1. Сколько координат определяют положение точки в пространстве, если она расположена в системе 3-х ортогональных плоскостей проекций
| Вид материала | Документы |
- Задание точки на чертеже в системе двух- трех плоскостей проекций. Линии связи. Задание, 503.91kb.
- Положение камеры Преобразования, определяющие положение и ориентацию объекта в мировой, 105.74kb.
- Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
- Построение линии пересечения взаимно перпендикулярных плоскостей, 26.08kb.
- Урок лекция по геометрии в 10 классе по теме «Декартовы координаты в пространстве», 53.59kb.
- Многие приходят в см, чтобы разбогатеть. Еще больше уходят, так и не разбогатев, 60.14kb.
- Темы лекций по начертательной геометрии для студентов очной формы обучения 1 курс, 26.7kb.
- Тематический план изучения курса физики 10 класса экстернат, 234.78kb.
- Математическая основа геоинформационных систем, 844.68kb.
- Урок-подорож, 108.55kb.
| ФГОУ ВПО «АКАДЕМИЯ ГРАЖДАНСКОЙ ЗАЩИТЫ МЧС РОССИИ» ПЕРЕЧЕНЬ ВОПРОСОВ аттестационного испытания по дисциплине «НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ» Специальность: «Защита в чрезвычайных ситуациях» ХИМКИ - 2010
|
|
| 3.Сколько координат имеет точка, расположенная в системе 2-х ортогональных плоскостей проекций? |
|
|
. |
| Ка 7.Какая координата точки не будет изменяться, если она перемещается в системе 3-х ортогональных плоскостей проекций параллельно: 1 – горизонтальной плоскости проекций, 2 – фронтальной плоскости проекций, 3 – профильной плоскости проекций? |
| 8.Какая координата точки будет изменяться, если она перемещается в системе 3-х ортогональных плоскостях проекций параллельно: 1 − фронтальной и профильной плоскостям проекций; 2 – горизонтальной и профильной плоскостям проекций; 3 – горизонтальной и фронтальной плоскостям проекций. |
| Ав 9.Сколько осей проекций будет иметь эпюр, отображающий пространственную систему 2-х (3-х) ортогональных плоскостей проекций? |
| Па 10.Сколько отображений в виде проекций будет иметь точка на эпюре, расположенная в системе 2-х ортогональных плоскостей проекций, если она равноудалена от них и расположена в: I четверти пространства; II четверти пространства; III четверти пространства; IV четверти пространства. |
| 11.Сколько плоскостей проекций должно быть при аксонометрическом способе проецирования? |
| 12.Сколько осей проекций должно быть при выполнении аксонометрической проекции? |
| 13.Аксонометрические оси проекций: а) имеют одну общую точку; б) имеют две общие точки; в) не имеют общей точки. |
| 14.Три отрезка прямых, исходящие из одной точки под произвольными углами могут быть приняты, за: а) аксонометрические оси проекций; б) ортогональные оси проекций; в) координатные оси. |
| 15.Сколько коэффициентов искажения по координатным осям должно быть при аксонометрическом способе проецирования? |
| 16.Изометрическое проецирование предполагает одним из условий наличие: а) неравенства коэффициентов искажения по осям; б) равенства коэффициентов искажения; в) равенства двух и неравенство одного коэффициентов искажения. |
| 17. Сколько осей проекций имеет безосный эпюр? |
| 18.По безосному эпюру двух точек: а) можно определить их положение относительно плоскости проекций, но нельзя их взаимного положения; б) можно определить их положение относительно плоскости проекций, и взаимное положение; в) можно определить только их взаимное положение. |
| 19.По приведенному безосному эпюру точек А и В определите их пространственное взаимно-относительное положение: 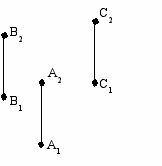 |
| 20.Как называется прямая расположенная в системе 3-х ортогональных плоскостей проекций, если она отображается в виде точки на 1) горизонтальной плоскости проекций; 2)- фронтальной плоскости проекций; 3) профильной плоскости проекций ? |
| 21.Как называется прямая, расположенная в системе ортогональных плоскостей проекций, если одна из её проекций изображена параллельно оси проекций 1)X; 2)Y? |
| Ответ-ключ: |
| 22.Как называется прямая, если две её проекции (горизонтальная и фронтальная) расположены перпендикулярно оси проекций X: |
| 23.Если в системе 3-х ортогональных плоскостей проекций прямая расположена параллельно 1)горизонтальной; 2)фронтальной плоскости проекций, то как изображается её профильная проекция? а |
| 24. |
| 25.Как изображаются на эпюре параллельные прямые? |
| 26. Как изображаются на эпюре пересекающиеся прямые? |
| 27.Как изображаются на эпюре скрещивающиеся прямые? |
| 28.Как надо расположить прямую в системе 3-х ортогональных плоскостей проекций, чтобы она имела только один след на 1) горизонтальной плоскости проекций; 2) фронтальной плоскости проекций; 3) профильной плоскости проекций? два следа на 1) горизонтальной плоскости проекций; 2) фронтальной плоскости проекций; 3) профильной плоскости проекций? |
| 29. Если в пространстве на прямой общего положения лежит точка, то на эпюре она расположена … |
| 30. Натуральная величина (Н.В.) отрезка прямой отображается на эпюре в виде его горизонтальной (фронтальной и профильной) проекции, если сам отрезок располагается в системе 3-х ортогональных плоскостей проекций? |
| 31. Натуральная величина отрезка прямой отображается на эпюре одновременно в двух его проекциях: горизонтальной и профильной, горизонтальной и фронтальной, фронтальной и профильной, если сам отрезок располагается в системе 3-х ортогональных плоскостей проекций: |
| 32. Сколько точек, на лежащих на одной прямой, задают плоскость? |
| 33. Задание плоскости следами частный случай какого способа? |
| 34. Если на эпюре, отображающем систему 2-х ортогональных плоскостей проекций горизонтальный и фронтальный след плоскости расположен // оси проекций Х, то какое положение в пространстве эта плоскость занимает? |
| 35. Если на эпюре, отображающем систему 3-х ортогональных плоскостей проекций, профильный след плоскости расположен // (перпендикулярно) оси проекций Z, то какое положение в пространстве эта плоскость занимает? |
| 36. Если на эпюре, отображающем систему 3-х ортогональных плоскостей проекций, горизонтальный и фронтальный следы плоскости расположены // оси проекций Х, то какое положение в пространстве эта плоскость занимает? |
| 37. Если горизонтальные (фронтальные, профильные) проекции трёх точек, задающих плоскость, расположены на прямой, образующей с осью проекций Х произвольный (отличный) от 90° и 0°) угол, то как расположена эта плоскость? |
| 38. Как расположена относительно плоскостей проекции а) горизонталь; 2) фронталь; 3) профильная прямая? |
| 39. Как расположена линия ската плоскости? |
| 40. Какая проекция горизонтали (фронтали) плоскости параллельна следу плоскости, если плоскость на эпюре задана следами? |
| 41. Какая проекция линии ската плоскости перпендикулярна следу плоскости, если плоскость на эпюре задана следами? |
| 42. Если точка на горизонтально (фронтально, профильно) проецируемой плоскости, то какая проекция точки совпадает со следом плоскости? |
| 43. Если точка лежит на горизонтальной (фронтальной, профильной) плоскости уровня, то какая проекция точки не совпадает со следами этой плоскости? |
| 44. Если прямая параллельна двум следам плоскости, то как расположена эта прямая по отношению к плоскости? |
| 45. Если прямая перпендикулярна двум следам плоскости, то как расположена эта прямая по отношению к плоскости? |
| 46. Если два следа одной плоскости соответственно параллельны двум следам другой плоскости, то как расположены эти плоскости в пространстве? |
| 47. Если горизонтальный и фронтальный следы одной плоскости соответственно параллельны горизонтали и фронтали другой плоскости, то как расположены эти плоскости в пространстве? |
| 48. Если две горизонтально (фронтально, профильно) проецирующие плоскости 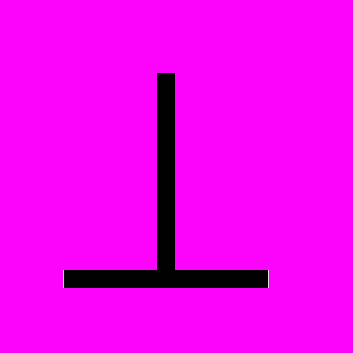 , то на эпюре какие их следы должны располагаться под углом 90°? , то на эпюре какие их следы должны располагаться под углом 90°? |
| 49. Если горизонтально проецирующая плоскость 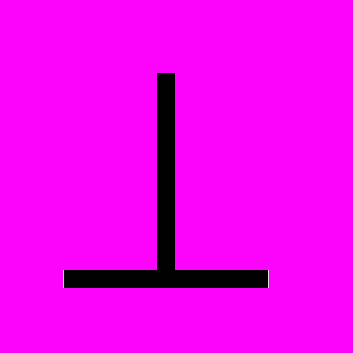 горизонтальной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? горизонтальной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? |
| 50. Если фронтально проецирующая плоскость 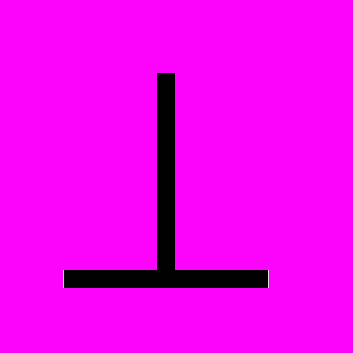 фронтальной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? фронтальной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? |
| 51. Если профильно проецирующая плоскость 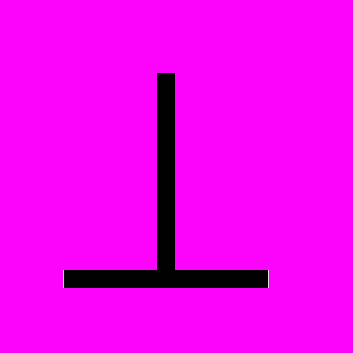 профильной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? профильной плоскости уровня, то на эпюре какие их следы должны располагаться под углом 90°? |
| 52. Как расположены следы двух перпендикулярных плоскостей: горизонтально проецирующей и фронтально проецирующей? |
| 53. Как расположены плоскости, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся другой плоскости? |
| 5 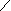 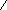 4. Как отобразится на эпюре прямой угол, если одна сторона прямого угла параллельна П1(но 4. Как отобразится на эпюре прямой угол, если одна сторона прямого угла параллельна П1(но 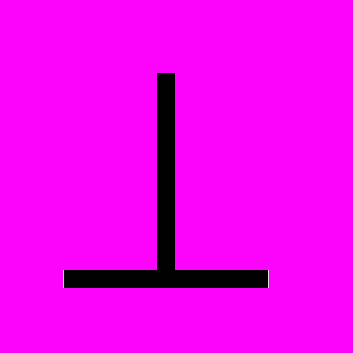 П2), а другая параллельна П2(но П2), а другая параллельна П2(но 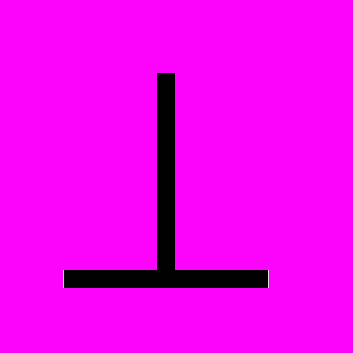 П1)? П1)? |
| 5 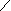 5. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 5. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 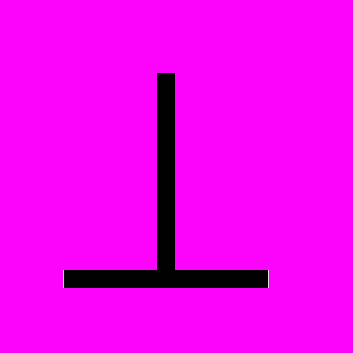 П1 , а вторая параллельна П1(но П1 , а вторая параллельна П1(но 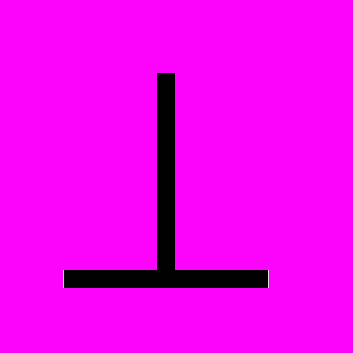 П2)? П2)? |
| 5 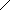 6. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 6. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 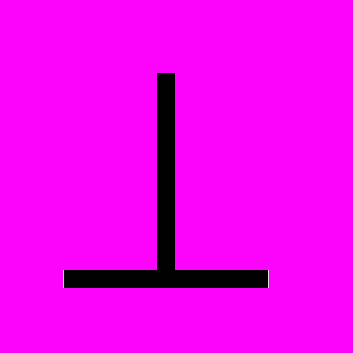 П2 , а вторая параллельна П2(но П2 , а вторая параллельна П2(но 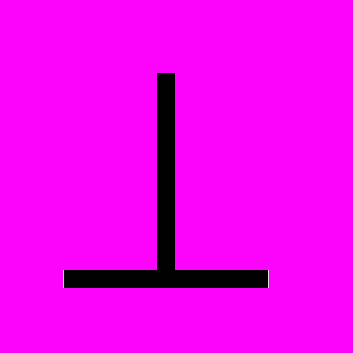 П1)? П1)? |
| 5 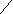 6. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 6. Как отобразится на эпюре прямой угол, если одна сторона прямого угла 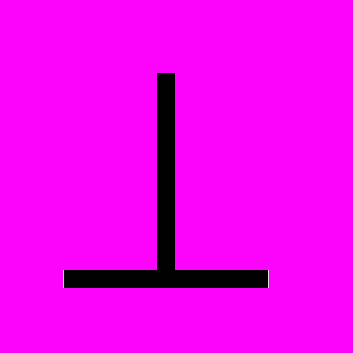 П3 , а вторая параллельна П3(но П3 , а вторая параллельна П3(но 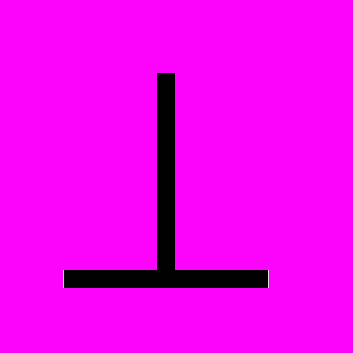 П1 П1 П2)? П2)? |
| 57. Как изображаются многогранники на эпюре? |
| 58. Что является образующей у линейчатых поверхностей: а) цилиндрических; б) конических? |
| 59. Сколько направляющих у линейчатых поверхностей под названием: а) цилиндроид; б)коноид? |
| 60. Наличие чего является общим условием образования линейчатых поверхностей: цилиндроида и коноида? |
| 60. Что представляют из себя направляющие поверхностей: а) цилиндроида; б) коноида? |
| 61. Наличие чего является общим условием образования линейчатых поверхностей: цилиндрической и конической? |
| 62. Образующие винтовой поверхности под названием прямой геликоид это какие прямые? |
| 63. Направляющие винтовой поверхности под названием прямой циклоид это какие линии? |
| 64. Что является основным условием образования поверхности вращения? |
| 65. Что является образующей торовой поверхности? |
| 66. С помощью каких линий строятся проекции точки, лежащей на поверхности сферы? |
| 67. Какая линия является образующей сферы? |
| 68. Если точку, находящуюся на сфере перемещать по её поверхности параллельно какой либо плоскости проекции по замкнутой траектории, то что получим в результате? |
| 69. Если точку, находящуюся на эпюре, перемещать по его поверхности по замкнутой траектории параллельной плоскости проекции, которая 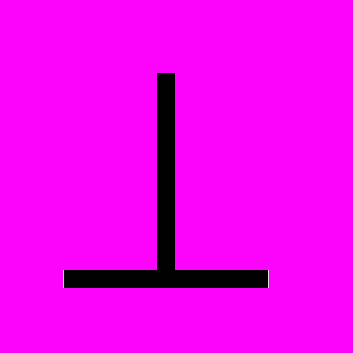 его оси вращения, то что получим в результате? его оси вращения, то что получим в результате? |
| 70. Что из себя представляет плоская кривая, лежащая на поверхности сферы, все точки которой равноудалены от её центра? |
| 71. Что из себя представляет плоская кривая, лежащая на поверхности тора (прямого кругового конуса, цилиндра), все точки которой равноудалены от его оси? |
| 72. На каких поверхностях вращения можно использовать прямые и плоские кривые линии при нахождении точки? |
| 73. Если на поверхности равномерно вращающегося прямого кругового цилиндра (конуса) находится точка и она равномерно перемещается по его образующей, то траектория её движения – это …? |
| 74. Если плоская кривая находится в горизонтальной (фронтальной, профильной) проецирующей плоскости, то какая её проекция совпадает со следом этой плоскости? |
| 75. Если плоская кривая находится в горизонтальной (фронтальной, профильной) плоскости уровня, то её проекция не совпадает со следом плоскости? |
| 76. На поверхности какого геометрического тела можно провести прямую? |
| 77. На поверхности какого геометрического тела нельзя провести прямую? |
| 78. Сколько видов допускается изображать на чертеже? |
| 79. Что называется главным видом? |
| 80. Невидимые контуры предмета изображают на видах какой линией? |
| 81. Видимые контуры предмета изображаются на видах какой линией? |
| 82. Как располагается секущая плоскость при выполнении ступенчатого (ломанного) разреза? |
| 83. Что называется простым разрезом? |
| 84. Какие размеры проставляются на чертеже, если изображения чертежа выполнены в масштабе 2:1 (1:2, 1:1)? |
| 85. Чем отличается сечение от разреза? |
| 86. Как изображается материал детали в сечении? |
| 87. К каком чертежу составляется спецификация? |
| 88. На каком формате допускается выполнять сборочный чертёж и спецификацию? |
| 89. Контур выносного (наложенного) сечения выполняется какой линией? |
| 90. Где указывается масштаб чертежа? |
| 91. По какому чертежу выполняется сборка изделия? |
| 92. По какому чертежу разрабатываются рабочие чертежи? |
| 93. Сколько видов аксонометрических проекций допускается ГОСТом? |
| 94. С помощью какой линии показывается резьба в разрезах и сечениях? |
| 95. Какое обозначение на чертеже имеет стандартная метрическая резьба? |
| 96. Чему равен угол между аксонометрическими осями в стандартной прямоугольной изометрии? |
| 97. Каким типом линий указывается на чертеже секущая плоскость при выполнении разрезов и сечений? |
| 98. Линейный размер изображения вида, выполненного с разрывом … |
| 99. На каком формате чертежа его основная подпись выполняется вдоль короткой стороны формата? |
^ МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ
ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ, ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ
И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ СТИХИЙНЫХ БЕДСТВИЙ
_______________________________________________________________
^ ФГОУ ВПО «АКАДЕМИЯ ГРАЖДАНСКОЙ ЗАЩИТЫ»
У Ч Е Б Н А Я П Р О Г Р А М М А
ПО ДИСЦИПЛИНЕ
" НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ИНЖЕНЕРНАЯ ГРАФИКА "
ХИМКИ – 2009 г.
Целевая УСТАНОВКА И ОРГАНИЗАЦИОННО-МетОДИЧЕСКИЕ УКАЗАНИЯ
Основными целями изучения дисциплины «Начертательная геометрия. Инженерная графика» являются:
овладение «языком» графического отображения пространственных объектов в виде проекционных моделей;
развитие пространственного воображения, образного и логического мышления;
формирование знаний и умений, необходимых для чтения и выполнения чертежа изделия.
В результате изучения дисциплины студенты должны:
^ Иметь представление:
-о предмете и методе начертательной геометрии;
-об основных способах проецирования;
-об образовании аксонометрических проекций;
-о конструкторской документации;
-о построении элементов геометрии детали;
Знать:
-теоретические основы построения проекционных моделей геометрических объектов (точка, прямая, плоскость, многогранники, поверхности) и материальных тел (трехмерные объекты);
-алгоритмы решения типовых позиционных и метрических задач;
-основные способы преобразования чертежа;
-правила оформления и выполнения рабочего чертежа детали, эскиза и сборочной единицы.
Уметь:
-графически отображать на чертеже геометрические объекты и их пространственные отношения;
-решать основные метрические и позиционные задачи;
-применять способы преобразования чертежа.
-выполнять построение разверток поверхностей;
-выполнять рабочие чертежи и эскизы деталей и простейших сборочных единиц, строить аксонометрические проекции.
Дисциплина «Начертательная геометрия. Инженерная графика» базируется на материале таких школьных предметов, как рисование, черчение, геометрия, стереометрия которые является основой для усвоения и понимания обучающимися «языка» графических изображений, представленных в виде проекционных моделей пространственных объектов.
Методика проведения занятий построена на последовательном изучении его разделов и тем путём чтения лекций, проведения практических занятий, самостоятельной работы обучающихся, консультаций.
Лекции проводятся с целью дать систематизированные основы знаний, объяснить теоретический материал курса, принципы и алгоритмы решения типовых задач.
Практические занятия проводятся для углубления и закрепления знаний, полученных на лекциях и в процессе самостоятельной работы обучающихся.
Самостоятельная работа обучающихся имеет целью подготовку к предстоящим занятиям, в т.ч. зачёту и экзамену, а также формирование и развитие интеллектуальных способностей, самостоятельности в поиске и приобретении новых знаний. Она должна носить систематический и непрерывный характер.
Самостоятельная работа предусматривает выполнение индивидуальных учебных заданий – графических работ (эпюров и чертежей). Последние выполняются и защищаются по требованиям кафедры.
В основе методического замысла по реализации целевых установок изучения дисциплины положена ориентация на формирование и развитие у обучающихся творческого мышления и интеллектуального потенциала.
Курс дисциплины обеспечивает освоение материала таких дисциплин как «Механика», «Основы строительного черчения и расчета конструкций». «Компьютерная графика», «Спасательная техника и базовые машины», «Автомобильная подготовка».
В процессе обучения осуществляется контроль успеваемости текущий и итоговый. Текущий контроль предназначен для проверки хода и качества усвоения учебного материала, управления образовательным процессом и стимулирования учебной работы обучающихся. Он проводится в ходе всех видов занятий в форме, избранной преподавателем: устные ответы, тесты, самостоятельные и контрольные работы.
Итоговый контроль предназначен для оценки достижения учебных целей по изучаемому курсу дисциплины и проводится путём принятия зачёта с оценкой в конце первого семестра, и экзамена в конце второго семестра обучения.
^ II. РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ ПО СЕМЕСТРАМ, ТЕМАМ И ВИДАМ УЧЕБНЫХ ЗАНЯТИЙ.
| Номера и наименование разделов и тем | Всего часов учеб ных заня тий по распи санию | В том числе учеб ных заня тий с пре пода вате лем | Из них по видам учебных занятий | ||||||
| Лек ции | Лабо раторные рабо ты | Прак тичес кие заня тия | Конт роль ные рабо ты | Время отво димое на са мосто ятель ную рабо ту | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| |||||||||
| Тема №1. Ведение в дисциплину Раздел 1. Геометрические объекты: задание, изображение на чертеже Тема № 2. Точка: задание, проекционная модель, пространственные отношения. Тема № 3. Прямая и плоскость: задание, проекционная модель, пространственные отношения. Тема № 4. Кривые линии, поверхности, многогранники: задание, проекционные модели. | 3 45 10 18 17 | 2 34 8 14 12 | 2 10 2 4 4 | - - - - - - | - 22 6 8 8 | - 2 - 2 - | 1 11 2 4 5 | ||
| Раздел № 2. . Инженерная графика: конструкторская документация, оформление и изображения чертежа Тема № 5. Чертеж, эскиз и аксонометрические проекции детали Тема № 6. Сборочный и рабочий чертеж. | 28 17 11 | 16 10 6 | 6 4 2 | - - - | 8 6 2 | 2 - 2 | 12 7 5 | ||
| Итого за семестр | 76 | 52 | 18 | - | 30 | 4 | 24 | ||
| 2 С Е М Е С Т Р | |||||||||
| Раздел №3. Способы преобразования Тема № 7. Способ замены плоскостей проекций (ЗПП) Тема № 8. Способ плоско параллельного переноса (ППП). Раздел № 4. Позиционные задачи Тема № 9. Пересечение прямой с геометрическими объектами: алгоритмы, проекционные модели. | 25 12 13 32 6 | 14 6 8 22 4 | 4 2 2 8 2 | - - - - - - | 8 4 4 14 2 | 2 - 2 - - | 11 6 5 10 2 | ||
| Тема № 10. Пересечение плоскости с геометрическими объектами: алгоритмы, проекционные модели. Тема № 11. Пересечение поверхностей, алгоритмы, проекционные модели Раздел № 5. Метрические задачи Тема № 12. Длина отрезка прямой и кратчайшего расстояния. Тема № 13. Угол между плоскостями, прямой и плоскостью. Тема № 14. Натуральная величина плоской фигуры, развертка геометрического тела. | 11 15 25 6 7 12 | 8 10 16 4 4 8 | 2 4 6 2 2 2 | - - - - - - | 6 6 8 2 2 4 | - - 2 - - - 2 | 3 5 9 2 3 4 | ||
| Итого за семестр | 82 | 52 | 18 | - | 30 | 4 | 30 | ||
| Всего по дисциплине | 158 | 104 | 36 | - | 60 | 8 | 54 | ||
^ III. СОДЕРЖАНИЕ РАЗДЕЛОВ И ТЕМ
Тема № 1. Введение в дисциплину.
Предмет и метод «Начертательной геометрии». Общие понятия и определения. Центральный и параллельный способы проецирования. Постоянные свойства ( и варианты) параллельного проецирования.
^ Раздел 1. Геометрические объекты: задание и изображение на чертеже
Тема № 2. «Точка: задание, проекционная модель, пространственные отношения».
Точка в ортогональной системе двух и трех плоскостей проекций, ее пространственные отношения. Эпюр Монжа. Построение недостающей проекции точки. Координаты точки. Безосный эпюр. Взаимоотносительное пространственное положение точек.
Тема № 3. «Прямая и плоскость: задание, проекционная модель, пространственные отношения».
Задание и проекционные модели прямой общего и частного положения, плоскости общего и частного положения. Особые линии плоскости. Пространственные взаимно-относительные положения точки, прямой и плоскости, их проекционные модели.
Тема № 4. «Кривые линии, поверхности, многогранники: задание, проекционные модели.
Кривая линия – общие понятия, задание и проекционная модель. Образование и задание на эпюре: линейчатой поверхности, в т.ч с плоскостью параллелизма, поверхности вращения, винтовой поверхности, геометрических тел (гранных и криволинейных). Построение проекционных моделей их пространственных отношений.
^ Раздел 2. Инженерная графика: конструкторская документация, оформление и изображения чертежа
Тема № 5. « Чертеж, эскиз и аксонометрические проекции детали».
ЕСКД. Образование, основные правила оформления чертежа. Изображение рабочего чертежа: виды, разрезы, сечения, выносные элементы, эскиз детали. Надписи и обозначения; нанесение размеров. Изображение и обозначение резьбы и элементов деталей. Стандартные аксонометрические проекции.
Тема №6 Сборочный и рабочий чертеж.
Основные правила и особенности выполнения и чтения сборочного и рабочего чертежа изделия. Изображение сборочной единицы. Спецификация
^ Раздел 3. Способы преобразования
Тема № 7. «Способ замены плоскостей проекций ».
Суть способа, пространственно-проекционная модель. Алгоритмы решения типовых задач. Примеры проекционного решения задач способом замены плоскостей проекций.
Тема № 8. «Способ плоско параллельного переноса».
Суть способа, пространственно-проекционная модель. Алгоритмы решения типовых задач. Примеры проекционного решения задач способом плоско параллельного переноса.
^ Раздел 4. Позиционные задачи
Тема № 9. «Пересечение прямой с геометрическим объектом»
Принцип решения задач на пересечение прямой с геометрическим объектом, пространственно – проекционные алгоритмы нахождения точки пересечения прямой с плоскостью, поверхностью и многогранником. Решение задач.
Тема № 10. «Пересечение плоскости с геометрическим объектом»
Принцип решения задач на пересечение плоскости с геометрическим объектом, пространственно – проекционные алгоритмы нахождения линии пересечения плоскости с плоскостью, поверхностью и многогранником. Решение задач.
Тема № 11. «Пересечение поверхностей»
Принцип решения задач на пересечение поверхностей, геометрических тел, пространственно – проекционные алгоритмы нахождения линии пересечения поверхностей, геометрических тел. Способ сфер: концентрических и эксцентрических. Теорема Монжа. Решение задач.
^ Раздел 5. Метрические задачи
Тема № 12. « Длина отрезка прямой и кратчайшего расстояния».
Определение длины отрезка прямой. Нахождение кратчайшего расстояния от точки до прямой и до плоскости. Пространственно – проекционные алгоритмы решения. Примеры решения задач.
Тема № 13. « Угол между плоскостями, прямой и плоскостью».
Определение угла наклона прямой к плоскости и угла между двумя пересекающимися плоскостями. Пространственно – проекционные алгоритмы решения. Примеры решения задач.
Тема № 14. «Натуральная величина плоской фигуры, развертка геометрического тела».
Обзор способов построения натуральной величины плоской геометрической фигуры.
Построение натуральной величины треугольника, способом вращения вокруг линии уровня. Развертка поверхности. Графические способы построения развертки геометрического тела. Построение развертки пирамиды и конуса.
