Математическая основа геоинформационных систем
| Вид материала | Документы |
- Темы фамилия применение геоинформационных технологий в создании муниципальных информационных, 37.02kb.
- 1. Истоки, определение и структура логистики как научной дисциплины. Этапы эволюции, 543.99kb.
- Вестник Новосибирского Государственного Университета том9, выпуск1, 2011г. серия, 177.45kb.
- Пояснительная записка к курсовой работе на тему «Исследование математических методов, 401.07kb.
- «Применение ит в математическом моделировании и симуляции», 78.3kb.
- Оглы Разработка технологической модели муниципальных геоинформационных систем для задач, 312.34kb.
- Седых Борис Александрович, гр. А2-05 (а-с52), иатэ нияу мифи с доклад, 28.96kb.
- В. м антонов В. А. Горно-геологическая информационная система на основе геолого-маркшейдерских, 257.18kb.
- Рабочая программа дисциплины 1 Пояснительная записка Учебно-методический комплекс, 321.52kb.
- Календарно-тематическое планирование по географии 6 класс, 895.04kb.
ГИС- 2.
МАТЕМАТИЧЕСКАЯ ОСНОВА ГЕОИНФОРМАЦИОННЫХ СИСТЕМ
Наличие математической основы карт является принципиальным отличием ГИС от других информационных систем. Именно математическая основа (МО) дает возможность интегрировать различные данные. Технологически МО является базой построения цифровых моделей и карт геоинформационных систем, обеспечивает топологическое соответствие пространственных объектов и явлений и их изображений на картах. Разработка, выбор и использование МО основаны на принятых в любой стране геодезических системах координат и высот, общей теории картографических проекций, а также масштабов, компоновок и разграфок карт.
При создании ГИС необходимо, чтобы исходные картографические материалы были приведены в геодезическую систему координат и картографическую проекцию базовой карты, принятые для данной ГИС, ее математическая основа обеспечивает оптимальные условия решения картографических задач ГИС [де Мерс Майкл, 1999].
2.1. Геодезические системы координат и высот.
Как известно, большинству из нас Земля представляется в форме, близкой к шару, но всем известно, что она не шар. Отличие, весьма существенное для точной навигации. Сложная поверхность Земли получила еще в 19 веке название геоида, Поверхность геоида совпадает с поверхностью морей и океанов в их спокойном состоянии и виртуально продолжается под Материками. Для практического применения широкое распространение получили две модели формы Земли: сферическая с упрощенным представлением ее в виде шара с радиусом 6371 ,1 км и сфероидальная в виде эллипса вращения (эллипсоида). Под ним понимают геометрическую фигуру, которая образуется при вращении эллипса вокруг своей малой оси. Размеры эллипсоида вращения, его ориентация и расположение относительно центра масс Земли могут варьироваться для достижения наибольшей точности приближения к реальной земной поверхности. Следует уяснить, что каждой используемой модели соответствует и своя система координат. Когда мы говорим о какой-либо системе координат, то подразумеваем и соответствующую модель эллипсоида. Но и это еще не все различия, которые нужно знать пользователю системы GPS. Если параметры эллипсоида подбираются для Земли в целом, то такой эллипсоид получил название общего земного эллипсоида (ОЗЭ). С целью же описания локальной (частичной) области поверхности Земли с большей точностью может использоваться эллипсоид с другими параметрами. Такой эллипсоид, законодательно принятый для измерений и обработки геодезических данных, называется референц-эллипсоидом (РЭ), а образуемая им система координат — референцной. В референц-эллипсоиде его малая ось совпадает с осью вращения Земли, но должна быть параллельна ей. Малая полуось всегда совпадает с осью воащения, а центр эллипсоида совпадает с центром массы Земли.
Уровенная поверхность - это поверхность, перпендикулярная к отвесным линиям, по которым к каждой точке данного небесного направлен вектор силы тяжести. Строгое определение геоида связано со знанием строения земной коры.
М.С.Молоденский предложил вместо геоида определять поверхность квазигеоида, которую можно строго определить без привлечения гипотез о строении земной коры и которая совпадает с поверхностью геоида на морях и океанах, отступая от нее на расстояние 2 метров на континентальной части Земли.
В геодезии измерения, выполненные на физической поверхности переносят на математическую, которая может быть описана соответствующими уравнениями. В этой связи изучают и используют общеземной эллипсоид и референц-эллипсоид.
Рис. 2. Изображения геоида, эллипсоида WGS -84 и местного эллипсоида
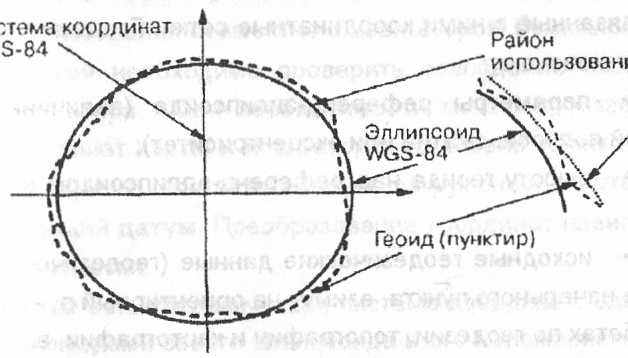
Эллипсоид вращения, плоскость экватора и центр которого с падают с центром масс Земли, называют общеземным эллипсопдом. Эллипсоид, на поверхность которого отображаются материал астрономо-геодезических и топографических съемок и который наиболее полно соответствует поверхности геоида, называют референц- эллипсоидом. В разных странах приняты референц-эллипсоиды, сколько различающиеся своими параметрами.
В картографии, чтобы отобразить на плоскости физическую поверхность Земли, необходимо перейти к математическим поверхностям - шару, эллипсоиду вращения и, в отдельных случаях, трехосному эллипсоиду. К элементам геодезической основы относят опорные пункты, определенные в системе геодезических координат, принятой в государстве, и связанные с ними координатные сетки. Геодезические системы координат включают: параметры референц-эллипсоида (величина большой или малой полуоси, сжатие или эксцентриситет); высоту геоида над референц-эллипсоидом в начальном пункте; исходные геодезические данные (геодезические широта и долгота начального пункта, азимут на ориентирный пункт).
В работах по геодезии, топографии и картографии, выполняем в России, используется эллипсоид Красовского начальным пункт которого является Пулково. Превышение геоида над референц-эллипсоидом в начальном пункте равно нулю.
В нашей стране принята Балтийская система высот. Счет высот в этой системе ведется от нуля Кронштадтского футштоха. В ппроцессе выполнения картосоставительских работ определяют геодезическую систему координат и систему высот, которые приняты при создании исходного картографического материала. Это выявляется по формулярам листов карт или по литературно-описательны м источникам. В случаях, когда геодезическая основа материала, используемого для создания карт, имеет другую по сравнению с базовой систему ординат, необходимо осуществить ее преобразование.
В России используются две общеземные системы координат ПЗ-90 и международная WGS-84 (Ворд геодетик систем 1984). Обе системы близки
к другу: ПЗ-90 используется в России для геодезического обеспечения орбитальных полетов, а WGS-84 применяется во всем мире для обработки спутниковых измерений GPS. К российским референцным системам ищятся СК-42 (Пулково) и СК-95. Обе системы используют эллипсоид Красовского (введен с 1946 г.) и применяются при выполнении геодезических гопографических работ.
При навигации и использовании ОРЗ-навигаторов очень важно понимать, что отображение GPS -позиций на картах с разными системами координат без их пересчета приведет к большим ошибкам. Поэтому используются картографические программы, позволяющие переводить данные, например, из системы WGS-84 в местные системы координат. У пользователей портативных навигаторов этой проблемы вообще нет. При использовании совместно с навигатором бумажной карты с координатной сеткой необходимо проверить совпадение систем координат карты и навигатора. При необходимости можно произвести настройку системы координат карты и навигатора, установив в нем параметры, называемые датумом, соответствующие загруженной карте, или выбрав пользовательский датум. Преобразование координат навигатор выполнит автоматически.
Датум есть геодезическая система координат, однозначно определяемая размерами своего эллипсоида и его положением по отношению
центру Земли (табл. 1).
Таблица 1. Параметры эллипсоидов в разных системах координат
| Система | Длина большой оси, м | Эксцентриситет |
| СК-42(СК-95) WGS -84 | 6378245 6378137 | 0,0066934216 0,0066943800 |
| П3-90 | 6378136 | 00066946619 |
Число разных датумов (а проще — систем координат), используемых в мировой картографии, более сотни. Разные датумы были предложены с целью получения наилучшего приближения определяемой ими модели к реальной поверхности Земли данного региона. К примеру, локальный Североамериканский датум НАД-27 разработан для наилучшего представления Северной Америки, а локальный Европейский датум ЕД-50 создан для использования в Европе. Локальные датумы нельз применять вне области, для которой они были разработаны.
2.2. Географические координаты.
Для определения положения любого объекта на поверхности Земли используется система из географических координат и двух особых точек — полюсов Северного и Южного. Полюса являются, как известно, точками пересечения оси вращения Земли с поверхностью эллипсоида. Наиболее наглядно географические координаты представляются в сферической модели Земли (рис. 3). В ней географические координаты (широта и долгота) определяются с помощью окружностей, образующихся при сечении шаровидной модели Земли плоскостям для широты — в горизонтальном направлении, а для долготы — в вертикальном.
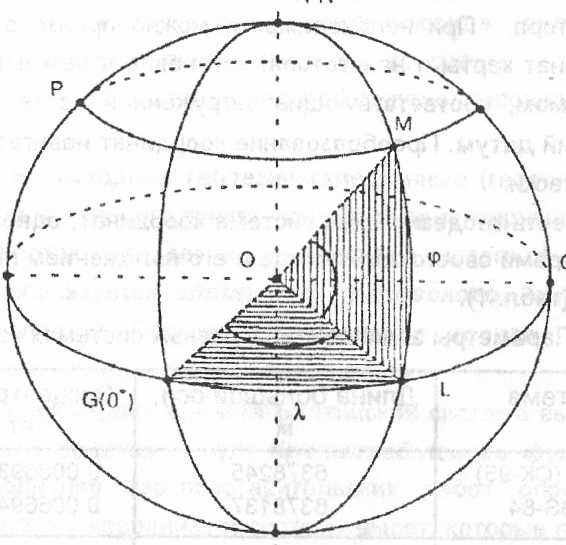Рис. 3. Определение географических координат. Окружность ЕКу, образуемая на поверхности шара горизонтальной секущей плоскостью, перпендикулярной земной оси и проходящей через центр шара, называется экватором. Он делит земной шар на северное и южное полушария. Окружности малых кругов, плоскости которых параллельно плоскости экватора, образуют параллели (РР’).
Окружности, образуемые плоскостями, проходящими через земную ось, получили название меридианов (географических или истинных). Среди всех меридианов надо выделить начальный (нулевой), называемый гринвичским, поскольку он проходит через астрономическую обсерваторию в Гринвиче (Англия). Этот меридиан делит земной шар на восточное и западное полушария.
Географической широтой некоторой точки на поверхности земного сфероида называется угол между плоскостью экватора и нормалью (отвесно линией) к этой поверхности. Для модели Земли в виде шара нормаль совпадает с земным радиусом ОМ, проведенным через данную точку М в центре шара. Широта измеряется дугой меридиана (угол МОЛ) от экватора до параллели данной точки. Широта принимает значения в диапазоне от О до 90°. Если точка находится в северном полушарии,
то широте приписывают наименование N (северное), если в южном - S.
Географической долготой какой-либо точки называется двугранный угол между плоскостями начального (нулевого) меридиана и меридиана, проходящего через заданную точку. Так, долгота точки М определяется углом ГОЛ. Долгота измеряется меньшей дугой экватора ЖЛ, а, к примеру, не дугой ЖЕКуЛ. Счет долгот ведут к востоку или западу от начального меридиана, от О до 180°. Если точка находится в восточном полушарии, то долготе приписывает наименование Е (восточная), если в западном — W (западная). Иногда, для обозначения полушарий точки, в координатах используются знаки +/-. Причем знак минус приписывают координатам, находящимся в южном и западном полушариях.
Для географических координат в навигаторах используются следуюiцие форматы:
- ddd.mm.ss.s - градусы, минуты, секунды;
- ddd.dddd - градусы, десятичные доли градусов;
- dd.mm.mmm — градусы, минуты, десятичные доли минут.
2.2. Картографические проекции
Картографические проекции - это математически определенный способ изображения поверхности земного шара или других планет на плоскости. Общее уравнение картографических проекций связывает географическую широту (В) и долготу (Л) с прямоугольными координатами икс и игрек на плоскости.
Все картографические проекции обладают искажениями, возникающими при переходе от сферической поверхности к плоскости.
По характеру искажений картографические проекции под:
разделяют следующим образом:
> равноугольные проекции, не имеющие искажений углов и направлений;
> равновеликие проекции, не содержащие искажений площадей;
> равнопромежуточные проекции, сохраняющие без искажений какое-либо одно направление (меридианы или параллели);
> произвольные проекции, в которых содержатся искажения углов и площадей.
Главный масштаб карты показывает степень уменьшения линейных размеров эллипсоида при его изображении на карте. Искажения масштаба проявляются в наличии частного масштаба карты в любой ее точке. Под этим понимается отношение длины бесконечно малого отрезка на карте к длине бесконечно малого отрезка на поверхности эллипсоида (шара).
Мерой искажений в картографической проекции в каждой точке карты служит бесконечно малый эллипс искажений. Существуют специальные карты, иллюстрирующие распределение искажений разных видов посредством изокол (изолиний равных искажений).
В зависимости от положения сферических координат, картографические проекции подразделяют на группы:
> нормальные проекции, в которых ось сферических координат сов падает с осью вращения Земли;
> поперечные проекции, у которых ось сферических координат ле-1 жит в плоскости экватора;
> косые проекции, когда ось сферических координат расположена под углом к земной оси.
Существующее различие требований к картам разного пространственного охвата, тематики и назначения, а также особенности формы картографируемой территории и ее положения на земном шаре привели к многообразию картографических проекций.
По виду меридианов и параллелей нормальной сетки различают следующие картографические проекции:
> цилиндрические, в которых меридианы изображены равноотстоящими параллельными прямыми, а параллели - прямыми, перпендикулярными к ним;
> конические, с прямыми меридианами, исходящими из одной точки, и параллелями, представленными дугами концентрических окружностей;
> азимутальные, в которых параллели изображаются концентрическими окружностями, а меридианы - радиусами, проведенными из общего центра этих окружностей;
> псевдоцилиндрические, где параллели представлены параллельными прямыми, а меридианы - в виде кривых, увеличивающих свою кривизну по мере удаления от прямого центрального меридиана;
> псевдоконические, в которых параллели представлены дугами концентрических окружностей, средний меридиан - прямой, а остальные меридианы - кривыми;
> поликонические, в которых параллели изображены эксцентрическими окружностями, центры которых лежат на прямом центральном меридиане, а остальные меридианы - кривыми линиями, увеличивающими кривизну с удалением от центрального меридиана;
> условные, у которых меридианы и параллели могут иметь различную форму.
Проекты, в которых требуется определение кратчайших маршрутов, особенно на длинные дистанции, нуждаются в азимутальных проекциях, поскольку в них возможно изображение больших кругов как прямых линий. Эти проекции чаще всего используют на картах воздушого сообщения, радиопеленгации, слежения за спутниками и картографирования небесных тел. Такие проекции стали популярны недавно, но и использование растет с расширением использования ГИС в этих областях.
Наиболее часто используют такие азимутальные проекции, как равновеликая Ламберта, стереографическая, азимутальная, эквидистантная, ортографпческая и гномоническая. Отметим, что некоторые из них сохраняют без искажений как направления, гак и площади. Это свойство может оказаться полезным для анализа таких крупных атмосферных явлений, как дымовые выбросы вулканов, которым свойственно двигаться по маршруту большого круга по мере рассеивания в атмосфере и движения по общим правилам воздушной циркуляции.
Есть много проекций для выбора - гораздо больше, чем перечислено здесь. Некоторые специальные проекции особенно подходят для отображения всей планеты или очень больших ее участков. Другие позволяют лучше координировать крупные картографические программы, такие, как создание топографических карт целого континента, которое выполняется небольшими фрагментами.
Для карт, создаваемых в виде серий листов, используют многогранные проекции, параметры которых могут меняться от листа к листу или группе листов. Иногда картографической проекцией ошибочно называют сетку параллелей и меридианов на карте. Сетки на карте - это система линий, служащая для определения координат объектов, их нанесения и поиска, ориентирования, прокладки направлений и маршрутов. В картографии (в том числе и цифровой) используют разны виды сеток:
> географическая сетка - это сеть меридианов и параллелей н земной шаре (эллипсоиде);
> картографическая сетка - изображение сети меридианов и параллелей на картах и планах, построенных в той или иной картографической проекции;
> прямоугольная сетка - сеть плоских прямоугольных координат заданной картографической проекции;
> километровая сетка - стандартная квадратная координатная сетка на топографической карте, линии которой проведены параллельно экватору и осевому меридиану через интервалы, соответствующие определенному числу километров (частный случай прям угольной сетки);
> указательная сетка - любая сетка на карте, предназначенная для поиска местоположения объектов, изображенных на карте по указателю географических названий.
Геоинформационные технологии содержат математический аппарат, позволяющий рассчитывать картографические проекции разных видов с заданным распределением искажении.
2.3. Системы координат для картографии.
Мы привыкли к картам как к способу наглядного отображения
поверхности Земли на бумажном листе, то есть на плоскости. Но не всякое изображение земной поверхности можно назвать картой и не
всякая карта пригодна для ориентирования и навигации. Картой в строгом смысле слова называется уменьшенное изображение земной поверхности на плоскости, выполненное по определенному математическому закону и показывающая ее размещение элементов объектов местности с их характеристиками. Отобразить сферическую поверхность на плоскости невозможно без разрывов и складок. Поэтому, построенное тем или иным способом изображение (проекция) будет обязательно иметь искажения.
Геометрическая сущность наиболее распространенных цилиндрических проекций заключается в том, что сетка меридианов и параллелей проектируется на боковую поверхность цилиндра. Затем поверхность цилиндра развертывается в плоскость. В зависимости от расположения цилиндра вокруг условного глобуса (Земли) различают две цилиндрические проекции. В продольной проекции Меркатора, нашедшей широкое применение в судовождении, ось цилиндра располагают по оси земного шара. В поперечной проекции Меркатора и проекции Гаусса-Крюгера ось цилиндра располагают в плоскости экватора.
Меркатор - (1512-1594) - фпамандский каргтюграф, изготовитель оптических инструментов. С 1552 г. работал в Германии. Карту в проекции, названной его именем, впервые предложил в 1559 г. Ввел понятие магнитного склонения, рассчитал координаты магнитных полюсов.
В продольной проекции Меркатора построены морские навигационные карты, причем слово «продольная» обычно опускают. В поперечной проекции создаются топографические карты. Различие указанных проекций карт вызвано в первую очередь требованиями обеспечения максимального удобства для пользователей и наилучшего соответствия используемым на суше и море методам ориентирования и навигации. Вспомним понятие масштаба. Он определяется как степень уменьшения размеров участков земной поверхности (в том числе и линий) относительно соответствующих им на местности. Различают масштабы численный, выраженный в виде дроби, и линейный, как графическое отображение первого. Численный масштаб, например 1:100 000, показывает, что одной единице длины на карте (см, м, км) соответствует 100 000 таких же единиц на местности. Если для Данного примера использовать младшую единицу в 1 см, то на местности ей будет соответствовать 1 км. Линейный масштаб приведен на рис. 4, где показан пример измерения расстояния 4,8 км.
Система координат необходима для определения расстояний и направлений на Земле. Географическая система координат, использующая широту и долготу, необходима для определения положений объектов, расположенных на сферической поверхности Земли или промежуточном глобусе. Поскольку чаще всего имеют дело с двухмерными картами, спроецированными с этого глобуса, требуется одна или несколько систем координат, соответствующих различным проекциям. Такие системы координат на плоскости называют картографическими (геодезическими) прямоугольными системам координат, они позволяют определять положение объектов на плоских картах.
Декартова система координат - это классические прямоугольные координаты. Построение системы известно по работе с графиками и числовыми осями. Она состоит из двух линий - абсциссы и ординаты. Абсцисса - горизонтальная линия, содержащая равномерно распределенные числа, начиная с 0, называемого началом координат, и продолжающаяся так далеко в двух направлениях, насколько это нужно для измерения расстояний. Величины называются координатами, они положительны справа от О и отрицательны слева. Вторая линия, ордината, обеспечивает движение по вертикали от той же нулевой начальной точки в положительном или отрицательном направлениях. Вместе они позволяют определять местоположение любой точки или объекта указанием величин Х и У. Приборы-дигитайзеры, используемые для ввода координат в ГИС, основаны на той же простой декартовой системе координат.
По традиции, первой называют координату Х, второй - У. Когда карта ориентирована севером вверх, как обычно, Х-координата называется отсчетом на восток, поскольку это соответствует расстоянию от начальной точки в восточном направлении. Аналогично, У-координата называется отсчетом на север, поскольку это соответствует расстоянию на север от начальной точки; нет западного или южного направлений. Вместо этого начальную точку размещают на карте гак, чтобы все значения были положительны, или, иначе говоря, чтобы все точки оказались в северо-восточном квадрате системы координат. Это позволяет читать координаты сначала вправо, затем вверх от начальной точки. В некоторых случаях, учитывая размер территории, ‘кет потребоваться введение смещенных (ненулевых) начал координат, чтобы обеспечить для каждого участка земли достаточно точное представление на плоской поверхности.
Численные значения плоских координат обычно не используют в анализе мелкомасштабных карт из-за сложного характера искажений.
Для таких карт требуется компенсация искажений, созданных при проецировании.
Несмотря на большое количество имеющихся проекций, подавляющее большинство систем координат ориентировано на использование равноугольных картографических проекций, обычно поперечной Меркатора, полярной стереографической и равноугольной конической Ламберта. Однако, если объект находится вблизи экватора, более полезной может оказаться проекция Меркатора.
В случаях использования в работе карт других стран, нужно установить, каковы проекции, набор координат и другие характеристики координатных систем в этих странах. Многие пользуются теми или другими из перечисленных выше типов, но перед вводом в ГИС требует знакомство с положениями начал координат и территориями, на которых они расположены. Наиболее широко распространенной в ГИС системой проекций и координат является универсальная поперечная Меркатора. Она используется в большинстве работ, связанных с дистанционным зондированием, подготовкой топографических карт, построением баз данных природных ресурсов, так как обеспечивает точные измерения метрической системе, принятой в большинстве стран. В ней основной единицей измерения длины является метр. В США до сих пор преобладают старые английские меры (дюймы, футы, ярды, мили и т.д.).
В России распространена система координат 1942 г. для проекцпи Гаусса-Крюгера, в которой ось Х указывает на север, а ось У на восток.
При выполнении топографических и геодезических работ применяется проекция Гаусса-Крюгера, в которой углы изображаются без искажении, а линейные искажения не зависят от направления. В основ построения единой системы плоских координат для России и стран СНГ - положено разделение поверхности северной части эллипсоида на ряд совершенно одинаковых сфероидических треугольников, ограниченных экватором и меридианами с разностью долгот 6°. Принцип построения картографической проекции Гаусса-Крюгера показан на рисунке 1. Как отмечалось ранее, при использовании проекции Гаусса-Крюгера в основу положено разделение поверхности общего земного эллипсоида на ряд одинаковых меридианных полос с заданной разностью долгот 6° граничных меридианов. Изображение на плоскости каждой шест градусной полосы представляет собой колонну листов Международной карты мира в масштабе 1: 1 000 000.
Изображение каждого треугольника в проекции Гаусса-Крюгера представляет собой шестигранную координатную зону. В качестве декартовых координат используют прямолинейные изображения осево меридиана (ось Х) и экватора (ось 9. В пределах каждой шестиградусной зоны размещается целое число трапеций карт в масштабах 1 1:1000 000 до 1:10 000. для того чтобы обеспечить выполнение топографо-геодезических работ на границе двух соседних зон, стандартная зона расширяется на 30’ по долготе к востоку и западу от граничного меридиана.
Координаты геодезических пунктов, находящихся в перекрытиях зон в каталогах координат приводятся дважды (в основной и соседних зонах). На топографических картах перекрытия отмечают соответствующими штрихами, показывающими выходы координатных линий соседней зоны.
При съемках городов и участков территории, отводимой под строительство крупных инженерных сооружений, желательно уменьшить величины линейных искажений, чтобы ими можно либо пренебречь, либо учесть. С этой целью можно ввести местную систему координат в проекции Гаусса-Крюгера со своим (нестандартным) осевым меридианом и своими размерами зоны по долготе. При этом структура формул проекции Крюгера не изменяется. Во всех случаях применения местных систем после завершения работ координаты пунктов должны быть переведены в государственную систему плоских координат в стандартной зоне.
Российские топографические карты наиболее часто употребляемых масштабов - 1:200 000, 1:100 000, 1:50 000 - выполнены именно в проекции Гаусса-Крюгера. Они являются, в свою очередь, основой для всех тематических работ, создаваемых в данном масштабе. На топографических картах система плоских прямоугольных координат зоны задается в виде координатной километровой сетки.
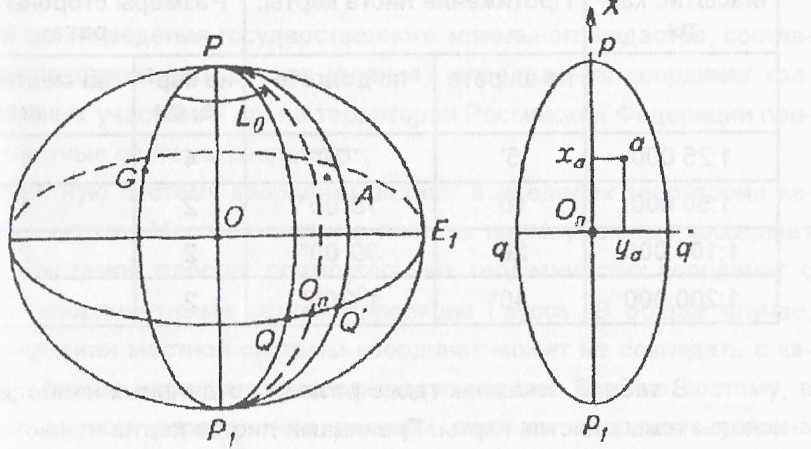
Рис. 5. Принцип построения проекции Гаусса—Крюгера.
1. разделенпе поверхности эллппсоида на сфероидические треугольники;
2. изображение сфероидическпх треугольников в проекции Гаусса-Крюгера.
Горизонтальные линии сетки параллельны экватору, а вертикальные — осевому меридиан. Эти линии проводятся на равных расстояниях одна от другой и образуют набор квадратов. для каждого масштаба установлены свои размеры квадратов сетки, которые приведены в табл.2.
Таблица 2. Размеры листов карты и сторон квадратов сетки
| Масштаб карты | Протяжение листа карты, | Размеры стороны квадрата | ||
| | по широте | по долготе | на карте, см | на местности, км |
| 1 25 000 | 5’ | 7’ 30” | 4 | 1 |
| 1:50 000 | 10 | 15’ 00” | 2 | 1 |
| 1:100000 | 20’ | З0, 00” | 2 | 2 |
| 1 :200 000 | 40’ | 1о0, 00,, | 2 | 4 |
В табл. 2 показаны также размеры отдельных наиболее часто используемых листов карты. Границами листов карты являются меридианы и параллели. Базовым листом карты является лист в масштабе 1:1000000 (<миллионка»), имеющий протяжение по широте в 4° и долготе в 6°. Карты более крупных масштабов образуются из «миллионки» соответствующей нарезкой (разграфкой). Для того чтобы можно было легко и быстро находить нужные листы карты, каждый из них имеет свое условное обозначение. Следует обратить внимание на то, что направление линий сетки не совпадает с направлениями север — юг и восток — запад, хотя и близко к ним. Наибольшие отклонения наблюдаются у границ зоны, где они достигают 30, Отклонение на правления истинного меридиана от вертикальной линии координатной сетки получило название сближения меридианов (Сб). Величина сбли жения меридианов зависит от местоположения точки на карте.
Для топографических карт ряда стран в шестиградусных зонах применяется проекция УТМ универсальная трансверсальная проекция Меркатора, называемая также проекцией Гаусса-Боага. Она отличается от проекции Гаусса-Крюгера тем, что в ней на среднем меридиане масштаб равен не единице, а 09996.
В проекции УТМ может использоваться как левая система координат (ось Х направлена на север, ось У - на восток), так и правая (ось идет на восток, ось У - на север).
При решении других задач (как правило, не топогеодезических) используют разные картографические проекции.
2.4. Местные системы координат
В целях ведения государственного земельного кадастра, составления землеустроительных карт (планов), определения координат границ земельных участков и др. на территории Российской Федерации применяют местные системы координат.
Местную систему координат задают в пределах территории кадастрового округа. Местная система плоских прямоугольных координат является системой плоских прямоугольных геодезических координат с местными координатными сетками проекции Гаусса. В общем случае, осевой меридиан местной системы координат может не совпадать с каким -либо осевым меридианом шестиградусных зон. Именно поэтому, в вышеприведённом определении местной системы координат указана проекция Гаусса, а не Гаусса—Крюгера. При разработке местных систем координат используют параметры эллипсоида Красовского.
В местных системах координат применяют Балтийскую систему высот. Редуцирование линейных измерений в проекцию Гаусса местной координатной сеткой и вычисление геодезических высот выполняют с помощью «Карты высот квазигеоида над эллипсоидом Красовского». Эта карта соответствует государственной референцной системе.
За основу местных систем координат может быть принята система координат СК-63, которая покрывает территорию большинства субъектов Российской Федерации несколькими самостоятельными блоками. В то же время, вместо блочного покрытия территории страны, местные системы координат можно устанавливать на территории кадастрового округа или кадастрового района.
Применение единой местной системы координат позволяет однозначно и без дополнительных преобразований вести Единый государственный реестр земель.
Местные системы координат имеют названия. Названием системы может являться ее номер, равный, например, коду (номер субъекта РФ или города, устанавливаемому в соответствии с «06щероссийским классификатором объектов административно-территориального деления».
В каждой местной системе координат устанавливаются следующие параметры координатной сетки проекции Гаусса:
-долгота осевого меридиана первой зоны;
- число координатных зон;
- координаты условного начала;
- угол поворота осей координат местной системы относительно государственной в точке местного начала координат;
- масштаб местной системы координат относительно плоско прямоугольной системы геодезических координат СК42 или СК95;
- высота поверхности (плоскости), принятой за исходную, которой приведены измерения и координаты в местной системе;
- референц-эллипсоид, к которому отнесены измерения местной системе
координат;
- соответствующие формулы преобразования плоских прямоугольных
геодезических координат.
Совокупность указанных параметров называют «КЛЮЧОМ» местной системы координат. В местной системе координат могут быть одна или несколько зон проекции Гаусса. В системе координат с несколькими зонами расстояние между соседними осевыми меридиан ми (ширина координатной зоны) составляет З0.
Условное начало Х, У в местных системах назначают так чтобы координаты в пределах зоны были положительными, а значения абсцисс не имели тысяч километров. Для всех местных систем координат масштаб изображения на осевом меридиане равен единице.
Каждая местная система координат территории кадастрового округа имеет тесную связь с единой государственной системой плоских прямоугольных координат посредством соответствующих, ран названных ключей перехода. При изменении (уточнении) координат пунктов геодезических сетей в государственной референцной системе ключи вычисляют заново при условии минимальных изменений координат пунктов в местной системе.
Контрольные вопросы и задания.
1. Что называют уроненной поверхностью и поверхностью геоида.
2. С какой целью введено понятие кеазигеопда?
З. В чем заключаются различия общеземного и референц-эллипсоида?
4. Чем различаются между собой общие земные эллипсоиды ПЗ-90 и WGS-84?
5. Зачем нужны исходные геодезические даты?
6. Что положено е основу геодезической системы координат?
7. Что называют геодезическими координатами? Проиллюстрируйте сказанное соответствующим чертежом.
8. В чем заключаются различия прямоугольных геодезических координат и плоских прямоугольных геодезических координат? Поясните, замеченные различия соответствующими чертежами.
9. Что представляет собой местная система плоских прямоугольных координат?
10. Что называют нормальной и геодезической высотой точки земной поверхности?
11. Как можно преобразовать плоские прямоугольные координаты из одной системы в другую?
12. Какие параметры координатной сетки называют ключом местной системы координат?