В квантовой физике

(для специальности «математика»)

программа

Ставрополь – 2006

Печатается по решению

редакционно-издательского совета

Ставропольского государственного университета

Математические модели в квантовой физике: Программа Ставрополь.: Издательство СГУ. 2006. С.

Пособие содержит пояснительную записку, тематический план, программу лекционного курса, литературу.

Рекомендуется для студентов университета, обучающихся по специальности «Математика», как курс, входящий в качестве курсов по выбору.

Составитель: старший преподаватель Озерецковский Г.А.

Рецензент: доктор физико-математических наук Дерябин М.И.

^

Издательство Ставропольского

государственного университета 2006.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Дисциплина «Курсы по выбору» (ЕН) (математические модели в квантовой физике) изучается на 4 курсе в 8 семестре.

Известной истиной, основанной на многолетнем опыте науки, является положение о том, что взаимодействие математики и физики может быть плодотворным для обеих наук. Тонкость и глубина современных физических теорий делают важным изучение их логической и математической структуры. Под этим знаменем ведущие университеты страны еще в конце 60-х годов 20 века ввели в программу подготовки математиков курс квантовой механики. Используя этот опыт, в предлагаемой программе предпринята попытка рассмотреть две из задач, возникающих в квантовой физике при создании математических моделей физических процессов в микромире. Речь идет о построении и исследовании математической модели механического движения микрочастицы и простейшей осцилляторной модели двухатомной молекулы, что позволяет рассчитать её энергетический колебательный спектр, удовлетворительно совпадающий с данными эксперимента.

Предлагаемая программа опирается на курс физики, изученный студентами на 3-м курсе и на курс теоретической механики, изучаемый ими на 4-м курсе. При этом знание квантовой механики не предполагается, а её основные положения в объеме, необходимом для решения основной задачи, излагаются в данной дисциплине. Рассматриваются также приложения квантовой механики, связанные с постановкой наиболее интересных математических задач. Например, реализация алгебры наблюдаемых как алгебры эрмитовых операторов в конечномерном комплексном пространстве

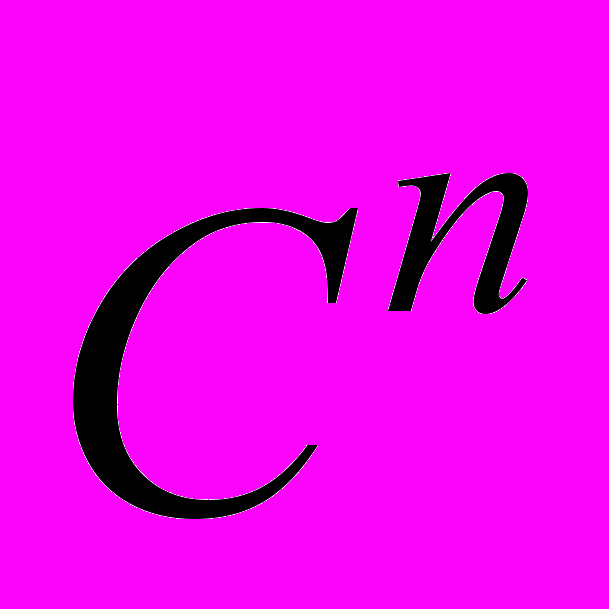, использование спектральной функции эрмитового оператора для описания множества значений физической величины т. д. Таким образом, предлагаемая программа может служить не только источником информации об используемых математических моделях в физике, но и примером практического применения теорем функционального анализа, изучаемого студентами на 4 курсе.

^ 1.2. Задачи, решаемые в процессе преподавания дисциплины

Данная учебная дисциплина имеет следующие задачи.

При построении математической модели движения микрочастицы необходимо, в соответствии с общей структурой физической теории ответить на следующие вопросы:

Как правильно выбрать способ математического описания состояния микрочастицы.
Как описать математически физические величины, которыми описывается сама микрочастица, её взаимодействие со средой и т. п.
Как выбрать уравнение эволюции изучаемой системы.

В результате решения этих задач возникает алгоритм описания движения любой нерелятивистской частицы.

При построении математической модели двухатомной молекулы необходимо решить следующие задачи:

Построить физическую модель классического гармонического осциллятора.
Построить математическую модель классического гармонического осциллятора.
По аналогии с классическим построить физическую модель квантового гармонического осциллятора
На базе физической модели построить операторную алгебру квантового осциллятора.
Исследовать свойства построенной математической модели и сравнить результаты расчетов с данными эксперимента.
Качественно наметить пути совершенствования математической модели.

^ 1.3 Соответствие учебной программы уровню подготовки выпускника, содержащейся в ГОС

Предлагаемая учебная программа опирается на цикл математических и общенаучных дисциплин, изучаемых в 1 – 6 семестрах, таких как: «Математический анализ» (1 – 2 семестры), «Геометрия» и «Алгебра» (1 – 3 семестры), «Физика» (5 – 6 семестры), «Теоретическая механика» (4 курс) и др. Это позволяет использовать достаточную математическую базу для использования алгебраических методов построения модели для строгого решения задачи об отыскании энергетического спектра двухатомной молекулы в первом приближении.

^

1.4. Место дисциплины в профессиональной подготовке выпускника.

Учебная дисциплина «Курсы по выбору (ЕН)» (Математические модели квантовой физики) изучается параллельно с изучением дисциплины «Концепции современного естествознания» и служит хорошим примером практического применения теории математического моделирования. Предлагаемая программа позволяет пройти все этапы математического моделирования при построении двух конкретных моделей: «Модель механического движения микрообъекта» и «Модель двухатомной молекулы».

^

1.5. Тематический план

№ п/п	Темы курса	Количество часов
№ п/п	Темы курса	Лекции	Практические занятия	СКР
1	Введение	2
2	Особенности поведения микрообъектов	2	4
3	Построение математической модели движения микрочастицы	4	6
4	Постановка новой задачи и её качественный анализ	2
5	Построение осцилляторной математической модели двухатомной молекулы	4	4
6	Математический анализ моле и решение задачи о энергетическом спектре двухатомной молекулы	2	2
	Итого часов	16	16

^ 1.6. Содержание дисциплины, структурированной по видам учебных занятий в последовательности, соответствующей тематическому плану.

Введение

Структура физической теории. Последовательность построения математической модели. Формулировка задачи о вычислении энергетического колебательного спектра двухатомной молекулы.

^ 2. Особенности поведения микрообъектов

Изучение особенностей движения микрообъектов на основе экспериментального изучения:

Излучения абсолютно черного тела;
Теплоемкости твердых тел;
Фотоэлектрического эффекта;
Комптоновского рассеяния электронов.

Выводы из анализа экспериментов:

Волновые свойства микрочастиц;
Дискретность состояний микросистем;
Ограничения на точность измерений;
Вероятностный характер закономерностей микромира.

^ 3. Построение математической модели движения микрочастицы

Волновая функция. Принцип суперпозиции состояний. Уравнение Шрёдингера. Описание поведения микрочастиц. Построение математической модели в координатном базисе. Описание состояний, описание наблюдаемых, связь с процедурой измерения. Математическое исследование модели (общий формализм).

^ Постановка задачи и её качественный анализ

Модель одномерного линейного гармонического осциллятора в классической физике и её применение. Квантово-механический одномерный линейный гармонический осциллятор и возможности его применения.

^ 5. Построение осцилляторной математической модели двухатомной молекулы

Операторная алгебра гармонического осциллятора. Генераторы алгебры и определяющие соотношения. Векторы состояния и их нормировка. Лестничные операторы, их действие на векторы состояния. Оператор числа частиц, его собственные векторы и собственные значения.

^ 6. Математический анализ модели и решение задачи вычисления энергетического колебательного спектра двухатомной молекулы

Изучение математических свойств построенной модели осциллятора. Вычисление энергетического спектра двухатомной молекулы. Исследование осцилляторной модели и её реализаций: проверка результатов применения модели на конкретной реализации – колебаний молекул. Ограниченность осцилляторной модели и пути её улучшения.

^

2. Требования к уровню освоения программы и формы контроля

В результате изучения КПВ «Математические модели в квантовой физике» студенты должны знать:

Постулаты квантовой механики;
Математический формализм квантовой механики в координатном базисе;
Алгебраический метод построения осцилляторной модели двухатомной молекулы.

Уметь:

Проверять коммутационные свойства операторов;
Выражать операторы наблюдаемых через лестничные операторы (в рамках изученных моделей);
Вычислять результаты действия операторов наблюдаемых на векторы состояния.

Быть ознакомлены с:

Алгебраическим методом извлечения информации о свойствах операторов наблюдаемых;
Логической и математической структурой квантовой механики;
Методами математического исследования моделей и их проверкой.

Формы контроля:

Самостоятельное решение задач, возникающих в процессе построения и изучения моделей на практических занятиях.
Ответы на контрольные вопросы по изучаемым темам.
Зачет в конце семестра.

3. Учебно-методическое обеспечение дисциплины

Обязательная литература

Л. Д. Фаддеев, О. А. Якубовский. Лекции по квантовой механике для студентов – математиков. –Л.: Издательство ЛГУ. 1980. –200 с.
А. В. Борисов. Основы квантовой механики. Учебное пособие по курсу «Физика» для студентов отделения математики механико–математического факультета. –М.: Издательство физического факультета МГУ. 1999. –88 с.

Дополнительная литература

1. Балашов В. В., Долинов В. К. Курс квантовой механики. – М.: Едиториал УРСС, 2002.

2. А. Боум. Квантовая механика. Основы и приложения. – М.: МИР. 1990. –720 с.

СОДЕРЖАНИЕ

1.Пояснительная записка

2.Тематический план

3.Содержание дисциплины

4.Литература

Blog

В квантовой физике

Содержание

КПВ: МАТЕМАТИЧЕСКИЕ МОДЕЛИ