Geum.ru

Xxxviii международная (Звенигородская) конференция по физике плазмы и утс, 14 18 февраля 2011 г. О преемственности квантовой механики и классической электродинамики

Вид материалаДокументы
Подобный материал:

XXXVIII Международная (Звенигородская) конференция по физике плазмы и УТС, 14 – 18 февраля 2011 г.



О ПРЕЕМСТВЕННОСТИ КВАНТОВОЙ МЕХАНИКИ И КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ


В.И. Коган*, А.А. Рухадзе

ИОФ им. А.М. Прохорова РАН
*РНЦ Курчатовский институт

На 36 и 37 конференциях в Звенигороде В.И. Коганом были представлены доклады [1] по интерпретации квантовой механики на основе классической электродинамики. Доклады вызвали неоднозначную реакцию. В настоящем сообщении оговорены постулаты и допущения, показывающие преемственность квантовой механики и классической электродинамики.

В монографии [2] решена задача о движении электрона в кулоновском поле положительного заряда. В кулоновском поле притяжения в классической механике [3] возможно движение нейтральной частицы по эллиптическим траекториям с периодом

(1)

Здесь 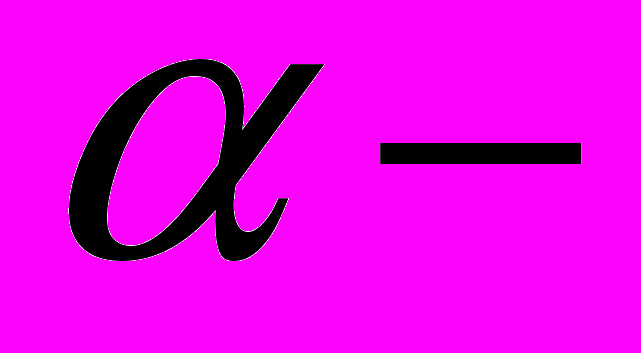характеристика потенциала (в случае заряда 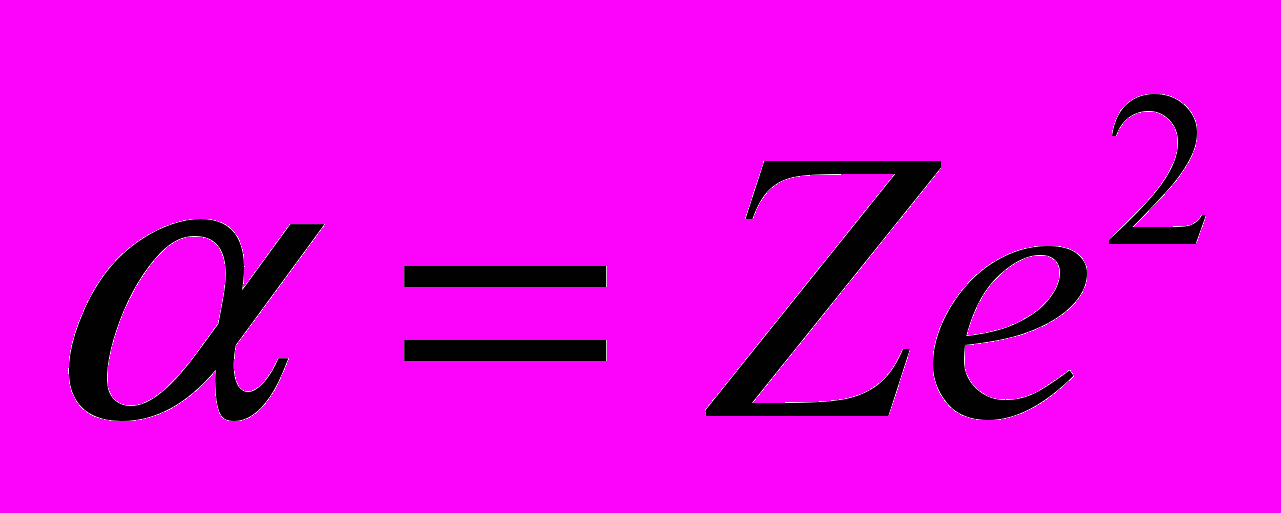), масса частицы, совершающего эллиптическое движение (в нашем случае масса электрона), 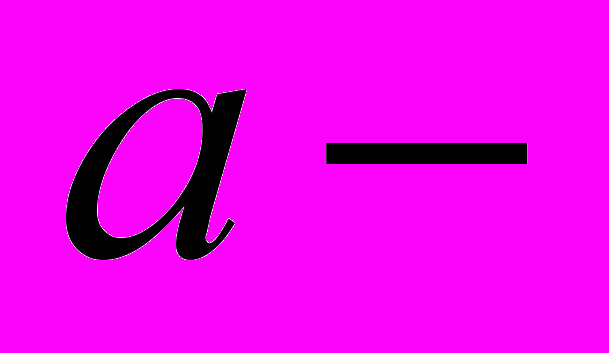полуось эллипса, уравнение которого в полярных координатах имеет вид [3]

(2)

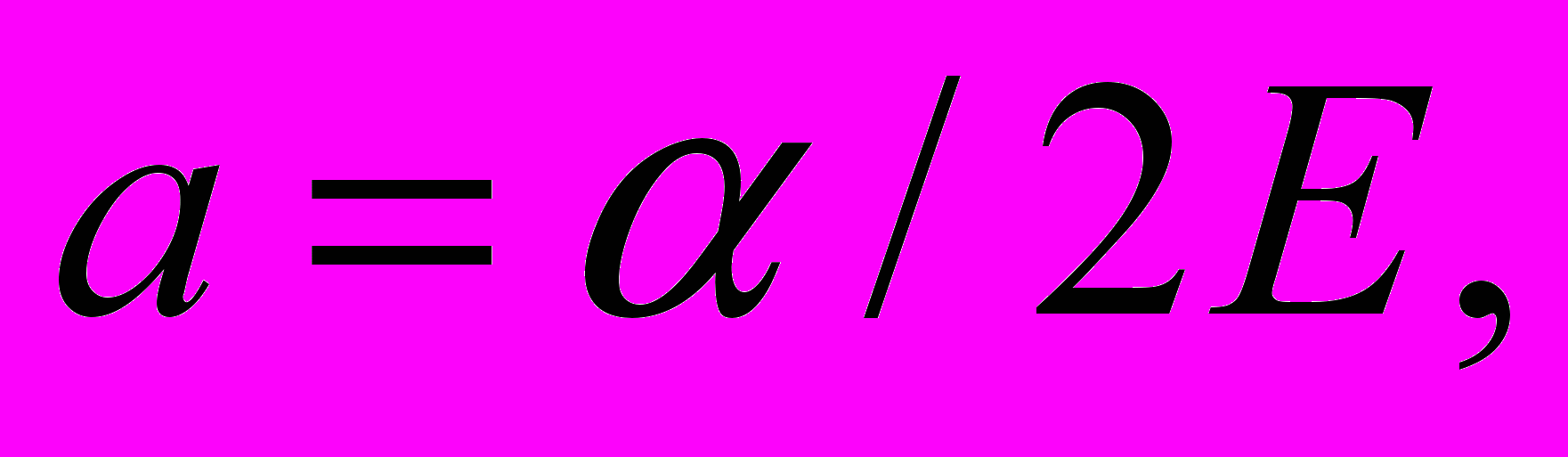
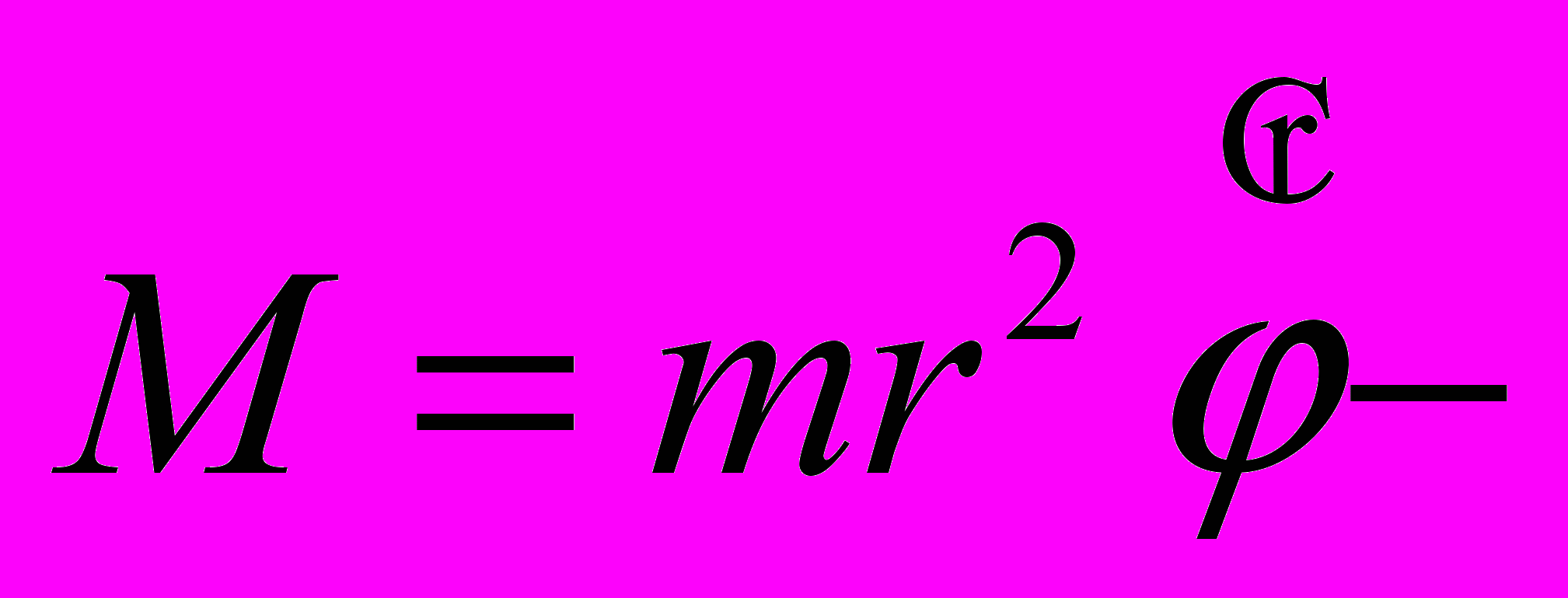где эксцентриситет, а параметр орбиты, момент количества движения, а кинетическая энергия частицы.

В случае поля заряда 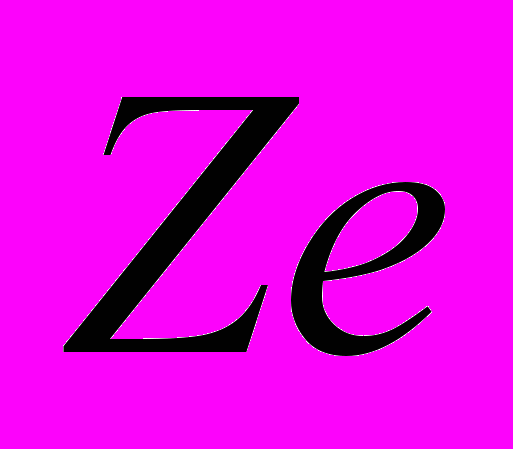в [2] вычислена интенсивность излучения электрона при движении по эллиптическим орбитам. В условиях, когда траектория электрона близка к параболе (такое движении в кулоновском поле ядра в [1] было названо параболическим ), т.е. когда в [2] приведена формула для интенсивности излучения на высоких гармониках частоты 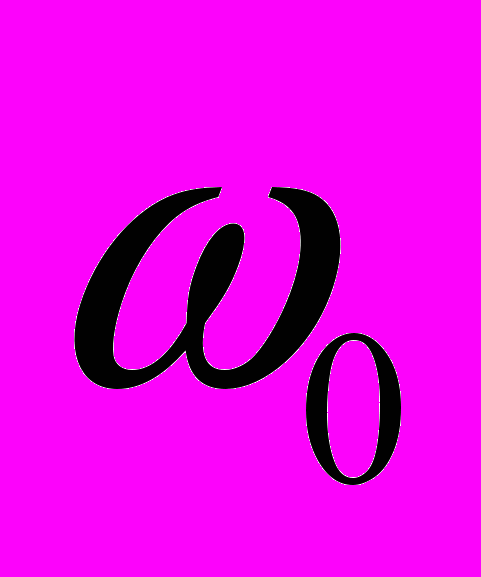, т.е. при где 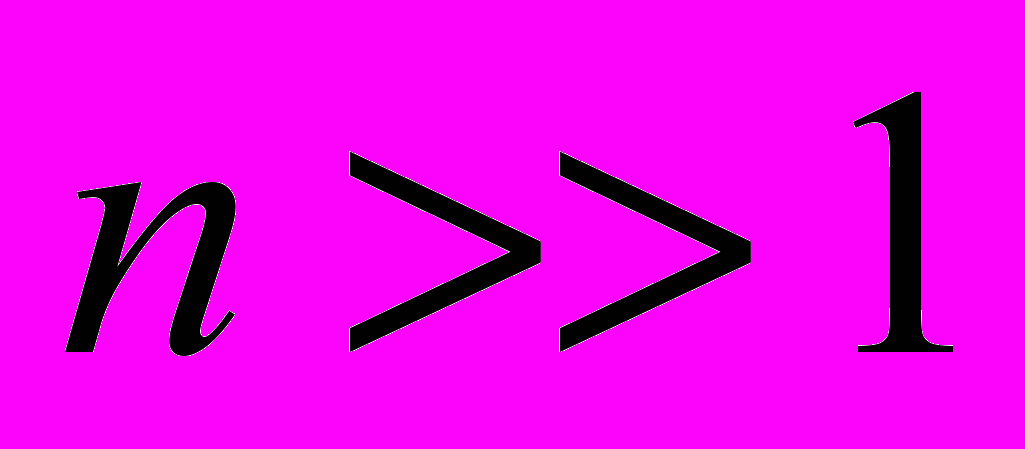. Показано, что интенсивность излучения электрона при , экспоненциально падает. Именно на это обстоятельство было обращено внимание в [1,2] и приведена асимптотическая формула в пределе больших частот

(3)

При получении формулы (3) было принято допущение, что можно трактовать как боровскую частоту, т.е. проведена замена . В этом допущении состоит суть работ [1] и, с нашей точки зрения, преемственность квантовой механики и классической электродинамики. Это допущение вполне логично, если учесть, что в квантовой теории водородоподобного атома возможны переходы между возбужденными состояниями и основным состоянием атома (т.е. излучение с частотой 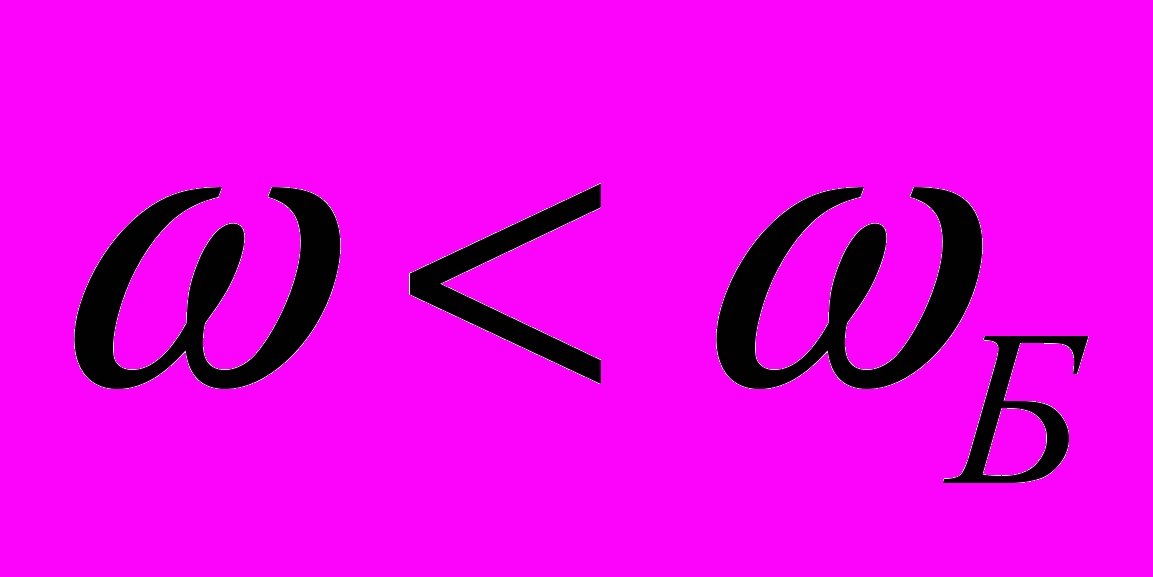), а основное состояние устойчиво (т.е. излучение невозможно).

Литература
  1. В.И. Коган, Тезисы 36 и 37 Международных конференций по физике плазмы и УТС, Звенигород. 2009, с.180 и 2010, с. 184.
  2. Л.Д. Ландау, Е.М. Лифшиц, Теория поля, М. Наука. 1988.
  3. Л.Д. Ландау, Е.М. Лифшиц, Механика, М.ФИЗМАТГИЗ. 1988.