Урок по теме: «Системы двух линейных уравнений с двумя неизвестными»
| Вид материала | Урок |
Содержание2. Какие уравнения, называются равносильными? 3 1. Покажем, что пара чисел х =0 у = -2 |
- Лекции по предмету "аналитическая геометрия и линейная алгебра", 82.08kb.
- Урок по теме «Системы линейных уравнений», 8.64kb.
- Системы линейных уравнений с двумя переменными как математические модели реальных ситуаций, 118.06kb.
- Программа решения системы линейных уравнений по методу Гаусса 7 2 Программа решения, 230.48kb.
- Урок в 7 классе по теме: «Системы линейных уравнений в решении алгебраических задач», 97.42kb.
- Вопросы к экзамену 1 семестр, 56.89kb.
- Контрольная работа по линейной алгебре и аналитической геометрии «Системы линейных, 383.4kb.
- 1. Матрица и расширенная матрица системы. Элементарные преобразования матриц. Решение, 8.16kb.
- Неравенств и, если «да», то найдите общее решение и частное решение двумя способами:, 11.47kb.
- Лекция № Тема 1: Системы линейных алгебраических уравнений. Метод Гаусса решения систем, 50.61kb.
Модульный урок по теме: «Системы двух линейных уравнений с двумя неизвестными» (Урок изучения нового материала) 7класса
учитель ЯКУБОВА И.Б.
| УЭ | Содержание работы | Указание к работе |
| УЭ-0 | Интегрирующая цель: познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач. В конце занятия вы должны ЗНАТЬ: Что такое система? УМЕТЬ: Выделять главное, решать системы двух линейных уравнений с двумя неизвестными разными способами. | Запишите в тетрадь тему урока Прочитайте цель урока. |
| УЭ-1 | Цель: определить исходный уровень знаний по теме: Системы двух уравнений с двумя неизвестными. Ответьте на вопросы: 1. Какие уравнения называются линейными уравнениями с двумя переменными? ^ 2. Какие уравнения, называются равносильными? 3.Какими свойствами обладает уравнения с двумя переменными? | Прочитайте цель урока. Ответьте на вопросы. Если ваш товарищ ответил не верно, то помоги ему. |
| У   Э-2 | Цель: познакомить со способом решения системы линейных уравнений с двумя неизвестными. Проблемный вопрос: Что значит решить систему уравнений? Задание 1. Послушайте объяснение учителя. Запишите формулу в тетрадь. Запишите определение в тетрадь. Задание 2. Проверим, является ли пара чисел х=10 ,у=15 решением системы: х + у=25 , 10+15=25- верное равенство 2х-у=5 20-15=5 – верное равенство. Задание 3.По образцу проверьте, является ли пара чисел х =-2, у = 1 решением системы 3х – у = - 7, -х +у=3 | Прочитайте цель урока. Внимательно слушайте объяснения учителя. Запишите решение в тетрадь. Обменяйтесь тетрадями и сверьте ответы. Исправьте ошибки. |
| УЭ-3 | Цель: совершенствовать навыки решения систем уравнений с двумя неизвестными. Исследуйте решение.  х+5у=7, х+5у=7 3х–2у=4 х=7-5у 3·(7-5у)-2у=4, 21-15у-2у=4, -15у-2у=4-21, -17у=-17, у=1 (х=7-5у) х=7-5·1=2 Найденная пара чисел х=2 , у=1 является решением данной темы. Ответ: х =2 ,у=1 Ответьте на проблемный вопрос | Прочитайте цель урока Если испытываете, затруднения обратись за помощью к товарищу или к учителю. Решение обсудите в классе используя, приложение №1 |
| У Э-4 | Цель: Оценить усвоение нового материала Внимательно просмотри этапы урока, выясните, что вам непонятно, уточните у товарища или учителя. Выполните итоговое задание. ^ 1. Покажем, что пара чисел х =0 у = -2 не удовлетворяет системе уравнений 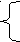5х+ у = -1, -3х – у = -2, ( т. е. не является ее решением) 2. Решим систему 2х-4у=14, -3х=2у =-9 способом подстановки. | Смотри приложение № 2. |
| УЭ-5. | Цель: определить уровень усвоения знаний. Введем основные понятия при решении системы уравнений с двумя неизвестными.
При каких значениях переменных х и у получится верное равенство? Впишите пропущенные слова.
х,у то принято в записи его решения на первое место ставить значения__________________, а на второе ____________________________ 3. Если ставиться задача, найти все общие решения двух или нескольких уравнений, то говорят, что надо____________________ 4. Решить систему, значит найти ________________ | Прочитайте цель. Выполните задание. Сделайте взаимопроверку используя, приложение №3 |
| УЭ-6 | Цель: Подведение итогов урока и определение домашнего задания. Если вы справились со всеми заданиями – вы молодец! Если у вас есть недоработки, возьмите модуль домой и закончите его. Для этого воспользуйтесь учебником. Смотри § 43. | Прочитайте цель. |
ПРИЛОЖЕНИЕ 1.
Решим систему уравнений х + 5у=7,
3х -2у =4
способом подстановки.
Поступим следующим образом.
Из одного уравнения выразим одно неизвестное через другое.
В данном случае удобнее из первого уравнения х =5у =7 выразить х через у:
х= 7 -5у.
В другое уравнение (в данном случае во второе 3х – 2у = 4) подставим вместо неизвестного его значение, выраженного из первого уравнения: 3·(7 – 5у)-2у = 4 . Решим полученное линейное уравнение с одним неизвестным:
21 – 15у 2у=4, -15у -2у =4 -21, -17у = -17, у=1.
Найденное значение неизвестного (у=1) подставим в выражении для другого неизвестного
(х=7-5у)
х= 7-5·1=2
Найденная пара чисел х=2 ,у =1 является решением данной системы.
Либо краткое решение дано в УЭ -3.
ПРИЛОЖЕНИЕ 2.
1).
5 · 0+.(-2) = -1 – верное равенство,
-3.0-(-2)=-2 –неверное равенство 2 ≠ -2.
Пара чисел х =0 , у=-2 не является решением данной системы.
2).
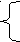2х-4у = 14, 2х =14+4у-3х+2у= -9 х =14+4у
2
х= 2 · (7 +2у) х=7+2у
2
-3 · (7+2у) +2у = -9,
-21-6у+2у = -9.
–4у =21—9, -4у=12,
у = 12: (-4) у= -3
х=7+2(-3), х=1
Ответ: х=1; у= -3.
ПРИЛОЖЕНИЕ 3.
- это уравнение в верное равенство.
- значение переменной х, на второе место у.
- надо решить систему уравнений.
- найти множество ее решений.
Критерии оценивания:
| №№ | Ф.И..ученика | Количество правильных ответов | Оценка | Комментарий |
| 1. | Бочеров Алексей | + + + - - | «5» | Вы молодец |
| «4» | Будьте внимательны | |||
| «3» | Надо потрудиться | |||
| «2» | Очень жаль, будем работать |