Обучение школьников способам решения проблем на уроках математики
| Вид материала | Урок |
- Чудинов Ю. В., Место рассказа в обучении младших школьников риторическим способам решения, 67kb.
- Задачи: провести диагностическое исследование уровня развития творческого мышления, 149.7kb.
- Методика использования дидактических игр на уроках математики для активизации познавательной, 25.3kb.
- Ионовой Надежды Валентиновны на заседании рмо учителей математики 2007 2008 учебный, 108.68kb.
- Реферат «развивающее обучение на уроках математики», 309.45kb.
- Для реализации компетентностного подхода в обучении на уроках математики можно применять, 161.54kb.
- Рабочая программа по курсу Формирование исследовательских умений на уроках математики, 51.16kb.
- Комплекс дидактических игр для активизации познавательной деятельности младших школьников, 456.29kb.
- Элективный курс «параметры и их практическая значимость» Учитель математики Маеренкова, 182.82kb.
- Обучение в сотрудничестве как способ активизации учебно-познавательной деятельности, 151.77kb.
ОБУЧЕНИЕ ШКОЛЬНИКОВ СПОСОБАМ РЕШЕНИЯ ПРОБЛЕМ НА УРОКАХ МАТЕМАТИКИ
С.Л. Николаева
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 49
Учебный предмет ”Математика” уникален в деле формирования личности. Образовательный, развивающий потенциал математики огромен. Не случайно ведущей целью математического образования является интеллектуальное развитие учащихся, формирование качеств мышления, необходимых человеку для полноценной жизни в обществе. Математика выступает именно как предмет общего образования, который позволяет наделять подрастающего человека способностями, необходимыми для свободной и безболезненной адаптации его к условиям жизни в современном обществе.
Развивает и формирует ученика не столько само знание, сколько метод его приобретения. Если учебная деятельность протекает только в рамках воспроизведения усвоенных знаний, то это не способствует развитию человека.
Появление мотивации познавательной деятельности наиболее успешно может быть вызвано проблемностью, созданной учителем в обучении. Кроме того, проблемное обучение способствует развитию интеллектуальных, творческих способностей учащихся. Проблемное обучение основано на получении новых знаний через решение теоретических и практических проблем.
Организация проблемного обучения осуществляется на основе проблемных вопросов, задач, заданий, проблемных ситуаций. Проблемная ситуация является важной составляющей проблемного обучения, во многих случаях именно с нее начинается весь процесс.
Последовательность этапов проблемного обучения, начиная с проблемной ситуации, выглядит следующим образом: проблемная ситуация – проблема – проблемная задача – решение проблемы.
Существуют разные способы создания проблемных ситуаций, наиболее часто используются следующие:
Первый способ: проблемная ситуация возникает при условии, если учащиеся не знают способы решения поставленной задачи, не могу ответить на проблемный вопрос, дать объяснение новому факту в учебной или жизненной ситуации.
Второй способ: проблемные ситуации возникают при столкновении учащихся с необходимостью использовать ранее усвоенные знания в новых практических условиях.
Третий способ: проблемная ситуация легко возникает в том случае, если имеется противоречие между теоретически возможным путем решения задачи и практической неосуществимости выбранного способа.
Основное различие между проблемным и традиционным обучением состоит в двух моментах: они различаются по цели и принципам организации педагогического процесса.
Цель традиционного типа обучения - усвоение результатов научного познания, вооружение учащихся знаниями основ наук, привитие им соответствующих умений и навыков.
Цель проблемного типа обучения не только усвоение результатов научного познания, системы знаний, но и самого пути процесса получения этих результатов, формирования познавательной самодеятельности ученика и развития его творческих способностей.
Деятельность учащихся при наличии проблемности выстраивается поэтапно: осознание проблемной ситуации, формулировка проблемы на основе осознания проблемной ситуации, высказывание и обоснование гипотез, решение проблемы через проверку гипотез, оценка способа решения. Каждый этап при осуществлении деятельности, свойственной этапу, представляет определенную сложность для учащихся.
Проблемное обучение может быть использовано на различных этапах учебного процесса, на этапе формирования умений и навыков. Наиболее часто на уроках математики оно используется при изучении нового материала. Ученик самостоятельно усваивает новое понятие, название которого учитель вводит после усвоения его сущности. При разрешении проблемной ситуации учащиеся проходят все основные этапы этого процесса: анализ, выдвижение версий и их обсуждение, решение проблемы с использованием версий, проверка правильности решения проблемы. Учитель организует деятельность и выступает в роли консультанта . В результате, у школьников появляются такие важные умения, как:
а) видеть проблему и осознавать ее;
б) сформулировать и переформулировать проблему;
в) выдвигать гипотезы;
г) обосновывать и доказывать выдвинутые гипотезы;
д) применять на практике найденный способ решения учебной проблемы.
Постоянная постановка перед учеником проблемных ситуаций приводит к тому, что он не «пасует» перед проблемами, а стремится их разрешить, тем самым мы имеем дело с творческой личностью всегда способной к поиску, войдя в жизнь, ученик будет более защищен от стрессов.
Структурными элементами проблемного урока являются:
| Этапы урока | Действия учителя | Действия учащихся |
| 1. Возникновение проблемных ситуаций и постановка проблемы | Создает проблемную ситуацию, формируем противоречия, ставит задачу. | Осознают противоречие, помогают формулировать проблему. |
| 2. Выдвижение предположений и обоснования гипотезы | Организует дискуссию, обсуждение различных вариантов, гипотез | Выдвигают различные гипотезы, варианты решения проблемы |
| 3. Доказательство гипотезы | Организует проверку, анализ различных подходов к решению проблемы. | Доказывают, спорят, аргументируют, убеждают, критически оценивают. |
| 4. Проверка правильности решения проблемы | Обосновывает правильных способ решения, аргументирует его преимущества. | Решают задачи, сотрудничают в достижении общего успеха. |
| 5. Рефлексия | Анализирует процесс и результаты совместной работы, вовлеченность детей. | Анализируют, оценивают процесс и результаты совместной деятельности, вовлеченность каждого. |
Хотелось показать технологию введения новых понятий и способов посредством создания проблемных ситуаций. Рассмотрим процесс обучения формулировке, обоснованию и доказательству гипотез на уроке «Решение систем линейных уравнений» в 7 классе.
Тема урока: Решение систем линейных уравнений
^ Цели урока:
- совместно с учащимися разработать способы решения систем линейных уравнений;
- организовать совместную деятельность, создающую условия для демонстрации учащимися умения формулировать гипотезы, формирования мышления, характерного для математической деятельности;
- воспитание чувства дружбы, взаимовыручки, умения работать в команде и ответственности за результаты совместной работы.
Ход урока:
1. I. Погружение в проблемную ситуацию.
Приветствие учащихся.
Повторение ранее изученного материала: (учащиеся сами определили круг вопросов, задавали друг другу)
- Что называется уравнением? (Уравнение – это равенство, содержащее одну или несколько переменных)
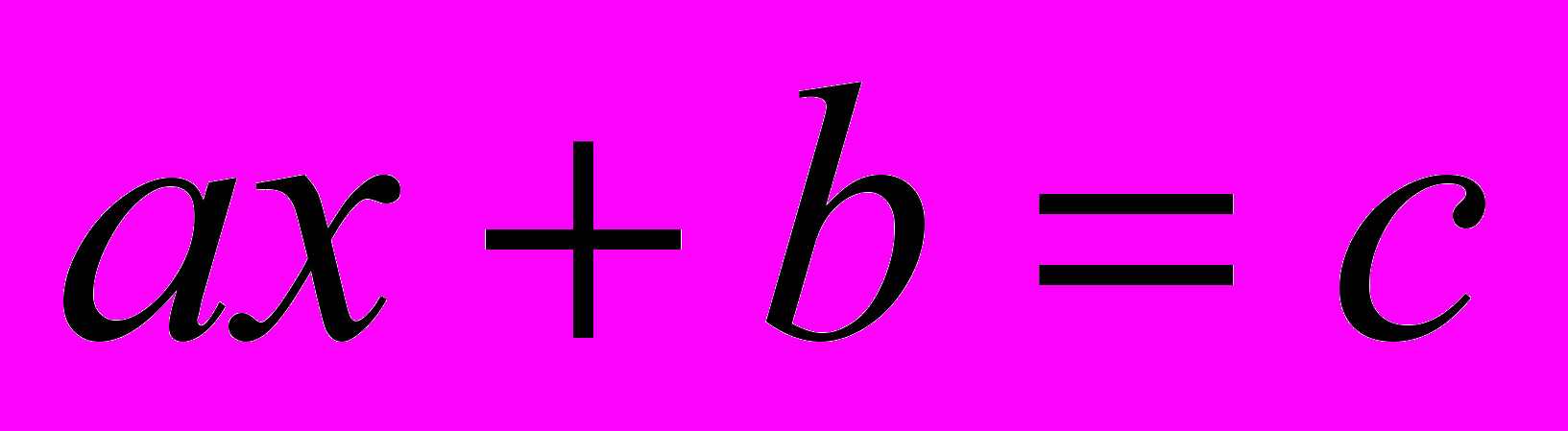- линейное уравнение с 1 переменной.
- Что называется линейным уравнением с 2 переменными? (
)
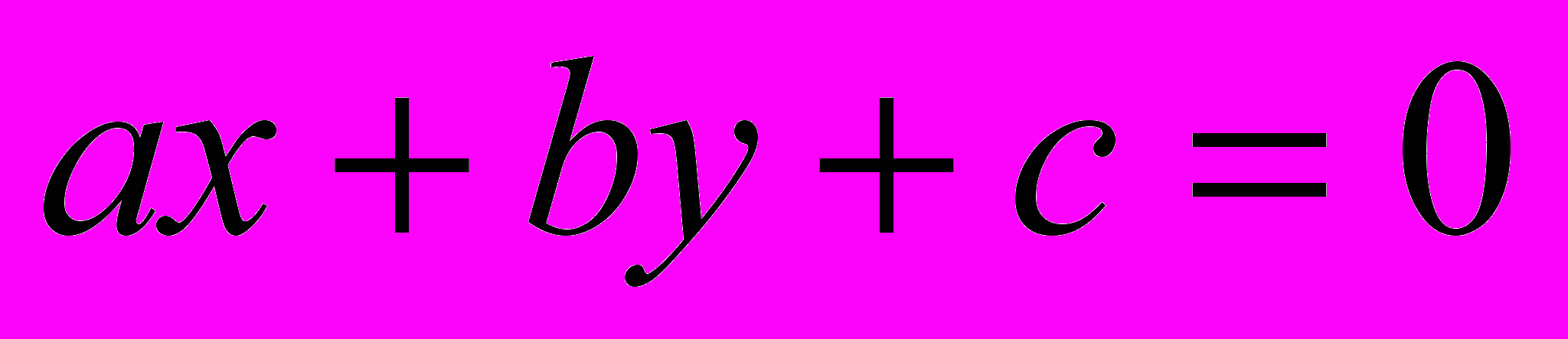- Приведите примеры линейных уравнений с 2 переменными.
- Что является решение линейного уравнения с 2 переменными?
Задача 1: Разность двух чисел равна 6. Найдите эти числа. (
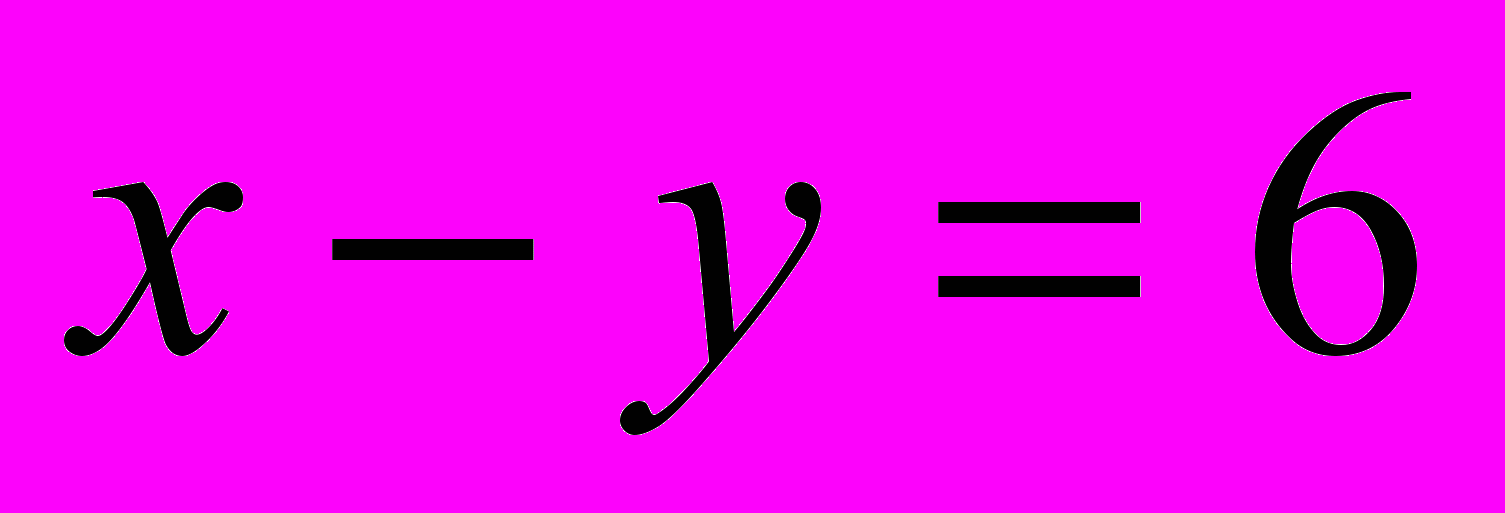)- Какие свойства уравнений вы знаете?
Свойства уравнений:
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
II. Создание проблемной ситуации.
Задача 2: Разность двух чисел равна 4, а их сумма равна 0.Найдите эти числа.
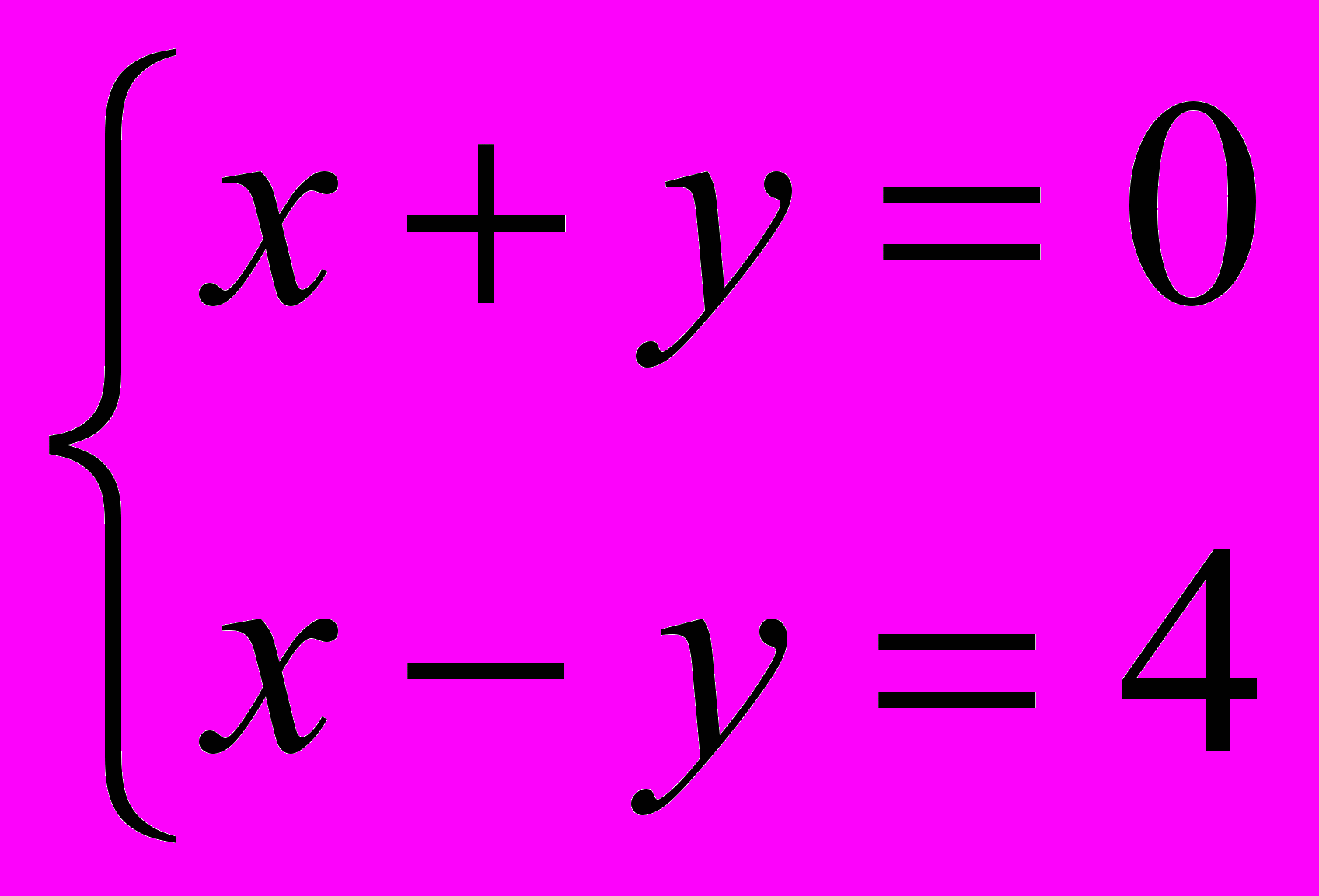
- Чем отличаются условия 1 и 2 задачи?
- Мы получили с вами 2 уравнения, они объединены одним условием. В алгебре говорят, что получили систему уравнений.
- Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно.
^ III. Работа по обоснованию версий в группах.
- Сейчас поработайте в группах, рассмотрите данную систему уравнений и попробуйте предложить способы решения данной системы. (Способы решения фиксируются на доске.)
- Решите систему уравнений одним из предложенных способов по желанию.
Представители каждой из команд выходят к доске и предлагают свой вариант решения системы уравнений.
Задача 3: Решите систему уравнений:
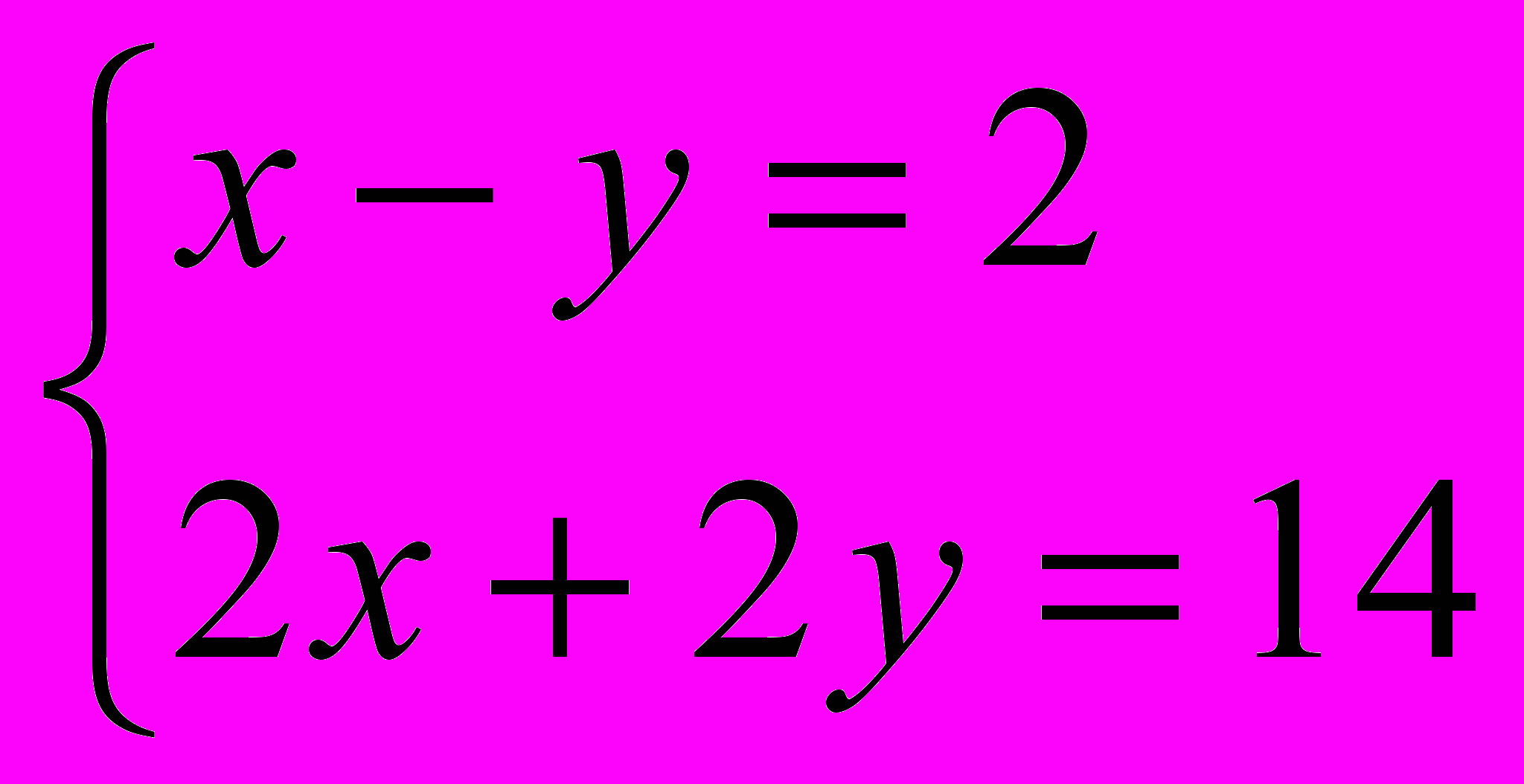
Ответ: (4;2)
Задание группам:
- Решите своим методом следующую систему уравнений.
- Попробуйте обосновать свой вариант решения и сформулировать правило (алгоритм) решения системы.
- Как узнать правильность предложенной вами гипотезы. (Как проверить, правильно ли решена система?)
- Что является решение системы линейных уравнений с 2 переменными?
- Предложите название своего метода решения системы.
^ VI. Представление результатов работы групп.
(представители каждой команды выходят к доске и предлагают свои варианты решения системы)
Вывод: ^ Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
- Итак, одна и та же система решена разными способами.
- Какой из них вам показался более удобным?
- В чем недостаток графического метода?
Все эти способы в математике имеют свои названия: графический, сложения, подстановка.
V. Итог урока:
- способы решения систем уравнений с 2 переменными;
- алгоритмы способов решения систем уравнений с 2 переменными;
- проверка решения.
VI. Оценивание работы в группе.
| Ф.И | | | | | | Балл |
| 1. Высказал(а) идею, версию | | | | | | 2 |
| 2. Сформулировал(а) гипотезу | | | | | | 2 |
| 3. Уточнил(а) гипотезу | | | | | | 1 |
| 4. Задавал(а) вопросы | | | | | | 1 |
| 5. Отвечал(а) на вопросы | | | | | | 1 |
| 6. Составлял(а) алгоритм | | | | | | 2 |
| 7. Представлял(а) группу | | | | | | 2 |
| 8. Оформлял(а) | | | | | | 1 |
| Итого | | | | | | |
| Оценка | | | | | | |
Оценка за количество баллов: от 12 до 9 – «5»
от 6 до 8 – «4»
от 2 до 5 – «3»
от 0 до 1 – «2»
^ VII. Рефлексия.
- На этом уроке я приобрел(а) следующие знания: _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
- Я научился(ась): ______________________________________________________________________________________________________________________________________________________________________________________
- Я продемонстрировал(а) умения: ______________________________________________________________________________________________________________________________________________________________________________________
- Мне нравятся уроки проблематизации за ______________________________________________________________________________________________________________________________________________________________________________________
^ Анализ урока.
Место урока в разделе учебного курса:
Данный урок первый в теме «Решение систем линейных уравнений с двумя переменными» проводился 21 апреля 2008г, продолжительность – 2 часа.
До этого урока дети решали только уравнения с одной и двумя переменными и не встречались с системами уравнений. Поэтому, для меня, как для учителя было важно, чтобы учащиеся в полной степени смогли самостоятельно овладеть новыми знаниями: система уравнений и разобраться в методах решения систем, отработать навыки решения систем различными способами.
Для работы на уроке ребята сами разделились на 4 группы по 5 человек и 1 группа – 6 человек.
^ Тип урока: урок – проблематизация.
Цели урока:
- совместно с учащимися разработать способы решения систем линейных уравнений;
- организовать совместную деятельность, создающую условия для демонстрации учащимися умения формулировать гипотезы, формирования мышления, характерного для математической деятельности;
- воспитание чувства дружбы, взаимовыручки, умения работать в команде и ответственности за результаты совместной работы.
^ Мотивы выбора структуры урока: в 7 «Б» классе, в котором проходил урок 30 учащихся, на уроке присутствовало 26 человек.
Для того, чтобы вовлечь всех учащихся в работу на уроке на этапе знакомства с новым материалом и формирования навыков решения систем уравнений был выбран данный тип урока. Для меня, занимая позицию лидера, было важно, заинтересовать детей, привлечь к участию в уроке, а именно, увидеть проблему, предложить свои гипотезы и версии. Главное – это формирование самостоятельных умений, способности принимать решения, брать на себя ответственность.
^ Ход урока:
1. Погружение в проблемную ситуацию.
Считаю, что на первом этапе – этапе погружения учащимся удалось довольно обширно повторить
ранее изученный материал. Они самостоятельно вспомнили основные ранее изученные темы по линейным уравнениям, очень активно задавали вопросы друг другу, отвечали и уточняли друг друга.
^ II. Создание проблемной ситуации.
На следующем этапе, во время обдумывания решения предложенной мною задачи учащиеся увидели существенное отличие между первой и второй задачами, они сразу высказали версию, что данная задача состоит не из одного условия, а двух, и для того чтобы решить эту задачу, необходимо составить два уравнения с двумя переменными.
Так же сами учащиеся во время обсуждения условия задачи и возможного ответа к задаче пришли к выводу, что ответ должен состоять из двух чисел, и эти числа должны являться решениями сразу двух уравнений.
Ребята быстро подобрали (устно) возможные варианты решения задачи, однако, поняли, что практически они не знают, как решать эту задачу.
^ III. Работа с версиями детей.
Была сформулирована проблема, и ребята начали в группах в течение 5 минут обсуждать возможные версии по решению данной системы. Затем представители групп озвучили свои версии. Все они были зафиксированы на доске:
- Из каждого уравнения выразить у через х, построить графики линейных функций, найти координаты точки пересечения.
- Из каждого уравнения выразить у через х, прировнять левые части уравнений, решить полученное уравнение (найти х), подставить найденное значение х в выражение для у (найти значение у).
- Сложить левые и правые части уравнений, решить полученное уравнение с одной переменной х, найти соответственное значение у.
- Из первого уравнения выразить у через х, подставить во второе уравнение и найти значение у.
^ IV. Работа по обоснованию версий в группах.
Для проверки правильности выдвинутых версий группам было дано задание решить новую систему одним из способов на основе личного, ими предложенного.
Так же каждая группа должна была:
- обосновать свой вариант решения, сформулировать и записать алгоритм решения системы данным методом;
- сделать вывод о том, что является решением системы уравнений с двумя переменными, как записать ответ;
- выдвинуть гипотезу о том, как проверить, правильно ли решена система и обосновать ее;
- предложить название своего метода решения системы.
^ VI. Сравнение лично полученного результата с научным.
Представители каждой из групп выходили к доске, предъявляли свое решение системы, алгоритм решения, обоснованную гипотезу.
Другие учащиеся совместно со мной, дополняли выступающих ребят, уточняли, задавали вопросы, записывали решение и алгоритм в тетради.
В результате, на доске было представлено четыре способа решения систем линейных уравнений, сформулированы четыре алгоритма решения систем, даны следующие названия способов решения:
- графический
- подстановка
- сложение
- сравнение
После выступления учащихся, я обобщила весь материал урока, мы еще раз повторили алгоритмы решения систем, и все вместе четко сформулировали и записали названия всех методов.
Мне, как педагогу было приятно видеть, что ребята сами самостоятельно вышли не только на три основных метода решения систем, которые предлагаются в программе 7 класса (графический, сложение, подстановка), но и смогли увидеть и предложить четвертый способ: способ сравнения.
^ VII. Итог урока. Рефлексия. Выставление оценок.
Дети работали с интересом, увлеченно. Было видно, что материал ими понят и усвоен хорошо. Учащиеся показали хорошие знания по предмету, ответственность друг за друга сплоченность.
Все поставленные задачи выполнены. В конце урока учащиеся в группах сами оценили свою работу по предложенной карте, которая была разработана мною, но согласована с детьми.
В результате за работу на уроке ребята получили следующие оценки:
«5» - 6 человек
«4» - 13 человек
«3» - 7 человек
«2» - 0 человек
В качестве рефлексии ребятам была предложено письменно ответить на вопросы. Вот некоторые цитаты из рефлексивных листов:
- На этом уроке я приобрел(а) следующие знания:
- я узнал, что такое система уравнений,
- что есть много способов решения систем уравнений;
- что является решением системы линейных уравнений,
- как решать системы линейных уравнений;
- как работать в группе, чтобы был результат работы;
- есть 4 вида решения систем линейных уравнений;
- новые знания по теме, которую раньше не изучали, научились составлять алгоритмы решения систем линейных уравнений;
- знания по новой теме;
- научился сам выводить способы решения систем линейных уравнений;
- можно самому выводить новые правила и изучать новую тему;
- хорошо разобралась в способах решения систем линейных уравнений
- я узнал, что такое система уравнений,
- Я научился(ась):
- работая в группе выводить правила решения систем;
- не бояться высказывать свою идею, гипотезу;
- работать в группе, изучать самостоятельно материал;
- решать системы линейных уравнений;
- составлять алгоритмы и самому находить способы решения;
- особых умений не было, подобные уроки у нас проводятся, и к этой форме работы мы привыкли, на этом уроке мы снова закрепляли умения работать в такой форме;
- представлять результаты работы группы перед классом;
- Я продемонстрировал(а) умения:
- правильно формулировать ответ на вопрос задачи, составлять алгоритм решения системы;
- отвечать на вопросы и помогать другим;
- представлять работу группы;
- оформления, формулирования, решения систем уравнений, построение графиков уравнений;
- рассуждать в группе, размышлять;
- организовать работу в группе;
- отстаивать свою точку зрения перед группой,
- выступать, доказывать свою точку зрения;
- работе в группе и по теме с прошлых уроков;
- доказывать гипотезы по решению систем уравнений;
- что-то попытаться сделать самому;
- выдвигать свои мнения и слушать других;
- работе в группе, оцениванию участников группы, смогла разобраться с темой урока.
- Мне нравятся уроки проблематизации за то, что:
- на них можно разобраться с темой и притом самостоятельно, я люблю работу в группе;
- на них очень интересно;
- можно разобраться с темой урока, работая в группе;
- необычные методы работы;
- мы сами ставим перед собой проблемы и сами пытаемся их решить;
- можно высказывать мнение об уроке;
- весь класс сам знакомится и изучает новый материал и самостоятельно получает новые знания;
- право выбирать самим форму работы, правила, которые формулируются простым, понятным языком одноклассников;
- каждый может высказать свою точку зрения, работу в группе;
- что ты можешь помочь другим разобраться в непонятных вопросах;
- такие уроки очень интересные, мы сами выводим новые для себя правила.
