Линейные д. У. Го порядка. Линейный диф-ый оператор

Вид материала

Документы

Содержание НАПОМНИМ СЛЕДУЮщЕЕ ПОНЯТИЕ. ЛИНЕЙНО НЕЗАВИСиМОЙ Определителем вронского ОПР.1. совокупность

Подобный материал:

• Программа курса :«Линейная алгебра и аналитическая геометрия», 38.96kb.
• Уроки №5-6 тема: " Программирование ветвящихся алгоритмов. Оператор выбора, 58.01kb.
• Лекция №20, 58.21kb.
• Векторы. Линейные операции над векторами. Скалярное произведение векторов. Векторное, 8.22kb.
• Программирование ветвлений на Паскале Оператор ветвления на Паскале, 166.05kb.
• Программа вступительного испытания в магистратуру «Программная инженерия» Утверждено, 109.24kb.
• Уравнения математической физики направление подготовки, 18.02kb.
• Дифференциальные уравнения, 23.51kb.
• Обыкновенные дифференциальные уравнения, 17.54kb.
• Урок: «типы алгоритмов. Линейные алгоритмы»    Тема: Типы алгоритмов. Линейные алгоритмы, 101.98kb.

§ 3. ЛИНЕЙНЫЕ Д.У. 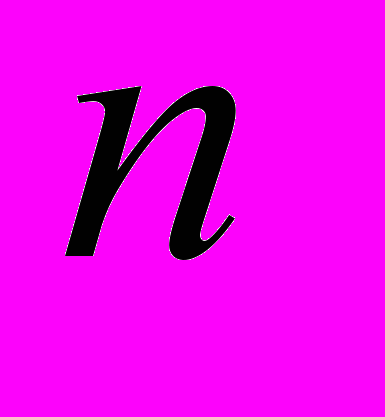-ГО ПОРЯДКА.


ЛИНЕЙНЫЙ Диф-ый ОПЕРАТОР.


ОПР.1 .ЛИНЕЙНЫМ Д.У. 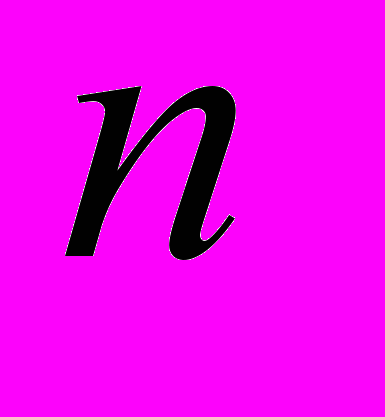-ГО ПОРЯДКА НАЗЫВАЕТСЯ УРАВНЕНИЕ ВИДА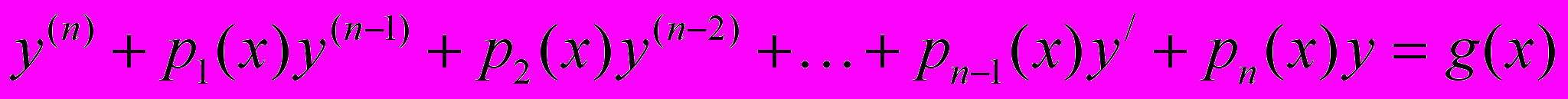



(1)

ВСЕ ПРОИЗВОДНЫЕ И САМА ФУНК-ИЯ 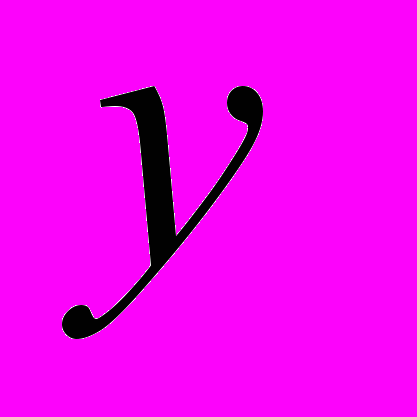ВХОДЯТ В УРАВНЕНИЕ В ПЕРВЫХ СТЕПЕНЯХ. 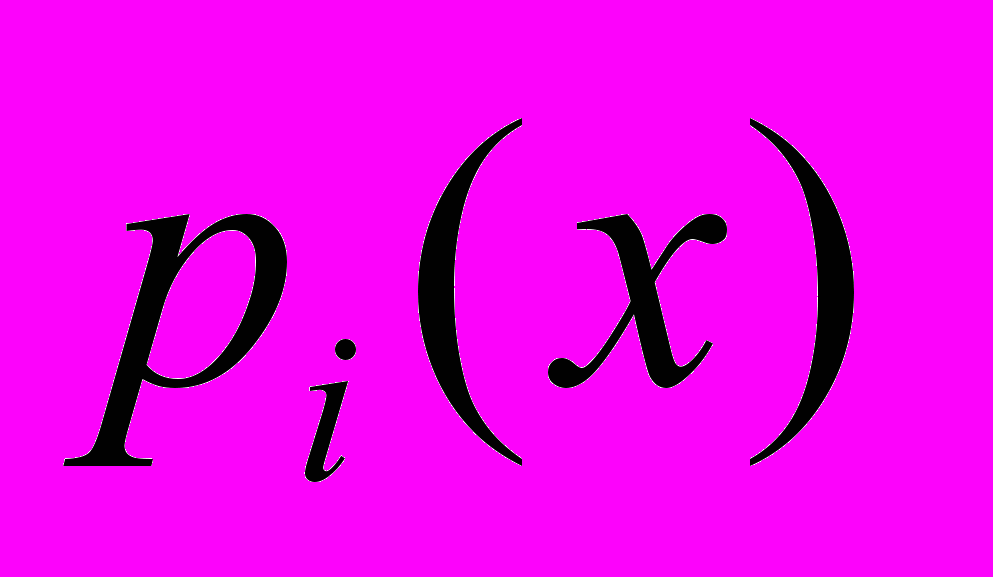-ВЕЩЕСТВЕННЫЕ ФУНКЦИИ.


ЕСЛИ 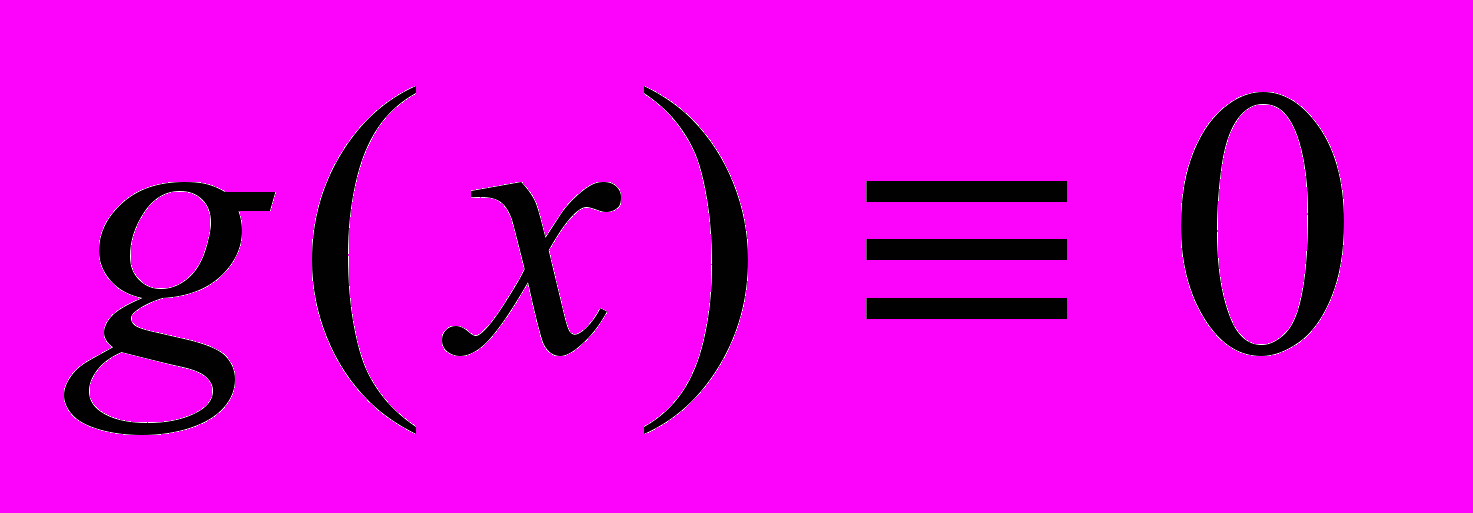, ТО УРавненИЕ НАЗЫВАЕТ­СЯ ОДНОРОДНЫМ.


(1)-НЕОДНОРОДНОЕ Линейное Д.У. 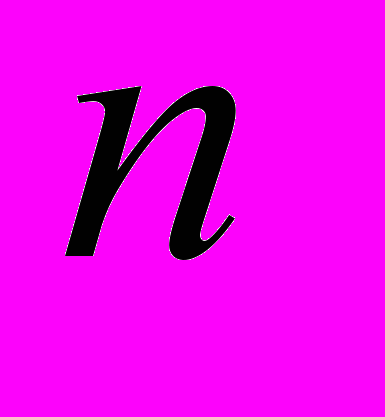-ГО ПОРЯДКА.


ЗАПИШЕМ ЛИНЕЙНОЕ ОДНОРОДНОЕ УРАВНЕНИЕ




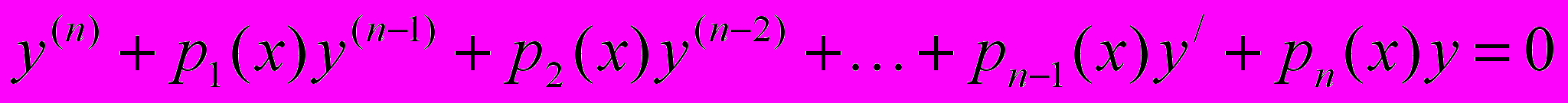
(2)


И ВВЕДЕМ ОБОЗНАЧЕНИЕ


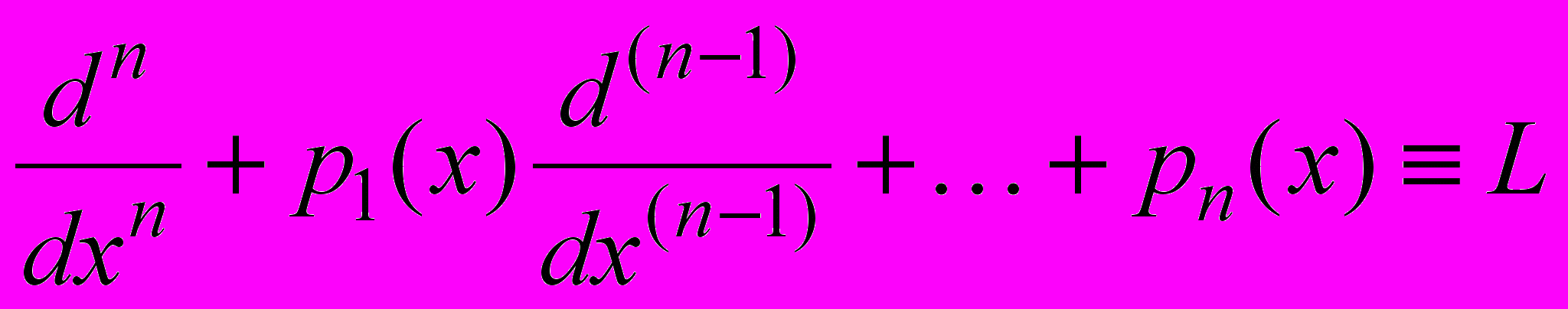(3)

И НАЗОВЕМ 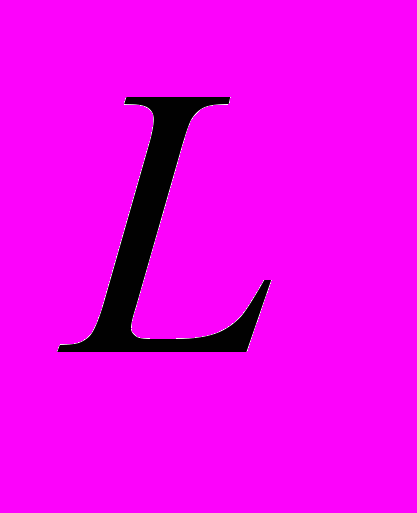- ЛИНЕЙНЫМ ДИФ-ЫМ ОПЕРАТОРОМ, ДЕЙСТВУЮЩИМ НА ФУНКЦИЮ .

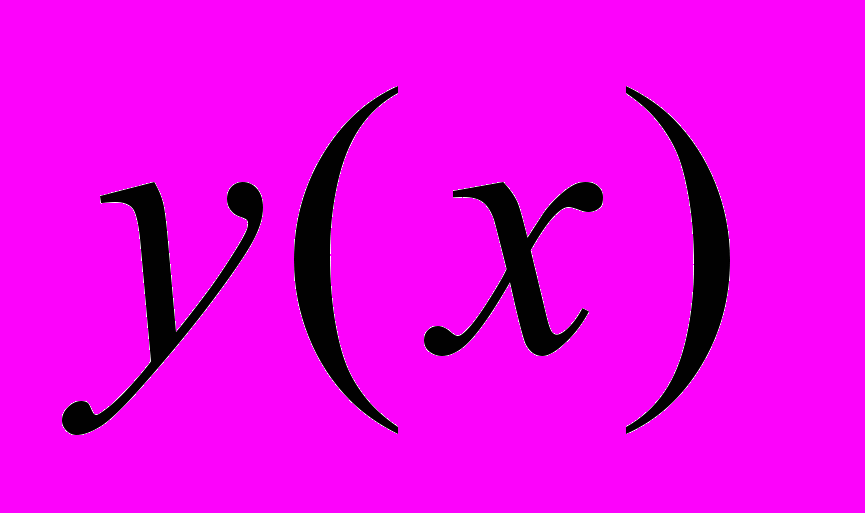С ПОМОЩЬЮ ОПЕРАТОРА Линейное Д.У. (1) ЗАПИШЕМ В ВИДЕ 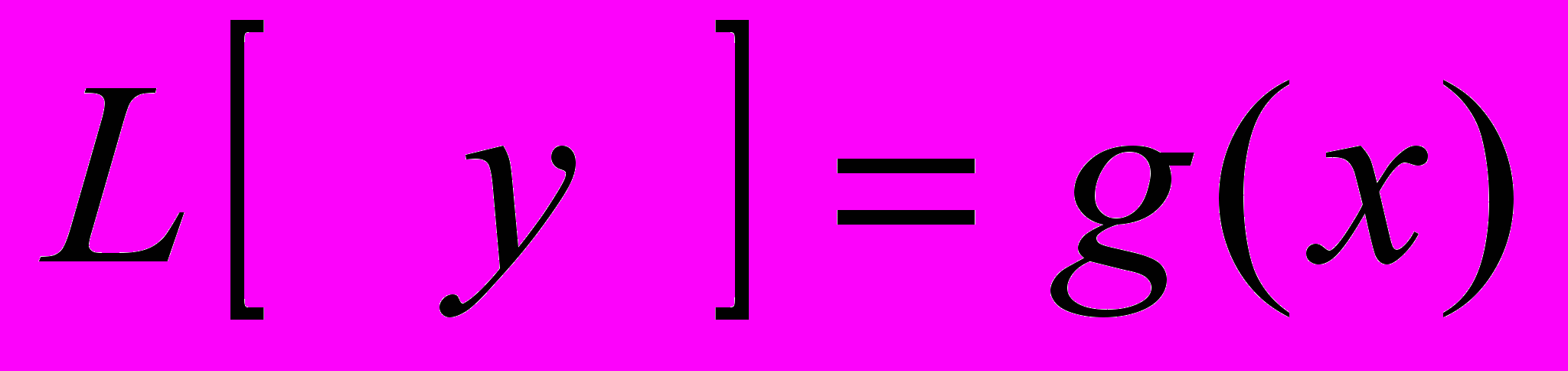- ЛИНЕЙНОЕ НЕОДНОРОДНОЕ Д.УРАВНЕНИЕ 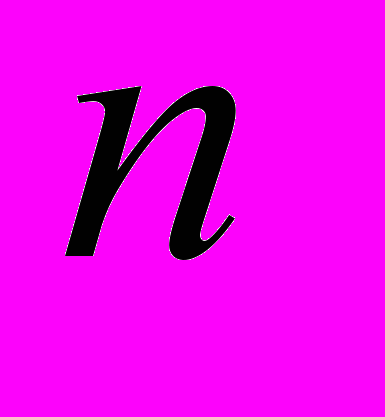- ГО ПОРЯДКА.


А (2) ЗАПИШЕТСЯ В ВИДЕ


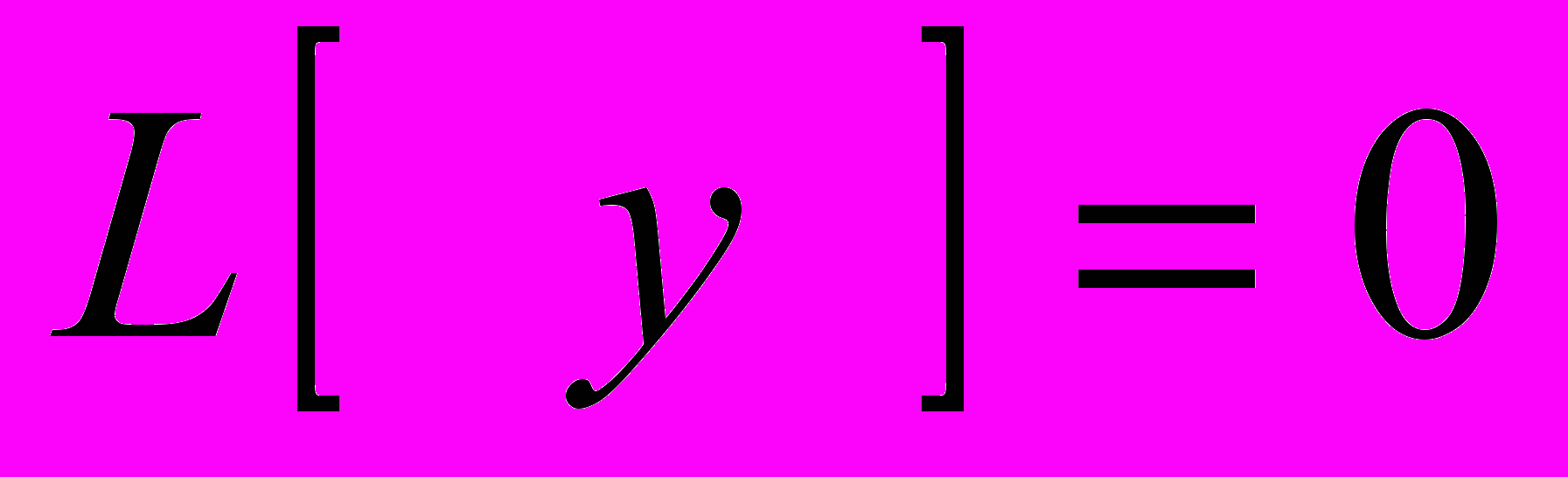(2^/)


ЛИНЕЙНЫЙ Д. ОПЕРАТОР КАЖДОЙ Ф-ИИ 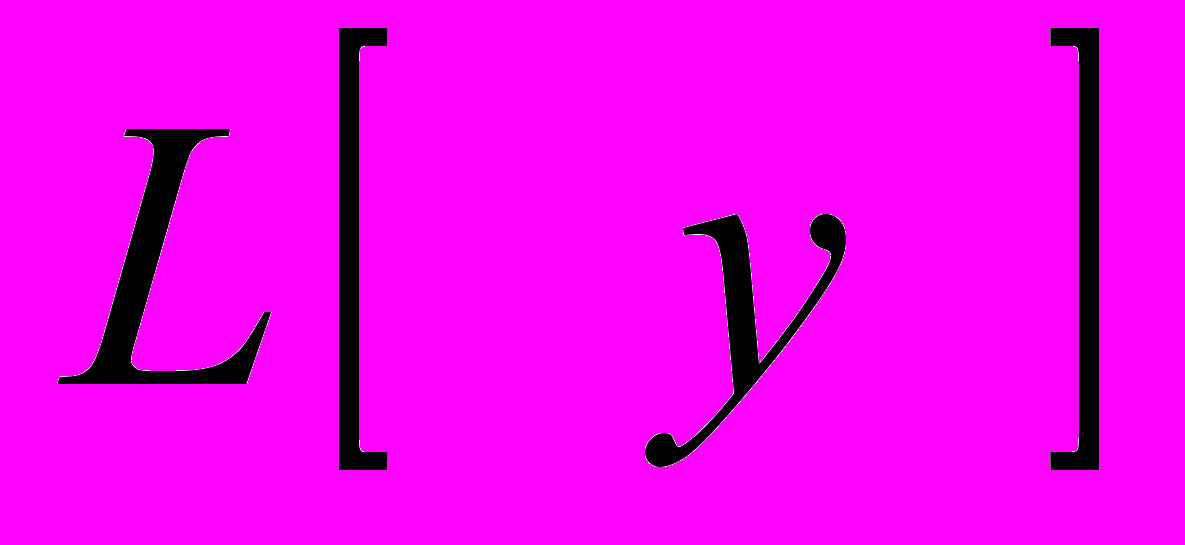СТАВИТ В СООТВЕТСТВИЕ НЕКОТОРУЮ ДРУГУЮ ФУНКЦИЮ.


^ НАПОМНИМ СЛЕДУЮщЕЕ ПОНЯТИЕ.

ГОВОРЯТ, ЧТО НА МНОЖЕСТВЕ 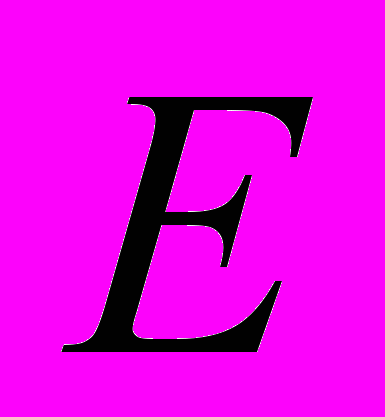ЗАДАН ОПЕРАТОР СО ЗНАЧЕНИЯ­МИ В МНОЖЕСТВЕ , ЕСЛИ КАЖДОМУ ЭЛЕМЕНТУ 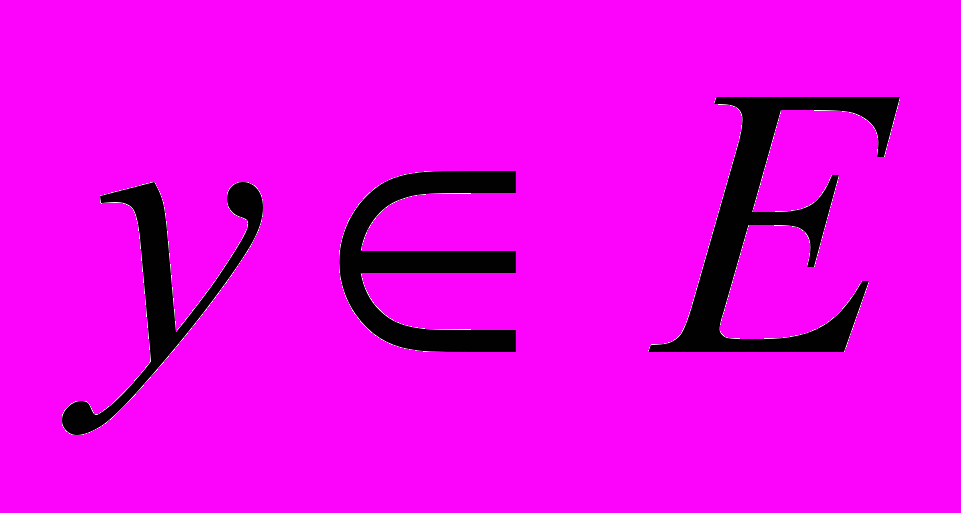ПО НЕКОТОРОМУ ЗАКОНУ ПОСТАВЛЕН В СООТВЕТСТВИЕ ОПРЕДЕЛЕННЫЙ ЭЛЕМЕНТ 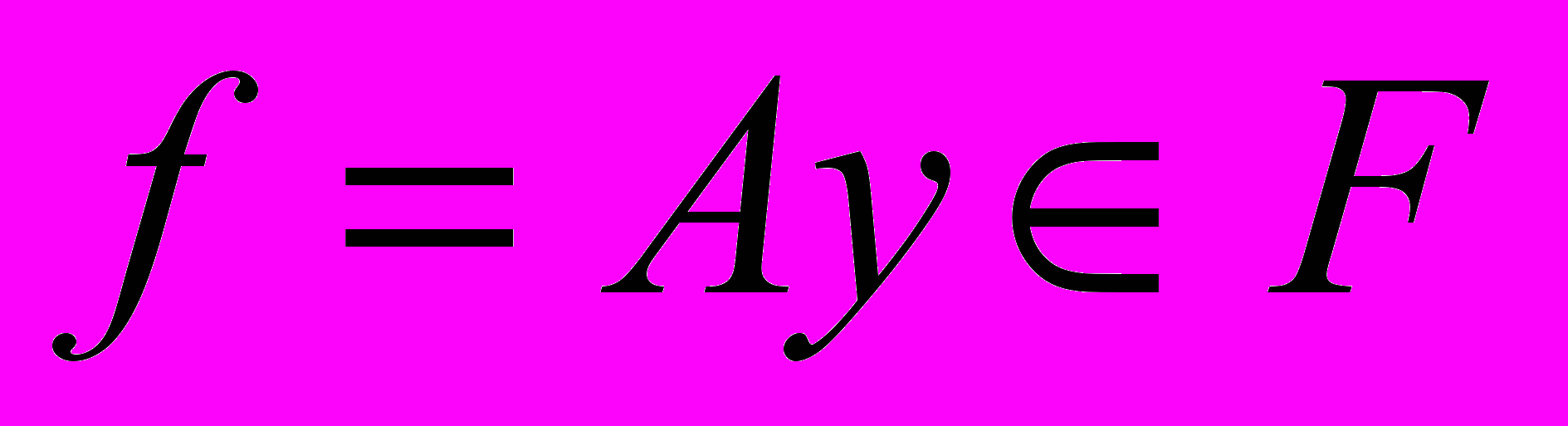. МНОЖЕСТВО 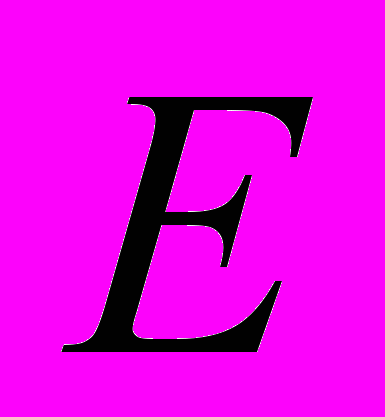НАЗЫВАЮТ ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ ОПЕРАТОРА .


ПУСТЬ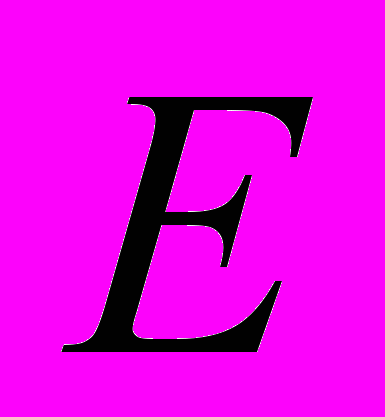- ЛИНЕЙНОЕ ПРОСТРАНСТВО. ОПЕРАТОР , ЗАДАННЫЙ НА 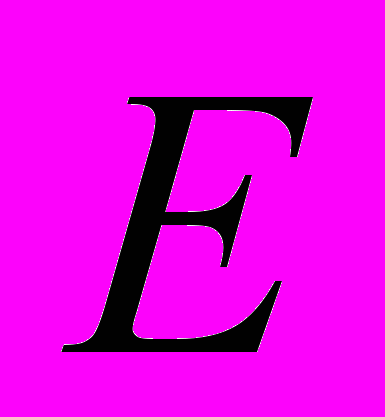НАЗЫВАЕТСЯ ЛИНЕЙНЫМ, ЕСЛИ ОН АДДИТИВЕН И ОДНОРОДЕН, Т.Е.

1) ,


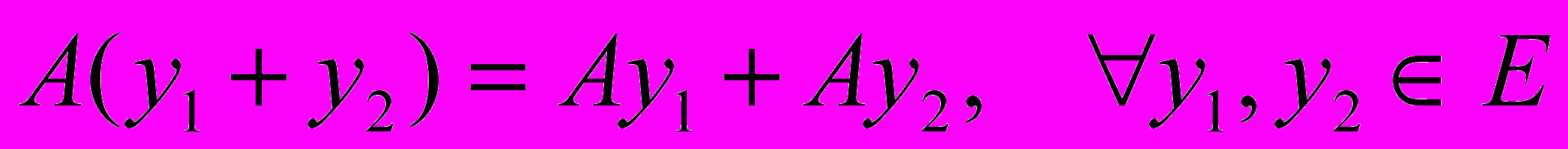2) 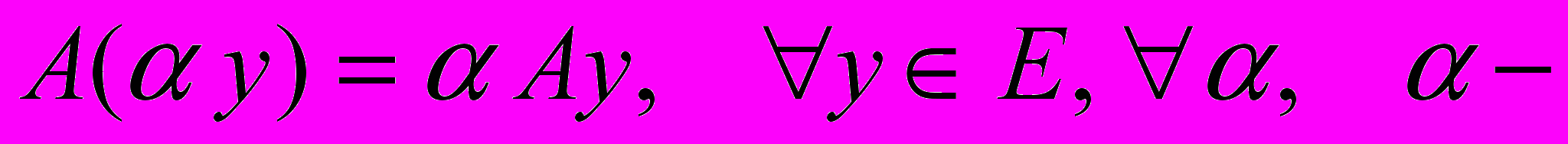ЧИСЛО.


пример.


.


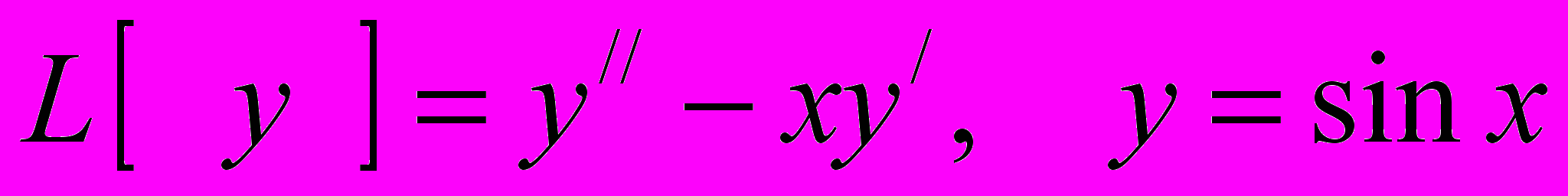
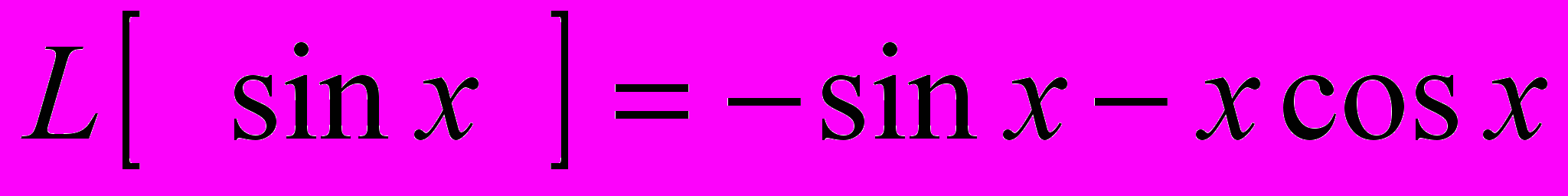Свойства решений однородного ур-ния

ТЕОРЕМА 1. ЕСЛИ 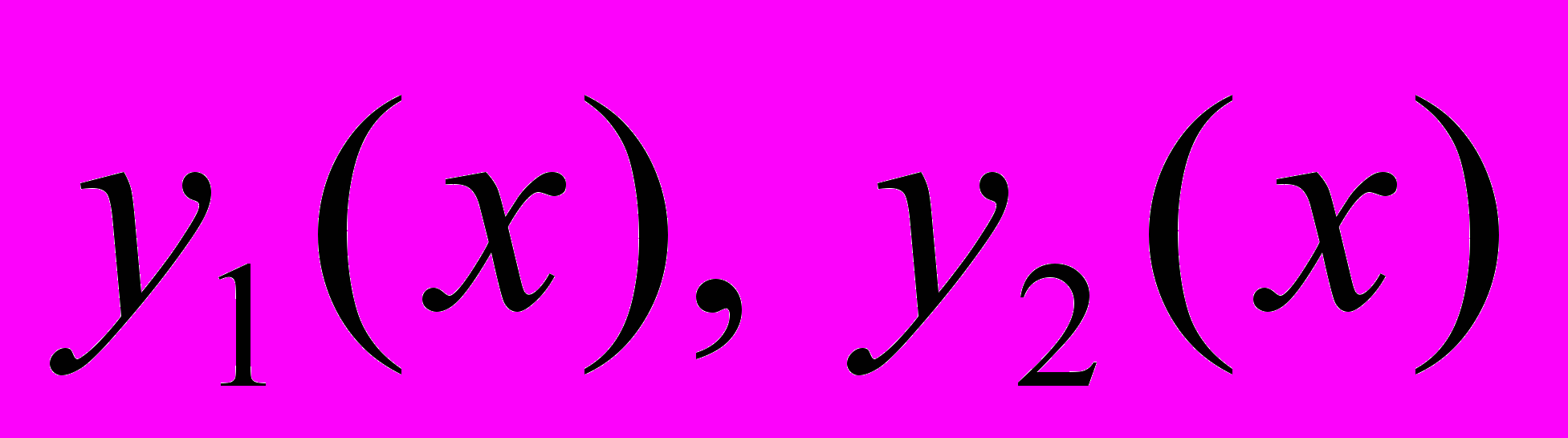РЕШЕНИЯ (2),

ТО 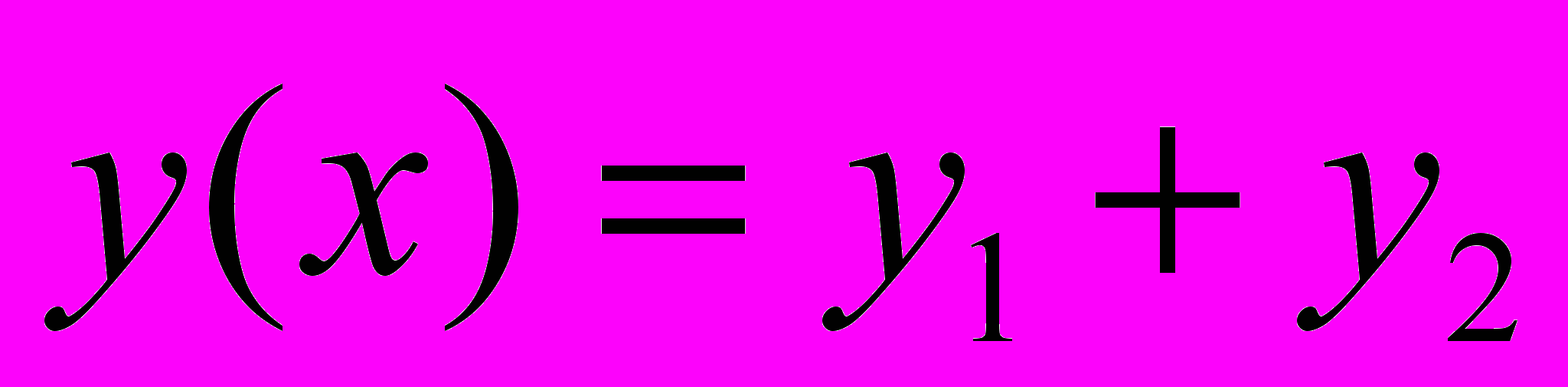- ТАКЖЕ БУДЕТ РЕШЕНИЕМ (2).


ДОК-ВО: ЗАМЕТИМ, ЧТО

.

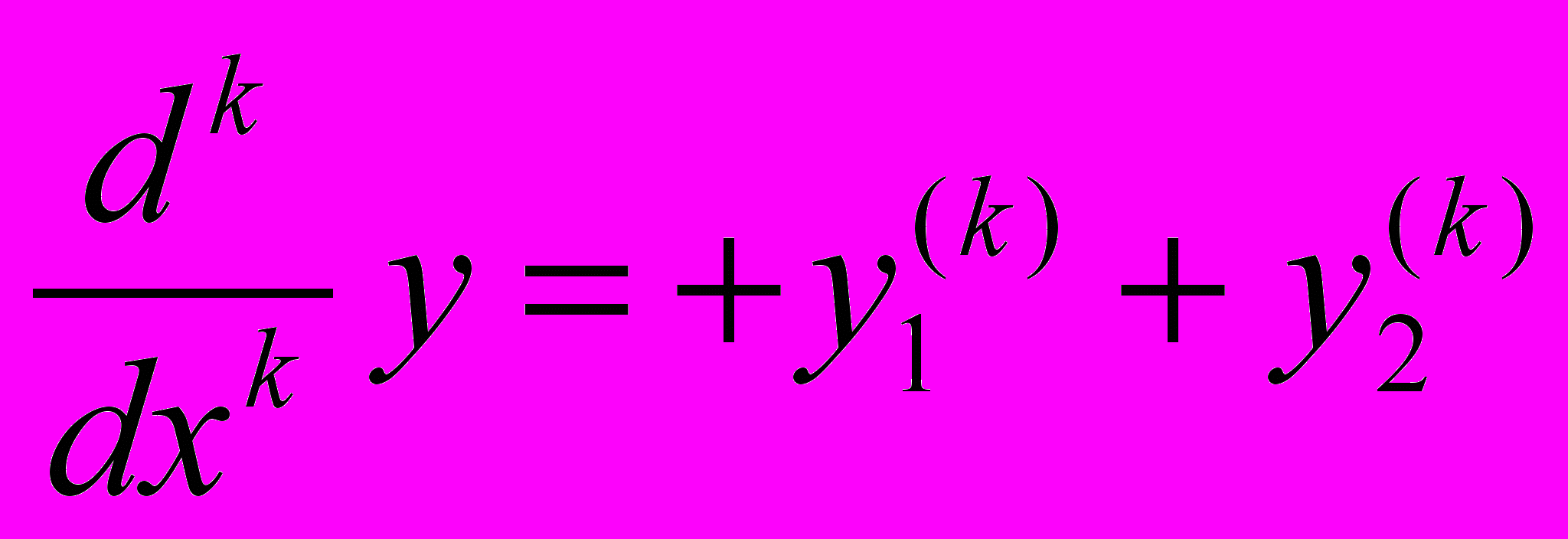тогда

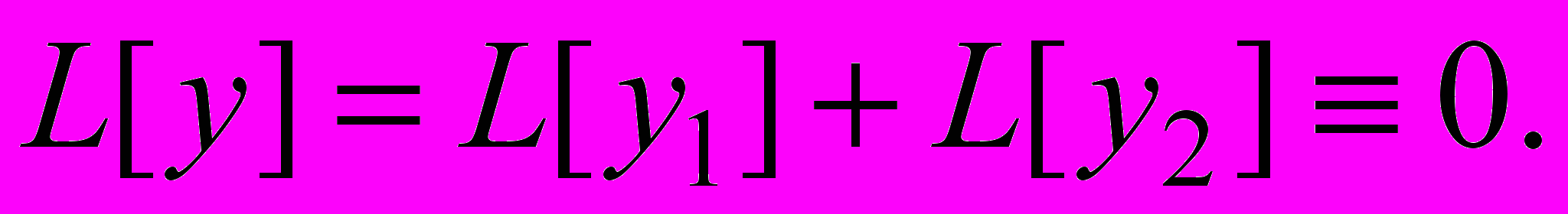
ТЕОРЕМА 2. ЕСЛИ 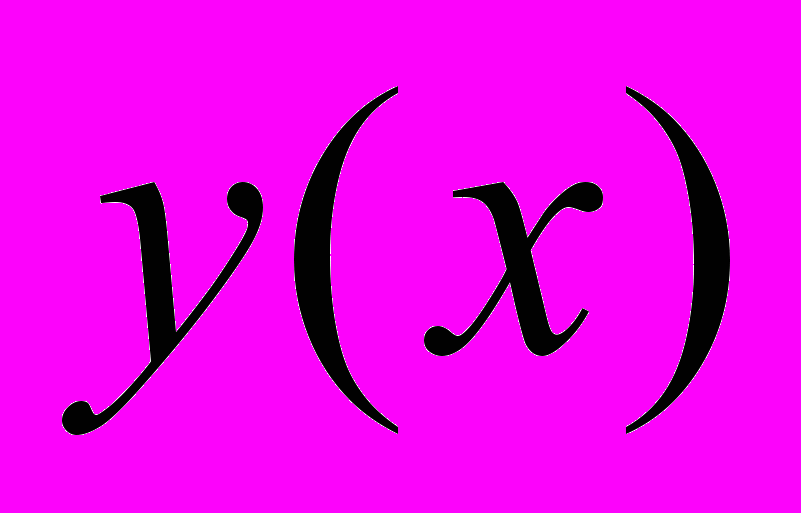РЕШЕНИЕ (2), ТО

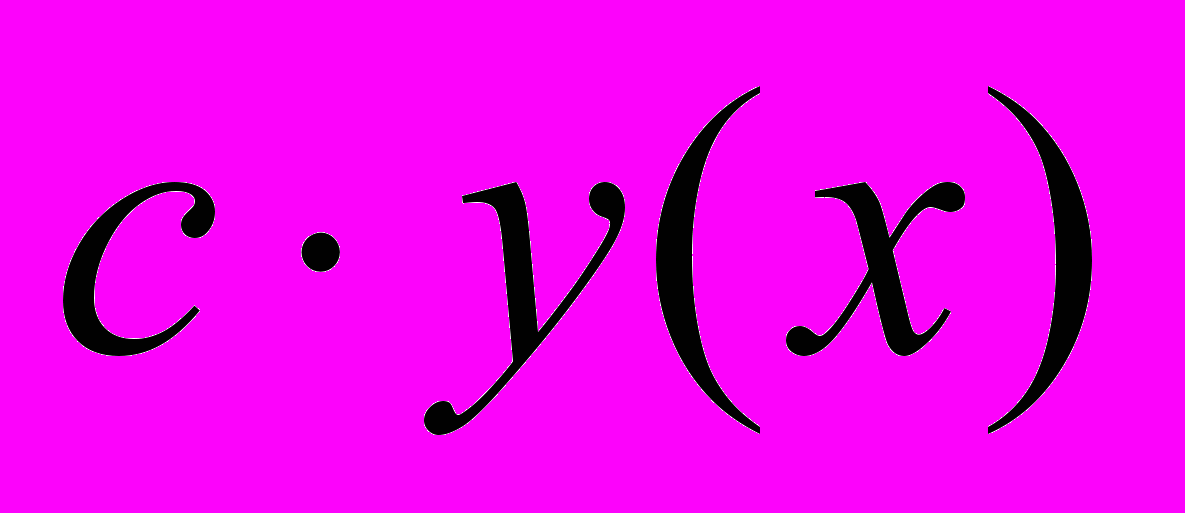, ГДЕ 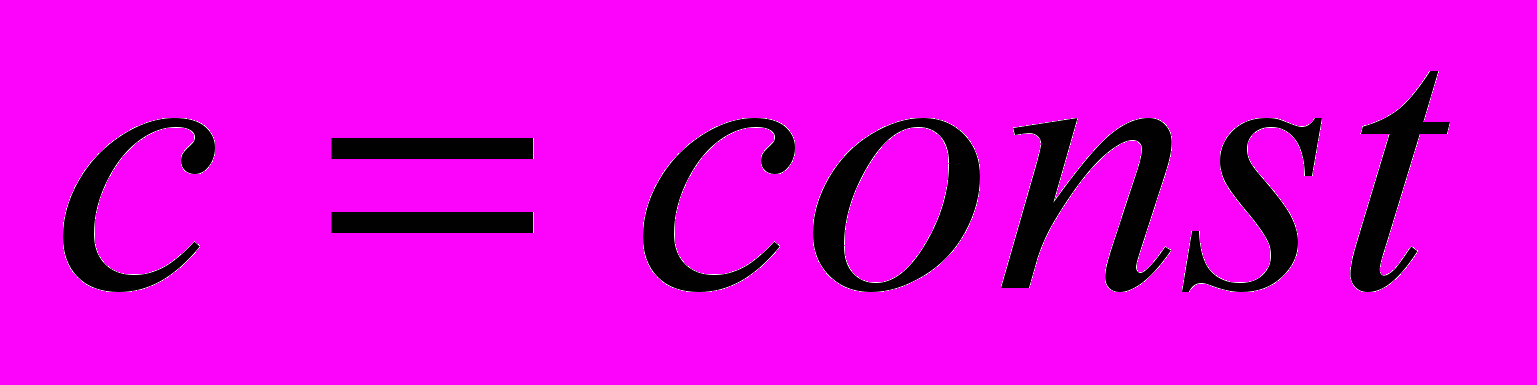- также БУДЕТ РЕШЕНИЕМ.


ДОК-ВО: ЗАМЕТИМ, ЧТО





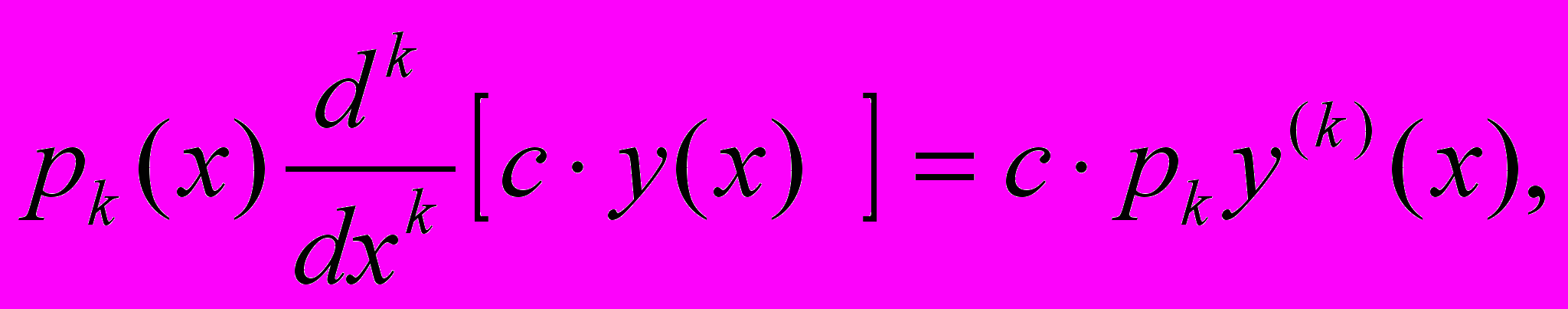
Тогда


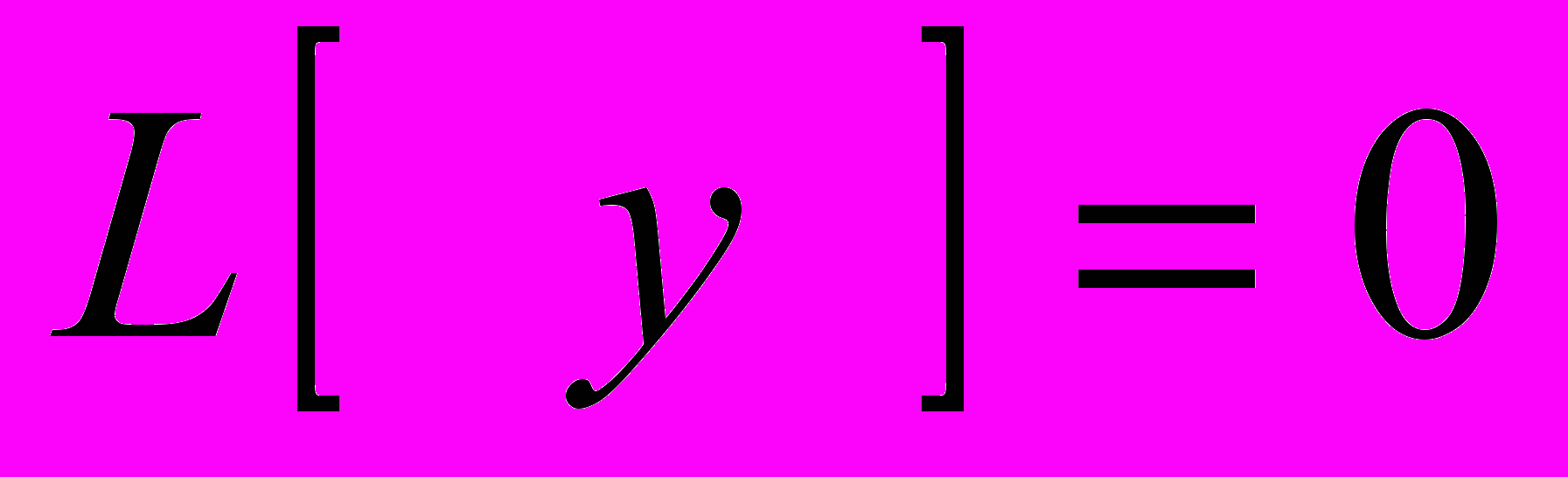
ЭТИ ДВА СВОЙСТВА И ЕСТЬ ПО ОПРЕДЕЛЕНИЮ СВОЙСТВА ЛИНЕЙНОСТИ.


В ИТОГЕ, ЕСЛИ 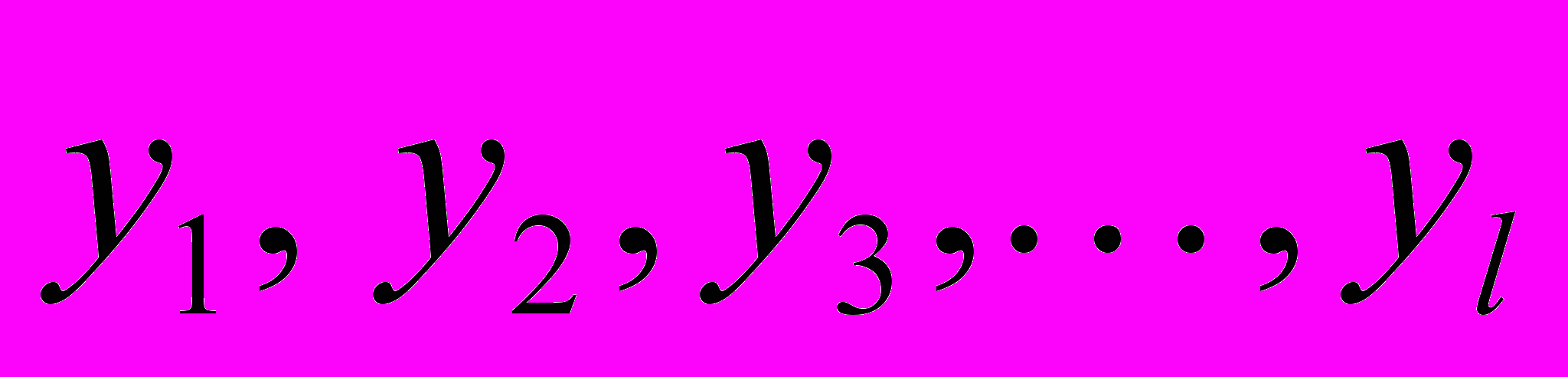РЕШЕНИЯ (2), ТО

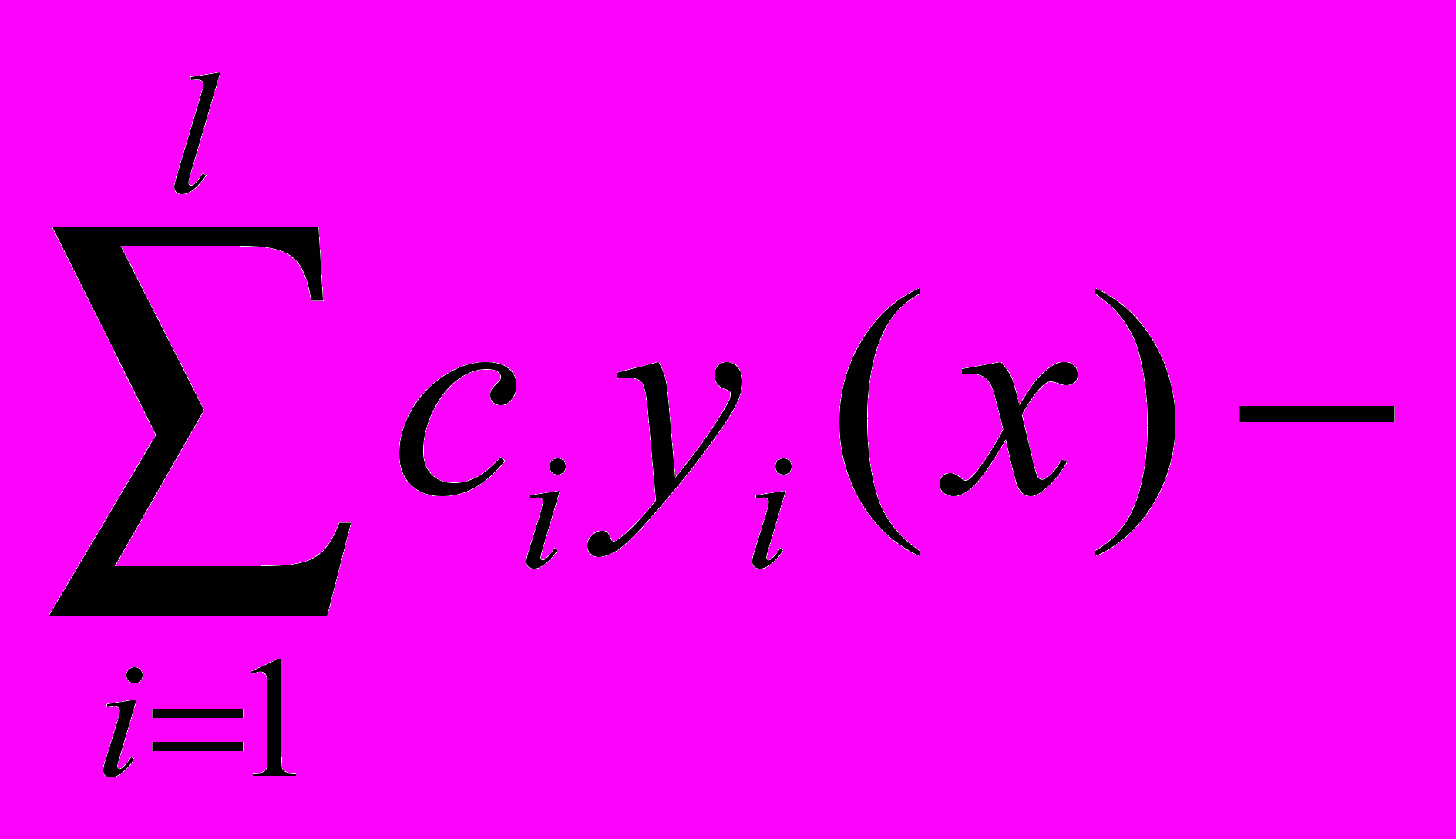ТАКЖЕ БУДЕТ РЕШЕНИЕМ (2):

.


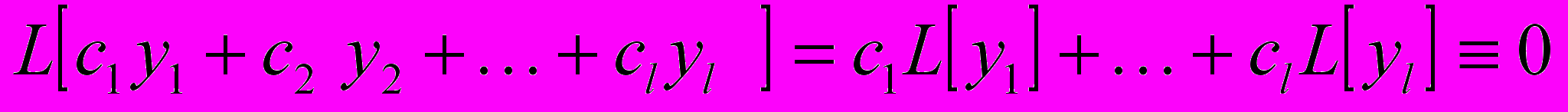теорема 3. если л.о.д.у.

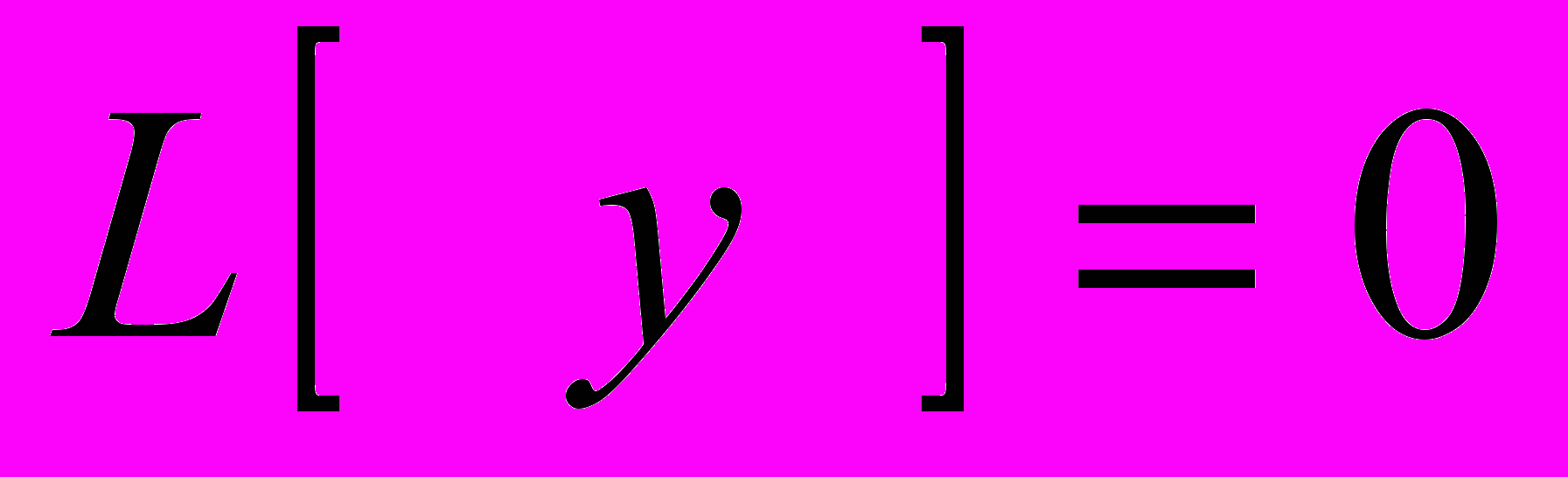
С ДЕЙСТВИТЕЛЬНЫМИ КОЭФФИЦИ­ЕНТАМИ



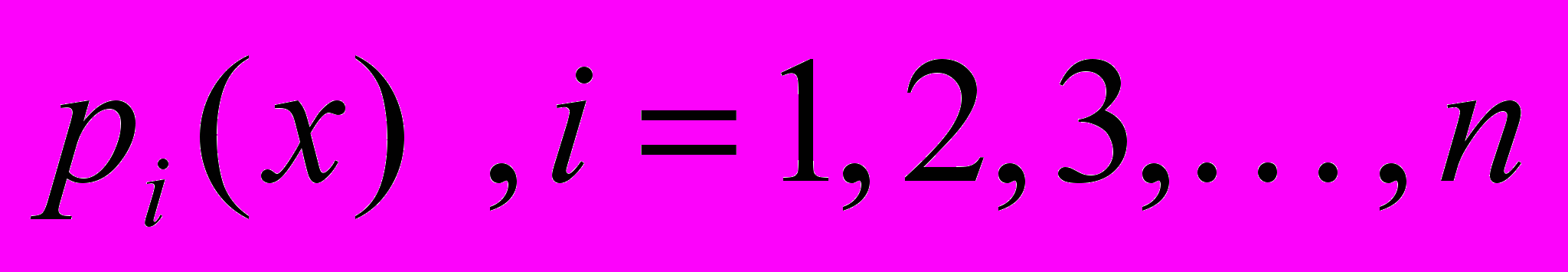
ИМЕЕТ КОМПЛЕКСНОЕ РЕШЕНИЕ

,


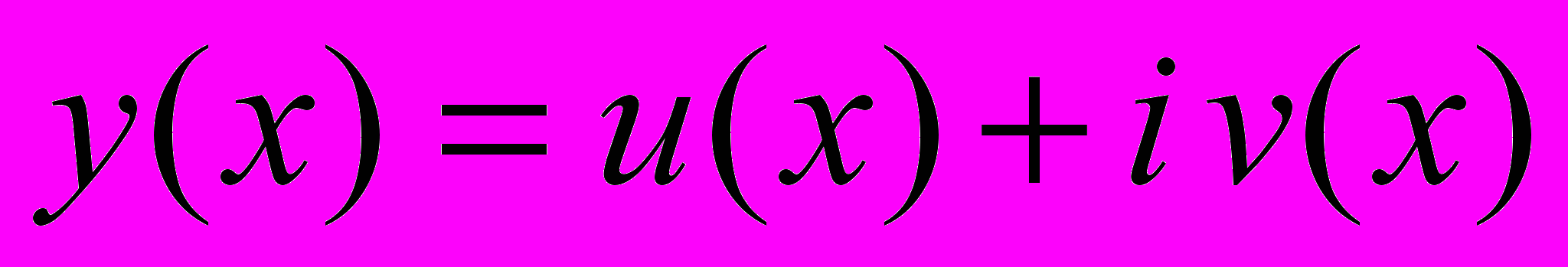ТО ДЕЙСТВИТЕЛЬНАЯ ЧАСТЬ ЭТОГО РЕШЕНИЯ 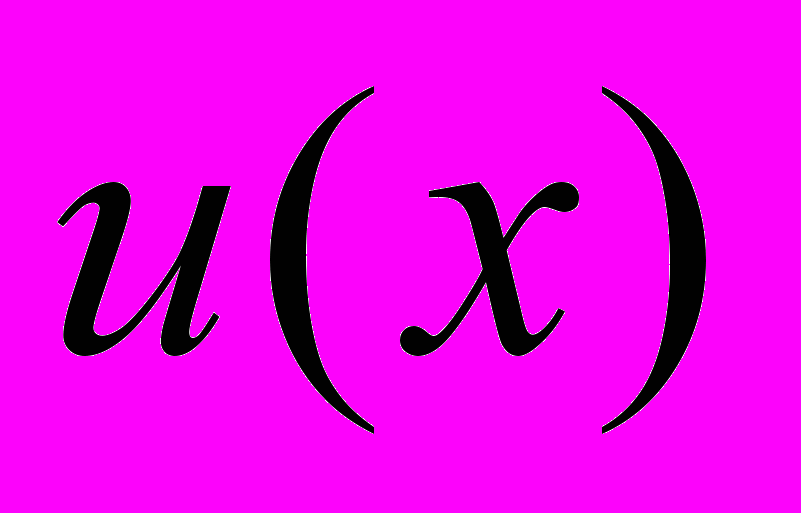И ЕГО МНИМАЯ ЧАСТЬ 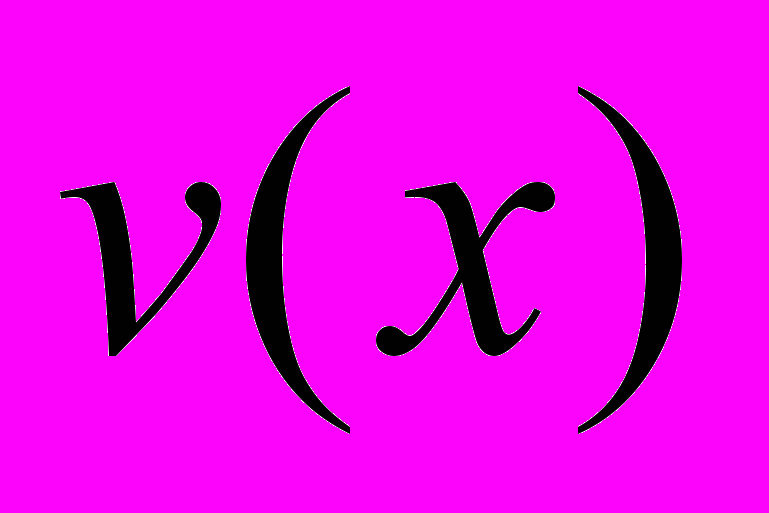В ОТДЕЛЬНОСТИ ЯВЛЯЮТСЯ РЕШЕНИЯМИ ТОГО ЖЕ ОДНОРОДНО­ГО УРАВНЕНИЯ.

док-во: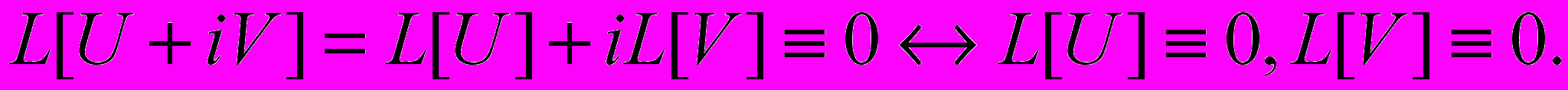

ТЕОРЕМА 4. ЕСЛИ Л.Д.У. 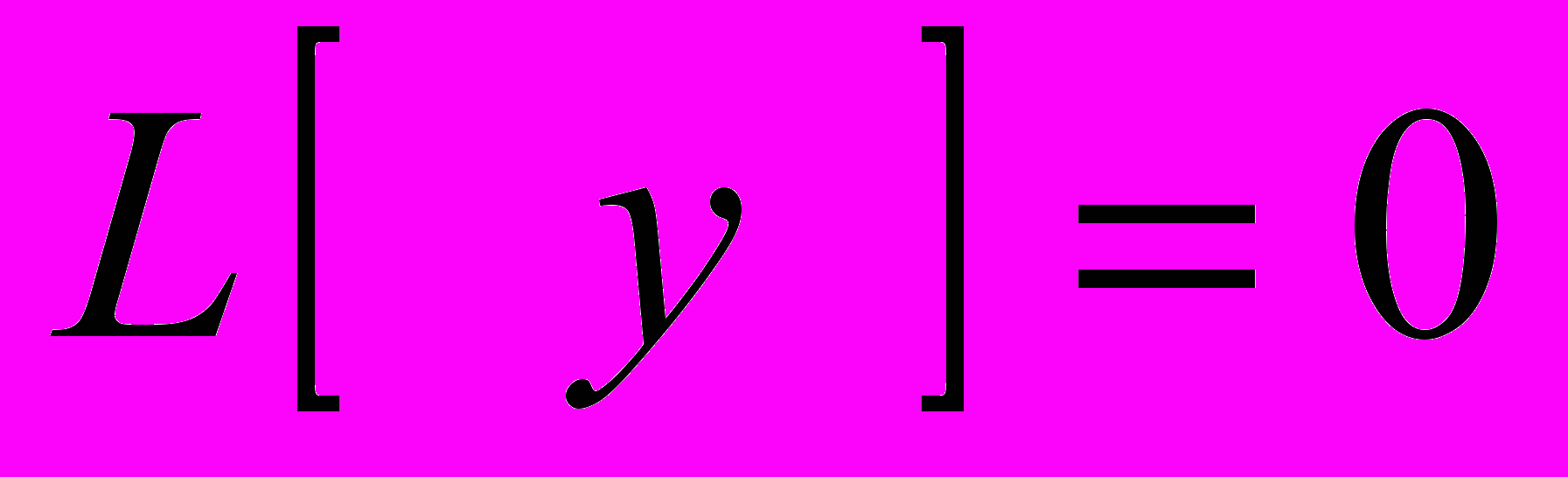ИМЕЕТ РЕШЕНИЕМ КОМПЛЕКСНУЮ ФункцИЮ 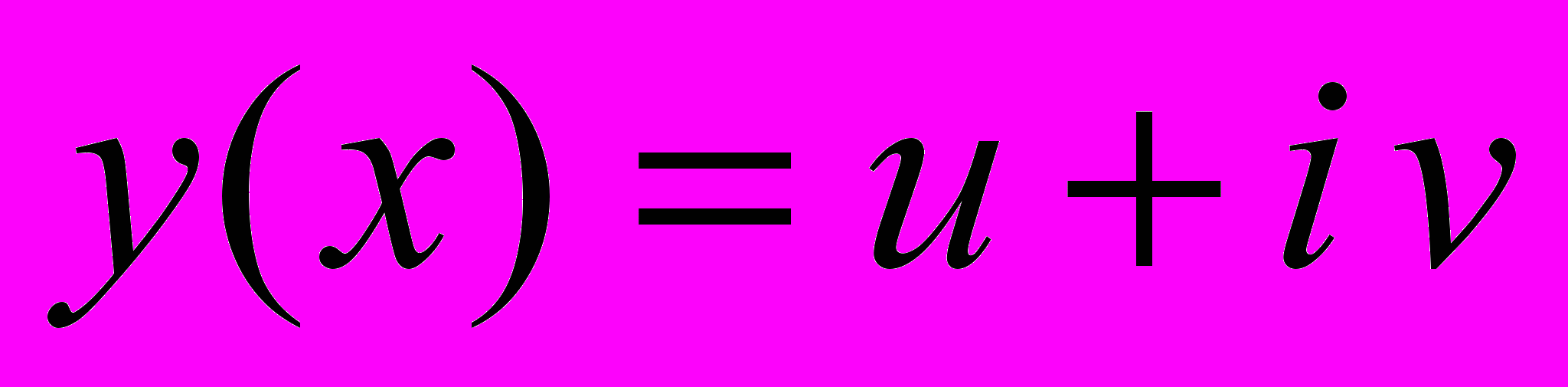, ТО КОМПЛЕКСНО-СОПРЯЖЕННАЯ ФункцИЯ 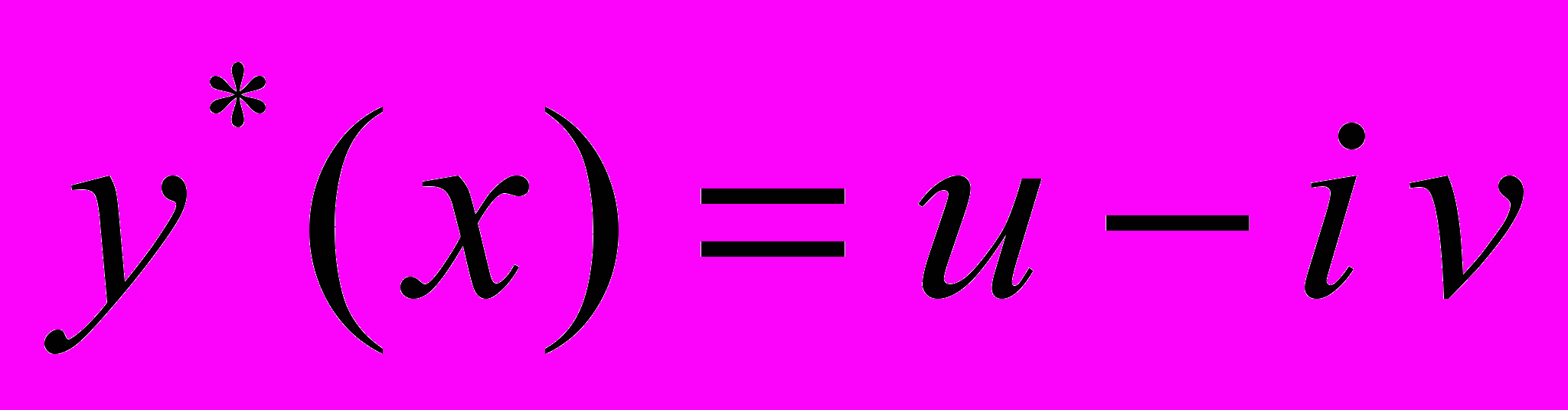ТОЖЕ РЕШЕНИЕ .


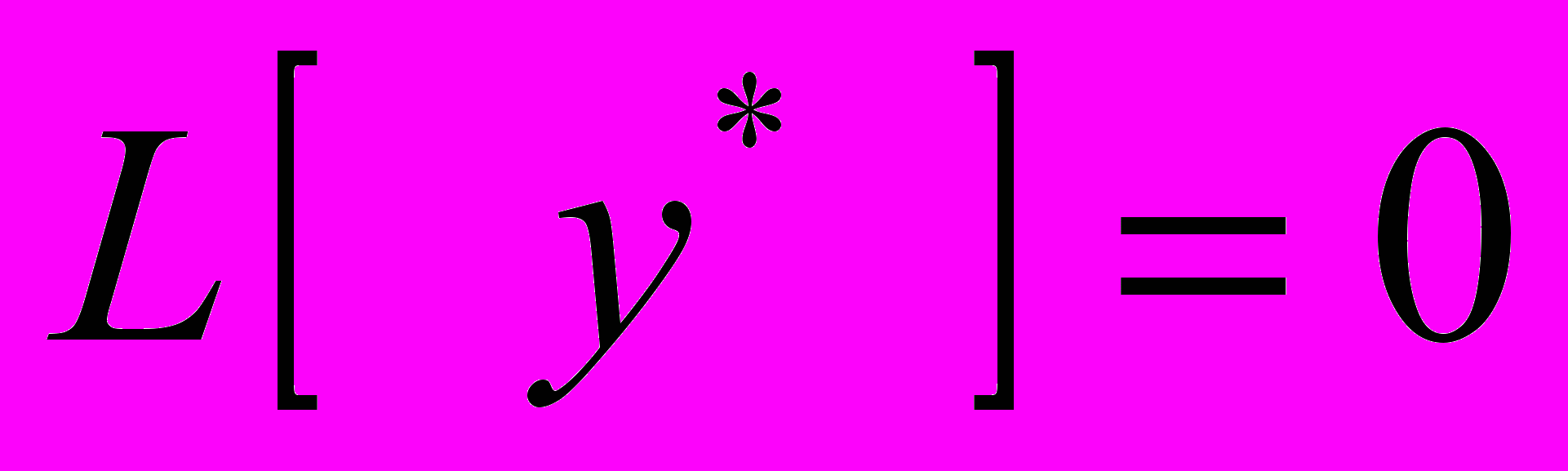Т.Е. ЕСЛИ 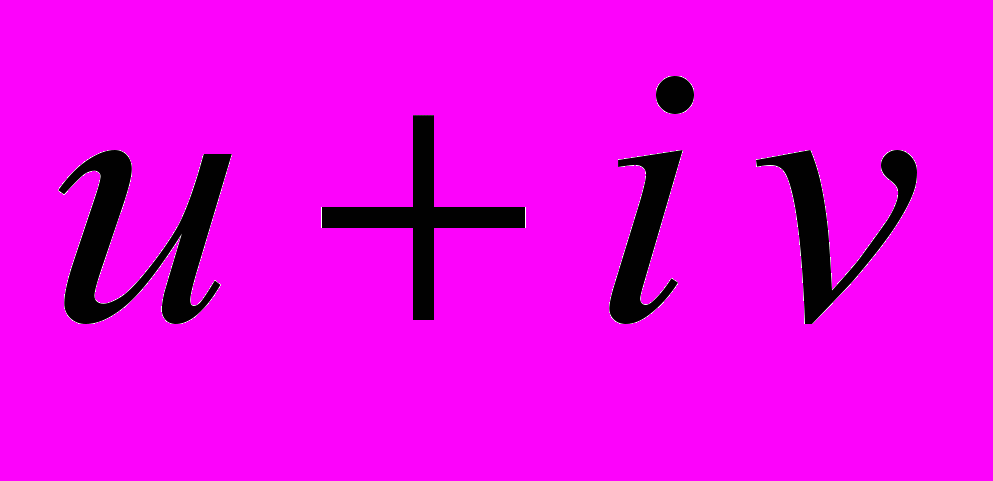РЕШЕНИЕ, ТО АВТОМАТИЧЕСКИ ЗНАЕМ ЕЩЕ ОДНО РЕШЕНИЕ 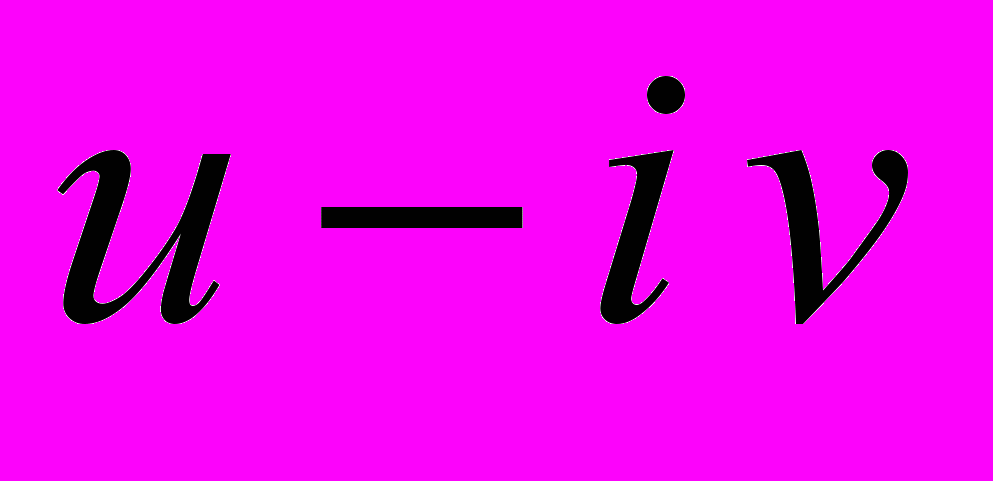ИЛИ ДВА ВЕЩЕСТВЕННЫХ РЕШЕНИЯ 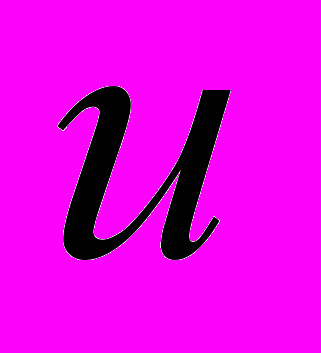И .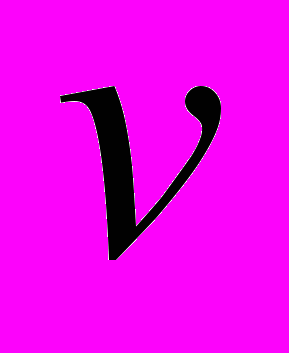


§ 4. ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ФУНКЦИЙ


ОПР. 1. БУДЕМ ГОВОРИТЬ, ЧТО Ф-ИИ



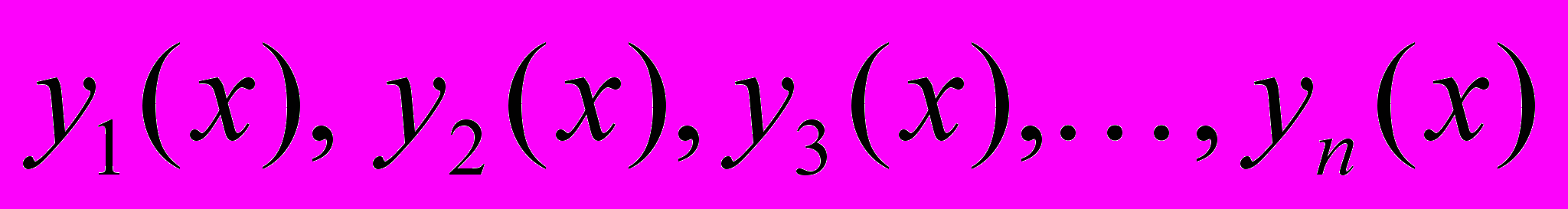
ЛИНЕЙНО ЗАВИСИМЫ НА ИНТЕРВАЛЕ

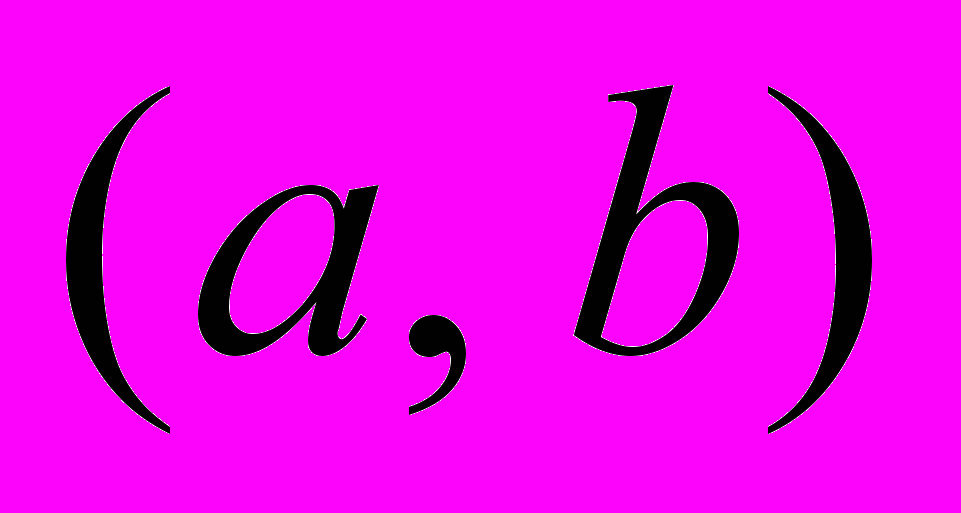, ЕСЛИ СУЩЕСТВУЮТ ПОСТОЯННЫЕ 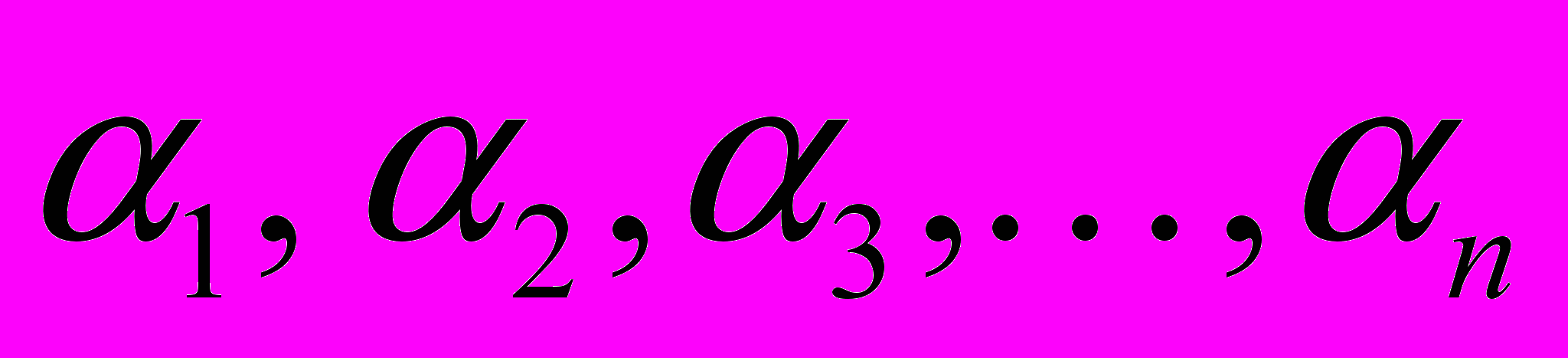- ТАКИЕ, ЧТО НА ЭТОМ ИНТЕРВАЛЕ ВЫПОЛНЯЕТСЯ ТОЖДЕСТВО ПО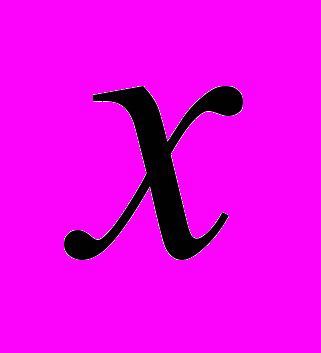


, (*)


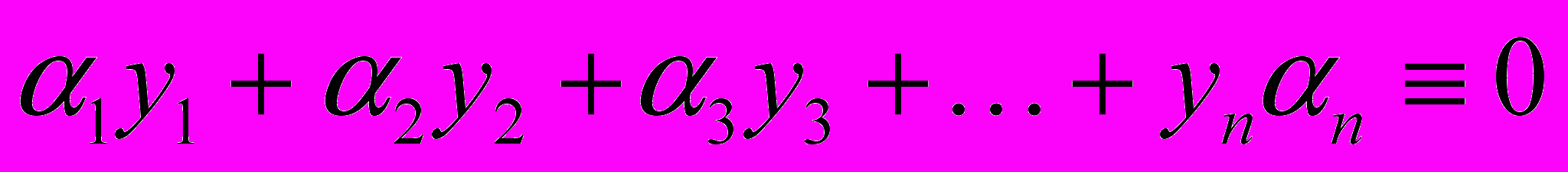ПРИЧЕМ ХОТЯБЫ ОДНО ИЗ ЧИСЕЛ ОТЛиЧНО ОТ НУЛЯ.


НАПРИМЕР, ЕСЛИ 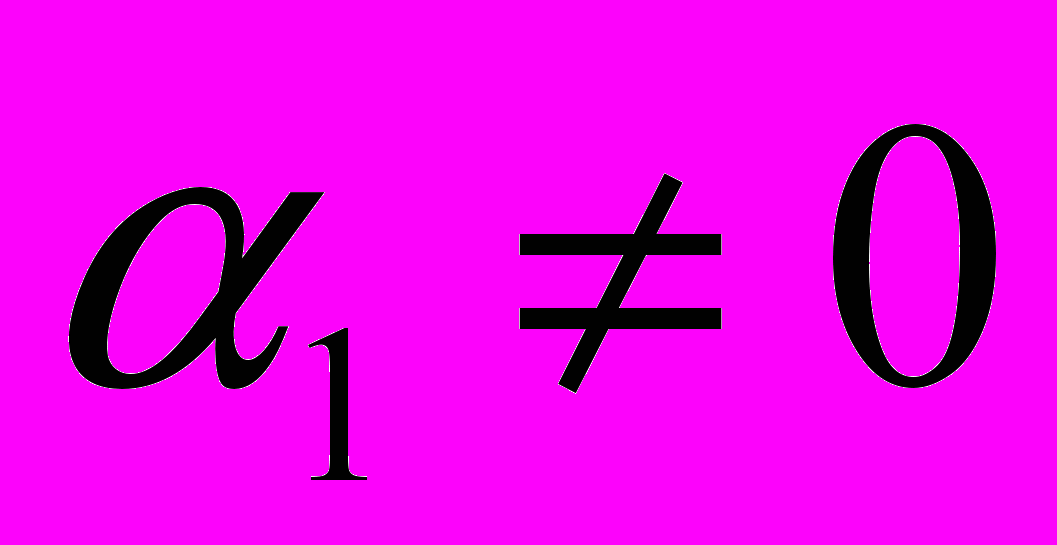, ТО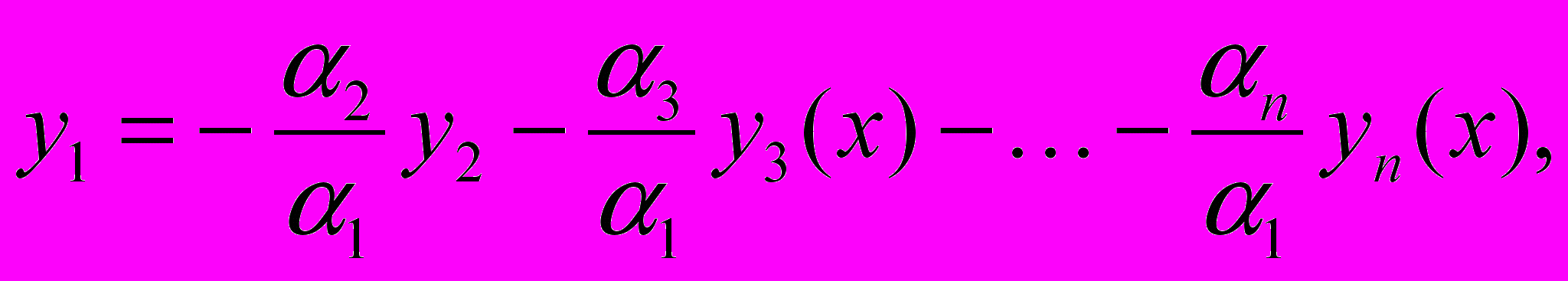



Т.Е. ОДНА ФУНКЦИЯ ВЫРАЖАЕТСЯ ЧЕРЕЗ ДРУГИЕ.


ОПР.2. ЕСЛИ ТОЖДЕСТВО (*) ВЫПОЛ­НЯЕТСЯ НА 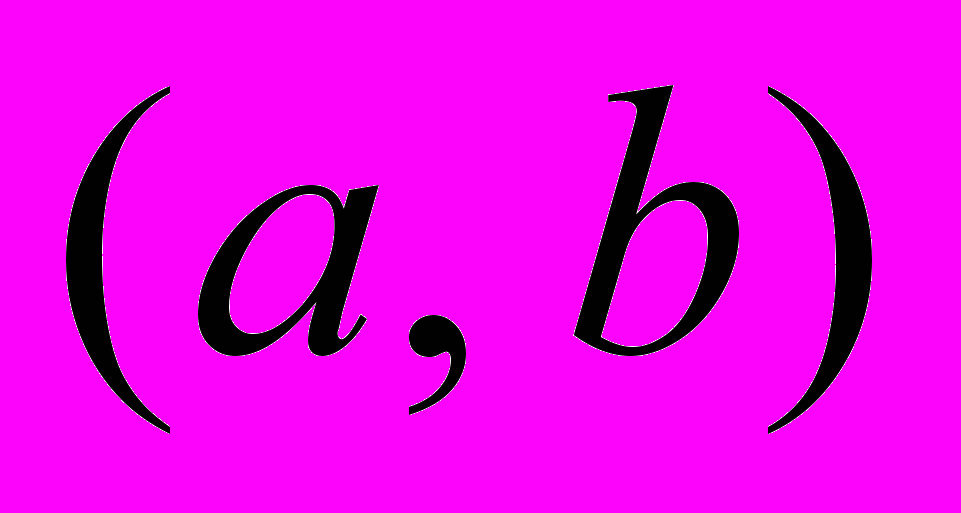ЛИШЬ кОГДА ВСЕ 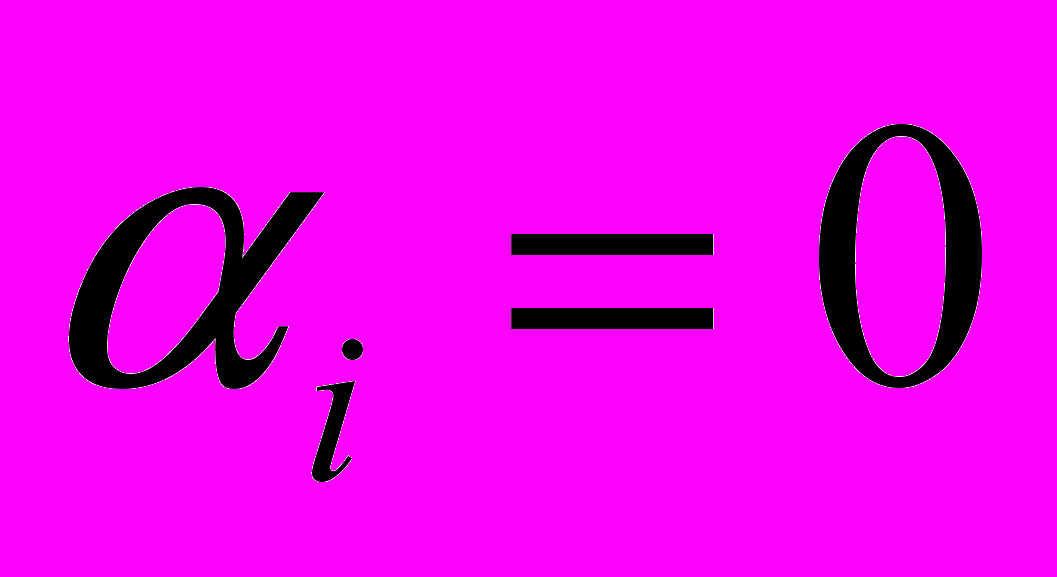, ТОГДА СОВОКУПНОСТЬ Ф-ИЙ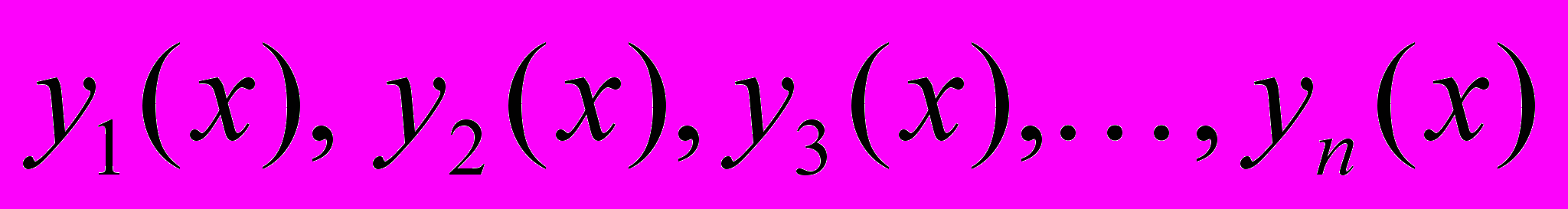



НАЗЫВАЕТСЯ ^ ЛИНЕЙНО НЕЗАВИСиМОЙ НА .


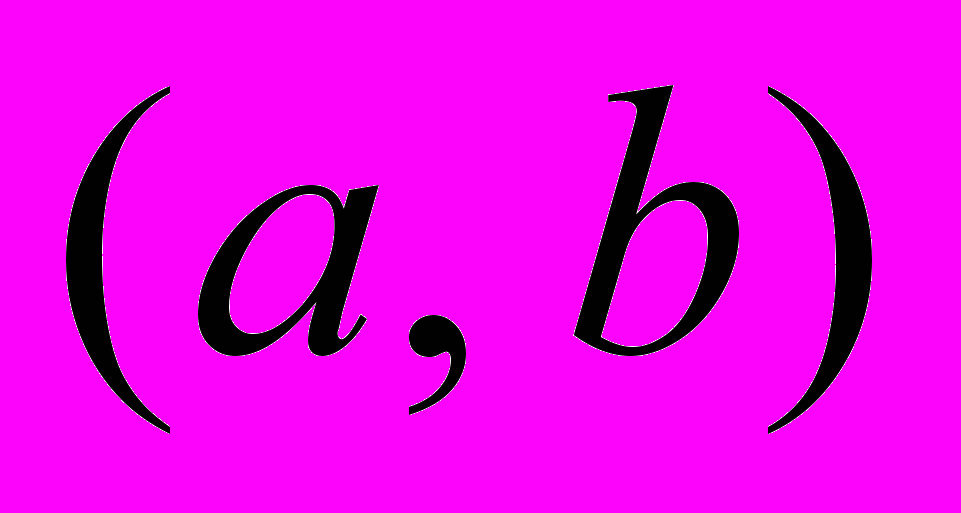ДЛЯ ДВУХ Ф-ИЙ ЛИН. ЗАВИСИМОСТЬ ОЗНАЧАЕТ ПРОПОРЦИОНАЛЬНОСТЬ

.


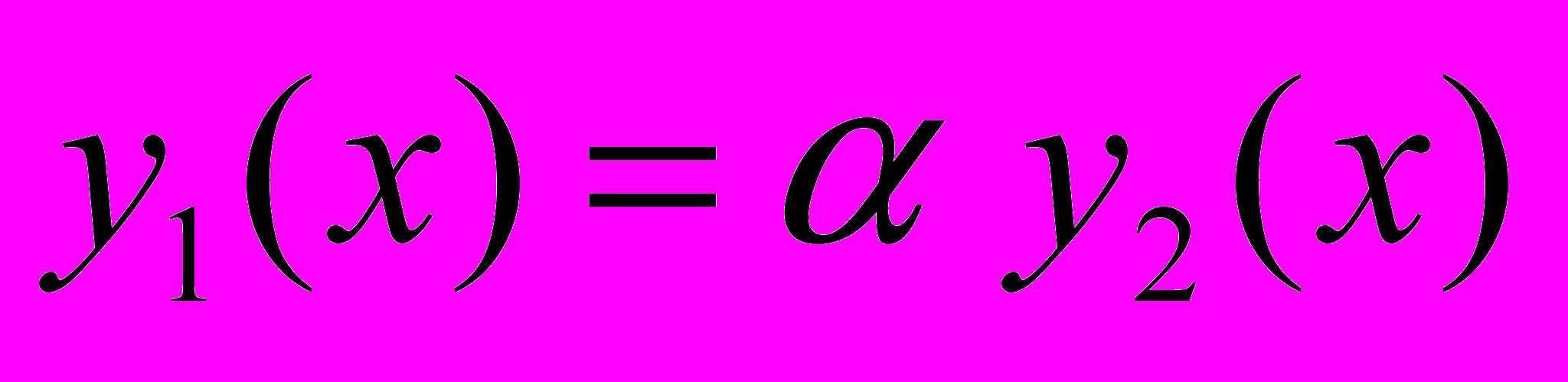В ОБЩЕМ СЛУЧАЕ СОВОКУПНОСТЬ Ф-ИЙ ИССЛЕДУЕТСЯ НА ЛИНЕЙНУЮ ЗАВИСИМОСТЬ С ПОМОЩЬЮ ОПРЕДЕЛИТЕЛЯ ВРОНСКОГО.


( Ю. ВРОНСКИЙ - 1778-1853 -ПОЛЬСКИЙ МАТЕМАТИК И ФИЛОСОФ)


ОПР.З. ПУСТЬ ИМЕЕМ СИСТЕМУ Ф-ИЙ





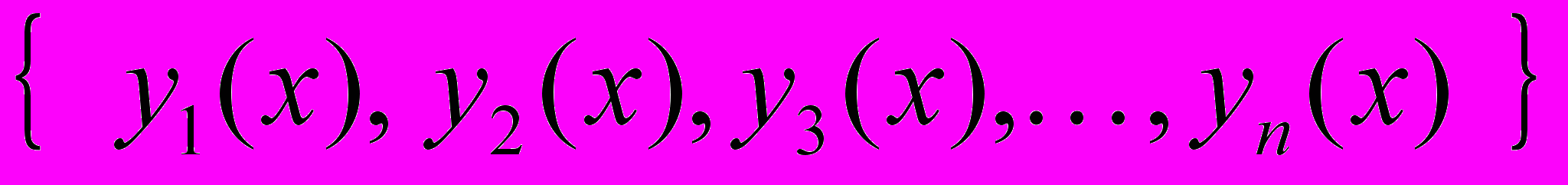
ОПРЕДЕЛЕННЫХ НА ИНТЕРВАЛЕ 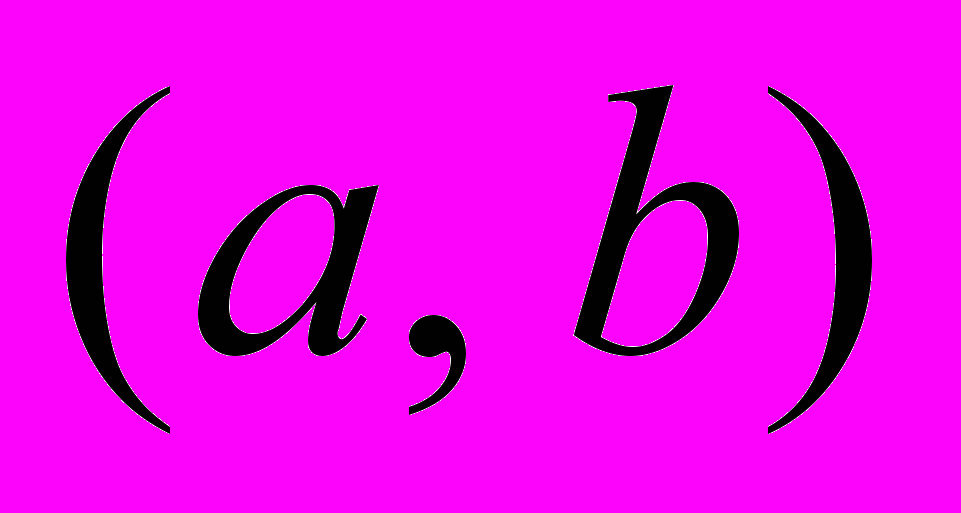ПОСТРОИМ МАТРИЦУ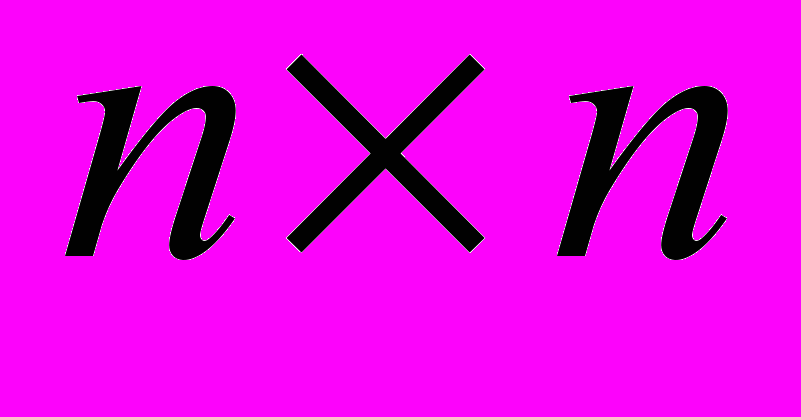




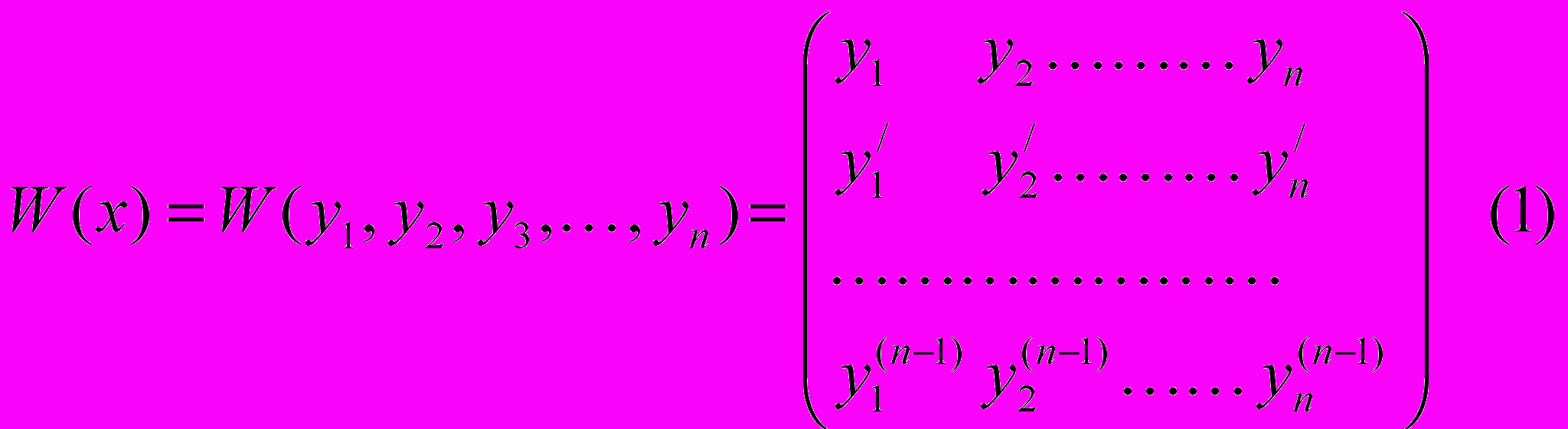
ОПРЕДЕЛИТЕЛЬ ЭТОЙ МАТРИЦЫ НАЗЫВАЕТСЯ ^ ОПРЕДЕЛИТЕЛЕМ ВРОНСКОГО ДЛЯ .


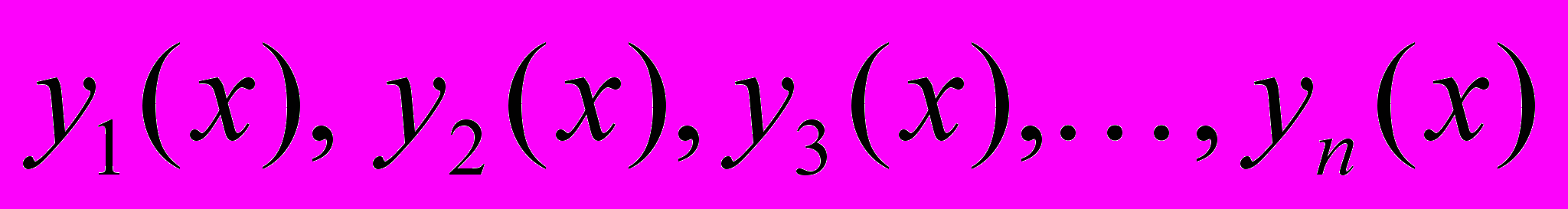ТЕОРЕМА 1 .(НЕОБХОДИМОЕ УСЛОВИЕ ЛИНЕЙНОЙ ЗАВИСИМОСТИ Ф-ИЙ)

ЕСЛИ Ф-ИИ 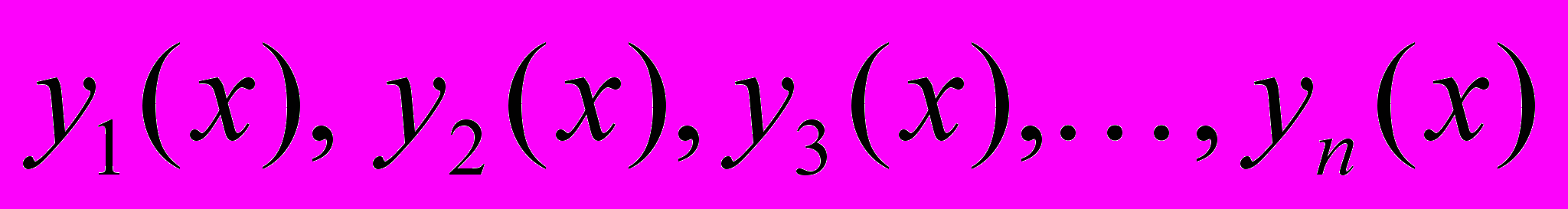, ИМЕЮЩИЕ ПРОИЗВОДНЫЕ ДО ПОЯДКА 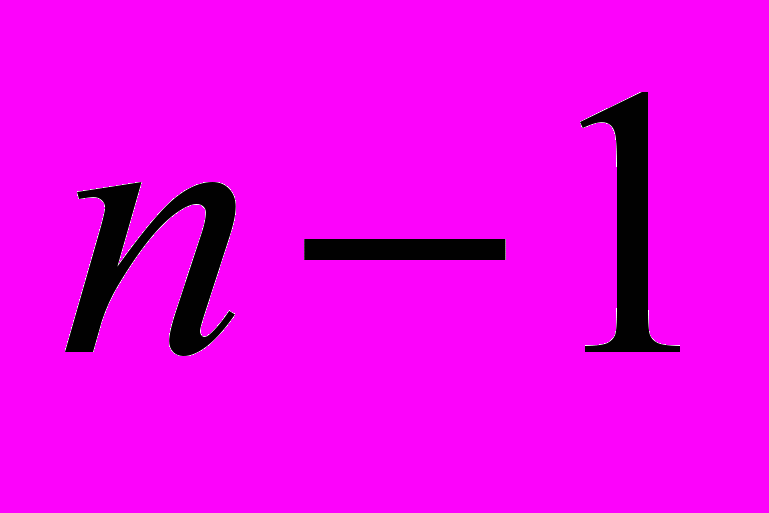- ВКЛЮЧИТЕЛЬНО, ЛИНЕЙНО ЗАВИСИМЫ НА ИНТЕРВАЛЕ 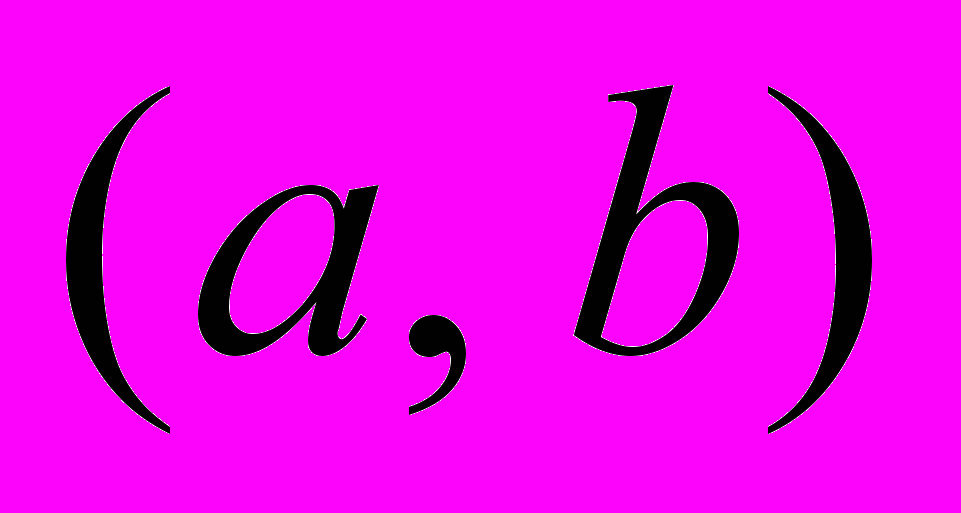, ТО НА ЭТОМ ИНТЕРВАЛЕ ОПРЕДЕЛИТЕЛЬ ВРОНСКОГО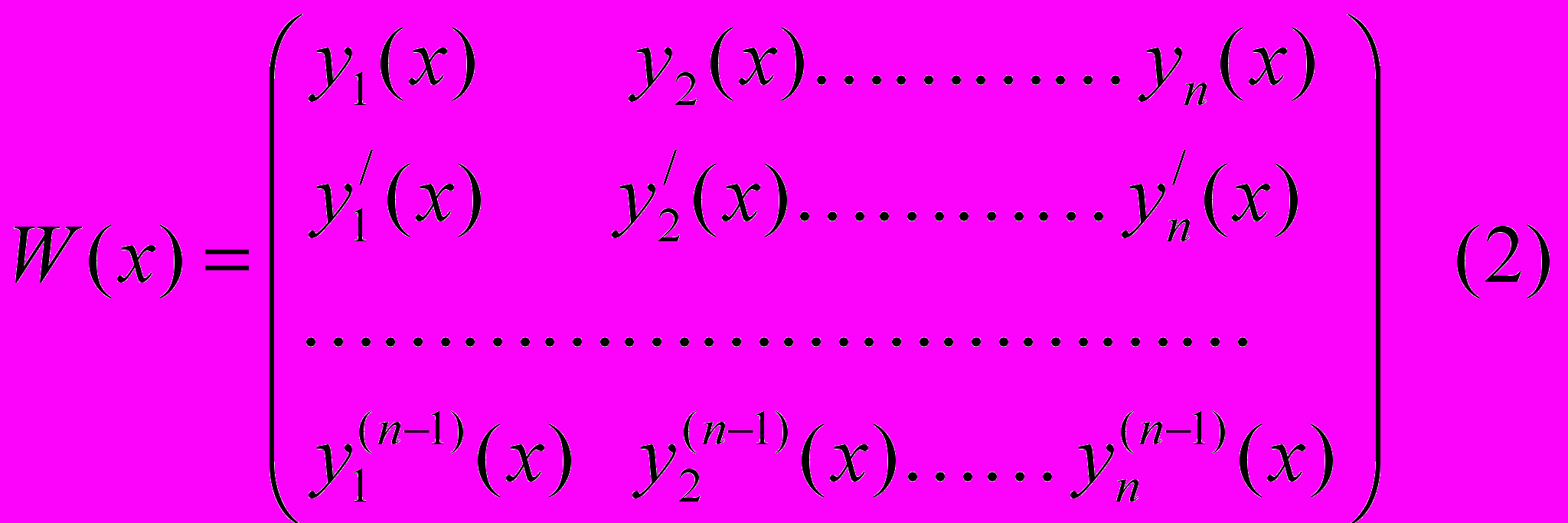





СИСТЕМЫ ФУНКЦИЙ 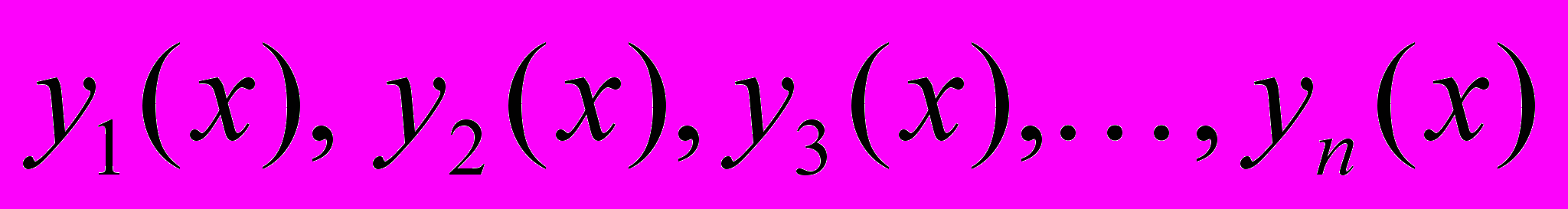, ТОЖДЕСТВЕННО РАВЕН НУЛЮ:


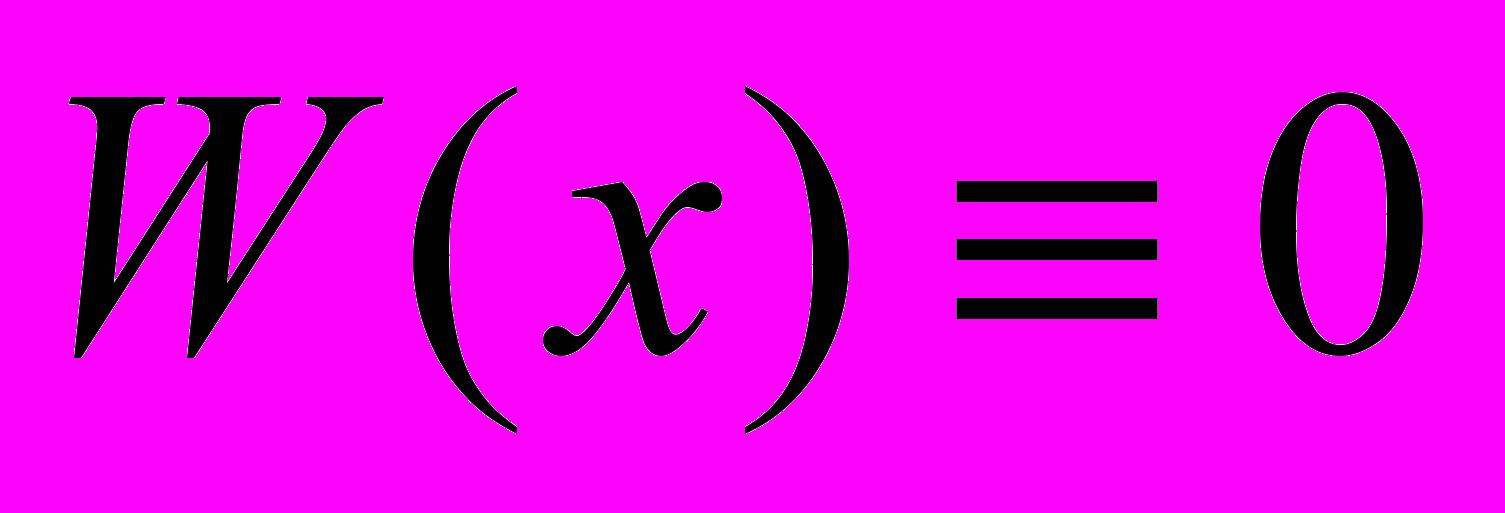НА .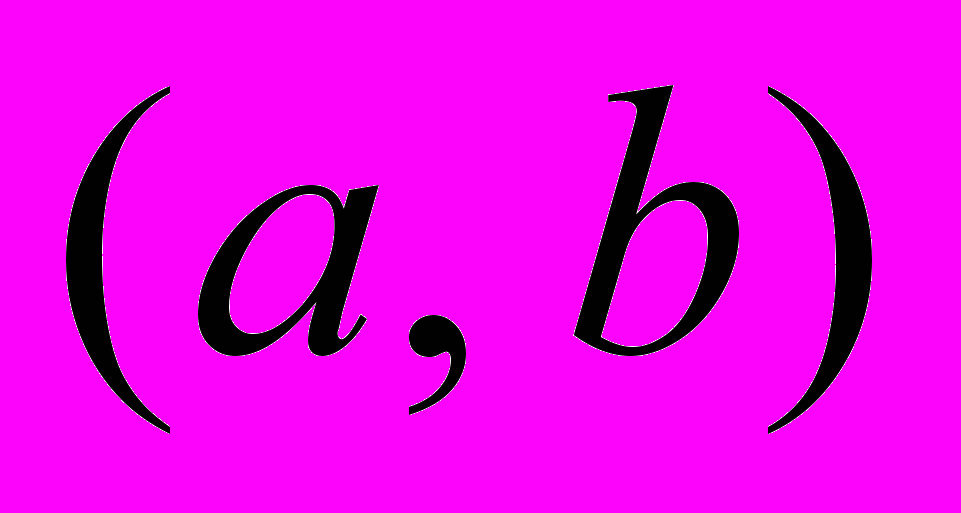


ДОК-ВО:


примеры. 1. дана система функций: 1,x,x²,…,x^n-1.

доказать, что функции линейно-независимы.


2. дана система функций: 1, sin²x, cos²x

доказать, что функции линейно-зависимы.


3. дана система функций: 1, e^x, e^2x,…,e^(n-1)x.

доказать, что функции линейно-независимы.

§ 5. структура общего решения ЛИНЕЙНОго однородного диф-го уравнения 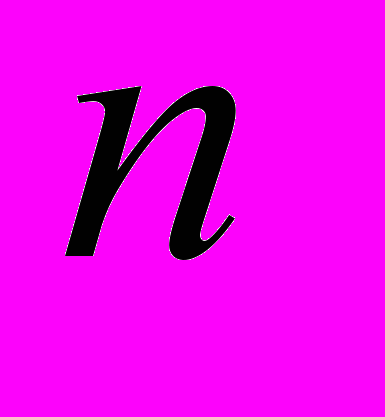-го порядка.


пусть дано л.о.д.у. 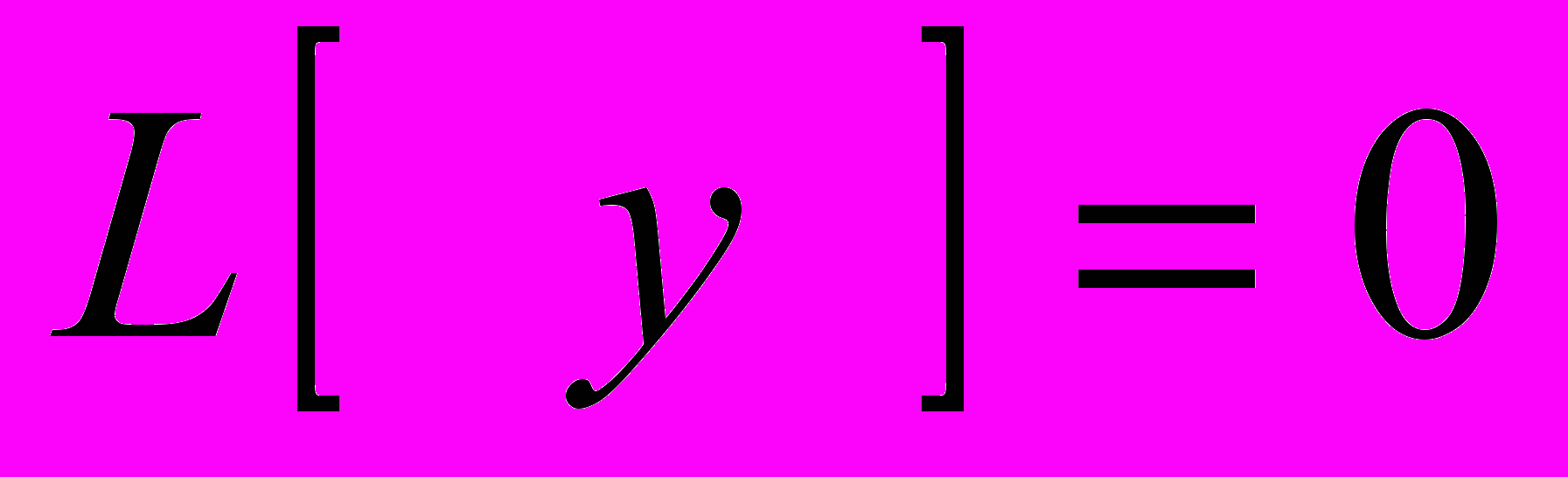. (1)


^ ОПР.1. совокупность 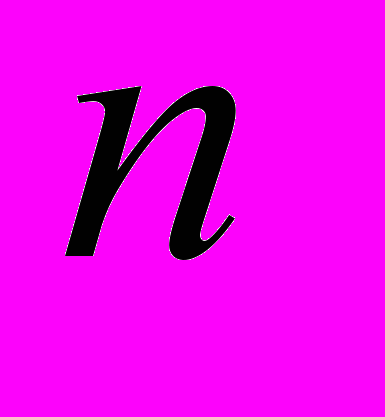линейно-независимых частных решений 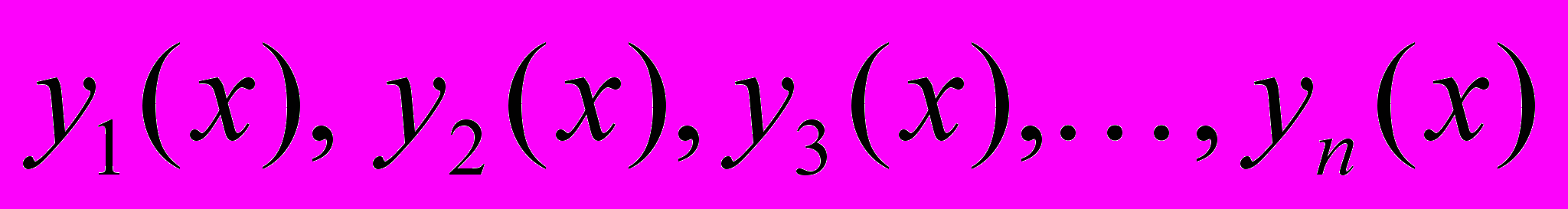уравнения (1) называется фундаментальной системой решений этого уравнения.


Теорема 1. общее решение уравнения (1) –есть линейная комбинация 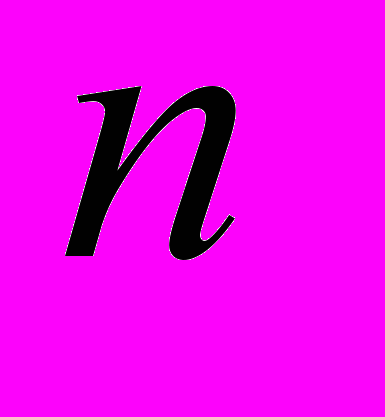линейно-независимых частных решений этого уравнения: 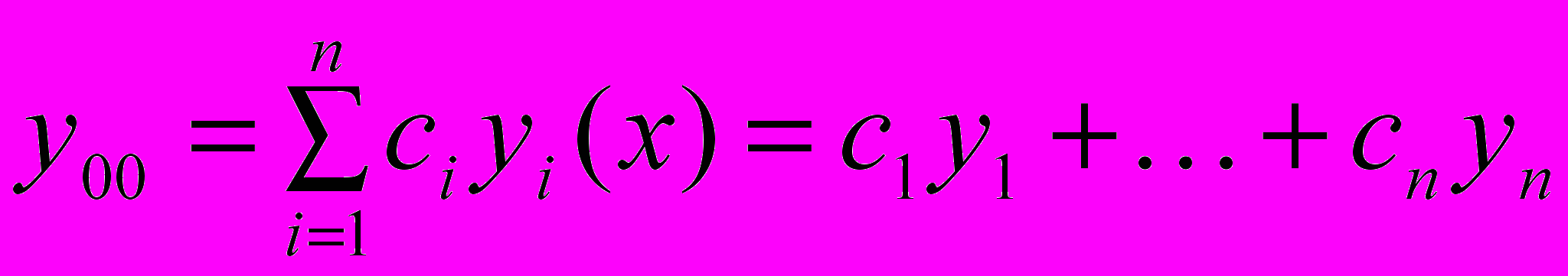(2) , где 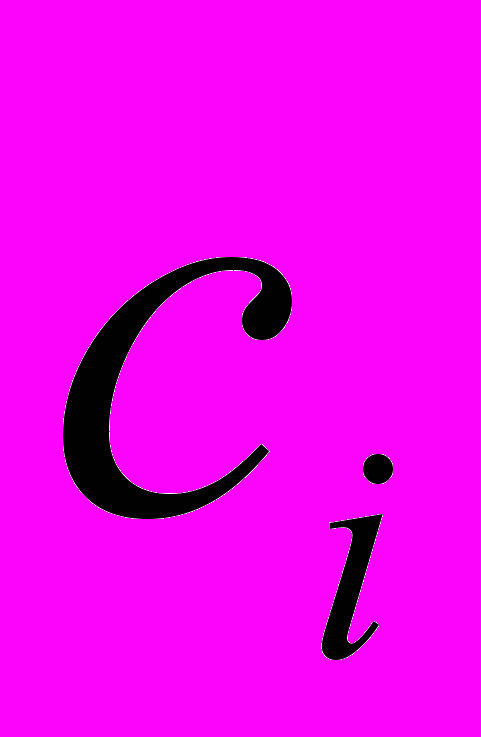произвольные постоянные.


Д-во: