Головоломок вишенка в коктейле
| Вид материала | Документы |
- Психологическое сопровождение замещающих семей, 219.46kb.
- Психологическая коррекция агрессивного поведения детей, 219.57kb.
- С. В. Левина Н. А. Задворочнова публичный доклад, 193.66kb.
- Проектный метод в деятельности доу, 187.91kb.
- Проектный метод в деятельности доу, 214.46kb.
- Альтергот Оксана Петровна. Детский сад является юридическим лицом, имеет полный пакет, 211.9kb.
1000 развивающих головоломок...
1. ВИШЕНКА В КОКТЕЙЛЕ
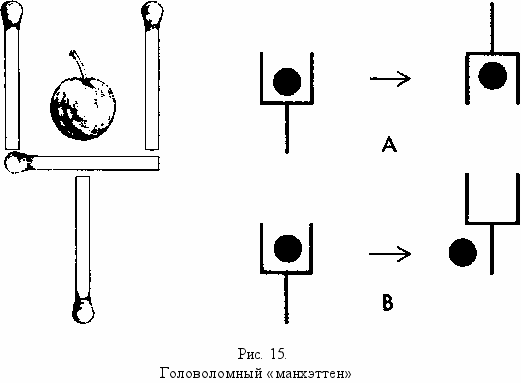
Это одна из тех редких чудесных головоломок, которые решаются мгновенно, если подойти к ним правильно. В формулировке задания есть изюминка, призванная направить ваши мысли по ложному экспериментальному пути. Известны случаи, когда умные люди бились над ней по двадцать минут и в конце концов приходили к заключению, что она не имеет решения.
Положите четыре спички так, чтобы изобразить фужер (см. рис. 15). Задача в том, чтобы передвинуть только две спички таким образом, чтобы фужер оказался в другом положении, а вишенка — снаружи. Фужер можно переворачивать как угодно, но он должен оставаться таким же, как исходный. На рисунке под буквой А показано, как можно переместить 2 спички, чтобы «перевернуть» фужер. Однако это не является решением, так как вишенка остается внутри. Под буквой В показан другой способ «опустошить» фужер. Однако и это не является решением, так как здесь перемещенными оказываются три, а не две спички.
^ 10. ЗАВЯЖИТЕ УЗЕЛ
Возьмите бельевую веревку длиной примерно 120 см. Завяжите на обоих концах петли, как показано на рис. 18. Петли должны быть такими, чтобы вы могли просунуть в них руки. Надев петли на запястья и натянув веревку, попытайтесь завязать узел в центре веревки. Вы можете делать с веревкой всё что угодно, кроме, естественно, высвобождения запястья из петли, разрезания веревки или нарушения существующих узлов. За исключением фокусников, этот трюк мало кому известен.
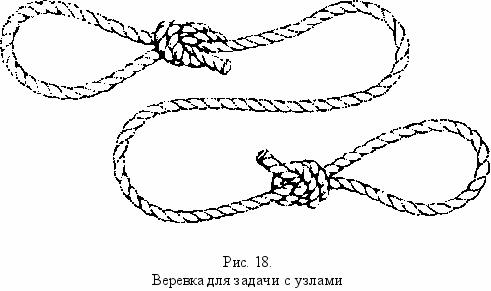
ОТВЕТЫ
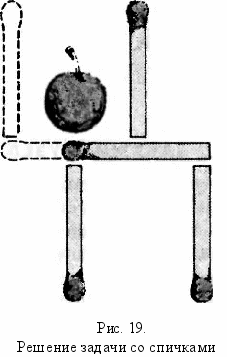
- На рис. 19 показано, как нужно передвинуть две спички, чтобы вишенка оказалась вне фужера.
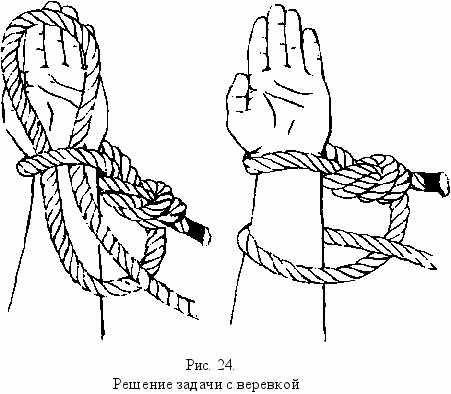
10. Чтобы завязать узел на веревке, натянутой между запястьями, вначале потяните её среднюю часть и проденьте под веревку, охватывающую левое запястье, как показано на рис. 24. Перекиньте петлю через левую руку, затем потяните обратно из-под веревки, охватывающей запястье. Теперь петля находится у вас на левой руке, как видно на правом рисунке. Если снять петлю с руки через левую ладонь, на веревке образуется узел.
Если наполовину повернуть петлю вправо после того, как вы первый раз пропустили её под веревкой, охватывающей запястье, но до того, как вы перекинули её через ладонь, получится узел-восьмерка. А если конец петли продеть через кольцо, прежде чем пере
кинуть петлю через руку, кольцо прочно завяжется на веревке после того, как вы завяжете любой узел.
Ван Каннингем и Б.Л. Шварц независимо друг от друга написали мне, что постановка задачи не запрещает второго решения. Сложите ладони, проденьте каждую из них через соответствующую петлю, а после этого просто разведите руки.
Арифметика на пальцах
тичном счете. Но точно так же можно использовать подобные знаки для счета и в любой другой системе. Действительно, пальцы прекрасно подходят для счета по самой простейшей системе счисления — бинарной, или двоичной. Согнутый или выпрямленный палец соответствует двум положениям переключателя в схемах современных компьютеров, использующих двоичный код. Фредерик Пол в статье How to Count on Your Fingers («Как считать на пальцах»), опублико
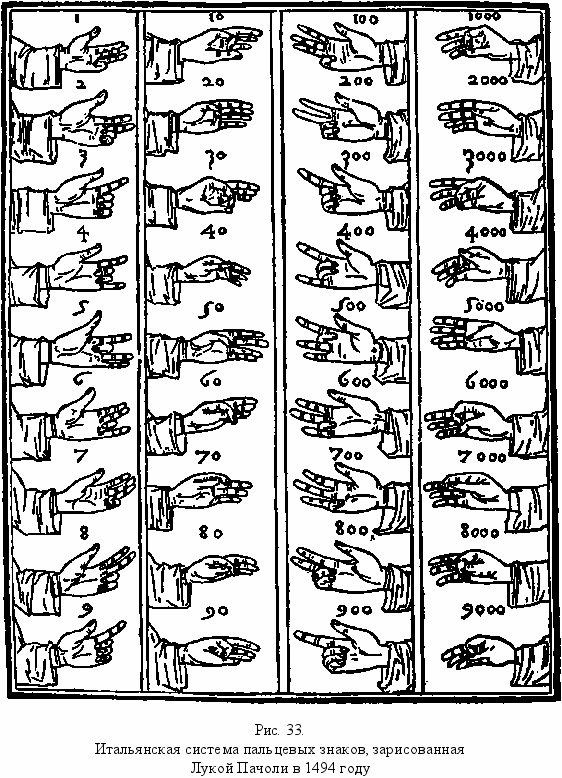
ванной в 1966 году в странном сборнике Digits and Dastards («Цифры и негодяи»), предлагает начинать счет со сжатых кулаков, повернутых тыльной стороной вверх. Вытянутый палец соответствует единице в двоичной системе, согнутый — нулю. Таким образом, чтобы посчитать от 1 до 1111111111 (что соответствует 1023 в десятичной системе), нужно начать с разгибания мизинца правой руки. Для выражения двойки в десятичной системе, то есть 10 в двоичной, нужно согнуть мизинец и вытянуть безымянный палец правой руки. Если вытянуты оба пальца — мизинец и безымянный, — это соответствует 11 в двоичной системе или трем в десятичной. На рисунке 34 изображено, как показать на двух руках 500 в двоичной системе. Немного потренировавшись, вы сможете использовать пальцы для быстрого счета в двоичной системе и даже, как поясняет Пол, для двоичного сложения и вычитания. Благодаря тому что символьная («булева») логика целиком построена на двоичной системе (истина-ложь), с помощью пальцев рук можно решать простые задачи из области математической логики.
0 11111 0 1
0 0
Рис. 34.
Число 500 в двоичном коде, показанное на пальцах

Любое число в двоичной системе, состоящее из одних единиц, обязательно будет на единицу меньше соответствующей степени двойки. Например, 1023 в десятичной системе, которое в двоичной пальцевой системе показывается распрямлением всех десяти пальцев, равно 210 — 1. Это навело Пола на мысль о занятной головоломке. Допустим, мы хотим вычесть некоторое число п из 1023 (или из любого другого числа, которое в двоичной системе выражается рядом единиц). Можете ли вы предложить крайне простой способ быстро произвести такое вычитание на пальцах?
Так как в Средневековье и эпоху Возрождения мало кто знал таблицу умножения дальше 5x5 (счетами также мало кто владел), существовало множество способов вычислить произведения чисел от 6 до 10. Один из распространенных методов, названный в труде 1492 года «древним правилом», — это использование комплементарных, или дополняющих, чисел на базе десяти (число, комплементарное п, равняется 10 — п). Чтобы перемножить 7 и 8, запишем числа, комплементарные им — 3 и 2. Каждое из них при вычитании из непарного ему дает 5 (8 - 3 = 7 - 2 = 5). Таково число десятков в произведении 7x8. Произведение 3x2 равно 6. Пятьдесят и 6 дают 56 — это и есть конечный результат умножения.
Для этого метода в качестве счетного инструмента часто использовались пальцы. Пальцам каждой руки присваивались значения от 6 до 10, начиная с мизинца. Чтобы умножить 7 на 8, соедините седьмой палец одной руки с восьмым другой, как показано сверху на рис. 35. Обратите внимание, что число, комплементарное 7, представлено тремя пальцами, расположенными над соприкасающимися на левой руке, а комплементарное 8 — на правой. Пять расположенных ниже пальцев символизируют 5 — число десятков в ответе. К пятидесяти нужно прибавить произведение верхних пальцев — 2x3, или 6. В результате получаем 56. Этот способ умножения на пальцах любых чисел от 6 до 10 широко практиковался в эпоху Возрождения и, говорят, до сих пор используется крестьянами в некоторых районах Европы и России.
Сегодня этот метод имеет значительную педагогическую ценность для начальной школы не только потому, что он увлекателен для детей, но и потому, что он тесно связан с алгебраическим умножением двучленов. Вместо использования чисел, комплементарных внутри десятка, мы можем представить 7 и 8 как дополнения к 5, записав их в виде двучленов (5 + 2) и (5 + 3), а затем провести умножение:
5 + 2
5 + 3 25+ 10
+ 15 + 6 25 + 25 + 6 = 56.
Первые два числа в нижнем ряду соответствуют сумме нижних пальцев, умноженной на 10, а 6 соответствует произведению верхних пальцев.
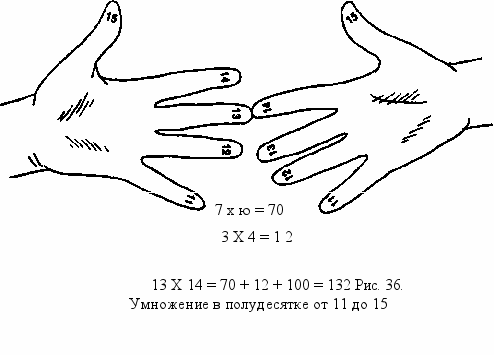
Пальцевый метод умножения легко обобщается для других полудесятков, больших 10, хотя нет никаких свидетельств того, что когда-либо в истории подобный метод применялся для чисел больше 10. Для всех полудесятков, заканчивающихся на 5, используется несколько иная процедура. Давайте рассмотрим следующий полудесяток от 11 до 15 и предположим, что нам нужно перемножить 14 и 13. Пальцам присваиваются значения от 11 до 15, и те пальцы, которые соответствуют перемножаемым числам, со-
5 X Ю = 50 7X8 = 90 + 6 = 56
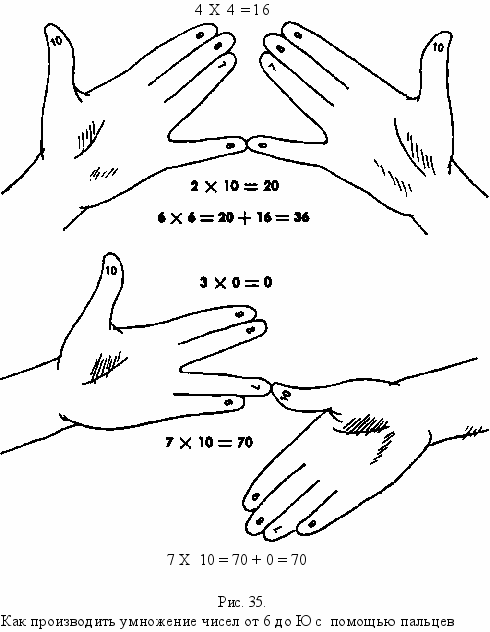
прикасаются, как показано на рис. 36. Семь расположенных ниже пальцев умножаются на 10, и получаем 70. Но теперь вместо того, чтобы добавить к этому числу произведение расположенных выше пальцев, мы не обращаем на них внимания, а перемножаем между собой нижние пальцы каждой руки, 4x3= 12. Сложив 12 и 70, получим 82. Последнее действие — прибавить 100 (константа). Ответ - 182.
Объяснить, каким образом этот метод работает, можно по-разному. Самое простое — рассмотреть его в понятиях умножения двучленов:
10 + 3
10 + 4 100 + 30
+ 40+12 100 + 70+ 12= 182.
Левые 100 — добавляемая константа, 70 — сумма нижних пальцев, умноженная на 10, а 12 — произведение нижних пальцев обеих рук.
Для всех полудесятков, оканчивающихся на 0, применяется первая процедура. Для чисел от 16 до 20 нижние пальцы имеют «ценность» 20, а добавляемая константа увеличивается до 200, как показано в примере перемножения 17 и 19 (см. рис. 37).
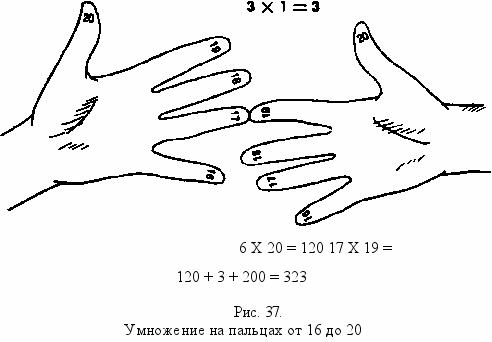
Перемножая шесть нижних пальцев на 20, получаем 120. Произведение верхних пальцев на обеих руках дает 3. К 123 добавляем константу 200 и получаем 323 — окончательный ответ. Биномная запись такова:
10 + 7
10 + 9 100 + 70
+ 90 + 63 100 + 160 + 63 = 323.
Если мы переместим влево 100 из 160, а 60 из 63 — в середину, то получим 200 + 120 + 3. Это соответствует подсчету на пальцах. Константа здесь — 200, сумма нижних пальцев, умноженная на 20, равна 120, а произведение верхних пальцев каждой руки равно 3.
^ Таблица на рис. 38, взятая из статьи Ферда У. Макэлвейна Digital Computer — Nonelectronic («Неэлектронный компьютер»), опубликованной в сборнике Mathematics Teacher за апрель 1961 года, дает значения нижних пальцев для каждого полудесятка, а также добавочные константы. Не забывайте, что для каждого полудесятка, оканчивающегося на 0, используется первая процедура, в которой участвуют верхние пальцы. Для полудесятков, оканчивающихся на 5, используется вторая процедура, где не участвуют верхние пальцы. Значения, придаваемые нижним пальцам для полудесятков, оканчивающихся на 5, равны \0(d — 1), где d — номер десятка. Для полудесятков, оканчивающихся на 0, это значение 1(W. Добавочная константа для полудесятков, оканчивающихся на 5, равна 100(d - I)2. Для полудесятков, оканчивающихся на 0, константа равна \00d(d — 1).
Данная таблица может быть продолжена для всех остальных полудесятков. Существует много способов записи общих формул для полной процедуры.
^ Значения Добавочная
Десяток Полудесятки нижних пальцев константа
| 1 | 1-5 | 0 | 0 |
| | 6-10 | 10 | 0 |
| 2 | 11-15 | 10 | 100 |
| | 16-20 | 20 | 200 |
| 3 | 21-25 | 20 | 400 |
| | 26-30 | 30 | 600 |
| 4 | 31-35 | 30 | 900 |
| | 36-40 | 40 | 1200 |
| 5 | 41-45 | 40 | 1600 |
| | 46-50 | 50 | 2000 |
Рис. 38.
Таблица значений пальцев и констант для умножения чисел до 50
^ Натан Альтшиллер Курт в книге Mathematics in Fun and in Earnest («Математика в шутку и всерьез») 1958 года издания предлагает следующую формулу:
(а + х)(а+у) = 2а(х +у) + (а-х)(а-у),
что может быть записано как
(а + х)(а +у) = а(х + у) + ху + а2,
где х и у — конечные цифры в числах, которые надо перемножить, а а может быть равно 5, 10, 15, 20, 25, 30, то есть первым числам каждого полудесятка.
Можно ли применять умножение на пальцах к числам из разных полудесятков, например, 17 х 64? Оказывается, да. К несчастью, этот процесс довольно сложен, требует придания различных значений пальцам каждой руки, поэтому я отсылаю интересующихся к упомянутой выше статье Макэлвейна, где описан этот метод. Конечно, всегда можно разбить большие числа на более мелкие части и провести с ними серию умножений на пальцах, а потом сложить промежуточные результаты для получения окончательного. Так, 9x13 можно представить как (9 х 6) + (9 х 7).
Во всем этом есть и философское зерно. Чистая математика в общепринятом понимании - продукт человеческого ума. Однако между ней и устройством мира существует удивительное соответствие. Особенно ярко оно проявляется в поведении физических тел, например камешков или пальцев, сохраняющих свою индивидуальность. Так, «2 + 2 = 4» это не просто закон чистой арифметики, независимой от реального мира, но и закон прикладной арифметики. Антропологи, изучающие различные культуры, постоянно стремятся привязать к обыденному народному сознанию науку, и в частности математику. Они заявляют, что, поскольку разные племена используют различные системы счета, математические законы являются строго культурными, как, например, правила перевозки грузов или игры в бейсбол. Они забывают о том, что различные системы исчисления, используемые разными народами, есть не более чем различные способы символического выражения и передачи одних и тех же чисел, которые подчиняются одним и тем же арифметическим законам, вне зависимости от того, кто пользуется ими — математик из Гарварда или абориген, считающий на пальцах.
Очевидно, что нет такого места на Земле или на других планетах, где бы два и два пальца вместе не составляли бы четыре. Единственное исключение я нашел в романе Дж. Оруэлла «1984». В описанной там жуткой сцене пыток Уинстон Смит, в конце концов, вынужден признать, что два плюс два равно пяти:
О'Брайен показал ему левую руку, спрятав большой палец.
— Пять пальцев. Вы видите пять пальцев?
-Да.
И он их видел, одно мимолетное мгновение, до того, как в голове у него все стало на свои места. Он видел пять пальцев и никакого искажения не заменсиг.
Точно такая же возможность рассматривалась Достоевским. «Но дважды два четыре — все-таки вещь пренесносная, — говорит герой повести «Записки из подполья». — Дважды два четыре — ведь это, по моему мнению, только нахальство-с. Дважды два четыре смотрит фертом, стоит поперек вашей дороги руки в боки и плюется. Я согласен, что дважды два четыре — превосходная вещь; но если уже все хвалить, то и дважды два пять — премилая иногда вещица».
Может, это и премило, однако не применимо ни к какому логически возможному миру. Это субъективное, противоречащее само себе заблуждение, которое может возникнуть лишь временно, и то под влиянием «коллективного солипсизма» (как называл это Ору-элл), когда любая истинность, в том числе и в науке, определяется без связи с абстрактными законами логики или с математическими законами построения внешнего мира.
ДОПОЛНЕНИЕ
Дж. Э. Линдон, проживающий в английском городе Эддлстоуне, является, на мой взгляд, величайшим современным английским автором юмористических стихов. Так как его произведения не слишком широко печатаются (единственным исключением в США служит опубликованная The Worm Runner's Digest), то большая их часть доступна лишь его знакомым, которым, я надеюсь, хватает ума их хранить. Приведенная ниже поэма, посвященная открытию арифметики, попала ко мне в 1968 году — вскоре после того, как эта глава появилась в Scientific American.
^ У ИСТОКОВ АРИФМЕТИКИ Дж. Э. Линдон
Шел первобытный Магг по лесу, Съедая всё, что мог поймать, И так набрел он на поляну, Где Огг надумал размышлять.
^ Смотрел, смотрел он всё на камни (их было двадцать и один), Костистый лоб свой тер забавно, угрюм, задумчив, недвижим.
О о о ° ° • о д 0 ф о о % 0
Какого черта Огг глядит — Тряхнул Магг головой — На сей расколотый гранит? — и грохнул булавой.
^ Огг тыкал в камни, а затем Стал пальцы загибать. Рассвирепев, воскликнул Магг: «Что, колесо опять?»
Огг, с гулом стукнув себя в грудь, Ответил: «Есть идея, Но записать её — никак, увы, я не умею.
^ Смотри: возьмем с тобой по три руки и пары глаз, и это — словно две руки, ноги и нос взять раз».
О«0О «О, Оо0 ,о„ „оо,,
Сложив прямоугольник вмиг, Продолжил Огг: «Смотри, здесь три по семь камней в рядах, А также... семь по три.
о о
о
о А о О о о О О о
о ©о Q ^ * о ©
о °о
о о О
^ И если верно для камней, что дважды два — четыре, так верно то для всех вещей, что есть иль будут в мире!»
Магг мрачно камни оглянул и рыкнул исподлобья: «Не понял я, что ты загнул, проверим-ка теорию!»
^ С трудом собравши жен своих (Огг — двух, а Магг — четыре плюс две руки и плюс нога), сказали: встаньте шире!
Все тщетно было, и тогда Магг взял свою дубину и стал порядок наводить в рядах своих любимых.
^ Триумф идеи налицо: Три по семь — семь по три! Огг в восхищении орет А Магг считает их.
Кусок гранита поострей, Огг от скалы отбил И высек сразу же на ней: «Здесь Огг закон открыл...»
^ Магг заскучал и прочь побрел, чтоб новых жен добыть: ведь сколько, чтоб открыть закон, придётся жен побить?!
ОТВЕТЫ
Единственное решение «венерианской» задачи 12 + 12 = 101 в троичной системе исчисления. Таким образом, у венерианцев должно быть по 3 пальца на каждой руке. (Венерианская сумма эквивалентна 5 + 5 = 10 в нашей, десятичной, системе.) Реймонд Де Мерс написал мне, что, если у венерианцев по три пальца на руках, то, скорее всего, они будут пользоваться шестеричной системой. Он считает, что более вероятно, исходя из условия задачи, что у них всего три пальца, на одной руке — один, а на второй — два.
Кеймерон Д. Андерсон из Уиндзора, Онтарио, Канада, и англичанин Гренвилл Тернер из Шеффилдского университета предположили, что венерианские символы могут означать не сложение, а умножение. Тогда решений у этой задачи может быть неограниченное число. Вы можете попробовать доказать, что решение для наименьшей основы системы счисления — это 13 х 13 = 171 в восьмеричной системе.
Во втором задании предполагается, что десять вытянутых пальцев обеих рук означают десять единиц в бинарной системе, что эквивалентно 210 — 1, или 1023 в десятичной, вам нужно найти простой метод вычитания из этого числа некоего меньшего п. Фредерик Пол в вышеупомянутой статье предлагает следующее: п необходимо просто выразить в двоичной системе, используя пальцы так, как описано. Теперь, загибая каждый вытянутый палец и вытягивая каждый загнутый — то есть заменяя двоичные единицы на нули и наоборот, — мы получим нужный нам ответ в бинарной системе.
