Geum.ru

«решение оптимизационных экономических задач методами линейного программирования»

Вид материалаРешение

Содержание


Научный руководитель
Негосударственное образовательное учреждение
«решение оптимизационных экономических задач методами линейного программирования»
Графический метод решения задачи ЛП.
Симплекс-метод решения задач ЛП. Пример
Решаем задачу методом потенциалов
Подобный материал:
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Смоленский гуманитарный университет


РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЭКОНОМИЧЕСКИХ ЗАДАЧ МЕТОДАМИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Курсовая работа

ВАРИАНТ №______


Смоленск

2010

Смоленский гуманитарный университет

Факультет компьютерных технологий, экономики и дизайна

Кафедра математического моделирования


РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЭКОНОМИЧЕСКИХ ЗАДАЧ МЕТОДАМИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Курсовая работа

ВАРИАНТ №_____


Исполнитель:

(Ф.И.О.студента)

Студент группы

(группа, подпись студента)

^ Научный руководитель: д.т.н., профессор Бешенков С.Н.

(Ф.И.О.руководителя, подпись)

Зав.кафедрой: д.т.н., профессор Бешенков С.Н.

(Ф.И.О.зав.кафедрой, подпись)

Дата допуска:


Смоленск

2010

^ НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Смоленский гуманитарный университет




К
УТВЕРЖДАЮ

Заведующий кафедрой

_____________________________

«____» ___________ 20 ____ г.

афедра математики и информатики

(наименование кафедры)


З А Д А Н И Е

на курсовую работу студента


Тема курсовой работы: ^ «РЕШЕНИЕ ОПТИМИЗАЦИОННЫХ ЭКОНОМИЧЕСКИХ ЗАДАЧ МЕТОДАМИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ»

Целевая установка


Основные вопросы, подлежащие разработке (исследованию):

1.

2.

3.

4.

5.


Основная литература литература: (согласно приложения).

Объем работы не более 25 машинописных листов (через полтора интервала).

Срок доклада руководителю о ходе разработки курсовой работы:

«___» ___________ 20 ___ г.

Срок представления законченной работы: «___» _____________ 20 ___ г.

Дата выдачи задания:

Руководитель: ________________________________________________________________

Задание получил: «___» _____________ 20 ___ г. студент ____________________________

_____________________________________________________________________________


Содержание Стр.

Введение А
  1. Общая постановка задачи линейного программирования (ЛП) Б
  2. Примеры экономических задач, приводящихся к задачам ЛП
  3. Геометрический метод решение задач ЛП
  4. Симплексный метод решения задач ЛП
  5. Теоремы двойственности и их использование в задачах ЛП
  6. Транспортная задача и её решение методом потенциалов
  7. Решение задач ЛП с использованием программы « »

Заключение

Литература (с соблюдением правил оформления библиографического перечня)

^ Графический метод решения задачи ЛП. Пример

При откорме каждое животное должно получить не менее А ед.питательного вещества S1, не менее В ед. вещества S2 и не менее С вещества S3 . Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 килограмме каждого вида корма и стоимость одного килограмма корма дана в таблицах 1 и 2.

Таблица 1

Питательные вещества
Количество единиц питательных веществ в 1 кг. корма
Необходимое количество питательных веществ

корм 1
корм 2

S1
1
2
5

S2
3
2
9

S3
6
8
28

Стоимость 1 кг. корма
6
10



Составить рацион минимальной стоимости.

Решение.

Обозначим через 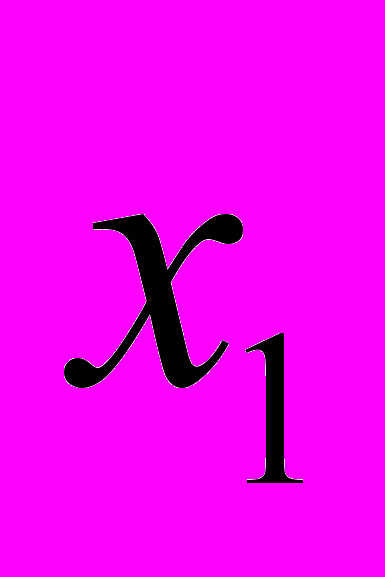-количество корма 1, а через 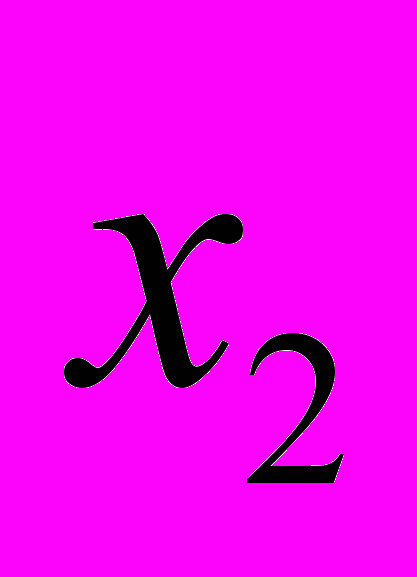-количество корма 2, которое следует ввести в рацион. Целевая функция задачи выражает требование минимизации затрат по закупке продуктов, содержащих необходимые питательные вещества. Она имеет вид: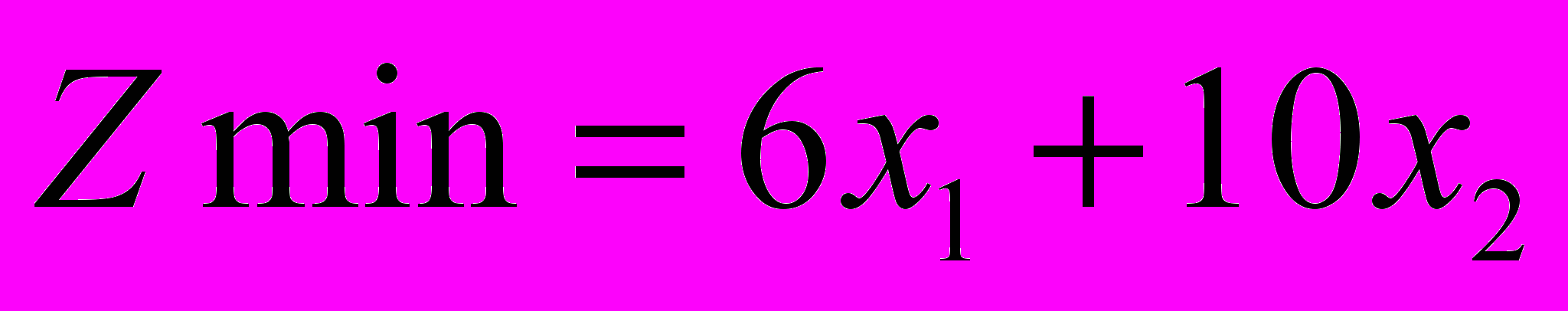



Ограничения задачи выражают требование содержания в кормах необходимого количества питательных веществ (S1, S2, S3) . Выглядят они так.



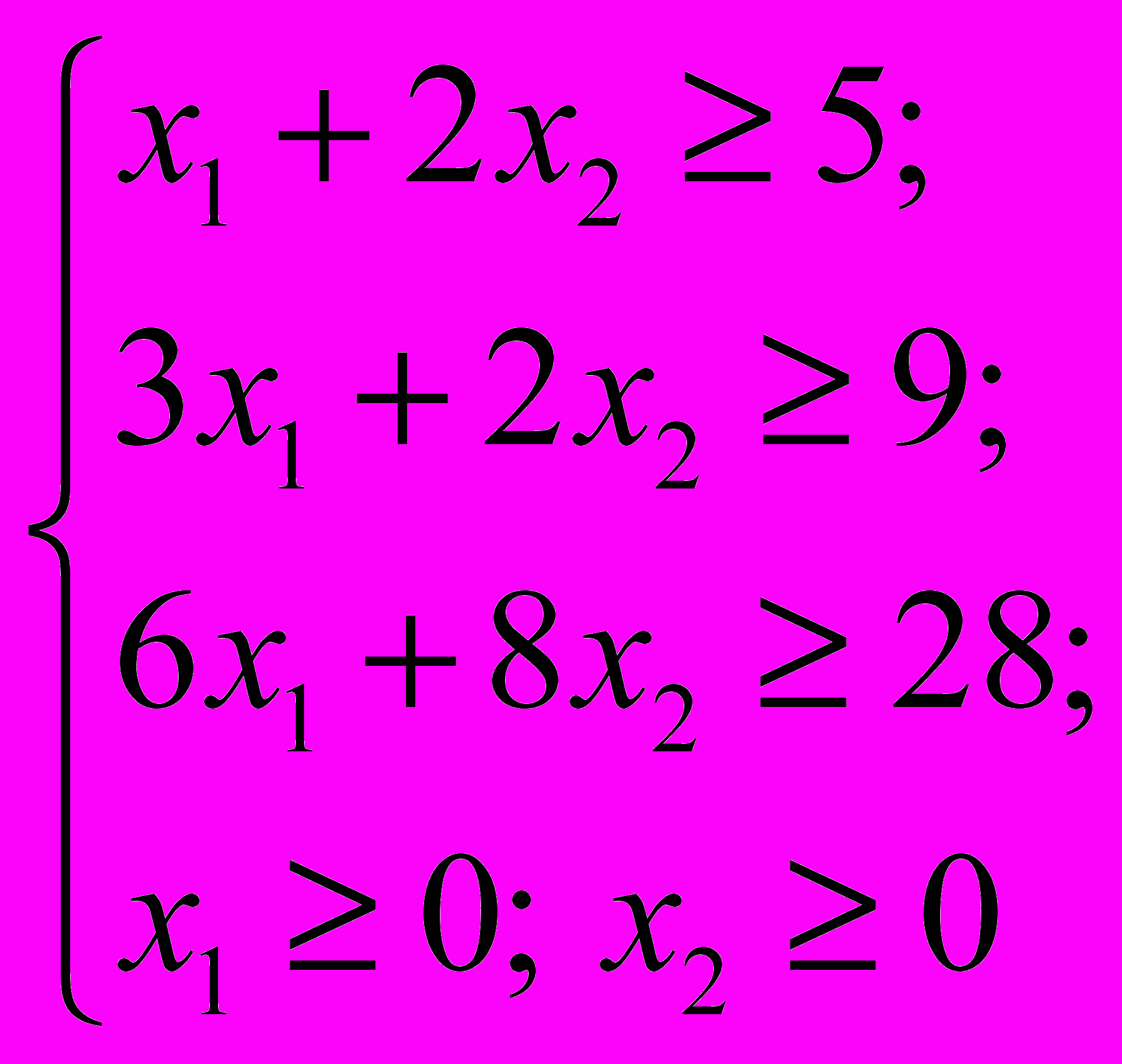
Построим область возможных решений, полученной задачи. Для этого найдем области плоскости 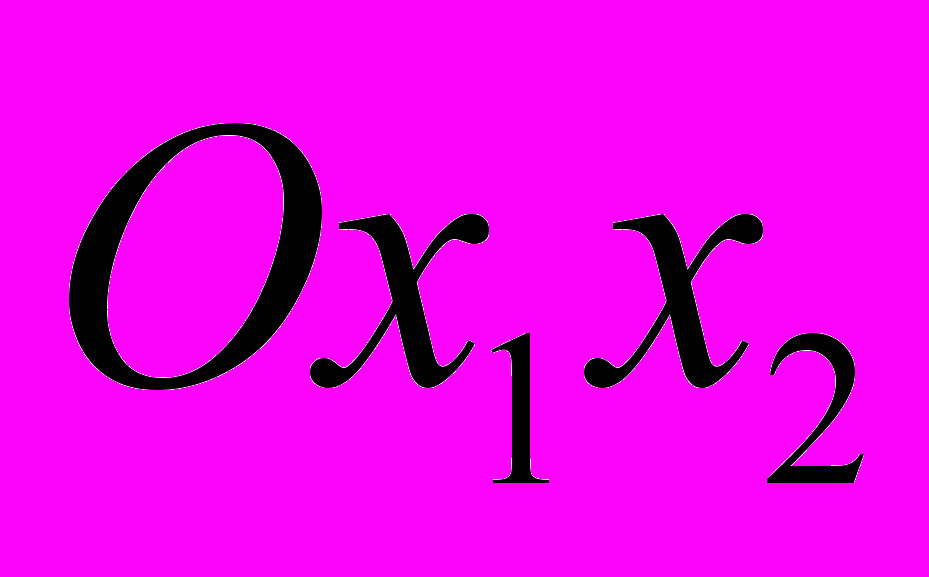, удовлетворяющие каждому неравенству, и выделим область, все точки которой удовлетворяют всем неравенствам системы (заштрихованная область). Получим область возможных решений.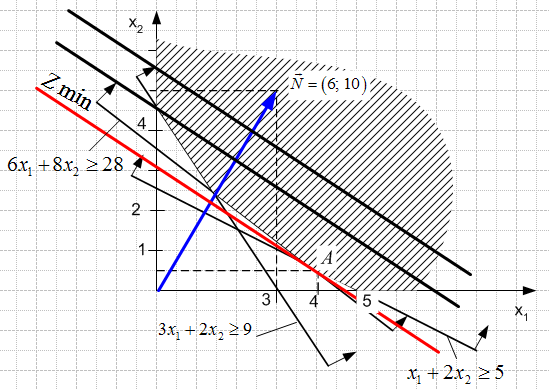



Построим вектор нормали 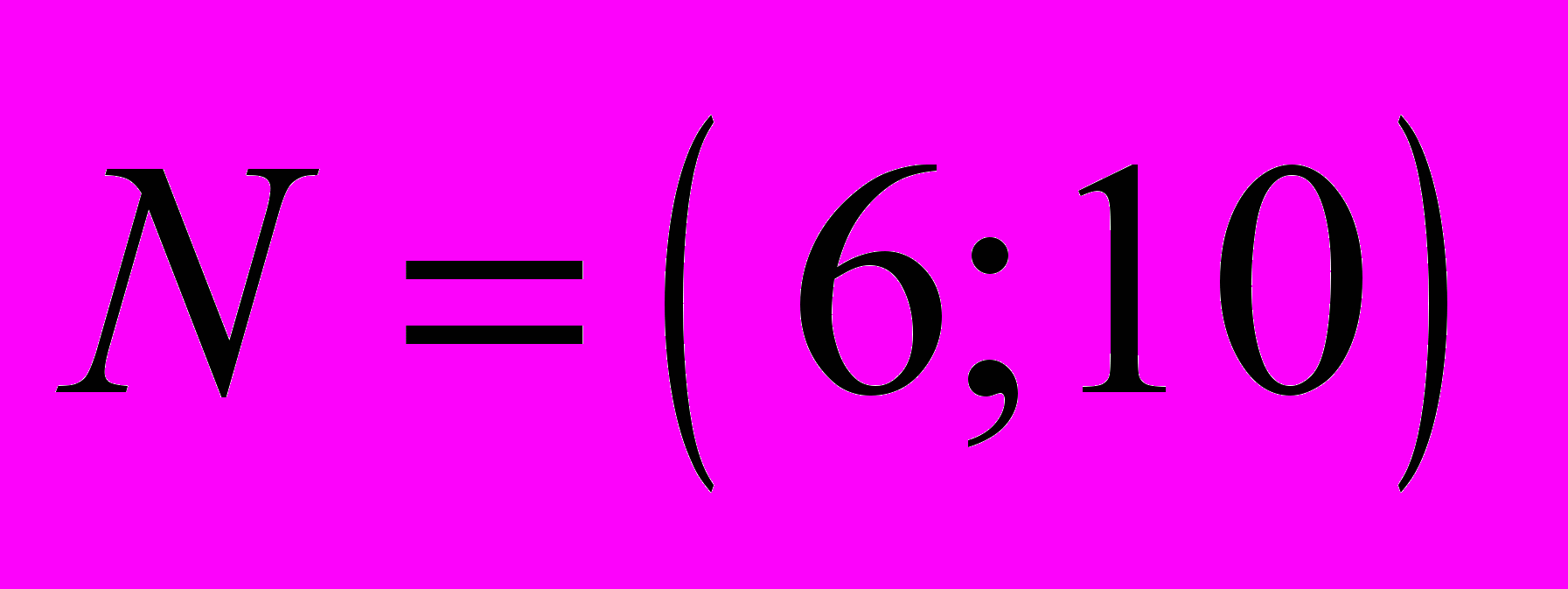к линиям уровня функции цели (на рисунке этот вектор для наглядности уменьшен в два раза). Это линии, на которых функция цели постоянна. Функция цели принимает минимальное значение в точке А. Найдем координаты этой точки, которая лежит на пересечении двух прямых. 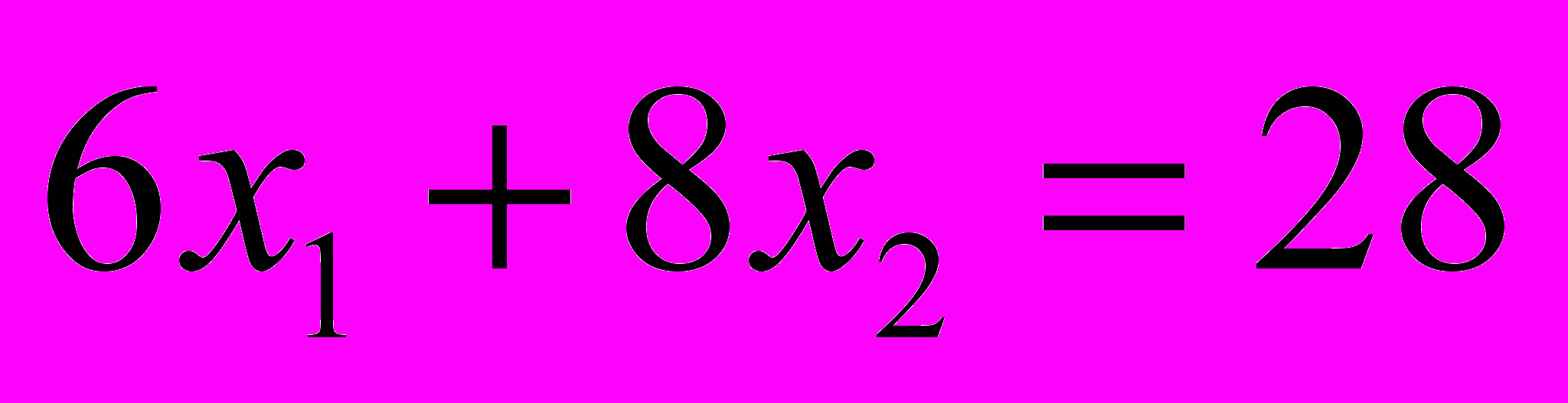и 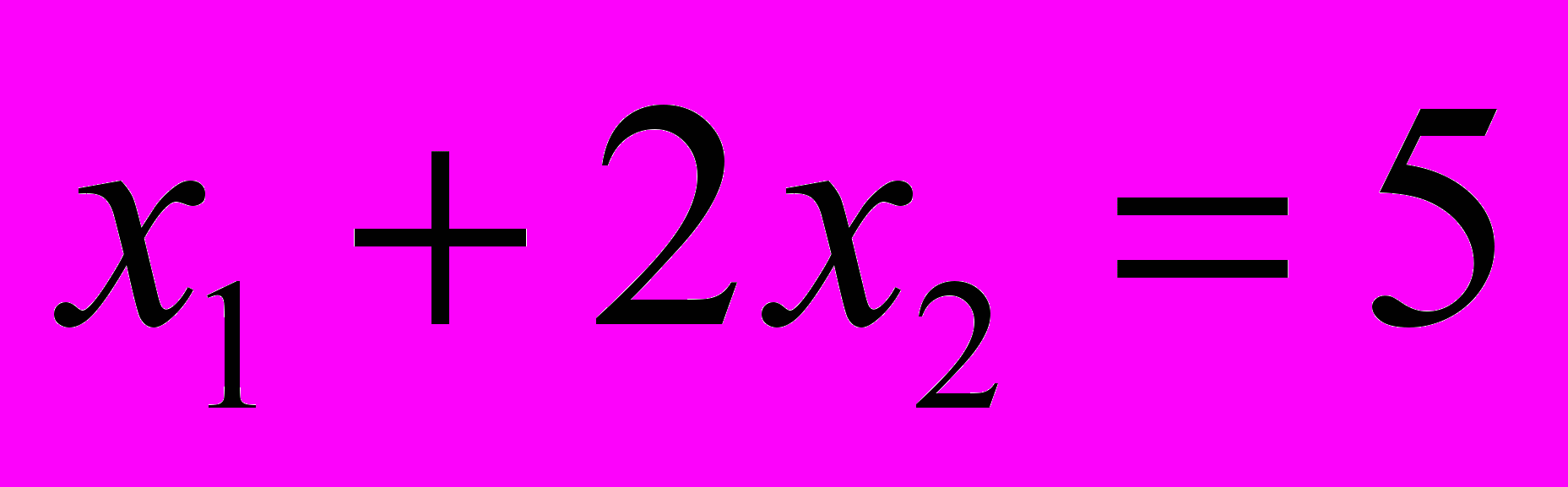. Решим систему этих уравнений.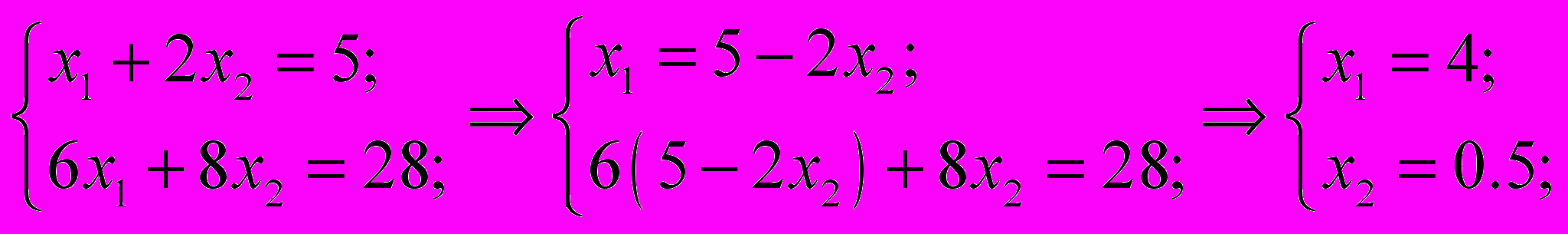



Таким образом, имеем оптимальный план закупки кормов 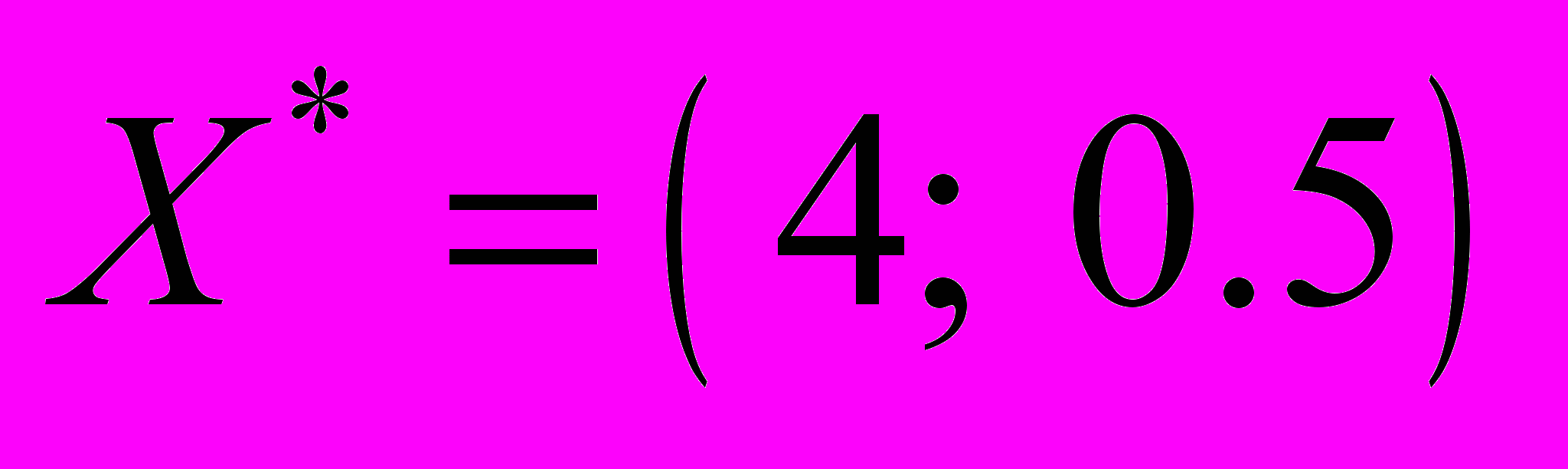, при котором затраты будут минимальны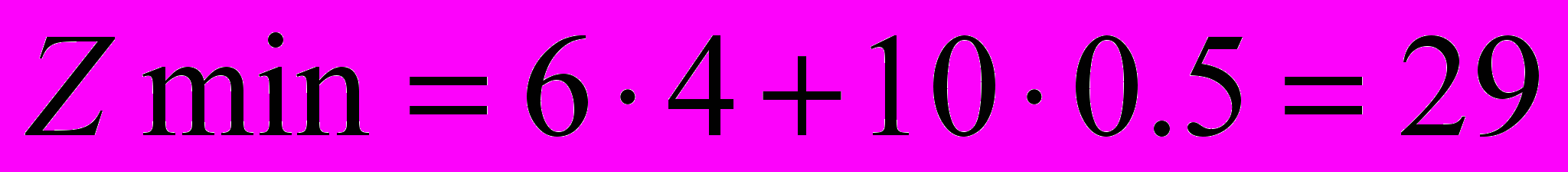

^ Симплекс-метод решения задач ЛП. Пример

Для изготовления 4-ёх видов продукции P1, P2, P3, P4 используют два вида сырья: S1 и S2 . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а так же величина прибыли, получаемая от реализации единицы продукции, приведены в таблице 2.

Таблица 2.

Вид сырья
Запас сырья
Количество единиц сырья, идущих на изготовление единицы продукции

P1
P2
P3
P4

S1
6
1
3
3
6

S2
10
2
1
2
8

Прибыль от единицы продукции
5
5
9
28

Составить план производства, обеспечивающий получений максимальной прибыли.

Решение. Составим математическую модель задачи. Обозначим через 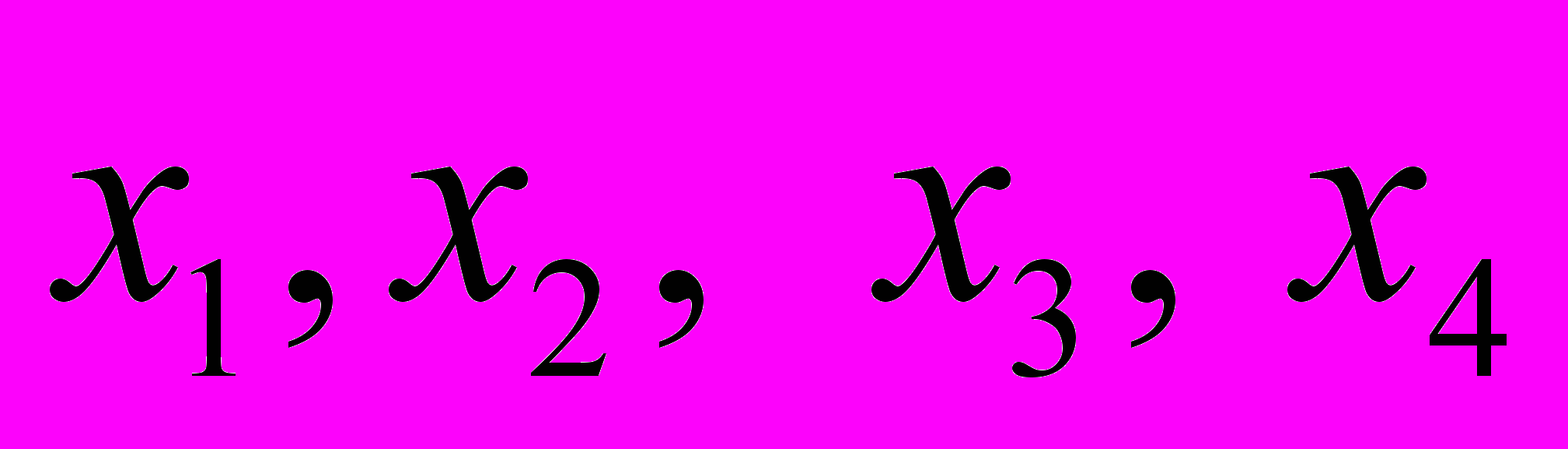количество продукции каждого вида, которую следует произвести. . Целевая функция задачи выражает требование максимизации полученной при реализации продукции прибыли. Она имеет вид: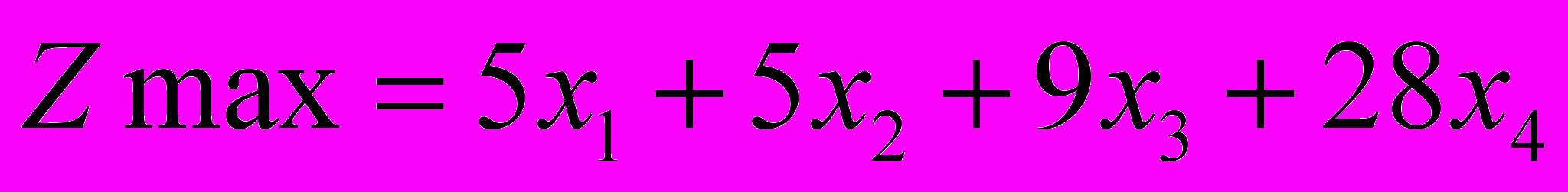



Ограничения задачи связаны с ограниченными запасами сырья. Выглядят они так.



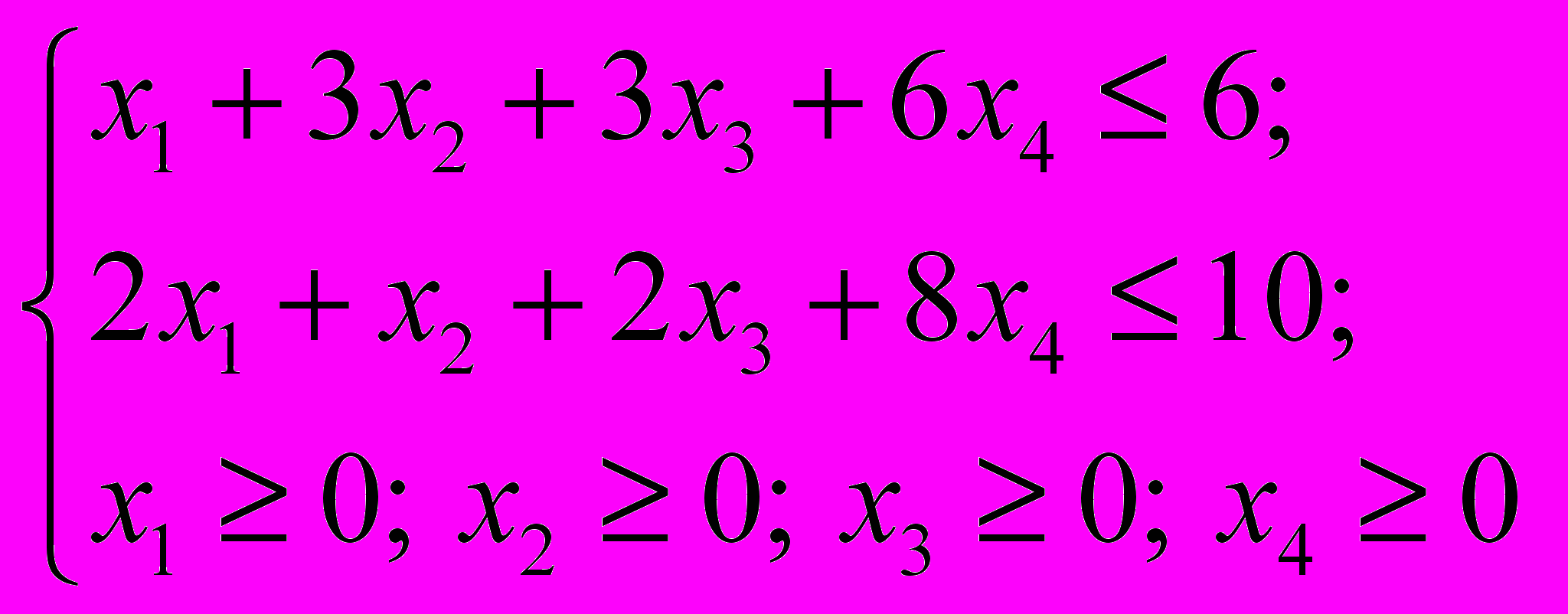
Решим задачу симплекс методом, для этого приведем ее к каноническому виду, вводя дополнительные переменные



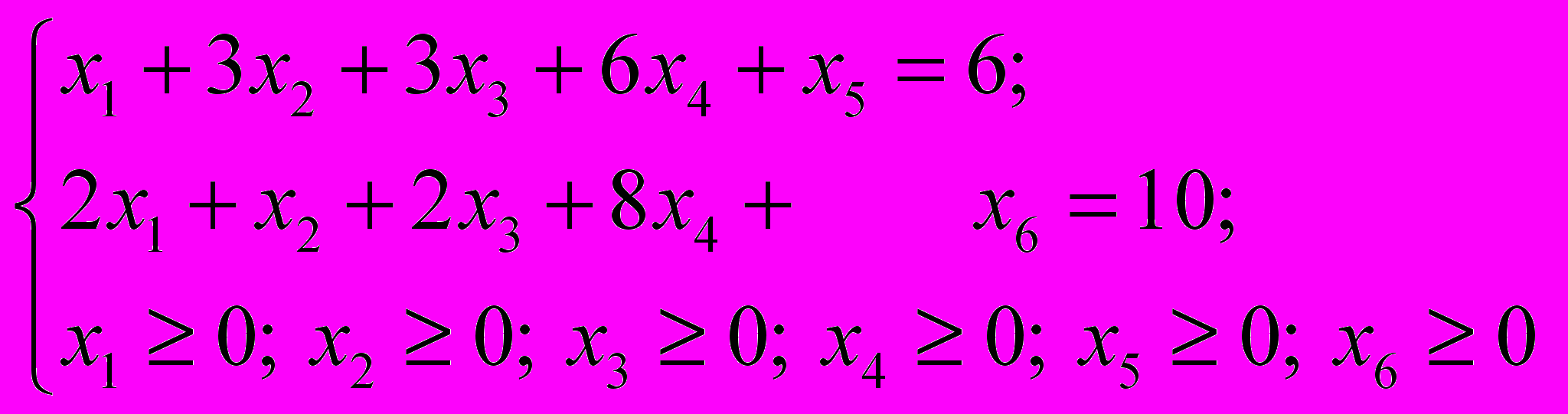
Перепишем функцию цели так

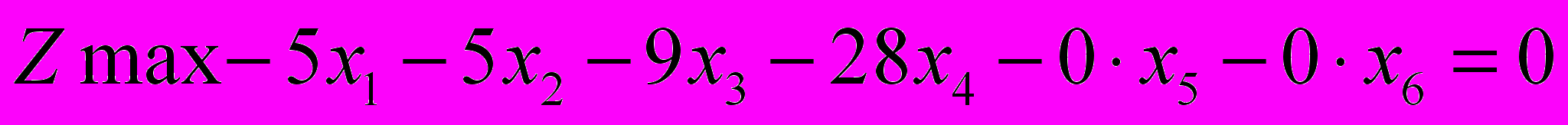
Занесем данные в таблицу Гаусса и выполним симплексные преобразования. Разрешающий элементы на каждом шаге преобразований выделены жирным шрифтом и цветом.
ХБ
А1
А2
А3
А4
А5
А6
А0
min

Исходная

Х5
1
3
3
6
1
0
6
1

система
Х6
2
1
2
8
0
1
10
1.25




Z
-5
-5
-9
-28
0
0
0
0

1-е

Х4
1/6
1/2
1/2
1
1/6
0
1
6

преобразование
Х6
2/3
-3
-2
0
-4/3
1
2
3




Z
-1/3
9
5
0
14/3
0
28
0

2-е

Х4
0
5/4
1
1
1/2
-1/4
1/2



преобразование
Х1
1
-9/2
-3
0
-2
3/2
3






Z
0
15/2
4
0
4
1/2
29



Среди значений индексной строки последней таблицы нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.


Оптимальный план задачи имеет вид: 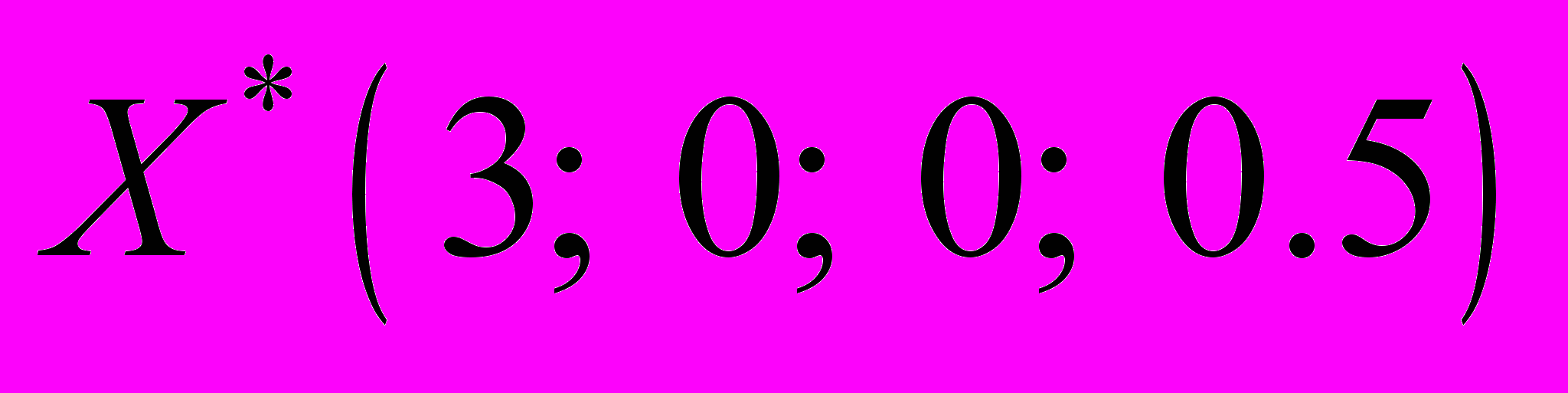. Целевая функция при этом равна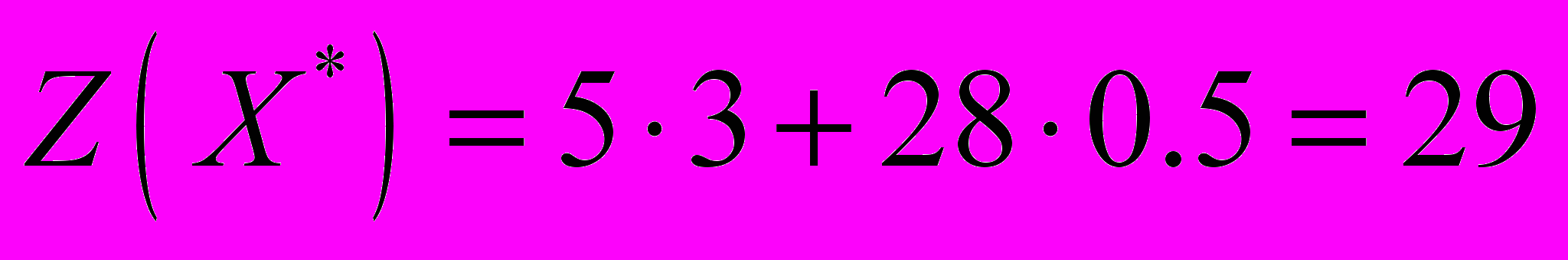

Теорема двойственности. Пример

а) Составить задачу двойственную к примеру 2.

б) найти её решение любым методом.

в) найти решение задачи 2, используя теорему двойственности.

Решение.

Между оптимальными решениями каждой из двойственной пары задач существует взаимосвязь, которая выражается следующими теоремами:

Теорема 1 (основная теорема двойственности).

Если одна из двойственной пары задач имеет оптимальное решение, то другая задача также имеет решение, причем максимальное значение целевой функции одной задачи равно минимальному значению целевой функции другой. Если же одна из задач не имеет решения, то система ограничений второй задачи противоречива.

Теорема 2 (теорема равновесия).

Если в оптимальном плане одной задачи значение какой-либо переменной строго больше нуля, то соответствующее ограничение другой задачи, при подстановке в него оптимального плана, становится равенством.

Обратно, если некоторое ограничение одной задачи, при подстановке оптимального плана, обращается в строгое неравенство, то соответствующая переменная в оптимальном решении другой задачи принимает значение равное нулю, т.е. для оптимальных планов 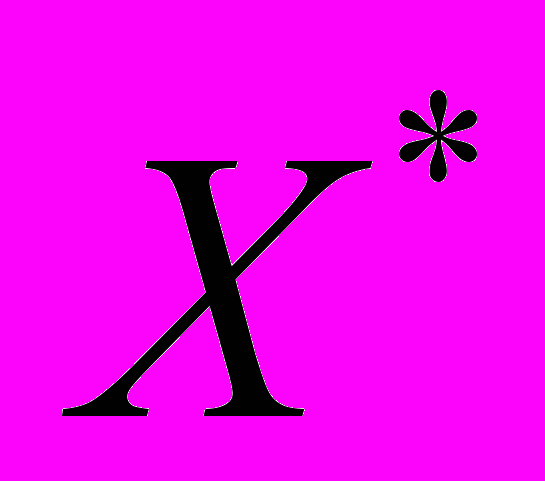и 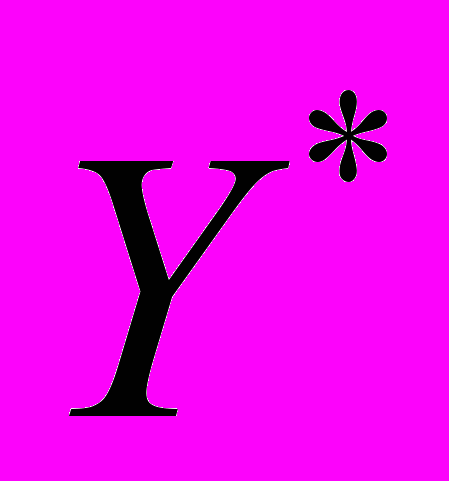соотношение между сопряженными ограничениями строится по принципу “строгому равенству соответствует строгое неравенство”.

а). Используя указанные теоремы, можно решение одной из пары двойственных задач получить непосредственно из решения другой.

Составим двойственную задачу.

Основная задача Двойственная задача.



б). Найдем решение двойственной задачи графическим методом.

Решим задачу графически. Нанесем на координатную плоскость 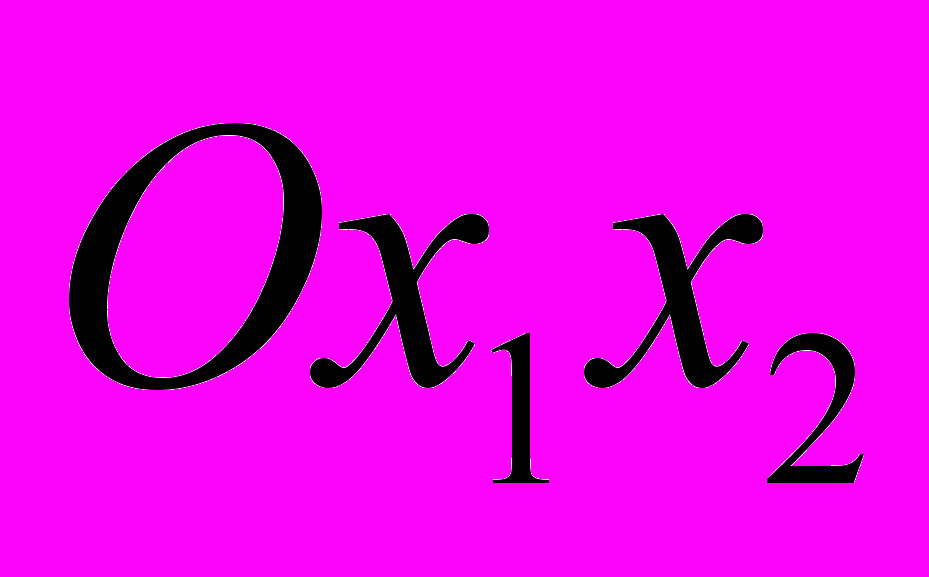систему ограничений, получим область возможных решений , все точки которой удовлетворяют всем ограничениям задачи, построим вектор нормали 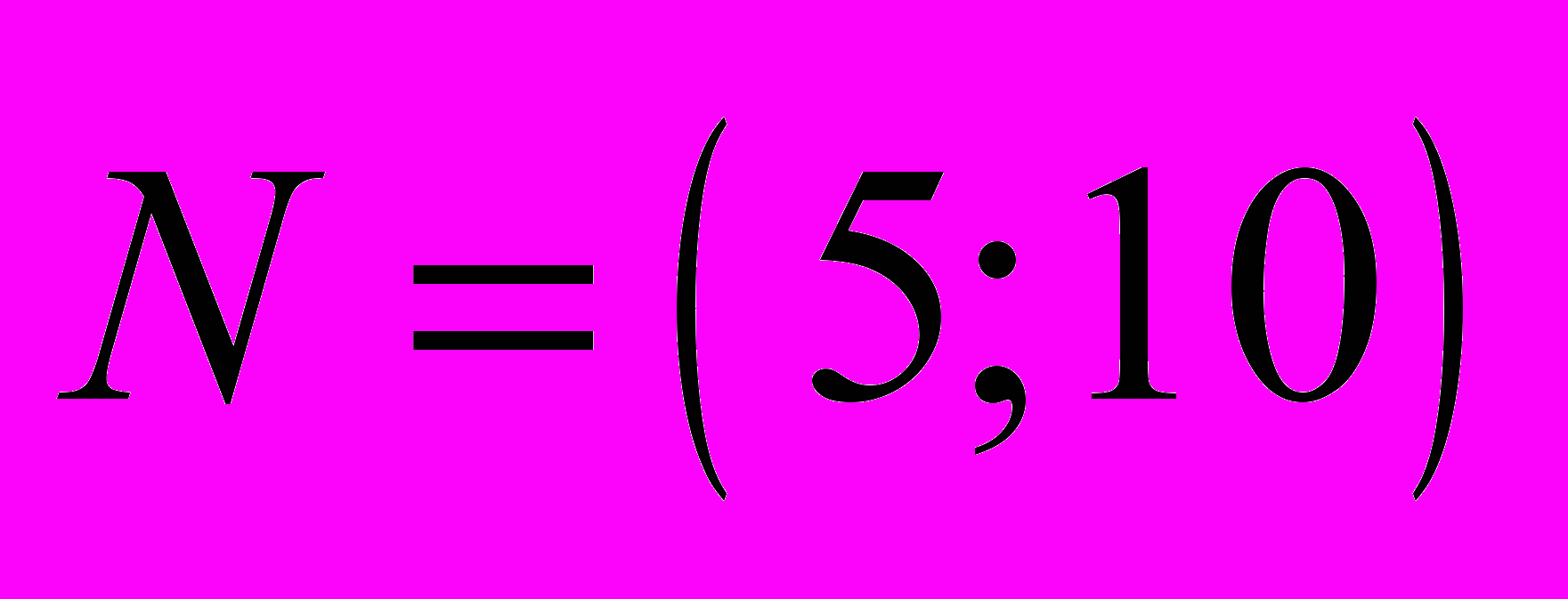к линиям уровня функции цели.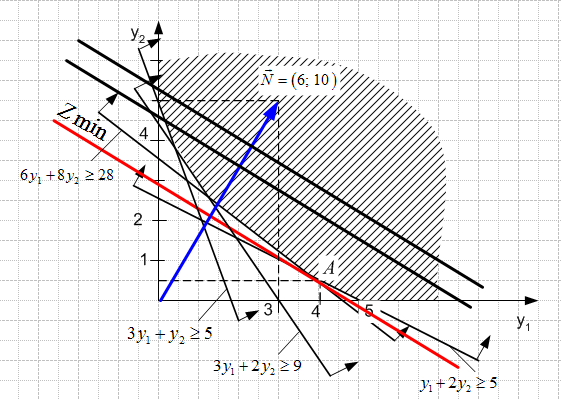



Построим вектор нормали 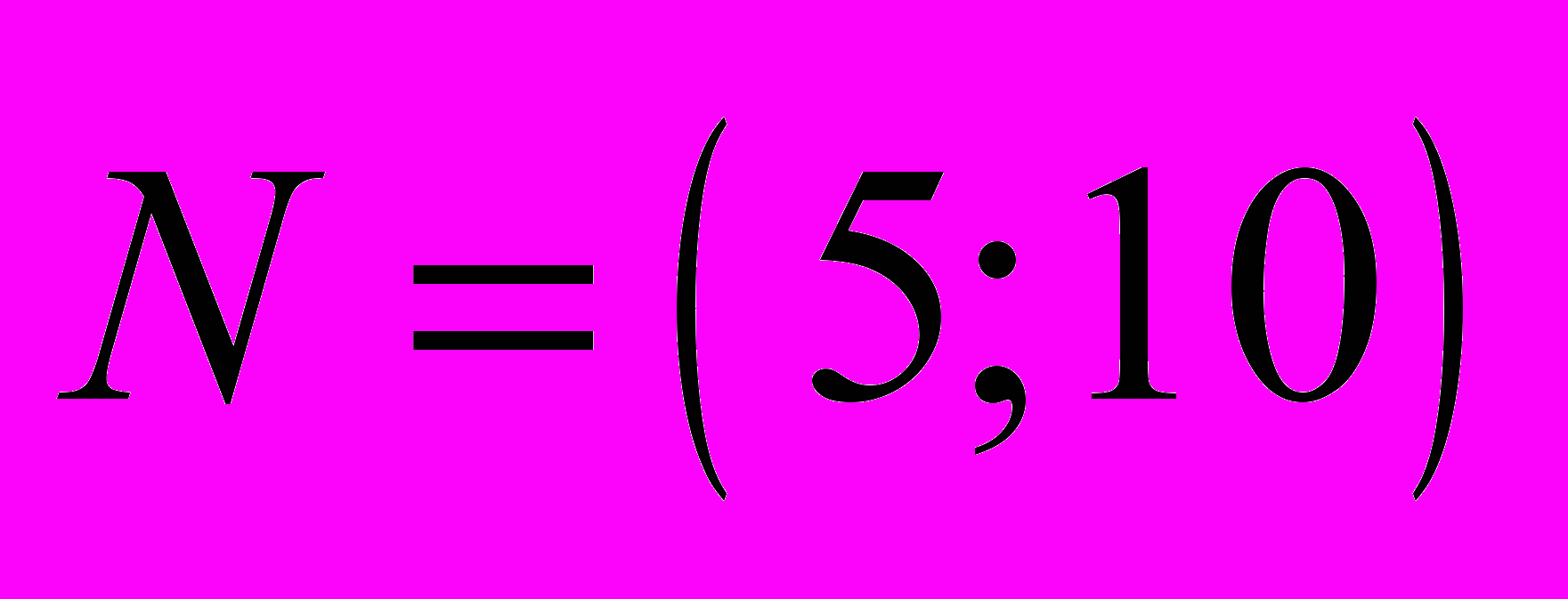к линиям уровня функции цели. Это линии, на которых функция цели постоянна. Функция цели принимает минимальное значение в точке А. Найдем координаты этой точки, которая лежит на пересечении двух прямых. 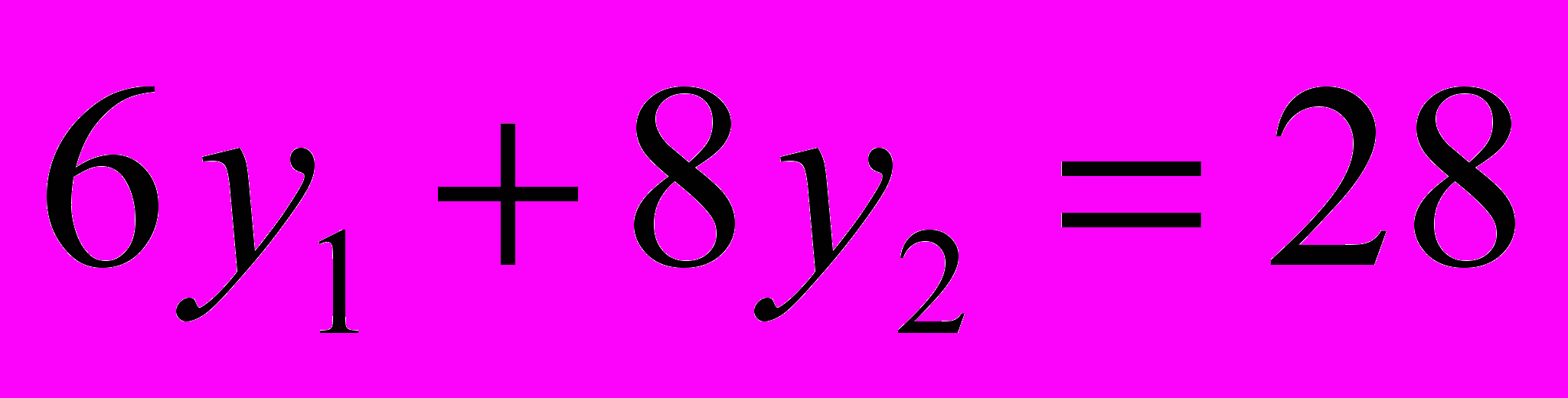и 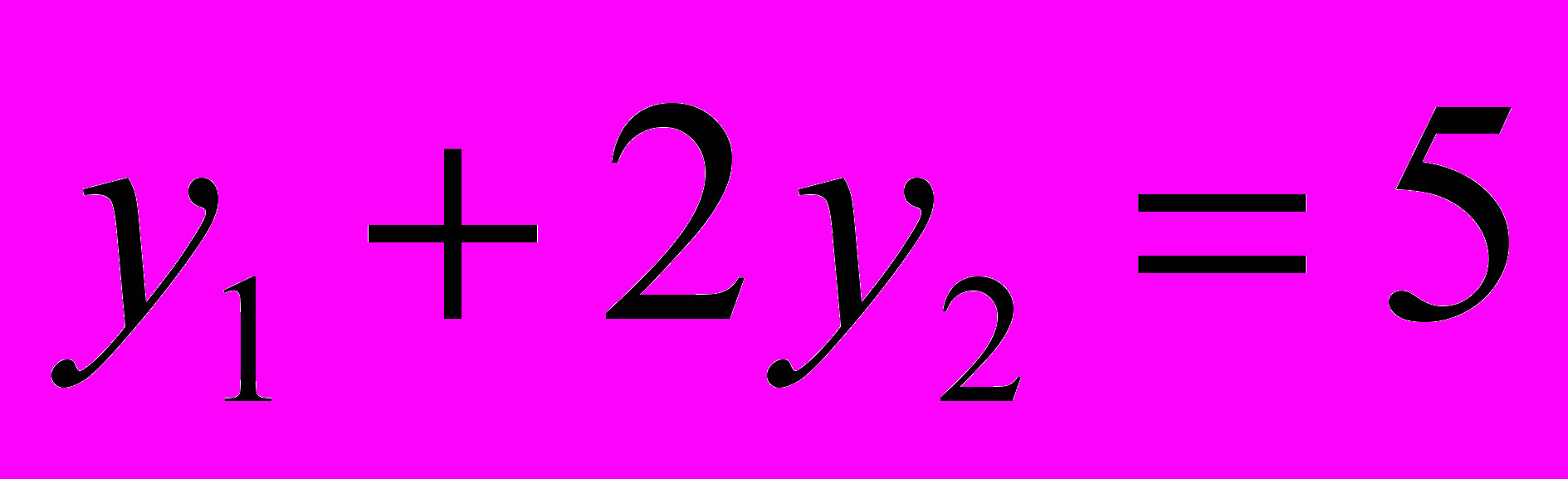. Решим систему этих уравнений.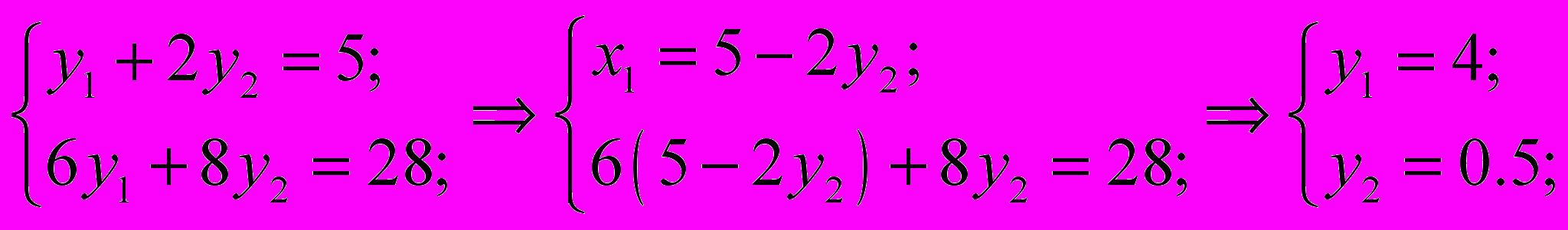



Таким образом, имеем оптимальный план закупки кормов 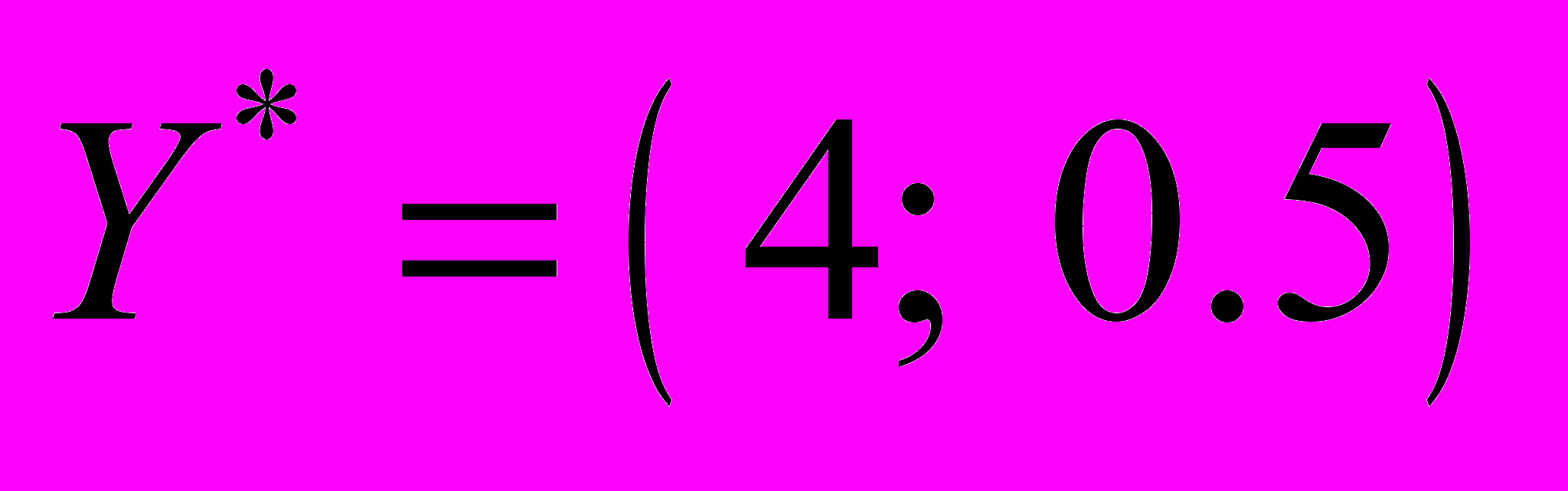, при котором затраты будут минимальны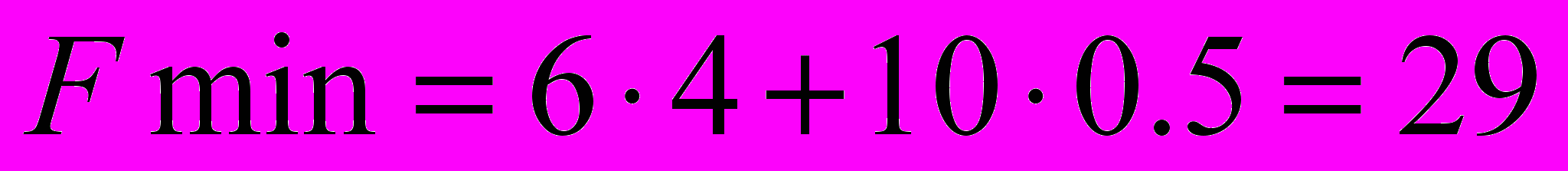

в) Найдем решение задачи 2, используя теорему двойственности.

Исходную задачу будем считать двойственно, а решенную графическим методом двойственную задачу будем считать основной

Так как для оптимальных планов 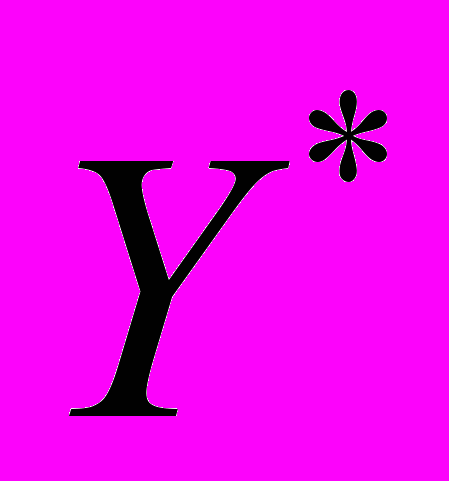и 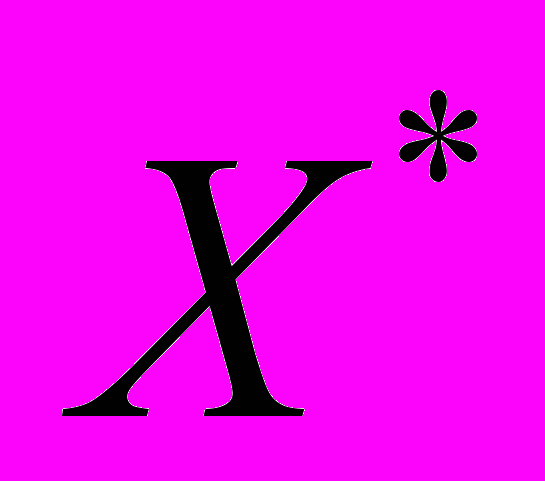соотношения между сопряженными ограничениями строится по правилу «строгому равенству соответствует строгое неравенство», то имеем: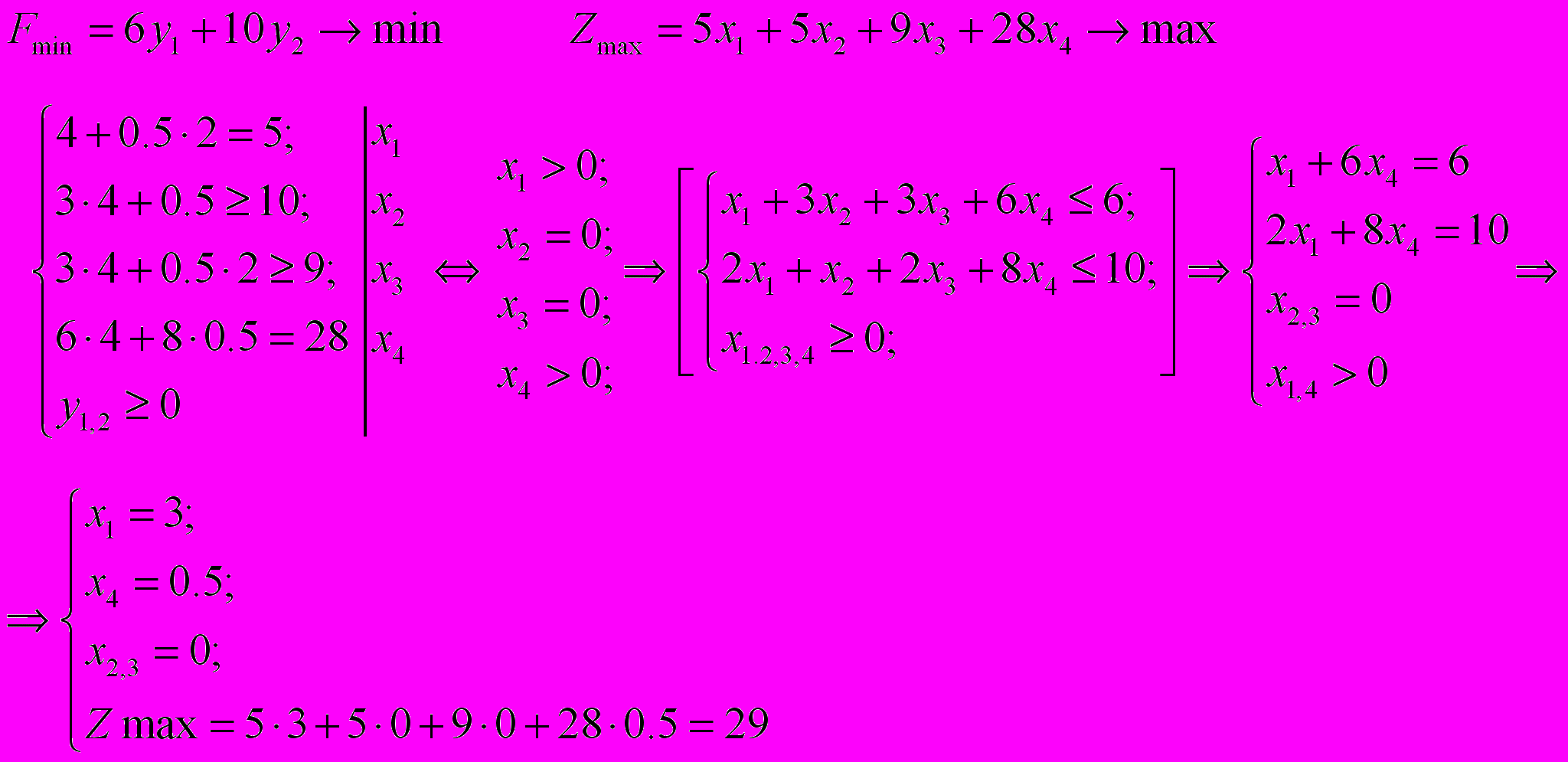




Оптимальный план двойственной задачи:

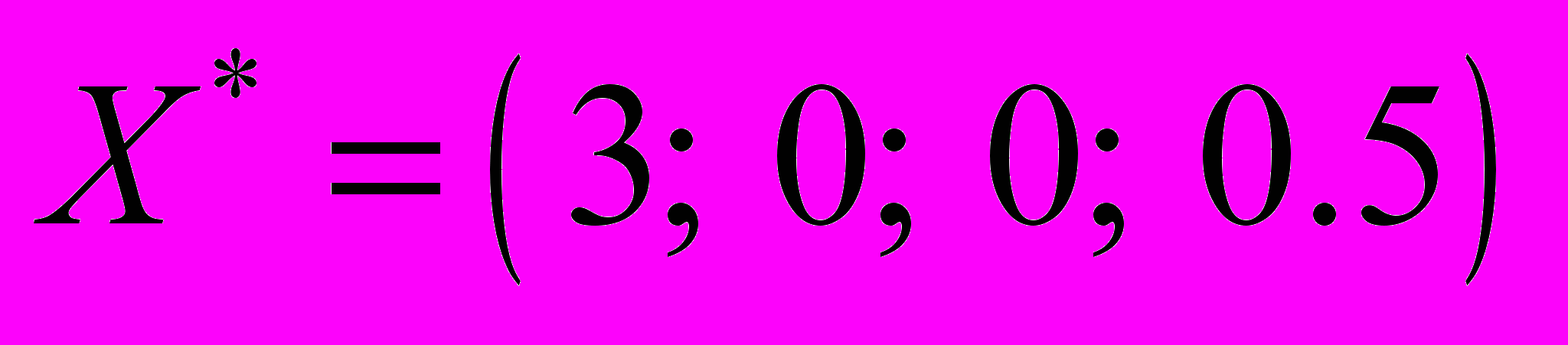
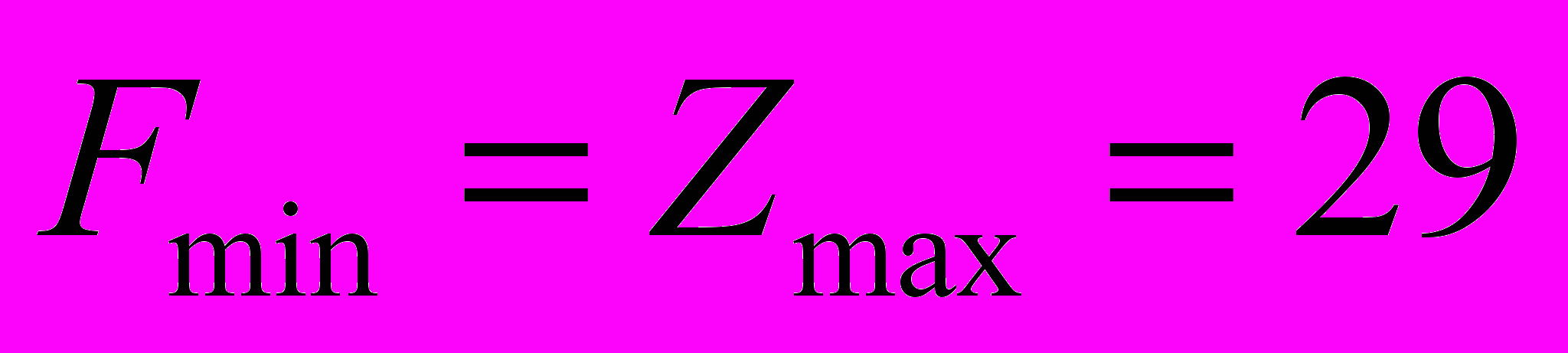
Транспортная задача. Пример

Исходные данные приведены в таблице 3, найти оптимальный план.

Таблица 3.

Мощность поставщиков
Мощность потребителей

40
40
30
40

80
5
4
3
4

70
3
2
5
5

30
1
6
3
2

Решение.

Проверим необходимое и достаточное условие разрешимости задачи.



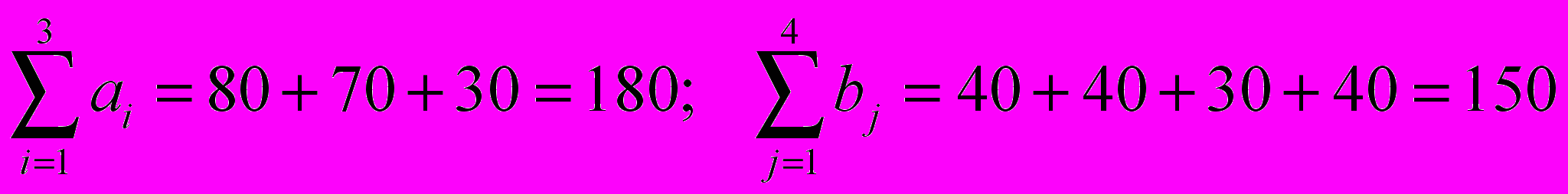
Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза у поставщиков. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительного (фиктивного) потребителя с потребностью 30 (180 - 150). Тарифы перевозки единицы груза от поставщика ко всем потребителям равны нулю.

Исходная таблица










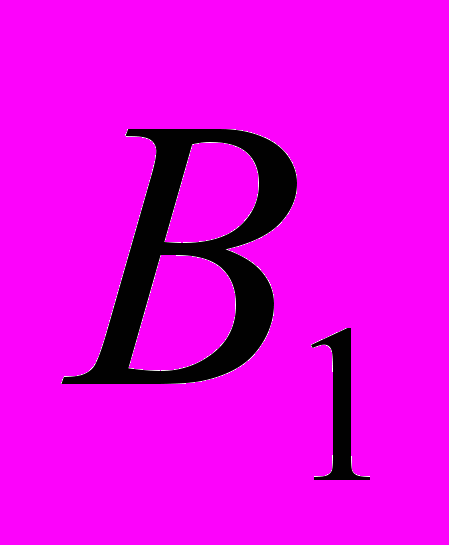
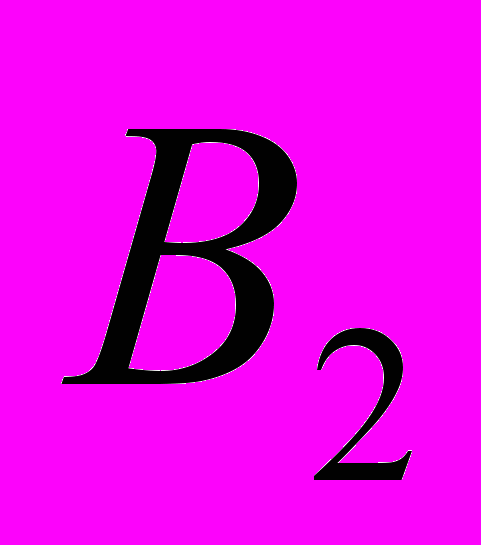
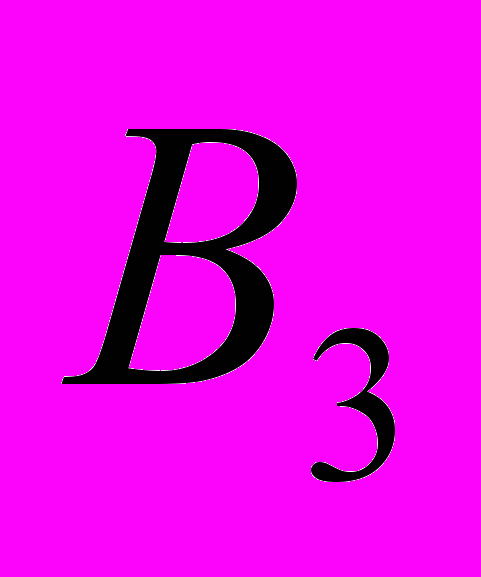
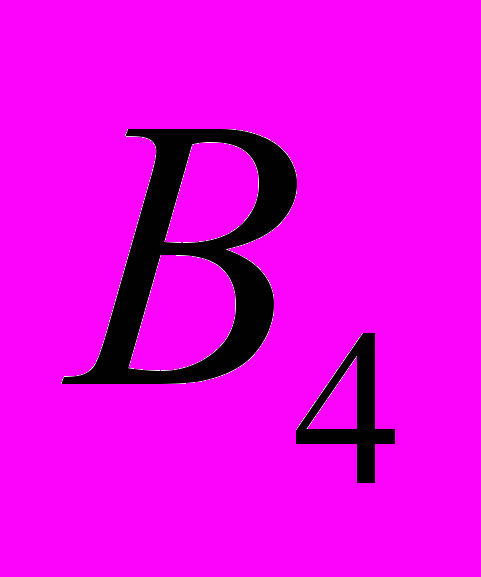
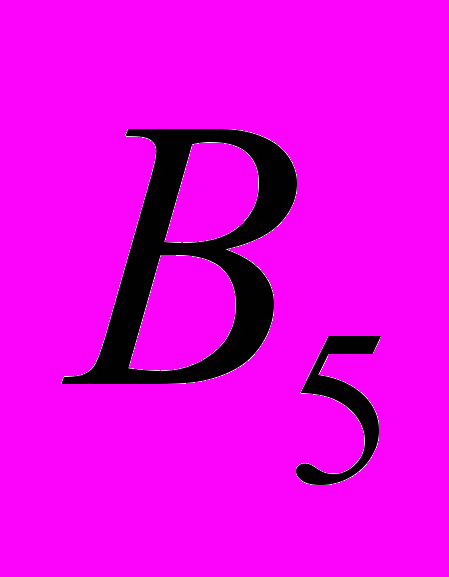
Запасы






5



4



3



4



0
80





















3



2



5



5



0
70





















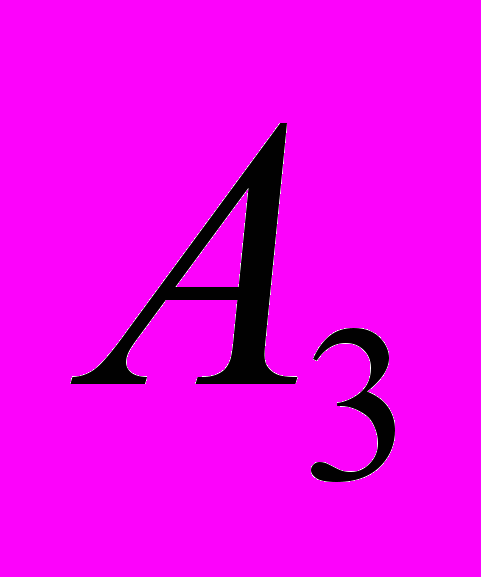
1



6



3



2



0
30
















Потребности
40
40
30
40
30




Используя метод минимального элемента, построим первый опорный план транспортной задачи.

Суть метода состоит в том, что из всей таблице стоимостей выбираем наименьшую и в эту клетку помещаем меньшее из чисел 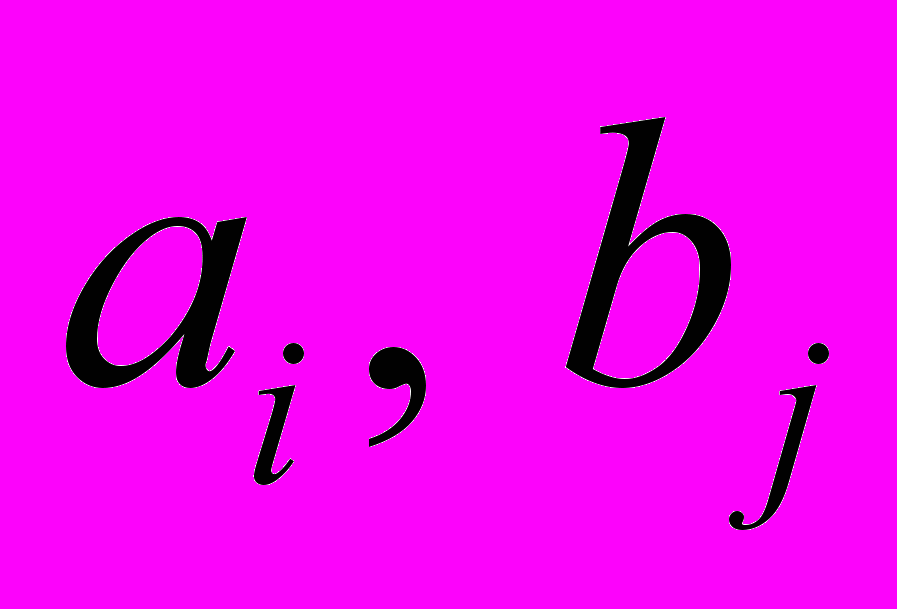. Затем из рассмотрения исключаем либо строку с поставщиком, запасы которого полностью израсходованы, либо столбец с потребителем, требования которого полностью удовлетворены










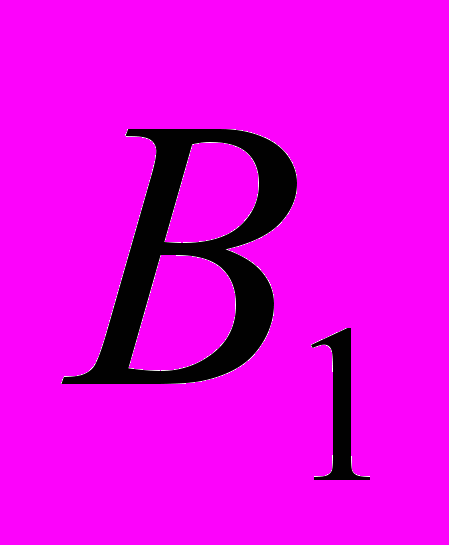
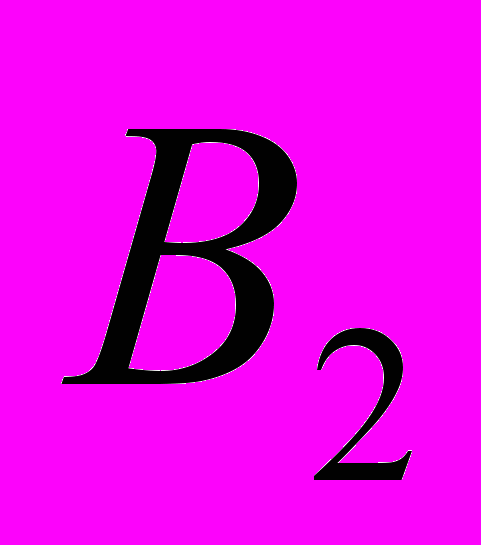
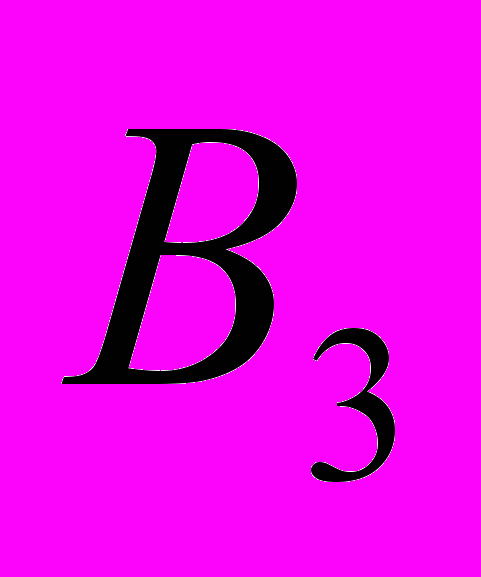
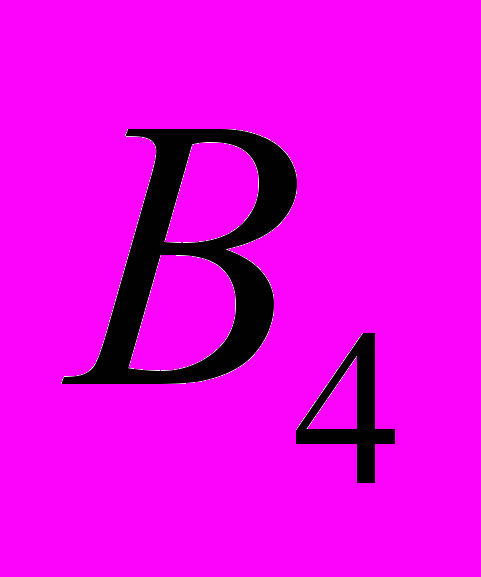
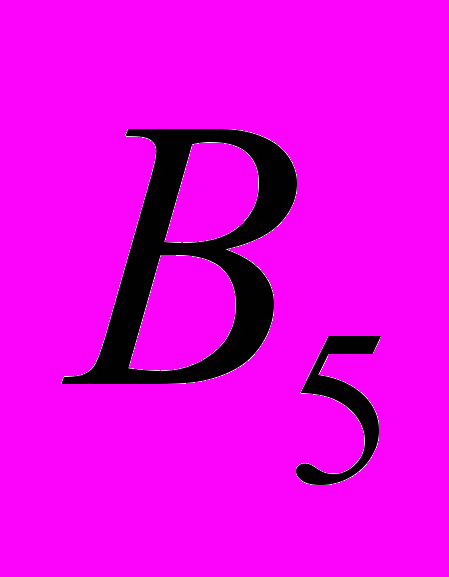
Запасы






5



4



3



4



0
80







30
20
30






3



2



5



5



0
70

10
40



20








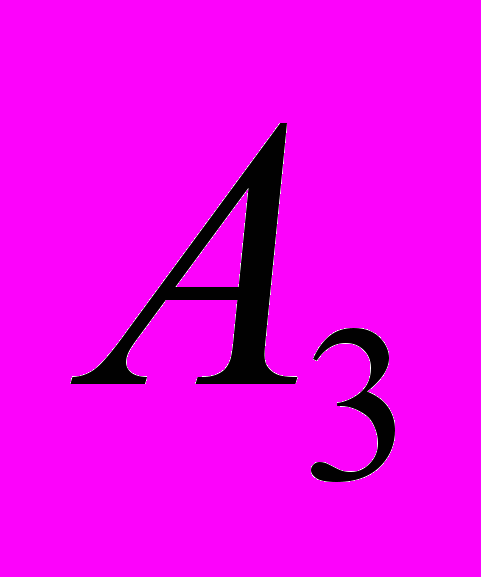
1



6



3



2



0
30

30












Потребности
40
40
30
40
30




Таким образом, получаем первоначальный опорный план.

Число занятых клеток таблице равно 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является вырожденным. Значение целевой функции для этого опорного плана равно::

F(x) = 330 + 420 + 030 + 310 + 240 + 520 + 130 = 410


^ Решаем задачу методом потенциалов. Полагая U1=0, определяем остальные потенциалы из соотношения Ui+Vj=Cij













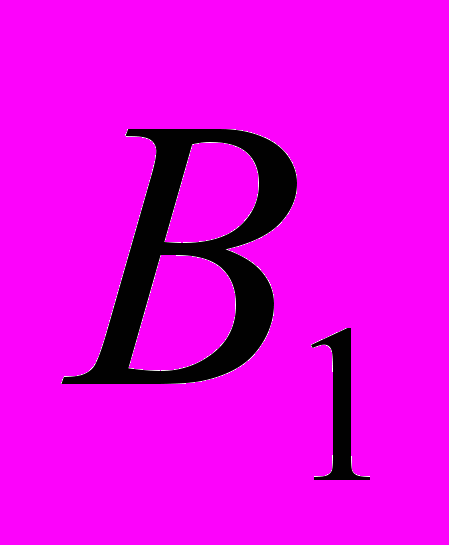
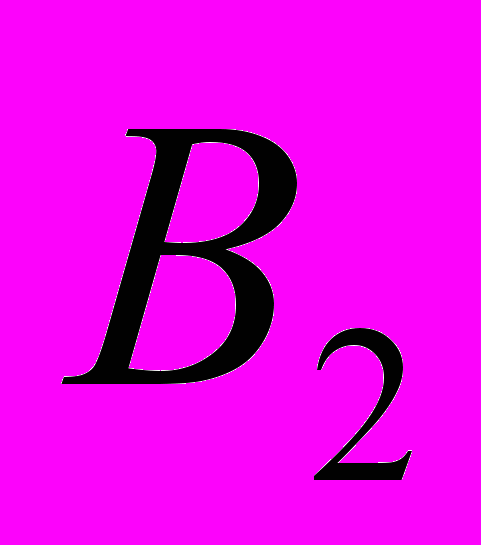
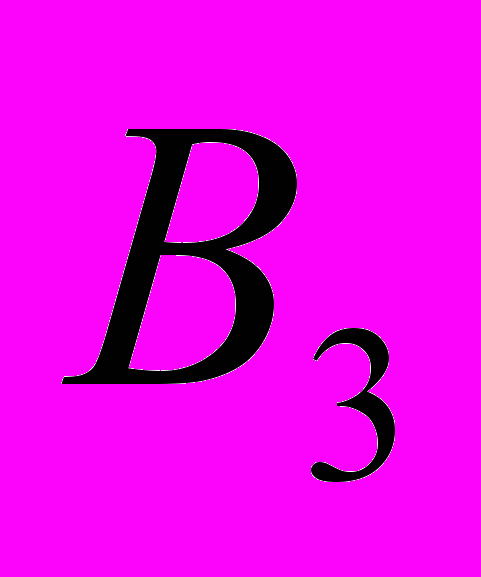
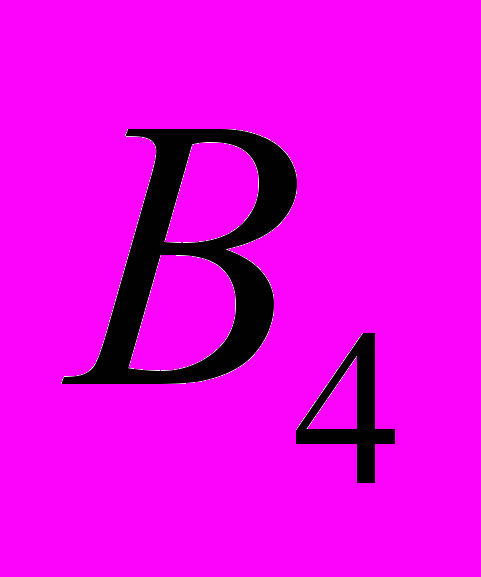
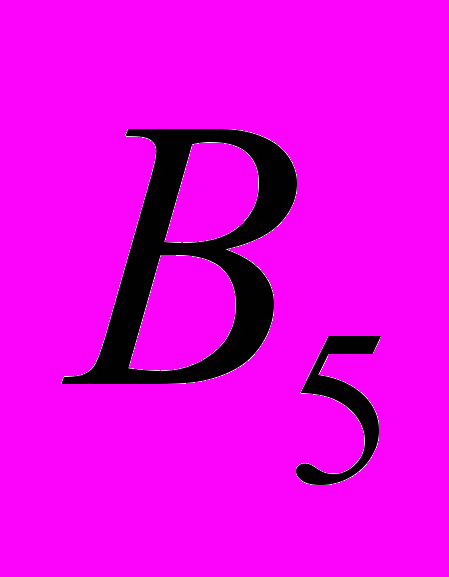
Ui






5



4



3



4



0
80
0







30
20
30






3



2



5



5



0
70
1

10
40



20








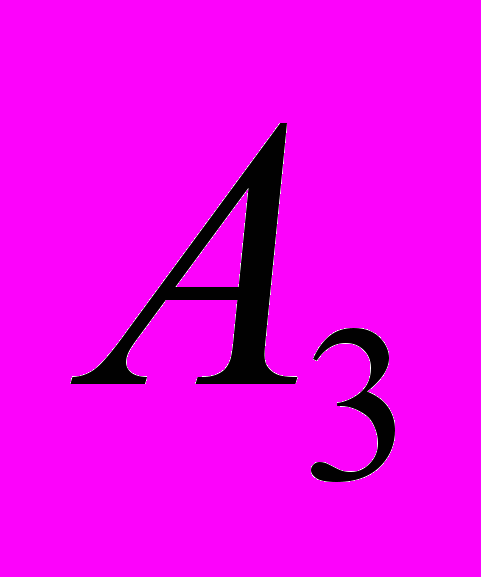
1



6



3



2



0
30
-1

30















40
40
30
40
30






Vj
2
1
3
4
0



Определим значения оценок 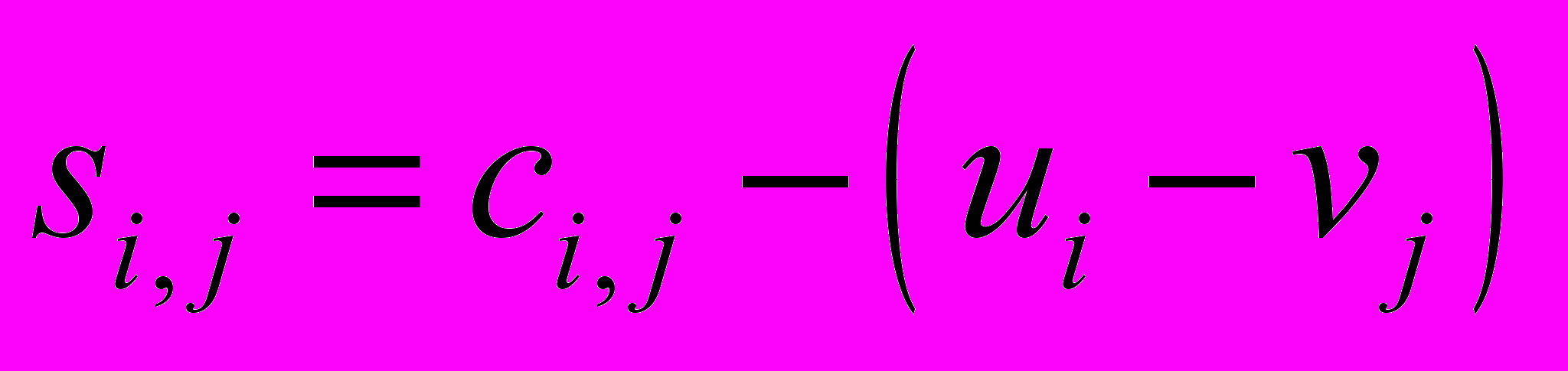в свободных клетках.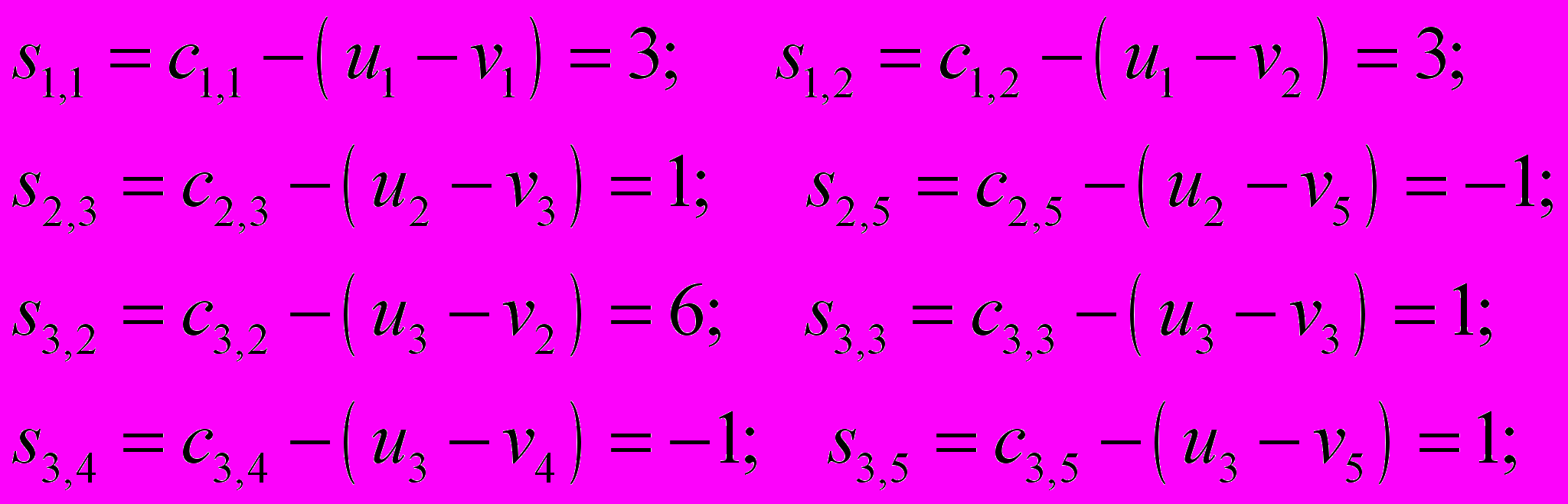



Полученный план не является оптимальным, так как имеются клетки с отрицательными оценками. Клетка (2; 5) является наиболее перспективной, поскольку имеет минимальный тариф. Ставим в ней + и создаем цикл.













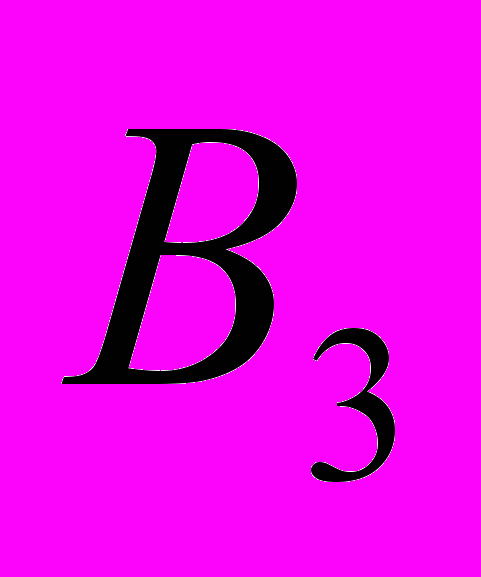
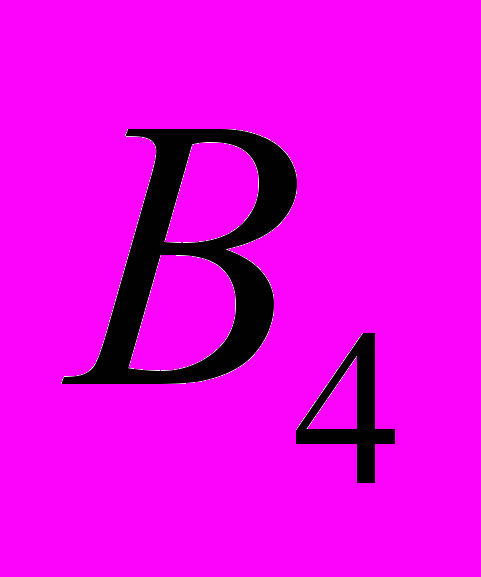
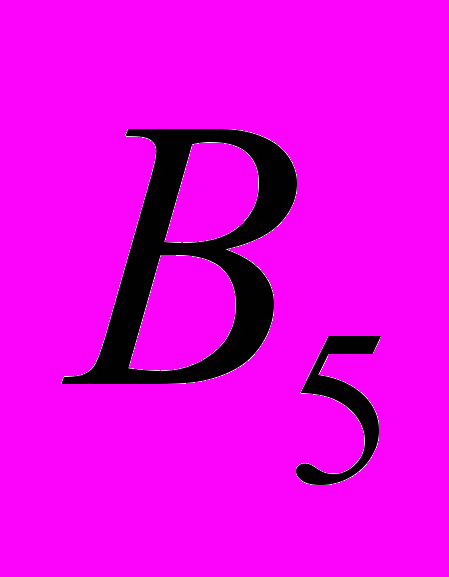
Ui






5



4



3



4



0
80
0







30
+20
- 30






3



2



5



5



0
70
1

10
40



-20
+






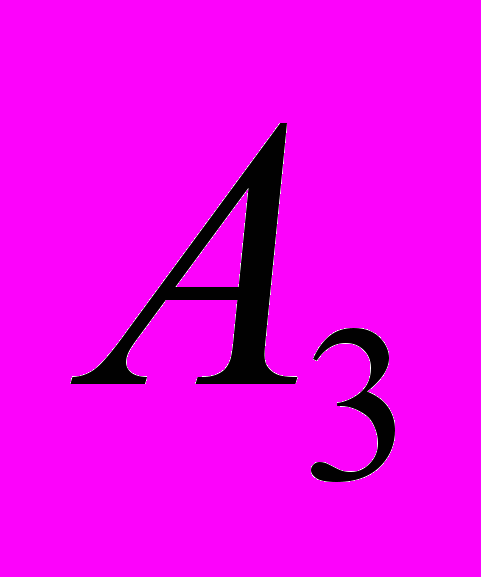
1



6



3



2



0
20
-1

30















40
40
30
40
30






Vj
2
1
3
4
0



В результате перемещения получим новый план













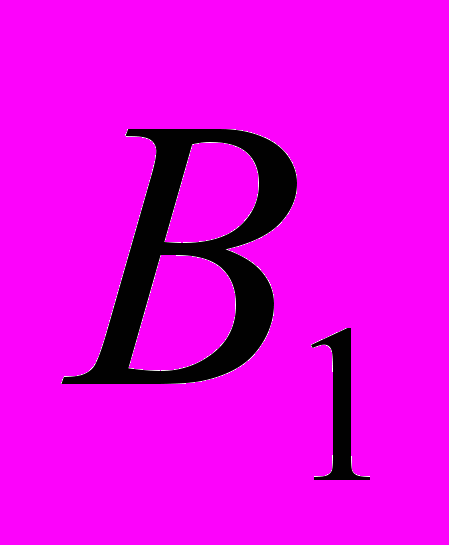
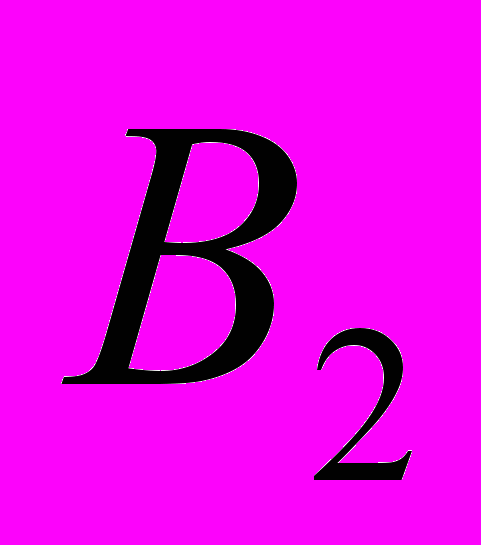
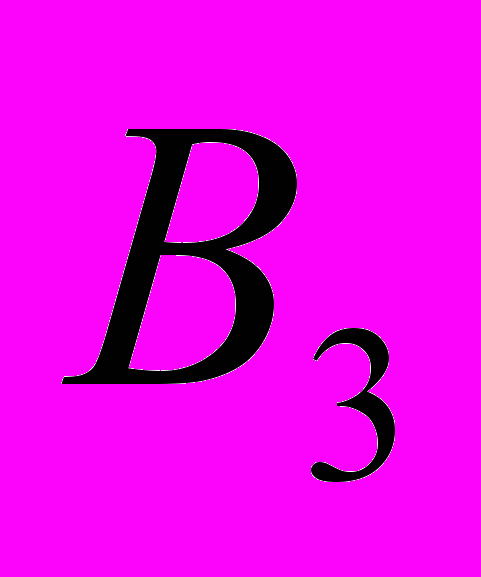
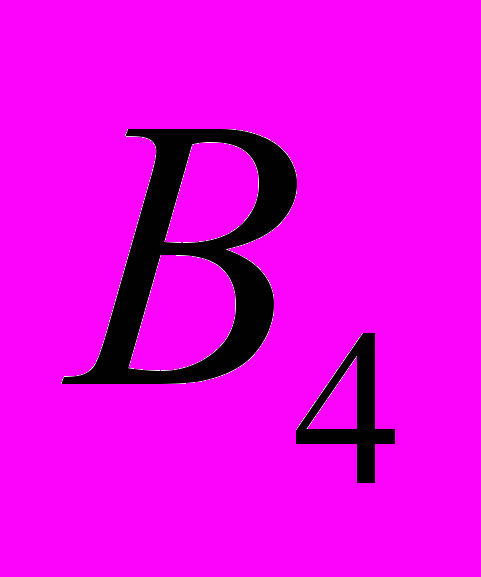
Ui






5



4



3



4



0
80
0







30
40
10






3



2



5



5



0
70
0

10
40






20






1



6



3



2



0
20
-2

30















40
40
30
40
30






Vj
3
1
3
4
0



Целевая функция F(x) = 330 + 440 + 010 + 310 +240 +020 + 130 = 390

Полагая U1=0, определяем остальные потенциалы из соотношения Ui+Vj=Cij

Определим значения оценок в свободных клетках.



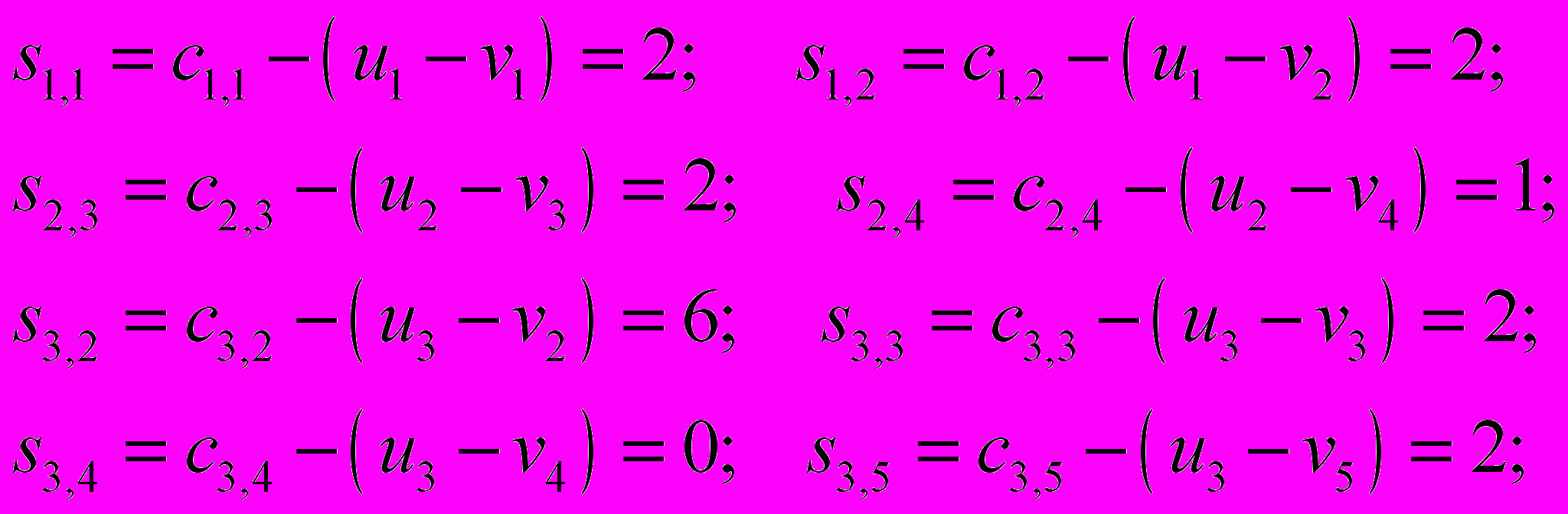
Так как все оценки неотрицательный, то получен оптимальный план. Задача решена.

Оптимальный план перевозок, т.е. количество груза, которое следует перевезти от каждого поставщика каждому потребителю при минимальных транспортных издержках F = 390 ден.ед. модно представить матрицей.




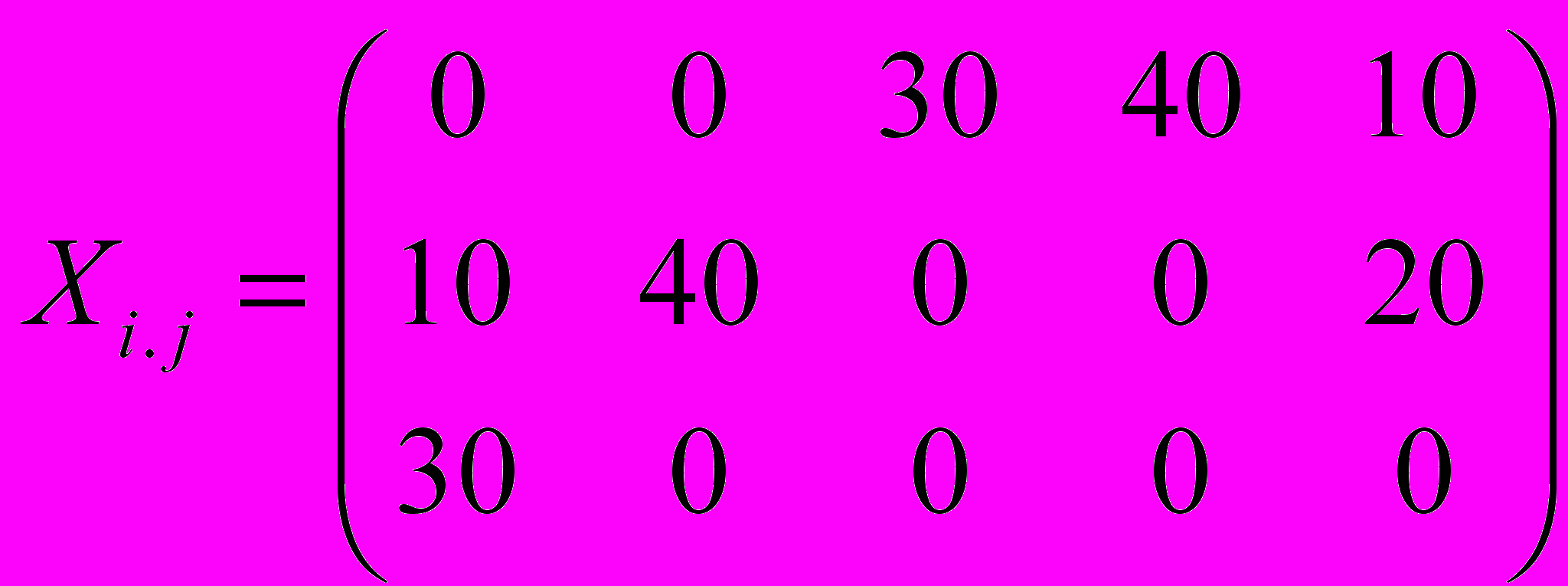
Литература
  1. Фомин Г.П. Методы и модели линейного программирования в коммерческой деятельности. Учебное пособие.- М.:Финансы и статистика, 2000 – 128 с.
  2. Коршунова Н.И., Пласунов В.С. Математика в экономике. Учебное пособие. М.: Вита-Пресс, 1996.
  3. Акулич И.Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986.
  4. Кузнецов А.В. и др. Высшая математика: математическое программирование.: высшая школа, 2001