Geum.ru

Использование возможностей программы GeoGebra при рассмотрении задач с экономическим содержанием

Вид материалаДокументы
Подобный материал:
Использование возможностей программы GeoGebra при рассмотрении задач с экономическим содержанием


Математические задачи с экономическим содержанием все чаще встречаются в образовательной практике. Это связано не только с профилизацией школ, но и с ориентацией математической подготовки на рассмотрение примеров, связанных с реальными процессами и системами. Достаточно рано можно знакомить учащихся с идеями, лежащими в основе задач линейного программирования, а использование информационных технологий обучения позволяет наглядно представить их решение.

В последнее время большой популярностью пользуются программы динамической геометрии, среди которых хочется выделить следующие: «Живая геометрия», «Математический конструктор», «GeoGebra». Первая и третья программы разработаны за рубежом, но русифицированы, вторая программа является отечественной разработкой достаточно высокого уровня. Программа GeoGebra выделяется тем, что, не уступая упомянутым аналогам, является бесплатной, т.е. доступна для свободного использования на самых разных уровнях, что для организации внеаудиторной работы может играть существенную роль.

Одной из типовых задач линейного программирования является задача об использовании ресурсов. Она имеет простую математическую модель, в рамках которой учащихся можно познакомить с идеями оптимизации. Кроме этого использование возможностей программ динамической геометрии позволяет рассмотреть окрестность задачи и проиллюстрировать некоторые существенные факты.

Рассмотрим задачу: фирма выпускает изделия двух типов, A и B. При этом используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы изделия А равны 2, 1, 0 и 3 единицы соответственно; а расход сырья каждого вида на изготовление единицы изделия В равны 3, 0, 1 и 1 единицы соответственно. Запасы сырья первого вида составляют 21 ед., второго вида – 4 ед., третьего вида – 6 ед. и четвертого вида – 14 ед. выпуск одного изделия А приносит доход 3 д.е., одного изделия B – 2 д.е. Составить план производства, обеспечивающий фирме наибольший доход.

Экономико-математическая модель задачи имеет вид:

х, ед. – количество изделий типа А, которое необходимо произвести;

y, ед. – количество изделий типа В, которое необходимо произвести.

Требуется максимизировать доход, выражающийся линейной функцией (целевой): .

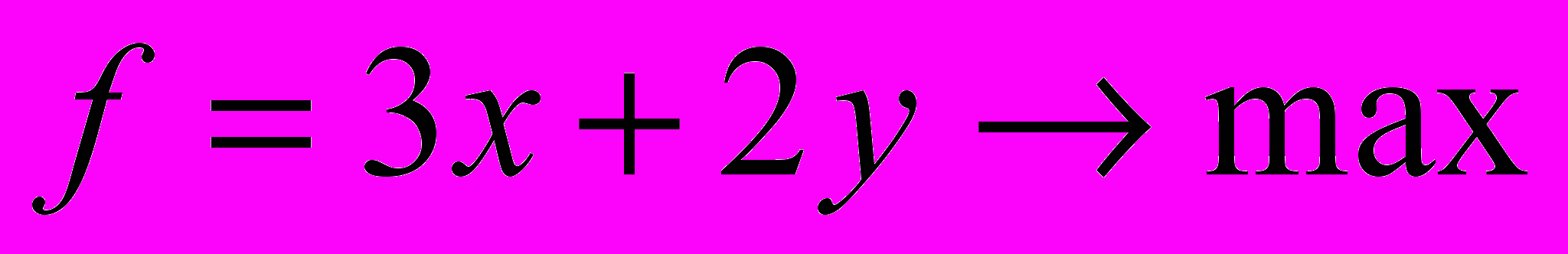При этом переменные х и y должны удовлетворять следующим линейным неравенствам, отражающим ограничения на запасы сырья: , , , , , .

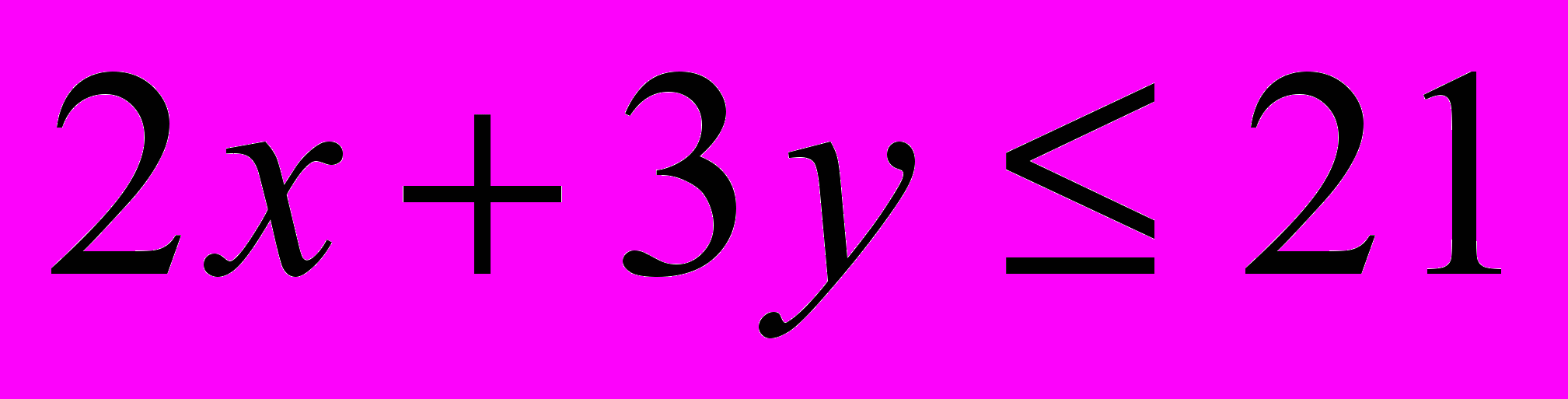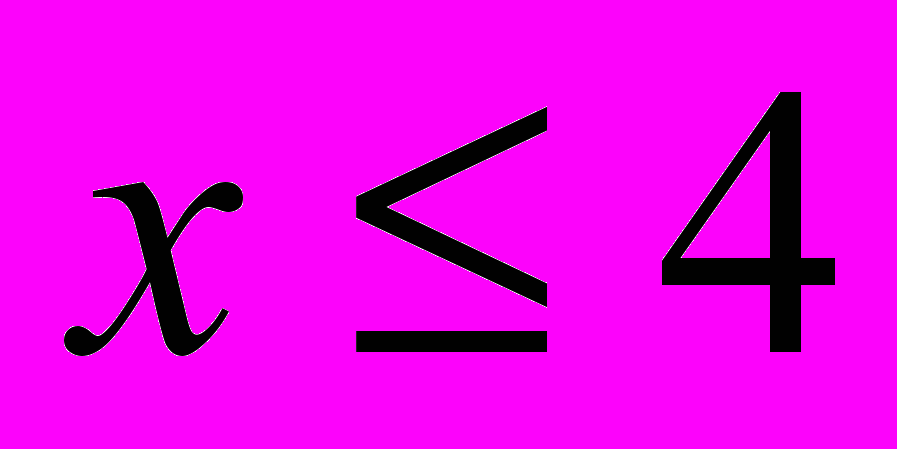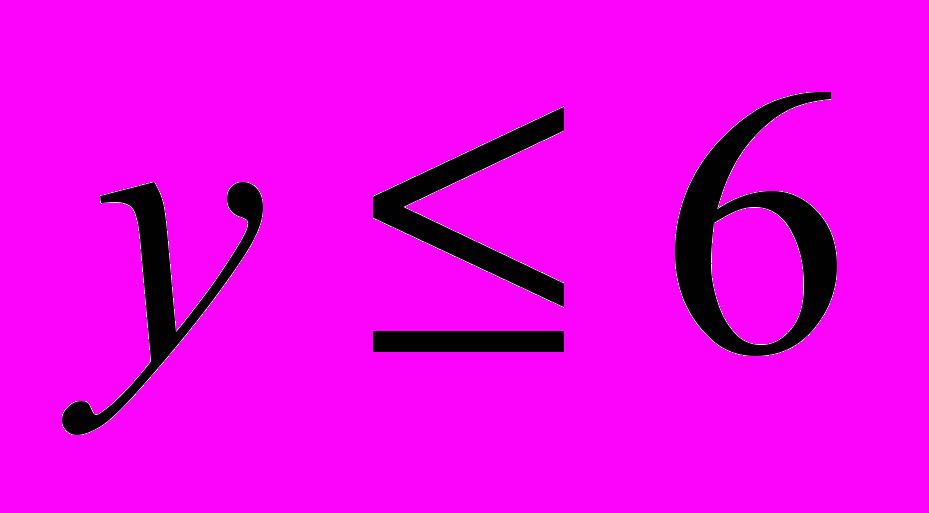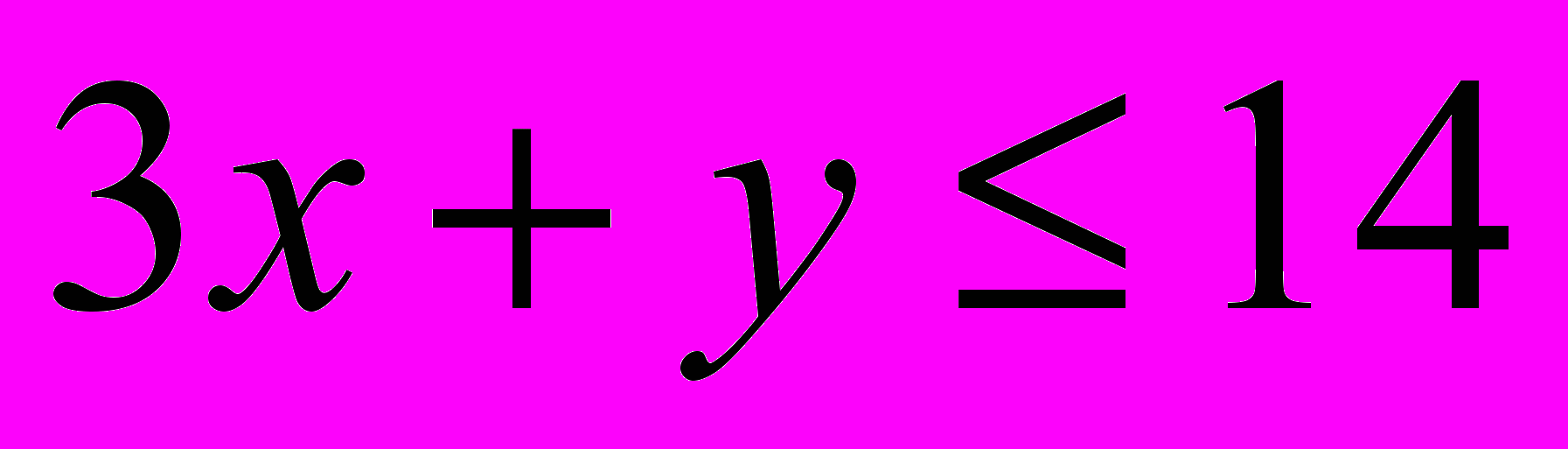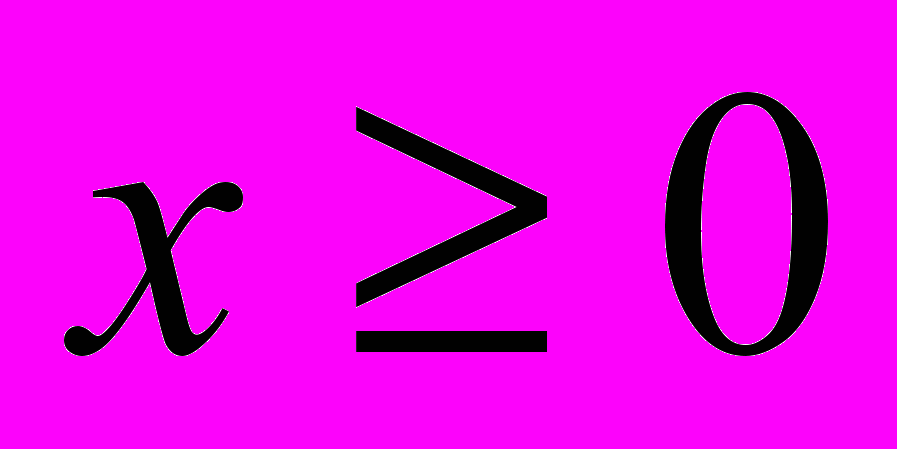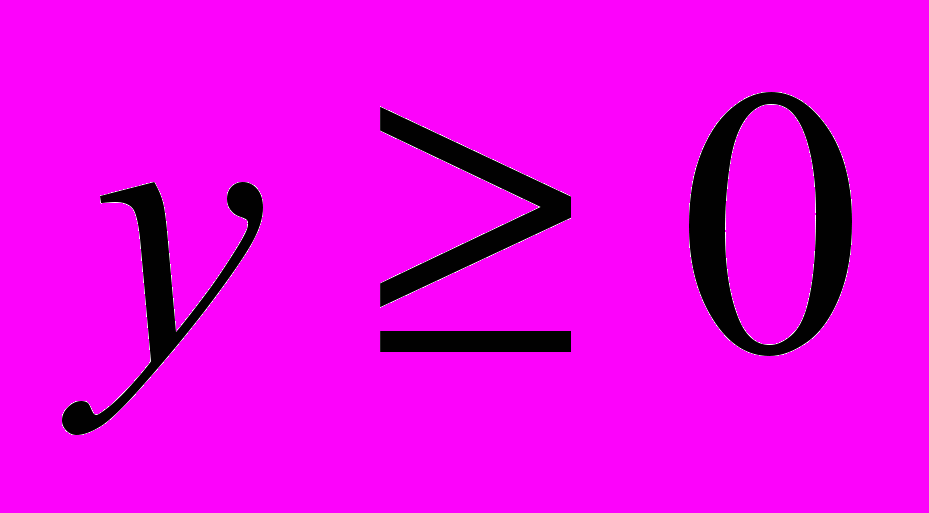Решение графическим методом требует небольших знаний из аналитической геометрии и может быть рассмотрено со способными учащимися уже в 7-8 классе. Школьники должны уметь строить прямую линию по ее общему уравнению, кроме этого может понадобиться решить систему двух линейных уравнений.

Совершенно очевидно, что современного школьника необходимо знакомить с возможностями применения различных программных средств к решению математических задач. Это позволит достичь самых разных образовательных целей: помогает формировать мотивацию, тренирует навыки самоконтроля, развивает исследовательские и творческие способности и т.д.

Рассмотрим возможности программы GeoGebra в применении к графическому решению задачи линейного программирования. Для работы с ней не требуется специальных знаний и достаточно опыта работы в универсальных редакторах (графическом, электронные таблицы). Кроме этого программу GeoGebra можно свободно и бесплатно скачать с официального сайта (ее объем 16 mb). В ходе занятия учитель в течение нескольких минут может продемонстрировать построение в программе области допустимых значений и опорную прямую, перемещая которую легко определяется точка, в которой целевая функция достигает максимума. После этого способные школьники самостоятельно смогут решать аналогичные задачи в программе.

На рисунке представлен динамический чертеж в виде найденного решения: целевая функция достигает максимума в точке С(3; 5) и принимает значение 19 д.е.




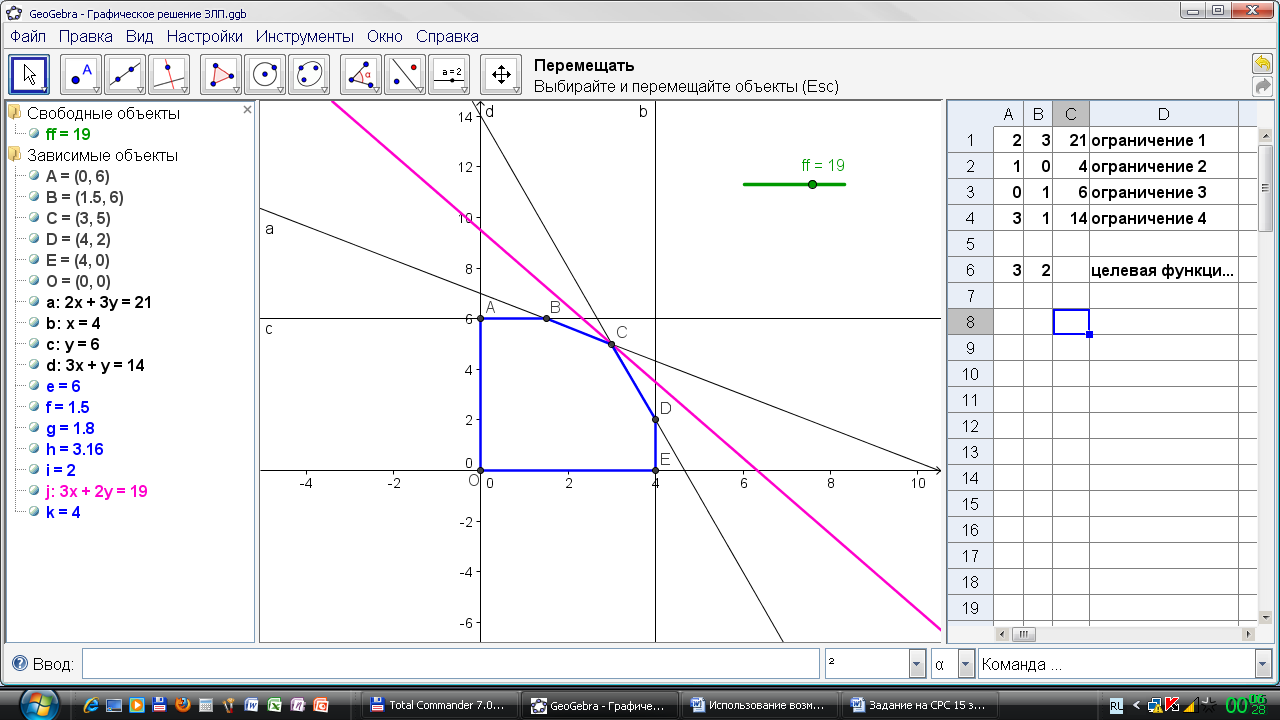
Рис. Динамический чертеж к задаче об использовании ресурсов


Для построения прямой достаточно ввести ее уравнение в строке ввода в виде 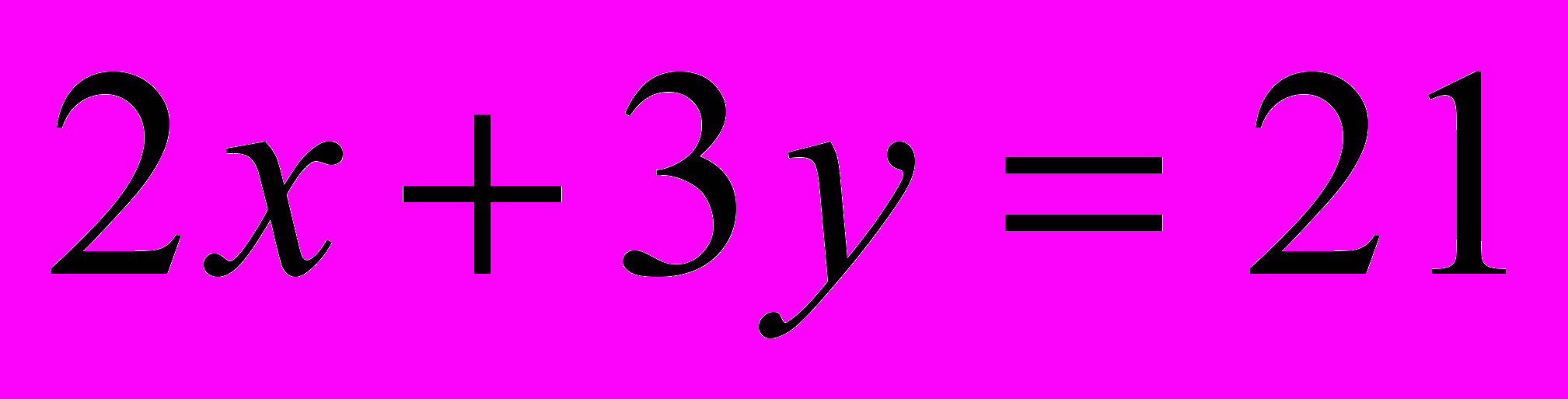. Для получения дополнительных возможностей с чертежом коэффициенты уравнения расположены в таблице, а само уравнение содержит ссылки на ее ячейки: 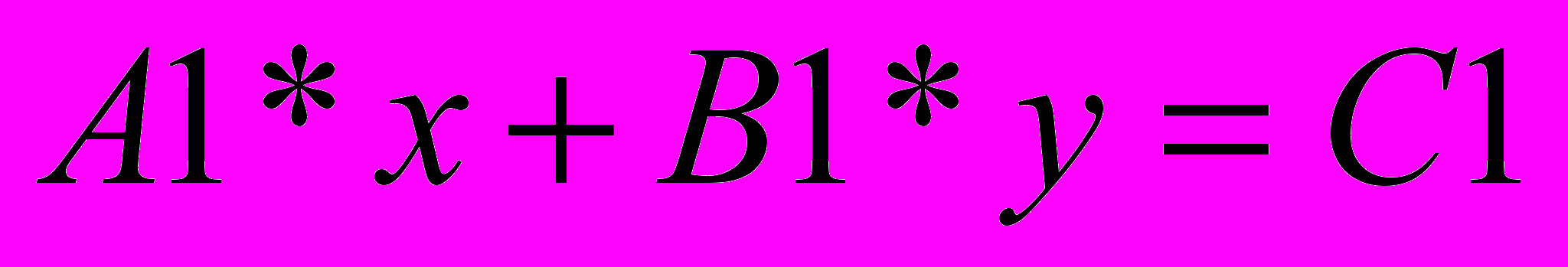. При изменении значений в ячейках таблицы меняется расположение соответствующей прямой. Такой подход позволяет обратить внимание учащихся на чувствительность найденного решения к небольшим изменениям условия (к малым шевелениям), что на практике всегда связано с погрешностью измерений. Чтобы опорная прямая, соответствующая различным уровням целевой функции, была подвижной, вводим параметр ff, значение которого меняется с помощью бегунка. Уравнение опорной прямой можно ввести в виде: 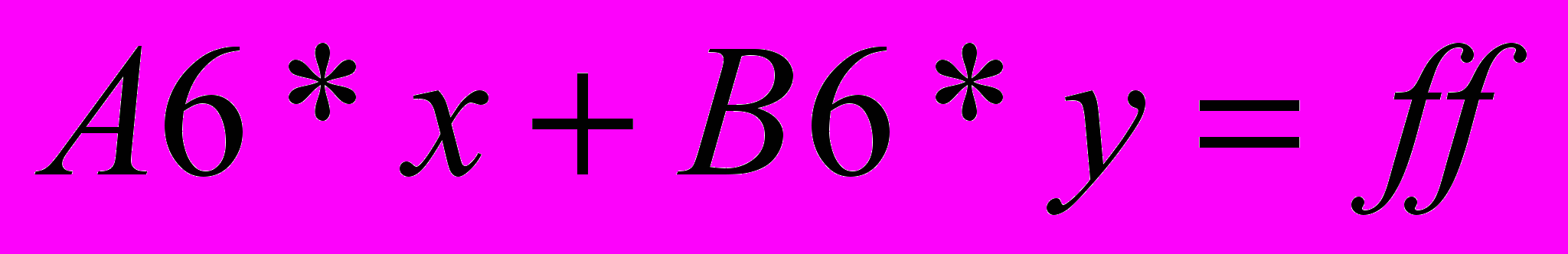. После небольшого изменения, например, на 0,1 в таблице коэффициентов целевой функции наглядно видно, что решение осталось прежним и даже более сильные колебания этих коэффициентов не меняют решения.

Достаточно очевидным по чертежу представляется выпуклость области допустимых решений и тот факт, что оптимальное решение находится в одной из вершин многоугольника. Отсюда следует возможность отыскания решения перебором вершин многоугольника, но в многомерном случае это потребует большого количества расчетов. Со школьниками можно обсудить вопрос определения количества этапов такого перебора. Также можно поговорить о неединственности решения или его отсутствии.

Таким образом, за небольшое время появляется возможность с помощью общедоступной программы динамической геометрии рассмотреть со школьниками применение методов аналитической геометрии к решению практико-ориентированных задач с экономическим содержанием.