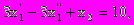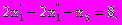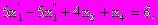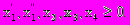Исследование операций

Вид материала

Исследование

Содержание Исследование операций Цель исследования операций 1.2. Прямые и обратные задачи исследования операций II. Линейное программирование

Подобный материал:

• Исследование операций " для подготовки специалиста по cпециальности 030100, 77.09kb.
• Журналы российской академии наук, 50.22kb.
• Журналы Российской академии наук, 48.74kb.
• Рабочей программы дисциплины Исследование операций по направлению подготовки 230700, 16.33kb.
• Формирование исследования операций как самостоятельной ветви прикладной математики, 99.74kb.
• Программа дисциплины Исследование операций для направления080200. 62 Менеджмент подготовки, 206.74kb.
• Исследование операций, 176.07kb.
• Программа учебной дисциплины «Математические модели в теории управления и исследование, 114.92kb.
• Исследование операций, 82.88kb.
• Учебной дисциплины «Теория игр и исследование операций» для направления 010100., 42.57kb.

УДК 519.85


Исследование операций


Учебное пособие представляет собой конспект лекций для студентов экономических специальностей по одноименной дисциплине. В каждой главе рассматриваются примеры решения задач, а в конце глав тесты и задачи, которые должны помочь усвоению материала.

I. Предмет и задачи исследования операций

1.1 Предмет исследования операций

Экономика, рынок - это сложные системы, состоящие из множества взаимосвязанных объектов. Если число объектов возрастает линейно, то число связей между ними возрастает по крайней мере по квадратичному закону. В этих условиях даже талантливые менеджеры не могут принимать обоснованные, оптимальные решения без привлечения новейших математических методов и электронно-вычислительной техники. Потребности практики обоснования решений в сложных условиях вызвали необходимость разрабатывать научные методы, которые объединены под общим названием “исследование операций”.

^ Исследование операций - это применение количественных методов обоснования решений во всех областях целенаправленной человеческой деятельности.

Чем сложнее, дороже, масштабнее планируемое мероприятие, тем менее допустимы в нем “волюнтаристские” решения и тем важнее становятся научные методы, позволяющие заранее оценить последствия каждого решения, отбросить недопустимые варианты и рекомендовать наиболее выгодные.

Под операцией далее будет пониматься всякое мероприятие, объединенное единым замыслом и направленное к достижению какой-либо цели. Операция есть всегда управляемое мероприятие, поскольку от менеджера зависит, какими выбрать параметры, характеризующие ее организацию.

Всякий определенный выбор этих параметров называется решением. Решения могут быть удачными и неудачными. Оптимальными называются решения, которые по тем или иным критериям (признакам) являются предпочтительными перед другими.

^ Цель исследования операций - предварительное количественное обоснование оптимальных решений.

Само принятое решение выходит за рамки исследования операций и относится к компетенции руководителя или групп лиц, которым предоставлено право выбора решения и на которых возложена ответственность за этот выбор.

Для применения количественных методов исследования операций в любой области всегда требуется какая-то математическая модель. При построении модели реальная операция неизбежно упрощается. Чем удачнее будет подобрана математическая модель, тем лучше она будет отражать характерные черты явления, тем успешнее будет исследование и полезнее вытекающие из него рекомендации (решения).

Общих способов построения моделей не существует. С одной стороны, математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых в основном зависит успех операции. С другой стороны, модель должна быть по возможности простой, не усложненной множеством мелких второстепенных факторов. Искусство строить математические модели есть именно искусство, и опыт в нем приобретается постепенно. Эта самая важная и ответственная часть исследования, требующая глубоких знаний не столько математики, сколько существа моделируемых явлений.

Известный специалист в области исследования операций Т.Л.Саати дал такое шутливое определение: “Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются еще худшие ответы другими способами”.

В связи с этим определением приведем “проблему лифта”, которая используется в качестве иллюстрации во многих книгах по исследованию операций. Суть этой проблемы проста. Служащие одной из фирм жаловались на слишком продолжительное время ожидания лифта, которым оснащено административное здание фирмы.

Была предпринята попытка решить возникшую проблему методами теории массового обслуживания. Полученное решение по ряду соображений оказалось неприемлемым. Дальнейшее исследование показало, что претензии служащих были необоснованны, так как в действительности время ожидания лифта было приемлемым. Тогда возникла идея установить на каждом этаже рядом со входом в лифт большие зеркала. Когда это было сделано, жалобы сразу же прекратились. Теперь люди в ожидании лифта рассматривали свои зеркальные отражения. Время при этом проходило незаметно.

Приведенный пример демонстрирует необходимость правильно оценивать возможности математического описания исследуемых явлений и помнить, что в сфере организационного управления далеко не все поддается формализации и, следовательно, адекватному отражению в математической модели.

С другой стороны, практические ситуации, в которых приходится принимать решения, бывают настолько сложными и важными, что даже небольшая помощь в обосновании решений, полученная математическими методами, является весьма существенной.


^ 1.2. Прямые и обратные задачи исследования операций

Задачи исследования операций делятся на два класса: прямые и обратные.

Прямые задачи отвечают на вопрос: что будет, если в заданных условиях будет принято решение 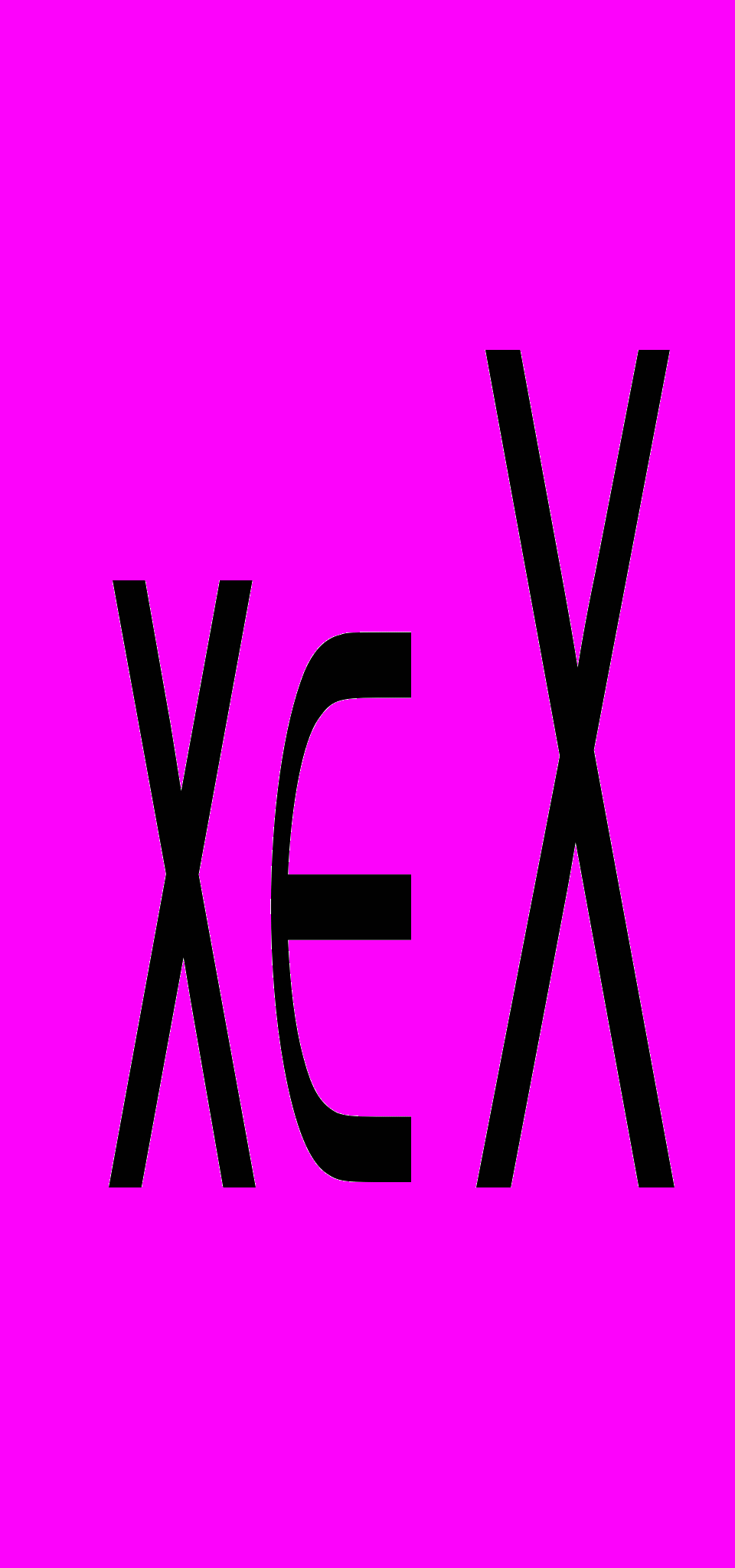?. В частности, чему будет равен, при данном решении х, выбранный показатель эффективности L(х).

Для решения прямой задачи строится математическая модель, позволяющая выразить показатель эффективности через заданные условия и выбранные х.

Обратные задачи отвечают на вопрос: как выбрать решение хХ для того, чтобы показатель эффективности L обратился в максимум? Очевидно, что прямые задачи решать проще обратных, - ведь для решения обратной задачи прежде всего надо уметь решать прямую. Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются.

Для решения обратных задач для многих экономических задач используются методы математического программирования. Они позволяют отыскать значения переменных, обеспечивающих экстремум показателя эффективности при наличии ограничений, накладываемых на эти переменные. Слово программирование в данном случае является неудачным переводом слова “program”, которое в рассматриваемом случае означает “планирование”.

В общем виде задача математического программирования может быть записана следующим образом:

найти максимум или минимум функции многих переменных

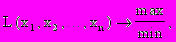(1.1)

при ограничениях

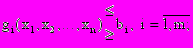(1.2)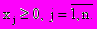

(1.3.)

Функция L(х₁, х₂, ..., х_n) называется целевой функцией, она характеризует эффективность исследуемой модели. Ограничения (1.2) и (1.3) определяют область допустимых значений вектора неизвестных переменных

х=/ х₁, х₂, ..., х_n/.

В зависимости от вида целевой функции и ограничений детерминированные задачи математического программирования подразделяются на задачи линейного программирования, нелинейного программирования, целочисленного программирования (рис. 1.1).




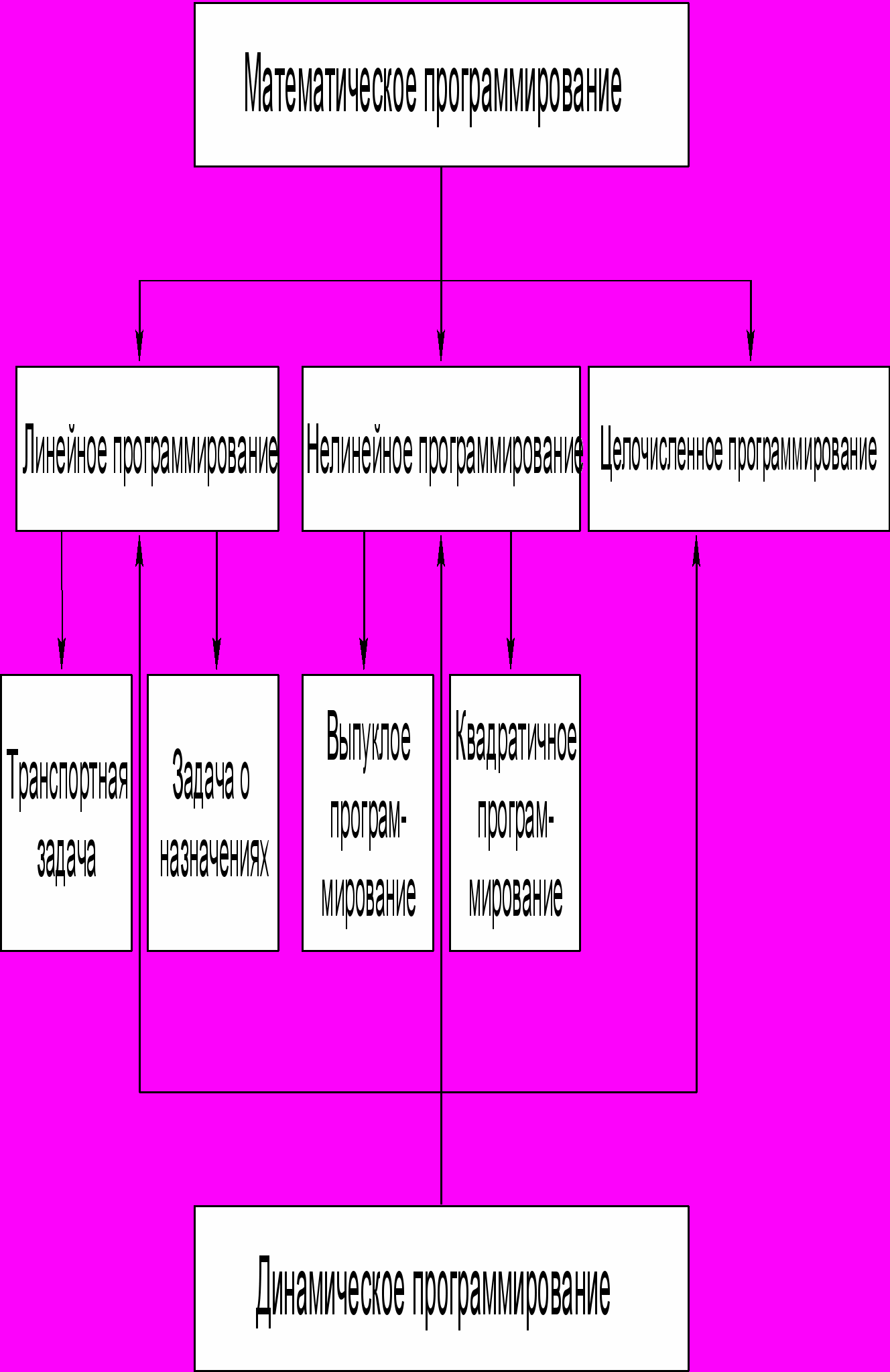
Рис. 1.1

К задачам линейного программирования относятся те, у которых целевая функция f(x) линейно зависит от неизвестных х₁, х₂, ..., х_n, а ограничения, налагаемые на эти неизвестные, имеют вид линейных равенств или неравенств. В линейном программировании существуют классы задач, структура которых позволяет разработать для их решения более простые специальные методы. Так в линейном программировании появились разделы транспортных задач и задач о назначениях.

Если целевая функция нелинейная или нелинейны ограничения, то данная задача относится к задачам нелинейного программирования.

Нелинейное программирование в свою очередь имеет подразделы выпуклого программирования (целевая функция и ограничения выпуклы) и квадратичного программирования (целевая функция квадратичная, а ограничения линейны).

Отдельным классом задач математического программирования являются задачи целочисленного программирования. В задачах целочисленного программирования искомые переменные могут принимать только целые числа.

Для оптимизации управления многошаговыми операциями разработан метод динамического программирования, которым можно решать многошаговые линейные, нелинейные и целочисленные задачи.

В случаях, когда в задачах содержатся кроме детерминированных параметров еще и неизвестные случайные параметры, требуется применять методы стохастического программирования.


^ II. Линейное программирование

2.1. Задачи линейного программирования

Пример 1. Фирма “Сатурн” изготавливает два вида продукции П₁ и П₂, реализация которых с учетом производственных возможностей фирмы неограниченна. Для производства используются ресурсы трех типов: трудовые, материальные, финансовые. Известно количество ресурсов, которое имеется в распоряжении фирмы, а также затраты каждого вида ресурсов для изготовления единицы продукции П₁ и П₂. Известна также прибыль на единицу каждого вида продукции. Эти данные представлены в таблице 2.1.

Таблица 2.1

Ресурсы	Затраты на	единицу продукции	Наличие
	П1	П2	ресурсов
Трудовые	2	8	28
Материальные	1	3	32
Финансовые	12	4	50
Прибыль на единицу продукции	3	5

Необходимо составить план распределения ресурсов.

Для решения задачи необходимо составить математическую модель данной операции. Для этого необходимо вначале ответить на следующие вопросы:

• какие параметры нужно определить в данной задаче?
  
• какой критерий оптимальности планирования необходим для данной задачи? (что характеризует эффективность исследуемой модели?)
  
• какие ограничения существуют при решении данной задачи.
  

Для рассматриваемой задачи планирования неизвестными являются планы выпуска продукции П₁ и П₂.

Поскольку выпуск продукции в постановке задачи не ограничен, то в качестве критерия необходимо взять получение максимально возможной прибыли.

Естественными являются ограничения на используемые ресурсы, которые не могут превышать их наличия.

После ответа на эти вопросы строится математическая модель.

1. Переменные (искомые величины) данной задачи обозначим через х₁ - план выпуска продукции П₁ и х₂ - план выпуска продукции П₂.
   
2. Целевая функция (прибыль) должна быть максимизирована
   

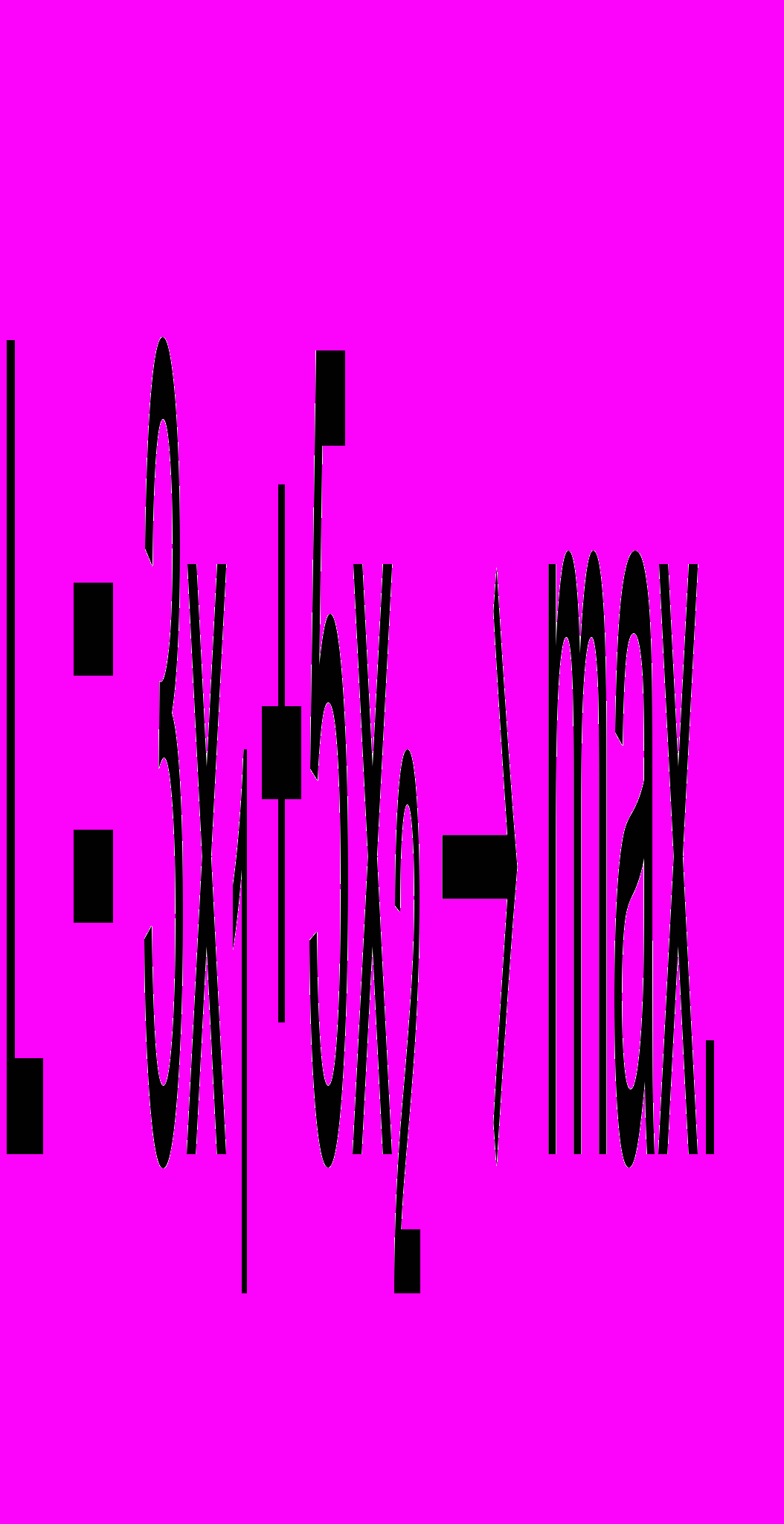
3. Ограничения на расходуемые ресурсы можно записать следующим образом
   

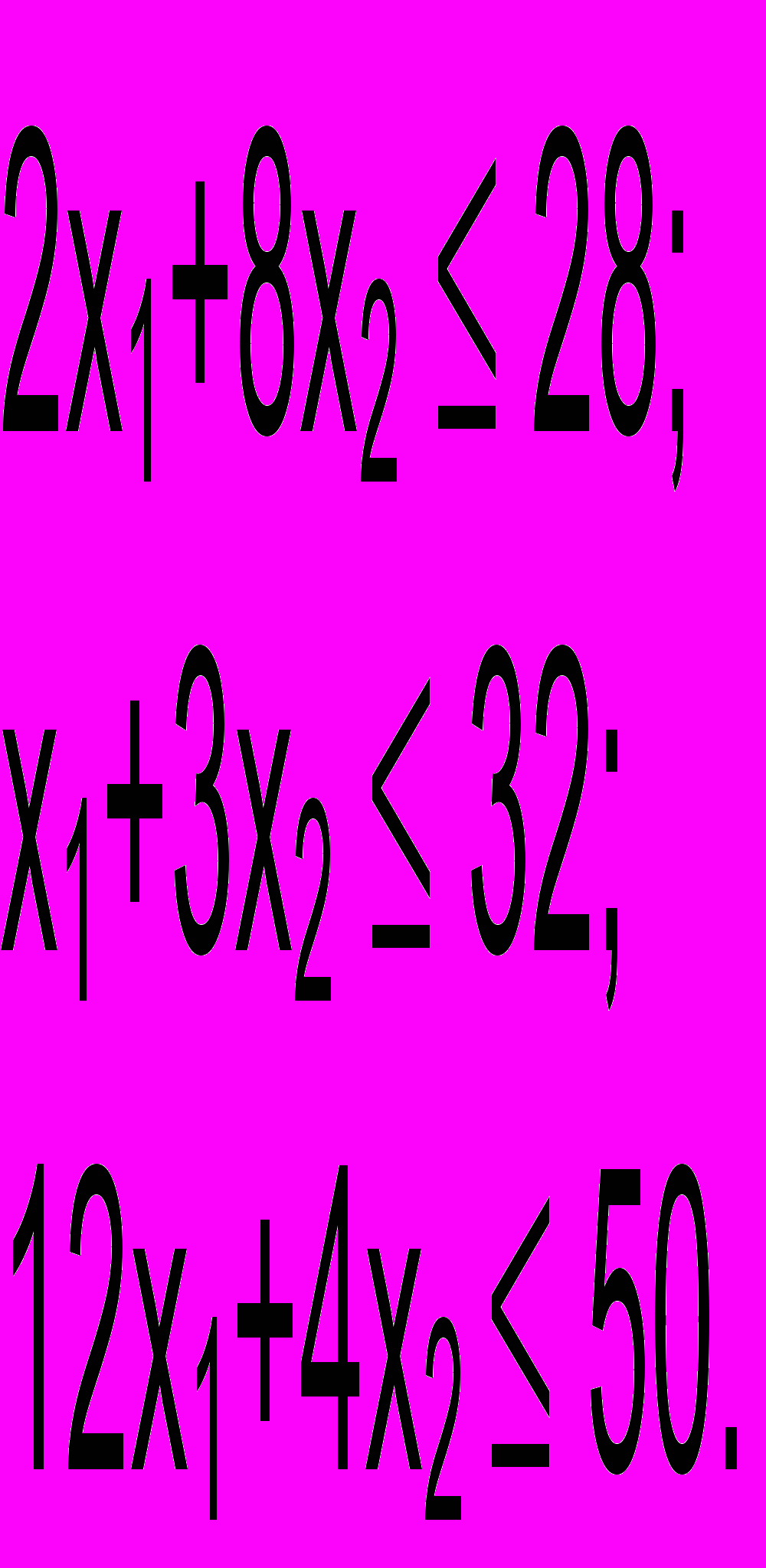
Кроме того, естественные ограничения заключаются в том, что планы выпуска продукции П₁ и П₂ не могут быть отрицательными, т.е. необходимо ввести ограничения на их знак:



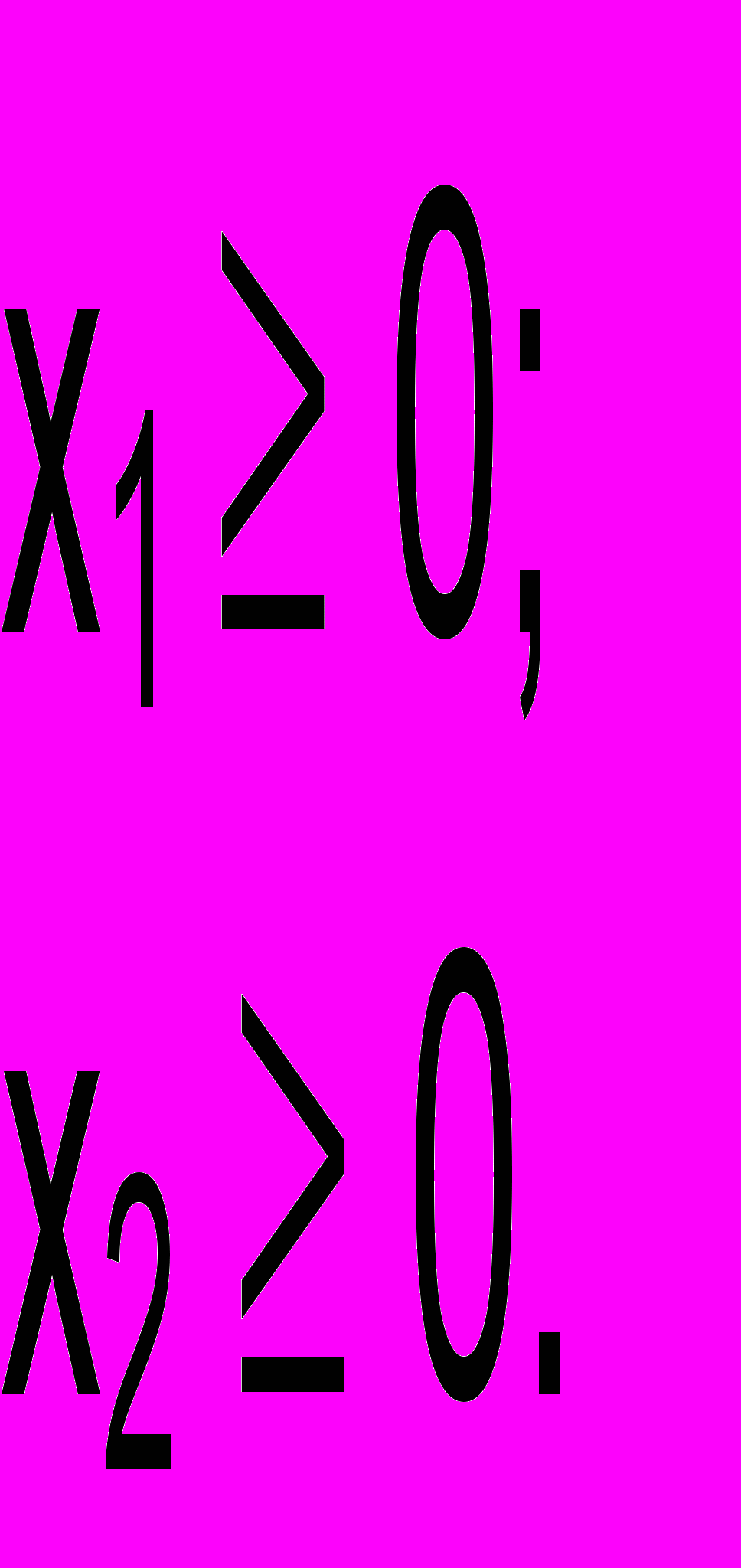
Таким образом, мы получили математическую модель рассматриваемой задачи: найти такие х₁ и х₂, , которые обеспечат



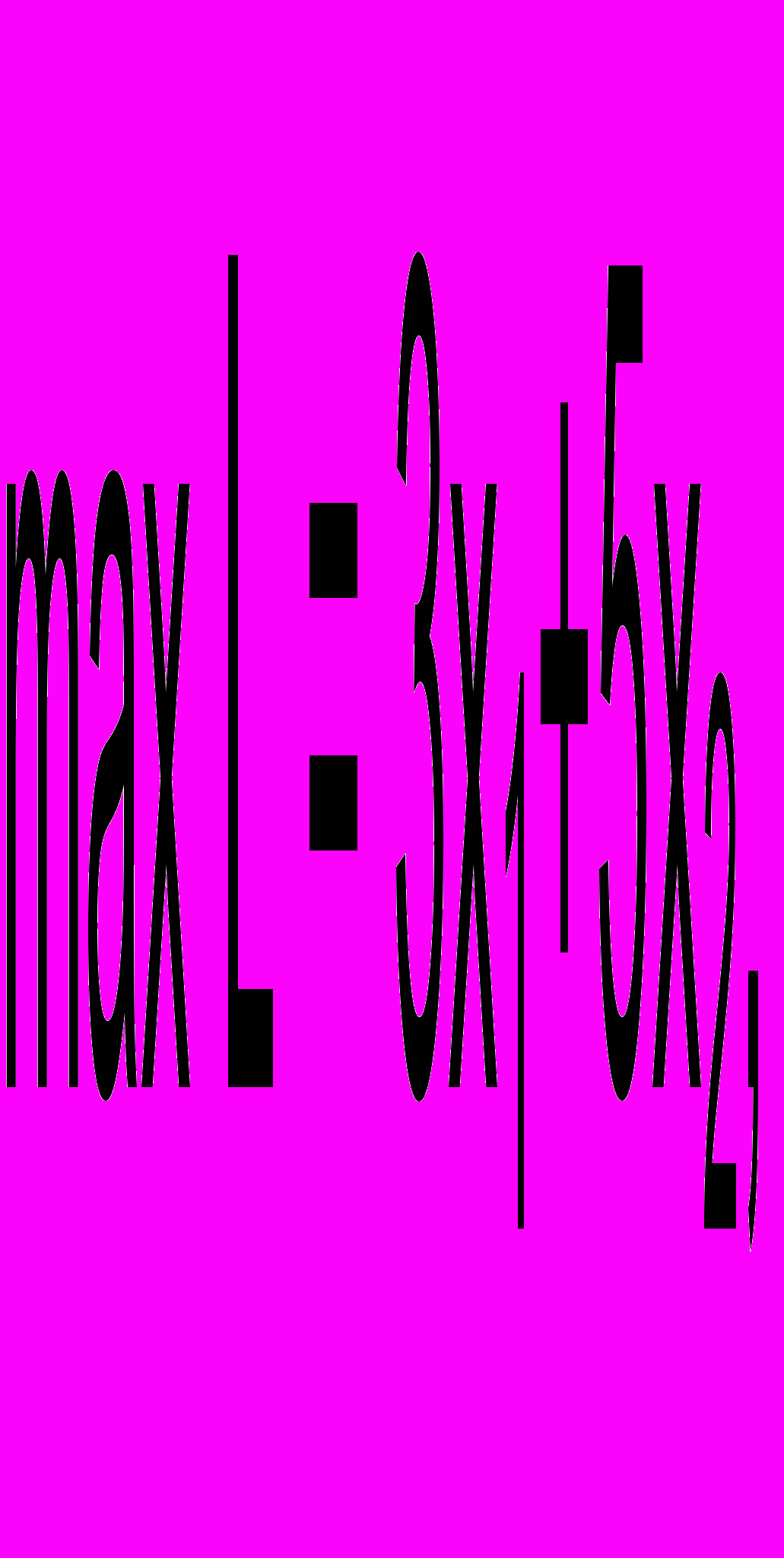
при ограничениях







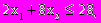
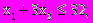
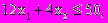
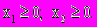
Данная модель является линейной, потому что входящие в нее функции (целевая функция и ограничения) линейны. Линейность предполагает наличие двух свойств - пропорциональность и аддитивность.

Пропорциональность означает, что вклад каждой переменной в целевую функцию и в любое ограничение прямо пропорционален величине этой переменной.

Аддитивность заключается в том, что целевая функция представляет собой сумму различных переменных, взятых с весовыми коэффициентами. Аналогично левая часть каждого ограничения также представляет собой сумму различных переменных, взятых с весовыми коэффициентами.

Пример 2. Фирма “Альтаир” располагает двумя видами станков, из них N₁ станков типа 1 и N₂ станков типа 2. Станки могут производить три вида продукции: П₁; П₂; П₃, но с разной производительностью. Данные а_ij производительности станков даны в таблице 2.2.

Каждая единица продукции П₁ приносит фирме доход С₁, продукции П₂ - С₂; продукции П₃ - С₃. Фирма имеет лицензию, согласно которой она должна производить в месяц не более ₁ единиц продукции П₁; ₂ - продукции П₂; ₃ - продукции П₃. Фирма уже получила заказы, согласно которым она должна производить в месяц не менее b₁ единиц продукции П₁; не менее b₂ продукции П₂ и не менее b₃ продукции П₃.

Требуется так распределить загрузку станков, чтобы обеспечить максимальный месячный доход.

Таблица 2.2

		Производительность				Наличие
Тип станка			Вид продукции			станков
	П1		П2	П3
1	а11		а12	а13		N1
2	a21		a22	a23		N2
Лицензия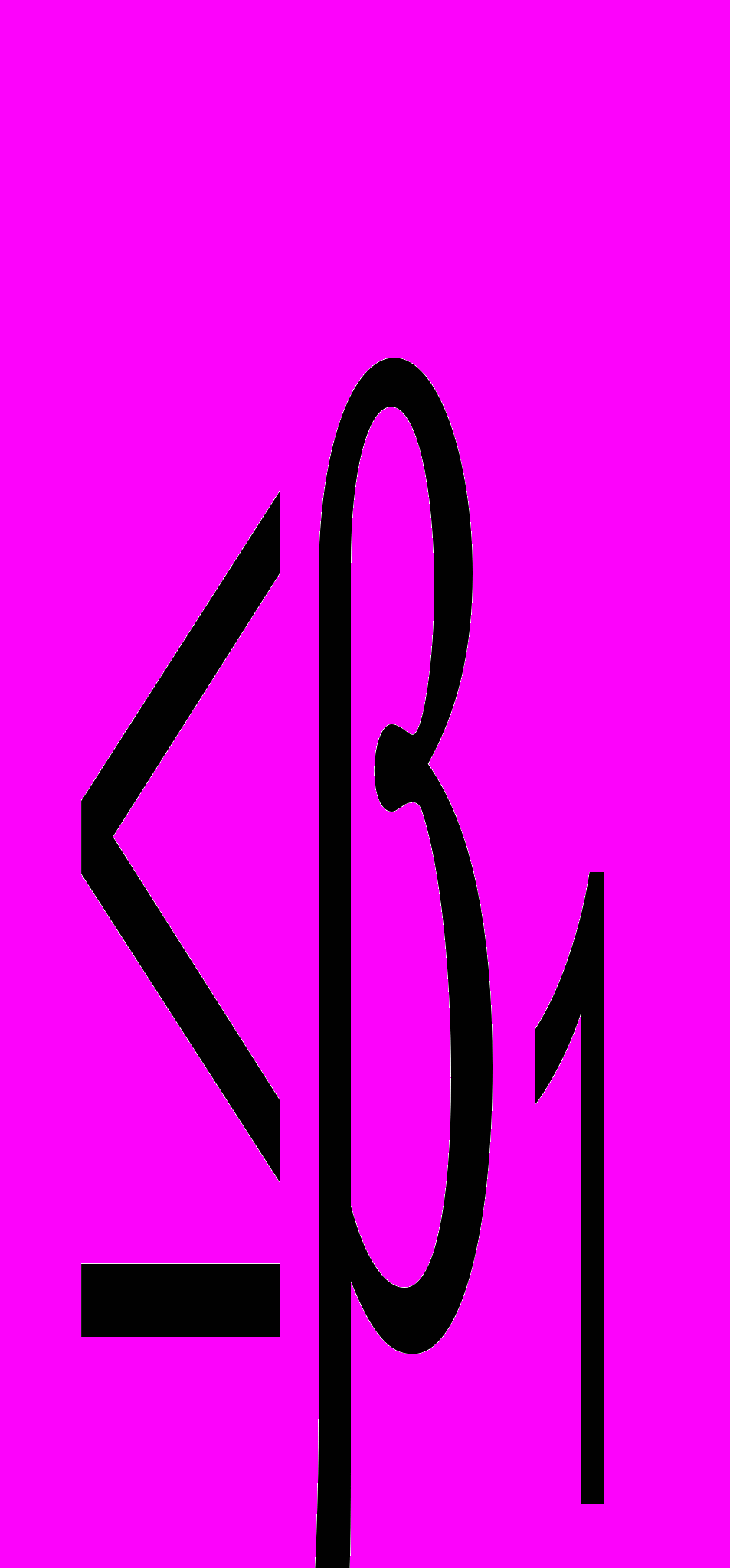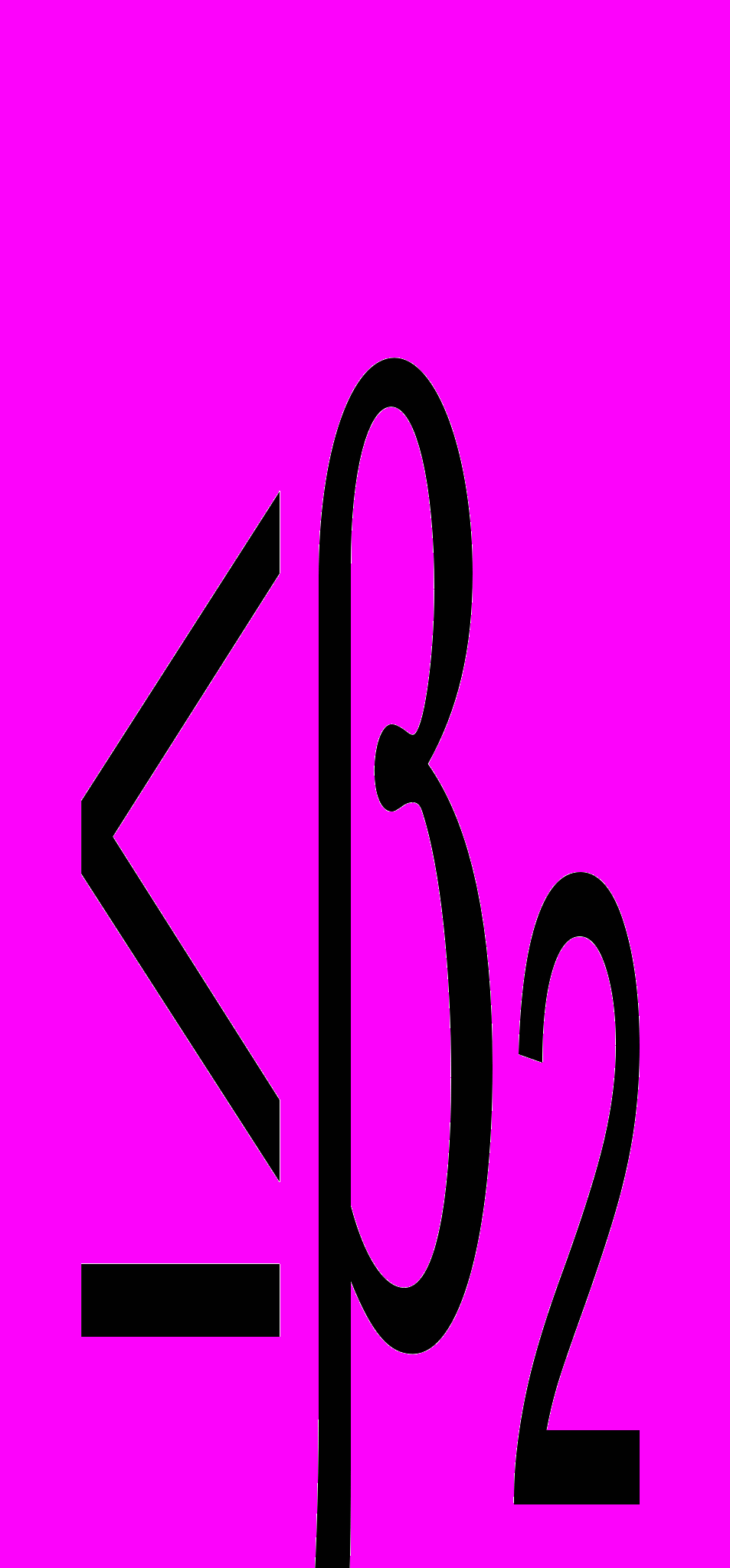
Заказы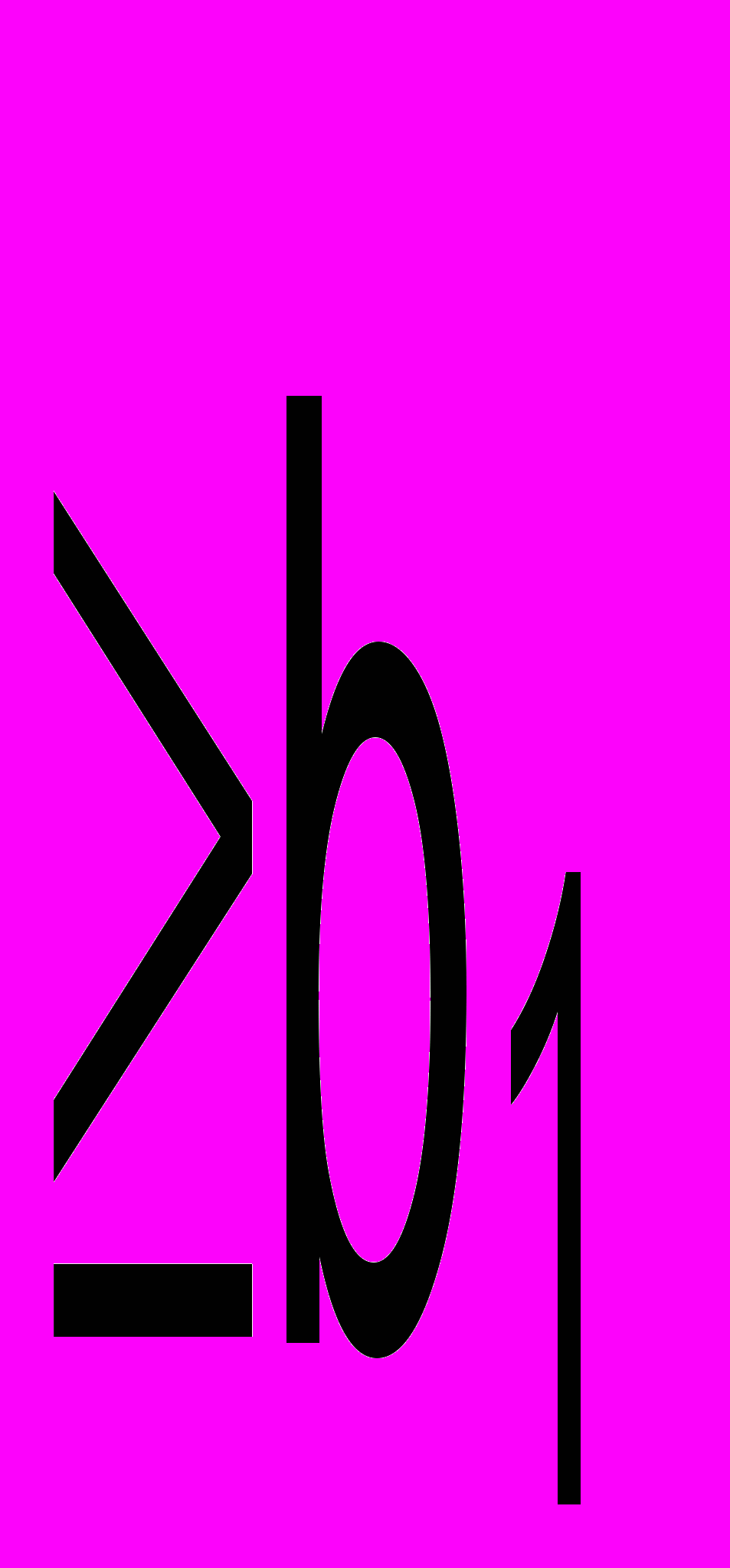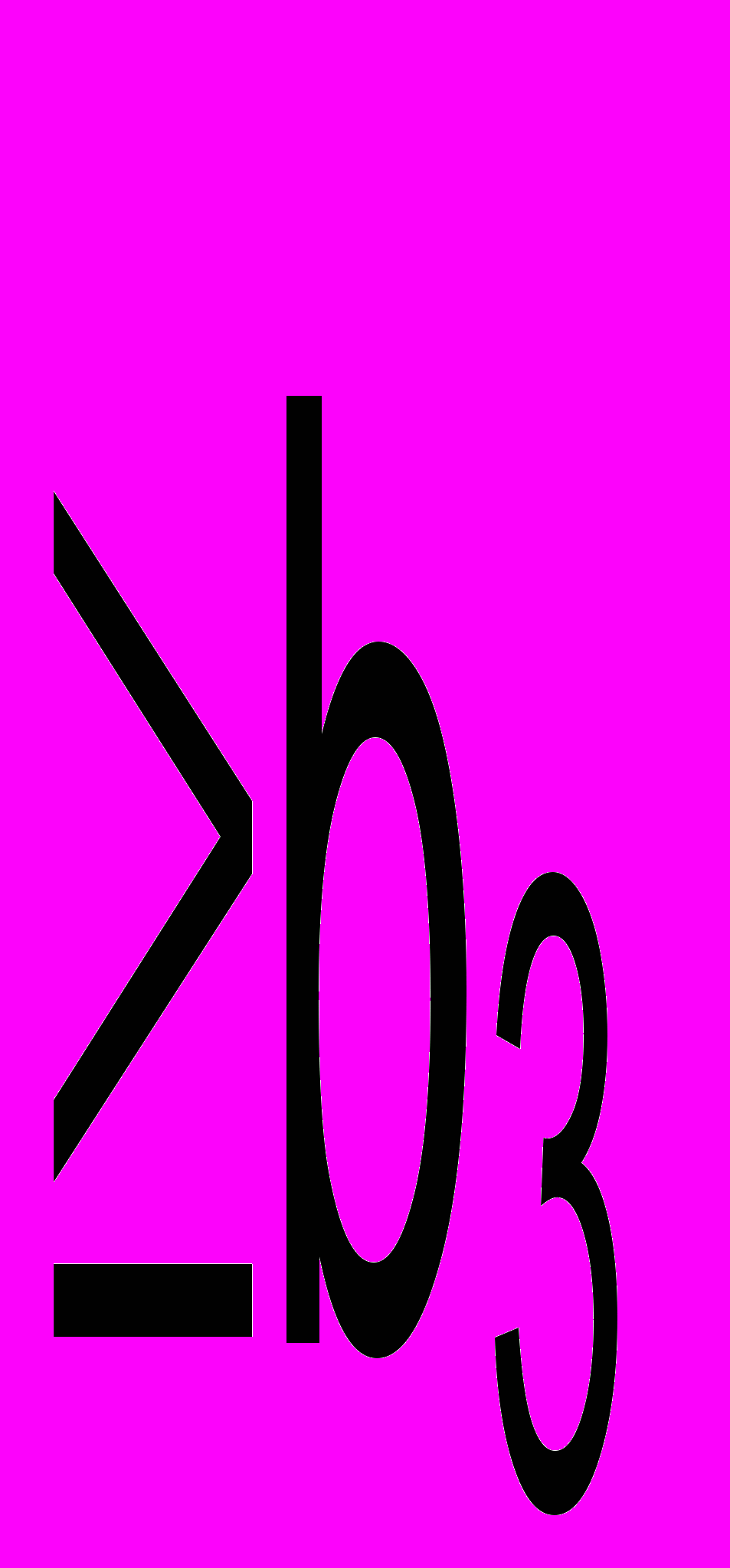
Прибыль	С1		С2	С3

В этой задаче неизвестными должны выступать не количество продукции каждого вида, а количество станков типов 1 и 2, занятых производством продукции каждого вида. Всего будет шесть неизвестных переменных:

х₁₁, х₁₂, х₁₃,

х₂₁, х₂₂, х₂₃,

где х_ij - количество станков i-го вида (i=1,2), занятых изготовлением продукции П_j (j=1,3). Запишем сначала ограничения, накладываемые на переменные х_ij.

Для обеспечения заказа необходимо, чтобы







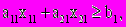
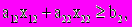
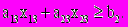
Для соблюдения плана, определяемого лицензией, необходимо, чтобы







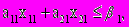
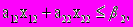
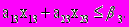
Ограничения, связанные с наличием станков





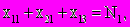
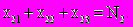
Естественные ограничения

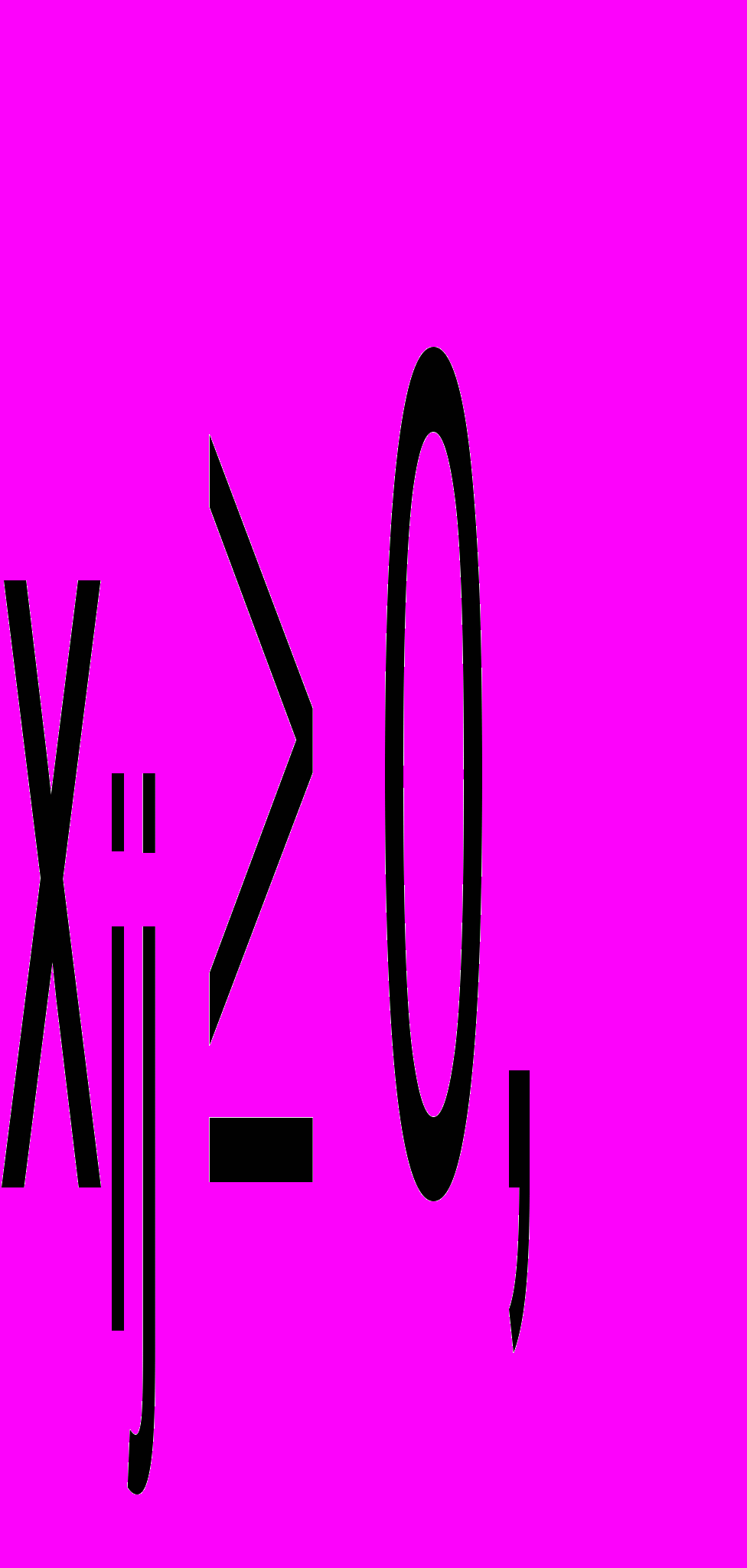i=1,2; j=1,2,3.

Целевая функция должна быть равна суммарному доходу от производства всех видов продукции:




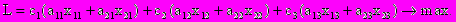
2.2. Стандартная форма задачи линейного программирования

Любую задачу линейного программирования можно свести к стандартной (канонической) форме, которая формулируется так: найти неотрицательные значения переменных х₁, х₂, ..., х_n, которые удовлетворяли бы условиям - равенством

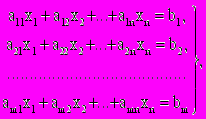(1.4)

где 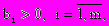и обращали бы в максимум линейную функцию этих переменных

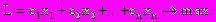(1.5)

Действительно, если в некоторых задачах в исходной постановке нужно целевую функцию L минимизировать, то изменив знак L на обратный, приходим к задаче максимизации (max -L),и наоборот. Например, минимизация функции



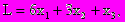
эквивалентна максимизации функции



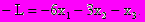
Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях переменных целевые функции будут равны по модулю, но их знаки будут противоположны.

Исходное ограничение, записанное в виде неравенства, можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения, когда знак неравенства <, или вычитая избыточную переменную, когда знак неравенства >.

Например, при исходном неравенстве



вводится остаточная переменная х₃, в результате чего исходное неравенство обращается в равенство



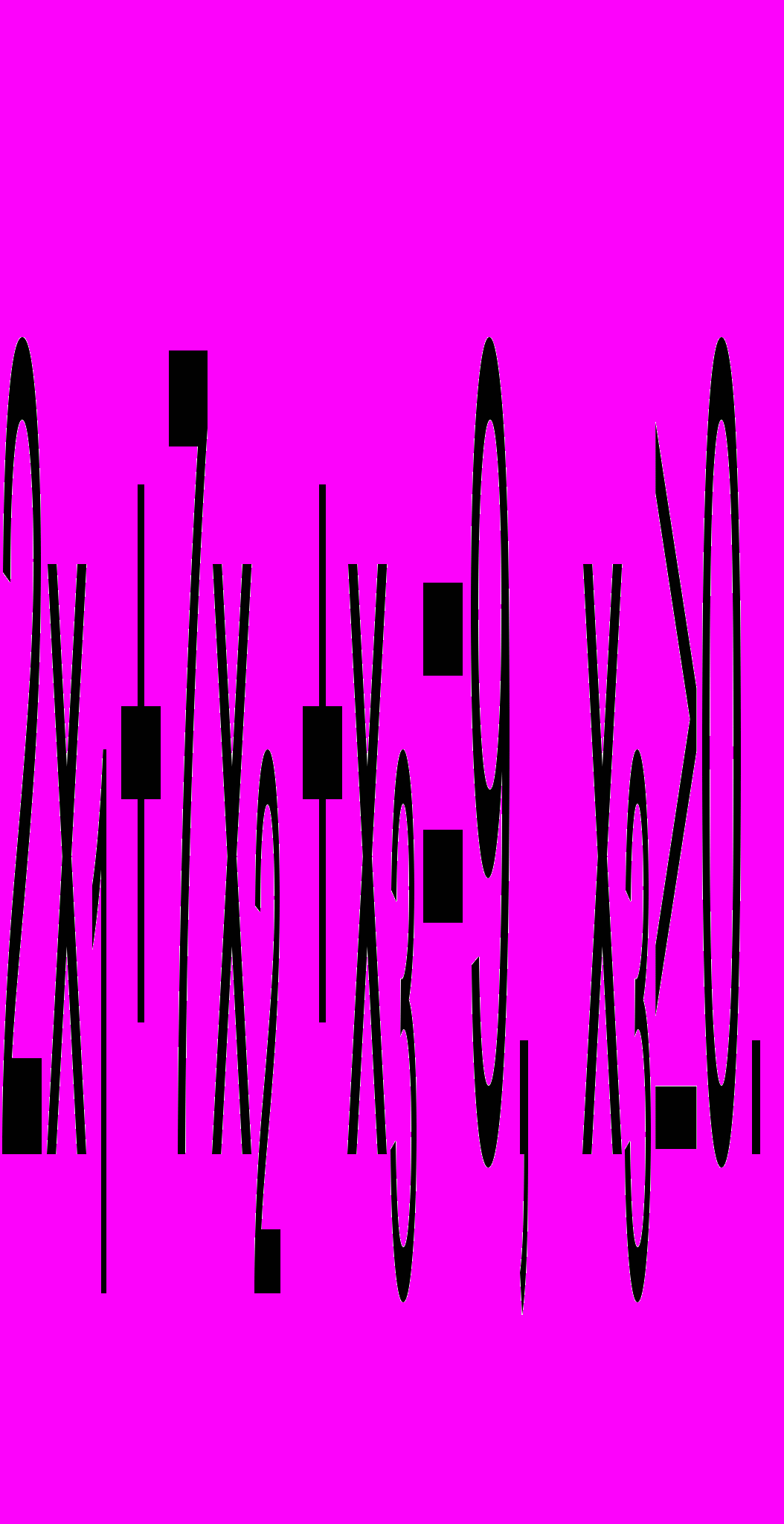
Если исходное ограничение определяет расход некоторого ресурса, то переменную х₃ следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.

Если исходное ограничение имеет вид другого типа



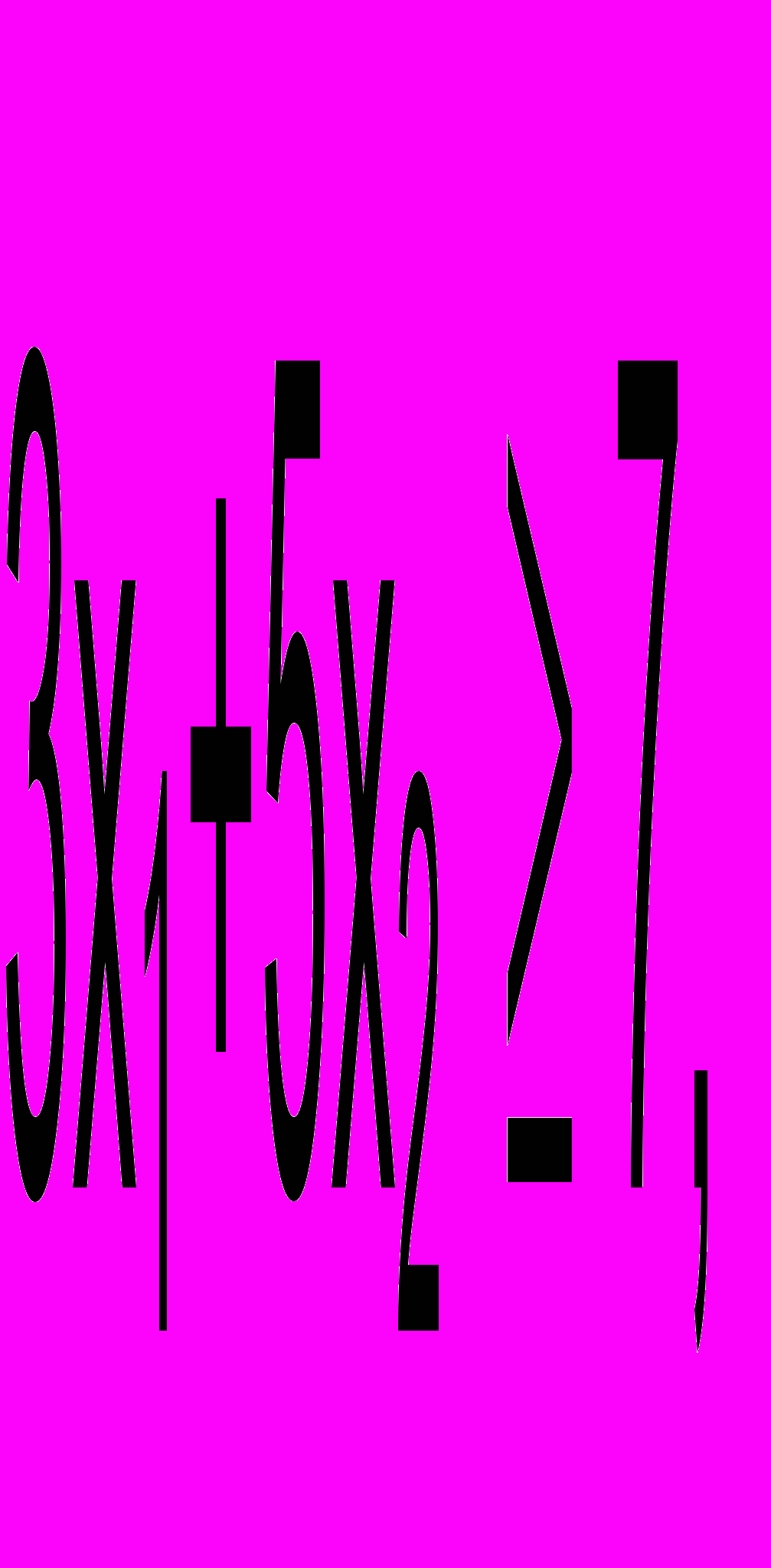
то вычитая из его левой части избыточную переменную х₄, получаем



Если в каком-то ограничении правая часть отрицательна, то, умножив обе части этого ограничения на -1, всегда можно сделать ее неотрицательной.

Например, равенство 2х₁+8х₂-3х₃=-6 эквивалентно равенству -2х₁-8х₂+3х₃=6.

Если ограничение с отрицательной правой частью имеет вид неравенства, то при умножении обеих частей неравенства на -1,необходимо также поменять знак неравенства на противоположный.

Например, неравенство 2х₁-5х₂>-3 эквивалентно неравенству -2х₁+5х₂<3.

Наконец, если какая-то переменная х_i не имеет ограничения в знаке, ее можно представить как разность двух неотрицательных переменных



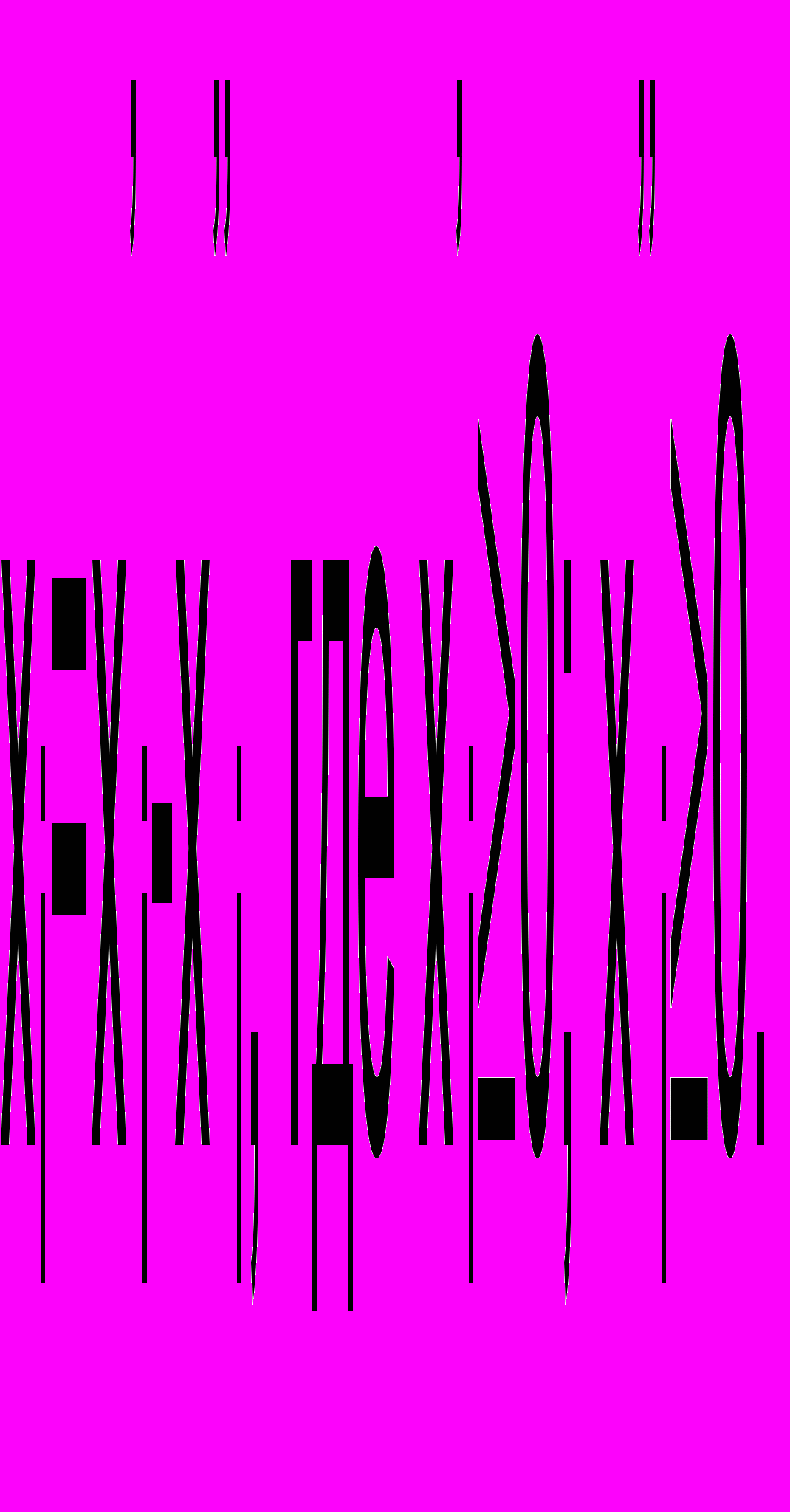
Такую подстановку следует использовать во всех ограничениях, которые содержат исходную переменную х_i, а также в выражении для целевой функции.

Пример. Представить следующую задачу линейного программирования в стандартной форме:



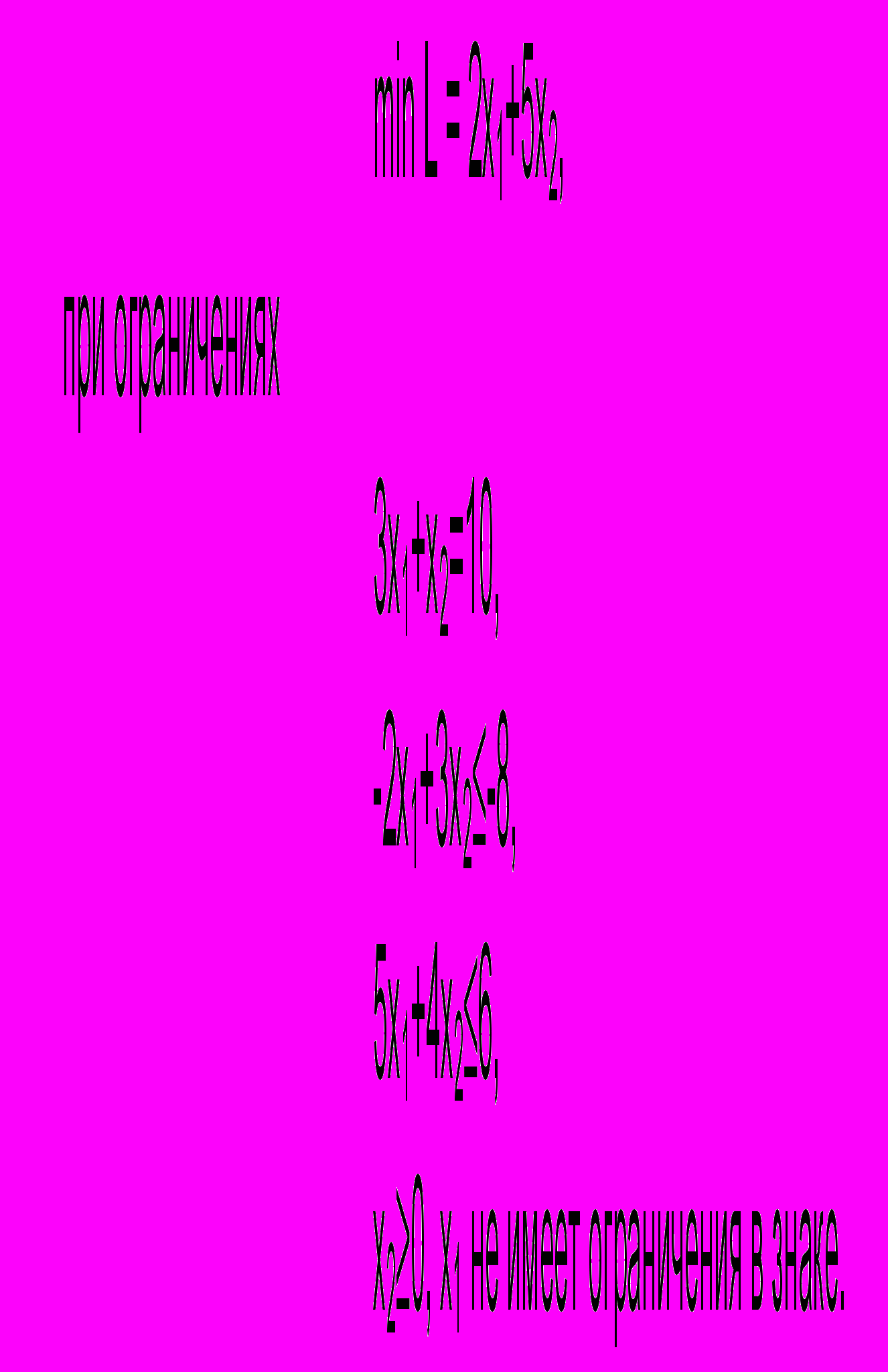
Решение. Умножим второе неравенство на -1 и вычтем избыточную переменную х₃, получим

2х₁-3х₂-х₃=8, х₃0.

Прибавим остаточную переменную к третьему неравенству:



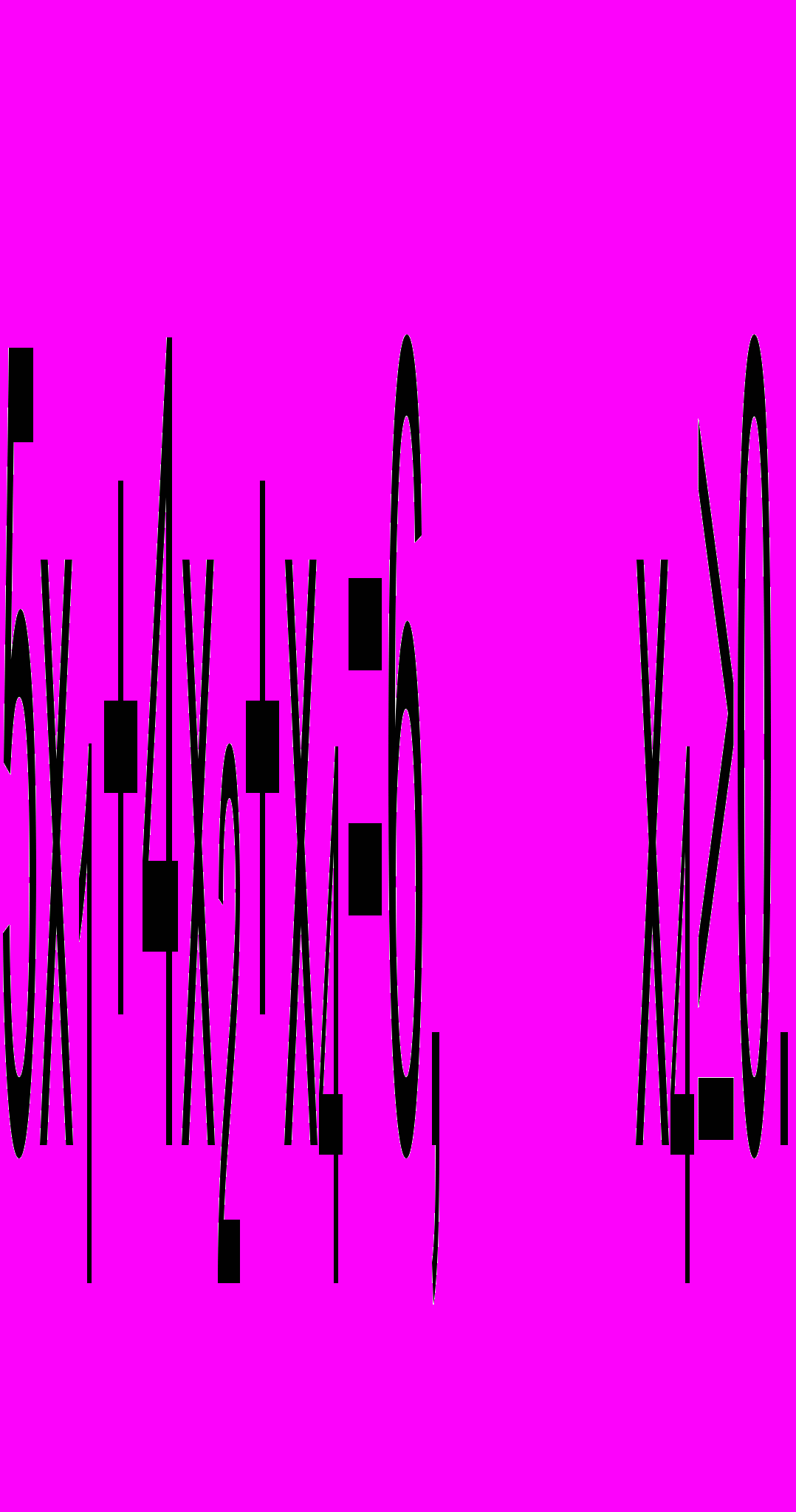
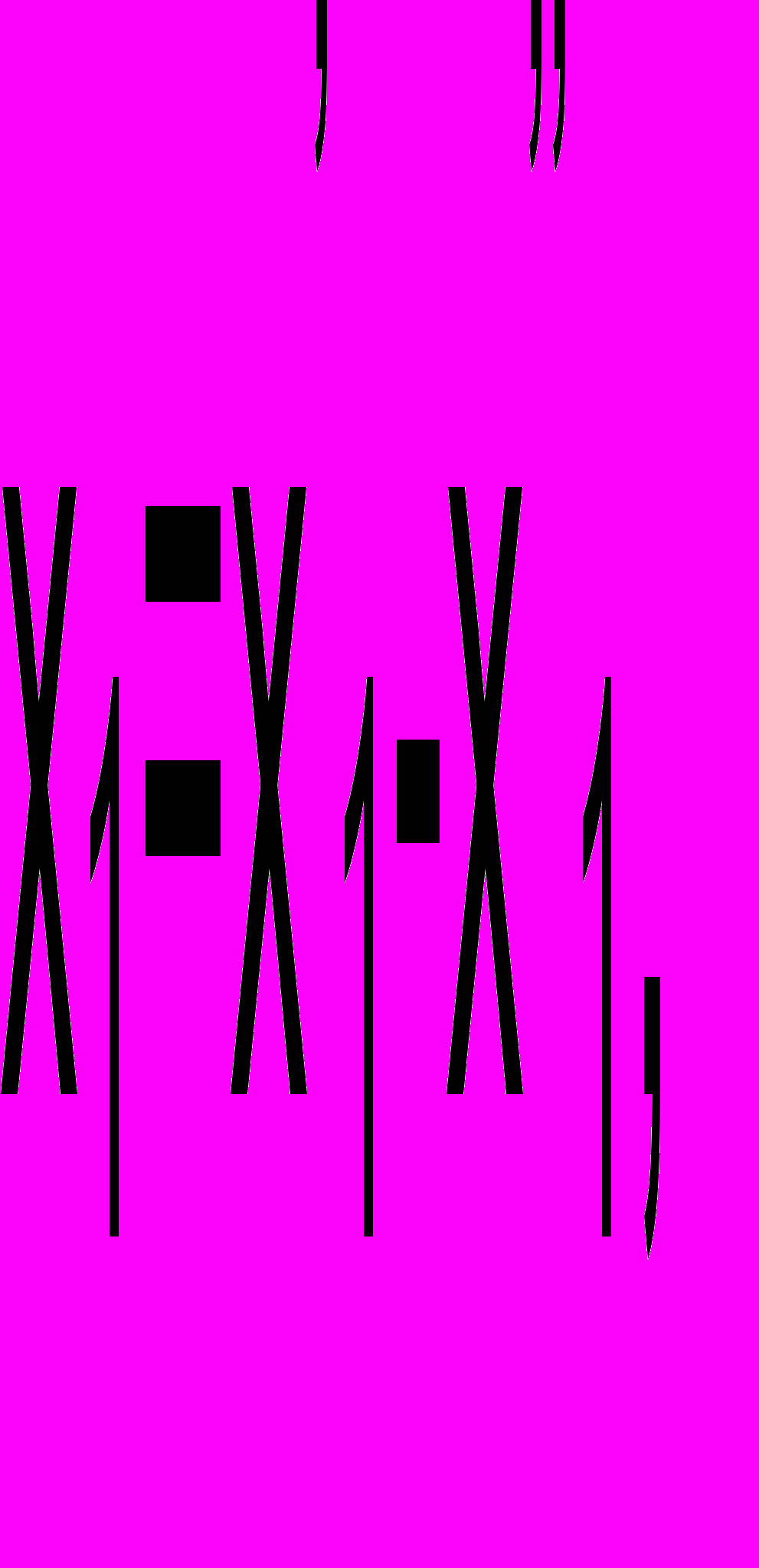
В целевой функции и во всех ограничениях осуществим подстановку Окончательно получаем исходную задачу линейного программирования в стандартной форме, если целевую функцию L заменим на -L.

max (-L)=-2x’₁+2x^’’₁-5x₂,

при ограничениях