Произведение векторов, их свойства и геометрический смысл

Вид материала

Литература

Содержание План-конспект урока

Подобный материал:

• Программа по аналитической геометрии и топологии. Раздел I: Векторная алгебра, 46.51kb.
• Программа для подготовки к экзамену теоретическая часть, 101.03kb.
• Аналитическая геометрия с элементами линейной алгебры, 54.48kb.
• Аналитическая геометрия с элементами линейной алгебры, 44.1kb.
• Векторы. Линейные операции над векторами. Скалярное произведение векторов. Векторное, 8.22kb.
• «Производная», 339.37kb.
• Вопросы к экзамену по дисциплине моделирование экономических процессов для студентов, 10.93kb.
• Дифференциальное исчисление Лекция 18. Производная, её геометрический и механический, 172.29kb.
• «Разработка алгоритма распознавания фонем русского языка с использованием вейвлет анализа, 243.45kb.
• Программа курса «Компьютерные технологии обработки и анализа медико-биологических данных», 12.71kb.

ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНО-ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

«ИЛЬИЧЕВСКОЕ ВЫСШЕЕ ПРОФЕССИОНАЛЬНОЕ УЧИЛИЩЕ

МОРСКОГО ТРАНСПОРТА»


ВЕКТОРНОЕ И СМЕШАННОЕ

ПРОИЗВЕДЕНИЕ ВЕКТОРОВ, ИХ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ


(Методическая разработка открытого урока)


Разработала Ткаченко Н. Н., преподаватель основ высшей математики І квалификационной категории

Рассмотрено на заседании методической комиссии портовых профессий

Протокол № _____ от ___________

Председатель методической комиссии

__________________ Гапонова Н. В.


Ильичевск

2008

СОДЕРЖАНИЕ

1. Аннотация 5
   
2. План-конспект урока 7-10
   
3. Приложение 11-14
   
4. Литература 15
   

АННОТАЦИЯ


Изучение темы «Векторы. Линии на плоскости и в пространстве» способствует дальнейшему воспитанию у учащихся математической культуры, выработке представления о роли и месте математики в современной цивилизации и мировой культуре, умению логически мыслить, оперировать абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.

Изучение аналитической геометрии позволит будущему специалисту сформировать необходимые компоненты мышления, которые понадобятся ему в будущей профессиональной деятельности.

Наиболее широко используются элементы данной темы математики в начертательной геометрии, физике, теоретической и технической механике, электротехнике, вычис­лительной технике.

В связи с простотой и легкостью восприятия материала посредством электронного варианта хода урока рекомендуется использовать данный метод для изучения темы «Векторное и смешанное произведение векторов, их свойства и геометрический смысл», а также для самостоятельного изучения учащимися данной темы.


^ ПЛАН-КОНСПЕКТ УРОКА


Тема программы: Векторы. Линии на плоскости и в пространстве.

Тема урока: Векторное и смешанное произведение векторов, их свойства и геометрический смысл.

Цель урока:

• сформировать фундаментальные знания по теме; познакомить учащихся с кругом задач, рассматриваемых в аналитической геометрии; развить практические навыки решения геометрических задач с применением алгебраического аппарата и привить навыки их использования в практической деятельности;
  
• развивать логическое мышление у учащихся, потребность в теоретических рассуждениях и обосновании своих действий, как в самой математике, так и в её приложениях; продолжать формировать абстрактное и наглядное мышление, наблюдательность;
  
• раскрыть (реализовать) интеллектуальный потенциал учащихся; воспитывать культуру мышления (точность знаний, аккуратность, строгость действий по алгоритму, творчество).
  

Тип урока: урок изучения нового материала

Вид урока: лекция

Дидактическое и материально-техническое обеспечение: мультимедийная доска, электронный вариант хода урока,компьютер, школьная доска, рабочая тетрадь

Межпредметные связи: физика – кинематика, статика теоретическая механика – равновесие тел


Методическая цель – методы и приемы работы с компьютерными и мультимедийными технологиями на уроке;


Литература:

Ильин В. А. Позняк Э. Г. Линейная алгебра: Учеб. для вузов – 4-е изд. – М. Наука. Физматлит. 1999

А. Г. Курош Лекции по общей алгебре – 1-е изд., М., 1962: 2-е изд., М.,1973

И. А. Каплан Практическое занятие по высшей математике – М, Наука, 1980


Ход урока

1. Организационная часть
   

• проверка наличия учащихся
  
• проверка готовности к занятиям
  

• сообщение темы раздела и урока.
  
• целевая установка учащихся
  

Тема нового раздела является частью курса аналитической геометрии. Аналитическая геометрия – это та часть геометрии, в которой основным аппаратом является аппарат элементарной алгебры. Алгебраический аппарат в геометрии удается применить благодаря методу координат, создателем которого является французский математик и философ Рене Декарт (1596-1650). Система координат Декарта дала возможность привлечь алгебру к геометрии и найти новые модели таким геометрическим абстракциям как точка, прямая, плоскость, кривая, поверхность.

Наряду с Декартом основоположником аналитической геометрии является также Ферма (1601-1665) – французский юрист и математик. Большой вклад в ее развитие внесли математики К. Ф. Гаусс (1777-1855) и Н. И. Лобачевский (1792-1856).

Аналитическая геометрия находит широкое приложение в физике и теоретической механике – барицентрические координаты, углы Эйлера, оптические свойства кривых второго порядка, определение положения и траекторий движения небесных тел и многое другое. (Открытие планеты Плутон)

При изучении данного курса, мы с вами познакомимся с новыми методами аналитической геометрии и приобретем навыки по использованию их при решении задач вашей профессиональной деятельности. Данный курс также позволит продолжать расширять и развивать умение логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.

• повторение пройденного материала, необходимого для проведения данного урока.
  

Повторение пройденного материала проводится в устной форме в виде опроса. Правильные ответы на вопросы дополняются учащимися и дублируются на мультимедийной доске.

Перечень вопросов, которые необходимо рассмотреть:

• Понятие векторных и скалярных величин;
  
• Сложение векторов;
  
• Длина вектора, заданного своими координатами;
  
• Определение скалярного произведения векторов;
  
• Применение скалярного произведения
  
• Скалярное произведение в координатной форме;
  

Перед тем, как перейти к следующему этапу, учащимся показывается, где можно применить скалярное произведение векторов при решении задач теоретической механики.

• сообщение алгоритма проведения урока
  

Рассмотреть другие виды произведения векторов, изучить их свойства и геометрический смысл. Закрепление материала проведем на примере решения технических задач.

2. Формирование новых знаний
   

• Изложение новой теоретической информации
  

Изложение новой теоретической информации ведется непосредственно при использовании мультимедийной доски и электронного варианта урока, составленного самим преподавателем. Электронный вариант хода урока по содержанию отвечает всем требованиям для изучения в полном объеме информации и имеет логическую структуру. Все объяснения преподавателя демонстрируются на мультимедийной доске. Данный вариант прилагается к основному плану урока.

Краткий ход изложение нового материала:

• Упорядоченная тройка векторов
  
• Правая (левая) тройка векторов
  
• Определение векторного произведения векторов.
  

На данном этапе следует отметить, что результатом векторного произведения векторов является вектор.

• Геометрический смысл векторного произведения
  

Основываясь на определении векторного произведения, учащимся самостоятельно предлагается определить геометрический смысл векторного произведения.

• Векторное произведение в координатной форме
  

Изученную ранее теорию определителей следует напомнить учащимся именно на данном этапе, когда непосредственно возникает связь теории определителей с аналитической геометрией.

• Векторное произведение векторов при решении задач теоретической механики
  
• Смешанное произведение векторов
  

Следует предложить учащимся самостоятельно определить – что будет являться результатом смешанного произведения векторов.

• Геометрический смысл смешанного произведения
  

Проведя аналогию с векторным произведением, учащиеся самостоятельно определяют геометрический смысл смешанного произведения.

Также учащимся предлагается прооперировать с абстрактными объектами и сделать вывод о взаимном расположении трех векторов, если их смешанное произведение равно нулю.

• Смешанное произведение в координатной форме
  

• Проверка доступности новой информации путем опроса нескольких учащихся по изложенной теме
  

Перечень вопросов:

1. Что является результатом скалярного произведения векторов?
   
2. Что является результатом векторного произведения векторов?
   
3. Что является результатом смешанного произведения векторов?
   
4. Какими методами аналитической геометрии следует воспользоваться, чтобы вычислить площадь параллелограмма (треугольника)?
   
5. Какими методами аналитической геометрии следует воспользоваться, чтобы вычислить угол между векторами?
   
6. Какими методами аналитической геометрии следует воспользоваться, чтобы вычислить объем параллелепипеда (пирамиды)?
   

• Ответы на вопросы учащихся
  

3. Закрепление новой информации
   

• Сообщение заданий и объяснение алгоритма их выполнения
  

Даны координаты вершин пирамиды



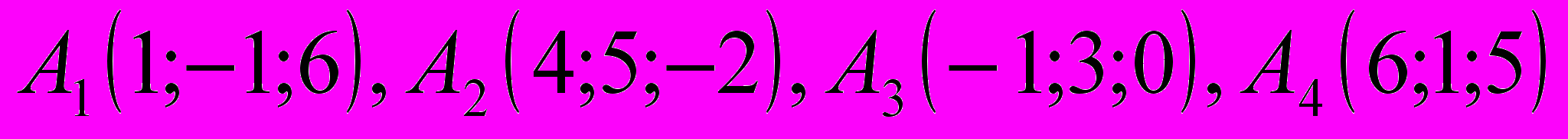
Методами векторной алгебры определить:

а) угол между ребрами А₁А₂ и А₁А₄,

б) площадь грани А₁А₂А₃

в) объем пирамиды

Решение задачи излагается учащимися у доски

• Задание для самостоятельной работы
  

Доказать, что четыре точки 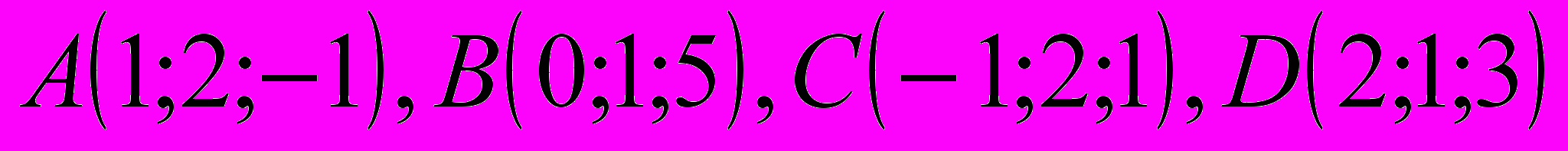лежат в одной плоскости

4. Подведение итогов
   

• Анализ типичных ошибок.
  
• Выставление и мотивация оценок
  
• Выдача домашнего задания.
  

Выучить основные определения, запись произведений векторов в координатной форме.

Задача 1.

Вычислить работу равнодействующей F сил 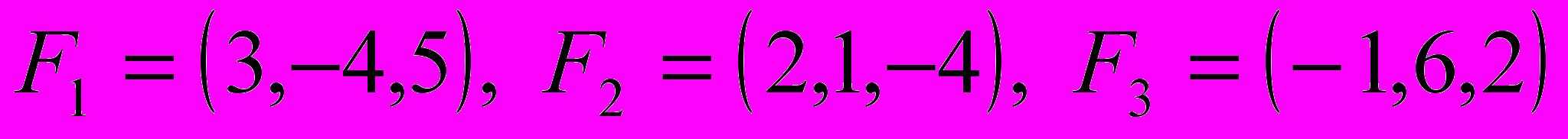, приложенных к материальной точке, которая под их действием перемещается прямолинейно из точки 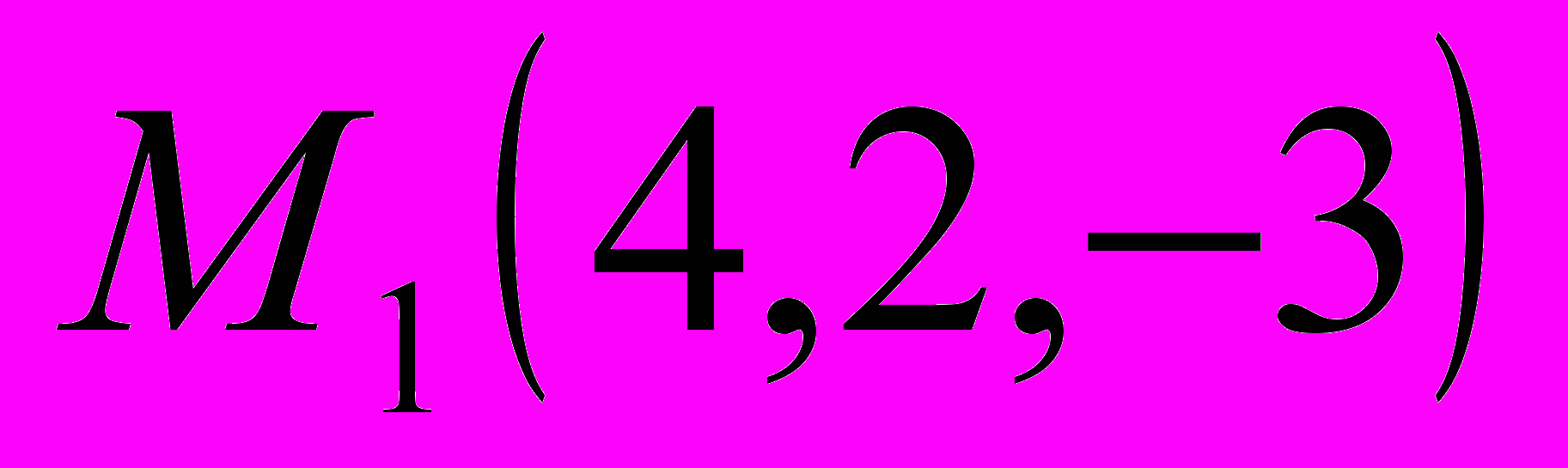в точку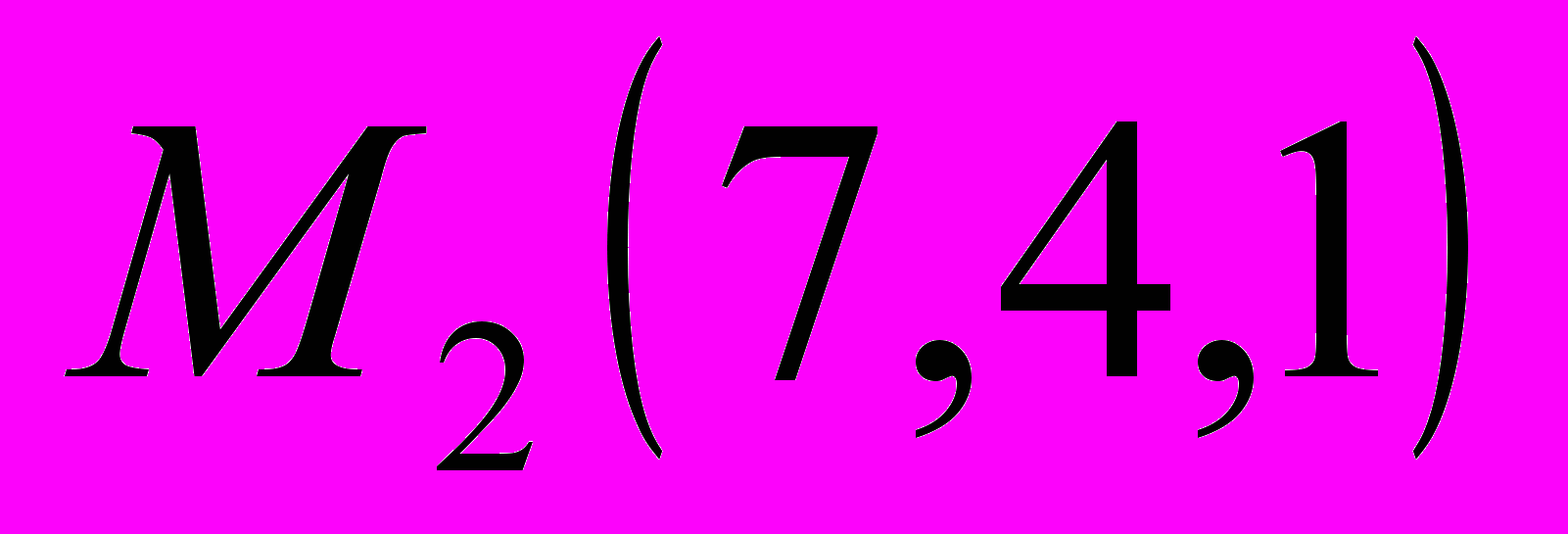

_{Задача 2}

Вычислить координаты вращающего момента М силы F=(3,2,1), приложенной к точке А(-1,2,4), относительно начала координат О


_{Решение всех приведенных задач прилагается.}


ПРИЛОЖЕНИЕ


Задача № 1

Даны координаты вершин пирамиды



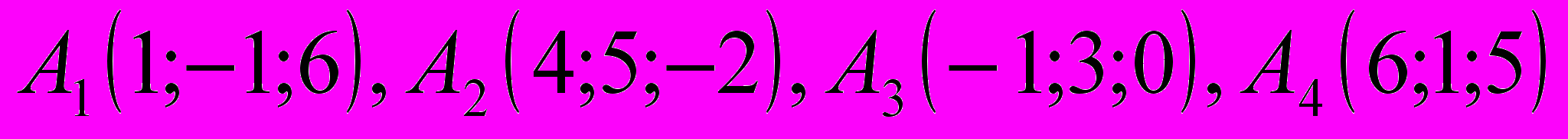
Методами векторной алгебры определить:

а) угол между ребрами А₁А₂ и А₁А₄,

б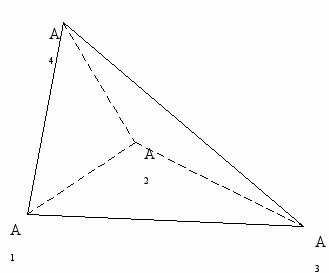) площадь грани А₁А₂А₃

в) объем пирамиды


а) угол между ребрами А₁А₂ и А₁А₄ найдем из скалярного произведения векторов 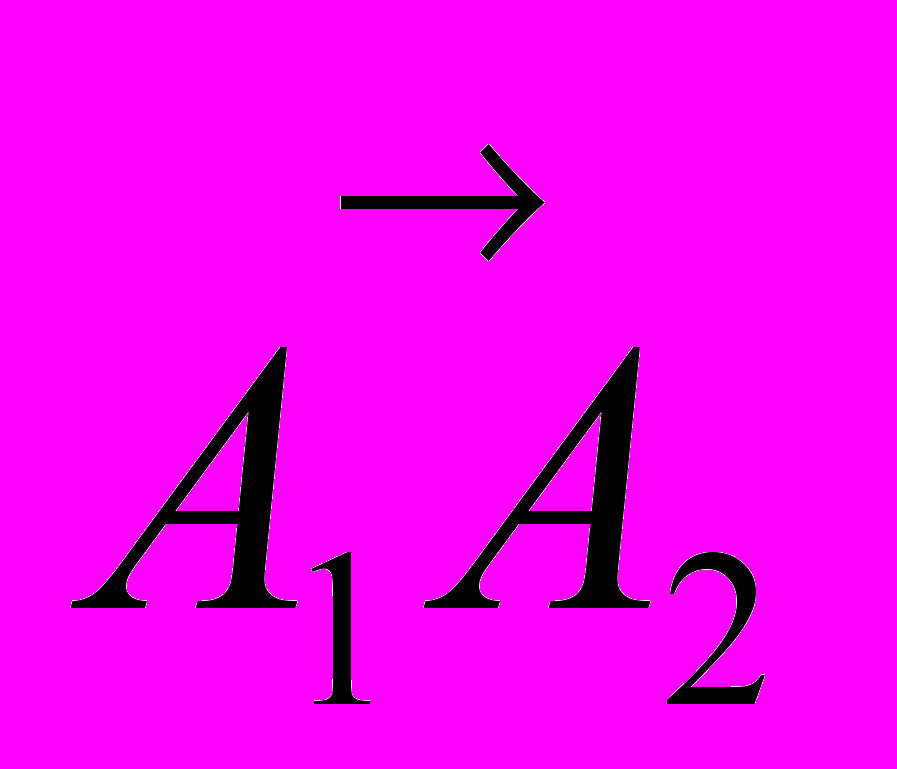и .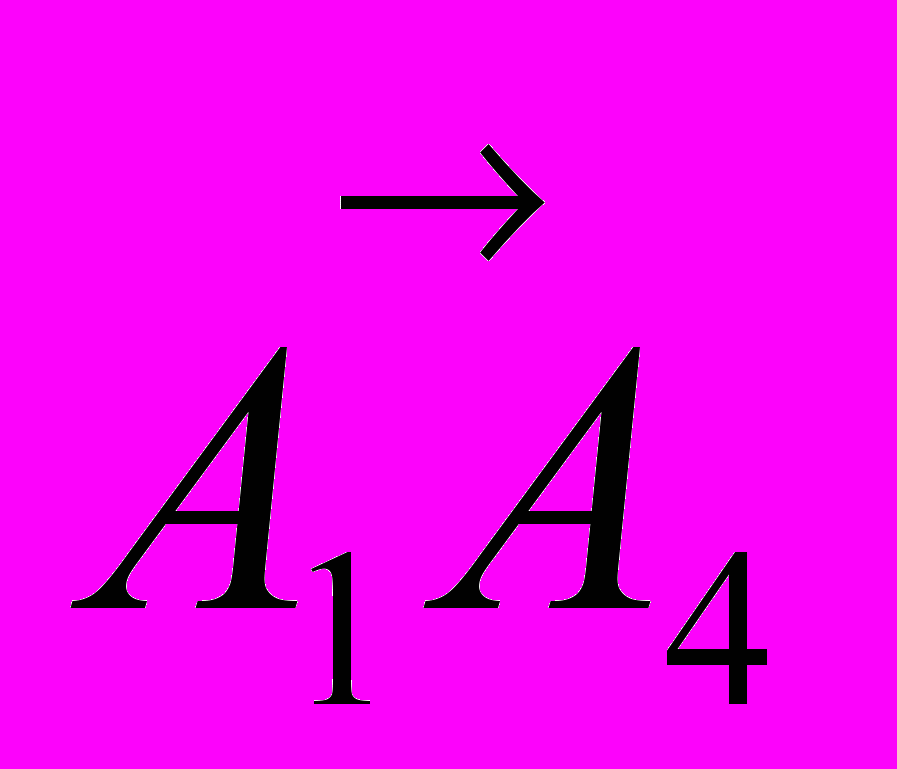

Для этого вычислим координаты и длины этих векторов, а также скалярное произведение векторов в координатной форме.







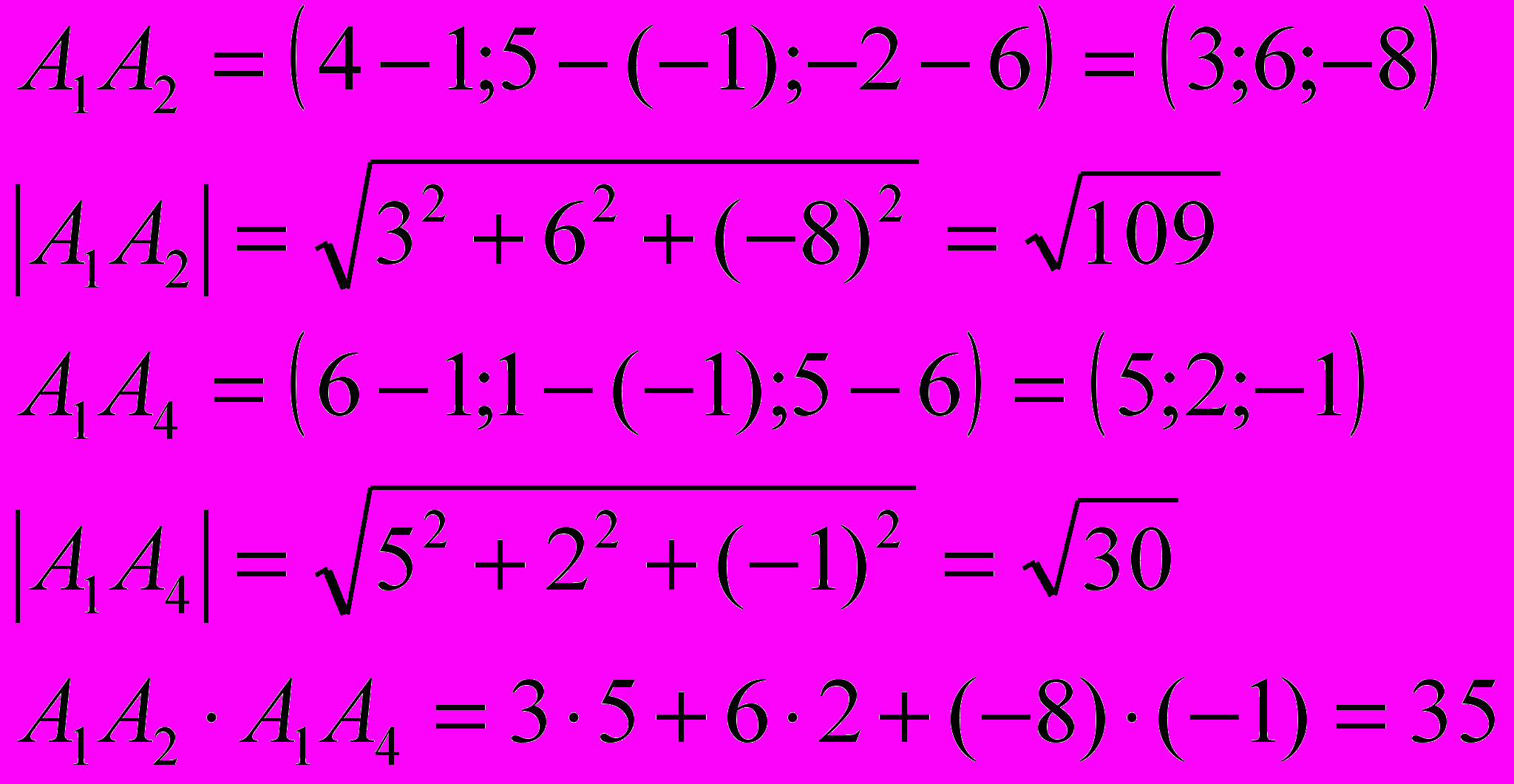
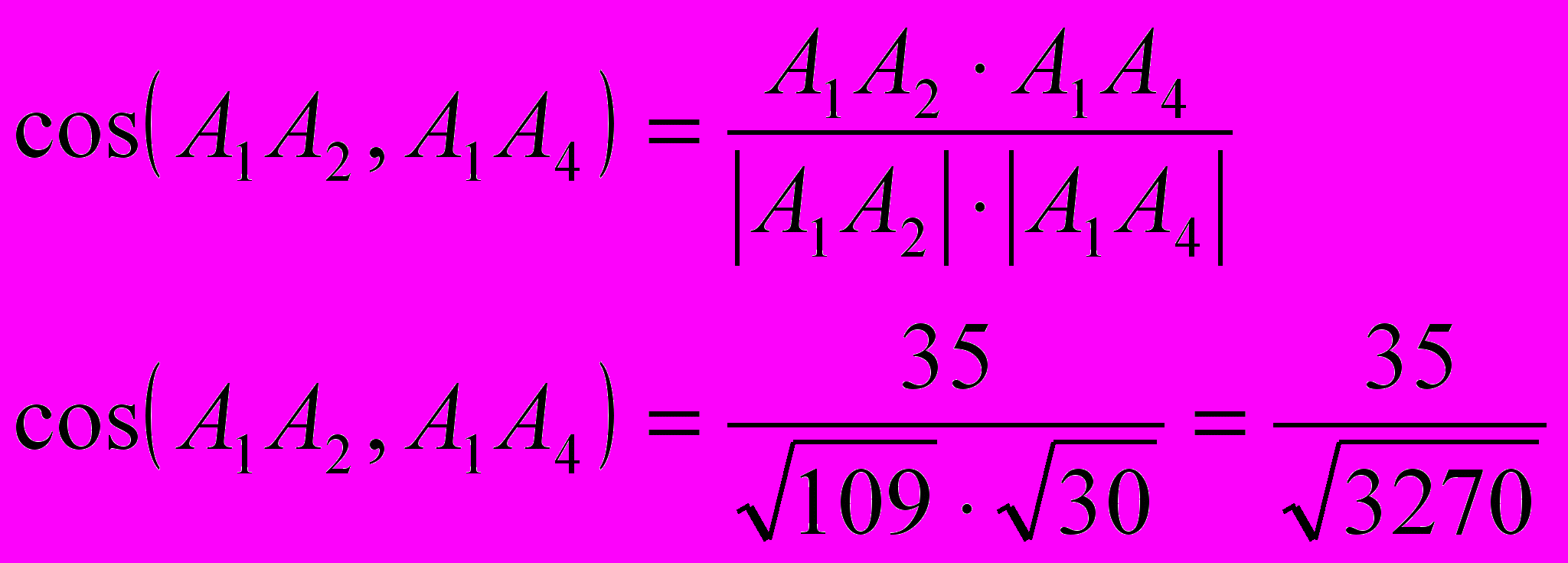
б) площадь грани А₁А₂А₃ найдем из геометрического смысла векторного произведения векторов 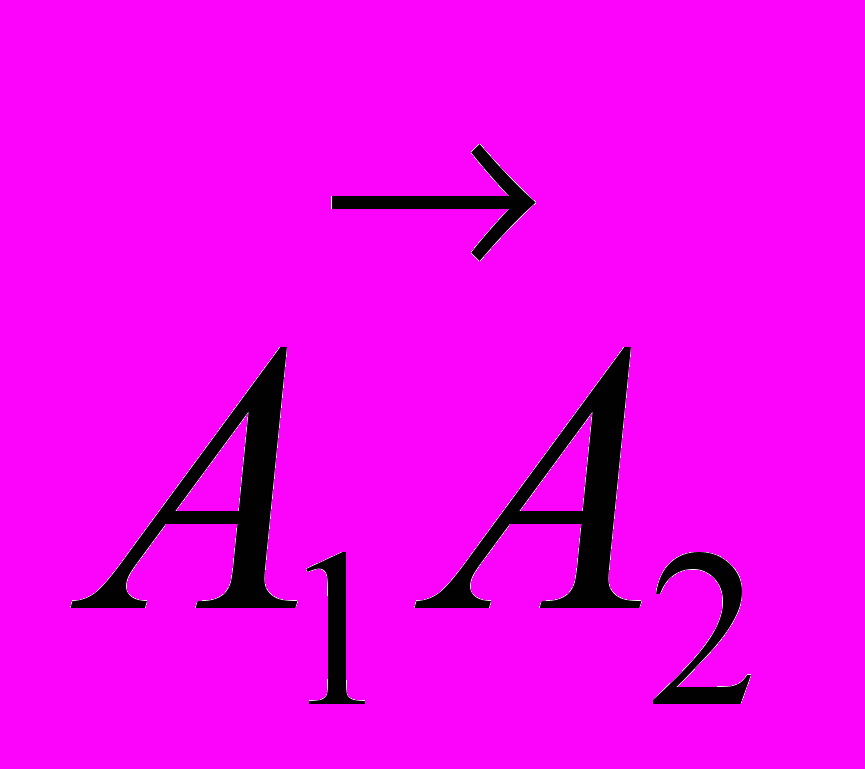и 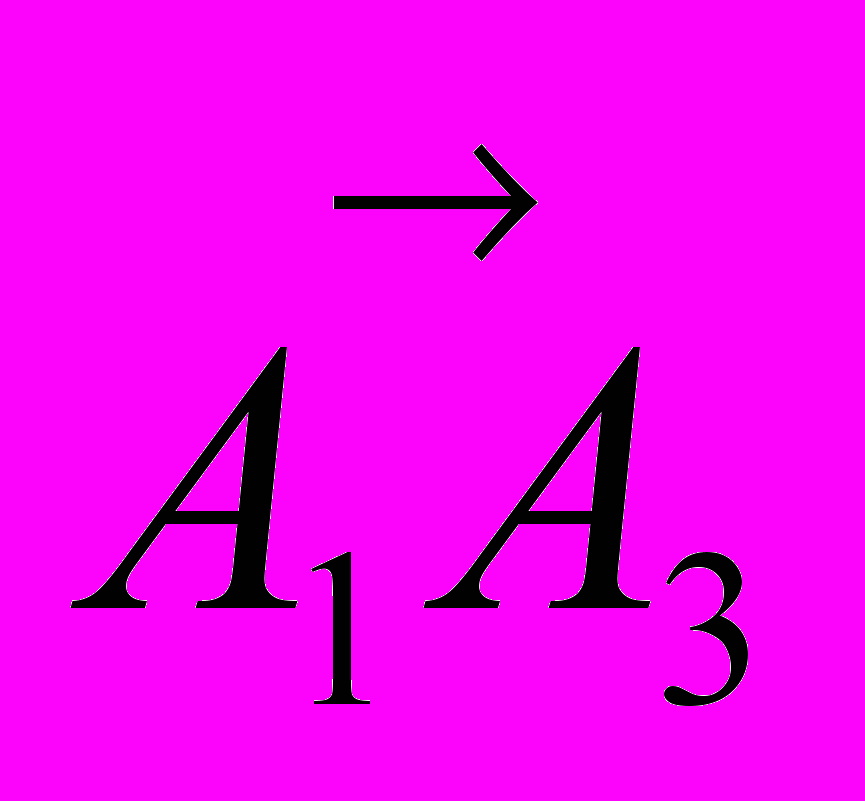. Так как координаты вектора 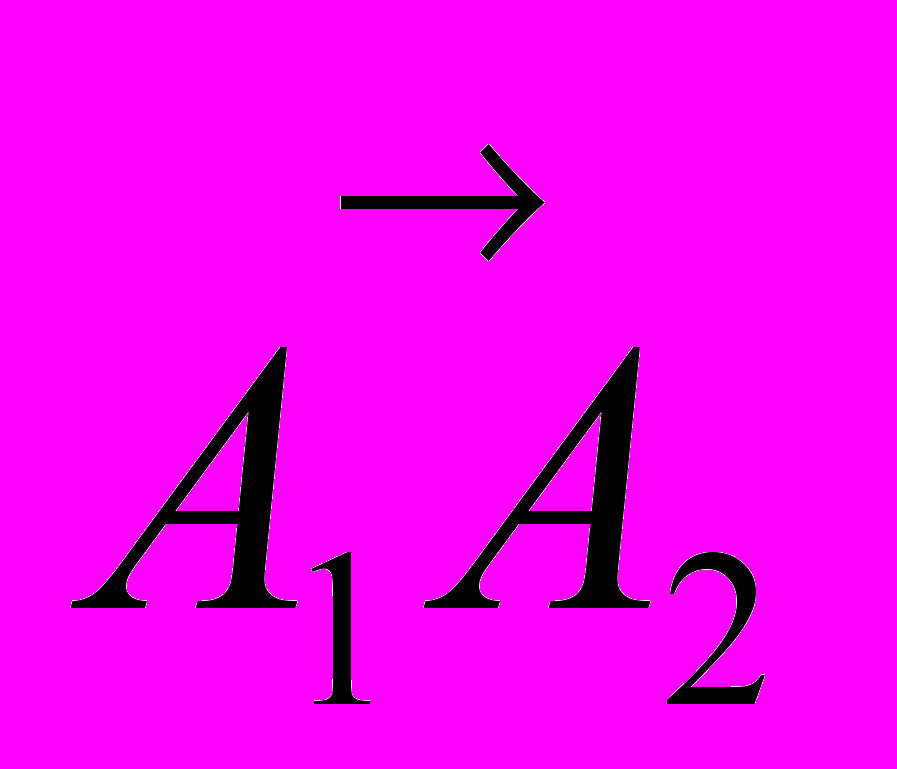найдены в предыдущем пункте, то вычислим только координаты вектора 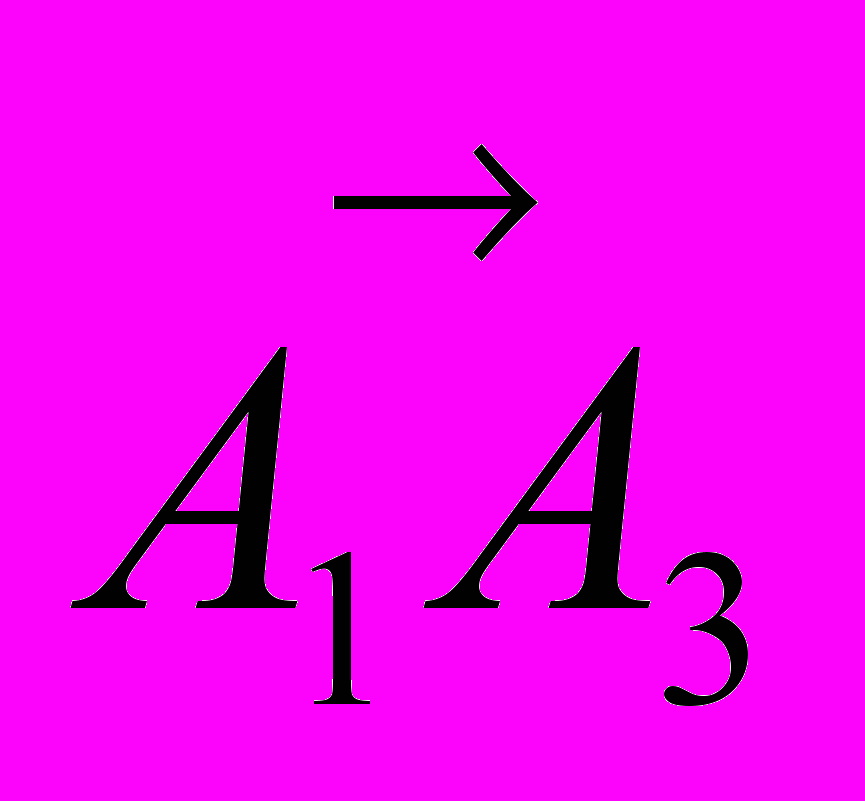и найдем координаты векторного произведения этих векторов.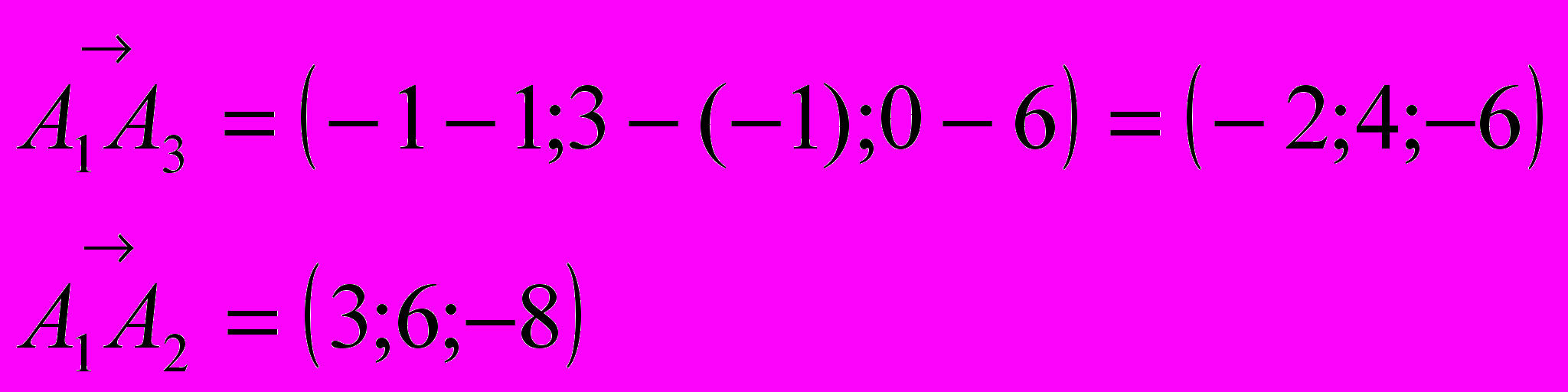










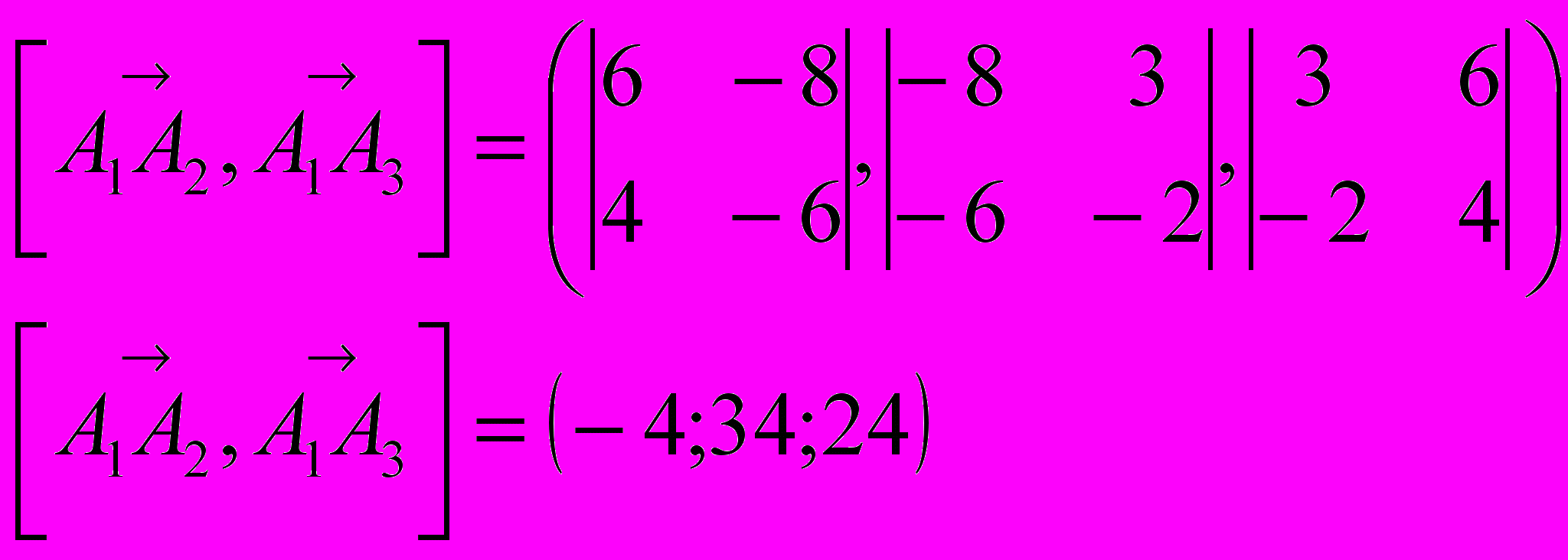
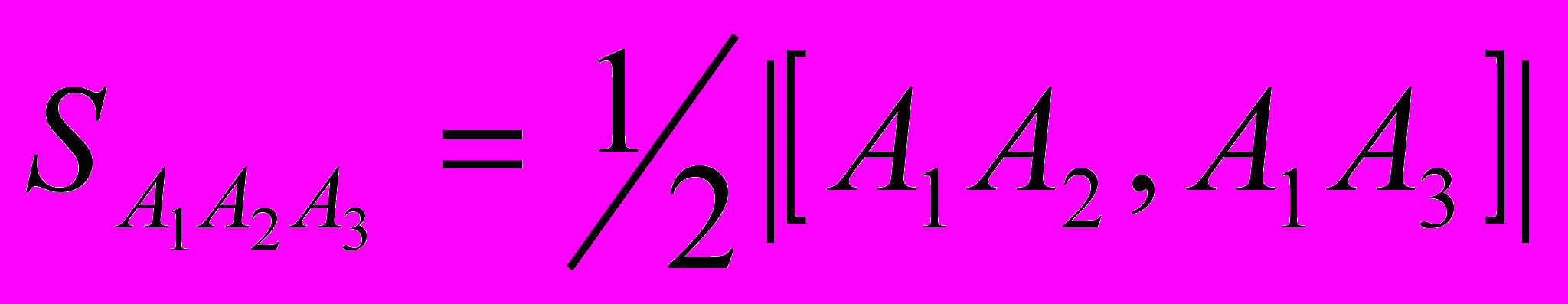
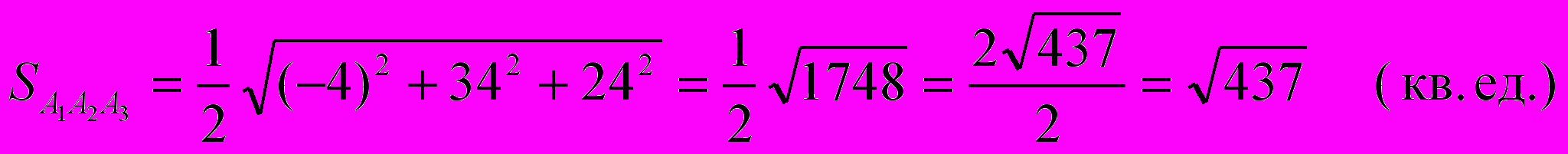
в) объем пирамиды найдем из геометрического смысла смешанного произведения векторов



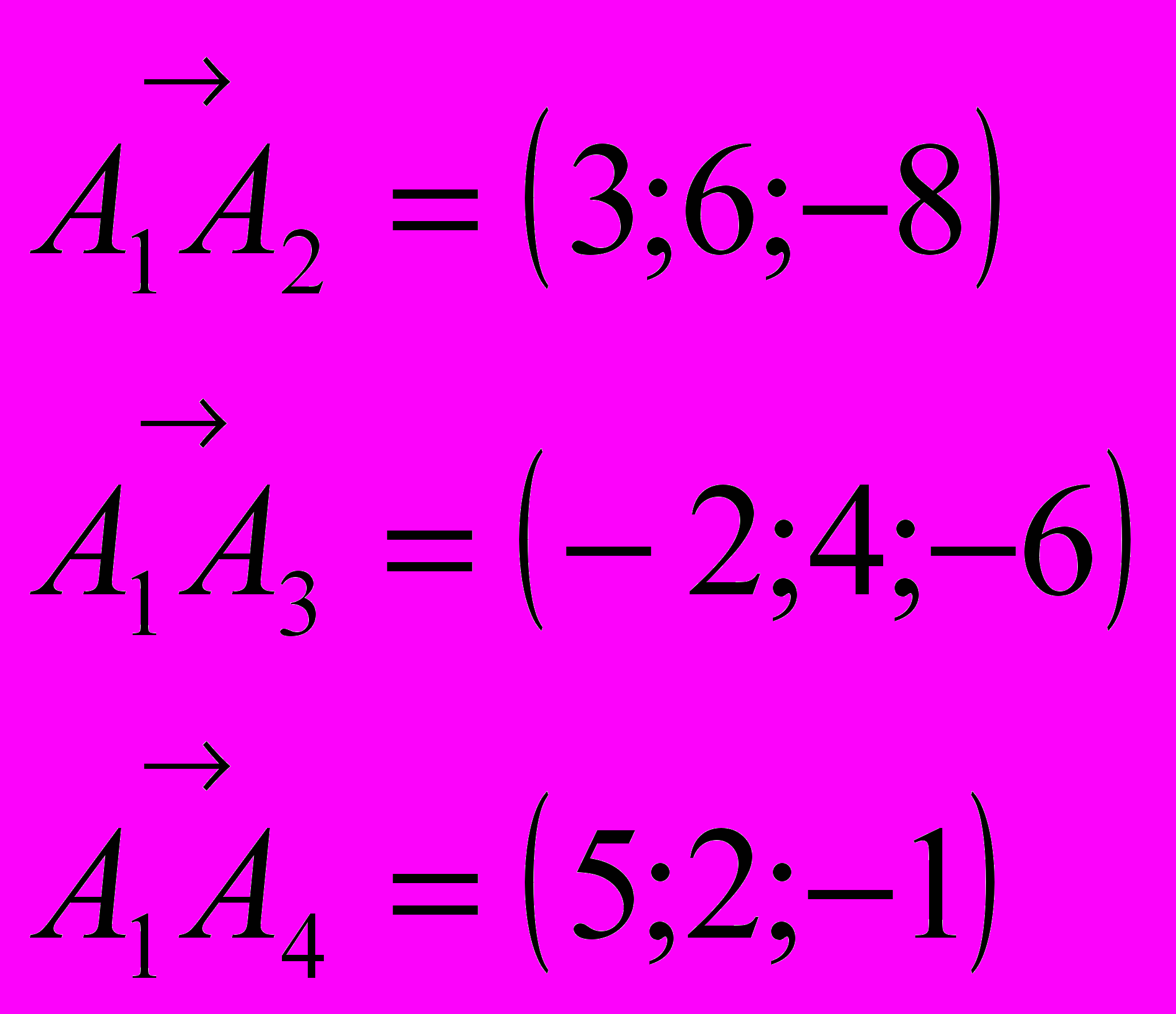
Координаты этих векторов были вычислены ранее. Смешанное произведение равно объему параллелограмма, построенного на приведенных к общему началу векторах.



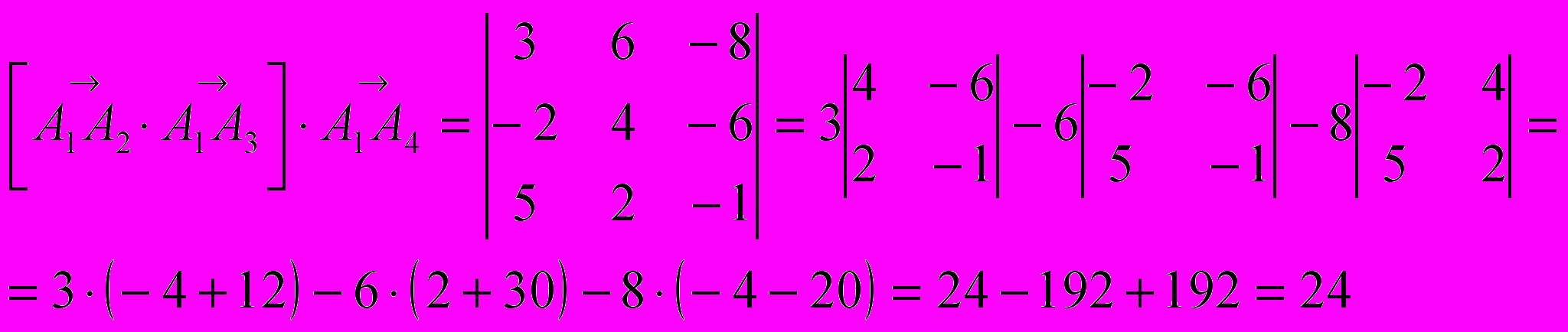
Тогда, объем пирамиды вычислим по формуле



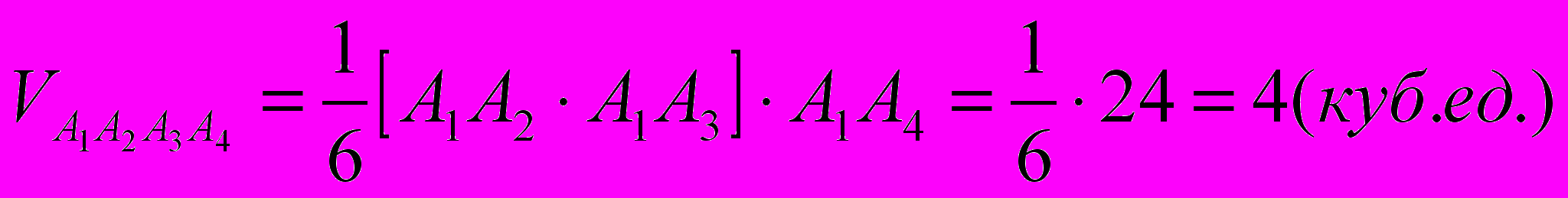
Задание № 2

Доказать, что четыре точки 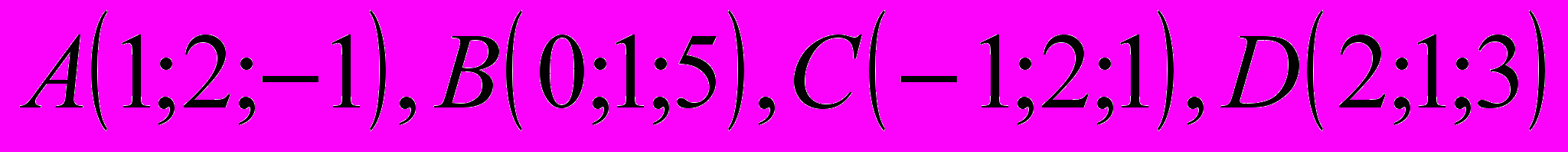лежат в одной плоскости


Решение

Для доказательства воспользуемся следствием из смешанного произведения векторов. В нем говорится, что если три вектора компланарны (т. е. лежат в одной плоскости), то их смешанное произведение равно нулю. А если вектора лежат в одной плоскости, то и все точки векторов лежат в одной плоскости.

Итак, рассмотрим три вектора 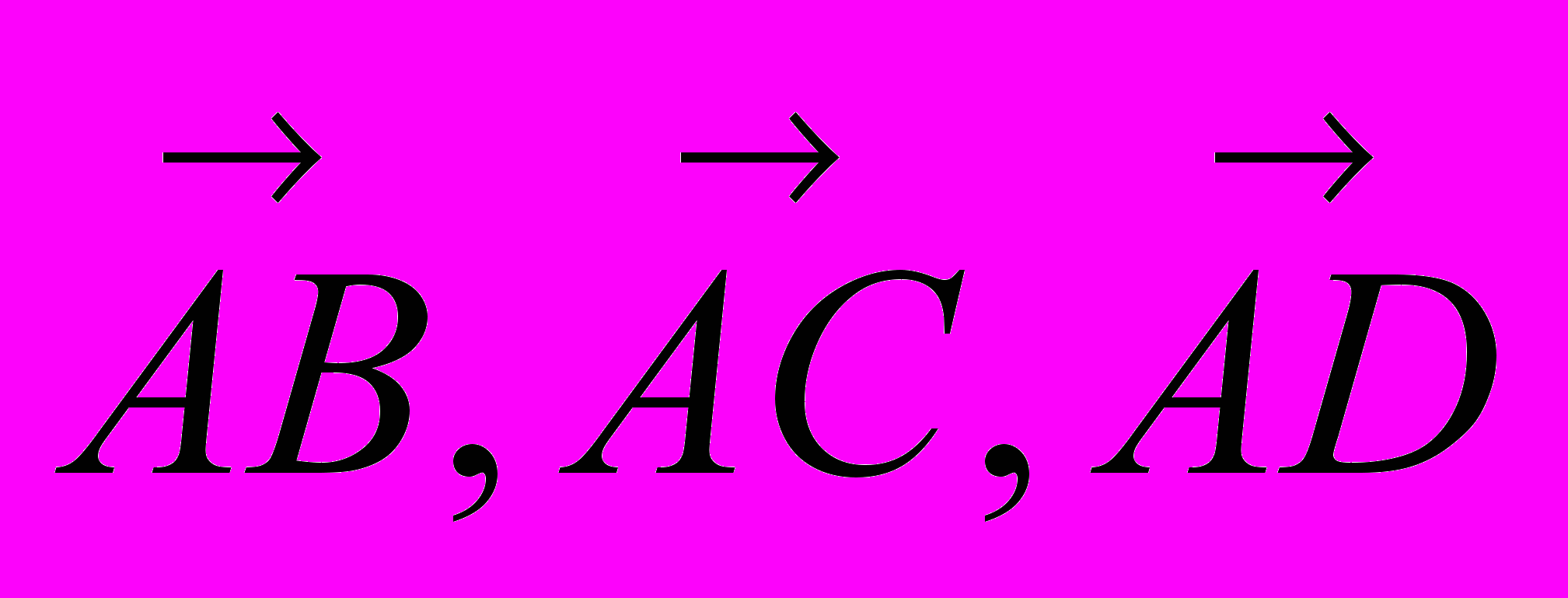и покажем, что их смешанное произведение равно нулю.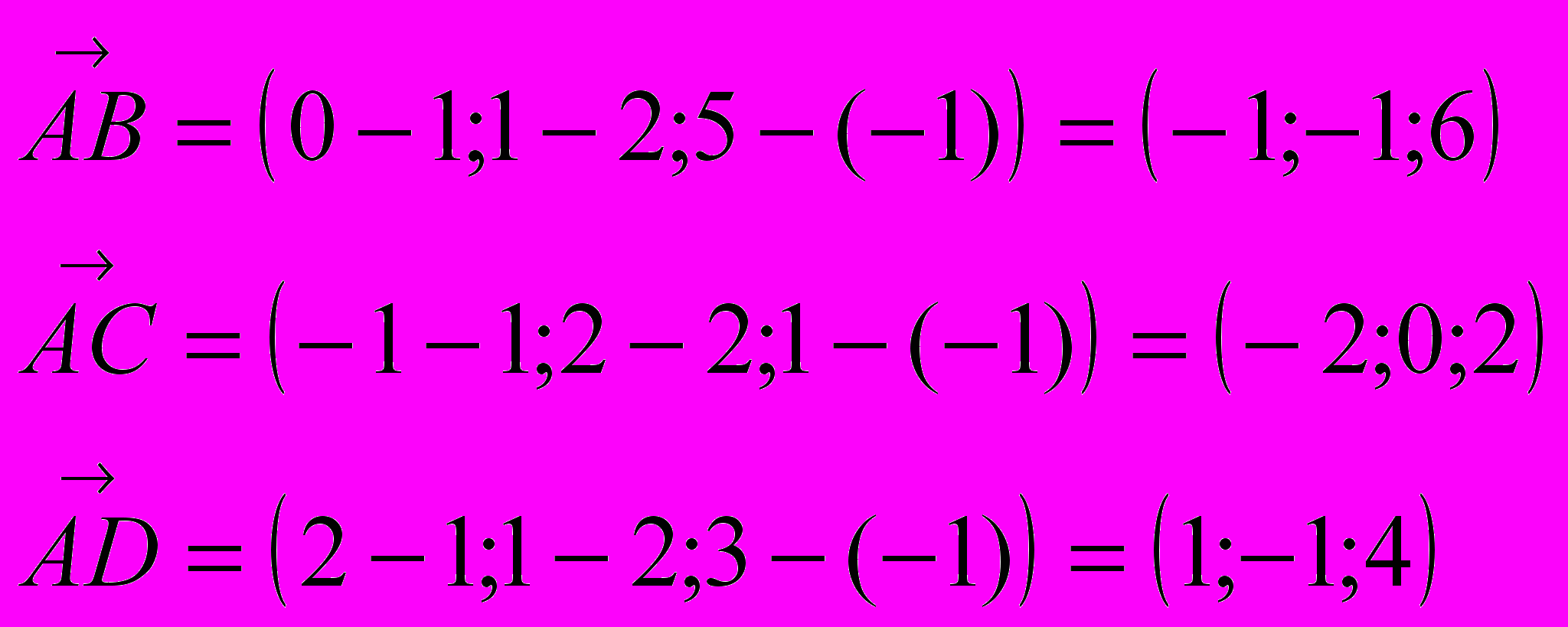








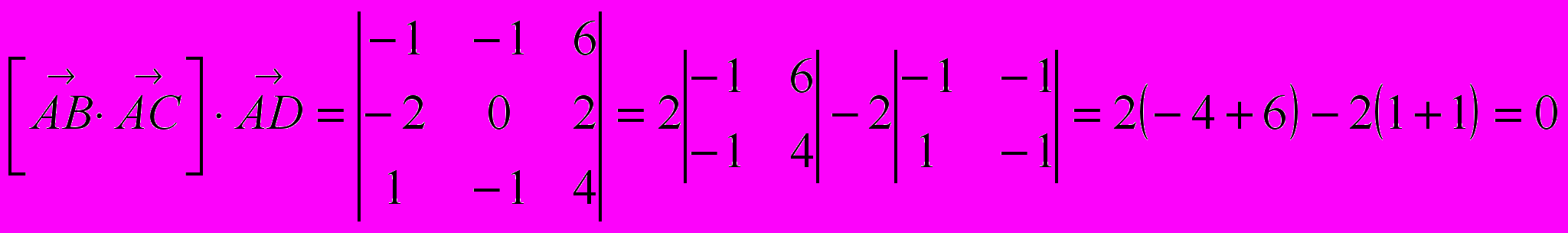
Смешанное произведение равно нулю, а значит, данные вектора лежат в одной плоскости.

Следовательно, четыре точки A, B, C и D с указанными координатами лежат в одной плоскости.


Задача № 3

Вычислить работу равнодействующей F сил 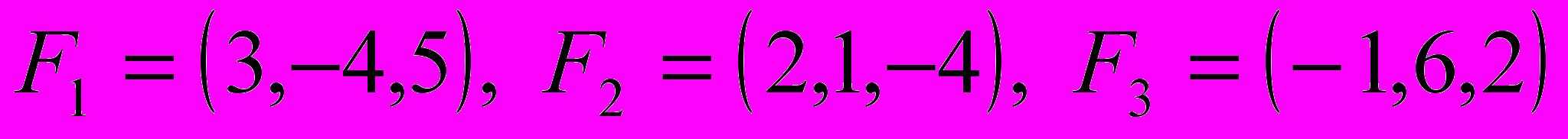, приложенных к материальной точке, которая под их действием перемещается прямолинейно из точки 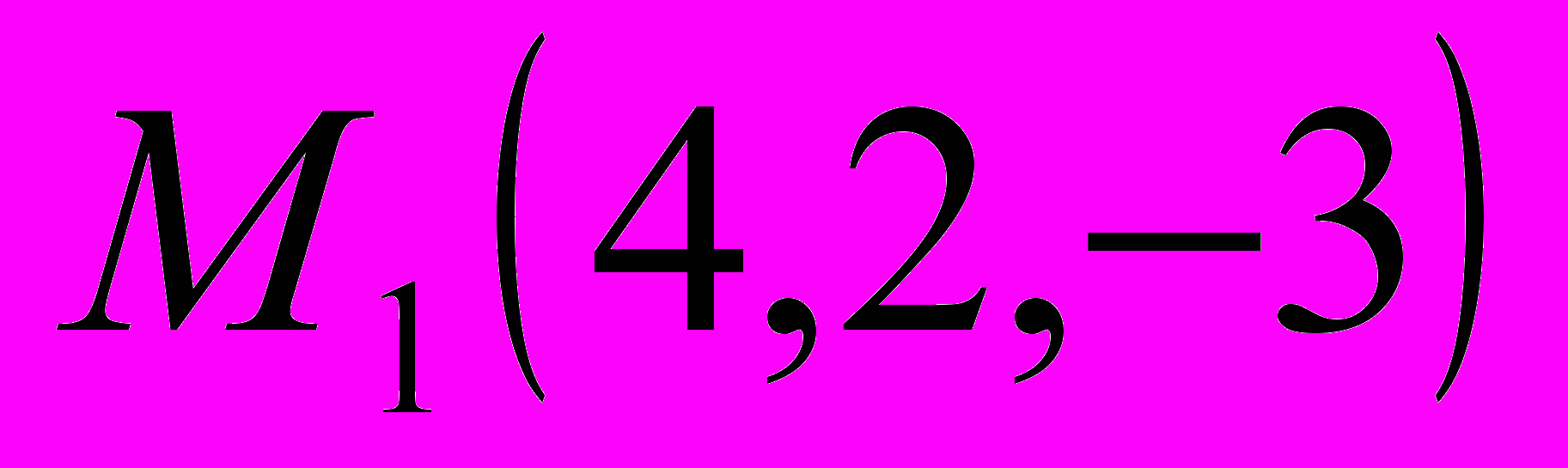в точку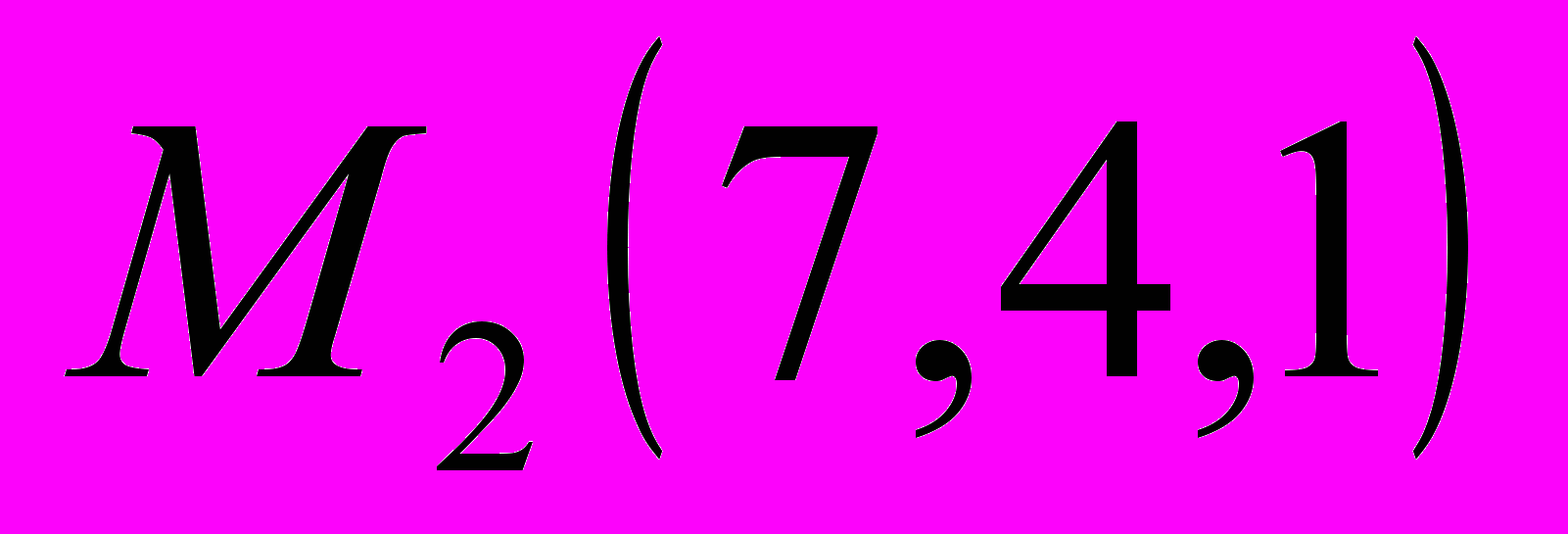


Решение

Так как



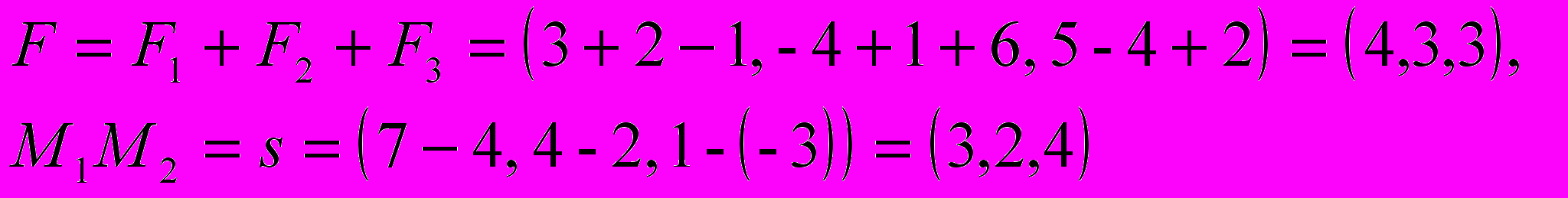
то



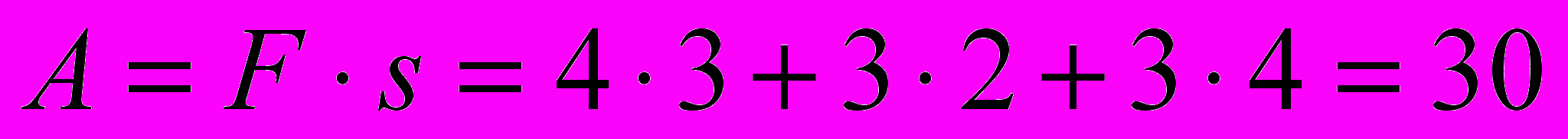
Задача № 4

Вычислить координаты вращающего момента М силы F=(3,2,1), приложенной к точке А(-1,2,4), относительно начала координат О


Решение






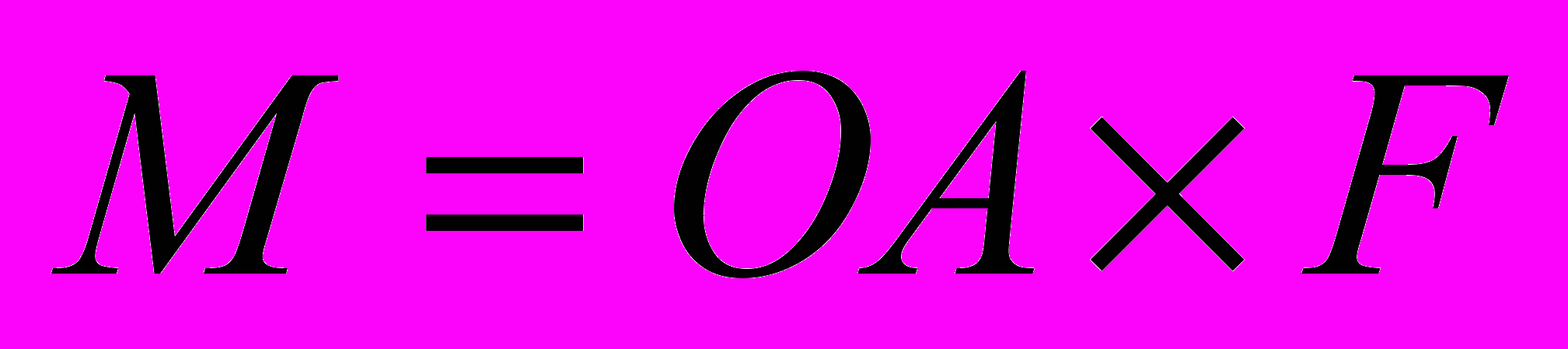
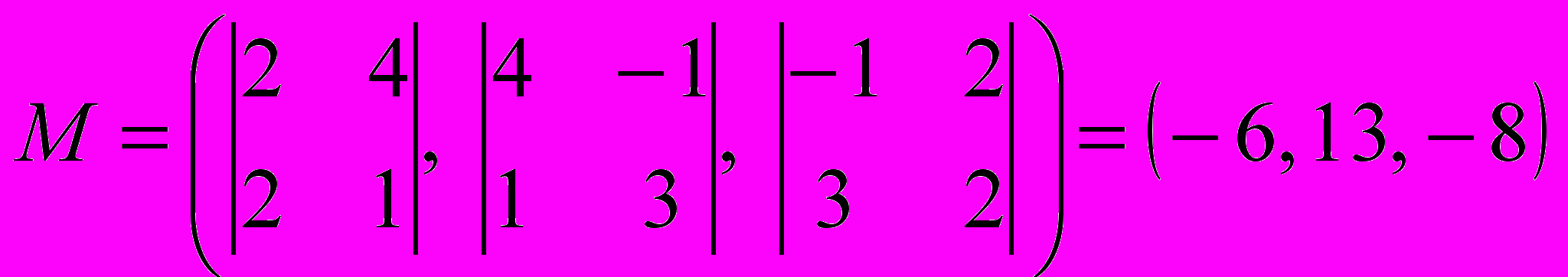
Литература

1. Ильин В. А. Позняк Э. Г. Линейная алгебра: Учеб. для вузов – 4-е изд. – М. Наука. Физматлит. 1999
   
2. А. Г. Курош Лекции по общей алгебре – 1-е изд., М., 1962: 2-е изд., М.,1973
   
3. И. А. Каплан Практическое занятие по высшей математике – М, Наука, 1980