Программа для подготовки к экзамену теоретическая часть
| Вид материала | Программа для подготовки |
СодержаниеПрактическая часть Типовые билеты |
- Программа для подготовки к зачету (экзамену) теоретическая часть, 113.03kb.
- Программа для подготовки к экзамену теоретическая часть, 254.95kb.
- Программа для подготовки к зачету I. Теоретическая часть, 68.7kb.
- Программа для подготовки к зачету теоретическая часть, 166.97kb.
- Рабочая программа по дисциплине «теоретическая фонетика» методические рекомендации, 327.76kb.
- Курс 5 Семестр 9 примерный перечень вопросов к экзамену теоретическая часть, 29.27kb.
- Программа для подготовки к зачету теоретическая часть, 54.03kb.
- Программа подготовки к государственному экзамену по специальности и специализации для, 176.35kb.
- Содержание введение теоретическая часть, 38.74kb.
- Содержание введение теоретическая часть, 38.73kb.
МОСКОВСКАЯ ФИНАНСОВО-ЮРИДИЧЕСКАЯ АКАДЕМИЯ
| Согласовано на 2008-2009 уч.год Начальник УМУ__________________С.В. Щедроткина «_____»_______________2009 г. | |
Дисциплина: Алгебра и геометрия
Специальность (направление): ВСЕ
Форма обучения: ВСЕ
Программа для подготовки к экзамену
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Список тем
- . Векторный анализ и аналитическая геометрия на плоскости
- Системы координат на плоскости.
- Векторы и линейные операции над ними.
- Проекция вектора на ось.
- Разложение вектора на компоненты.
- Скалярное произведение векторов, его свойства, физический и геометрический смысл.
- Преобразование координат вектора при повороте системы координат. Основные задачи аналитической геометрии.
- Прямая линия на плоскости.
- Направляющий вектор.
- Общее уравнение прямой, различные формы уравнения прямой. Параллельность и перпендикулярность прямых.
- Уравнение окружности.
- Основные задачи на прямую и окружность.
- Кривые второго порядка: эллипс, гипербола, парабола. Канонические уравнения кривых второго порядка.
- Системы координат на плоскости.
- Векторный анализ и аналитическая геометрия в пространстве
- Векторы в пространстве.
- Векторное произведение векторов, его свойства, физический и геометрический смысл.
- Смешанное произведение трех векторов, его свойства и геометрический смысл.
- Уравнение плоскости.
- Уравнение прямой в пространстве.
- Уравнение сферы.
- Основные задачи на плоскость, сферу и прямую в пространстве.
- Поверхности второго порядка. Канонические уравнения поверхностей второго порядка.
- Векторы в пространстве.
- Матрицы и детерминанты
- Обобщение понятия "вектор".
- Векторы-столбцы и векторы-строки. Матрицы.
- Произведение строки на столбец.
- Произведение матрицы на столбец.
- Произведение матриц.
- Свойства линейных операций над матрицами.
- Определитель (детерминант) матрицы. Свойства детерминанта. Способы вычисления детерминанта.
- Вычисление детерминанта раскрытием по строке (столбцу).
- Единичная матрица.
- Обратная матрица. Вычисление элементов обратной матрицы.
- Вырожденная матрица. Ранг матрицы.
- Обобщение понятия "вектор".
- Системы линейных алгебраических уравнений.
- Связь матриц с системами линейных алгебраических уравнений (СЛАУ).
- Матрица и расширенная матрица СЛАУ.
- Вырожденные и невырожденные СЛАУ.
- Теорема Кронекера-Капелли.
- Решение невырожденной СЛАУ обращением матрицы.
- Решение невырожденной СЛАУ методом Крамера.
- Решение вырожденных СЛАУ..
- Однородные СЛАУ.
- Связь матриц с системами линейных алгебраических уравнений (СЛАУ).
- Элементы теории множеств.
- Понятие множества.
- Точечные и числовые множества.
- Основные операции над множествами.
- Декартово произведение множеств.
- Соответствие между множествами.
- Мощность множества.
- Понятие множества.
- Алгебраические структуры.
- Алгебраические операции на множестве.
- Свойства операций.
- Группа. Примеры.
- Кольцо. Примеры.
- Поле. Примеры.
- Алгебраические операции на множестве.
- Числовые множества. Комплексные числа
- Натуральные числа.
- Кольцо целых чисел.
- Поле рациональных чисел.
- Поле действительных чисел.
- Определение комплексного числа.
- Поле комплексных чисел.
- Алгебраические операции с комплексными числами.
- Модуль и аргумент комплексного числа.
- Геометрическое представление комплексных чисел.
- Формула Эйлера.
- Понятие о функции комплексного переменного.
- Натуральные числа.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Типовые задачи
- Операции с векторами на плоскости.
Даны векторы
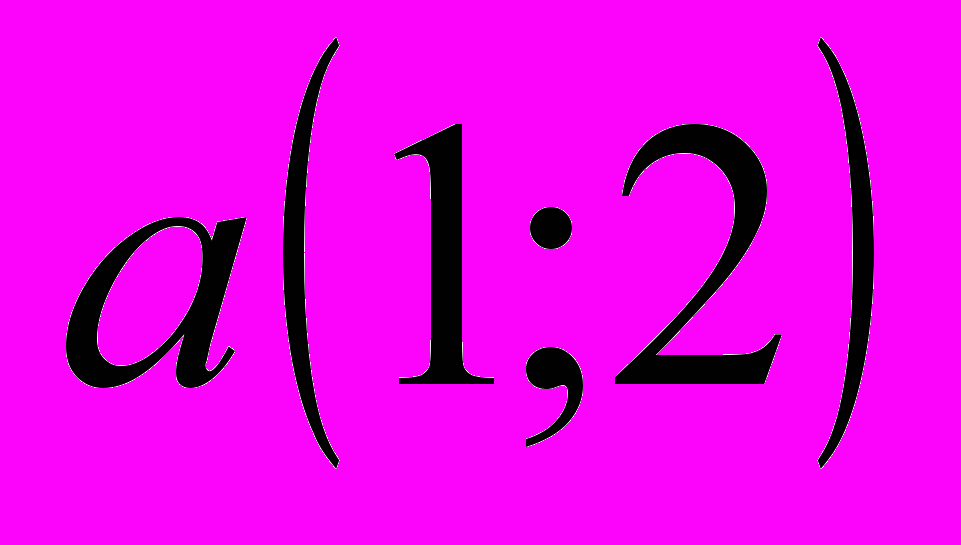 и
и 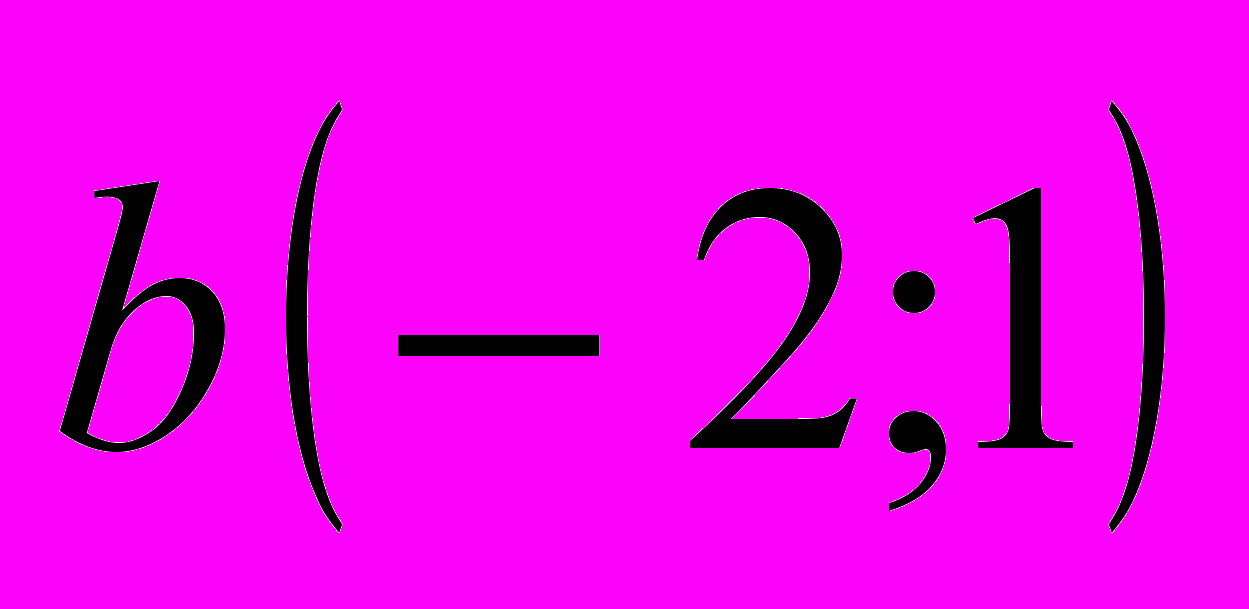 . Найти:
. Найти:- длины этих векторов;
-
 ;
;
- скалярное произведение данных векторов и угол между ними.
- Операции с векторами в пространстве
Даны векторы
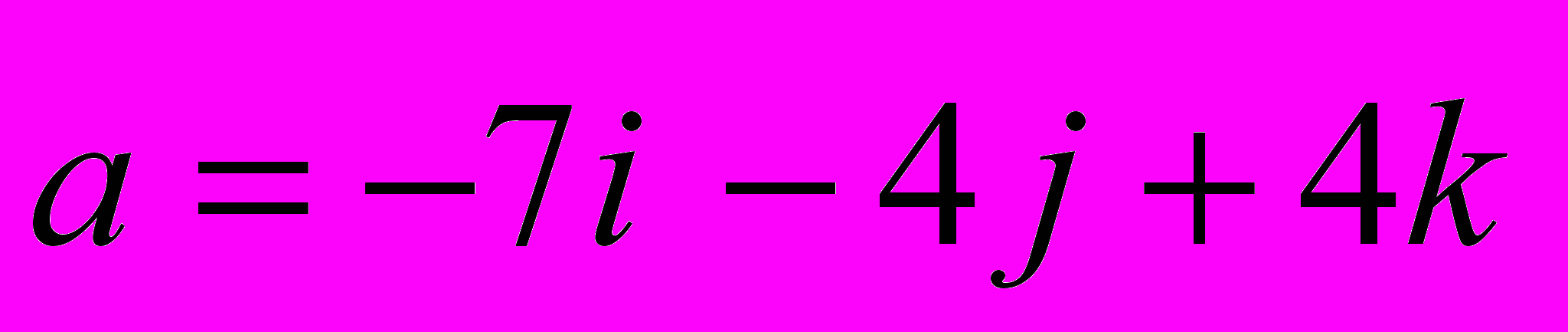 и
и 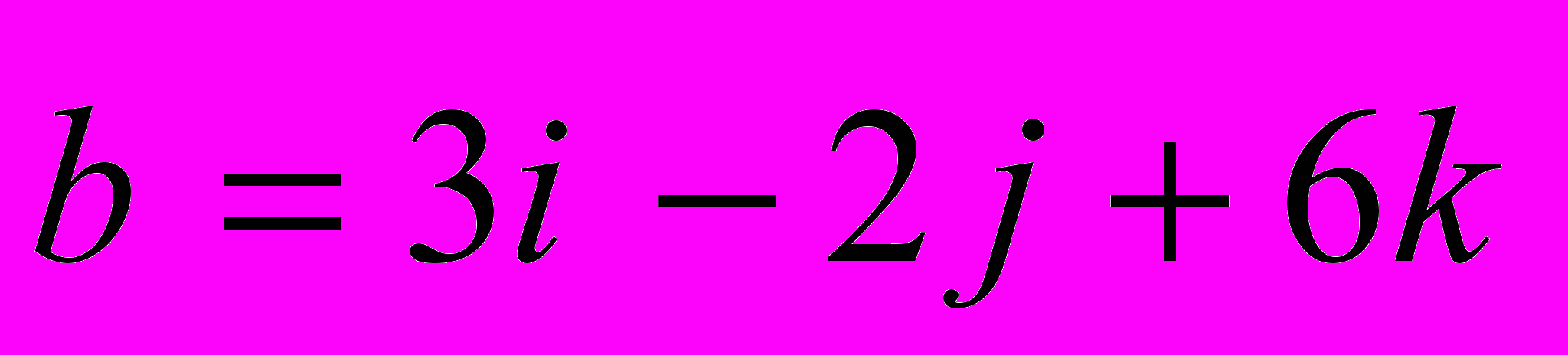 . Найти:
. Найти:- длины этих векторов;
-
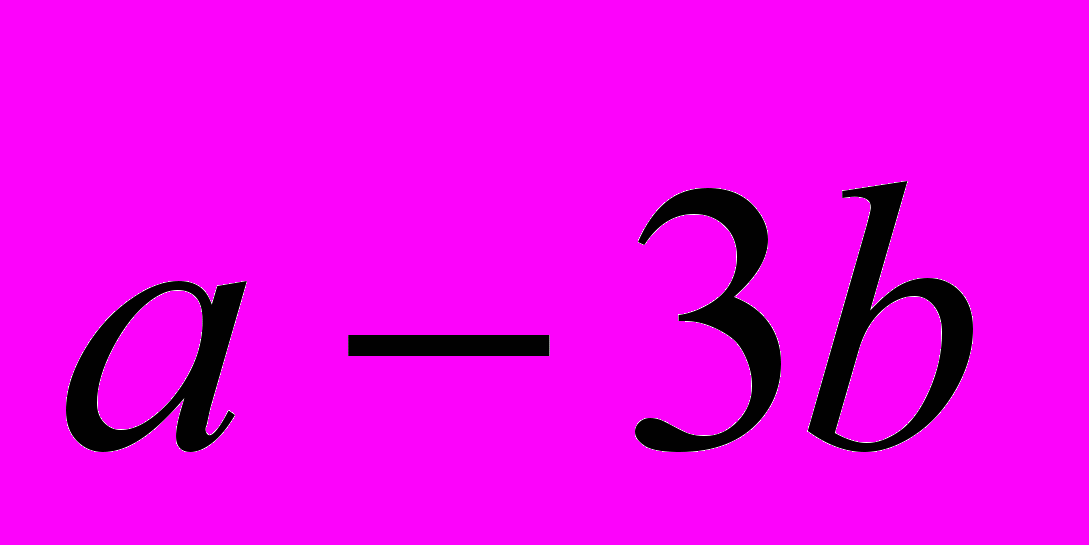 ;
;
- скалярное произведение данных векторов и угол между ними.
- Векторное и смешанное произведение векторов.
- Определить объём параллелепипеда, построенного на векторах
 (1;0;1),
(1;0;1),  (4;-1;-1),
(4;-1;-1),  (1;0;1).
(1;0;1).
- Определить объём параллелепипеда, построенного на векторах
- Прямые и окружности на плоскости.
- Составить уравнение прямой, представленной на рисунке.
- Составить уравнение прямой, представленной на рисунке.
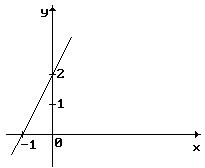
- Определить угловой коэффициент "k" и величину отрезка "b", отсекаемого прямой
 на оси OY.
на оси OY.
- Даны уравнения прямых:
а) x+y+1=0; б) x+y=0; в) 2·x+y+2=0; г) y=2·x
Какие из заданных прямых параллельны?
- Составить уравнение прямой, если известно, что прямая проходит через точку М(1;1) и имеет угловой коэффициент к=1.
- Найти длину отрезка, заключенного между точками пересечения прямой
3у+4х-12=0 с осями координат.
- Определить угол между прямыми х–2у–2=0 и у=–2 х+3.
- Составить уравнение прямой, проходящей через точки
 и
и  .
.
- Определить, с какими из прямых а) у=3; б) у=-х; в) х=5; г) у=2х пересекается окружность х2 +у2=25.
- Определить координаты центра и радиус окружности х2 +у2 –4х+8у–16=0.
- Составить уравнение окружности, проходящей через точку М(-1;1) и центр которой лежит в точке С(-4;5).
- Определить координаты центра окружности, заданной уравнением
 .
.
- Составить уравнение касательной к окружности
 в точке (3;–1).
в точке (3;–1).
- Составить каноническое уравнение окружности, представленной на рисунке.
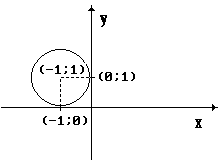
- Кривые второго порядка .
- Определить координаты фокусов эллипса 25x2+9y2=900.
- Определить координаты фокуса и уравнение директрисы параболы х2 =4у .
- Определить, какая кривая задается уравнением:
- Определить координаты фокусов эллипса 25x2+9y2=900.
-
 ;
;
-
 ;
;
-
 ;
;
-
 .
.
- Прямые, плоскости и сферы.
- Определить, какое из уравнений а) 2x-3y+z+1=0; б) x+2y-6=0; в) x+3y=0 определяет плоскость, параллельную оси OZ.
- Найти координаты нормального вектора к плоскости 2·x-3·y+z-6=0.
- Определить взаимное расположение прямых
 и
и  .
.
- Определить, какое из уравнений а) 2x-3y+z+1=0; б) x+2y-6=0; в) x+3y=0 определяет плоскость, параллельную оси OZ.
- Поверхности второго порядка.
- Определить, какая поверхность задаётся уравнением
- Определить, какая поверхность задаётся уравнением
-
 ;
;
-
 ;
;
-
 .
.
- Определители (детерминанты).
Вычислить определители:
-
 ;
;
-
 ;
;
-
 .
.
- Операции с квадратными матрицами.
Даны матрицы:
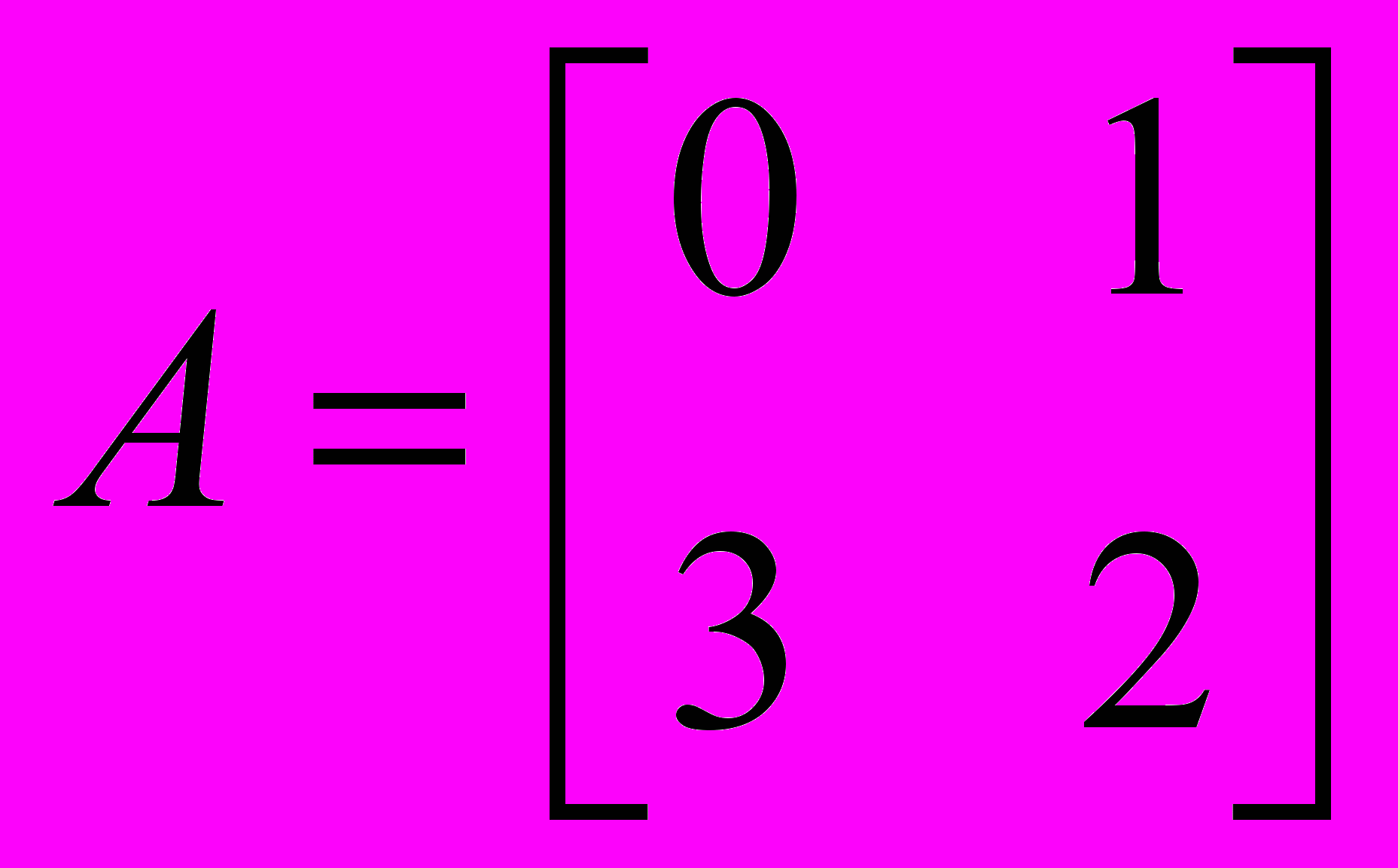 и
и 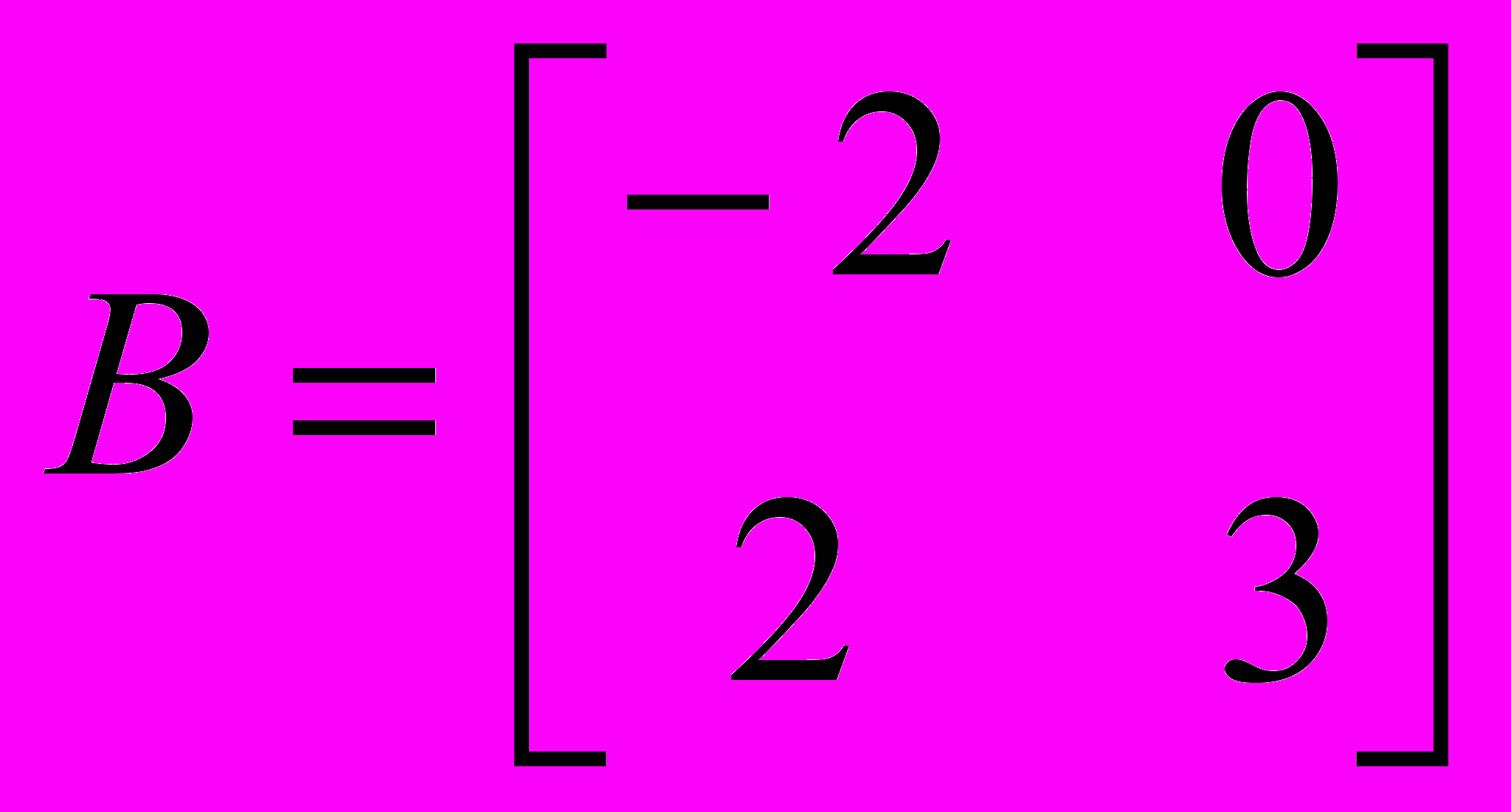 . Найти:
. Найти:- 5А – В;
- 3АT 2B;
- АВ.
- Операции с прямоугольными матрицами
- Даны матрицы А=
 и В=
и В= . Найти их произведение.
. Найти их произведение.
- Даны матрицы А=
- Ранг матрицы. Расширенная матрица системы уравнений. Частные определители.
- Определить ранг матрицы
 ;
;
- Вычислить частные определители системы
 .
.
- Определить ранг матрицы
- Обратные матрицы.
- Найти обратную матрицу для матрицы
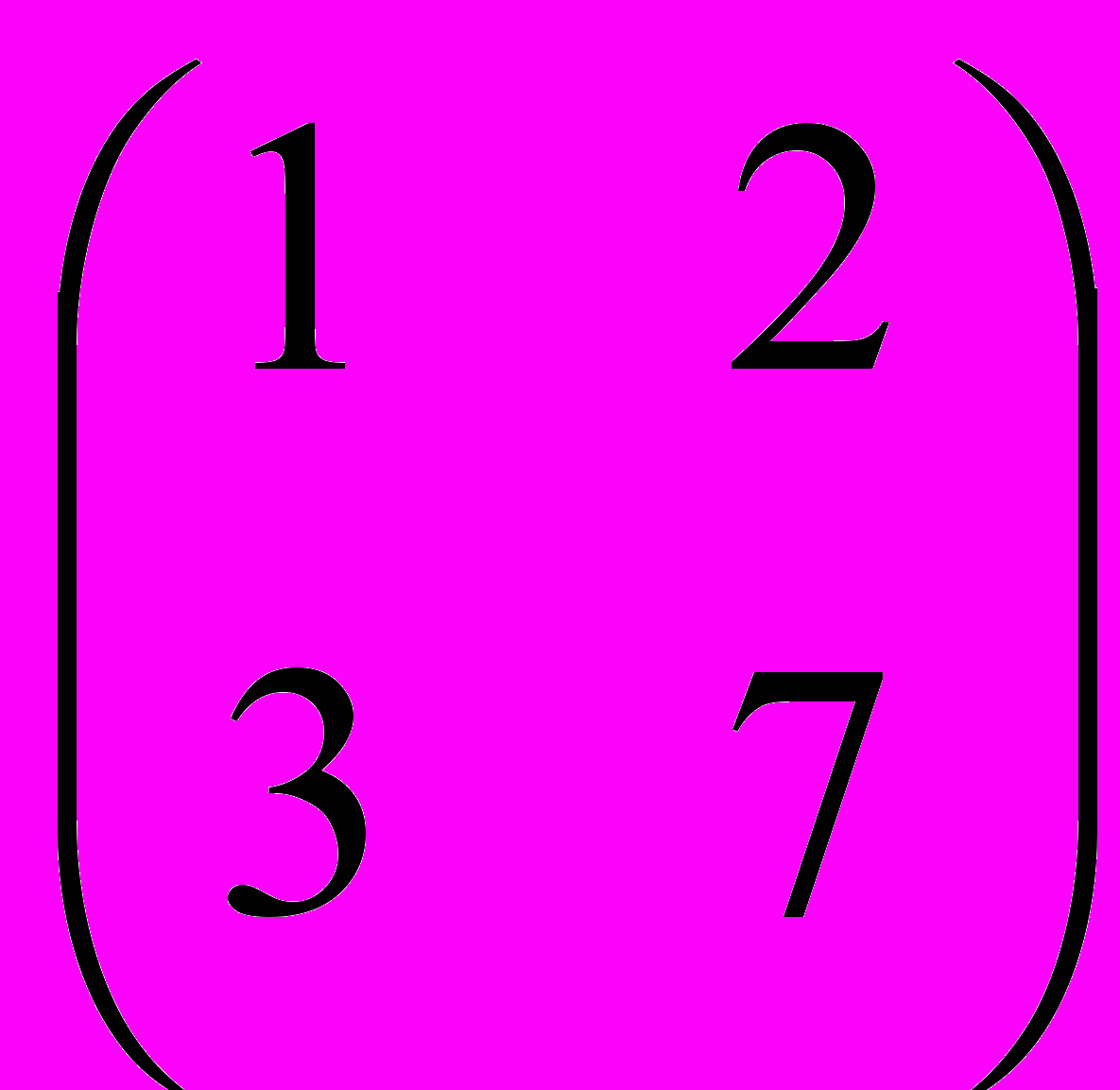 .
.
- Найти обратную матрицу для матрицы
- Системы линейных алгебраических уравнений
- Решить систему
 методом Крамера.
методом Крамера.
- Решить систему
- Элементы теории множеств.
- ; Определить результаты операций
 , если
, если 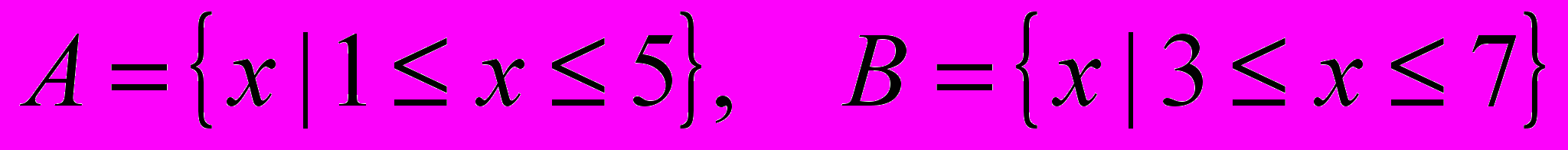
- . Пусть А – множество натуральных чисел, кратных 2; В – множество натуральных чисел кратных 3. Найти АВ, АВ, А\В, В\А.
- Пусть А – множество точек круга единичного радиуса с центром в начале координат; В – множество всех точек координатной плоскости. Изобразить множества АВ, АВ, А\В, В\А
- Сравнить мощность множества четных натуральных чисел с мощностью множества целых чисел, больших -100000.
- ; Определить результаты операций
- Алгебраические структуры.
- Выяснить, составляет ли группу множество положительных и отрицательных чисел, кратных трем с заданной операцией сложения по обычным правилам.
- Выяснить, составляет ли Абелеву группу множество невырожденных матриц 3х3 с заданной операцией умножения.
- Составляет ли множество векторов в пространстве с заданными операциями сложения и векторного умножения кольцо? Составляет ли это множество поле? Почему?
- Выяснить, составляет ли группу множество положительных и отрицательных чисел, кратных трем с заданной операцией сложения по обычным правилам.
- Комплексные числа.
- найти все значения

- записать в алгебраической и в тригонометрической формах значения выражения

- найти все решения уравнения

- найти все значения
ТИПОВЫЕ БИЛЕТЫ
Билет № 1
| 1. | Вычислить определитель:  |
| 2. | Найти произведение АВ, если А=  , В= , В= . . |
| 3. | Найти комплексные корни уравнения  |
| 4. | Найти обратную матрицу  . . |
| 5. | Пусть А = { (x, y) | x2+y2 > 0}; В = {(x, y) | y > -1 } Изобразить множества АÇВ, ВÈА, А\В, В\А |
| 6. | Определить площадь треугольника, построенного на векторах  =(2;0;2), =(2;0;2),  =(-3;-1;-1). =(-3;-1;-1). |
| 7 | Определить объём параллелепипеда, построенного на векторах  =(3;0;0), =(3;0;0),  =(0;2;0), =(0;2;0),  =(0;0;-7). =(0;0;-7). |
| 8. | Уравнение прямой, проходящей через точки  и и  имеет вид… имеет вид… |
| 9. | Найти точку пересечения прямой, заданной точкой A(1,2,-4) и направляющим вектором  , и плоскости, заданной уравнением 2x + 3y - z -1 = 0. , и плоскости, заданной уравнением 2x + 3y - z -1 = 0. |
| 10 | Определить координаты фокусов гиперболы 7х2–9у2=63 |
Билет № 2
| | Пусть А ={0;2;11;47} В={ 3n-2 | 0 |
| | Вычислить определитель:  |
| | Найти произведение АВ, если  , ,  , , |
| | Найти все комплексные значения  |
| | Ранг матрицы  равен… равен… |
| | Выяснить, составляет ли группу множество целых (положительных и отрицательных) четных чисел с операцией сложения. |
| | Решить систему линейных уравнений:  |
| | Уравнение окружности, проходящей через точку М(-1;1) и центр которой лежит в точке С(-2;3), имеет вид… |
| | Прямая х-2у-2=0 пересекается с прямой у=-2 х+3 под углом… |
| | Определить поверхность, заданную уравнением  . . |
5. СПИСОК литературЫ.
- Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – 2-е изд. – М.: Айрис-пресс, 2004. -608 с.: ил. –(Высшее образование).
- Дорофеева А.В. Высшая математика. Гуманитарные специальности: Учеб. Пособие для вузов.- 2-е изд., перераб. и доп. – М. : Дрофа, 2003. – 384 с.: ил.
- Зимина О.В., Кириллов А.И., Сальников Т.А. Высшая математика / под ред. А.И. Кириллова. – 3-е изд., испр. – М.: ФИЗМАТЛИТ, 2003. – 368 с. – (Решебник) – ISBN 5-9221-0441-1.
Зав. каф. «Общих математических
и естественнонаучных дисциплин» ___________________А.Ю. Байков
