Программа для подготовки к зачету I. Теоретическая часть
| Вид материала | Программа для подготовки |
СодержаниеII. Типовые задачи. III. Типовые билеты |
- Программа для подготовки к зачету (экзамену) теоретическая часть, 113.03kb.
- Программа для подготовки к зачету теоретическая часть, 166.97kb.
- Программа для подготовки к зачету теоретическая часть, 54.03kb.
- Программа для подготовки к экзамену теоретическая часть, 101.03kb.
- Программа для подготовки к экзамену теоретическая часть, 254.95kb.
- Рабочая программа по дисциплине «теоретическая фонетика» методические рекомендации, 327.76kb.
- Содержание введение теоретическая часть, 38.74kb.
- Содержание введение теоретическая часть, 38.73kb.
- Программа для подготовки к сдаче вступительного экзамена в аспирантуру по специальности, 174.75kb.
- Л. И. Горбунова, Г. С. Келлер культурология часть I человек – общество культура, 2386.47kb.
МОСКОВСКАЯ ФИНАНСОВО-ЮРИДИЧЕСКАЯ АКАДЕМИЯ
| Согласовано на 2008-2009 уч.год Начальник УМУ __________________С.В. Щедроткина «_____»_______________2009 г. | |
Дисциплина: Математика и информатика ( 1 часть из 2)
Специальность (направление): реклама.
Форма обучения: все
Программа для подготовки к зачету
I. Теоретическая часть.
- . Векторы. Определения, свойства, линейные операции, разложение вектора по базису.
- Скалярное произведение. Определения, свойства, решение в координатной форме.
- Уравнения прямой на плоскости. Отображение уравнений на графиках.
- Основные задачи на прямую на плоскости.
- Уравнения плоскости в пространстве.
- Основные задачи на плоскость.
- Уравнения прямой в пространстве.
- Основные задачи на прямую в пространстве.
- Квадратные матрицы. Операции с матрицами..
- Детерминант (определитель) матрицы. Свойства, способы вычисления.
- Обратная матрица.
- Матричный способ записи и решения систем линейных алгебраических уравнений.
- Правило Крамера для решения систем линейных уравнений.
- Функция. Основные элементарные функции. Построение графиков элементарных функций.
- Предел функции в точке и в бесконечности.
- Первый и второй замечательные пределы, их следствия.
- Неопределенные выражения. Приемы раскрытия неопределенных выражений.
- Непрерывность функции в точке. Точки разрыва функции и их классификация.
- Основные свойства функции, непрерывной в точке. Непрерывность функции на отрезке.
- Производная и дифференциал. Определение, геометрический смысл.
- Основные правила дифференцирования.
- Таблица производных основных элементарных функций.
- Правила дифференцирования сложной и неявной функций.
- Производные высших порядков. Определение, правила нахождения.
- Правило Лопиталя.
- Первообразная. Неопределенный и определенный интегралы. Формула Ньютона-Лейбница
- Основные методы интегрирования.
- Таблица неопределенных интегралов от простейших функций.
- Интегрирование подстановкой.
- Интегрирование тригонометрических выражений.
- Интегрирование по частям.
- Вычисление площади плоской криволинейной трапеции.
II. Типовые задачи.
- Операции с векторами на плоскости.
Даны векторы
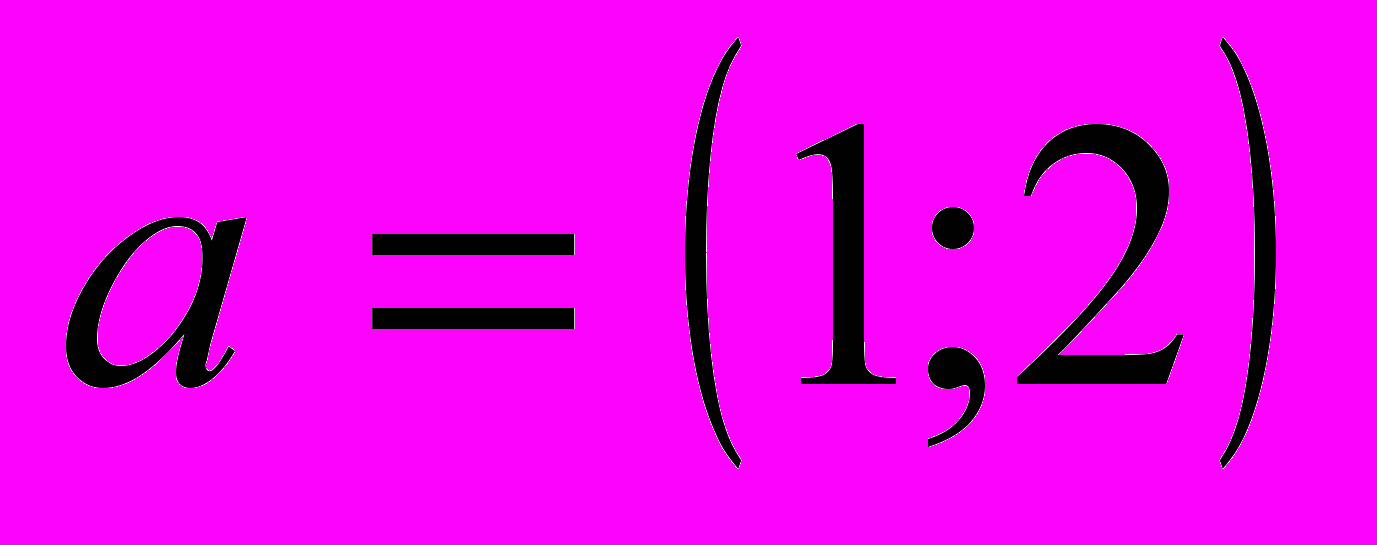 и
и 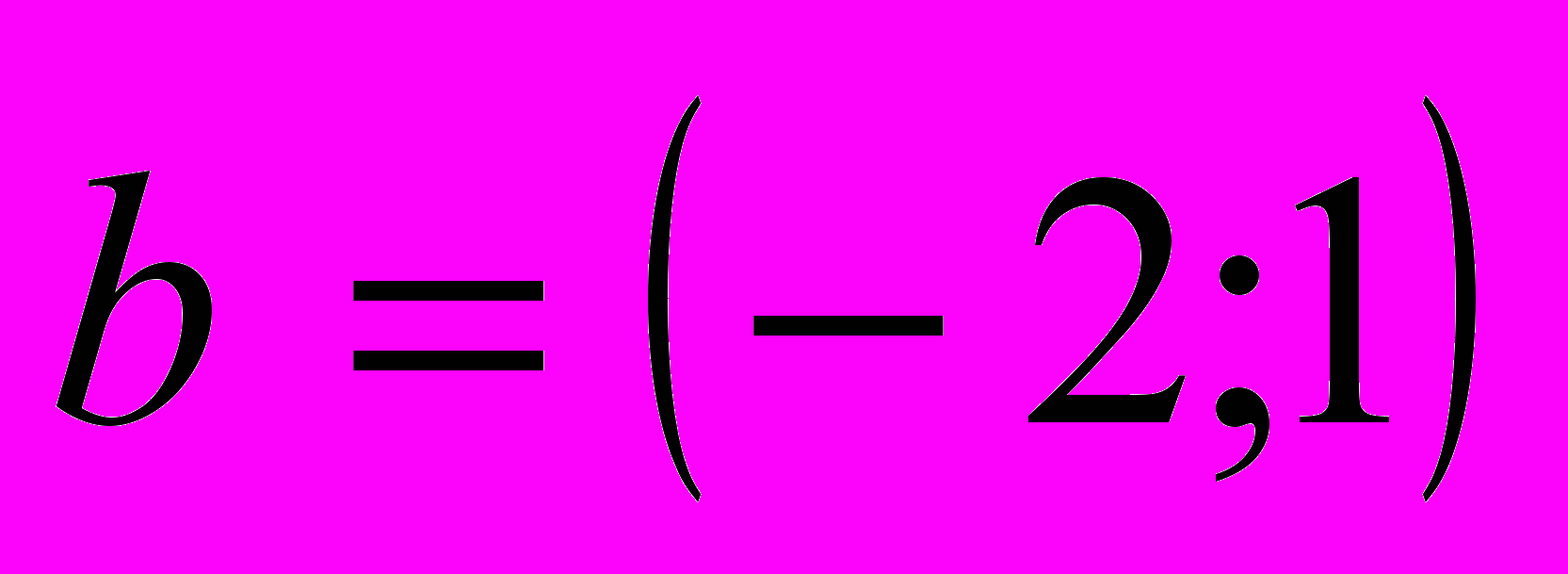 . Найти:
. Найти:- длины этих векторов;
-
 ;
;
- скалярное произведение данных векторов и угол между ними.
- Операции с векторами в пространстве
Даны векторы
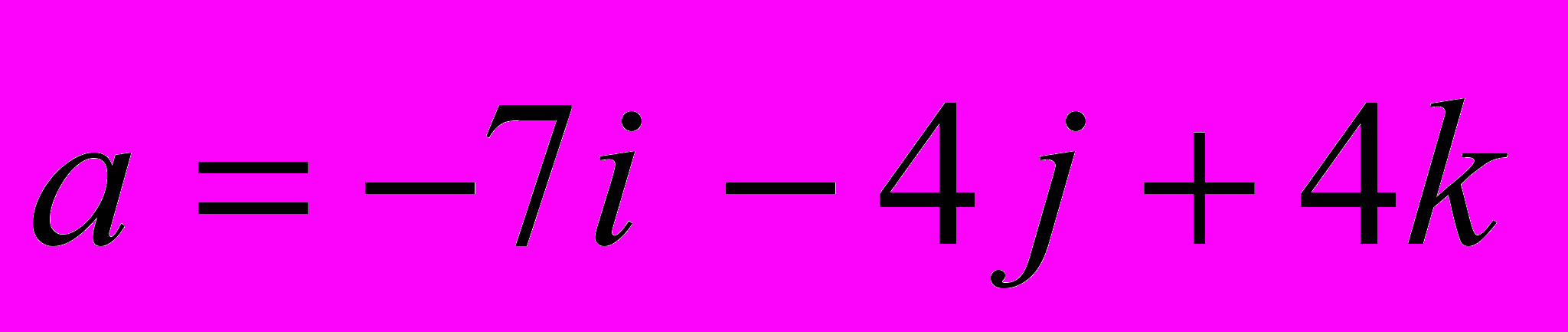 и
и 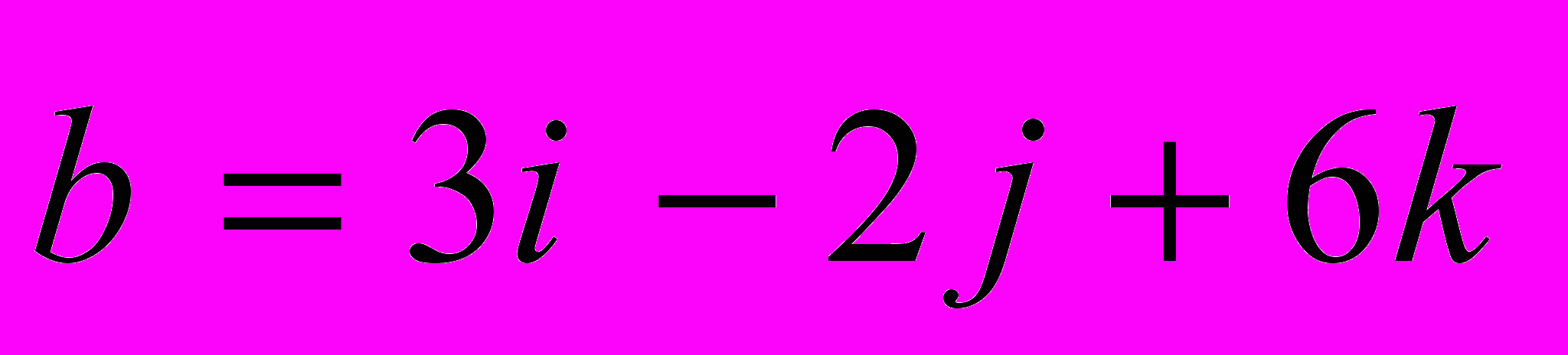 . Найти:
. Найти:- длины этих векторов;
- |
 |;
|;
- скалярное произведение данных векторов и угол между ними
- Прямые и окружности на плоскости.
- Составить уравнение прямой, представленной на рисунке.
- Составить уравнение прямой, представленной на рисунке.
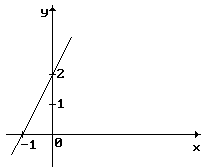
- Определить угловой коэффициент "k" и величину отрезка "b", отсекаемого прямой
 на оси OY.
на оси OY.
- Даны уравнения прямых:
а) x+y+1=0; б) x+y=0; в) 2·x+y+2=0; г) y=2·x
Какие из заданных прямых параллельны?
- Составить уравнение прямой, если известно, что прямая проходит через точку М(1;1) и имеет угловой коэффициент к=1.
- Найти длину отрезка, заключенного между точками пересечения прямой
3у+4х-12=0 с осями координат.
- Определить угол между прямыми х–2у–2=0 и у=–2 х+3.
- Составить уравнение прямой, проходящей через точки
 и
и 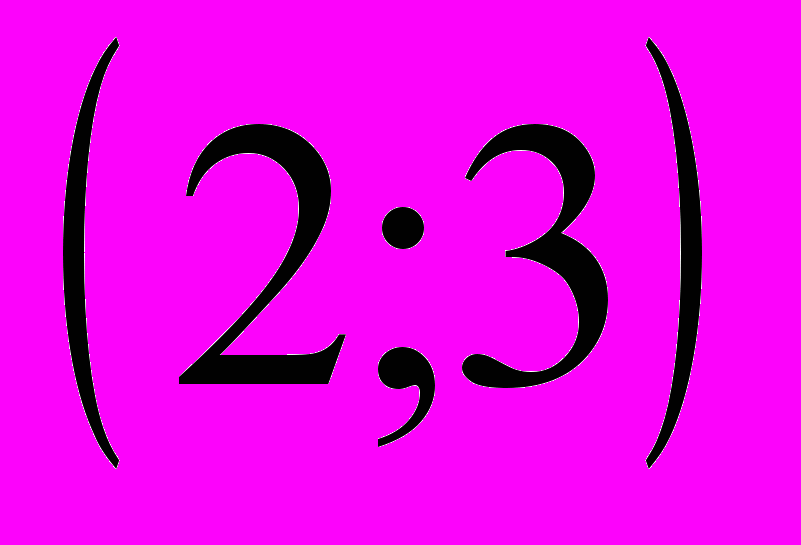 .
.
- Определить, с какими из прямых а) у=3; б) у=-х; в) х=5; г) у=2х пересекается окружность х2 +у2=25.
- Составить уравнение окружности, проходящей через точку М(-1;1) и центр которой лежит в точке С(-4;5).
- Определить координаты центра окружности, заданной уравнением
 .
.
- Составить уравнение окружности, представленной на рисунке.

- Определители (детерминанты).
Вычислить определители:
-
 ;
;
-
 ;
;
-
 .
.
- Операции с квадратными матрицами.
Даны матрицы:
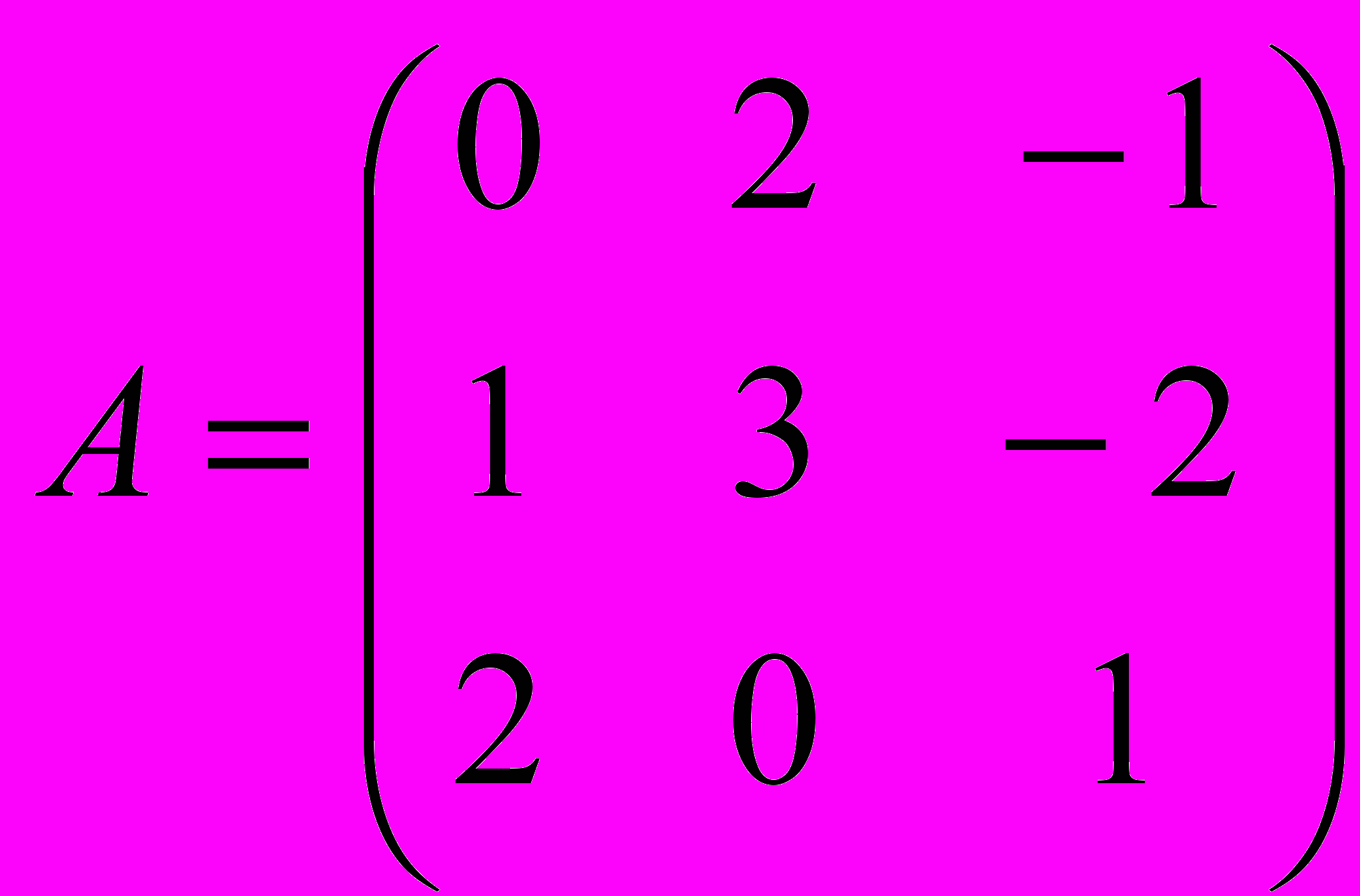 и
и 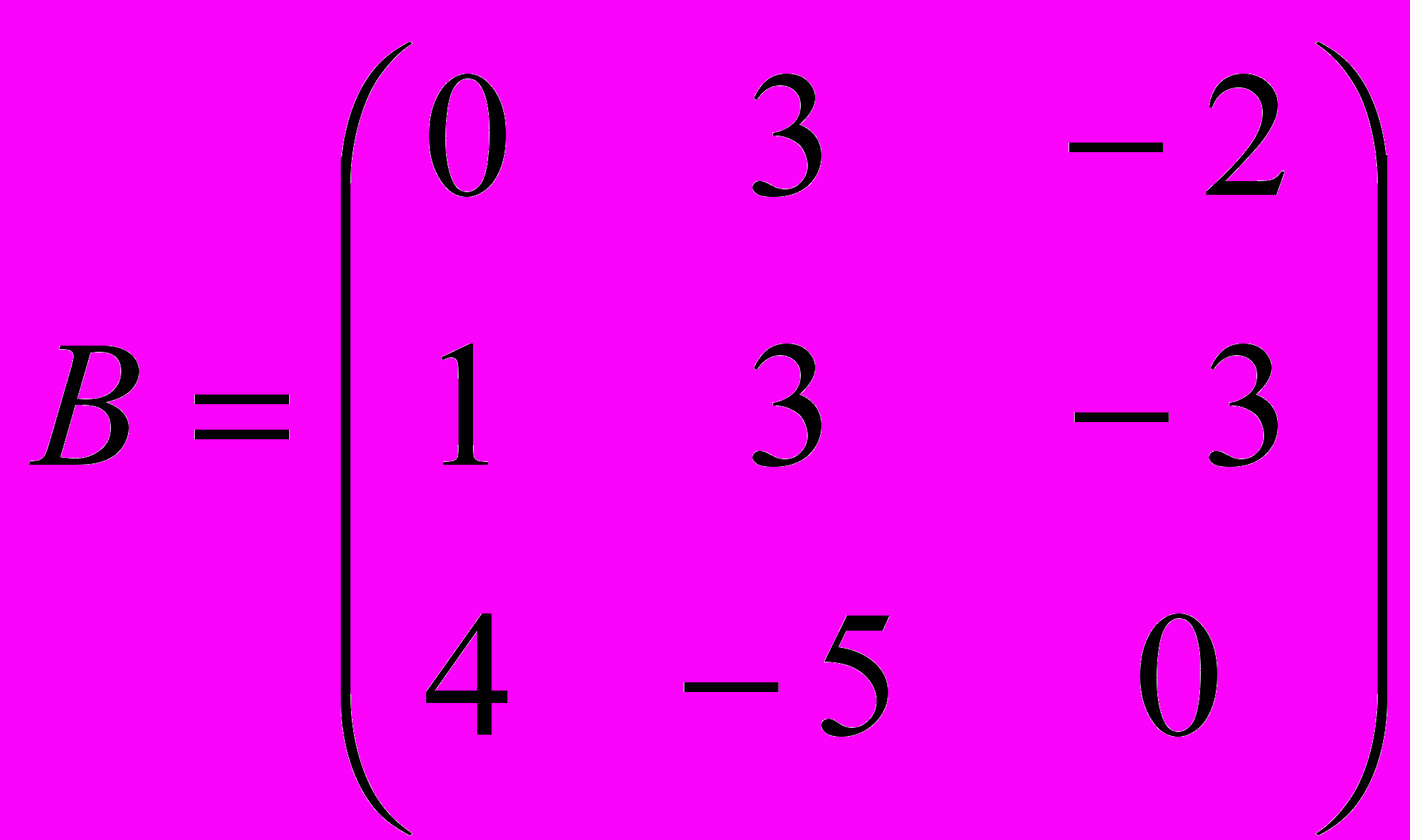 . Найти:
. Найти:- 5А – В;
- 3Аt – 2B;
- АВ.
- Обратные матрицы.
- Найти обратные матрицу для матрицы
 .
.
- Найти обратные матрицу для матрицы
- Системы линейных алгебраических уравнений
- Решить систему
 методом Крамера.
методом Крамера.
- Решить систему
- Пределы дробно-рациональных функций и замечательные пределы
Вычислить пределы:
-
 .
.
-

-
 .
.
- Производные элементарных функций
- Найти производную функции
 .
.
- Найти производную функции
- Геометрический смысл производной. Уравнение касательной
- Составить уравнение касательной к графику функции
 в точке (1;2).
в точке (1;2).
- Составить уравнение касательной к графику функции
- Возрастание, убывание, экстремумы функции одной переменной.
- Исследовать на экстремум функцию y=2x2+6x-7.
- Определить наибольшее и наименьшее значение функции
 на отрезке
на отрезке  .
.
- Исследовать на экстремум функцию y=2x2+6x-7.
- Табличные интегралы
- Вычислить интеграл
 .
.
- Вычислить интеграл
- Интегрирование подстановкой
- Вычислить интеграл
 .
.
- Вычислить интеграл
- Интегрирование по частям
-
- Геометрический смысл интеграла
К
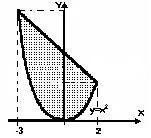
аким интегралом задается площадь заштрихованной части фигуры, изображенной на чертеже?
III. Типовые билеты
Типовой билет № 1
| | Найти произведение матриц  |
| | Вычислить определитель  |
| | Вычислить  . . |
| | Решить систему линейных уравнений:  |
| | Выяснить какие из прямых, заданных уравнениями параллельны: а) х+4у-7=0; в) 12у=3х+3; с) 8у=9-4х; д) 4х+у=7. |
| | Из прямых а) х+у-7=0, в) у=2х+3 с) 2у=9-4х д) 2х+у=0 параллельны… |
| | Вычислить предел:  |
| | Вычислить производную  |
| | Исследовать на экстремум функцию y=-3x2+x-11 |
| | Вычислить интеграл  |
Типовой билет № 2
| | Найти произведение матриц  |
| | Вычислить определитель  |
| | Найти обратную матрицу  |
| | Решить систему линейных уравнений:  |
| | Даны векторы  (-2;-4) и (-2;-4) и  (-3;-7). Найти скалярное произведение (-3;-7). Найти скалярное произведение  |
| | Вычислить предел:  |
| | Вычислить производную  |
| | Исследовать на экстремум функцию y=2x2+6x-7 |
| | Определить промежутки выпуклости, вогнутости и точки перегиба функции  . . |
| | Вычислить интеграл  |
ЛИТЕРАТУРА.
- Демин И.И. Математика. Учебно-методическое пособие для экономистов. – М.: МФА, 2002 – 130 с.
- Демин И.И. Математика. Учебно-методическое пособие для гуманитарных специальностей. – М.: МФА, 2002 – 90 с.
- Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – 2-е изд. – М.: Айрис-пресс, 2004. -608 с.: ил. –(Высшее образование).
- Зимина О.В., Кириллов А.И., Сальников Т.А. Высшая математика / под ред. А.И. Кириллова. – 3-е изд., испр. – М.: ФИЗМАТЛИТ, 2003. – 368 с. – (Решебник) – ISBN 5-9221-0441-1.
- Кремер Н.Ш. и др.Высшая математика для экономистов. Учебник, ЮНИТИ, М.,2002г.
- Щипачев В.С. Задачи по высшей математике. учебное пособие. Высшая школа, М.,1997

