Geum.ru

Программа для подготовки к зачету (экзамену) теоретическая часть

Вид материалаПрограмма для подготовки

Содержание


Практическая часть
Типовые билеты типовой билет №1
Типовой билет №2
Подобный материал:
МОСКОВСКАЯ ФИНАНСОВО-ЮРИДИЧЕСКАЯ АКАДЕМИЯ



Согласовано на 2008-2009 уч.год

Начальник УМУ




__________________С.В. Щедроткина


«_____»_______________2009 г.





Дисциплина: Методы решения оптимизационных задач в бизнесе

Специальность (направление): Прикладная информатика в экономике

Форма обучения: все


Программа для подготовки к зачету (экзамену)


ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Список вопросов

    1. Что такое оптимизация?
    2. Что такое параметры плана?
    3. Понятие одномерной и многомерной оптимизации.
    4. Какая функция называется целевой?
    5. Чем отличаются условная и безусловная оптимизация?
    6. Какая функция называется непрерывной?
    7. Какая функция называется гладкой?
    8. Какая функция называется непрерывной?
    9. Какая функция называется выпуклой?
    10. Какое множество называется выпуклым?
    11. Понятие проекции точки на множество.
    12. Свойства проекции точки на множество.
    13. Теоремы отделимости и их приложения.
    14. Понятие конуса.
    15. Теорема Фреше.
    16. Понятие строго выпуклой функции.
    17. Понятие сильно выпуклой функции.
    18. Теорема Вейерштрасса и её следствия.
    19. Выпуклая экстремальная задача.
    20. Теорема о глобальном экстремуме.
    21. Классификация численных методов оптимизации функций одной переменной.
    22. Предварительная локализация экстремума.
    23. Особенности решении задач одномерной оптимизации.
    24. Сходимость методов оптимизации.
    25. Условия остановки численных методов.
    26. Расскажите метод перебора. В чем заключаются достоинства метода? Постройте алгоритм метода.
    27. Расскажите метод общего поиска. В каких случаях его можно применять? Постройте алгоритм метода.
    28. Расскажите метод золотого сечения. В каких случаях его можно применять? Постройте алгоритм метода.
    29. Выведите значение пропорции золотого сечения.
    30. Докажите, что точка золотого сечения, отсекающая меньший отрезок, делит больший отрезок также в пропорции золотого сечения.
    31. Особенности решения задач многомерной оптимизации.
    32. Понятия локального и глобального экстремума.
    33. Расскажите метод покоординатного спуска.
    34. Каким свойством обладает вектор-градиент?
    35. Расскажите метод градиентного спуска.
    36. Расскажите метод наискорейшего спуска. Каковы достоинства метода?
    37. Расскажите метод штрафных функций.
    38. Методы поиска глобального экстремума.
    39. Каковы характерные особенности задач математического программирования?
    40. Опишите структуру общей задачи линейного программирования.
    41. Записать стандартную постановку задачи линейного программирования.
    42. Записать каноническую постановку задачи линейного программирования.
    43. Как перейти от стандартной постановки задачи линейного программирования к канонической?
    44. Какое решение задачи называется допустимым? Оптимальным?
    45. Как формулируется в общем виде задача рационального распределения материальных ресурсов?
    46. Какова структура модели рационального распределения материальных ресурсов?
    47. Как формулируется в общем виде задача о рационе питания?
    48. Какова структура модели задачи о рационе питания?
    49. Как формулируется в общем виде задача о раскрое?
    50. Какова структура модели задачи о раскрое?
    51. От каких факторов зависит математическая модель рационального раскроя материалов?
    52. Как формулируется задача оптимизации состава исходных компонентов при составлении смесей?
    53. Какова структура модели задачи о смесях?
    54. Как формулируется в общем виде задача оптимальной загрузки производственных мощностей?
    55. Какова структура модели задачи об оптимальной загрузке производственных мощностей?
    56. Как формулируется в общем виде задача на выбор оптимального портфеля ценных бумаг?
    57. Как формулируется в общем виде транспортная задача?
    58. Сформулируйте двойственную задачу линейного программирования.
    59. Теорема двойственности.
    60. В чем состоит идея геометрического метода? Когда его можно применять?
    61. Какая область называется областью допустимых решений? Основное свойство области допустимых решений?
    62. Свойство вектора-градиента.
    63. Может ли задача линейного программирования не иметь решения? Иметь бесконечное множество решений? В каких случаях это происходит?
    64. В чем состоит идея симплексного метода?
    65. Расскажите геометрический смысл симплекс-метода.
    66. Какое решение называется опорным? Способы выбора опорного решения?
    67. Что такое базисные переменные? Свободные переменные? Каков их геометрический смысл?
    68. По каким критериям выбирается разрешающий столбец? Разрешающая строка? Разрешающий элемент?
    69. Сформулируйте условие оптимальности плана задачи линейного программирования.
    70. В чем заключается сущность транспортной задачи?
    71. Какая модель транспортной задачи называется закрытой? Открытой?
    72. Как привести открытую модель транспортной задачи к закрытой?
    73. При каком условии любая транспортная задача будет иметь решение?
    74. Какими методами может строиться первоначальный план прикрепления потребителей к поставщикам?
    75. Постройте схему алгоритма метода северо-западного угла.
    76. Постройте схему алгоритма потенциалов.
    77. В каком случае базисный план транспортной задачи является оптимальным?
    78. Для решения каких задач применяется модель транспортной задачи?
    79. Какие экономические показатели могут быть использованы в качестве критерия при оптимизации транспортных процессов?
    80. Информация, необходимая для решения задач оптимизации транспортных процессов.
    81. Ограничения, имеющиеся в модели транспортной задачи.
    82. Всегда ли транспортную задачу можно сбалансировать?
    83. Могут ли для балансировки транспортной задачи понадобиться как фиктивные поставщики, так и фиктивные пункты потребления?
    84. 'Информация, необходимая для решения задачи регионального развития и размещения складской системы.
    85. Можно ли решить транспортную задачу симплекс-методом?
    86. Перечислите основные разделы математического программирования. Для каких задач они применяются? Приведите примеры.
    87. Сущность динамического программирования.
    88. Задача о нахождении кратчайшего в требуемом смысле пути.
    89. Сущность стохастического программирования.
    90. Сущность выпуклого программирования.
    91. Сущность квадратичного программирования.
    92. Сущность целочисленного программирования.
    93. Для решения задач из каких разделов математического программирования можно использовать инструмент Поиск решения MS Excel?
    94. Постановка задачи оптимального управления.
    95. Необходимое условие оптимальности управления.
    96. Уравнение Беллмана.
    97. Принцип максимума Понтрягина.
    98. План решения задач оптимального управления.
    99. История развития задач на минимум и максимум.
    100. Уравнение Эйлера.
    101. Необходимые условия оптимальности первого порядка в простейшей задаче вариационного исчисления.
    102. Принцип Гамильтона.
    103. Задачи вариационного исчисления с ограничениями.
    104. Вариационное исчисление и современные задачи оптимального управления.
    105. Перечислите основные вариационные методы.
    106. Что делать, если в меню Сервис MS Excel нет команды вызова Поиска решения?
    107. Опишите структуру окна инструмента Поиск решения в табличном процессоре MS Excel.
    108. Какие параметры можно настроить для инструмента Поиск решения в MS Excel?
    109. Какие типовые задачи линейного программирования можно решать с помощью инструмента Поиск решения в MS Excel?
    110. Как проанализировать результат решения, полученного с помощью инструмента Поиск решения в MS Excel?
    111. Как выполнить анализ «Что будет, если…» с помощью инструмента Поиск решения в MS Excel?
    112. Как решать задачи оптимизации в среде MathCAD?
    113. Какие функции используются при решении задач оптимизации в среде MathCAD?


ПРАКТИЧЕСКАЯ ЧАСТЬ

Типовые задания

      1. Одномерная унимодальная целевая функция u = 3 x4 + 4 x3 – 12 x2 – 5 задана на множестве [–3; 2]. Найти с точностью  значение проектного параметра х, доставляющего минимум целевой функции. Использовать метод перебора. Реализовать метод в табличном процессоре MS Excel. Принять = 0,01.
      2. Одномерная унимодальная целевая функция u = 2x – 5 x – 3 задана на множестве
        [–3; 4]. Найти с точностью  значение проектного параметра х, доставляющего минимум целевой функции. Использовать метод общего поиска. Реализовать метод в табличном процессоре MS Excel. Принять  = 0,01.
      3. Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой из машин I, II и III. Время обработки в часах для каждого из изделий А и В приведено ниже:
I
II
III

А
0,5
0,4
0,2

В
0,25
0,3
0,4

Время работы машин I, II и III, соответственно, 40, 36 и 36 часов в неделю. Прибыль от изделий А и В составляет, соответственно, 5 и 3 тыс. руб.

Составить производственную программу, обеспечивающую максимальную прибыль.
      1. Решить задачу графически


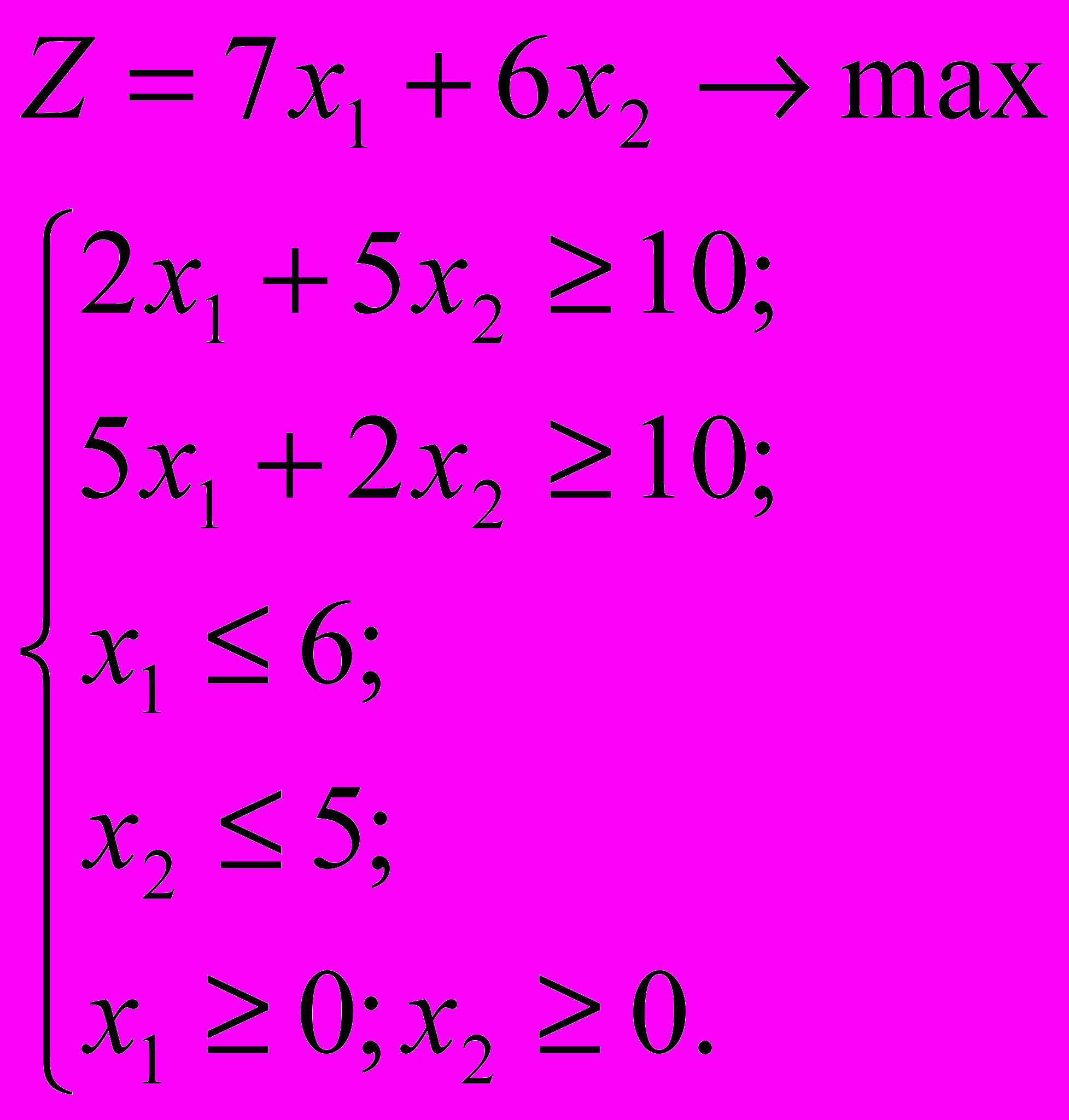
      1. Решить задачу симплекс-методом


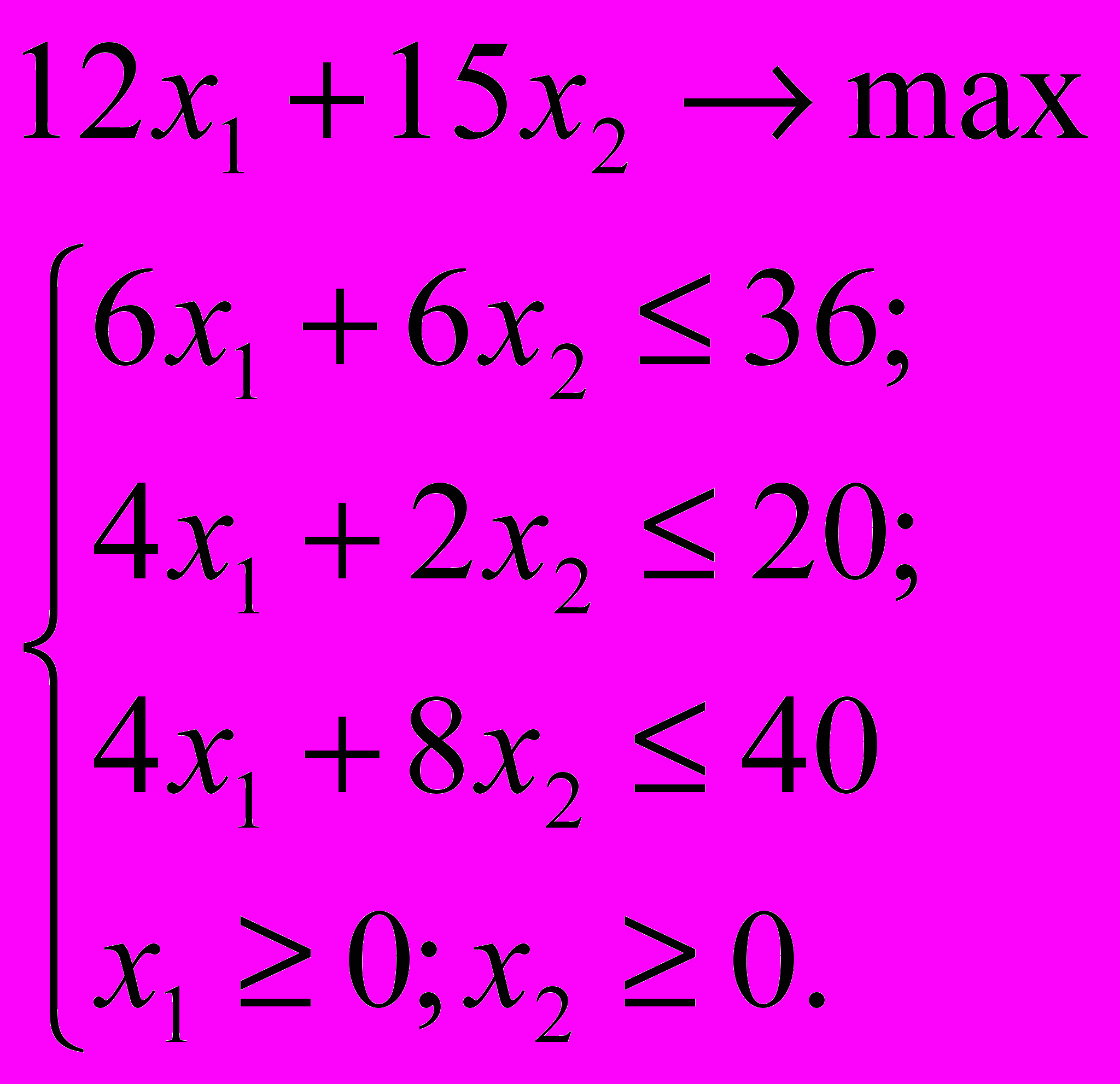
      1. Груз, хранящийся на трех складах необходимо развести по пяти магазинам. Для перевозки грузов требуется 40, 30 и 35 машин соответственно. Первому магазину требуется 20, второму – 34, третьему – 16, четвертому – 10 и пятому – 25 машин. Стоимость пробега одной машины за 1 км равна 5 единицам. Расстояния от складов до магазинов указаны в таблице:

Склады
Магазины

1
2
3
4
5

I
2
6
3
4
8

II
1
5
6
9
7

III
3
4
1
6
10

Составьте оптимальный по стоимости план перевозок грузов от складов до магазинов. Решить методом потенциалов.
      1. Решить задачи 1-5, используя инструмент Поиск решения.
      2. Решить задачи 1-5 в среде MathCAD

ТИПОВЫЕ БИЛЕТЫ

ТИПОВОЙ БИЛЕТ №1

  1. Симплекс-метод.
  2. Одномерная целевая функция u = x2 2x – 1 определена на множестве
    [–5; 1]. Найти с точностью  значение проектного параметра х, доставляющего минимум целевой функции. Использовать метод золотого сечения. Реализовать метод в табличном процессоре MS Excel. Принять  = 0,01.
  3. Решить задачу в среде MathCAD.

В городе имеется два асфальтовых завода, которые производят в сутки 30 и 40 тонн асфальта. Для выполнения планового объема работ трем дорожно-строительным участкам ежесуточно необходимо по 25, 30 и 15 тонн асфальта соответственно. Стоимость перевозки 1 тонны асфальта приведена в таблице:

Завод
Дорожный участок

1
2
3

1
100
150
200

2
200
200
300

Составить схему перевозки асфальта, при которой транспортные расходы будут минимальны.

ТИПОВОЙ БИЛЕТ №2

  1. Классификация численных методов оптимизации функций одной переменной.
  2. На 4-х элеваторах A, D, C, D находится зерно в количестве 100, 120, 150 и 130 т, которое нужно доставить на четыре сельскохозяйственных предприятия для посева Предприятию 1 необходимо – 140, 2 – 130, 3 – 90 и 4 – 140 т зерна. Стоимость доставки потребителям от поставщиков приведена в таблице:

Элеваторы
Сельскохозяйственные предприятия

1
2
3
4

A
4
5
5
7

B
8
7
5
4

C
9
6
4
5

D
3
2
9
3

Составьте оптимальный по стоимости план перевозок зерна.

Решить методом потенциалов.
  1. Решить задачу, используя инструмент Поиск решения.



СПИСОК ЛИТЕРАТУРЫ

  1. Сухарев А.Г., Тимохов А.В., Федоров В.В. Введение в методы оптимизации: Учеб. пособие для вузов. – М.: Высш. шк., 2008. – 368 с.
  2. Пантелеев А.В. Методы оптимизации в примерах и задачах: Учеб. пособие. – М.: Высш. шк., 2008. – 544 с.
  3. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. – 319 с.
  4. Алексеев Е.Р. Mathcad 12. – М.: НТ Пресс, 2005. – 345 с.