Geum.ru

Рабочая программа дисциплины «линейная алгебра» Рекомендуется для направления подготовки 080100 Экономика

Вид материалаРабочая программа

Содержание


2. Место дисциплины в структуре ООП
3. Требования к результатам освоения дисциплины
4. Объем дисциплины и виды учебной работы
Аудиторные занятия (всего)
Самостоятельная работа (всего)
5. Содержание дисциплины
Умножения геометрических векторов
Метод координат
Кривые и поверхности второго порядка
2. Линейные пространства
2.2. Линейные отображения и матрицы
2.6. Системы линейных уравнений
2.7. Собственные векторы и собственные числа матрицы.
3. Комплексные числа
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
5.3. Разделы дисциплин и виды занятий
6. Лабораторный практикум
8. Примерная тематика курсовых работ –
10. Материально-техническое обеспечение дисциплины
11. Методические рекомендации по организации изучения дисциплины
...
Полное содержание
Подобный материал:
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ

РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ

«ЛИНЕЙНАЯ АЛГЕБРА»

Рекомендуется для направления подготовки

080100 Экономика

Квалификация выпускника - бакалавр

Санкт-Петербург

2011 год


1. Цели и задачи дисциплины: накопление необходимого запаса сведений по математике (основные определения, теоремы, правила), а также освоение математического аппарата, помогающего моделировать, анализировать и решать экономические задачи, помощь в усвоении математических методов, дающих возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов; развитие логического и алгоритмического мышления, способствование формированию умений и навыков самостоятельного анализа исследования экономических проблем, развитию стремления к научному поиску путей совершенствования своей работы.


^ 2. Место дисциплины в структуре ООП: дисциплина «Линейная алгебра» относится к циклу Б.2.1. Математический цикл, Базовая часть. Входные знания, умения и компетенции студентов должны соответствовать курсу математики общеобразовательной школы. Дисциплина «Линейная алгебра» является предшествующей для следующих дисциплин: математический анализ, теория вероятностей м математическая статистика, методы оптимальных решений, информатика, математические методы и модели, микроэкономика, макроэкономика, статистика, эконометрика.


^ 3. Требования к результатам освоения дисциплины:

    Процесс изучения дисциплины направлен на формирование следующих компетенций:

– способен понимать сущность и значение информации в развитии современного информационного общества, сознавать опасности и угрозы, возникающие в этом процессе, соблюдать основные требования информационной безопасности, в том числе защиты государственной тайны (ОК-12);

– владеет основными методами, способами и средствами получения, хранения, переработки информации, имеет навыки работы с компьютером как средством управления информацией, способен работать с информацией в глобальных компьютерных сетях (ОК-13);

расчетно-экономическая деятельность

способен собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1);

способен на основе типовых методик и действующей нормативно-правовой базы рассчитать экономические и социально-экономические показатели, характеризующие деятельность хозяйствующих субъектов, (ПК-2);

способен выполнять необходимые для составления экономических разделов планов расчеты, обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3);

аналитическая, научно-исследовательская деятельность

способен осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК-4);

способен выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы (ПК-5);

способен на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты (ПК-6);

способен использовать для решения аналитических и исследовательских задач современные технические средства и информационные технологии (ПК-10);

организационно-управленческая деятельность

способен использовать для решения коммуникативных задач современные технические средства и информационные технологии (ПК-12);

педагогическая деятельность

способен преподавать экономические дисциплины в образовательных учреждениях различного уровня, используя существующие программы и учебно-методические материалы (ПК-14);

способен принять участие в совершенствовании и разработке учебно-методического обеспечения экономических дисциплин (ПК-15).


В результате изучения дисциплины студент должен:

Знать: основы линейной алгебры, необходимые для решения экономических задач;


Уметь: применять методы математического анализа и моделирования, теоретического и экспериментального исследования для решения экономических задач;


Владеть: навыками применения современного математического инструментария для решения экономических задач; методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов.


^ 4. Объем дисциплины и виды учебной работы

Общая трудоемкость дисциплины составляет 6 зачетных единиц.


Вид учебной работы
Всего часов

(1 семестр)

^ Аудиторные занятия (всего)
108

В том числе:
-

Лекции
60

Практические занятия (ПЗ)
48

Семинары (С)



Лабораторные работы (ЛР)



^ Самостоятельная работа (всего)
108

В том числе:
-

Контрольная работа №1
10

Тест №1
20

Контрольная работа №2
10

Тест№2
22

Контрольная работа №3
10

Экзамен
36

Общая трудоемкость час

зач. ед.
216

5+1


^ 5. Содержание дисциплины

5.1. Содержание разделов дисциплины

1. Аналитическая геометрия

Геометрические векторы. Определение геометрических векторов, линейные операции, линейно зависимые и линейно независимые системы векторов, базисы, координаты вектора, действия с векторами в координатах.

^ Умножения геометрических векторов. Скалярное произведение, определение и формула в ортонормированном базисе. Определители второго и третьего порядков. Векторное и смешанное произведение, определение, формулы и геометрические приложения.

^ Метод координат. Прямоугольные координаты на плоскости и в пространстве. Преобразование прямоугольных координат. Расстояние между точками, деление отрезка в заданном отношении. Понятие об уравнении линий и поверхностей. Различные формы уравнения прямой на плоскости. Основные задачи на прямую линию на плоскости. Уравнения плоскости. Уравнения прямой в пространстве. Основные задачи на плоскость и прямую в пространстве.

^ Кривые и поверхности второго порядка. Общий вид уравнения второго порядка, инварианты. Окружность, эллипс, гипербола, парабола. Определение вида кривой по уравнению. Полярные координаты на плоскости. Представление о поверхностях второго порядка.

^ 2. Линейные пространства

2.1. Векторное пространство 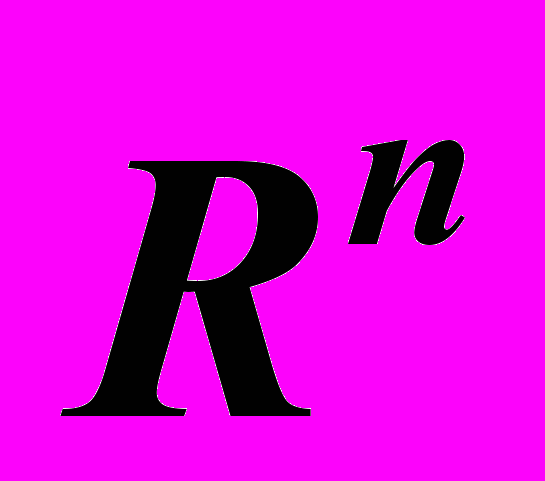. Определение и свойства линейных операций над -мерными векторами, векторное пространство 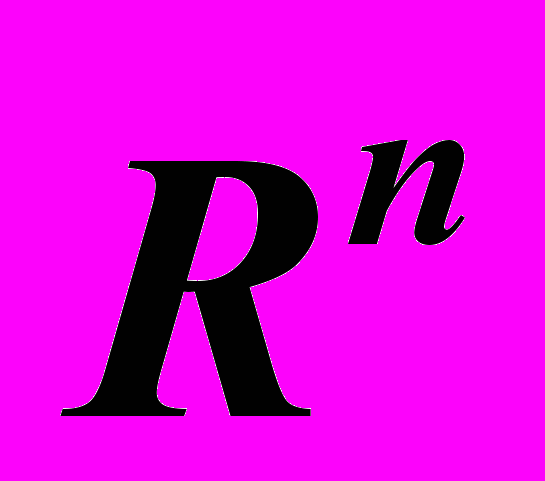. Линейно зависимые и линейно независимые системы векторов. Скалярное умножение, неравенство Коши, норма (длина) -мерного вектора. Ортогональность, угол между векторами. Базисы, координаты вектора относительно базиса, размерность. Ортогональные и ортонормированные базисы, процедура ортогонализации. Подпространства и линейные оболочки. Ранг системы векторов. Эквивалентные системы векторов, элементарные преобразования систем векторов.

^ 2.2. Линейные отображения и матрицы Линейные отображения (преобразования, операторы). Матрицы, связь матриц с линейными отображениями. Алгебра линейных отображений и алгебра матриц. Транспонирование матрицы и его свойства. Симметричные матрицы. Понятие о сопряженном и самосопряженном линейном отображении.

2.3. Определители. Определение и элементарные свойства определителей. Определитель произведения матриц. Разложение определителя по строке (столбцу). Вычисление определителей с помощью элементарных преобразований. Определитель и линейная независимость системы векторов. Геометрический смысл определителя.

2.4. Ранг линейного отображения и ранги матриц. Образ и ядро линейного отображения. Ранг линейного отображения. Ранг матрицы. Ранг матрицы и линейная независимость системы векторов.

2.5. Обратная матрица. Обратимые линейные отображения. Обратная матрица. Признаки существования обратной матрицы. Вычисление обратной матрицы с помощью элементарных преобразований и с помощью союзной (присоединенной) матрицы. Преобразование координат вектора и элементов матрицы при переходе к новому базису. Ортогональные матрицы.

^ 2.6. Системы линейных уравнений. Координатная, векторная и матричная формы записи системы линейных уравнений. Исследование систем линейных уравнений. Теоремы Кронекера-Капелли, Крамера, Фредгольма. Решение систем линейных уравнений методом элементарных преобразований (методом Гаусса). Решение однородных систем линейных уравнений.

^ 2.7. Собственные векторы и собственные числа матрицы. Определение собственных векторов и собственных чисел линейного отображения и квадратной матрицы. Собственные подпространства. Вид матрицы линейного отображения в базисе из собственных векторов. Понятие о характеристическом и минимальном многочлене квадратной матрицы. Квадратичные и билинейные формы. Критерий Сильвестра положительной определенности квадратичной формы. Приведение квадратичной формы к сумме квадратов. Основные понятия линейной балансовой модели. Элементы теории неотрицательных матриц.

^ 3. Комплексные числа

Комплексные числа. Алгебраическая и тригонометрическая форма записи. Модуль и аргумент. Экспонента от комплексного числа, формула Эйлера. Основная теорема алгебры. Разложение на множители многочлена с вещественными коэффициентами.


^ 5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами

№ п/п
Наименование обеспечиваемых (последующих) дисциплин
№ № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин

1
2
3

1
Математический анализ
+
+



2
Теория вероятностей и математическая статистика

+
+
+

3
Методы оптимальных решений
+
+



4
Информатика



+



5
Математические методы и модели
+
+



6
Микроэкономика
+
+



7
Макроэкономика
+
+



8
Статистика
+
+



9
Эконометрика
+
+




^ 5.3. Разделы дисциплин и виды занятий

№ п/п
Наименование раздела дисциплины
Лекц.
Практ.

зан.
СРС
Всего

час.

1
Аналитическая геометрия

18
18
30
66

2
Линейные пространства
38
24
32
94

3
Комплексные числа


4
6
10
20


^ 6. Лабораторный практикум не предусмотрен.

7. Практические занятия (семинары)

№ п/п
№ раздела дисциплины
Тематика практических занятий (семинаров)
Трудо-емкость

(час.)

1
1
Геометрические векторы, линейные операции, базисы, координаты вектора, скалярное произведение, решение геометрических задач с помощью векторов.
2

2
1
Определители второго и третьего порядков. Векторное и смешанное произведение. Вычисление площадей и объемов.

2

3
1
Расстояние между точками, деление отрезка в заданном отношении. Задачи на составление уравнений линий на плоскости. Основные задачи на прямую линию на плоскости
2

4
1
Прямая на плоскости
2

5
1
Контрольная работа
2

6
1
Плоскость и прямая в пространстве.
2

7
1
Полярные координаты.
2

8
1
Кривые второго порядка.
2

9
1
Поверхности второго порядка. Метод сечений.
2

10
2
Действия с n-мерными векторами.
2

11
2
Алгебра матриц.
2

12
2
Вычисление определителей.
2

13
2
Ранг матрицы.
2

14
2
Обратная матрица. Матричные уравнения.
2

15
2
Системы линейных уравнений. Формулы Крамера.
2

16
2
Системы линейных уравнений. Метод Гаусса.
2

17
2
Решение неопределенных и однородных систем линейных уравнений.
2

18
2
Контрольная работа.
2

19
5
Собственные векторы и собственные числа матрицы.
2

20
5
Знакомство с линейной балансовой моделью.
2

21
5
Матрицы прямых и полных затрат.

2

22
3
Действия с комплексными числами в алгебраической и тригонометрической формах.
2

23
3
Извлечение корней из комплексного числа, решение квадратных уравнений.
2

24
3
Контрольная работа.
2


^ 8. Примерная тематика курсовых работ – курсовые работы не предусмотрены.

9. Учебно-методическое и информационное обеспечение дисциплины:

а) основная литература
  1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1984.
  2. Бугров Я.С. Никольский С.М. Высшая математика: Задачник. – М.: Наука, 1982.
  3. Высшая математика для экономистов. Под ред. Кремера Н.Ш., – М.: ЮНИТИ, 1998.


б) дополнительная литература
  1. Математика в экономике: учебно-методическое пособие. Под ред. Н.Ш Кремера. C М.: Финстатинформ, 1999.
  2. Солодовников А.С., Бабайцев В.А., Бранков А.В. Математика в экономике. – М.: Финансы и статистика, 1998.
  3. Воеводин В.В. Линейная алгебра. – М.: Наука, 1980.
  4. Идельсон А.В., Блюмкина И.А. Аналитическая геометрия. Линейная алгебра. – М.: ИНФРАМ, 2000.
  5. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. – М.: Высшая математика, 1982.
  6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учебник. – М.: Гос.Изд.физ-мат.литература,1983.
  7. Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты). – М.: Высшая школа, 1983.


в) программное обеспечение не предусмотрено


г) базы данных, информационно-справочные и поисковые системы:
  1. ссылка скрыта
  2. ссылка скрыта
  3. ссылка скрыта


^ 10. Материально-техническое обеспечение дисциплины:

Документ-сканер, принтеры, компьютеры и пакеты программ обработки результатов тестирования.


^ 11. Методические рекомендации по организации изучения дисциплины:

В течение семестра проводятся три контрольных работы (по аналитической геометрии, линейной алгебре и по комплексным числам) и два теста (по аналитической геометрии и линейной алгебре). Максимальное число баллов за контрольную работу равно 10, за тест – 35. Максимальное число баллов, которое можно получить за работу в семестре, равно 100. Минимальное число баллов, при котором тест или контрольная работа считаются сданными, равно 20 для теста и 5 для контрольной работы. В течение семестра необходимо заработать не менее 55 баллов. Максимальное число баллов, которое можно получить на экзамене, также равно 100. Итоговая оценка (в баллах) вычисляется по формул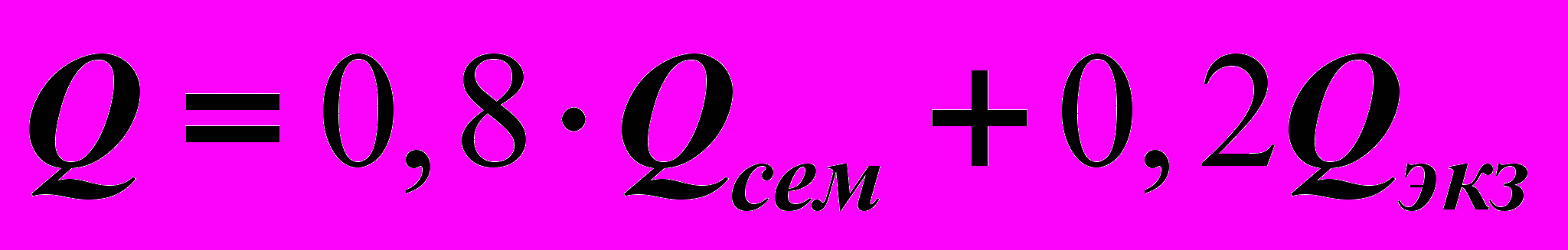е , где 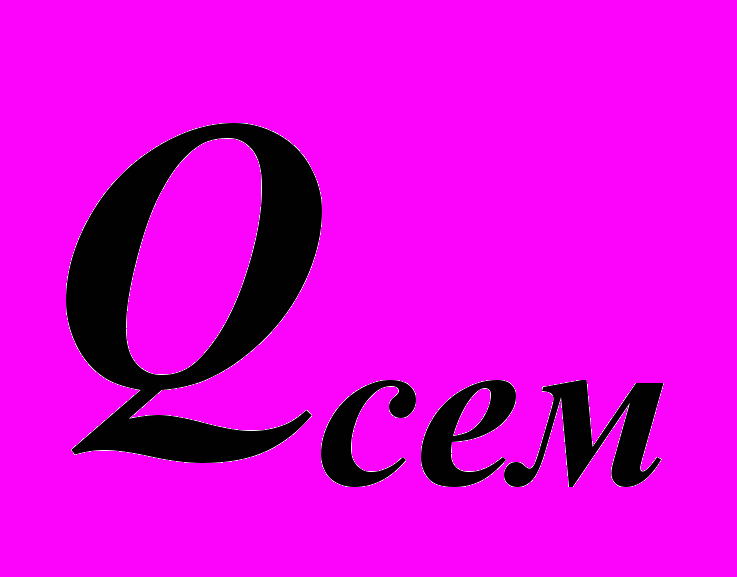– баллы, полученные за работу в семестре, а 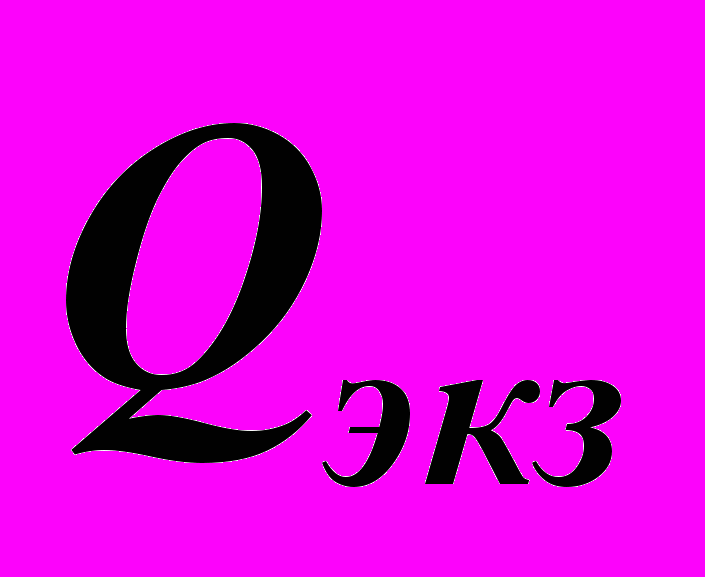– за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:



Итоговое количество баллов
оценка

до 55
неудовлетворительно

от 55 до 70
удовлетворительно

от 70 до 85
хорошо

от 85
отлично


^ Примеры заданий теста №1.


Ответ ДА или НЕТ.

Прямая задана уравнением 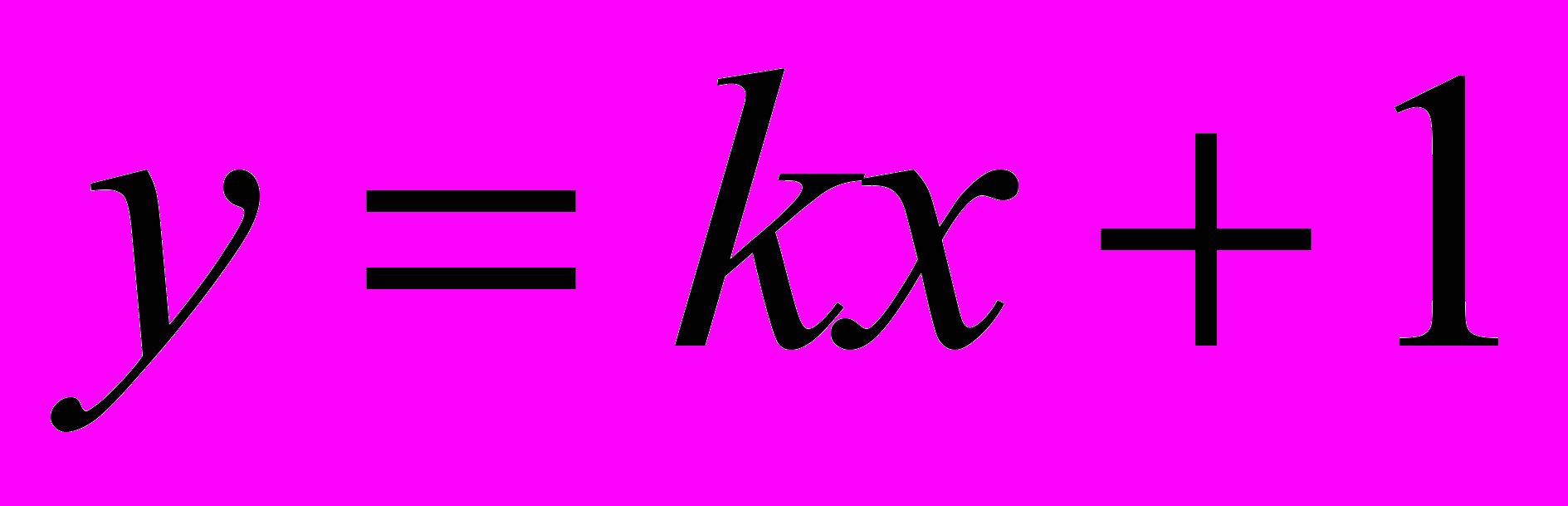. Верно утверждение:

Существует значение 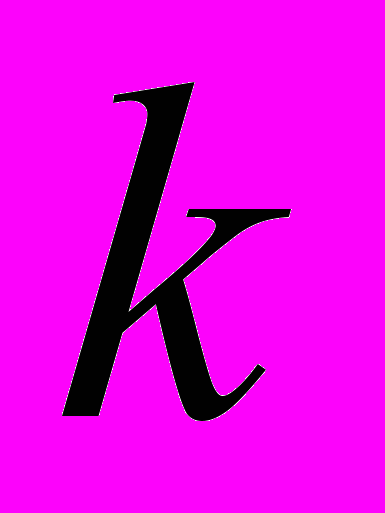, при котором прямая проходит через точку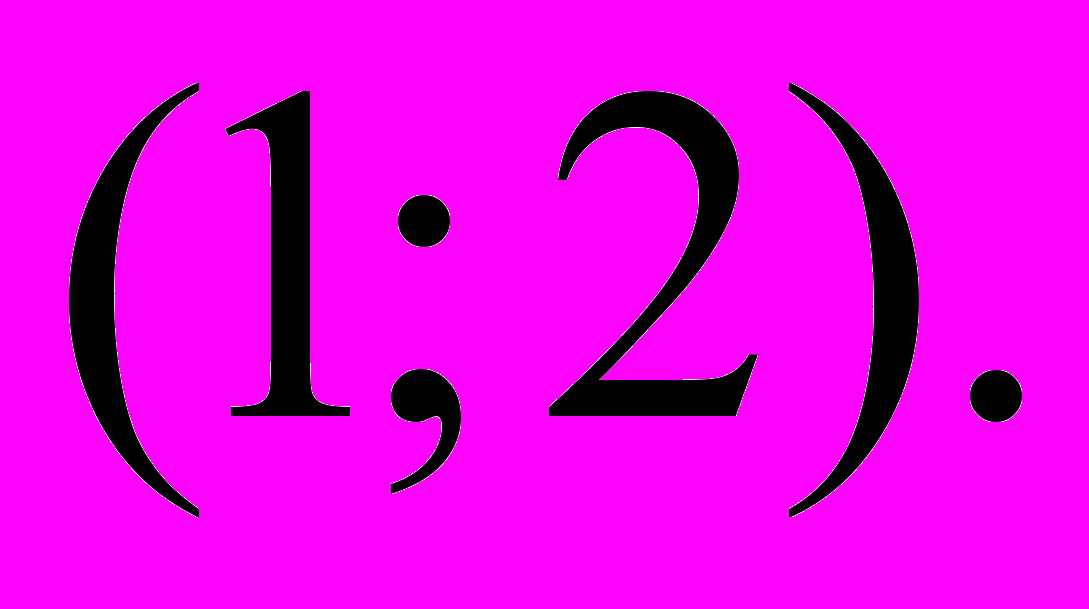

Абсцисса точки пересечения прямой с осью 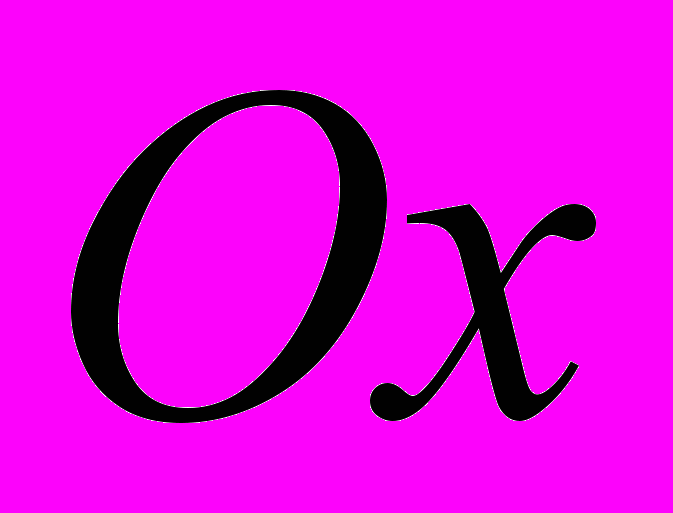положительна только при отрицательных значениях .

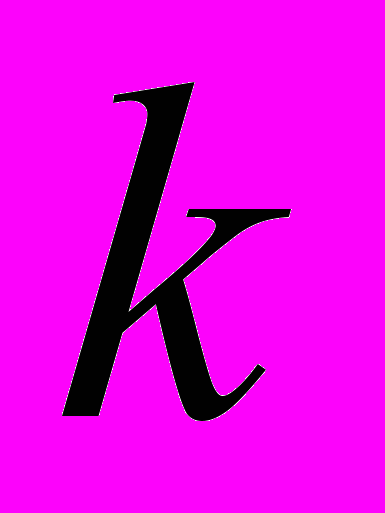При 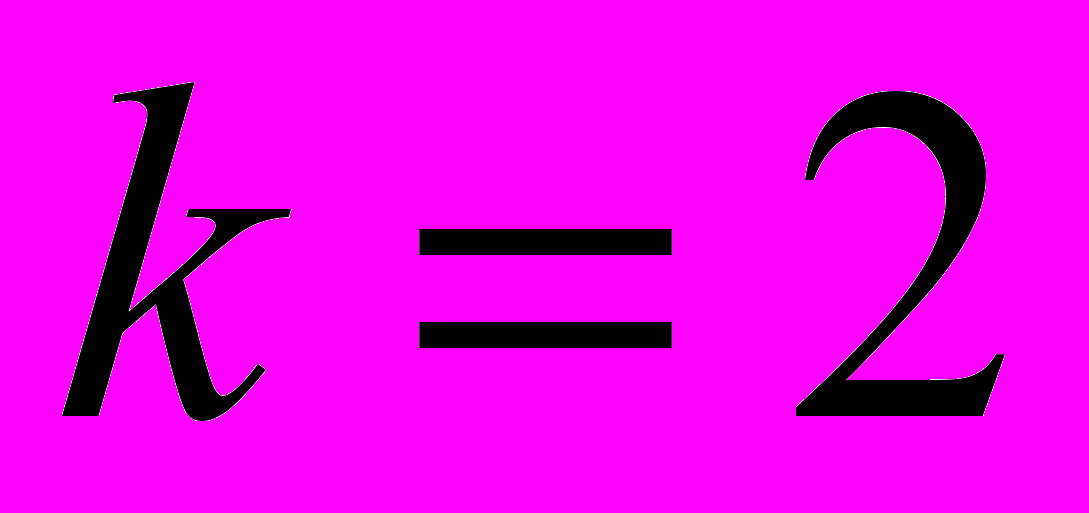данная прямая перпендикулярна прямой .

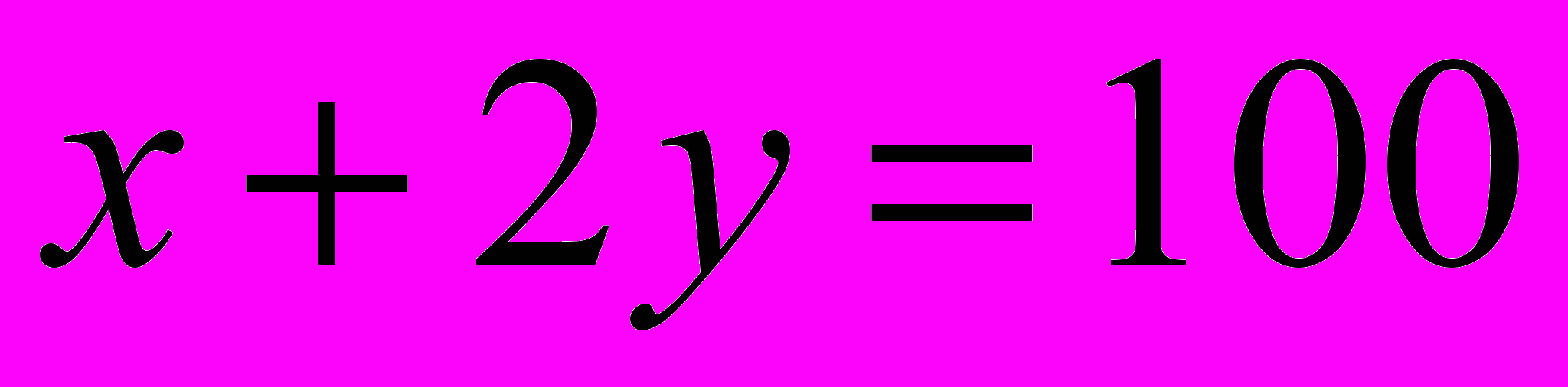Если 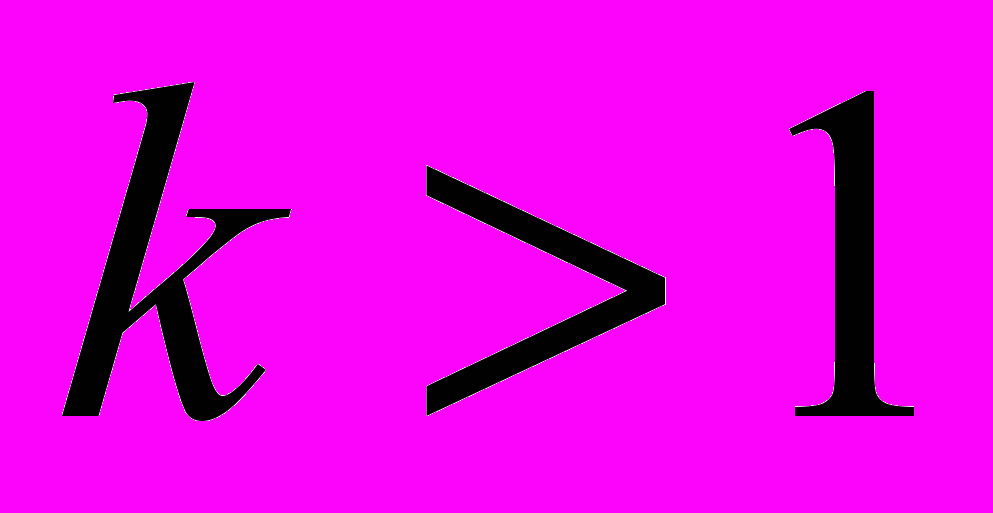, то прямая пересекает ось абсцисс в точке с координатой больше, чем .

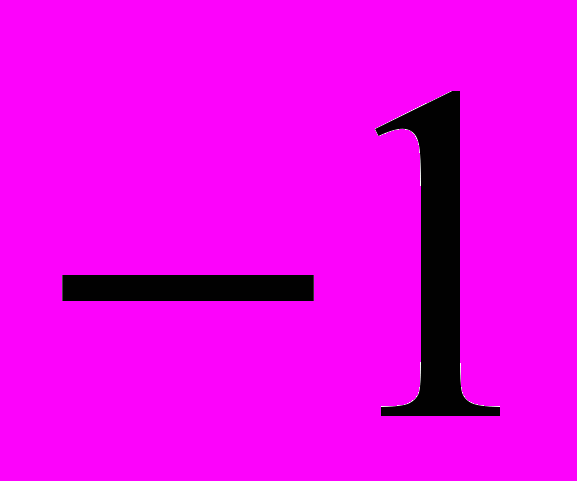Существует значение 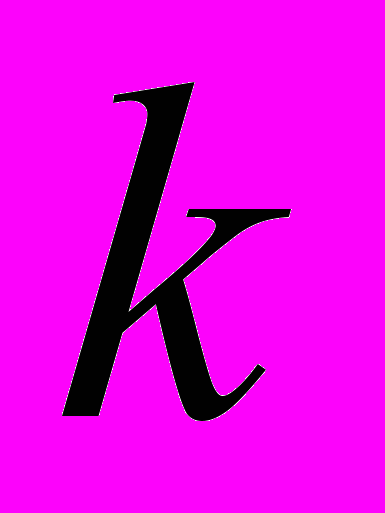, при котором прямая проходит через точк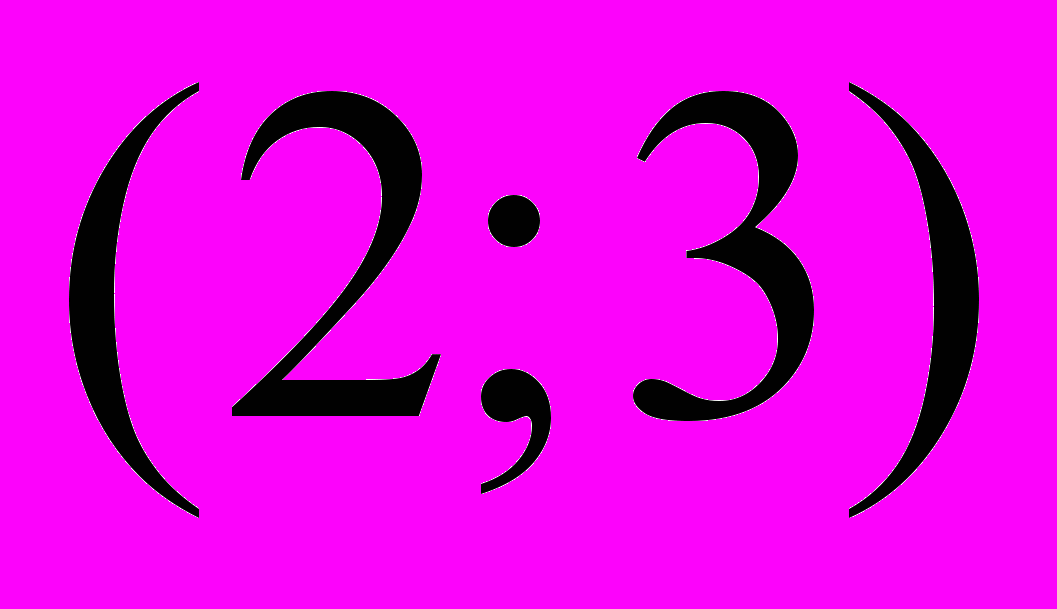и и .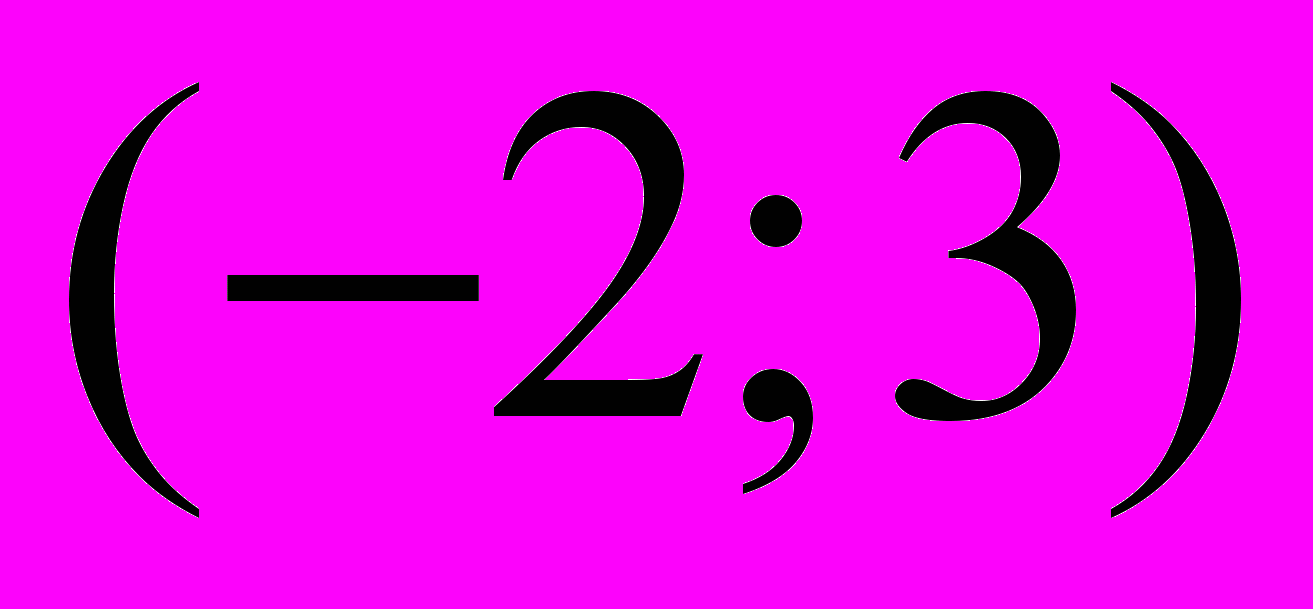


Выбор одного ответа.


На координатной плоскости имеется отрезок, соединяющий две точки с абсциссами разных знаков. Тогда этот отрезок…

А. обязательно пересекает ось ординат

Б. обязательно пересекает ось абсцисс

В. обязательно пересекает каждую из осей координат

Г. не пересекает ни одну из осей координат


Задачи с числовым ответом.


Найдите радиус окружности, касающейся оси 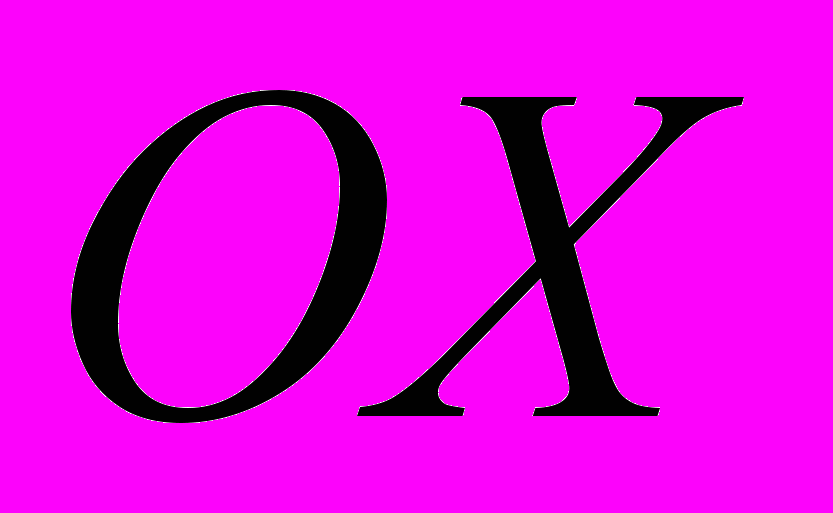в точке 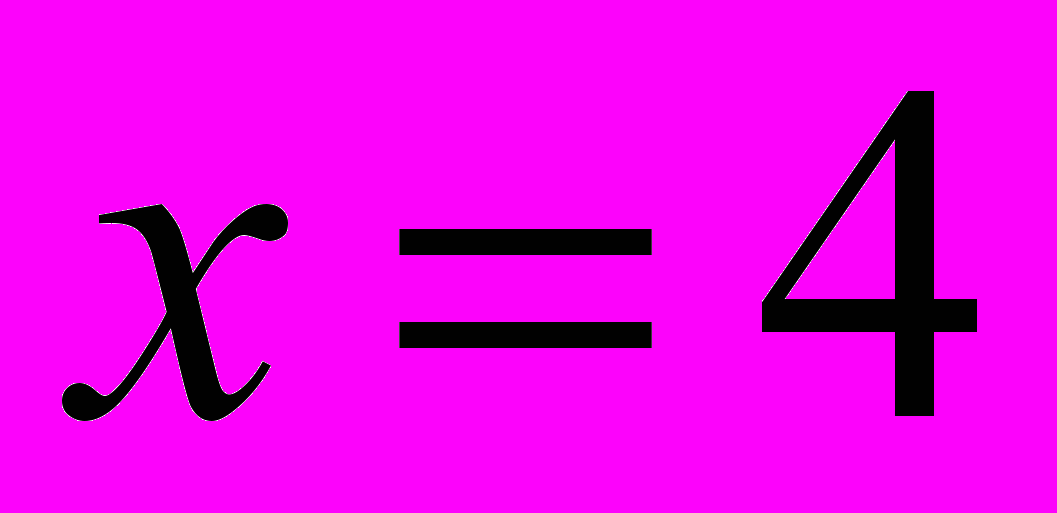, если центр окружности лежит на прямой .


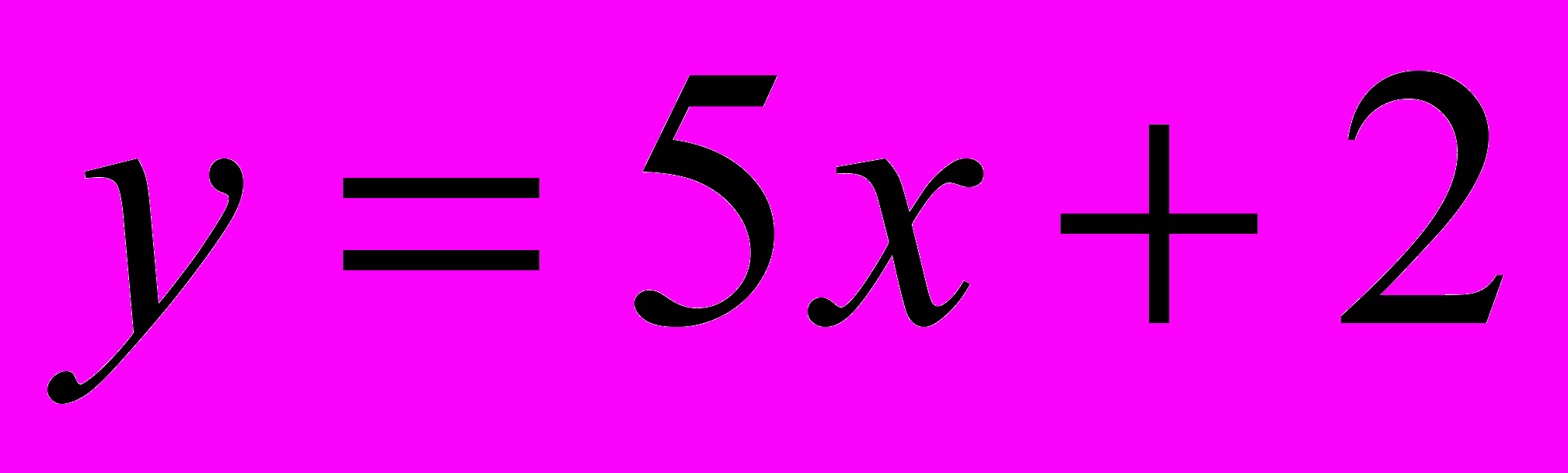Примеры заданий теста №2.


Ответ ДА или НЕТ.


Дана система 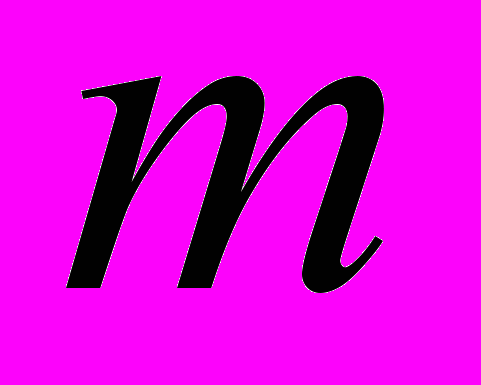линейных уравнений с 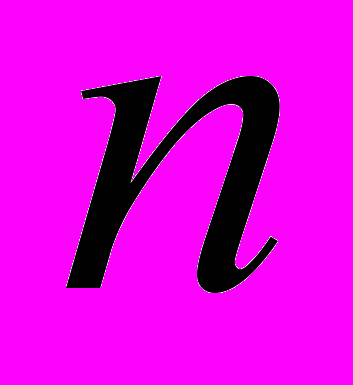неизвестными. Пусть ранг матрицы этой системы равен 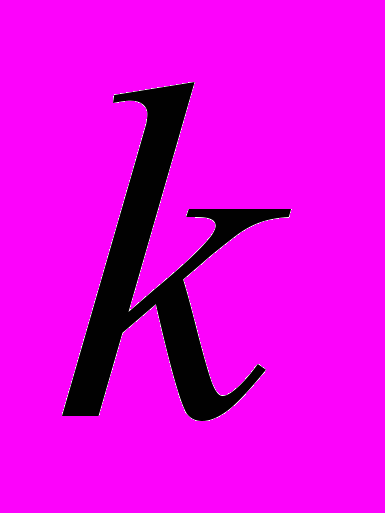, а ранг расширенной матрицы системы равен 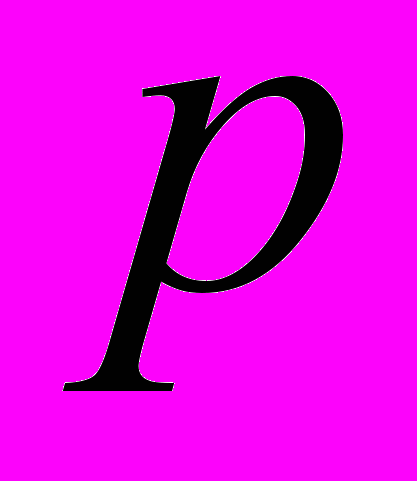. Правильными утверждениями являются…

если система имеет хотя бы одно решение, то

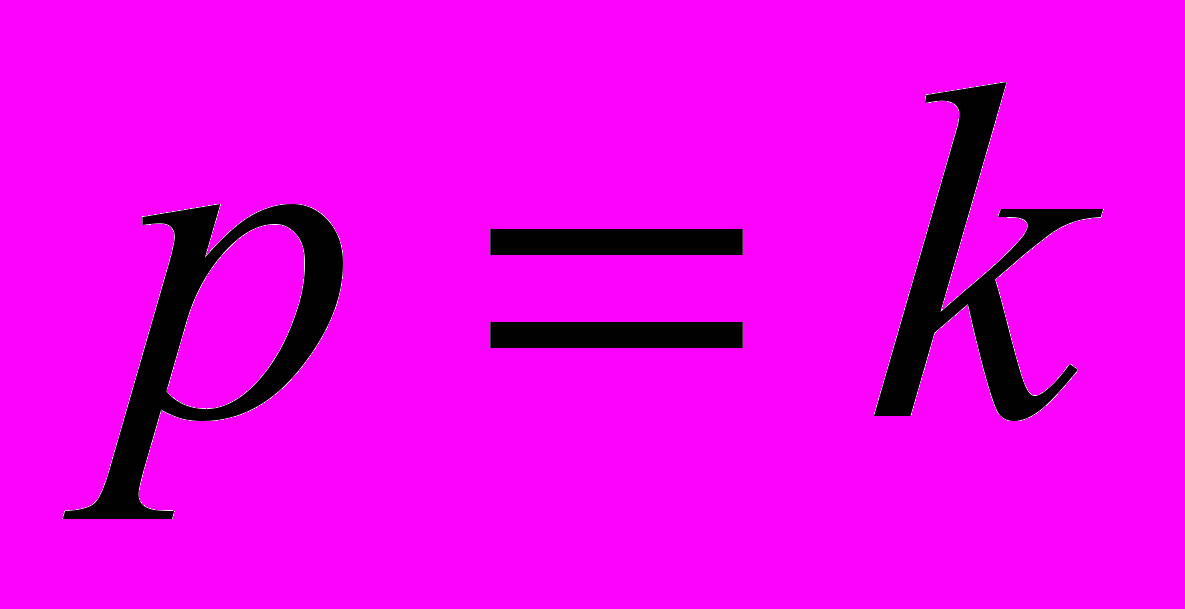
есл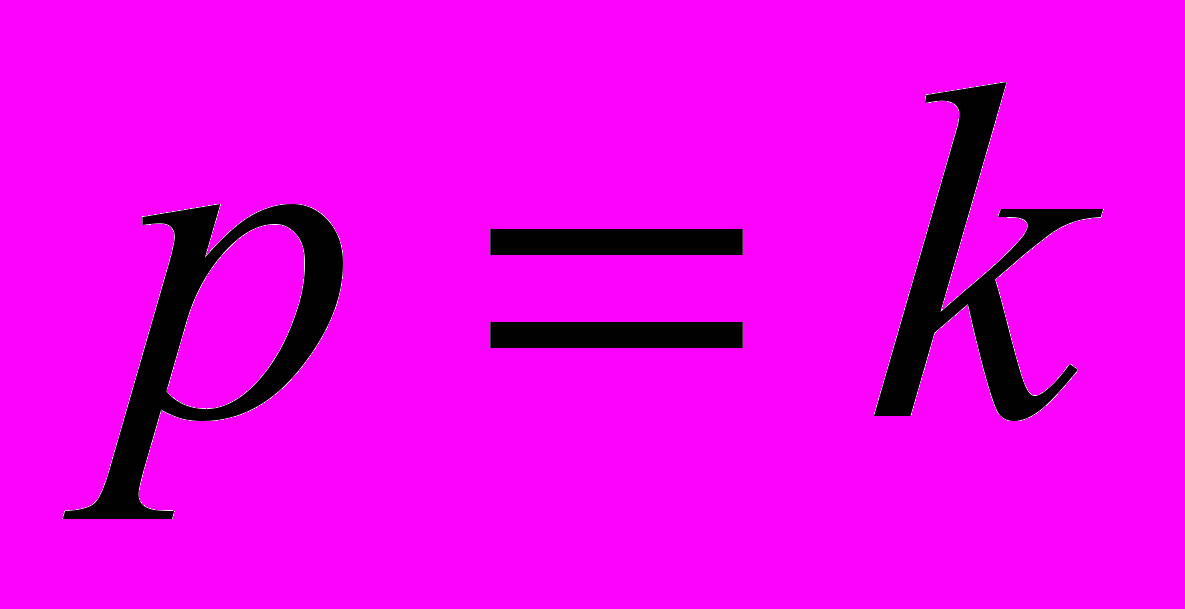и и 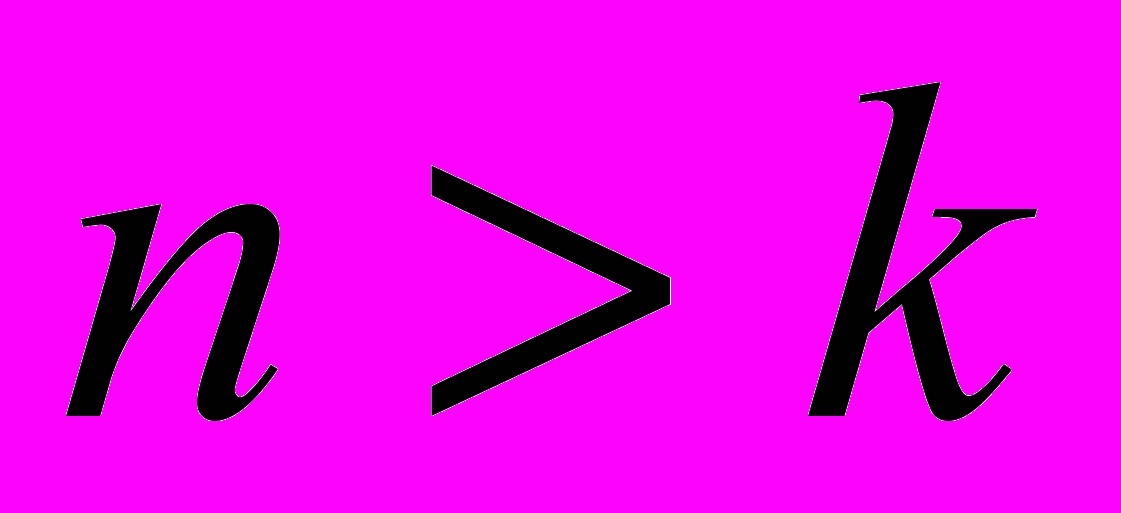, то система имеет бесконечное множество решений

если 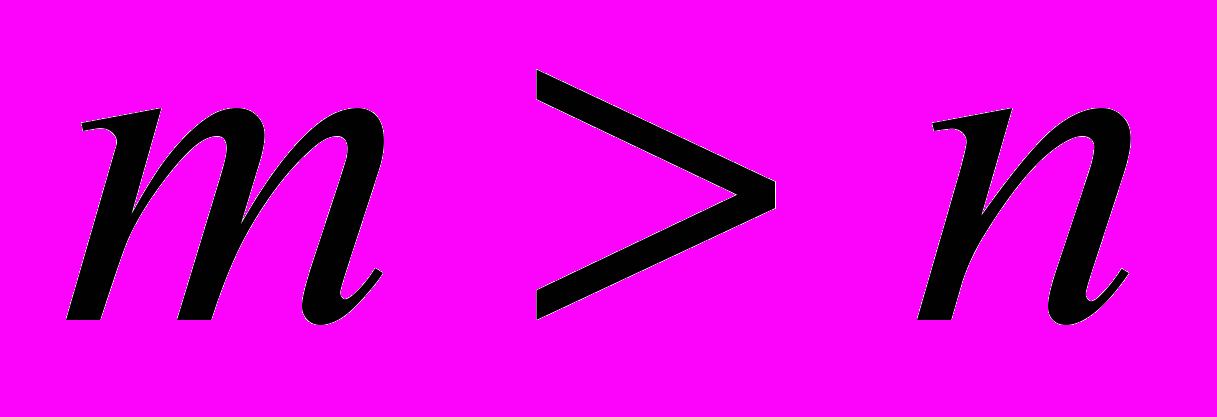, то система не имеет решений

если 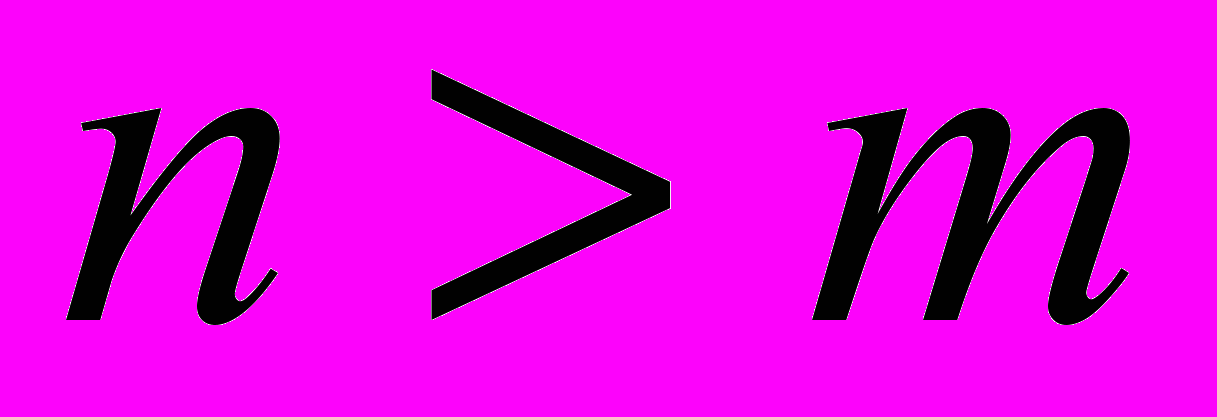, то система имеет хотя бы одно решение


Выбор одного ответа.


Некоторый элемент определителя равен 2, его алгебраическое дополнение равно 5. Если этот элемент определителя увеличить на 3, то новый определитель будет больше исходного…

А. на 15

Б. на 3

В. на 6

Г. в 15 раз


Задачи с числовым ответом.


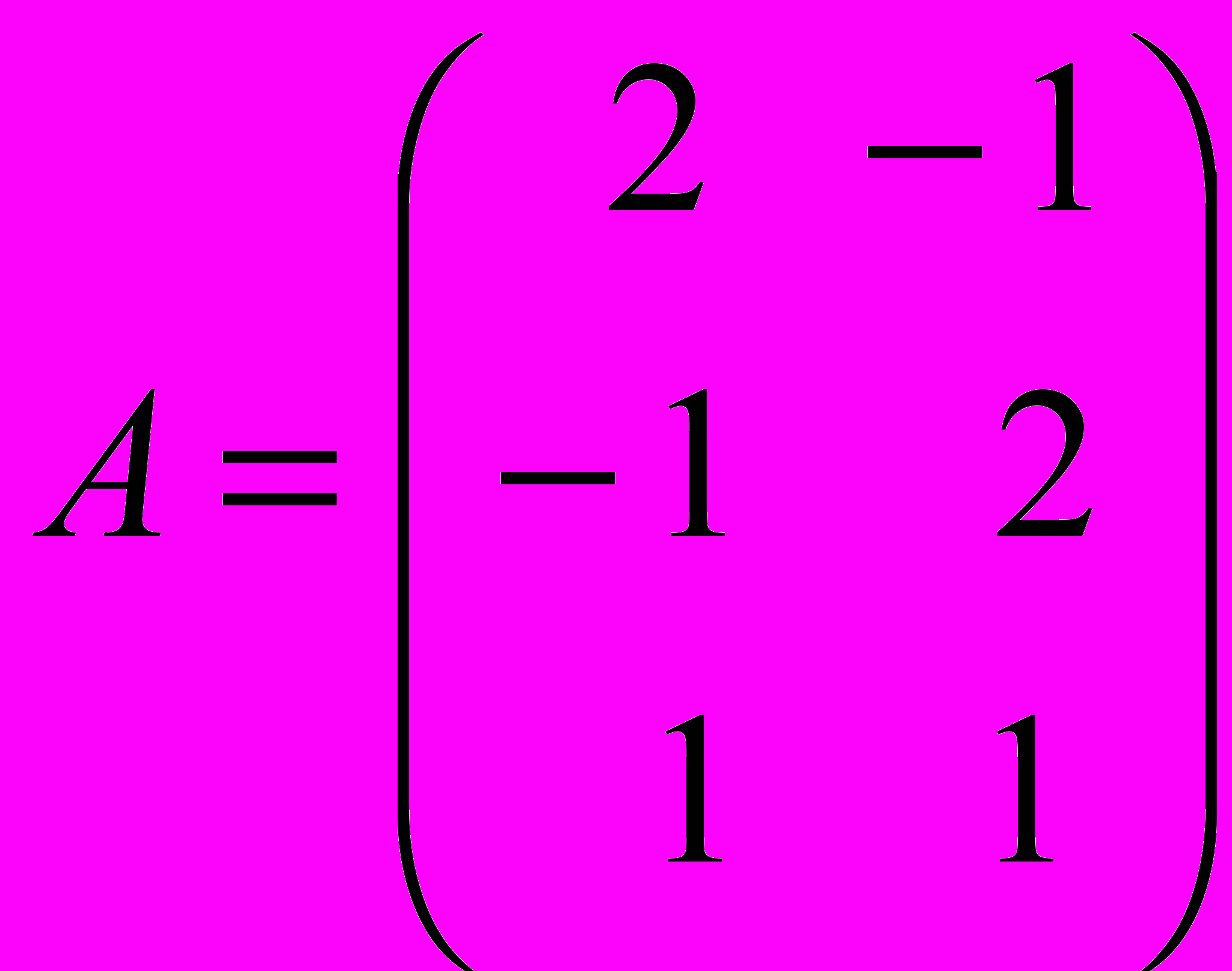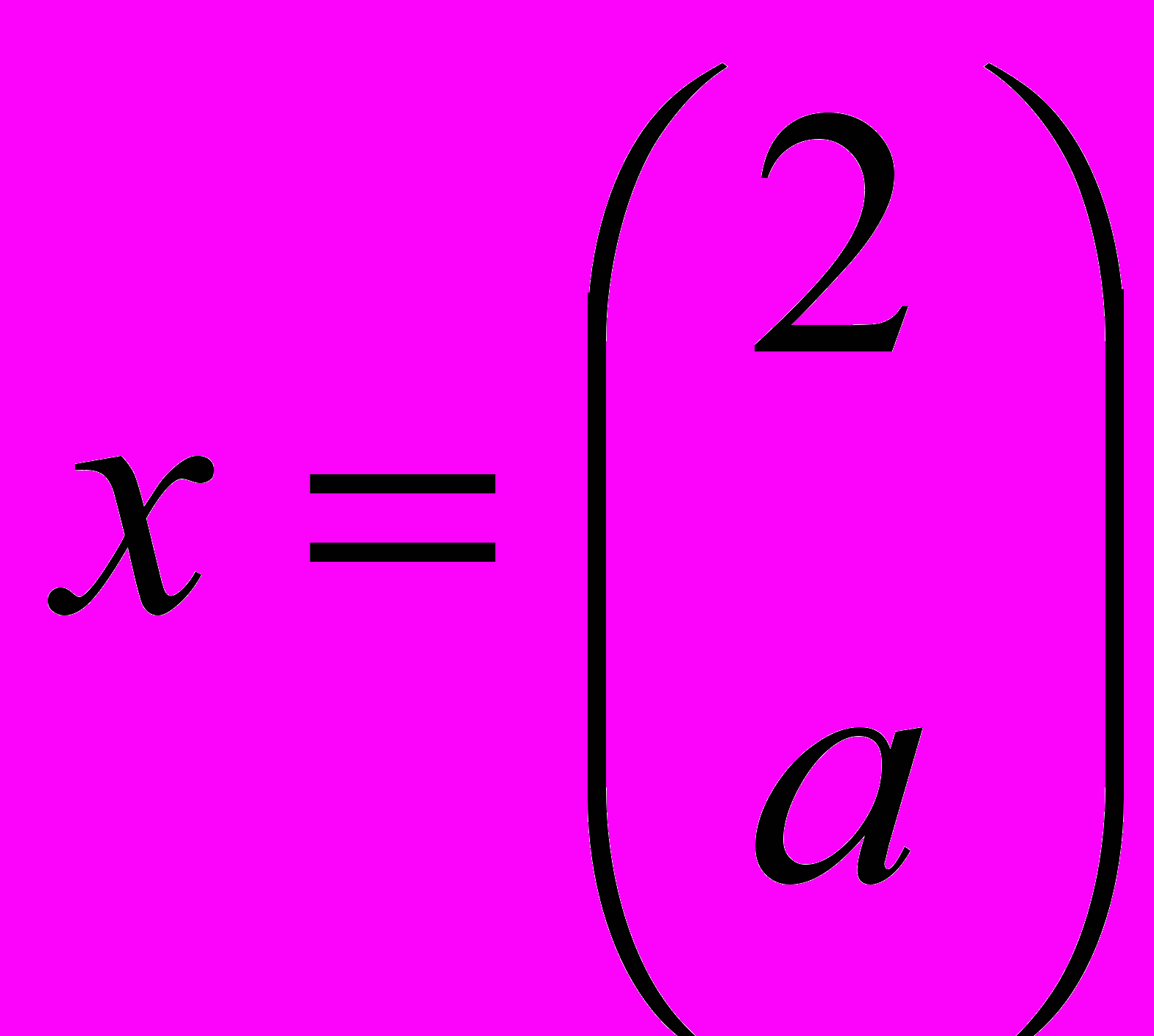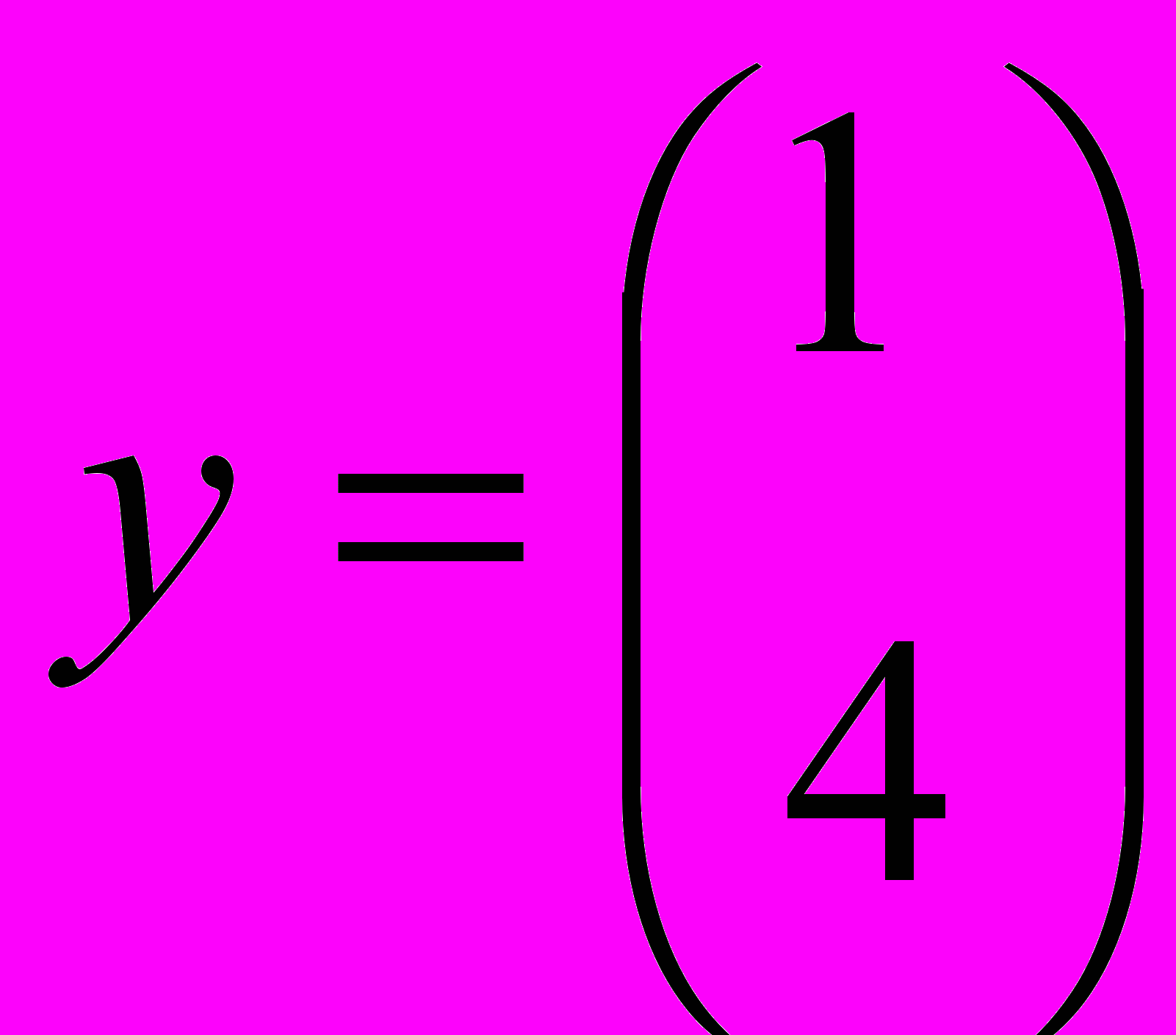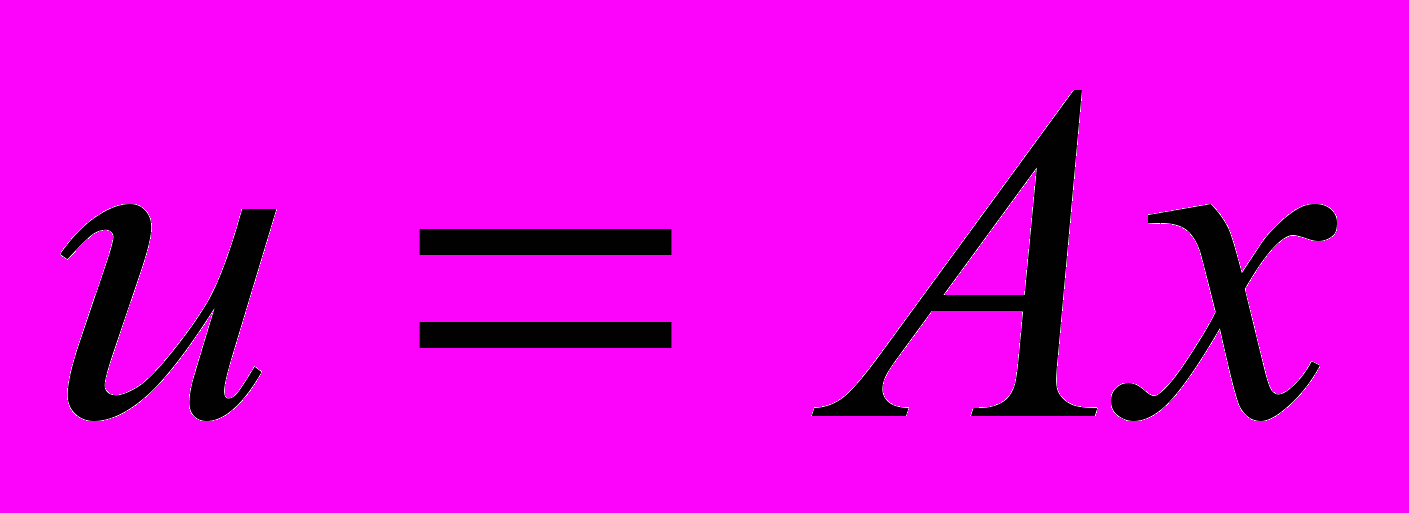Даны матрица и два вектора и . Найти значение параметра , при котором векторы и 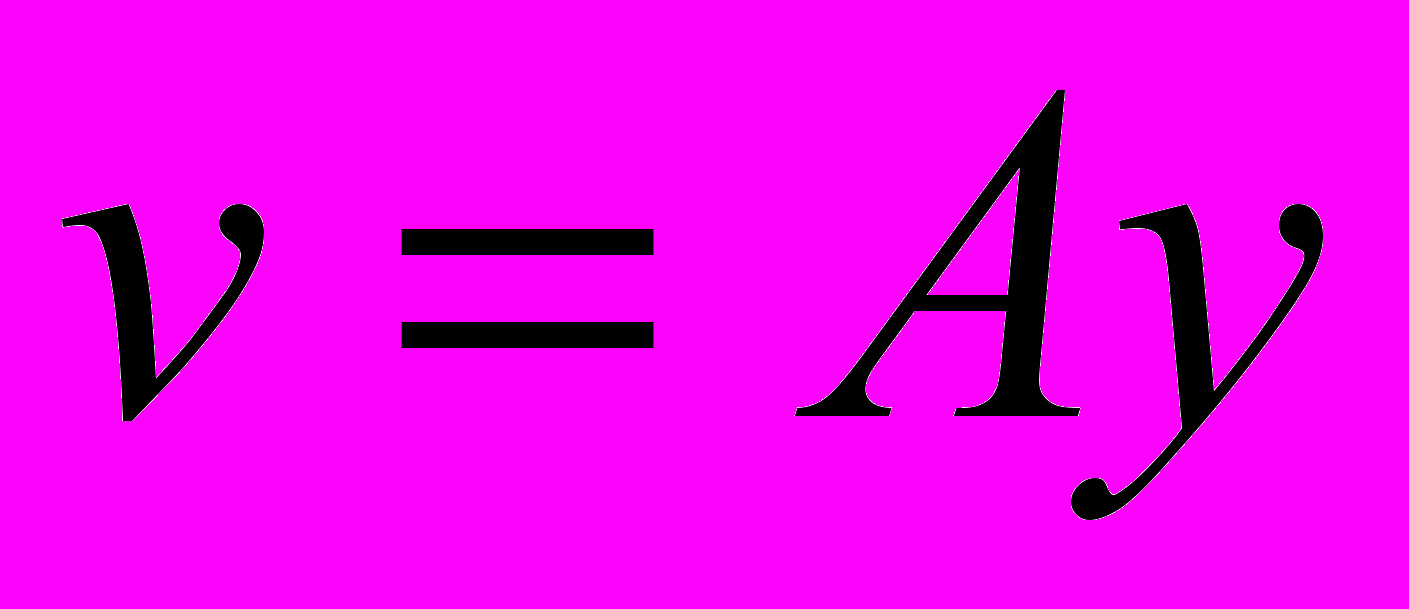перпендикулярны.


Примеры заданий контрольной работы №1.


Задача №1.

Даны две смежные вершины параллелограмма 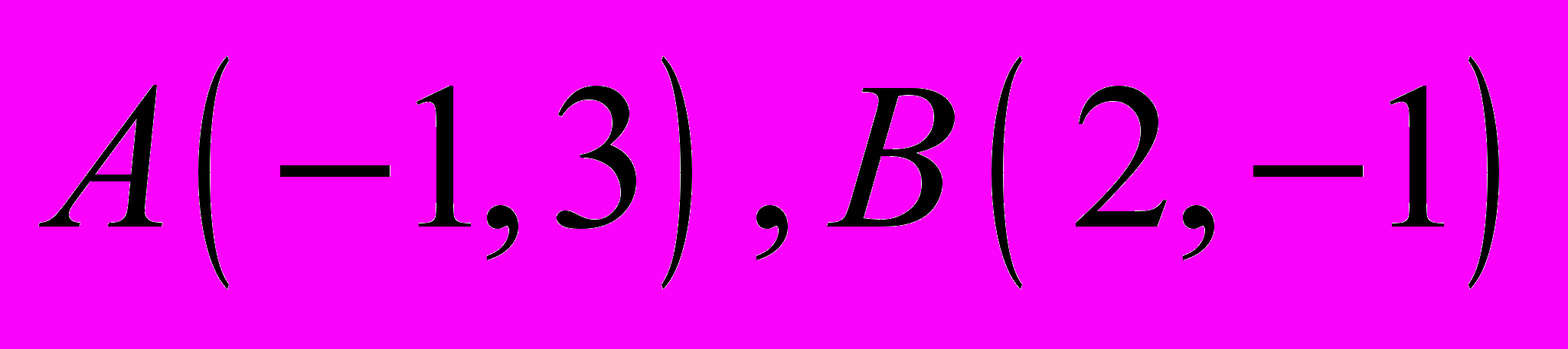. Найти две другие его вершины при условии, что диагонали параллелограмма параллельны осям координат.


Задача №2.

Даны две противоположные вершины квадрата 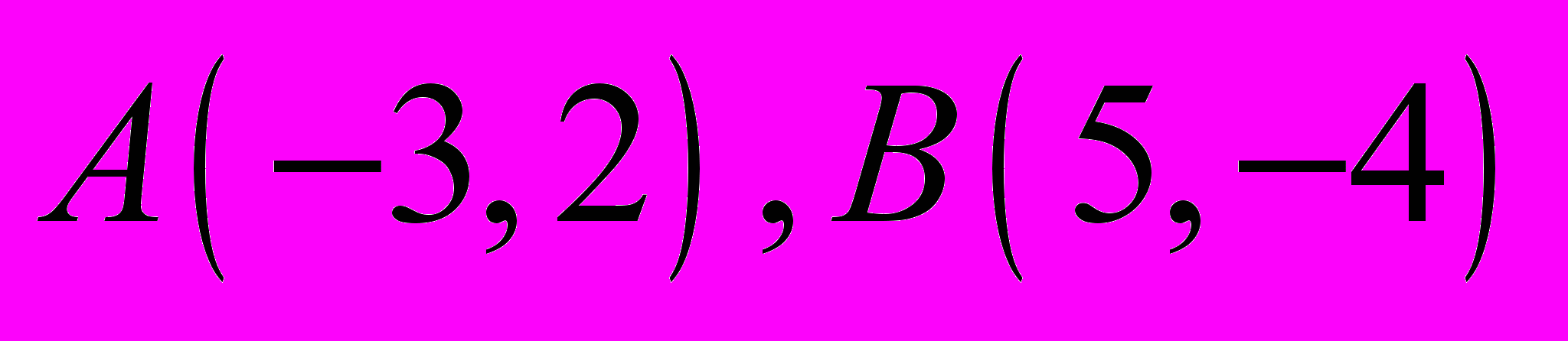. Найти две другие его вершины и .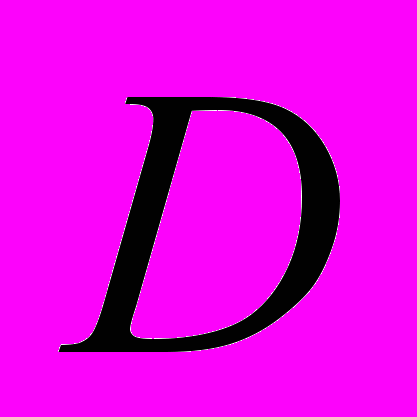


Задача №3.

Через точку 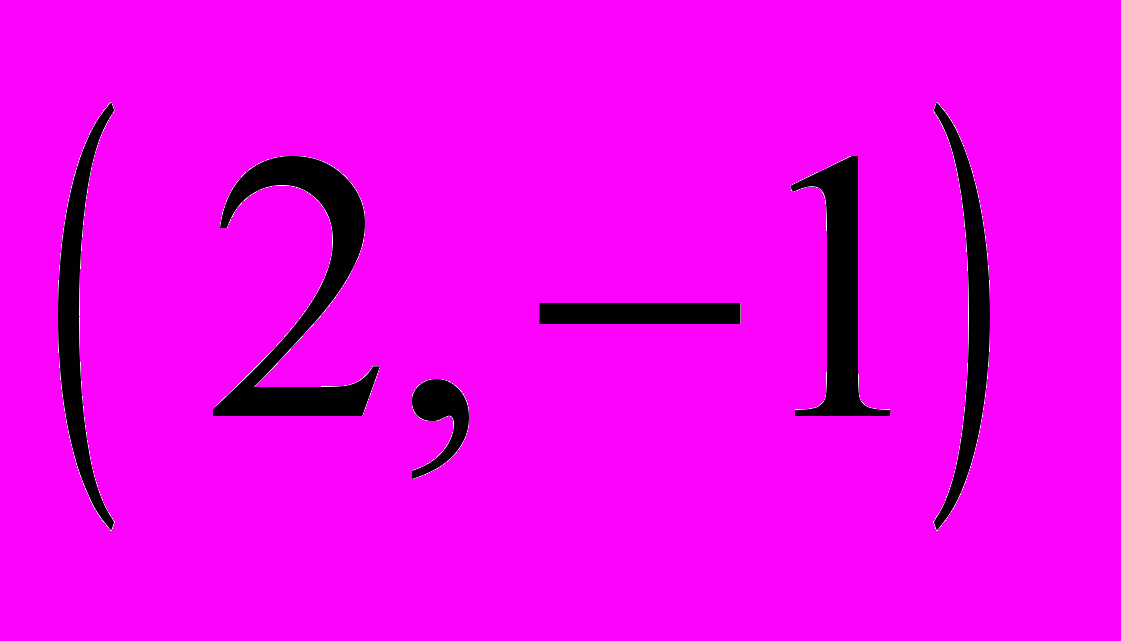провести прямую, отрезок которой между осями координат делился бы в данной точке пополам.


Задача №4.

Найти уравнения прямых, проходящих через точку 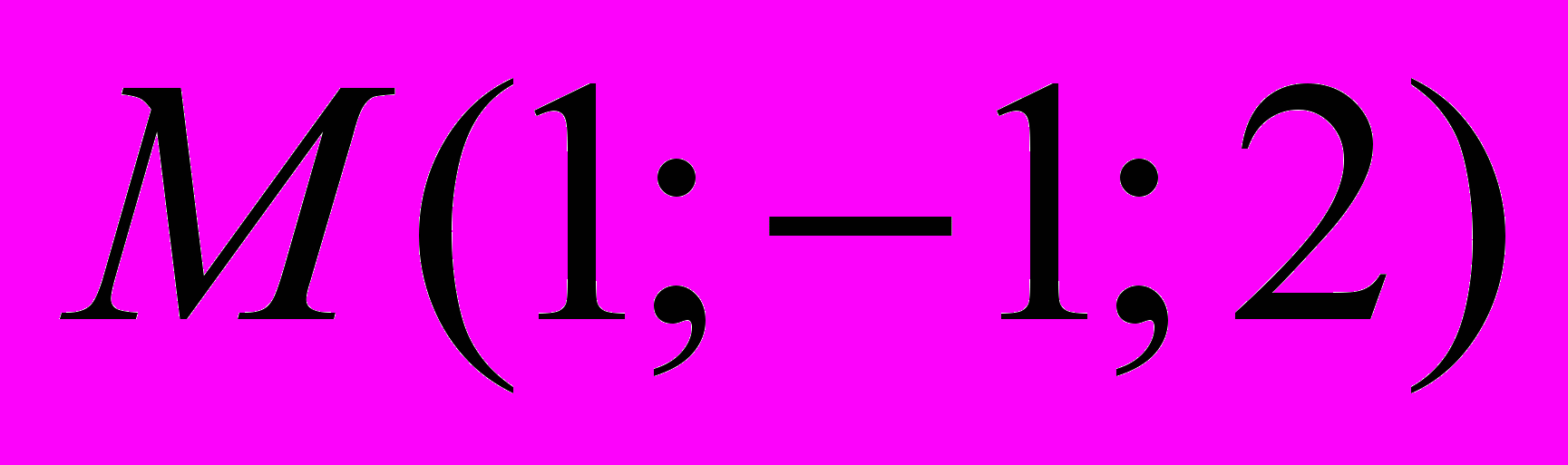параллельно линиям пересечения плоскости 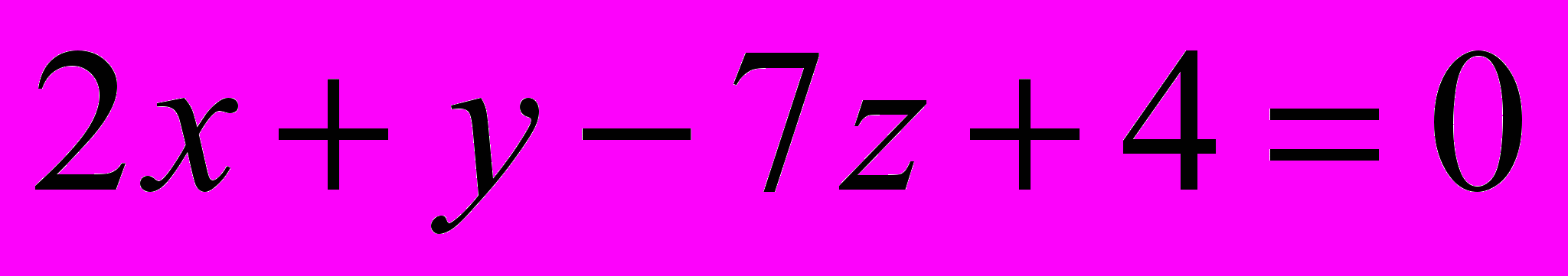с координатными плоскостями.


Примеры заданий контрольной работы №2.


Задача №1.

Вычислить .


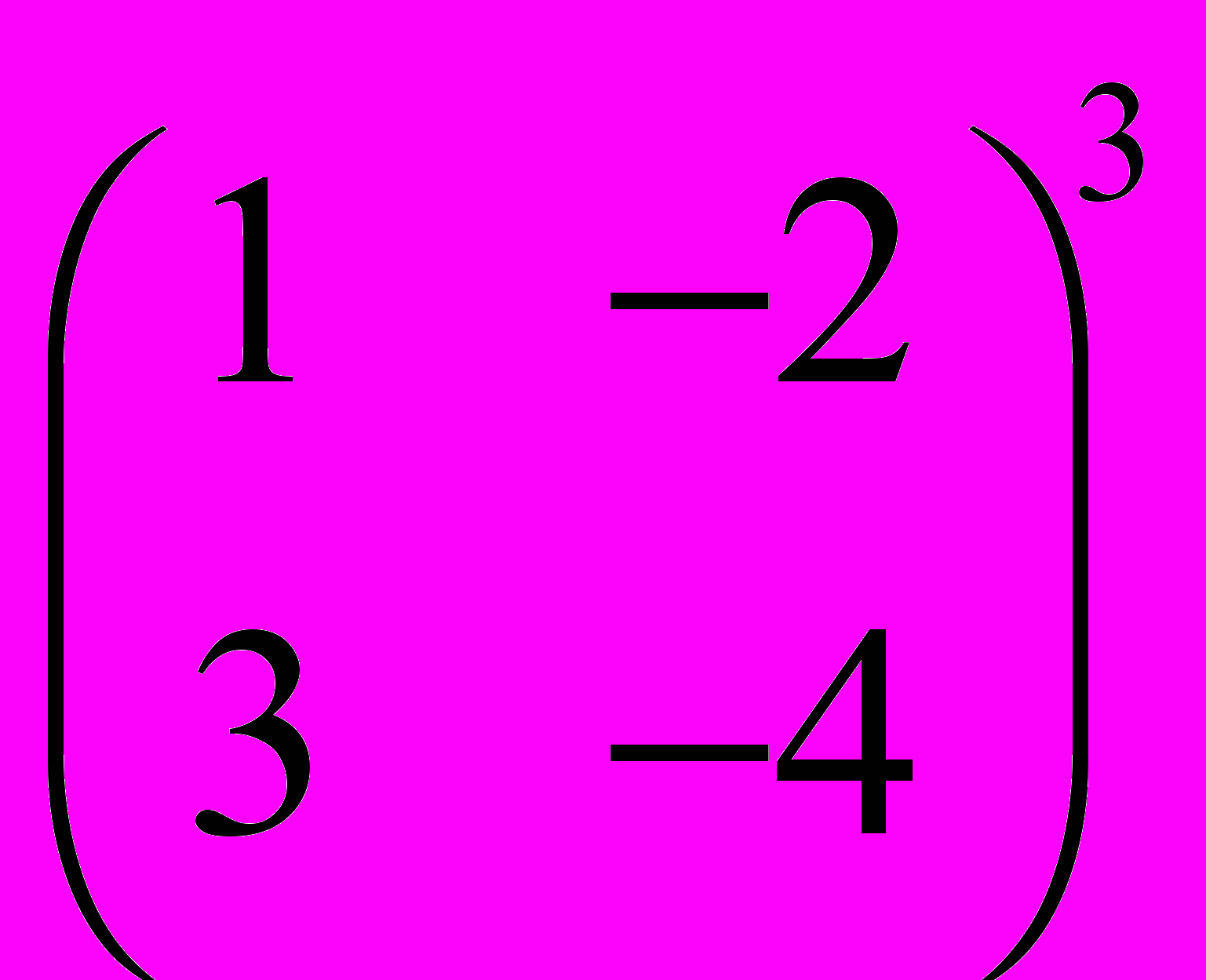Задача №2.

Решить матричное уравнение:.


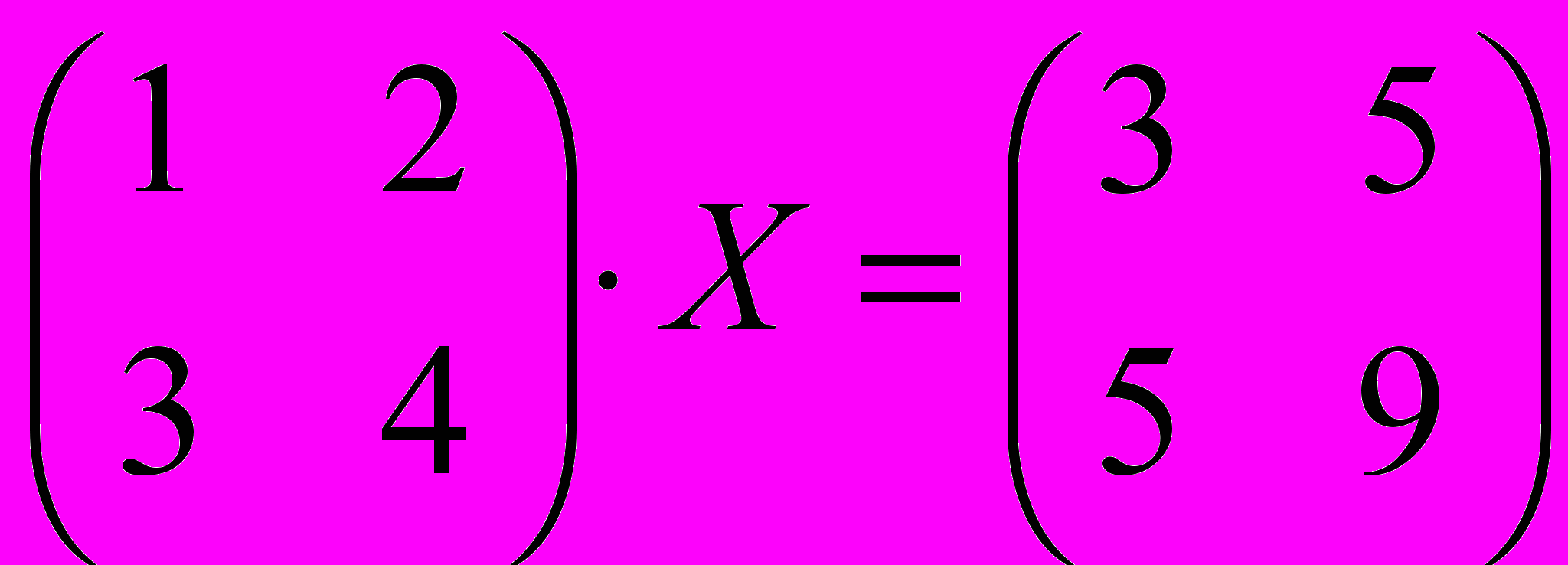Задача №3.

Решить систему уравнений .

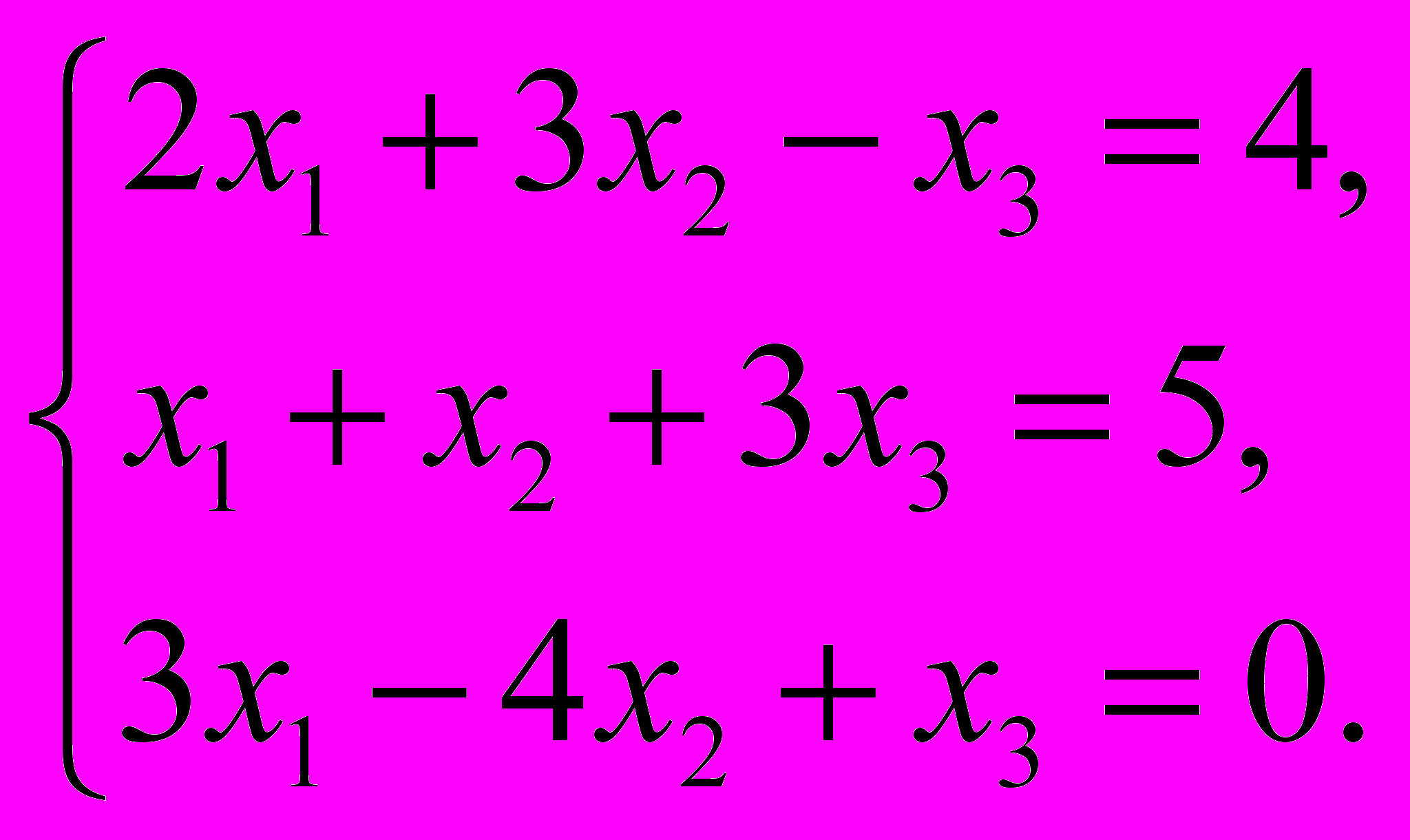Задача №4. Решить систему уравнений .


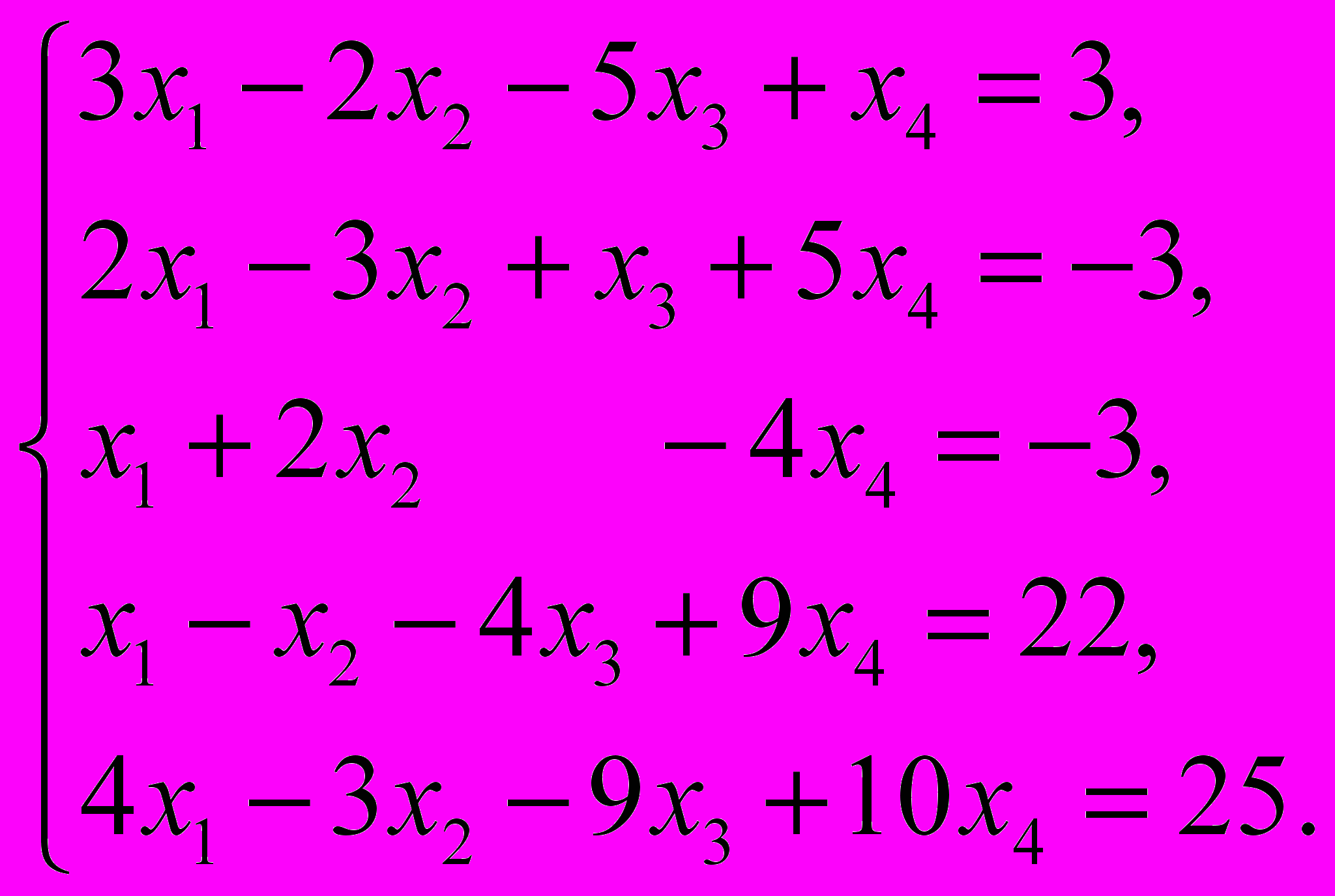Примеры заданий контрольной работы №3.


Задача №1.

Найти алгебраическую форму числа .


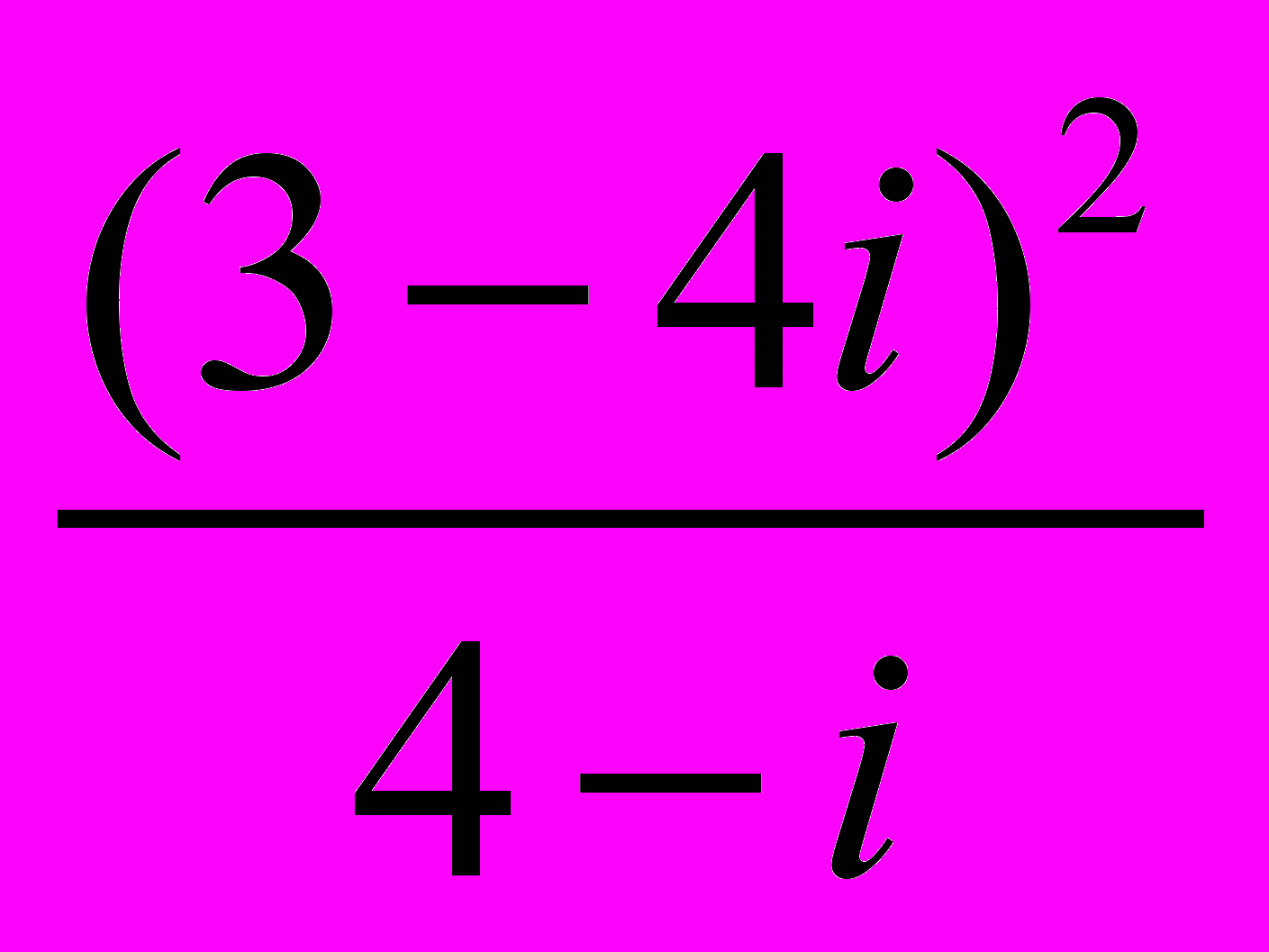Задача №2.

Найти тригонометрическую и показательную форму числа .


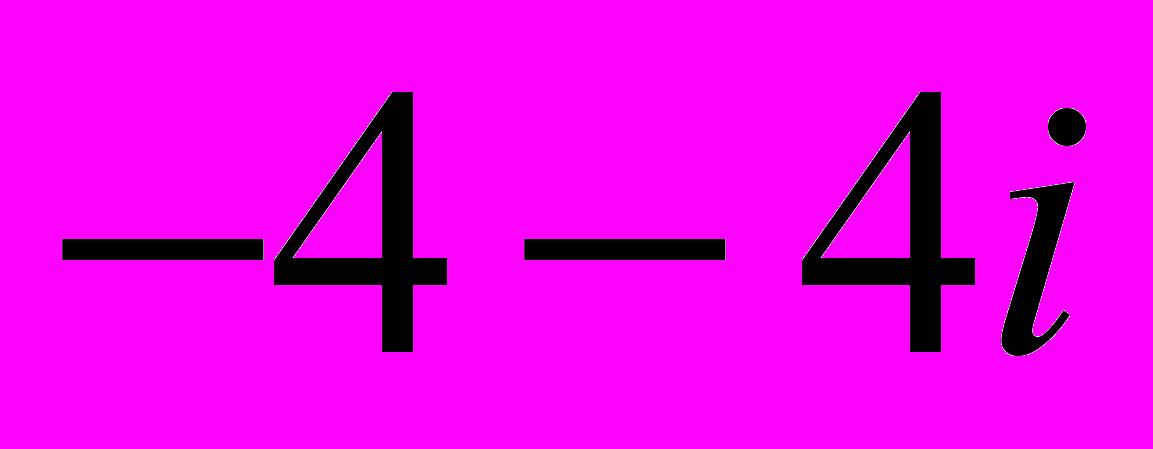Задача №3.

Найдите все корни 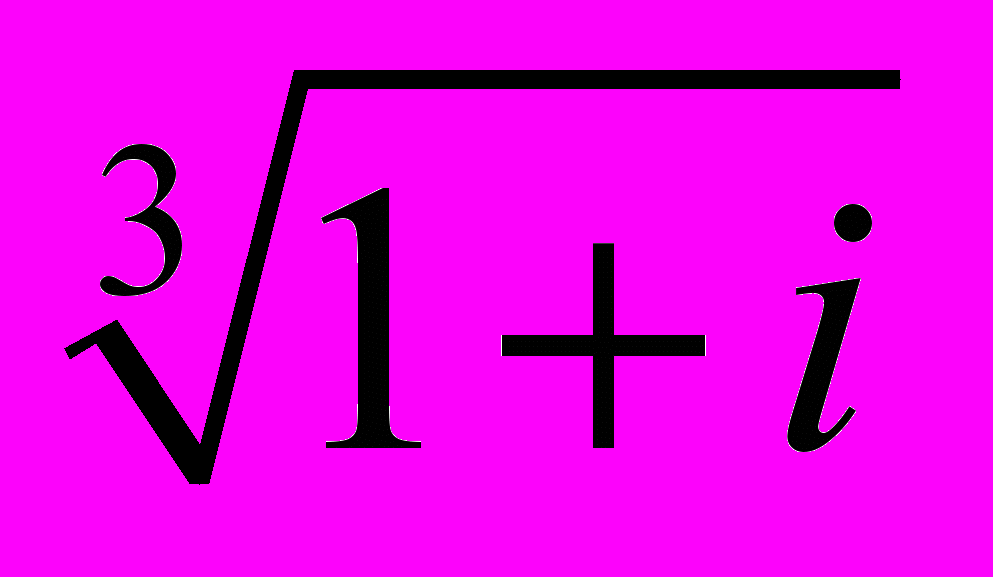и изобразите их на плоскости.


Задача №4.

Разложите многочлен 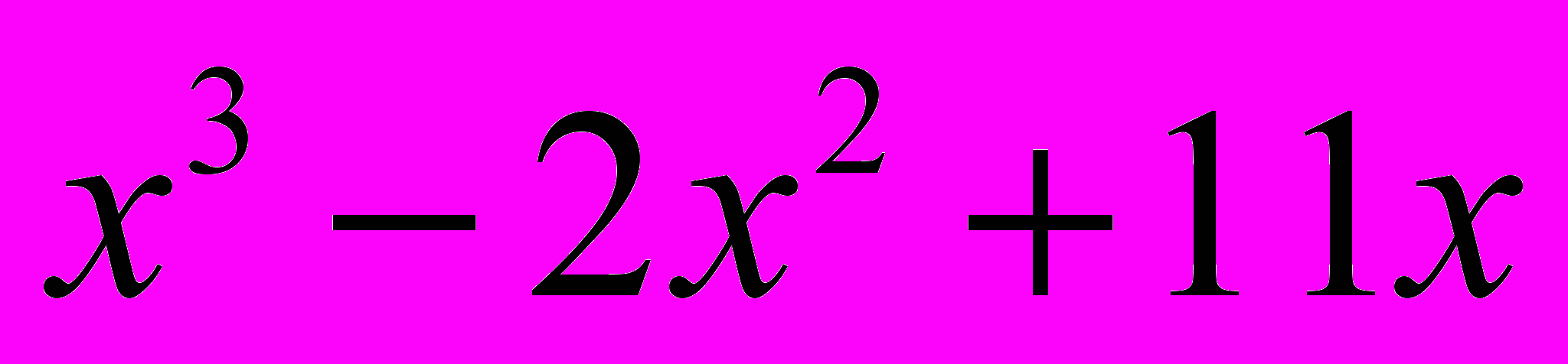на линейные множители.


Разработчики:

СПбГУЭФ доцент В. Г. Дмитриев


СПбГУЭФ профессор Г. В. Савинов


Эксперты:


ЭМИ РАН директор Л. А. Руховец


СПбГМТУ профессор В. Б. Хазанов