Программа дисциплины «Линейная алгебра» для направления 080100. 62 «Экономика»

Вид материала

Программа дисциплины

Содержание 2. Цели освоения дисциплины 3. Компетенции обучающегося, формируемые в результате освоения дисциплины 4. Место дисциплины в структуре образовательной программы 5. Тематический план учебной дисциплины 1.3Самостоятельная работа 6. Формы контроля знаний студентов 6.1 Критерии оценки знаний, навыков 7. Содержание дисциплины Линейная алгебра Аналитическая геометрия Линейная алгебра Линейная алгебра. Линейная алгебра Линейная алгебра Аналитическая геометрия Линейная алгебра Линейная алгебра 8. Образовательные технологии 9.2 Вопросы для оценки качества освоения дисциплины Практические задачи ... Полное содержание

Подобный материал:

• Программа дисциплины «Линейная алгебра» для направления 080100. 62 «Экономика», 212.6kb.
• Программа дисциплины «Линейная алгебра» для направления 080100. 62 «Экономика», 230.6kb.
• Рабочая программа дисциплины «линейная алгебра» Рекомендуется для направления подготовки, 177.83kb.
• Программа по дисциплине Линейная алгебра для студентов 1 курса дневного отделения факультета, 212.1kb.
• Рабочая учебная программа дисциплины (модуля) Линейная алгебра, 227.98kb.
• Программа дисциплины «дифференциальные и разностные уравнения» Для направления 080100., 179.24kb.
• Программа дисциплины «Территориальное стратегическое планирование» для направления, 384.7kb.
• Программа дисциплины Инвестиции для направления 080100. 62 Экономика подготовки бакалавра, 578.6kb.
• Правительство Российской Федерации Государственное образовательное бюджетное учреждение, 416.73kb.
• Программа дисциплины «Математический анализ» для направления 080100. 62 «Экономика», 400.03kb.

1. Область применения и нормативные ссылки

Настоящая программа учебной дисциплины устанавливает минимальные требования к знаниям и умениям студента и определяет содержание и виды учебных занятий и отчетности.

Программа предназначена для преподавателей, ведущих данную дисциплину, учебных ассистентов и студентов направления 080100.62 «Экономика» подготовки бакалавра.

Программа разработана в соответствии с:

• Рабочим учебным планом университета по направлению 080100.62 «Экономика» подготовки бакалавра, утвержденным в 2010г.
  

^

2. Цели освоения дисциплины

Целями освоения дисциплины «Линейная алгебра» являются изучение разделов матричной алгебры, решение систем линейных уравнений и векторного анализа, позволяющие студенту ориентироваться в таких дисциплинах, как «Теория вероятностей и математическая статистика», «Методы оптимальных решений», «Математические модели в экономике». Курс "Линейная алгебра" будет использоваться в теории и приложениях многомерного математического анализа, дифференциальных уравнений, математической экономики, эконометрики. Материалы курса могут быть использованы для разработки и применения численных методов решения задач из многих областей знания, для построения и исследования математических моделей таких задач. Дисциплина является модельным прикладным аппаратом для изучения студентами факультета Экономики математической компоненты своего профессионального образования.
^

3. Компетенции обучающегося, формируемые в результате освоения дисциплины

В результате освоения дисциплины студент должен:

• Знать теорию решения матричных уравнений, элементы векторного анализа и аналитической геометрии
  
• Уметь применить аппарат линейной алгебры в задачах формирования экономических моделей и решении прикладных задач, используемых в курсах «Математические модели в экономике» и «Теория игр».
  
• Иметь навыки в решении систем линейных уравнений и построении диагональных квадратичных форм.
  

В результате освоения дисциплины студент осваивает следующие компетенции:

Компетенция	Код по ФГОС/ НИУ	Дескрипторы – основные признаки освоения (показатели достижения результата)	Формы и методы обучения, способствующие формированию и развитию компетенции
Обще профессиональные компетенции	ОК-10	Основательная теоретическая математическая подготовка, а также подготовка по теоретическим, методическим и алгоритмическим основам курса Линейной алгебры, позволяющая выпускникам работать с современной научно-технической литературой, быстро адаптироваться к новым теоретическим и научным достижениям в области экономического моделирования, использовать аппарат Линейной алгебры при решении прикладных и научных экономических задач	Уверенно владеть теоретическим аппаратом , изложенном в курсе Линейной алгебры:, Владеть методам и средствами решения матричных уравнений, систем линейных уравнений; Иметь представление о функциональных возможностях наиболее распространенных алгоритмов решения прикладных задач Линейной алгебры, а также необходимые умения по их использованию.
2..Профильно-ориентированные компетенции	ОК-11	Профильно-ориентированные компетенции определяются отдельно для каждого из разделов курса Линейной алгебры.	Умение работать с аппаратом матричной алгебры, системами линейных уравнений, основами векторного анализа
3. Рабочие компетенций	ОК-12	Компетенций, которыми должен обладать выпускник университета с позиций работодателя. Такие компетенции определяют степень готовности выпускника выполнять те или иные конкретные практические работы, связанные с использованием изученного аппарата Линейной алгебры.	Умение формировать математическую модель экономической задачи, Умение применить необходимое программное обеспечение при решении прикладной экономической задачи

^

4. Место дисциплины в структуре образовательной программы

Основные положения дисциплины должны быть использованы в дальнейшем при изучении следующих дисциплин:

• Методы оптимальных решений
  
• Дискретная математика
  
• Математические модели в экономике
  
• Теория игр
  
  
  

^

5. Тематический план учебной дисциплины

Тематический план учебной дисциплины

№	1.1Название темы	1.2Всего часов	Аудиторные часы		^ 1.3Самостоятельная работа
			Лекции	Сем. и практ. занятия
1	Преобразования матриц и системы линейных урав­не­ний.	15	3	3	4
2	Определитель.	15	3	3	4
3	Линейные пространства.	17	4	4	4
4	Алгебра матриц.	12	2	2	4
5	Ранг матрицы.	12	2	2	3
6	Структура множества реше­ний системы линейных урав­нений.	14	2	2	4
7	Линейные операторы.	16	3	3	3
8	Линейные, билинейные и квадратичные формы.	12	2	2	3
9	Элементы аналитической геометрии.	18	5	5	4
1	Евклидовы пространства.	12	2	2	4
1	Самосопряженные опера­торы.	10	2	2	4
1	Аффинные пространства.	9	2	2	3
	ИТОГО	108	32	32	44

^

6. Формы контроля знаний студентов

Тип контроля	Форма контроля	1 год				Параметры **
		1	2	3	4
Текущий (неделя)	Контрольная работа	5	10			письменная работа 80 минут
Промежуточный	Домашнее задание		+			Представлена в виде реферата.
Итоговый	Экзамен		+			Устный экзамен

^

6.1 Критерии оценки знаний, навыков

По текущему контролю выдвигаются следующие критерии оценки знаний

По контрольной номер 1 студент должен продемонстрировать умение работы с матрицами, операции над ними – умножение и обращение матриц

По контрольной номер 2 студент должен продемонстрировать умение решать системы линейных уравнений методами Крамера и Гаусса

В домашнем задании студент должен самостоятельно разработать алгоритм нахождения собственных векторов с помощью квадратичных форм.

Оценки по всем формам текущего контроля выставляются по 10-ти балльной шкале.
^

7. Содержание дисциплины

Раздел 1. Преобразования матриц и системы линейных уравнений

Количество часов – лекции – 3, семинары – 3, самостоятельная работа - 4

Темы лекций и семинаров

Матрицы. Матрица и расширенная матрица системы линейных уравнений. эле­ментар­ные преобразования матриц. Обратимость элементарных преобразований. При­ведение матриц к ступенчатому виду элементарными преобразованиями. Метод Гаусса решения систем линейных уравнений. Решение систем линейных уравнений со ступен­чатой матрицей системы. Общее ре­шение систем линейных уравнений. Главные и сво­бодные неизвестные. Геометрическая интер­претация систем линейных уравнений в случае двух или трех неизвестных. Ненулевые решения однородной системы уравне­ний.

Литература

1. Бурмистрова Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.
   
2. Рейнов Ю.И. Линейная алгебра, Изд.-тво ВШЭ, 2006 г.
   

Раздел 2 Определитель

Количество часов – лекции – 3, семинары – 3, самостоятельная работа - 4

Темы лекций и семинаров


Определитель и элементарные преобразования. Построение определителя раз­ложением по столбцу. Определитель транспонированной матрицы. Вычисление опре­делителя разложением по строке.

Литература

Ильин В.А., Позняк Э.Г. ^ Аналитическая геометрия. – М.: Наука, любое издание.


Раздел 3 Линейные пространства

Количество часов – лекции – 4, семинары – 4, самостоятельная работа - 4

Темы лекций и семинаров


Простейшие следствия аксиом линейного пространства. Подпространство ли­нейного пространства. Простейшие свойства линейно зависимых векторов. Базис и ко­ординаты векторов. Существование базиса конечномерного пространства. Размерность линейного пространства.


Литература: Бурмистрова Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.


Раздел 4 Алгебра матриц

Количество часов – лекции – 2, семинары – 2, самостоятельная работа - 4

Темы лекций и семинаров


Сумма матриц. Умножение матрицы на число. Произведение матриц. Матрич­ная за­пись системы уравнений. Свойства арифметических операций над матрицами. Обратная мат­рица и формулы Крамера. Построение обратной матрицы элементарными преобразованиями. Преобразование координат при замене базиса.


Литература:

Рейнов Ю.И. Линейная алгебра, Изд.-тво ВШЭ, 2006 г.


Раздел 5 Ранг матрицы

Количество часов – лекции – 2, семинары – 2, самостоятельная работа - 3

Темы лекций и семинаров


Ранг матрицы. Ранг ступенчатой матрицы. Неизменность ранга при элементар­ных пре­образованиях. Теорема о ранге матрицы. Критерий линейной независимости системы строк (столбцов). Ранг произведения матриц. Определитель произведения матриц.


Литература:

Ильин В.А., Позняк Э.Г. ^ Линейная алгебра. – М.: Наука, любое издание.

.

Раздел 6 Структура множества решений системы линейных уравнений

Количество часов – лекции – 2, семинары – 2, самостоятельная работа - 4

Темы лекций и семинаров


Векторная запись системы уравнений. Теорема Кронекера-Капелли о совмест­ности системы линейных уравнений. Размерность пространства решений однородной системы линейных уравнений. Структура множества решений системы линейных урав­нений. Теорема о выборе главных и свободных неизвестных.


Литература .

Рейнов Ю.И. Линейная алгебра, Изд.-тво ВШЭ, 2006 г.


Раздел 7 Линейные операторы

Количество часов – лекции – 3, семинары – 3, самостоятельная работа - 3

Темы лекций и семинаров


Матрица линейного оператора. Преобразование матрицы линейного оператора при за­мене базиса. Собственные векторы и собственные значения линейного оператора. Приведение матрицы линейного оператора к диагональному виду. Характеристический многочлен линейного оператора. О корнях характеристического многочлена линейного оператора. Свойства собствен­ных векторов с одинаковыми и различными собствен­ными значениями.


Литература: Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.


Раздел 8 Линейные, билинейные и квадратичные формы

Количество часов – лекции – 2 семинары – 2, самостоятельная работа - 3

Темы лекций и семинаров


Формула линейного функционала. Матрица билинейной формы. Матрица сим­метрич­ной билинейной формы. Преобразование матрицы билинейной формы при за­мене базиса. Един­ственность симметричной билинейной формы, порождающей квадра­тичную форму. Критерий Сильвестра положительной определенности квадратичной формы. Закон инерции для квадра­тичных форм.


Литература: Бурмистрова Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998


Раздел 9 Элементы аналитической геометрии

Количество часов – лекции – 5 семинары – 5 самостоятельная работа - 4

Темы лекций и семинаров


Прямоугольная система координат на плоскости. Расстояние между точками. Деление отрезка в данном отношении. Векторы. Равенство векторов. Координаты век­тора. Сложение век­торов. Умножение вектора на число. Разложение вектора плоскости по двум неколлинеарным векторам. Скалярное произведение векторов. Общее уравне­ние прямой на плоскости. Условие параллельности и перпендикулярности прямых. Па­раметрическое и каноническое уравнения прямой. Расстояние от точки до прямой. Преобразование координат точки при замене системы координат. Разложение вектора по трем некомпланарным векторам. Векторное произведение векторов. Смешанное произведение векторов. Общее уравнение плоскости. Условие параллель­ности и пер­пендикулярности плоскостей. Уравнение прямой в пространстве. Взаимное располо­жение прямой и плоскости, двух прямых.


Литература : 1..Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры – М.:

Наука

2. Ильин В.А., Позняк Э.Г. ^ Аналитическая геометрия. – М.: Наука


Раздел 10 Евклидовы пространства

Количество часов – лекции – 2, семинары – 2 самостоятельная работа - 4

Темы лекций и семинаров


Скалярное произведение. Неравенство Коши-Буняковского. Неравенство тре­угольника. Длина вектора и угол между векторами. Ортогональность векторов. Незави­симость попарно ор­тогональных векторов. Ортогональная проекция вектора на подпро­странство. Построение орто­нормированного базиса ортогонализацией произвольного базиса. Матрица скалярного произве­дения в ортонормированном базисе. Ортогональ­ные матрицы. Геометрическая интерпретация ортогональных матриц.


Литература: Бурмистрова Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.


Раздел 11 Самосопряженные операторы

Количество часов – лекции – 2, семинары – 2, самостоятельная работа - 4

Темы лекций и семинаров


Сопряженность операторов в евклидовом пространстве. Матрицы сопряженных опера­торов. Собственные векторы и собственные значения самосопряженных операто­ров. Ортонор­мированный базис из собственных векторов самосопряженного оператора. Приведение квадра­тичной формы к каноническому виду.


Литература: Бурмистрова Е.Б., Лобанов С.Г. ^ Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.


Раздел 12 Аффинные пространства

Количество часов – лекции – 2, семинары – 2, самостоятельная работа - 3

Темы лекций и семинаров


Преобразование координат точки при замене системы координат. Линейные отображе­ния. Линейные операторы, связанные с линейными отображениями. Геомет­рические свойства линейных отображений. Аффинные и изометрические отображения.


Литература: Рейнов Ю.И. Линейная алгебра, Изд.-тво ВШЭ, 2006 г.

^

8. Образовательные технологии

Образовательные технологии для данного курса не используются

9. Оценочные средства для текущего контроля и аттестации студента

1. Тематика заданий текущего контроля

Текущий контроль состоит из двух контрольных работ. Примерные виды заданий Контрольных будут следующими

По контрольной №1


1. Решить уравнение А² – 2(В^Т  С)^Т = D^TX, где

А=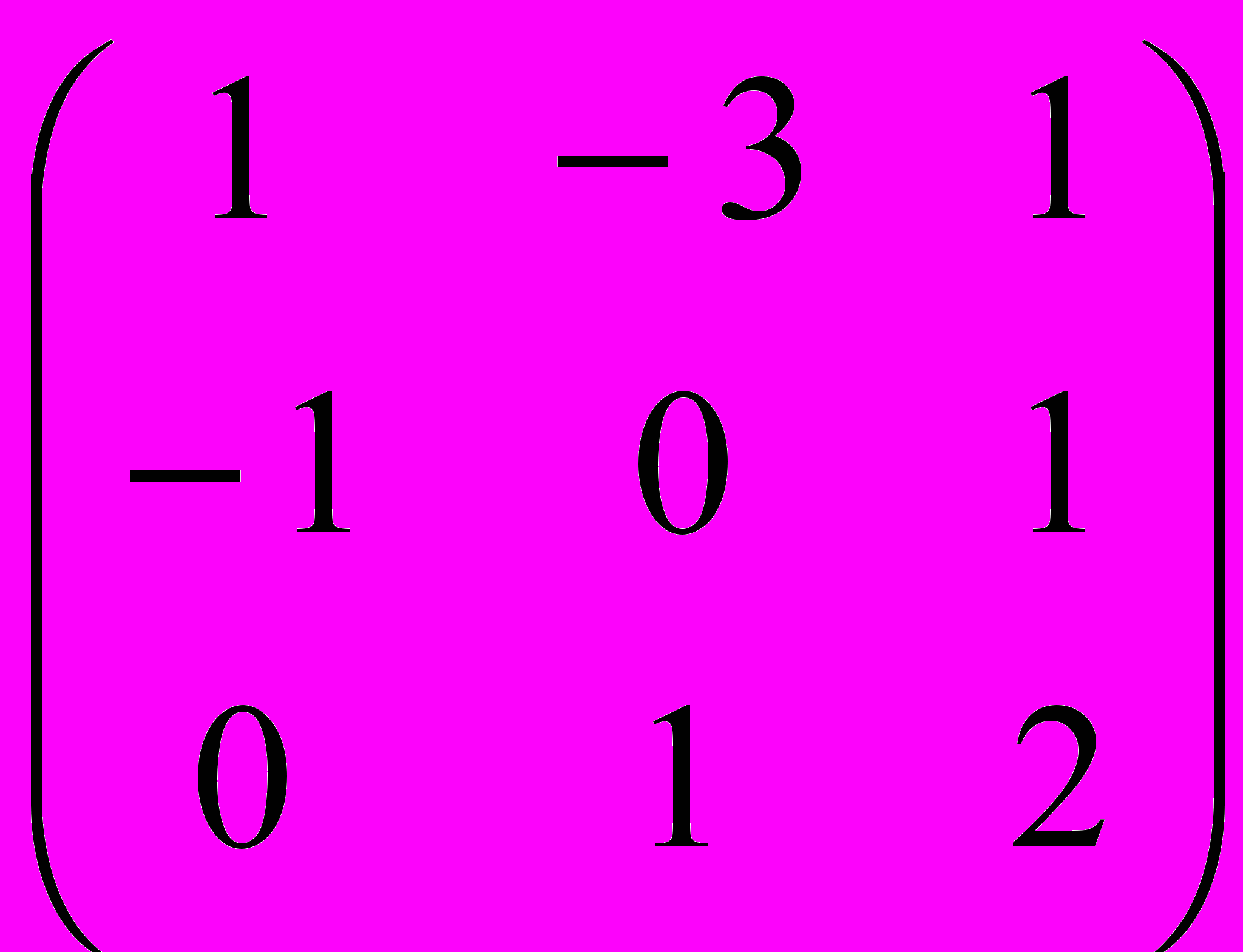,,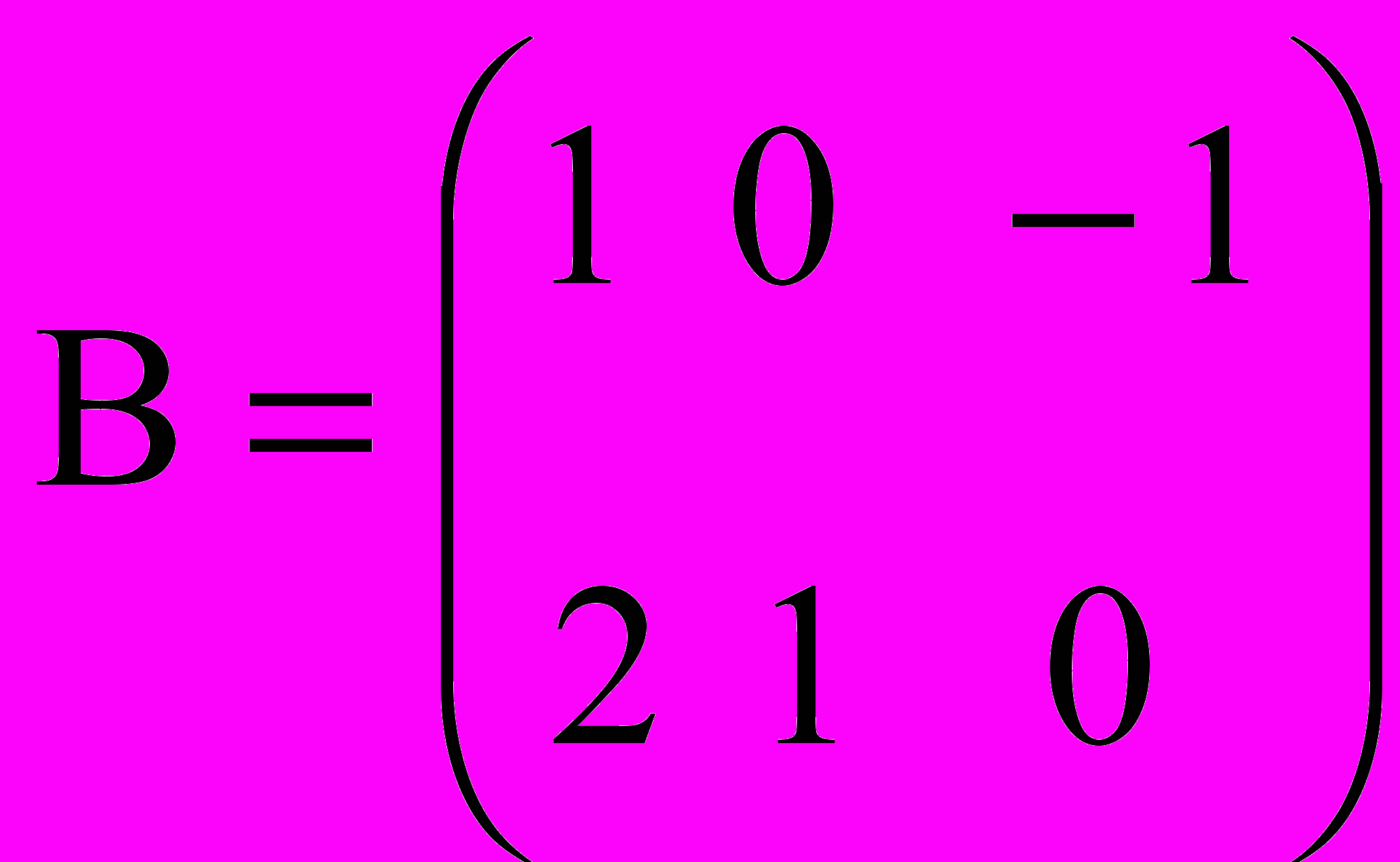,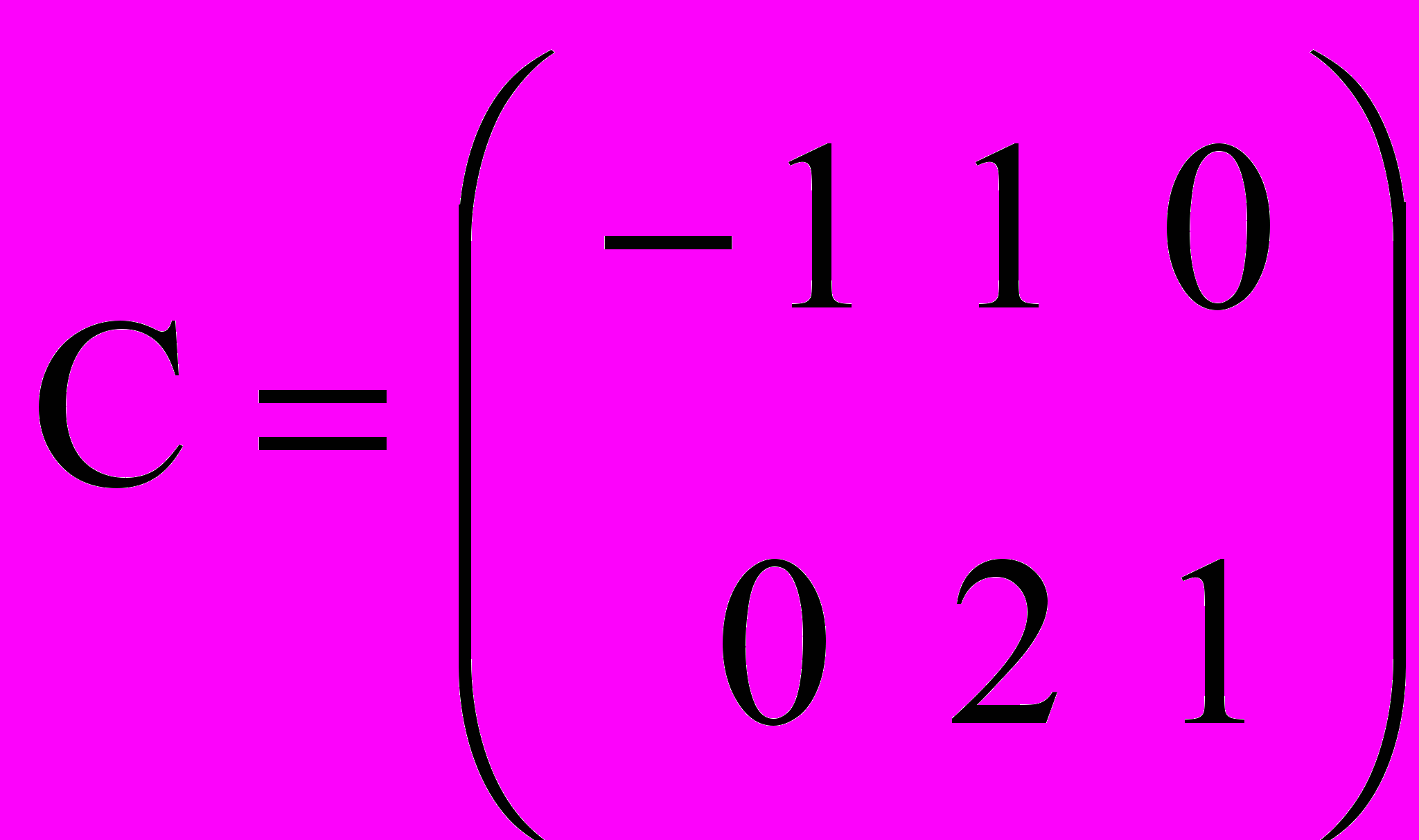D=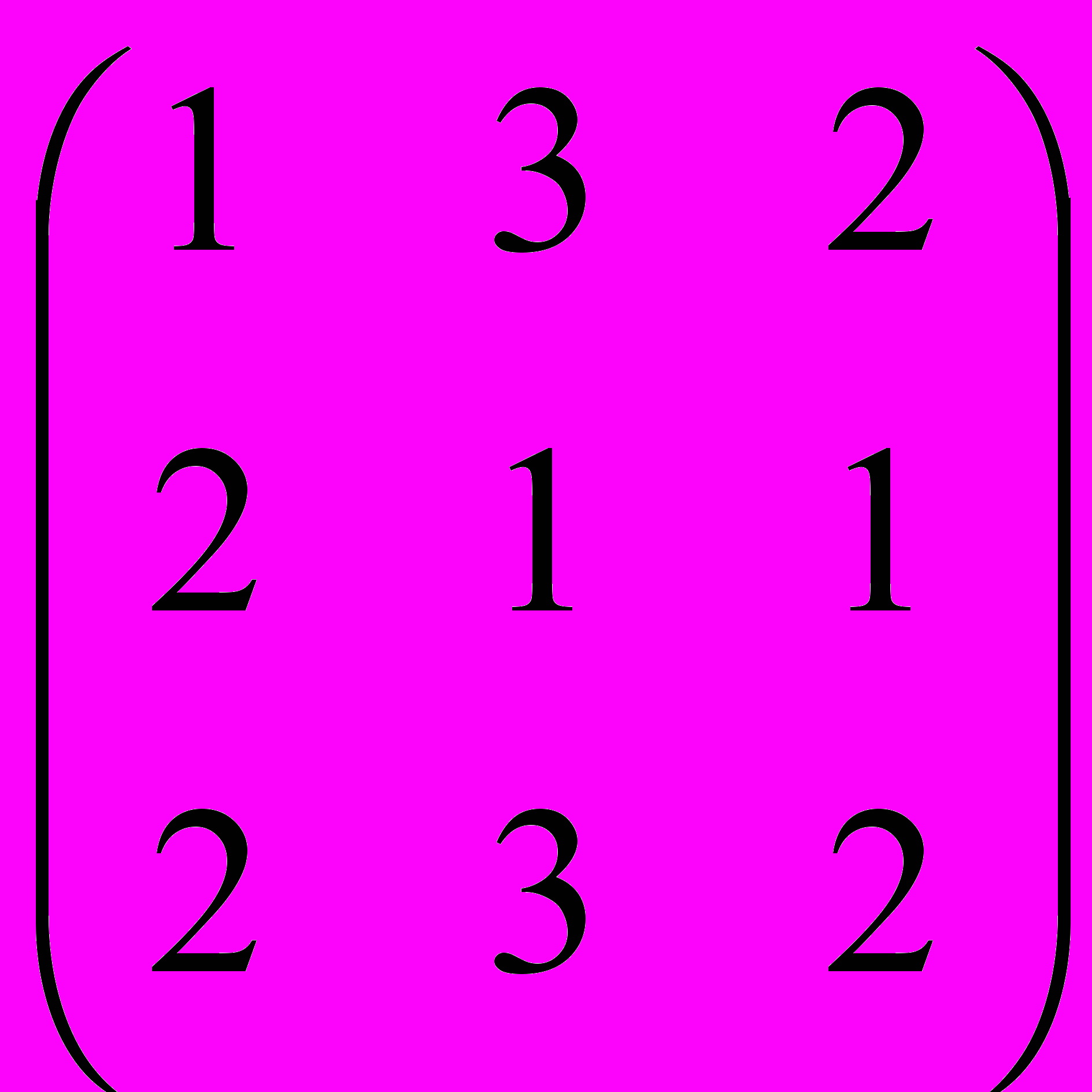

2. Вычислить определитель




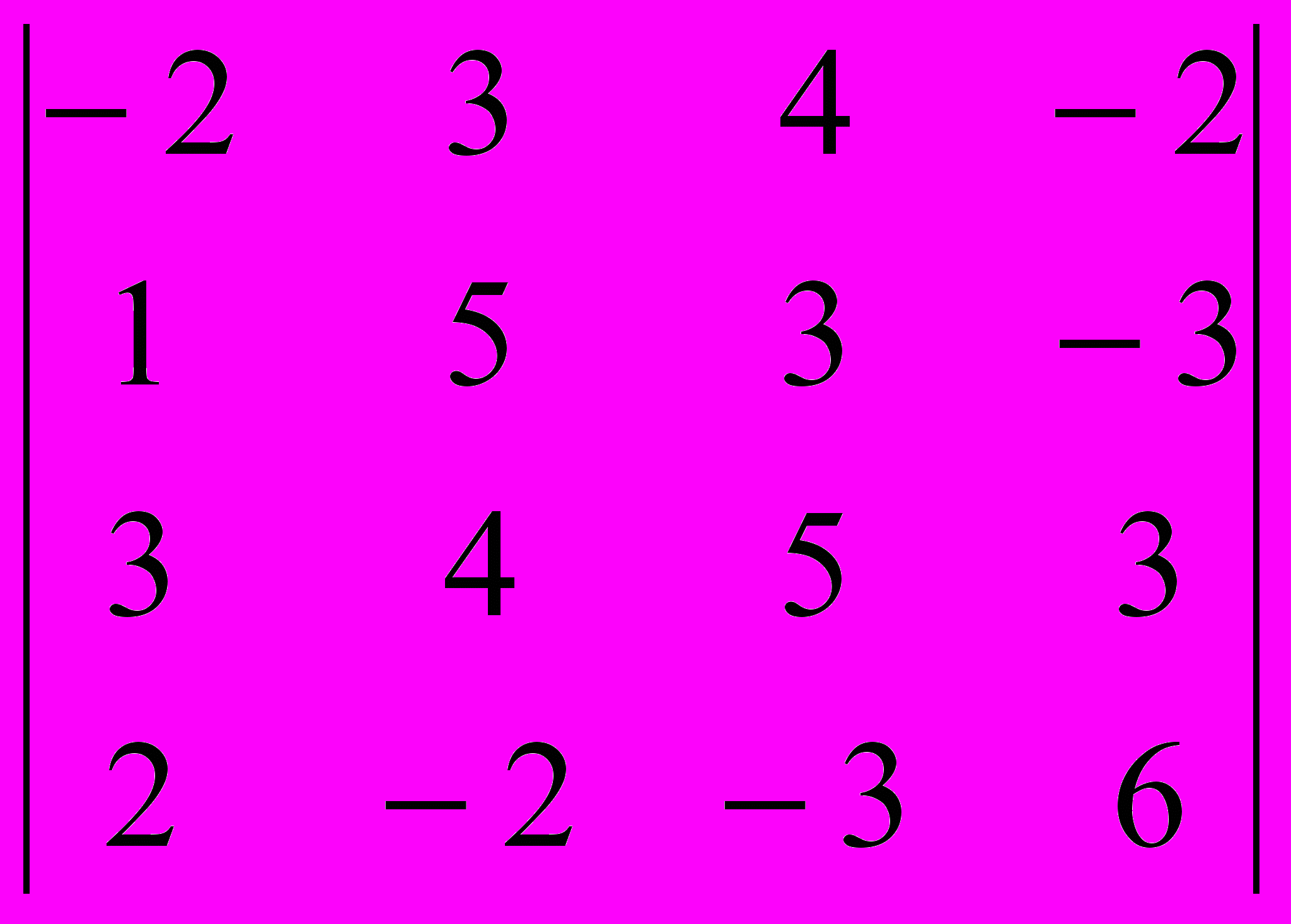
По контрольной № 2


1. Найти общее решение системы уравнений, как сумму частного решения и ФСР




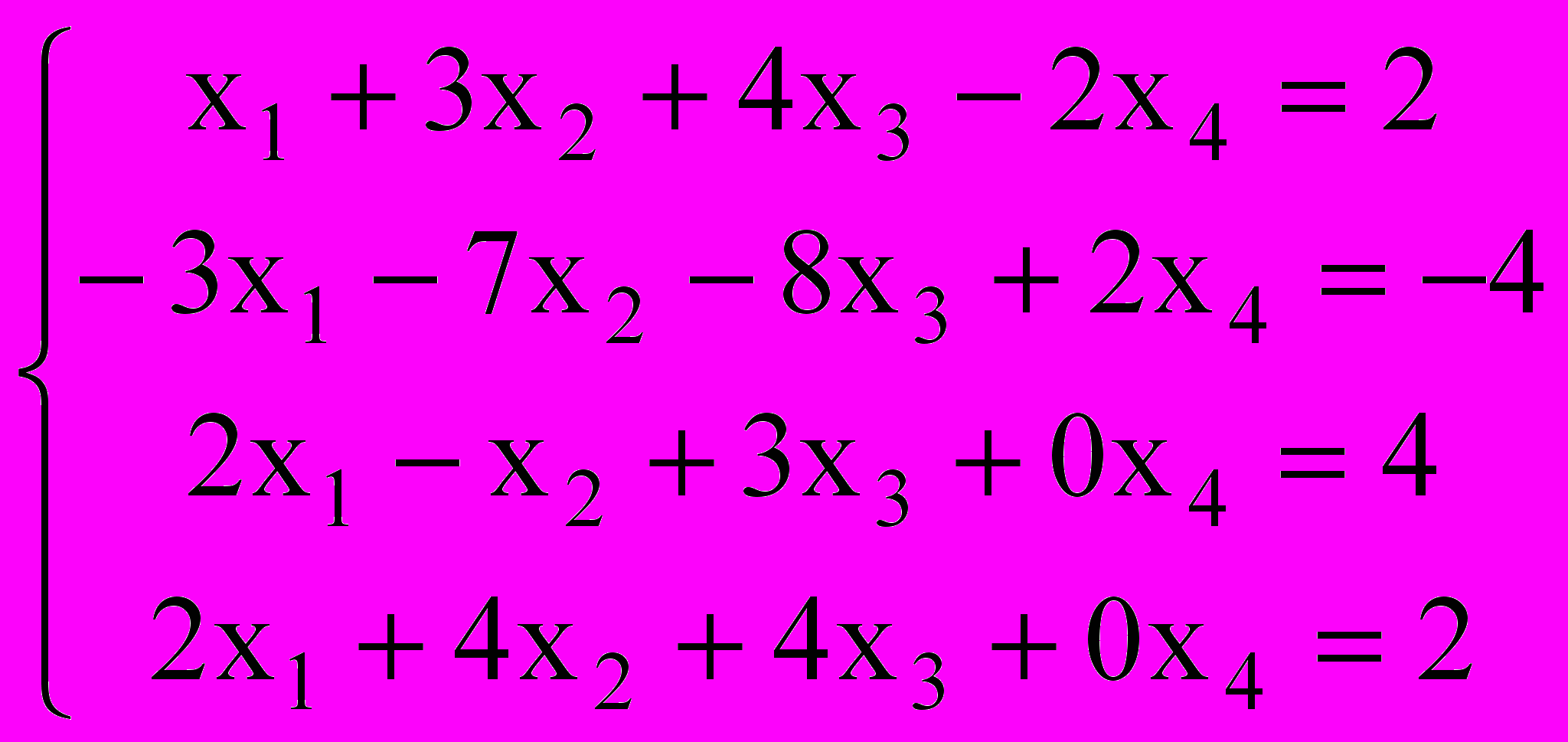
2. Найти ортогональное преобразование квадратичной формы, ее каноническую форму и исследовать форму на положительность, отрицательность или знакопеременность.




^

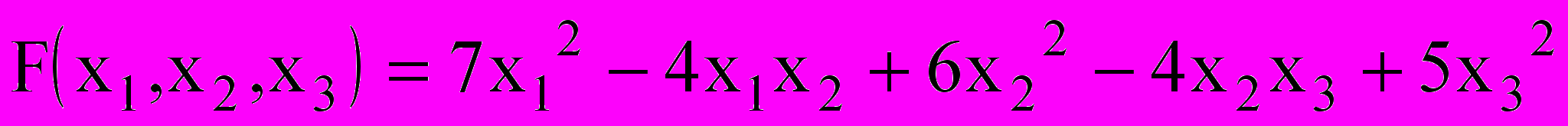
9.2 Вопросы для оценки качества освоения дисциплины

Формулировки

1. Матрица и ее виды – треугольная, диагональная, трапециевидная
   
2. Матрица и ее виды - симметричная, кососимметричная, клеточная
   
3. Матрица и ее виды - инволютивная, идемпотентная, ортогональная
   
4. Определение линейного пространства над полем К.
   
5. Транспонированная, обратимая и обратная матрица
   
6. Определитель n-го порядка
   
7. Свойства определителя (формулировка не менее 6-ти свойств)
   
8. Минор элемента и алгебраическое дополнение
   
9. Взаимная и обратная матрица
   
10. Однородная и неоднородная система линейных уравнений и их решение.
    
11. Несовместная, совместная, определенная и неопределенная системы уравнений.
    
12. Частное и общее решение системы. Равносильные системы.
    
13. Минор k-ого порядка матрицы
    
14. Определение ранга матрицы
    
15. Определение базисных строк и столбцов матрицы.
    
16. Определение элементарных преобразований над строками матрицы
    
17. Свойства элементарных преобразований над строками матрицы ( 3 свойства )
    
18. Элементарные преобразования системы линейных уравнений ( 3 свойства )
    
19. Определение базисных и свободных переменных, фундаментальной совокупности
    
20. решений, частного и общего решения неоднородной системы.
    
21. Формулировка Теоремы о числе решений
    
22. 12)Альтернативы Фредгольма
    
23. Собственное число и собственный столбец матрицы
    
24. Характеристический многочлен матрицы
    
25. Свойства собственных чисел матрицы
    

Доказательства

1. Любая матрица представима в виде суммы симметричной и кососимметричной (n=2)
   
2. Показать, что если матрица обладает двумя из свойств: симметричная,
   
3. ортогональная, иволютивная, то она обладает и третьем свойством.
   
4. Доказать, что (А + В)С = АС + ВС и А(ВС) = (АВ)С
   
5. Доказать, что (АВ)^Т= В^ТА^Т
   
6. Показать, что пространство матриц является линейным пространством
   
7. Доказательство одного из свойств определителя (из доказанных на лекции)
   
8. Каждая ортонормированная матрица имеет обратную матрицу.
   
9. Матрица, обратная к ортогональной матрице, будет ортогональной матрицей.
   
10. АА^Т =I, AA^-1 =I. A^-1(A^-1)^T= I? I = I I = (AA^-1)^T(AA^-1)= (A^-1)^T A^T A A^-1= (A^-1)^T A^-1
    
11. Произведение ортогональных матриц есть ортогональная матрица.
    
12. Теорема о взаимной матрице
    
13. Доказательство единственности обратной матрицы
    
14. Доказательство теоремы Крамера
    
15. Доказательство эквивалентности метода обратной матрицы и формул Крамера
    
16. Если ранг матрицы коэффициентов равен числу неизвестных, то система АХ=0 имеет
    
17. единственное (тривиальное) решение.
    
18. Для того чтобы однородная система имела ненулевое решение, необходимо и
    
19. достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.
    
20. Однородная система n уравнений с n неизвестными имеет ненулевое решение тогда и
    
21. только тогда, когда определитель этой системы был равен нулю.
    
22. Для того чтобы однородная система имела ненулевое решение, необходимо, чтобы
    
23. число уравнений системы было меньше числа неизвестных.
    
24. Теорема о связи собственных чисел и корнях характеристического многочлена
    

^

Практические задачи

1. Нахождение обратной матрицы (при n = 3)
   
2. Нахождение коммутирующей матрицы (при n = 2)
   
3. Пример на альтернативы Фредгольма (для систем 2 х 3)
   
4. Пример на нахождение ранга матрицы (для квадратных матриц 3 Х 3)
   
5. Пример на построение фундаментальной совокупности решений
   
6. Пример на нахождение собственных чисел и собственных корней характеристического многочлена
   

^

9.3 Примеры заданий итогового контроля

Типовой экзаменационный билет состоит из 3-х теоретических и 2-х практических заданий

ТИПОВОЙ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ

1. Доказать теорему Крамера

2. Дать определение квадратичной формы

3. Сформулировать свойства собственных чисел матрицы

4. Найти оператор, сопряженный с ортогональным

5. В некотором ортонормированном базисе евклидова пространства 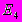система элементов 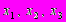представлена столбцами координат

.

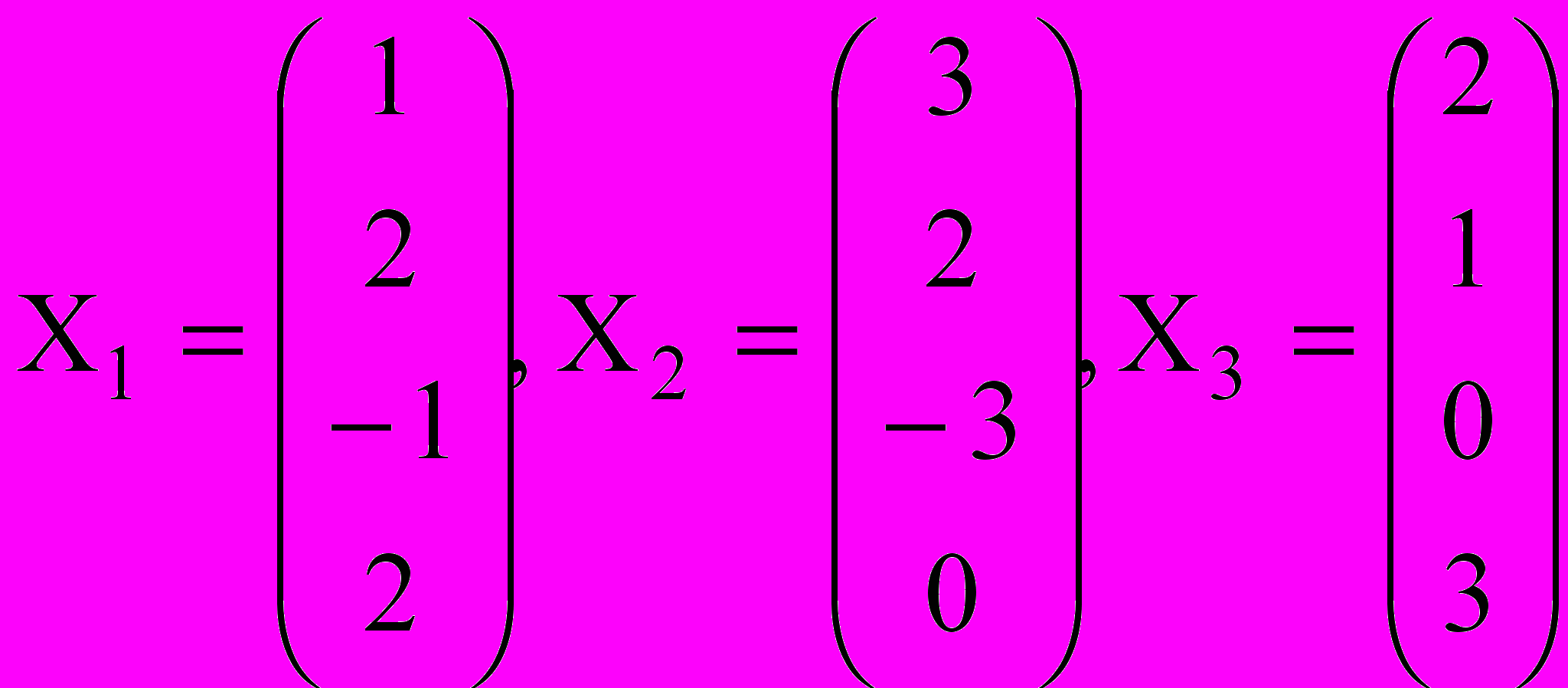Требуется:

1. найти размерность и базис линейной оболочки ;
   
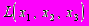2. указать в линейной оболочке 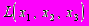ортонормированный базис и достроить его до ортонормированного базиса евклидова пространства.
   

.
^

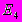10. Порядок формирования оценок по дисциплине

: По курсу предусмотрены две контрольные работы и домашнее задание, как формы текущего и промежуточного контролей (возможно проведение контрольной работы во внеаудиторное время) и контроль текущей работы в течение двух модулей. Студенты, не выполнившие контрольные работы и домашнее задание, к экзамену не допускаются, в экзаменационную ведомость проставляется оценка неудовлетворительно .

Форма итогового контроля – письменный экзамен, к которому допускаются студенты, выполнившие контрольные работы и домашнее задание. Студенты, посетившие менее 80% аудиторных занятий, выполняют на экзамене дополнительную письменную контрольную работу.

Все формы контроля оцениваются в 10-балльной шкале.

. Для получения результирующей оценки итогового контроля используются следующие весовые множители:

• Q₁ - оценки за 2 контрольные работы – 30% итоговой оценки
  
• Q₂ - оценка за домашнее задание – 20% итоговой оценки
  
• Q₃ - оценки контроля текущей работы в течение двух модулей – 10% итоговой оценки
  
• Q_{4 -} оценки письменного экзамена – 40% итоговой оценки, с округлением результата до целых единиц.
  

Итоговая оценка Q = 0.3Q₁ + 0.2Q₂ + 0.1Q₃ + 0.4Q₄


Экзаменационная оценка, в свою очередь, складывается из пяти составляющих со следующими весовыми множителями:

• G₁- за легкий теоретический вопрос на знание определений – 20% экзаменационной оценки;
  
• G₂ -за легкий вопрос по теории – 10% экзаменационной оценки;
  
• G₃ -за вопрос на доказательство теорем – 40% экзаменационной оценки;
  
• G₄ - за легкую задачу – 10% экзаменационной оценки;
  
• G₅ - за трудную задачу – 20% экзаменационной оценки;
  

Экзаменационная оценка Q₄ = 0.2G₁ + 0.1G₂ + 0.4G₃ + 0.1G₄ + 0.2G₁


Полученный после округления этой величины до целого значения результат и выставляется как результирующая оценка по 10-балльной шкале по учебной дисциплине "Линейная алгебра" в экзаменационную ведомость (оценкам 1, 2, 3 в 10-балльной системе соответствует оценка «неудовлетворительно » в пятибалльной системе, оценкам 4, 5 – «удовлетворительно », оценкам 6, 7 – «хорошо », оценкам 8, 9, 10 – «отлично »).


^

11 Учебно-методическое и информационное обеспечение дисциплины

11.1 Базовые учебники

2. Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра. – М.: Изд-тво ВШЭ, 1998 г.
   
3. Рейнов Ю.И. Линейная алгебра, Изд.-тво ВШЭ, 2006 г.
   

^ 11.2 Основная литература

2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры – М.: Наука, любое издание.
   
3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, любое издание.
   
4. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, любое издание.
   
5. Сборник задач по математике для ВТУЗов. Линейная алгебра и основы математиче­ского анализа (под редакцией А.В. Ефимова и Б.П. Демидовича) – М.: Наука, любое издание после1981.
   
6. Шевцов Г.С. Линейная алгебра. Учебное пособие. – М.: Гардарики, 1999.
   

^ 11. 3 Дополнительная литература

2. Александров П.С. Лекции по аналитической геометрии, пополненные необходимыми све­дениями из алгебры. – М.: Наука, 1968.
   
3. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. – М.: Изд-во Моск. ун-та, 1998.
   
4. Погорелов А.В. Геометрия. – М.: Наука, 1983.
   
5. Скорняков Л.А. Элементы линейной алгебры. Учебное пособие. – М.: Наука, 1980.
   

11.4 Справочники, словари и энциклопедии

Справочники, словари и энциклопедии не используются

11.5 Программные средства

Компьютерное программное обеспечение отсутствует

11.6 Дистанционная поддержка дисциплины

Дистанционная поддержка дисциплины отсутствует

12. Материально-техническое обеспечение дисциплины

Материально-техническое обеспечение курса отсутствует


Автор программ: к.т.н., доцент Рейнов Ю.И.