Кафедра: "ВТ"

Вид материала

Доклад

Содержание 2 этап. Преобразование входных сигналов. x Выбор алгоритма обучения нейронной сети 5 этап. Итоговое вычисление границ прогнозируемого значения. P=P T и предполагаемое значение i-го критерия на момент T

Подобный материал:

• 28-29 октября 2010 г. Девятая международная научно-практическая конференция „Норма, 51.26kb.
• Правительстве Российской Федерации» Кафедра «Макроэкономика» Кафедра «Микроэкономика», 147.21kb.
• План курсовых мероприятий тогирро на 2011 год Содержание Кафедра стратегического менеджмента, 2958.17kb.
• Программа профессиональной переподготовки специалистов для выполнения нового вида профессиональной, 34.84kb.
• Программа производственной преддипломной практики Для студентов Vкурса, обучающихся, 449.19kb.
• Кафедра автоматики и автоматизации производственных процессов, 1002.67kb.
• Кафедра стратегического менеджмента в образовании, 2593.09kb.
• Основной образовательной программы (ооп) высшего профессионального образования бакалавриат, 76.22kb.
• Бакалаврская программа № по направлению психология кафедра, 389.94kb.
• Бакалаврская программа № по направлению психология кафедра, 359.07kb.

1 этап. Подготовка выходных данных.

Выходными данными являются: z_i=y_i-p_i , где y_i - реальное значение прогнозируемой величины на некоторую дату, p_i - рассчитанное на эту дату с помощью линейного анализа.


^ 2 этап. Преобразование входных сигналов.

x_i^j*=(x_i^j-M(X_i))/(X_i), где x_i^j - j-я координата некоторого критерия X_i, M(X_i) - выборочная оценка математического ожидания, (X_i) - выборочная оценка среднего квадратичного отклонения.


3 этап. Выбор функций, участвующих в аппроксимации зависимости, из следующего набора функций:

_n

- f(x,a)=c₁/(c₂+((a_i*x_i))^m), где m - четное, с₁<>0, c₂>0;

_n ⁱ⁼¹

- f(x,a)=COS((a_i*x_i));

_nⁱ⁼¹

- f(x,a)=SIN((a_i*x_i));

_n ⁱ⁼¹ _n

- f(x,a)=(a_i*x_i)^m-1*c₁/(c₂+((a_i*x_i))^m), где m - четное, с₁<>0, c₂>0;

ⁱ⁼¹ _n ⁱ⁼¹

- f(x,a)=c₁/(c₂+EXP(-(a_i*x_i))), где с₁<>0, c₂ >= 1;

_n ⁱ⁼¹

- f(x,a)=c₁/LN(c₂+((a_i*x_i))^m), где m - четное, с₁<>0, c₂>0;

ⁱ⁼¹

x_i (i=1,...,n) - значение i-го критерия на некоторую дату; a_i (i=1,...,n) - параметр при i-ом критерии; c₁, c₂ - константы, m - целочисленная константа m>0.

Данный набор функций, предоставляемый для участия в нелинейном анализе, в будущем может быть расширен. Единственными ограничениями являются следующие требования к функциям: они должны быть везде дифференцируемы и области их значений должны быть ограничены сверху и снизу. При выборе пользователем функций, участвующих в нелинейном анализе, система выдает рекомендации, т.к. при определении констант выбранных пользователем функций, может возникнуть ситуация, когда итоговая функция будет иметь область значений только в отрицательной или положительной полуплоскостях, либо будет ограничена по значению таким образом, что значения погрешности выйдут за данные границы, в перечисленных случаях прогноз априори будет некорректен. Помимо этого система предоставляет уже готовые наборы функций наилучшим образом зарекомендовавших себя на соответствующих рынках. Например, для рынка облигаций это: _{n n n}

f(x,a) = sin((a_i*x_i))+1/(1+exp(-(b_i*x_i)))-1/(1+exp(-(c_i*x_i))),

^{i=1 i=1 i=1}

а для рынка акций:

_{n n n n}

f(x,a)=sin((a_i*x_i))+1/(1+exp(-(b_i*x_i)))-1/(1+exp(-(c_i * x_i)))-1/ln(1+((d_i*x_i))²).

^{i=1 i=1 i=1 i=1}

Таким образом, аппроксимирующую функцию в общем виде можно представить как:

_{k n}

F(x,a)=(f_j((a_ij*x_i)), где k - кол-во функций, n - кол-во критериев.

^{j=1 i=1}

Архитектура нейронной сети в общем виде представлена на рис.3. Здесь _j - линейные сумматоры, вычисляющие сумму произведений входных данных и искомых параметров, f_j - нелинейные функции, используемые для аппроксимации,  - итоговый сумматор. Данная сеть имеет простую архитектуру. Вообще, делались попытки предоставить возможность аналитику увеличивать число скрытых уровней, но, как показал опыт, это не привело к улучшению качества прогноза, а только привело к усложнению системы.




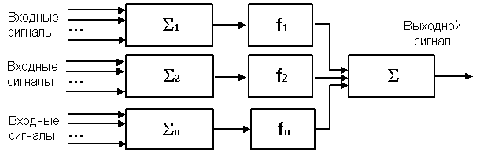
Рис.3


4 этап. ^ Выбор алгоритма обучения нейронной сети, основанного на методах обратного распространения ошибки, градиентного спуска, сопряженных градиентов, Ньютона, квазиньютоновский метод.

Методы оценивались по времени, затрачиваемому на обучение, и величине погрешности. Для градиентных методов были разработаны собственные алгоритмы, оптимизирующие процедуру выхода из локальных минимумов. Наилучшим образом зарекомендовали себя метод градиентного спуска и квазиньютоновский метод.


^ 5 этап. Итоговое вычисление границ прогнозируемого значения.

P=P_{линейное}+P_{нелинейное}+-E_{нелинейное}, где

P - итоговое прогнозируемое значение, P_{линейный} и P_{нелинейное} - значения линейного и нелинейного анализов, E_{нелинейное} - погрешность, полученная на этапе нелинейного анализа:

За время эксплуатации итоговая погрешность прогноза не превышала:

1. для рынка облигаций при прогнозировании цен 0,3%, доходности - 2%;
   
2. для рынка акций при прогнозировании цен 1,2%;
   
3. для валютного рынка -1,3%.
   

Таким образом, посредством применения нелинейного анализа удалось существенно снизить погрешность прогноза по сравнению с полученной на этапе линейного анализа.


4.5. Задача оптимального распределения свободных средств банка.


Задача состоит из двух идентичных по реализации этапов:

• оптимальное распределение средств внутри рынка;
  
• оптимальное распределение средств между рынками.
  

Первым шагом определяются горизонт портфеля - ^ T и предполагаемое значение i-го критерия на момент T - x_i^T и его погрешностьx_i^T (i=1,...,n), где n - количество значимых критериев.

В качестве основы математической модель рынка взята теория Марковица. Но в теории Марковица используются вероятностные характеристики рынка, что целесообразно для устойчивого, развитого рынка. Но данная задача будет решена успешнее, если использовать в ней результаты прогноза. Математическая модель выглядит следующим образом:

для выборки x_i^t, y^t_j (i=1,...,n), (j=1,...,k), (t=t₁,...,t₂) T>t₁ и T>=t₂

E=(p,s)

V=s^T*C_p*s

s_j>=0, s_j=1 (j=1,...,k),

где y^t_j - значение доходности j-го элемента на дату t; E - доходность портфеля; p - вектор-строка прогнозируемой доходности элементов портфеля; s - вектор-столбец искомых долей k элементов портфеля; V - риск портфеля; C_p=||c_pij||, где c_pij=M[(Y_i - P_i)*(Y_j-P_j)], Y_i и Y_j - выборки доходности элементов i и j, P_i и P_j - рассчитанные доходности элементов i и j.

На данный момент рассматриваемой системой решаются задачи нахождения портфеля с минимальным риском, т.е. Vmin и нахождения портфеля с минимальным риском при некоторой фиксированной доходности, т.е. Vmin и E>=Eф, где Eф - некоторая константа. Данные задачи, в общем случае, являются задачами квадратичного программирования, которые в данной системе решаются с помощью метода проекции градиента, для реализации которого разработан алгоритм, оптимизированный для решения данной конкретной задачи.


4.7. Выводы.


Все рассмотренное выше подтверждает, что нейросетевые экспертные системы являются эффективным инструментом анализа и предсказания поведения финансовых рынков, в том числе и для решения задачи оптимального распределения свободных средств банка. Можно ожидать, что в недалеком будущем реализованные на их основе подсистемы анализа и прогноза займут достойное место в составе АБС крупнейших банков и информационных АСУ корпораций, базирующихся на технологиях клиент-сервер. Первые шаги по внедрению данных методов уже сделаны.


5. Заключение.


Так что же такое "нейронная сеть"?

Нейронная сеть - это взаимосвязанная совокупность простых обрабатывающих элементов (нейронов, или узлов), которые с определенной (практически обусловленной) степенью приближения реализуют функции нейронов живых организмов. Как правило, передаточные функции всех нейронов в сети фиксированы, а веса являются параметрами сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы сети, а некоторые выходы - как внешние выходы сети. Подавая любые числа на входы сети, мы получаем какой-то набор чисел на выходах сети. Таким образом, работа нейросети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами сети. Нейронные сети обладают способностью к обучению, то есть являются информационно активными системами.