Тематико-календарный план лекций по дисциплине „ Высшая математика Ікурс

Вид материала

Закон

Содержание Элементы теории вероятностей. Понятия случайной величины (СВ). Законы распределения НСВ Понятия статистического оценивания. Предельные законы (теоремы) теории вероятностей. Планирование эксперимента и дисперсионный анализ. Однофакторный корреляционный анализ. Тематико-календарный план Дифференциальное исчисление. Интегральное исчисление. Определенный интеграл. Дифференциальные уравнения. Математическое моделирование некоторых процессов. Элементы теории вероятностей. Понятия случайной величины (СВ). Законы распределения НСВ Понятия статистического оценивания. Предельные законы(теоремы) теории вероятностей. Планирование эксперимента и дисперсионный анализ. Однофакторный корреляционный анализ. ... Полное содержание

Подобный материал:

• Анализа и теории функций календарный план учебных занятий по дисциплине «Высшая математика», 30.38kb.
• Тематико-календарный план лекций по эпидемиологии для студентов 5 курса «Общественное, 400.05kb.
• Календарный план проведения лекций и практических занятий по курсу «общая электротехника, 32.76kb.
• Календарный план учебных занятий по обязательной дисциплине «Дискретная математика, 109.62kb.
• Календарный план лекций по курсу «математический анализ» Для специальности «Математика», 39.98kb.
• Календарный рейтинг-план дисциплины оценки календарный рейтинг-план по дисциплине, 478.45kb.
• Календарный рейтинг-план дисциплины оценки календарный рейтинг-план по дисциплине, 349.54kb.
• Предложения в тематико-экспозиционный план раздела (полное и сокращенное наименование, 54.48kb.
• Календарный план учебных занятий по дисциплине "Высшая алгебра и аналитическая геометрия", 94.97kb.
• Завершинский Константин Фёдорович (Культурология), 835.52kb.

ТЕМАТИКО-КАЛЕНДАРНЫЙ ПЛАН

лекций по дисциплине „Высшая математика"

І курс, I семестр______/_______ уч. год

(фармацевтический факультет

специальность 7.110201 - фармация)

* Все занятия 2-х часовые

Всего часов - 14

№ лекции	Темы лекций и их содержание	Дата	Лектор
1	^ Элементы теории вероятностей. Случайные события и операции над ними. Классическое и ста­тистическое определение вероятностей. Формула добавления и перемножения вероятностей. Формула Байеса. Схема после­довательных независимых испытаний Бернулли. Формула Ла­пласа.
2	^ Понятия случайной величины (СВ). Дискретные и непре­рывные СВ. Закон распределения дискретных СВ (ДСВ). Способы зада­ния распределения ДСВ. Непрерывные СВ (НСВ). Понятия о функции распределения и функции плотности распределения НСВ.		-„”-
3	^ Законы распределения НСВ (биномиальный, Пуассона, рав­номерный, нормальный, Х2-распределение, t-распределение). Точечные и интервальные оценки параметров нормально рас­пределенного признака. ^ Понятия статистического оценивания. Точечные и интервальные оценки. Возможный интервал для математического ожидания и для дисперсии нормально рас­пределенного признака.		-„”-
4	^ Предельные законы (теоремы) теории вероятностей. Неравенство Чебышева. Закон больших чисел: теорема Чебы-шева. Применение теоремы Чебышева в теории измерений. Центральная предельная теорема и ее прикладное значение.		-„”-
5	Статистическая проверка гипотез (общее рассмотрение ста­тистической проверки гипотез). 1. Основные понятия и терминология. 2. Формирование гипотез про: 2.1. Согласования эмпирического закона распределения с теоретическим. 2.2. Равенство дисперсий двух нормальных совокупностей. 2.3. Равенство центров распределения двух независимо нормальных совокупностей (для равных и неравных дисперсий).		-„”-
6	^ Планирование эксперимента и дисперсионный анализ. План эксперимента. Модель дисперсионного анализа. Одно-факторный дисперсионный анализ.		-„”-
7	^ Однофакторный корреляционный анализ. Функциональная и статистическая связь между признаками. Корреляционная связь. Коэффициент корреляции и его оценка (глубина - сила корреляционной связи и ее надежность). Однофакторный регрессионный анализ. Оценка параметров уравнения регрессии методом наименьших квадратов. Интервальные оценки параметров линейной рег­рессии и линии регрессии.		-„”-

^ ТЕМАТИКО-КАЛЕНДАРНЫЙ ПЛАН

лекций по дисциплине „Высшая математика"

І курс, I семестр ______/______уч. год

(фармацевтический факультет

( специальность 7.110206 - клин.фармация)

* Все занятия 2-х часовые

Всего часов - 38

№ лекции	Темы лекций и их содержание	Дата	Лектор
1	1. Введение в дисциплину „Высшая математика". 2. Некоторые понятия и терминология математического анализа. Общие сведения о функциях. Множество и его элементы. Числовые множества. Функция одной переменной. Область определения и область значения функции. Элементарные функции. Функции многих пере­менных. Предел функции. Теоремы о пределах. Непрерывные функции.		Ас. Юрий Р.Ф.
2	^ Дифференциальное исчисление. Производная и дифференциальная функции, их физическое и геометрическое содержание. Производные и дифференциалы высших порядков. Частные производные и полный диффе­ренциал (первого и высших порядков). Применение полного дифференциала для приближенных вы­числений и оценка погрешностей косвенных измерений (об­щие подходы).		-„”-
3	^ Интегральное исчисление. Определение и основные свойства неопределенного интеграла. Вычисление неопределенного интеграла непосредственно, методом подстановки и частями. ^ Определенный интеграл. (Определение и основные свойст­ва). Формула Ньютона-Лейбница.		-„”-
4	^ Дифференциальные уравнения. Определение, общее и частное решение. Уравнения первого порядка с отделяемыми переменными.		-„”-
5	^ Математическое моделирование некоторых процессов. Моделирование дифференциальными уравнениями процес­сов в физике, химии и т.п. (радиоактивный распад; поглоще­ние ионизирующего излучения (з-н Бугера-Бера; размноже­ние бактерий; растворение врачебного вещества из таблеток; химические реакции 1-го и 2-го порядков)).		-„”-
6	^ Элементы теории вероятностей. Случайные события и операции над ними. Классическое и статистическое определение вероятностей. Формула добав­ления и перемножения вероятностей. Формула Байеса. Схе­ма последовательных независимых испытаний Бернулли. Формула Лапласа.		-„”-
7	^ Понятия случайной величины (СВ). Дискретные и непре­рывные СВ. Закон распределения дискретных СВ (ДСВ). Способы задания закона распределения для ДСВ. Непрерывные СВ (НСВ). Понятие о функции распределе­ния и функции плотности распределения НСВ.		-„”-
8	^ Законы распределения НСВ (биномиальный*, Пуассона*, равномерный*, нормальный, х2-распределение, t-распреде-ление). Точечные и интервальные оценки параметров нормально распределенного признака.		-„”-
9	^ Понятия статистического оценивания. Точечные и интервальные оценки. Возможный интервал для математического ожидания и для дисперсии нормально распределенного признака.		-„”-
10	^ Предельные законы(теоремы) теории вероятностей. Неравенство Чебышева. Закон больших чисел: теорема Че-бышева. Применение теоремы Чебышева в теории измере­ний. Центральная предельная теорема и ее прикладное зна­чение.		-„”-
11	Статистическая проверка гипотез (общее рассмотрение статистической проверки гипотез). 2. Основные понятия и терминология. 2. Формирование гипотез о: 2.1. Согласовании эмпирического закона распределения с теоретическим (по критерию согласия х2).		-„”-
12	Продолжение темы лекции № 11 2.2. Равенство дисперсий двух нормальных совокупностей (при помощи F-критерия). 2.3. Равенство центров распределения двух независимых нормальных совокупностей (по критериям F, t).		-„”-
13	^ Планирование эксперимента и дисперсионный анализ. План эксперимента. Модель дисперсионного анализа. Одно-факторный дисперсионный анализ.		-„”-
14	^ Однофакторный корреляционный анализ. Функциональная и статистическая связь между признаками. Корреляционная связь. Коэффициент корреляции и его оце­нивания (глубина - сила корреляционной связи и ее надеж­ность).		-„”-
15	^ Однофакторный регрессионный анализ. Оценивание параметров уравнения регрессии методом наи­меньших квадратов. Интервальные оценки параметров ли­нейной регрессии и линии регрессии.		-„”-
16, 17	^ Ряды динамики. Классификация временных рядов. Основные количественные характеристики (статистики) и цепные и базисные показате­ли временного ряда и сравнение его уровней: - средний уровень моментного временного ряда - ряда динамики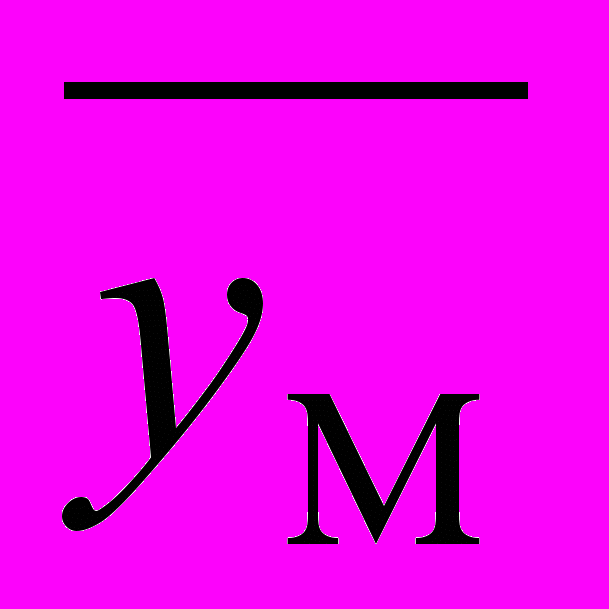 . - средний уровень интервального ряда с равными промежутка- ми времени - среднее арифметическое показателя. 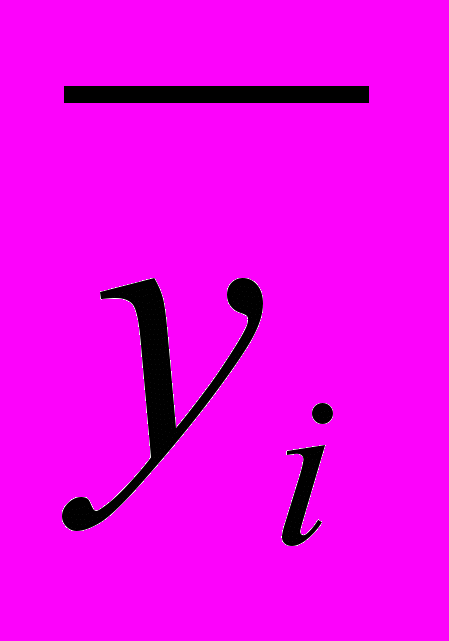. - среднеквадратичное отклонение уровней ряда - S; - коэффициент вариации - v; и цепные и базисные показатели временного ряда и сравне­ние его уровней; - абсолютный прирост и и i0 - базисного) показателей; - темп роста (Kt - цепного и К„- базисного) показателей; - темп прироста (Ті, - цепного и Tiо - базисного) показателей.		-„”-
18	Понятия о выравнивании (отыскание уравнений регрессии) для временных рядов (тренда). Моделирование линейного тренда.		-„”-
19	Заключительная лекция.		-„”-

^ ТЕМАТИЧЕСКИЙ И КАЛЕНДАРНЫЙ ПЛАНЫ

практических занятий по высшей математике

I курс, I семестр______/______ уч. год

(специальность 7.110206 – клин.фармация)

*Все занятия 2-х часовые

Всего часов - 38

№№ зан. п/п	Дата занятия	^ Темы занятий и их содержание
1		1. Введение в дисциплину „Высшая математика" Ознакомление студентов с таким: 1.1. Цель и задача предмета. 1.2. Особенности изучения предмета (виды занятий, методика подготовки к занятиям). 1.3. Виды конечного (на отдельных этапах изучения предмета) и итогового контролей. 2. Тема №1.* Понятие функции. Граница функции. Непрерывные функции. Производная функции. Производные простых функций. Примечание: Номер темы представлен соответственно Методическим указаниям (МУ) к практическим занятиям по высшей математики.
2		Тема №2. Производные сложных функций. Производные высших порядков. Дифференциал функции.
3		Тема №3. Исследование функций с помощью производных. Построение графиков функций.
4		1. Самоподготовка к контрольной работе по темам №№ 1-3. 2. Контрольная работа №1. (темы №№ 1-3)
5		Тема №4. Функции многих переменных. Частные производные. Полный дифференциал. Тема №5. Приближенные вычисления и оценка погрешностей косвенных измерений с помощью полного дифференциала.
6		1. Самоподготовка к контрольной работе по темам №№ 4,5. 2. Контрольная работа №2. (темы №№ 4-5)
7		Тема №6+№7. Неопределенный интеграл. Вычисление неопределенного интеграла (непосредственное, заменой переменной и по частям). Тема №8. Определенный интеграл. Вычисление площади и энергии с помощью определенного интеграла.
8		Тема №9. Понятие о дифференциальных уравнениях (ДУ). ДУ первого порядка с разделяющимися переменными. Однородные ДУ первого порядка.
9		Тема №10. 1. Закрепление знаний-умений по темам №№ 6-9 и решений типовых упражнений (см. Приложение в МУ). Самоподготовка к контрольной работе №3. 2. Контрольная работа №3 (по материалам тем №№ 1-9).
10		Тема №11+№12. (Приобретение практических навыков в применении теорем сложения и умножения вероятностей, формул полной вероятности и Байеса для вычисления вероятности случайных событий; формирование знаний о способах представления закона распределения дискретной случайной величины (ДСВ) и расчетов числовых характеристик ДСВ: М, D, ).
11		Тема №13. Непрерывные случайные величины (НСВ) и их числовые характеристики. Примеры распределений непрерывных случайных величин: равномерный, экспонентный и нормальный (Гаусса). Стандартное нормальное (нормированное) распределение.
12		1. Самоподготовка к контрольной работе по темам №№ 11-14. 2. Контрольная работа №4 (по темам №№ 11-14).
13		Тема №14. Основные понятия математической статистики. Генеральная и выборочная совокупности. Выборочный метод. Представление выборки. Основные понятия о точечных оценках характеристик (ТОХ) случайных величин (толкования, статистическое содержание, требования к ТОХ, применение).
14		Тема №15. Статистическая проверка гипотез (общие понятия и терминология). Тема №16. Статистическая проверка гипотез относительно средних и дисперсий независимых нормальных генеральных совокупностей.
15		Закрепление практических навыков по темам №15 и №16: 1. Оценка достоверности разности средних с помощью Z и t критериев. 2. Проверка гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей с помощью Р- критерия. 3. Проверка гипотезы о согласовании эмпирического закона распределения F*(х) с теоретическим при помощи критерия согласия 2
16		Тема №17. Однофакторный дисперсионный анализ (ОДА).
17		Тема №18. Однофакторные корреляционный (ОКА) и регрессионный (ОРА) анализы.
18		1. Самоподготовка к контрольной работе по темам №№ 15-18. 2. Контрольная работа №5 (по темам №№ 15-18).
19		Итоговое занятие по дисциплине „Высшая математика". 1. Определение итоговой оценки по практическим занятиям дисциплины „Высшая математика" и характеристик на экзамен. 2. Получение допуска к экзамену по дисциплине „Высшая математика".

^ ТЕМАТИЧЕСКИЙ И КАЛЕНДАРНЫЙ ПЛАНЫ

практических занятий по высшей математике

I курс, I семестр_______/_______ уч. год

(специальность 7.110201 – фармация)

* Все заняття 2-х часовые

Всего часов - 72

№№ зан. п/п	Дата занятия	Вид занятия		^ Темы занятий и их содержание
1		семинар (С)		Введение в дисциплину „Высшая математика" Ознакомление студентов с таким: 1.1. Цель и задача предмета. 1.2. Особенности изучения предмета (виды занятий, методика подготовки к занятиям). 1.3. Виды конечного (на отдельных этапах изучения предмета) и итогового контролей. 2. Тема №1.* Понятие функции. Граница функции. Непрерывные функции. Производная функции. Производные простых функций. Примечание: Номер темы представлен соответственно Методическим указаниям (МУ) к практическим занятиям по высшей математики.
2		практическое(П)		Тема №1. (Приобретение практических навыков).
3		С		Тема №2. Производные сложных функций. Производные высших порядков. Дифференциал функции.
4		П		Тема №2. (Приобретение практических навыков).
5		С		Тема №3. Исследование функций с помощью производных. Построение графиков функций.
6		П		Тема №3. (Приобретение практических навыков).
7		П		1. Самоподготовка к контрольной работе по темам №№ 1-3. 2. Контрольная работа №1. (темы №№ 1-3)
8		С		Тема №4. Функции многих переменных. Частные производные. Полный дифференциал.
9		П		Тема №4. (Приобретение практических навыков).
10		С		Тема №5. Приближенные вычисления и оценка погрешностей косвенных измерений с помощью полного дифференциала.
11		П		Тема №5. (Приобретение практических навыков).
12		П		1. Самоподготовка к контрольной работе по темам №№ 4,5. 2. Контрольная работа №2. (темы №№ 4-5)
13		С		Тема №6+№7. Неопределенный интеграл. Вычисление неопределенного интеграла (непосредственное, заменой переменной и по частям).
14		П		Тема №6+№7. (Приобретение практических навыков).
15		С		Тема №8. Определенный интеграл. Вычисление площади и энергии с помощью определенного интеграла.
16		П	Тема №8. (Приобретение практических навыков).
17		С	Тема №9. Понятие о дифференциальных уравнениях (ДУ). ДУ первого порядка с разделяющимися переменными. Однородные ДУ первого порядка.
18		П	Тема №9. (Приобретение практических навыков).
19		П	Тема №10. 1. Закрепление знаний-умений по темам №№ 6-9 и решений типовых упражнений (см. Приложение в МУ). Самоподготовка к контрольной работе №3. 2. Контрольная работа №3 (по материалам тем №№ 1-9).
20		С	Элементы теории вероятностей и математической статистики. Тема №11. Основные понятия теории вероятностей. Классическое и статистическое определения вероятности. Случайные события и операции над ними. Формулы сложения и умножения вероятностей.
21		С	Тема №12. Формула полной вероятности. Формула Байеса. Дискретные и непрерывные случайные величины и их числовые характеристики. Примеры распределений дискретных случайных величин: биномный, Пуассона.
22		П	Тема №11+№12. (Приобретение практических навыков в применении теорем сложения и умножения вероятностей, формул полной вероятности и Байеса для вычисления вероятности случайных событий; формирование знаний о способах представления закона распределения дискретной случайной величины (ДСВ) и расчетов числовых характеристик ДСВ: М, D, ).
23		С	Тема №13. Непрерывные случайные величины (НСВ) и их числовые характеристики. Примеры распределений непрерывных случайных величин: равномерный, экспонентный и нормальный (Гаусса). Стандартное нормальное (нормированное) распределение.
24		П	Тема №13. Усвоение понятий и знаний о свойствах М, D,  и их вычисление; умений установления связи между произвольным нормальным и стандартным нормальным (нормированным) распределениями; навыков вычисления вероятности значений НСВ с помощью таблиц функции Лапласа.
25		П	1. Самоподготовка к контрольной работе по темам №№ 11-14. 2. Контрольная работа №4 (по темам №№ 11-14).
26		С	Тема №14. Основные понятия математической статистики. Генеральная и выборочная совокупности. Выборочный метод. Представление выборки. Основные понятия о точечных оценках характеристик (ТОХ) случайных величин (толкования, статистическое содержание, требования к ТОХ, применение).
27		С	Тема №15. Статистическая проверка гипотез (общие понятия и терминология).
28		С	Тема №16. Статистическая проверка гипотез относительно средних и дисперсий независимых нормальных генеральных совокупностей.
29		П	Закрепление практических навыков по темам №15 и №16: 1. Оценка достоверности разности средних с помощью Z и t критериев. 2. Проверка гипотезы о равенстве генеральных дисперсий двух нормальных совокупностей с помощью F-критерия. 3. Проверка гипотезы о согласовании эмпирического закона распределения F*(х) с теоретическим при помощи критерию согласия 2.
30		П	Тема №17. Однофакторный дисперсионный анализ (ОДА).
31		С	Тема №18. Однофакторные корреляционный (ОКА) и регрессионный (ОРА) анализы.
32		П	Закрепление знаний и практических навыков по теме №18.
33		П	1. Самоподготовка к контрольной работе по темам №№ 15-18. 2. Контрольная работа №5 (по темам №№ 15-18).
34		С	Самоподготовка по теме: „Элементы теории массового обслуживания".
35		П	Ликвидация академзадолжености по разделу „Математическая статистика".
36		П	Итоговое занятие по дисциплине „Высшая математика". 1. Определение итоговой оценки по практическим занятиям дисциплины „Высшая математика" и характеристик на экзамен. 2. Получение допуска к экзамену по дисциплине „Высшая математика".