Е. Б. Замятина Распределенные системы и алгоритмы Курс лекций

Вид материала

Курс лекций

Содержание Лекция 14. Алгоритмы выбора сайтов Алгоритм смещения S1 обнаружил, что сайт S S3 посылает «ответ» сайту S Выбор с помощью алгоритма для деревьев Алгоритмы выбора для кольцевых архитектур

Подобный материал:

• Века. Вопросы к семинарам и диспутам. Часть вторая е. И. Замятин. Роман-антиутопия, 78.14kb.
• С. В. Лапина Социология Курс лекций, 2085.17kb.
• Е. В. Беляева Этика Курс лекций, 693.52kb.
• С. В. Лапина Культурология Курс лекций, 3263kb.
• О. В. Свидерская Основы энергосбережения Курс лекций, 2953.76kb.
• С. М. Забелов > П. С. Забелов Административное право Курс лекций, 3268.19kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.17kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.24kb.
• Курс лекций для студентов заочного факультета самара, 1339.16kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.

Лекция 14. Алгоритмы выбора сайтов

Во многих распределенных системах один из сайтов играет роль координатора при выполнении распределенного алгоритма. Иногда координатором является сайт, который инициировал выполнение алгоритма. Но не всегда один и тот же сайт на протяжении всего вычисления может оставаться координатором. Можно привести следующие причины смены координатора.

1. Выход из строя оборудования на сайте – координаторе, в связи с чем, этот сайт не может продолжать управлять процессами в распределенной системе.

2. Метод координации, реализованный на сайте, оказался неэффективным.

3. Изменения в интенсивности использования различных сайтов системы, приводящие к тому, что координация из прежнего места становится менее эффективной, чем координация с других сайтов.


В подобных случаях требуется выбор нового координатора. Выбор среди сайтов нужно проводить и тогда, когда должен быть выполнен централизованный алгоритм и не существует заранее известного кандидата на роль инициатора алгоритма. Например, в случае процедуры инициализации системы, которая должна быть выполнена в начале или после сбоя системы. Так как множество активных сайтов может быть неизвестно заранее, то невозможно назначить один сайт раз и навсегда на роль лидера.

Активные (функционирующие в данный момент) сайты должны самоорганизоваться и провести выборы координатора. Для выбора нужна какая-то информация о кандидатах. Для простоты будем считать, что с каждым сайтом связано некоторое число – оценка est (estimate). Выбран должен быть сайт с максимальным (или в отдельных задачах – минимальным) значением оценки.

Максимальное значение нетрудно найти, если все локальные оценки собрать в одном месте. Но сложность заключается в том, что неясно, кто бы мог взять на себя сбор информации, а также зависимость процедуры сбора от архитектуры системы.

Алгоритм смещения

Алгоритм предназначен для динамического выбора координатора на основе локальных оценок сайтов. Предполагается, что каналы связи надежны, а сайты иногда могут прерывать (например, из-за отказов) свое функционирование.

Сайты обмениваются сообщениями с тремя возможными значениями: «выборы», «ответ», «координатор». Сообщение «выборы» посылается для объявления выборов. Сообщение «ответ» посылается в ответ на объявление выборов. Сообщение «координатор» посылается для объявления идентификатора нового координатора.

Алгоритм выборов может начать любой сайт S_i , который определил, что текущий координатор S_C не функционирует (например, если ему слишком долго приходится ожидать сообщения от координатора).

Алгоритм состоит из следующих шагов.

1. Сайт S_i рассылает сообщение «выборы» всем другим сайтам, имеющим большую оценку est(S_j), чем у него. Он ожидает, что они отправят ему сообщения «ответ».

2. Ожидание сайтом S_i ответов длится не более чем время T. Если за это время ответы не получены, то сайт S_i объявляет себя координатором и уведомляет об этом сайты с меньшей оценкой, чем est(S_i) путем отправки им сообщений «координатор». Если же ответы получены, то сайт S_i ожидает еще некоторое ограниченное время прихода сообщения «координатор» (возможно, кто-то из «старших» товарищей возьмет на себя функции координатора). Если он не дождался сообщения «координатор», сайт S_i начинает новые выборы.

3. Если сайт S_i получает сообщение «координатор», то он записывает идентификатор сайта, с которого это сообщение было получено, и в дальнейшем общается с этим сайтом как с координатором.

4. Если сайт S_j получает сообщение «выборы» и намерен участвовать в выборах, то он возвращает сообщение «ответ», после чего начинает новые выборы (напомним, его оценка est(S_j) больше, чем оценка est(S_i) сайта, проводящего сейчас выборы).

5. Если происходит рестарт сайта S_C , то он начинает выборы. В том случае, если его оценка est(S_C) является наивысшей, он объявляет себя координатором и сообщает об этом другим сайтам. Это происходит, несмотря на то, что какой-то сайт в период неработоспособности S_C выиграл выборы и функционирует сейчас как координатор. Происходит смещение «временщика». Поэтому этот алгоритм выбора можно назвать алгоритмом смещения (английское название – the bully algorithm; слово bully имеет значения: задира, забияка, хвастун, хулиган, первоклассный, великолепный).





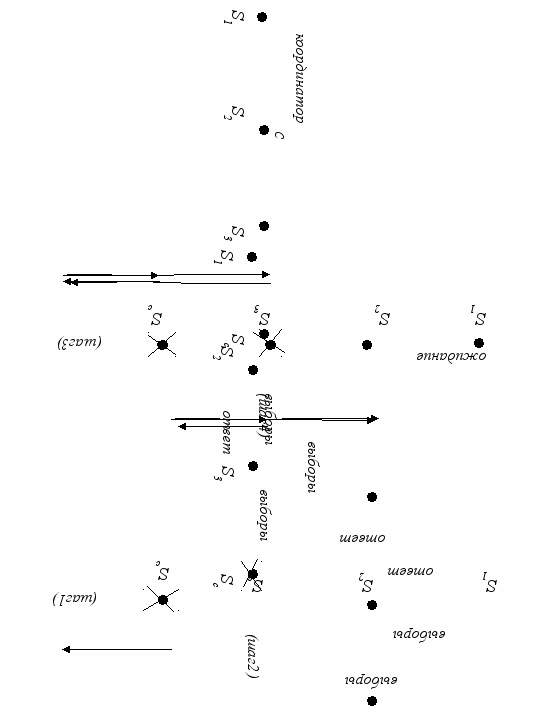
Рис. 29. Пример выполнения алгоритма выбора «смещение»


На рис. 29 изображены четыре шага выполнения алгоритма. Алгоритм начинается с того, что сайт S₁ обнаружил, что сайт S_C не выполняет свои функции координатора. Тогда он объявляет выборы, посылая соответствующие сообщения на сайты S₂ и S₃ . Те посылают сайту S₁ «ответы» (шаг 1) и начинают собственные выборы (шаг 2). На рисунке предполагается, что оценки est сайтов увеличиваются слева направо.

Сайт S₃ посылает «ответ» сайту S₂ , но сам дождаться ответа от S_C не может, так как тот не функционирует. Поэтому S₃ решает взять на себя функции координатора. Но ему не везет: он тоже выходит из строя (шаг 3), не успев послать сообщение «координатор».

Тем временем истекает период ожидания сайтом S₁ окончания выборов. Сообщения «ответ» он получил, а сообщение «координатор» – нет. Тогда он начинает новые выборы, по окончании которых координатором (C) становится сайт S₂ .


Во всех приведенных ниже алгоритмах процесс на сайте p имеет переменную state с возможными значениями coordinator (координатор) и lost (проигравший). Иногда мы будем предполагать, что state имеет значение sleep (спящий), когда p еще не выполнил ни одного шага алгоритма, и значение cand (кандидат), если p вступил в вычисление, но еще не знает, победил он или проиграл. Некоторые алгоритмы используют дополнительные состояния, такие как active, passive и др., которые будут указаны в самом алгоритме.

Важность уникальных идентификаторов в задаче выбора состоит в том, что они могут использоваться не только для адресации сообщений, но и для оценки сайтов. При разработке алгоритма выбора можно, например, потребовать, что сайт с наибольшей (или наоборот, с наименьшей) оценкой должен победить. Тогда задача состоит в поиске идентификатора с наибольшей оценкой с помощью децентрализованного алгоритма. В этом случае задачу выбора называют задачей поиска экстремума.

Выбор с помощью алгоритма для деревьев

Если топология распределенной системы – дерево или доступно остовное дерево системы, выбор можно провести с помощью алгоритма, приведенного в лекции 12. В этом алгоритме требуется, чтобы все концевые вершины были инициаторами алгоритма. Чтобы преобразовать алгоритм на случай, когда некоторые сайты также являются инициаторами, добавляется фаза wake-up. Сайты, которые хотят начать выборы, рассылают сообщение <wakeup> всем другим сайтам.

Когда сайт получит сообщение <wakeup> через каждый канал, он начинает выполнять алгоритм из лекции 12, который расширен таким образом, чтобы вычислять идентификатор сайта с наибольшей оценкой, и чтобы каждый сайт выполнял процедуру return(OK). Когда сайт выполняет эту процедуру, он знает идентификатор координатора; если этот идентификатор совпадает с идентификатором процесса, он становится координатором, а если нет – проигравшим.

В тексте алгоритма логическая переменная sent («отправлено») используется, чтобы каждый сайт послал сообщения <wakeup> не более одного раза, а переменная counter (счетчик) используется для подсчета количества сообщений <wakeup>, полученных сайтом.


var is_sent : boolean init false ;

counter: integer init 0 ;

rec_p[q] : boolean для всех q  Out(this) init false ;

m : integer init this ;

state : (sleep, coordinator, lost) init sleep ;

begin if this - инициатор then

begin is_sent := true ;

forall q  Out(this) do send <wakeup> to q

end ;

while counter < card(Out(this)) do

begin receive <wakeup> ; counter := counter + 1 ;

if not is_sent then

begin is_sent := true ;

forall q  Out(this) do send <wakeup> to q

end

end ;

(* Начало алгоритма из лекции 12 *)

while card{q : rec_p[q]} > 1 do

begin receive (token, r) from q ; rec_p[q] := true ;

if est(r) > est(m) then m := r

end;

send (token, m) to q₀ with rec_p[q₀] ;

receive (token, r) from q₀ ;

if est(r) > est(m) then m := r; (* return(OK) с ответом m *)

if m = this then state := coordinator else state := lost ;

forall q  Out(this), q  q₀ do send (token, m) to q

end


Когда хотя бы один сайт инициирует выполнение алгоритма, все сайты посылают сообщения <wakeup> всем своим соседям, и каждый сайт начинает выполнение алгоритма для дерева после получения сообщения <wakeup> от каждого соседа. Все процессы завершают алгоритм для дерева с одним и тем же значением оценки, а именно, с наибольшей оценкой сайта. Единственный сайт с такой оценкой закончит выполнение в состоянии координатор, а все остальные сайты – в состоянии проигравший.

Через каждый канал пересылается по два сообщения <wakeup> и по два сообщения <tok,r>, откуда сложность сообщений равна 4N–4. В течение D единиц времени после того, как первый процесс начал алгоритм, каждый процесс послал сообщения <wakeup>, следовательно, в течение D+1 единиц времени каждый процесс начал волну. Легко заметить, что первое решение принимается не позднее, чем через D единиц времени после начала волны, а последнее решение принимается не позднее D единиц времени после первого, откуда полное время равно 3D+1.

Если порядок сообщений в канале может быть изменен (т.е. канал – не FIFO), процесс может получить сообщение (token, r) от соседа прежде чем он получил сообщение <wakeup> от этого соседа. В этом случае сообщение (token, r) может быть временно сохранено или обработано как сообщения (token, r), прибывающие позднее.

Алгоритмы выбора для кольцевых архитектур

В алгоритме Лелана для распределенной системы с архитектурой кольца (ориентированного цикла) каждый инициатор вычисляет список идентификаторов всех инициаторов, после чего выбирается инициатор с наибольшей оценкой est(). Каждый инициатор посылает маркер, содержащий его идентификатор, по кольцу, и этот маркер передается всеми сайтами. Предполагается, что каналы подчиняются дисциплине FIFO, и что инициатор должен сгенерировать свой маркер до того, как он получит маркер другого инициатора (когда сайт получает маркер, он после этого не инициирует алгоритм).

Когда инициатор p получает свой собственный маркер, маркеры всех инициаторов прошли через p, и p выбирается лишь в том случае, если p имеет наибольшую оценку среди инициаторов. Напоминаем, что нужно различать внешнее и внутреннее обозначения сайтов. Здесь p и q – внешние обозначения. Они используются при необходимости процессами, выполняющимися на других сайтах. Собственный сайт p в своем процессе обозначается идентификатором this. При этом, разумеется, p и this имеют одно и то же значение (например, числовое или код). В приведенном ниже алгоритме переменная state задает состояние сайта.

Алгоритм Лелана:


var List_p : set of integer init {est(this)} ;

state: (sleep, coordinator, lost);

begin if this - инициатор then

begin state := cand ; send (token, this) to Next_p ; receive (token, q) ;

while q  this do

begin List_p := List_p  {q} ;

send (token, q) to Next_p ; receive (token, q) ;

end ;

if this = max (List_p) then state := coordinator

else state := lost

end

else repeat receive (token, q) ; send (token, q) to Next_p ;

if state = sleep then state := lost

until false

end


Так как порядок маркеров в кольце сохраняется (из предположения о каналах FIFO), и инициатор q отправляет (token, q) до того как получит (token, p), то инициатор p получает (token, q) прежде, чем вернется (token, p). Отсюда следует, что каждый инициатор p заканчивается со списком List_p, совпадающим с множеством всех инициаторов, и единственным выбираемым сайтом становится инициатор с наибольшей оценкой.

Все не-инициаторы приходят в состояние проигравший, но навсегда остаются в ожидании сообщений (token, r). Ожидание может быть прервано, если лидер посылает по кольцу специальный маркер, чтобы объявить об окончании выборов.

Алгоритм Чанга-Робертса, приведенный ниже, устраняет из кольца маркеры тех сайтов, для которых очевидно, что они проиграют выборы. В этом смысле он улучшает алгоритм Лелана. Т.е. инициатор p удаляет из кольца маркер (token, q), если est(q) < est(p). Инициатор p становится проигравшим, когда получает маркер с идентификатором q, таким что est(q) > est(p), или координатором, когда он получает маркер с идентификатором p.


var state : (sleep, coordinator, lost);

begin if this - инициатор then

begin state := cand ; send (token, this) to Next_p ;

repeat receive (token, q) ;

if q = this then state := coordinator

else if est(this) < est(q) then

begin if state = cand then state := lost ;

send (token, q) to Next_p

end

until state = coordinator

end

else repeat receive (token, q) ; send (token, q) to Next_p ;

if state = sleep then state := lost

until false

end (* Только координатор может завершить выполнение программы. Он передает сообщение всем сайтам, чтобы сообщить им свой идентификатор. *)


Пусть p₀ – инициатор с наибольшим идентификатором. Все процессы являются либо не-инициаторами, либо инициаторами с идентификаторами меньшими p₀, поэтому все процессы передают дальше маркер (token, p₀), отправленный p₀. Следовательно, p₀ получает свой маркер обратно и становится выбранным.

Не-инициаторы не могут быть выбраны, так как все они приходят в состояние проигравший самое позднее, когда через них передается маркер p₀. Инициатор p с оценкой est(p) < est(p₀) не может быть выбран; p₀ не передаст дальше маркер (token, p), поэтому p никогда не получит свой собственный маркер. Такой инициатор p приходит в состояние проигравший самое позднее, когда через него передается маркер (token, p₀).




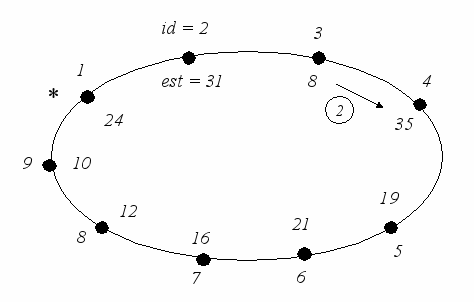
Рис. 30. Иллюстрация к алгоритму Чанга-Робертса


На рис. 30 изображен некоторый момент выполнения алгоритма Чанга-Робертса. На кольце расположены сайты. На внешней стороне кольца указаны их идентификаторы, на внутренней – величины оценок, на основе которых производится выбор координатора. Кружок с числом 2 – маркер (token, 2), переносящий номер сайта, для которого оценка имеет значение «31», стрелка указывает направление движения маркера. Начальный сайт при выполнении алгоритма указан звездочкой – это сайт 1 с оценкой est(1) = 24.