Е. Б. Замятина Распределенные системы и алгоритмы Курс лекций

Вид материала

Курс лекций

Содержание Лекция 12. Волновые алгоритмы распространения информации Волновой алгоритм - это распределенный алгоритм, который удовлетворяет следующим трем требованиям Алгоритм для кольцевой архитектуры Алгоритм для структуры – дерева Алгоритм голосования Алгоритм «Эхо» R все вершины, смежные с вершиной start, затем смежные со смежными и так далее. В описанном ниже методе Expand(R R): begin if Out(R) Алгоритм Финна Распространение информации с обратной связью M (одно и то же для всех процессов), которое должно быть распространено, т.е. все процессы должны принять M A – волновой алгоритм. Чтобы преобразовать A X, ) – частичный порядок, то c

Подобный материал:

• Века. Вопросы к семинарам и диспутам. Часть вторая е. И. Замятин. Роман-антиутопия, 78.14kb.
• С. В. Лапина Социология Курс лекций, 2085.17kb.
• Е. В. Беляева Этика Курс лекций, 693.52kb.
• С. В. Лапина Культурология Курс лекций, 3263kb.
• О. В. Свидерская Основы энергосбережения Курс лекций, 2953.76kb.
• С. М. Забелов > П. С. Забелов Административное право Курс лекций, 3268.19kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.17kb.
• И. М. Вашко Организация и охрана труда Курс лекций, 2301.24kb.
• Курс лекций для студентов заочного факультета самара, 1339.16kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.

Лекция 12. Волновые алгоритмы распространения информации

Многие задачи в распределенных системах решаются путем пересылки сообщений согласно некоторой схемы, которая гарантирует участие всех сайтов. Эта схема зависит от топологических особенностей системы, т.е. от вида графов, представляющих связи между узлами – сайтами.

Распределенные алгоритмы обычно допускают большой набор возможных трасс вычислений благодаря недетерминированности как в процессах, так и в подсистеме передачи. Трасса вычисления – это набор событий, частично упорядоченных отношением причинно-следственного предшествования. Волновой алгоритм обменивается конечным числом сообщений со всеми сайтами и затем на основе этого выполняет специальную процедуру return(OK).

Волновой алгоритм - это распределенный алгоритм, который удовлетворяет следующим трем требованиям:

1. Конечность. Каждое вычисление содержит конечное число событий.
   
2. Успешное завершение. Каждое вычисление содержит хотя бы одно событие return(OK).
   
3. Зависимость. В каждом вычислении каждому событию вызова процедуры return(OK) предшествует (в смысле причинно-следственной связи) какое-либо событие на каждом сайте.
   

Выполнение волнового алгоритма называется волной. Кроме того, в выполнении алгоритма различаются сайты инициаторы и сайты не-инициаторы. Сайт является инициатором, если он начинает выполнение своего локального алгоритма самопроизвольно, т.е. при выполнении некоторого условия, внутреннего по отношению к процессу. Не-инициатор включается в алгоритм только когда прибывает сообщение и вызывает выполнение локального алгоритма сайта. Начальное событие инициатора – внутреннее событие или событие посылки сообщения, начальное событие не-инициатора – событие получения сообщения.

Обычно при применении волновых алгоритмов в сообщение могут быть включены дополнительные переменные и другая информация. Многие приложения используют одновременное или последовательное распространение нескольких волн; в этом случае в сообщение должна быть включена информация о волне, которой оно принадлежит. Кроме того, процесс может хранить дополнительные переменные для управления волной, или волнами, в которых он в настоящее время активен.

Алгоритм для кольцевой архитектуры

Если сайты распределенной системы соединены однонаправленными каналами связи так, что образуют граф – ориентированный цикл, применим следующий волновой алгоритм.

Суть его в следующем. Один из сайтов – инициатор посылает маркер token своему единственному соседу по выходу (в ориентированном цикле каждый сайт имеет в точности один вход и один выход; выход одного сайта соединен с входом соседнего). Маркер, как правило, не имеет «содержания». Важен лишь факт отсылки маркера или поступления маркера.

Любой сайт (кроме инициатора), получив маркер, тут же отправляет его соседу. Инициатор, получив маркер, завершает процесс. Завершение процесса заключается в том, что сайт не посылает далее маркер, а выполняет некоторую процедуру return(OK) – успешный возврат. Рис. иллюстрирует работу этого алгоритма.





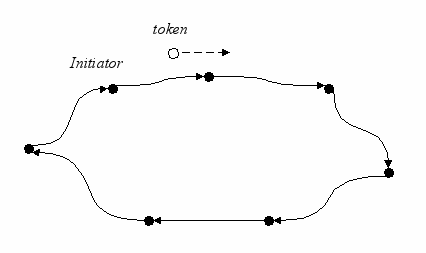
Рис. 22. Перемещение маркера по кольцу


Опишем волновой алгоритм для кольцевой архитектуры, используя языковые средства из лекции 6.

Структура распределенной системы задается формулой

System := dcycle(n)(Node[1..n]).

В системе имеется n сайтов с именами Node[i]. У каждого сайта имеется один входной полюс и один выходной полюс. Выходной полюс сайта Node[i], i  n, соединен каналом связи с входным полюсом сайта Node[i + 1]. Выходной полюс сайта Node[n] соединен с входным полюсом сайта Node[1].

Алгоритм (рутина) узла – инициатора:

routine Initiator

initial

out token;

endi

event;

if message = token then return(OK)

ende

endrout.

Здесь идентификатор message обозначает пришедшее на вход рутины сообщение. Этот идентификатор не описывается, он является системной переменной без определенного типа. Реально пришедшее на вход сообщение, «скрывающееся» за этим идентификатором, тип может иметь (кроме абстрактных сообщений). Поэтому в операциях сравнения сначала сравниваются (динамически) типы левой и правой частей, а при совпадении типов – значения.

Рутины остальных узлов имеют вид:

routine OtherNode

event;

if message = token then out token;

ende

endrout.

Таким образом «волна», начатая инициатором, заканчивается, когда возвращается к инициатору. Описанный распределенный алгоритм выполняется за время O(n).

Алгоритм можно расширить на случай двунаправленного цикла. Каждый узел имеет двух соседей и связи между ними симметричны (ненаправленны). Поэтому, следует ввести понятия «левого» и «правого» соседа. Инициатор направляет маркер только одному, например, правому соседу, и ожидает возвращения маркера слева. Также поступает и любой другой сайт.

Метод можно использовать и еще для более широкого класса архитектур распределенных систем, в которых существует гамильтонов цикл, проходящий через все сайты. Однако формулировка соответствующего алгоритма будет более сложной: для каждого сайта должен быть определен «сосед справа в гамильтоновом цикле».

Алгоритм для структуры – дерева

Предположим, что соединение сайтов распределенной системы каналами образует граф – неориентированное дерево. Из теории графов известны следующие факты для деревьев:

1) дерево – связный ациклический граф;

2) количество вершин в дереве на единицу больше, чем количество ребер;

3) в нетривиальном дереве имеется, по крайней мере, две вершины, степени которых равны единице; эти вершины называются висячими или терминальными; остальные вершины имеют степень, не меньше 2.

В описываемом алгоритме инициаторами являются все висячие вершины (рис. 23). Любой инициатор может передать маркер только одному соседнему сайту. Любой другой сайт v (не инициатор), имеющий степень deg(v), генерирует маркер только в том случае, если получил маркеры от deg(v) – 1 соседа, т.е. от всех смежных сайтов, кроме одного. Тогда сайт v отправляет маркер тому единственному соседу, от которого маркера еще не было (вполне возможно, что этот сосед просто задержался с передачей).

Если задержавшийся сосед все же передаст маркер, т.е. сайт v получит deg(v) маркеров, то сайт v выполнит процедуру return(OK). Выполнение процедуры return(OK) любым из сайтов завершает работу распределенного алгоритма.




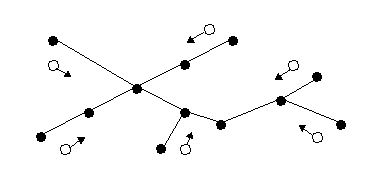
Рис. 23. Шаг 1. Маркеры, инициированные висячими вершинами дерева




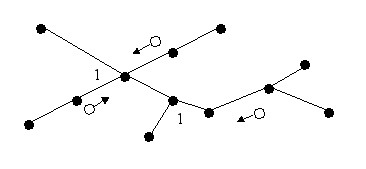
Рис. 24. Шаг 2. Продвижение маркеров по дереву




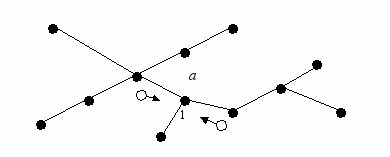
Рис. 25. Шаг 3. Заключительное перемещение маркеров


Описанный алгоритм не столь очевиден, как алгоритм для кольцевой архитектуры. Поэтому нам нужны гарантии его правильности, а именно, гарантии того, что если какой-либо из сайтов выполнил процедуру return(OK), все остальные сайты v_i получили, по крайней мере, по deg(v_i) – 1 маркеров и сгенерировали или готовы сгенерировать выходные маркеры.

Рисунки 23 – 25 иллюстрируют на примере некоторого дерева продвижение маркеров. На шаге 2 вершины, уже получившие маркеры, обозначены соответствующими числами. После выполнения шага 3, вершина, обозначенная «a» и имеющая степень 3, получит последние два маркера. Количество полученных маркеров станет равным трем, и будет выполнена процедура return(OK).

Отметим, что эти рисунки и приведенные выше комментарии к ним справедливы для случая, когда перемещение любого маркера по любому ребру дерева требует одного и того же времени, а генерация маркера происходит мгновенно. Инициаторы также одновременно генерируют свои маркеры.

В противном случае процесс закончится в какой-либо другой (не висячей) вершине дерева. Если же какая-либо из висячих вершин – инициаторов сильно запоздает с генерацией своего маркера, то может возникнуть непредусмотренная ситуация получения маркера висячей вершиной.

Сказанное еще раз подтверждает то, что выполнение распределенного алгоритма не является строго детерминированным во времени, но, тем не менее, при правильном построении алгоритма может быть детерминированным по результатам.

Алгоритм голосования

Алгоритм голосования применяется для распределенных систем, имеющих структуры полных графов. В этом случае инициатором может быть любой сайт. Для графа – звезды его тоже можно использовать, но инициатором должна быть центральная вершина звезды. Могут быть и другие варианты структуры, важно, чтобы от инициатора к любому сайту вел прямой канал связи.

Существо алгоритма заключается в следующем.

Инициатор отправляет по одному маркеру каждому соседнему сайту (по терминологии теории графов – каждой смежной вершине). Каждый сайт, получивший маркер, отправляет его обратно (если у него нет причин этого не делать). Инициатор подсчитывает полученные обратно маркеры и сравнивает их количество с известным ему количеством соседних сайтов. Когда эти числа сравняются (единогласное решение), инициатор выполняет процедуру return(OK).

Легко модифицировать этот алгоритм на случаи голосования по простому большинству, квалифицированному большинству и т.д.

Структура распределенной системы задается формулой

System := compl(n)(Node[1..n](P[1..n – 1])).

Здесь у каждого сайта Node[i] имеется набор полюсов P[1..n – 1]. Эти полюсы связаны каналами передачи данных с соответствующими полюсами остальных сайтов. Таким образом, все каналы изолированы друг от друга. Маркер, передаваемый сайтом Node[i] через полюс P[j], попадет только в один канал и, соответственно, только на один сайт.

Рутина сайта – инициатора:

routine Initiator

initial

integer counter;

counter := 0;

out token;

endi

event;

if message = token then

if (counter = n – 2) then return(OK)

else counter := counter + 1 endi

ende

endrout.

Здесь оператор out token означает передачу маркеров token всем смежным сайтам.

Рутины остальных сайтов имеют вид:

routine OtherNode

event;

case of polus

if message = token then out token through polus endi

endc

ende

endrout.

Здесь оператор case of – оператор распознавания входа. Идентификатор polus обозначает полюс, на который пришло сообщение, подобно тому, как само сообщение «скрывается» за идентификатором message. Оператор out token through polus возвращает маркер token через тот полюс сайта, на который пришел этот маркер, т.е. инициатору алгоритма.

Описанный распределенный алгоритм выполняется за время O(n).

Алгоритм «Эхо»

Алгоритм «Эхо» может работать для любой топологии распределенной системы. Как и предыдущий алгоритм, в нем имеется один инициатор.

Алгоритм использует метод прохода по графу, называемый «поиск (или просмотр графа) в ширину», описанный, в частности, в учебнике Л.Н.Королева, А.И.Микова «Информатика. Введение в компьютерные науки» для поиска множества R достижимых вершин из данной вершины start.

Метод состоит в том, чтобы продвигаться от начальной вершины по ширине всего фронта, включив сначала в множество R все вершины, смежные с вершиной start, затем смежные со смежными и так далее. В описанном ниже методе Expand(R) расширения множества R множество Out(R) – это множество всех вершин, смежных с вершинами из R, так сказать, достижимых за один шаг. В частности, может оказаться, что все они уже принадлежат R и тогда дальнейшее расширение невозможно. На этом процесс прекращается.


Expand( R):

begin

if Out(R)  R then

begin Out(R)  R;

Expand(R)

end

end;


Первый вызов – Expand(Out(start)); Предполагается, что Out() =  ,   .


В алгоритме «Эхо» инициатор посылает маркеры всем своим соседям. Любой сайт s (не инициатор), получивший первый раз маркер от одного из своих соседей (обозначим этого соседа pre), рассылает маркеры всем соседним сайтам, кроме того, от которого получил маркер. Соседи поступают точно так же. Волна удаляется от инициатора.

Дальнейший процесс рассмотрим на примере дерева. Волна доходит до некоторых из висячих вершин. Висячей вершине отправлять маркер дальше некуда. Тогда она возвращает его той вершине, от которой получила (вот оно «эхо»). Вершины, получившие «эхо» от своих соседей, возвращают маркеры своим вершинам pre. Те, в свою очередь, генерируют «эхо» своим предшественникам. Наконец «эхо» доходит до инициатора. Инициатор, получив «эхо» от всех своих соседей, выполняет процедуру return(OK).

Ниже приведен распределенный алгоритм, состоящий из описаний процесса вычислений для сайта – инициатора и описаний процессов для сайтов – не-нициаторов. В тексте описания процесса тот сайт, на котором этот процесс выполняется (свой сайт), обозначен идентификатором this (в традициях языка Симула-67). Множество Out(this) – это множество сайтов, смежных по выходу с сайтом this, т.е. тех сайтов, на которые с сайта this можно отправить сообщения по однонаправленным или двунаправленным каналам связи. Функция card( ) задает число кардинальности (мощность) множества, являющегося аргументом этой функции. Переменные, встречающиеся в текстах процессов – локальные (по экземпляру для каждого процесса): обмен информацией между процессами происходит только посредством сообщений, разделяемые переменные отсутствуют. Начальные значения счетчиков counter равны 0.


Процесс для инициатора:

begin for u  Out(this) do out token to u ;

while counter < card(Out(this)) do

begin receive token; counter := counter + 1 end ;

return(OK)

end ;


Процессы для не-инициаторов:

begin receive token from u ; pre(this) := u ; counter := counter + 1 ;

for (u  Out(this))&(u  pre(this)) do out token to u ;

while counter < card(Out(this)) do

begin receive token; counter := counter + 1 end ;

out token to pre(this)

end


Фазовый алгоритм

Фазовый алгоритм является децентрализованным алгоритмом для произвольных ориентированных графов. Двунаправленные связи тоже могут присутствовать, но они должны быть заданы парой параллельных встречных однонаправленных каналов (дуг графа). Алгоритм требует, чтобы процессам на сайтах был известен диаметр d графа, либо его оценка сверху.

Переменные в тексте алгоритма имеют следующий смысл.

counter_out – счетчик, подсчитывающий количество маркеров token, посланных каждому из соседей по выходу. Если таких соседей у некоторого сайта, например, три, то за каждой единицей счетчика стоит три посланных маркера – по одному на каждого соседа.

counter_in – массив счетчиков, по одному счетчику на каждого соседа по входу. Хранит количество маркеров, посланных соседями.

this – сайт, процесс которого исполняет данный алгоритм.

Out() – множество вершин, смежных по выходу.

u – некоторый сайт, передавший маркер.

Функция min, примененная к массиву, выбирает из него минимальный элемент.


var counter_in: array [0..d] of integer init 0;

counter_out: integer init 0 ;


begin if this - инициатор then

begin for r  Out(this) do out token to r ;

counter_out := counter_out + 1

end;

while min(counter_in) < d do

begin receive token from u ;

counter_in [u] := counter_in [u] + 1 ;

if (min(counter_in)  counter_out) & (counter_out < d) then

begin for r  Out(this) do out token to r ;

counter_out := counter_out + 1

end

end ;

return(OK)

end


Алгоритм может использоваться в ориентированных сетях произвольной топологии, где каналы могут передавать сообщения только в одном направлении. В этом случае, соседи s являются соседями по входу (процессы, которые могут посылать сообщения s) и соседями по выходу (процессы, которым s может посылать сообщения).

В фазовом алгоритме каждый процесс посылает ровно d сообщений каждому соседу по выходу. Только после того, как k сообщений было получено от каждого соседа по входу, (k + 1)-ое сообщение посылается каждому соседу по выходу.

Алгоритм Финна

Алгоритм Финна – еще один волновой алгоритм, который можно использовать в ориентированных сетях произвольной топологии. Он не требует того, чтобы диаметр сети был известен заранее, но подразумевает наличие уникальных идентификаторов процессов. В сообщениях передаются множества идентификаторов процессов, что приводит к довольно высокой битовой сложности алгоритма.

Процесс сайта s содержит два множества идентификаторов процессов, Inc(s) и NInc(s). Неформально говоря, Inc(s) – это множество процессов u таких, что событие в u предшествует последнему произошедшему событию в s, а NInc(s) – множество процессов u таких, что для всех соседей r процесса u событие в r предшествует последнему произошедшему событию в s. Эта зависимость поддерживается следующим образом.

Изначально Inc(s) = {s}, а NInc(s) = . Каждый раз, когда одно из множеств пополняется, процесс s посылает сообщение, включая в него Inc(s) и NInc(s). Когда s получает сообщение, включающее множества Inc(s) и NInc(s), полученные идентификаторы включаются в версии этих множеств в процессе s. Когда s получит сообщения от всех соседей по входу, s включается в NInc(s). Когда два множества становятся равны, s выполняет процедуру return(OK). Из неформального смысла двух множеств следует, что для каждого процесса u такого, что событие в u предшествует некоторому событию e, выполняется следующее: для каждого соседа r процесса u событие в r также предшествует событию e.

При разработке распределенных алгоритмов для различных приложений часто в качестве подзадач возникает несколько общих проблем для сетей процессов. Эти элементарные задачи включают в себя широковещательную рассылку информации – broadcasting (например, посылка начального или заключительного сообщения), достижение глобальной синхронизации между процессами, запуск выполнения некоторого события в каждом процессе, или вычисление функции, входные данные которой распределены между процессами.

Распространение информации с обратной связью

Важным применением волновых алгоритмов является случай, когда некоторая информация должна быть передана всем процессам и определенные процессы должны быть оповещены о завершении передачи. Эта задача распространения информации с обратной связью (PIF – propagation of information with feedback) формулируется следующим образом.

Формируется подмножество процессов из тех, кому известно сообщение M (одно и то же для всех процессов), которое должно быть распространено, т.е. все процессы должны принять M. Определенные процессы должны быть оповещены о завершении передачи; т.е. должно быть выполнено специальное событие notify, причем оно может быть выполнено только когда все процессы уже получили сообщение M. Алгоритм должен использовать конечное количество сообщений.

Оповещение в PIF-алгоритме можно рассматривать как событие return(OK).

Любой волновой алгоритм может использоваться как PIF-алгоритм. Действительно, пусть A – волновой алгоритм. Чтобы использовать A как PIF-алгоритм, возьмем в качестве процессов, изначально знающих M, инициаторы A. Информация M добавляется к каждому сообщению A. Это возможно, поскольку по построению стартеры A знают M изначально, а последователи не посылают сообщений, пока не получат хотя бы одно сообщение, т.е. пока не получат M. Событию return(OK) в волне предшествуют события в каждом процессе; следовательно, когда оно происходит, каждый процесс знает M, и событие return(OK) можно считать требуемым событием notify в PIF-алгоритме.

Синхронизация

Волновые алгоритмы могут использоваться для случаев, когда должна быть достигнута глобальная синхронизация процессов. Задача синхронизации формулируется следующим образом. В каждом процессе q должно быть выполнено событие a_q , и в некоторых процессах должны быть выполнены события b_p , причем все события a_q должны быть выполнены по времени раньше, чем будет выполнено какое-либо событие b_p . Алгоритм должен использовать конечное количество сообщений.

В алгоритмах синхронизации события b_p будут рассматриваться как события return(OK).

Любой волновой алгоритм может использоваться как алгоритм синхронизации. Действительно, пусть A – волновой алгоритм. Чтобы преобразовать A в алгоритм синхронизации, потребуем, чтобы каждый процесс q выполнял a_q до того, как q пошлет сообщение в A или примет решение в A. Событие b_p происходит после события return(OK) в p.

Вычисление нижней грани

Продемонстрируем применение волновых алгоритмов для вычисления функций, значения которых зависят от входов процесса на каждом сайте. В качестве представителей таких функций будут рассмотрены алгоритмы, вычисляющие нижнюю грань по всем входам, которые должны быть извлечены из частично упорядоченного множества.

Как известно из курса математики, если ( X, ) – частичный порядок, то c называют нижней гранью a и b, если c  a, c  b, и  d : ( d  a & d  b  d  c). Допустим, что X таково, что нижняя грань всегда существует; в этом случае нижняя грань является единственной и обозначается как a  b. Так как  – бинарный оператор, коммутативный и ассоциативный, то операция может быть обобщена на конечные множества: inf { a₁, ..., a_k} = a₁  ...  a_k .

Задача вычисления нижней грани в распределенной системе формулируется следующим образом. Каждый процесс на сайте q содержит вход a_q , являющийся элементом частично упорядоченного множества X. Потребуем, чтобы определенные процессы вычисляли значение inf {a_q } по всем сайтам и чтобы эти процессы знали, когда вычисление завершается. Они записывают результат вычисления в переменную out и после этого не могут изменять ее значение.

Событие write, которое заносит значение в out, рассматривается в алгоритме вычисления нижней грани как событие return(OK).

Любой волновой алгоритм может быть использован для вычисления нижней грани.

Это можно показать следующим образом. Допустим, что дан волновой алгоритм A. Назначим каждому процессу q дополнительную переменную v_q , которой придадим начальное значение a_q . Во время волны эти переменные переприсваиваются следующим образом. Всякий раз, когда процесс q посылает сообщение, текущее значение v_q включается в сообщение. Всякий раз, когда процесс q получает сообщение со значением v, переменной v_q присваивается значение v_q  v. Когда в процессе p происходит событие return(OK), текущее значение v_p заносится в out_p.

Теперь нужно показать, что в результат заносится правильное значение. Обозначим правильный ответ через L, т.е. L = inf {a_q}. Для события a в процессе q обозначим через v^(a) значение v_q сразу после выполнения a. Так как начальное значение v_q равно a_q , и в течение волны оно только уменьшается, неравенство v^(a)  a_q сохраняется для каждого события a в q. Из присваивания v следует, что для событий a и b, a  b  v^(a)  v^(b). Кроме того, так как v всегда вычисляется как нижняя грань двух уже существующих величин, неравенство L  v выполняется для всех величин в течение волны. Таким образом, если d – событие return(OK) в p, значение v^(d) удовлетворяет неравенству L  v^(d) и, так как событию d предшествует хотя бы одно событие в каждом процессе q, v^(d)  a_q для всех q. Отсюда следует, что L = v^(d).

Известна теорема о нижней грани: Если  – бинарный оператор на множестве X, причем он:

1. коммутативен, т.е. a  b = b  a,
   
2. ассоциативен, т.е. (a  b)  c = a  (b  c),
   
3. идемпотентен, т.е. a  a = a,
   

то существует отношение частичного порядка  на X такое, что  – функция нижней грани.

Среди операторов, удовлетворяющих этим трем критериям – логическая конъюнкция и дизъюнкция, минимум и максимум целых чисел, наибольший общий делитель и наименьшее общее кратное целых чисел, пересечение и объединение множеств. Отсюда следует, что операции &, , min, max, НОД, НОК,  и  над величинами, локальными по отношению к сайтам, могут быть вычислены за одну волну.