Украина. Министерство образования и науки автономной республики крым крымское республиканское высшее учебное заведение
| Вид материала | Лекции |
СодержаниеВариация альтернативного признака Меры вариации Размах вариации Среднее линейное отклонение Группы пр-тий по объему товарооборота, тыс.грн. Моментные ряды динамики Наименование показателей |
- Украина. Министерство образования и науки автономной республики крым крымское республиканское, 793.81kb.
- Автономной Республики Крым Крымское республиканское высшее учебное заведение «Феодосийский, 80.78kb.
- Автономной Республики Крым Крымское Республиканское высшее учебное заведение «Феодосийский, 196.04kb.
- Автономной Республики Крым Крымское республиканское высшее учебное заведение «Феодосийский, 130.23kb.
- Автономной Республики Крым Крымское республиканское внешкольное учебное заведение «Центр, 323.55kb.
- Автономной Республики Крым профессиональное училище сервиса и дизайна» В. А. Дзоз, 68.84kb.
- Украина Автономная Республика Крым Министерство образования и науки, молодежи и спорта, 77.93kb.
- Украина Автономная Республика Крым Министерство образования и науки, молодежи и спорта, 46.62kb.
- Внедрение облачных вычислений как метод предотвращения ddoS-атак, 54.83kb.
- Автономной Республике Крым в 2012 году крымской акции «Успех года» Всоответствии, 189.22kb.
M o = 20 + 9 * 20,1 – 4,9 / (20,1 – 4,9) + ( 20,1 – 15,5) = 26 лет 9 месяцев
Ме = 40 + 9 * 100/2 – 40,5 / 15,2 = 45 лет 6 месяцев
Л.1с. 85…94
Л. 6 Показатели вариации
Вариацией называют изменение признака у единиц совокупности.
Вариация наряду с применением средних и относительных величин имеет большое практическое значение.
Вариация альтернативного признака выражается в том, что одни единицы обладают данным признаком, а др. нет.
Например: одни изделия являются годными, а другие нет.
Меры вариации
Показатели вариации относятся к числу обобщающих показателей. В статистике чаще всего применяются следующие показатели вариации:
- размах вариации (R)
- среднее линейное отклонение (
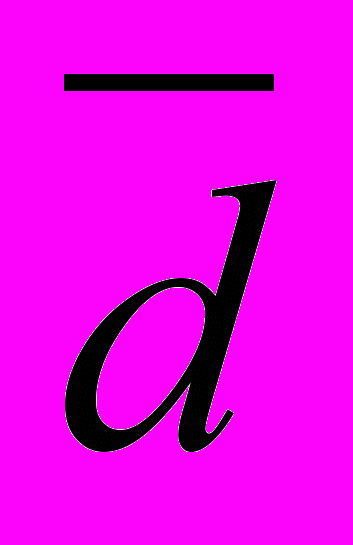 )
)- Дисперсия (δ2)
- среднее квадратическое отклонение (δ)
Размах вариации – это разность между max и min значениями признака
R = Rmax – Rmin
Размах вариации характеризует пределы изменения варьирующего признака. Легкость расчета размаха вариации приводит к тому, что он нередко используется в экономике.
Индивидуальное значение признака отклоняется от средней в ту или иную сторону.
Среднее линейное отклонение = средней арифметической из абсолютных отклонений (модулей) значений признака всех единиц от средней арифметической:
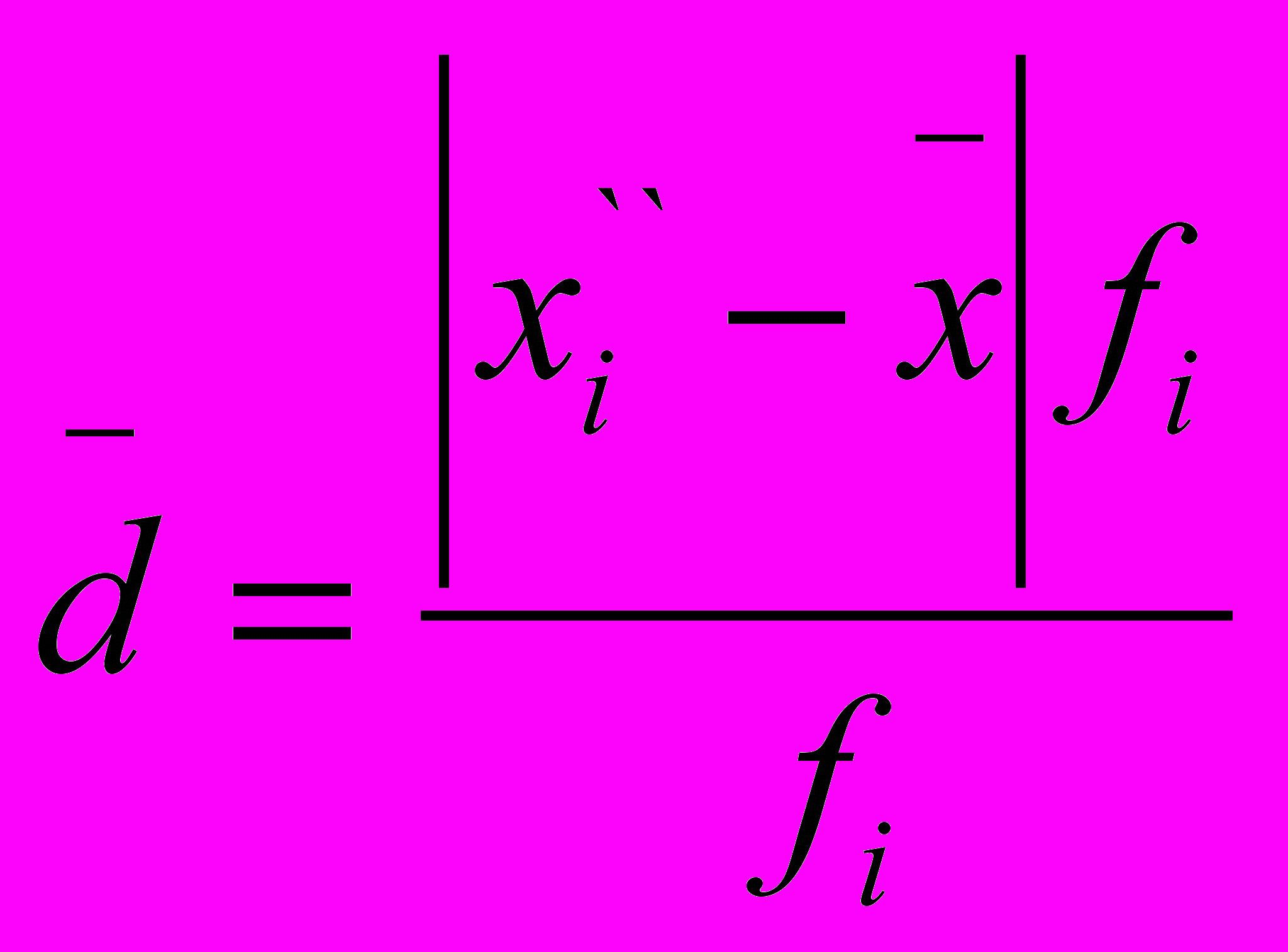
В статистике широко используется показатель вариации называемый дисперсией.
Дисперсия – средний квадрат отклонений индивидуальных значений признака от средней арифметической:
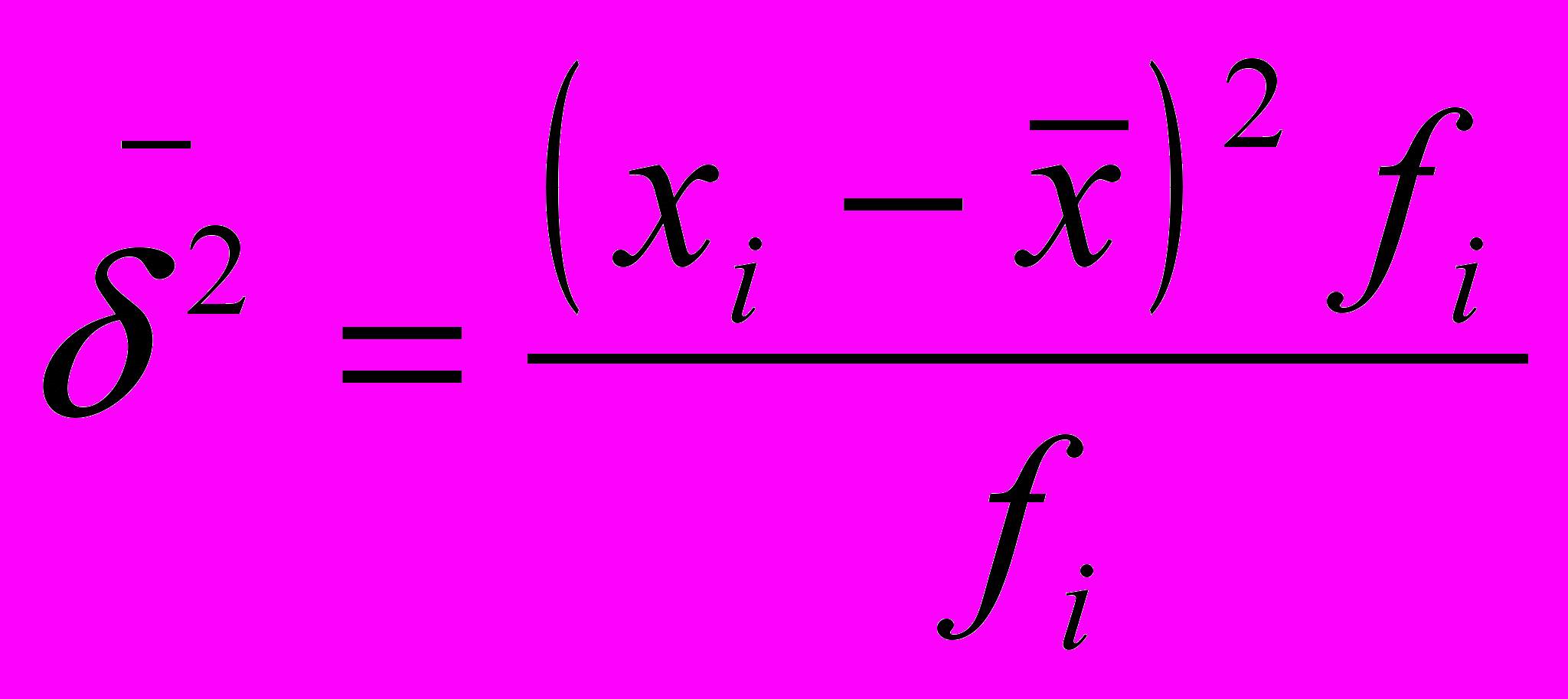
Корень квадратный из дисперсии среднего квадрата отклонений представляет собой среднее квадратическое отклонение:
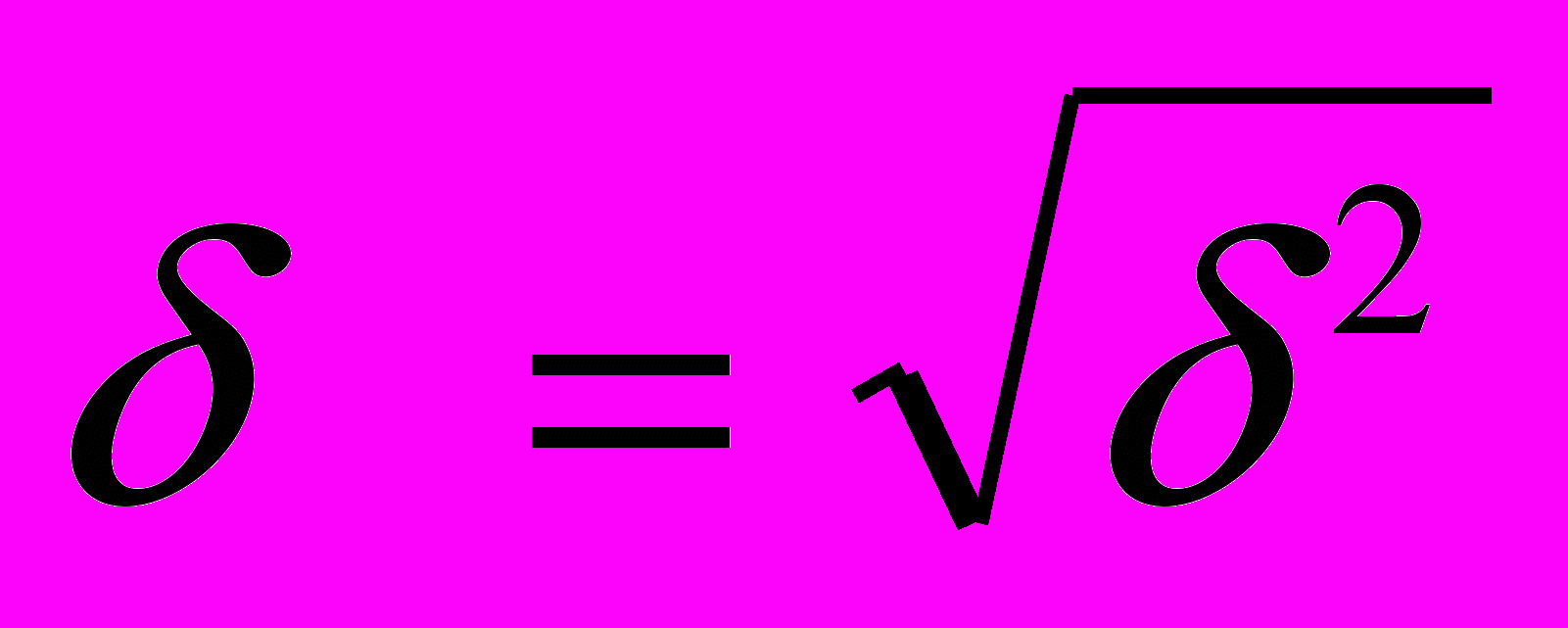
Пример.
| Группы пр-тий по объему товарооборота, тыс.грн. | Число пр-тий fi | Центр. значение xi | xi fi | xi - 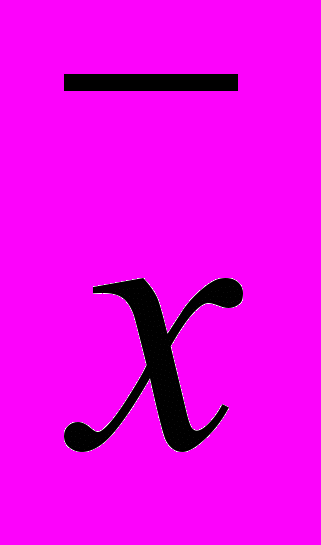 | x /i – x fi | (x/i - 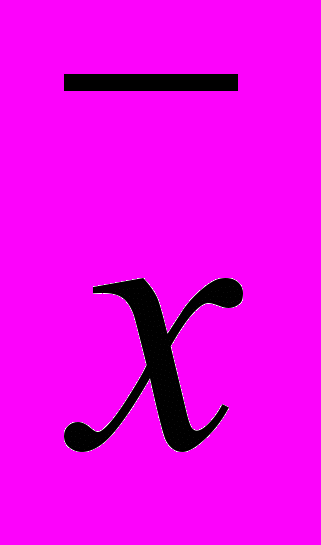 )2 )2 | (x/i - 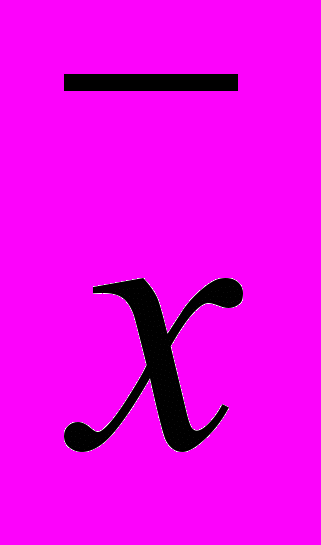 )2 fi )2 fi |
| 90-100 | 28 | 95 | 2660 | 10 | 280 | 100 | 2800 |
| 100-110 | 48 | 105 | 5040 | 0 | 0 | 0 | 0 |
| 110-120 | 20 | 115 | 2300 | 10 | 200 | 100 | 2000 |
| 120-130 | 4 | 125 | 500 | 20 | 80 | 400 | 1600 |
| Итого | 100 | | 10500 | | 560 | | 6400 |
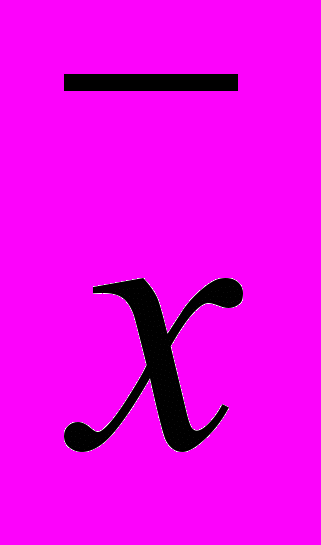 = x /i fi / Σ fi = 10500 / 100 = 105
= x /i fi / Σ fi = 10500 / 100 = 105Среднее отклонение
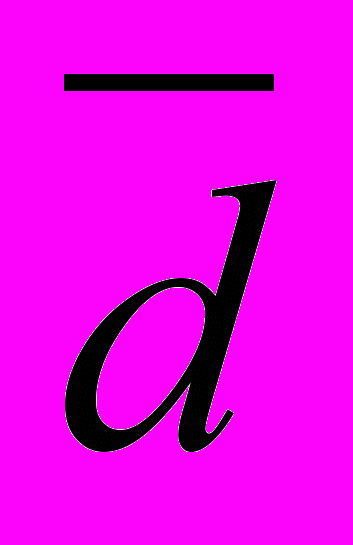 = 560 /100 = 5,6
= 560 /100 = 5,6Дисперсия δ2 = 6400 / 100 = 64
δ =
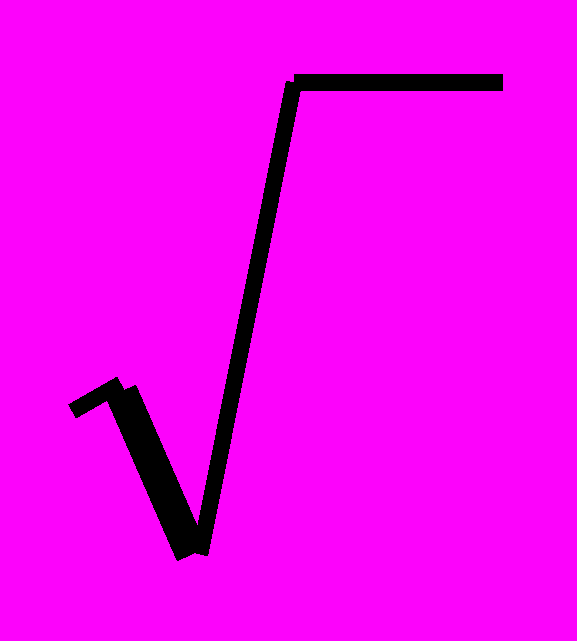 64 = 8 тыс. грн.
64 = 8 тыс. грн.Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой изучаемое явление.
Л.1с. 101…117
Л. 6. Ряды динамики
Рядами динамики называются стат. данные, отображающие развитие изучаемого явления во времени.
Ряды динамики подразделяются на:
- моментные и интервальные;
- полные и неполные;
- ряды абсолютных, относительных и средних величин.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Их особенностью является то, что в их уровни могут входить одни и те же единицы изучаемой совокупности. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет:
Таблица 1
| Дата | На 01.01.03 | На 01.04.03 | На 01.07.03 | На 01.10.03 | На 01.01.04 |
| Число работников, чел. | 100 | 150 | 120 | 130 | 125 |
Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени.
Их особенностью является то, что каждый их уровень складывается из данных за более короткие интервалы времени.Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупненных периодов.
Таблица 2
| Год | 1998 | 2000 | 2001 | 2002 | 2003 |
| Объем товарооборота, тыс. грн. | 10,2 | 15,0 | 17,3 | 18 | 20,4 |
В полных рядах динамики даты (периоды) следуют друг за другом с равными интервалами (таблица 1).
В не полных рядах динамики равный интервал не соблюдается (таблица 2).
По форме представления уровней ряды динамики делятся на:
- ряды абсолютных величин ( кг, шт, грн.);
- ряды относительных величин (%);
- ряды средних величин (грн/чел, грн/ед).
Для расчета показателей динамики на постоянной базе каждый последующий уровень (уi) ряда сравнивается с одним и тем же базисным уровнем (у о ) и называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень (уi) ряда сравнивается с предыдущим (уi-1) и называются цепными.
Для количественной оценки динамики соц-экономических явлений применяются показатели:
- абсолютные приросты (∆ )
- коэффициент роста (Кр)
- темпы роста (Тр)
- коэффициент прироста (Кпр)
- темпы прироста (Тпр).
| Наименование показателей | Базисный | Цепной |
| Абсолютный прирост,∆ | ∆ б = уi - yo | ∆ ц = yi - yi -1 |
| Коэффициент роста, Кр | Крб = yi / yo | Kpц = yi / yi - 1 |
| Темп роста, Тр | 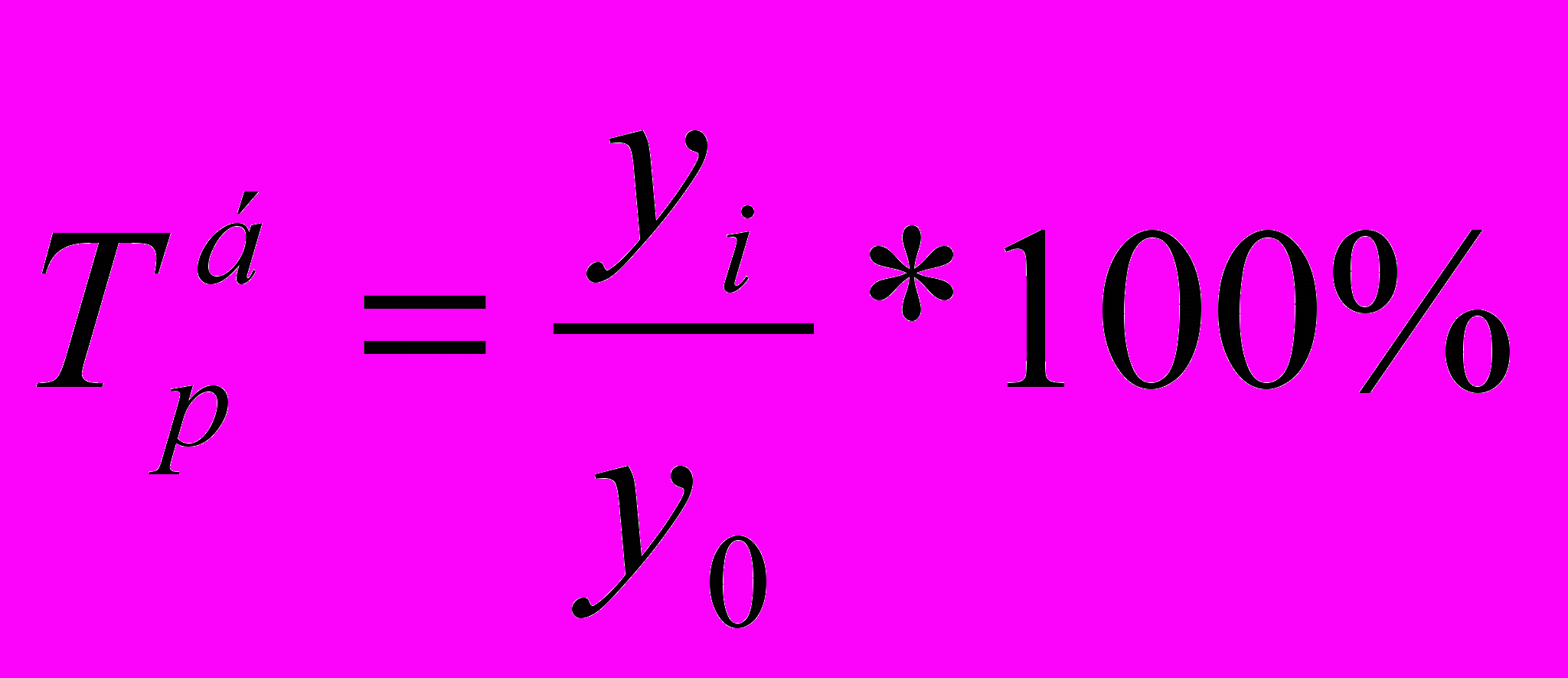 Трб = Крб * 100% | 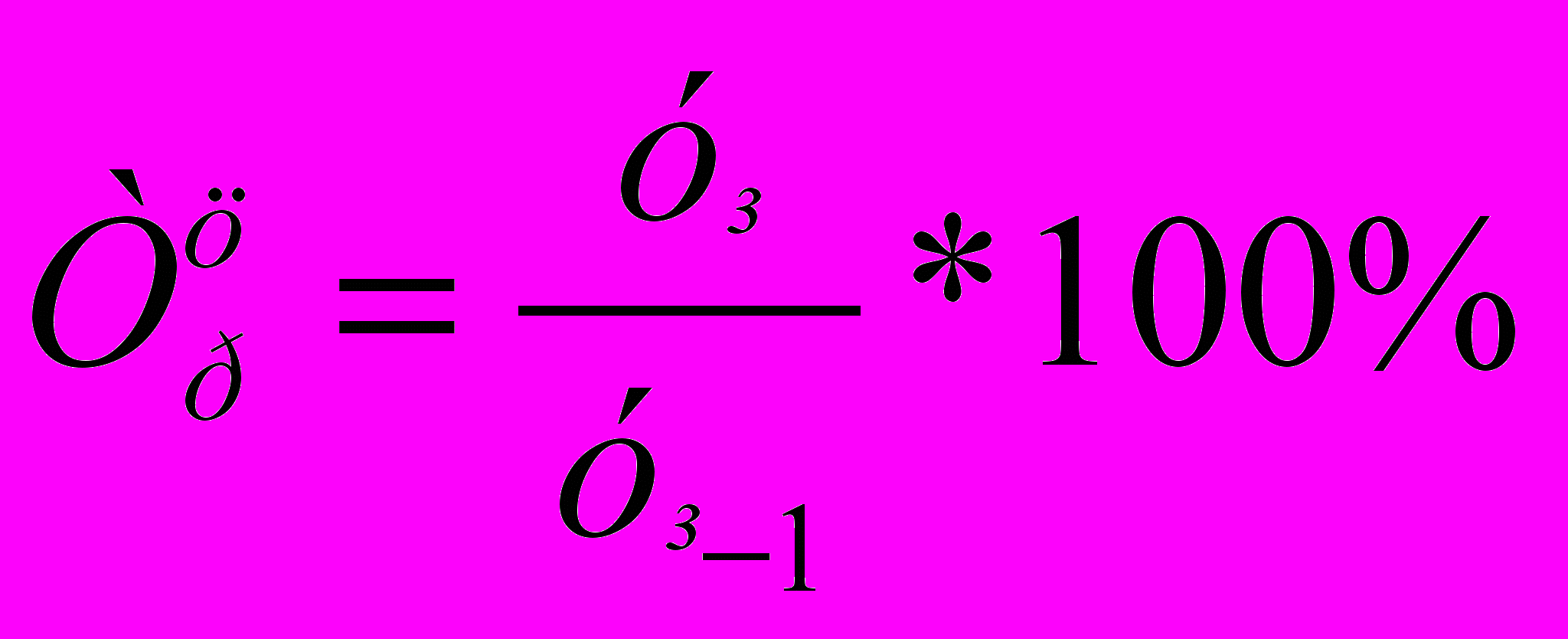 Трц = Крц * 100% |
| Коэффициент прироста, Кпр | Кпрб = Крб -1 | Кпрц = Крц - 1 |
| Темп прироста, Тпр | Тпрб = Трб - 100 | Тпрц = Трц - 100 |
| Абс.значение 1% прироста | Аб = y0 / 100 | Ац = yi – 1 / 100 |
Пример:
| Показатель | 2001г. | 2002г. | 2003г. | 2004г. |
| Товарооборот, тыс.грн. | 885,7 | 932,6 | 980,1 | 1028,7 |
| Абс.прирост, тыс.грн. ∆б = yi – y0 ∆ц = yi – yi - 1 | - - | ∆б = 932,6 -885,7=46,9 ∆ц = 46,9 | ∆б =980,1-885,7=94,4 ∆ц = 47,5 | ∆б = 143 ∆ц = 48,6 |
| Коэфф.роста Крб =yi / y0 Крц = yi / yi - 1 | - - | Крб = 1,053 Крц = 1,053 | Крб = 1,106 Крц = 1,051 | Крб = 1,161 Крц = 1,049 |
| Темп роста Трб = Крб * 100 Трц = Крц * 100 | - - | Трб = 105,3% Трц = 105,3% | 110,6% 105,1% | 116,1% 104,9% |
| Коэфф.прироста Кпрб = Крб -1 Кпрц = Крц - 1 | - - | 0,053 0,053 | 0,106 0,051 | 0,161 0,049 |
| Темп прироста Тпрб = Трб – 100 Тпрц = Трц - 100 | - - | 5,3 5,3 | 10,6 5,1 | 16,1 4,9 |
| Абс.значение 1% прироста Аб = y0 / 100 Ац = yi – 1 / 100 | - - | 8,86 8,86 | 8,86 9,33 | 8,86 9,80 |
Средний уровень ряда характеризует типическую величину абсолютных уровней.
В интервальных рядах средний уровень у определяется по формуле (таблица 2):
У = Σyi / n = y1 + y2 + y3 +… +yn
У = 10.2 + 15 + 17.3 + 18 + 20.4 / 5 =
В моментном ряду(таблица 1):
У = ½ у1 + у2 + у3 +… + ½yn / n-1
У = ½ 100+150+120+130+ ½ 125 / 5 -1=
Средний абсолютный прирост:
∆у = Σ ∆ уц I / n ;
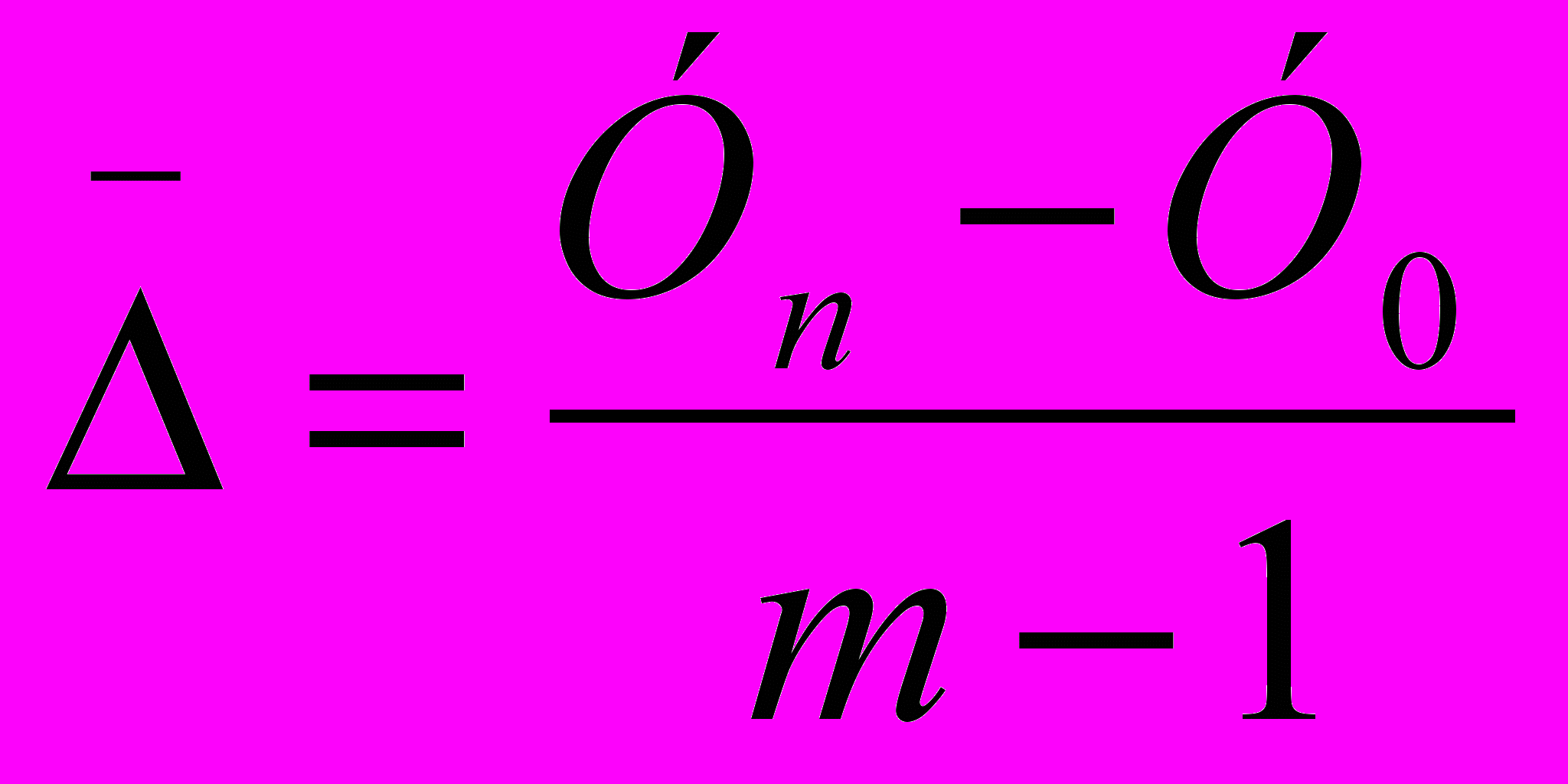
Средний темп роста:
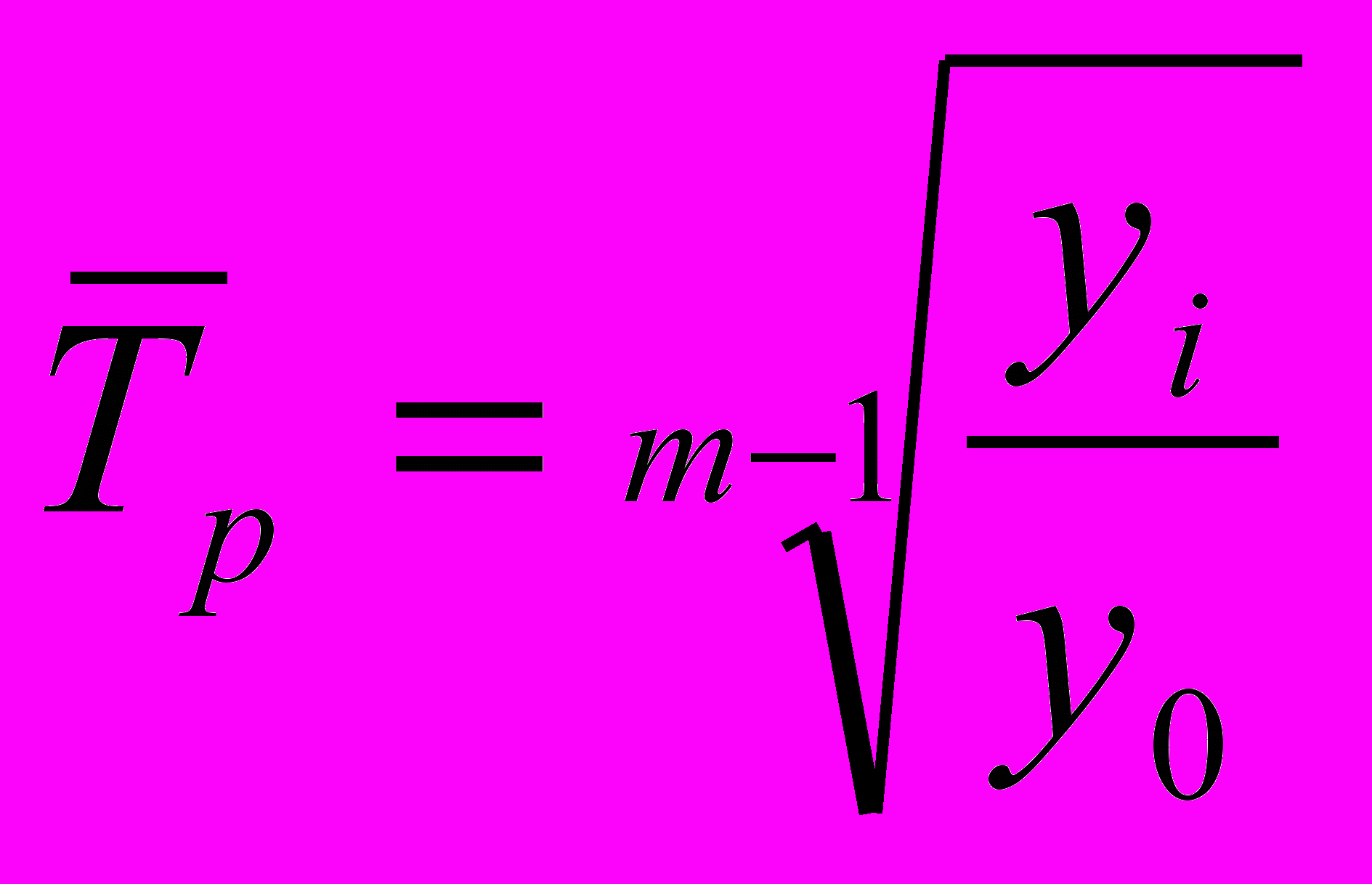
Средний темп прироста:
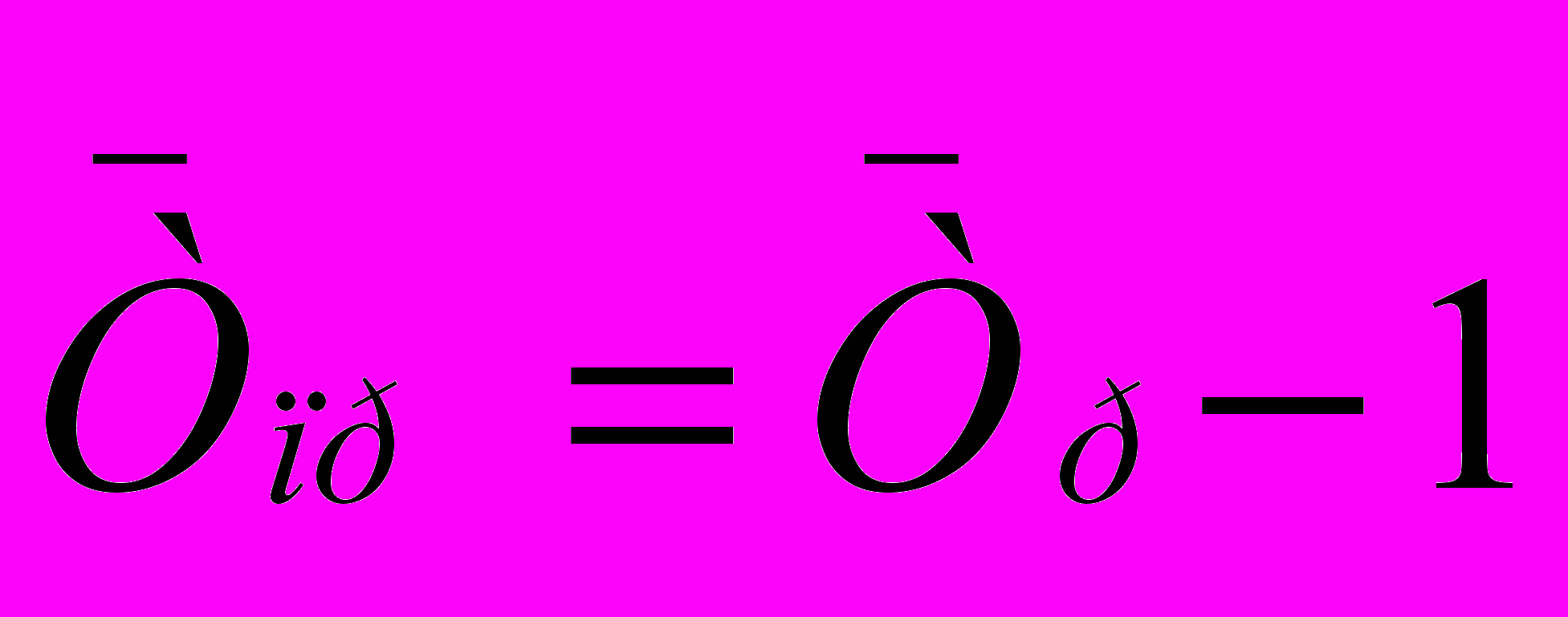
Л. 8. Индексы
Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях, отличается от уровня того же явления в других условиях.
Различие условий может проявляться во времени (индексы динамики), в пространстве (территориальные индексы), в выборе в качестве базиса сравнение какого-либо условного уровня (планового показателя) соответственно вводят индексы ? выполнения плана.
Все индексы делятся на два класса:
- Элементарные (индивидуальные).
- Сложные.
Под индивидуальными понимают относительные числа, характеризующие изменение во времени показателей, относящихся к однородному явлению.
Например, если требуется показать динамику цены с помощью индивидуальных индексов, то берут цену отчетного периода и делят ее на цену сравниваемого периода.
Применение сложных индексов является дальнейшим развитием метода средних. В той области явлений, где требуется, применение индексного метода стат-ка встречается, с совокупностями разнородных элементов.
Пример: определить:
- показатели изменения цены и количества реальных товаров
- на сколько изменится уровень цены для всей совокупности товаров во 2 квартале по сравнению с 1кварталом.
| Товар | Ед. Измер. | I квартал | II квартал | ||||
| Цена, ед. | Кол-во | Ст-ть,грн. | Цена,ед. | Кол-во | Ст-ть,грн. | ||
| А Б В | кг кг кг | 3 10 200 | 100 20 10 | 300 200 2000 | 2 12 160 | 150 10 20 | 300 120 3200 |
| Итого | | | | 2500 | | | 3620 |
Для определения изменения цены и количества необходимо рассчитать индивидуальные индексы в агрегатной форме:
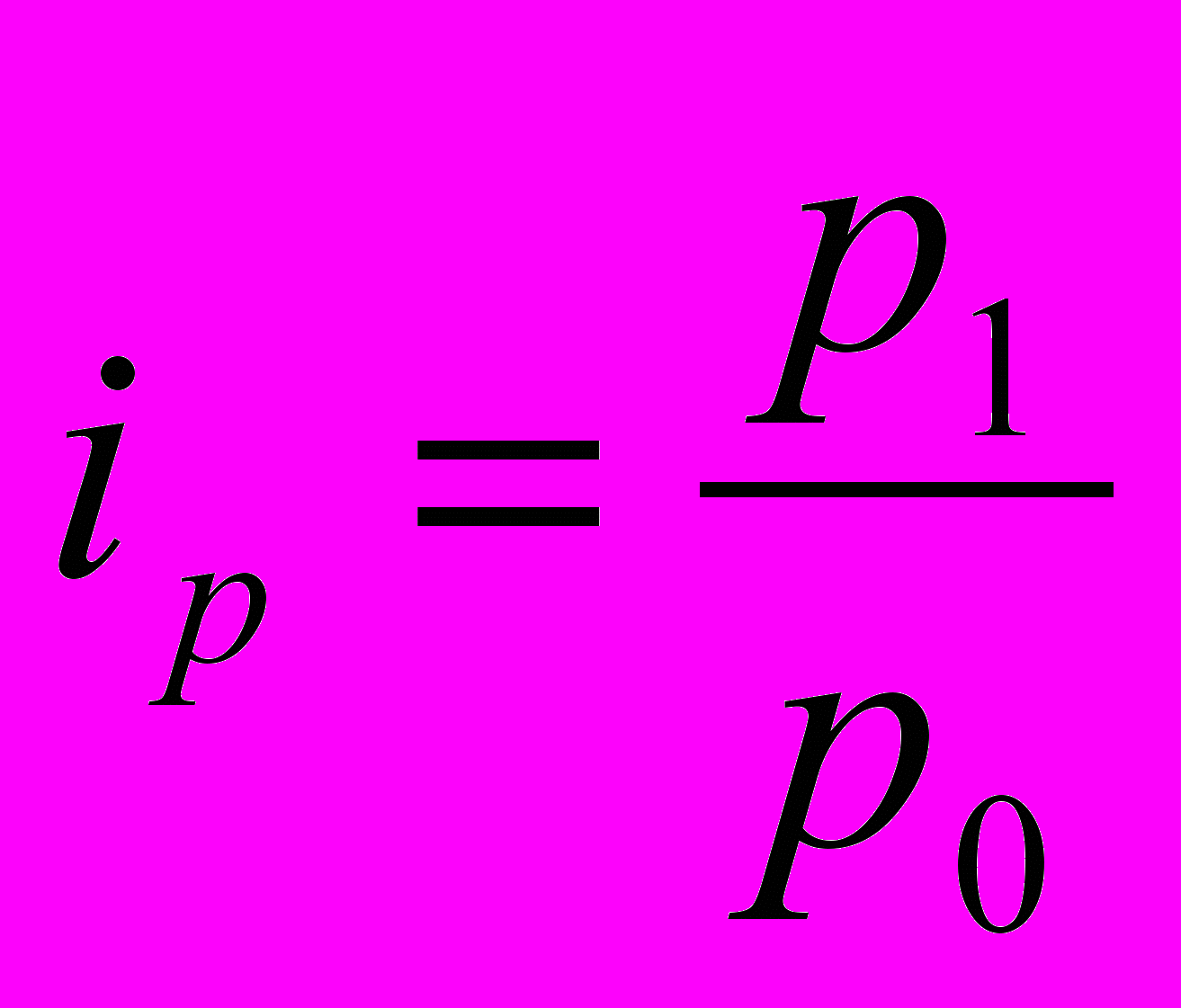 ,
, где iр – индивидуальный индекс цены
Р1 – цена текущего периода
Р0 – цена базисного периода
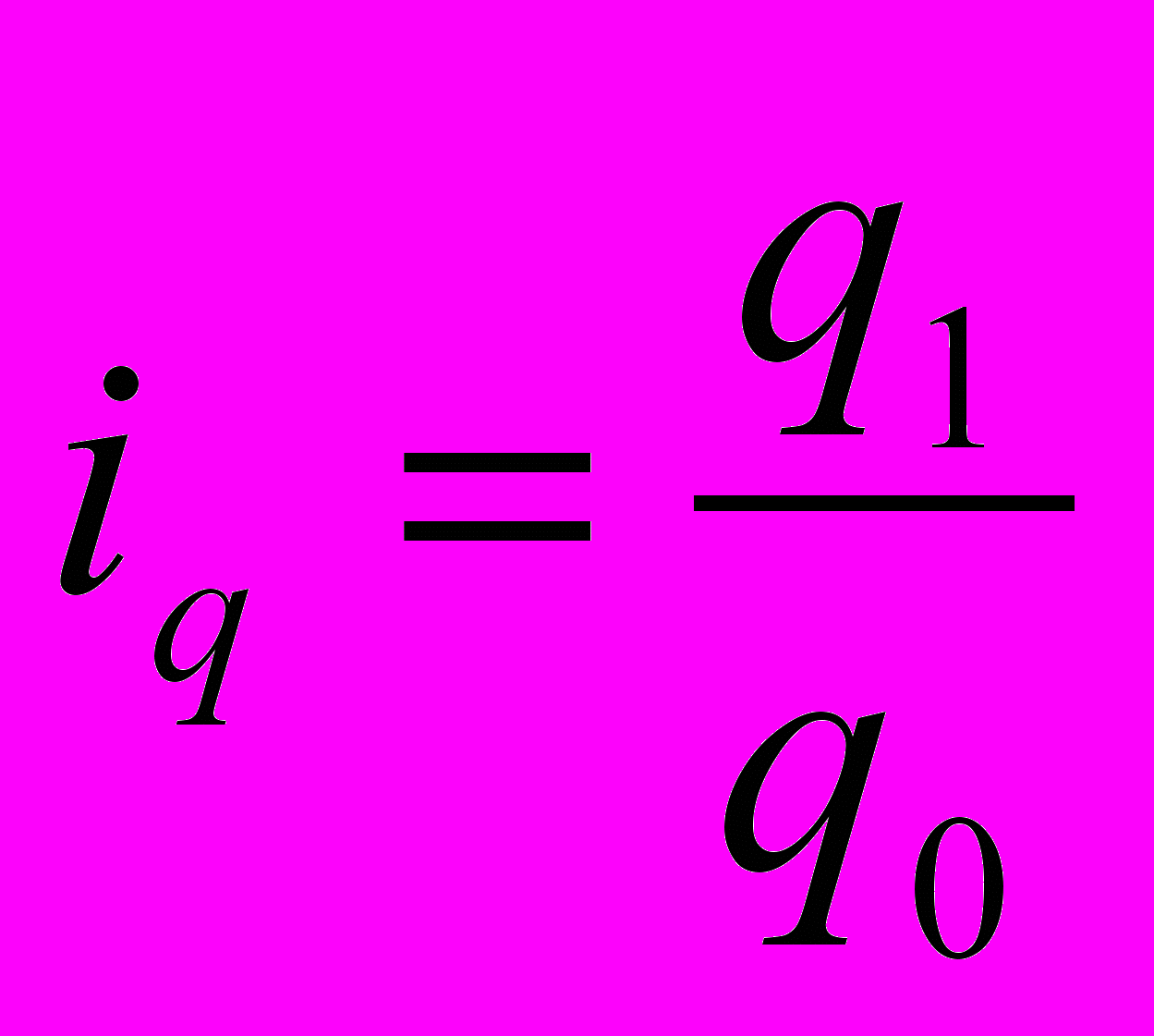 , ,
, ,где iq – индивидуальный индекс количества
q 1 – количество текущего периода
q 0 – количество базисного периода
ip = 2/3 = 0.67
цена на товар А во II квартале по сравнению с I уменьшилось в 0,33 раза или на 33%
ip = 12 / 10 = 1.2
ip = 160 / 200 = 0.8
iq = 150 / 100 = 1.5
количество произведенного товара А во II квартале по сравнению с I увеличилось в 1,5 раза или на 50%
iq = 10 / 20 = 0.5
iq = 20 / 10 = 2
Обязательным условием для вычисления индивидуальных индексов является max однородность того объекта, для которого их исчисляют.
Индивидуальные индексы являются величинами относительными (динамики) и, следовательно, могут быть и цепными и базисными и выражаются в % и в коэффициентах.
Вся трудность в решении вопроса об индексах возникает, тогда, когда приходится давать общую характеристику изменения уровня цен в совокупности товаров.
Товарная масса представляет собой совокупность разнородных элементов, поэтому нельзя просто вычислить среднюю цену, т.к.придется складывать цены разных товаров.
Следовательно, необходимо перейти к показателю стоимости товаров, который равен произведению цены на количество.
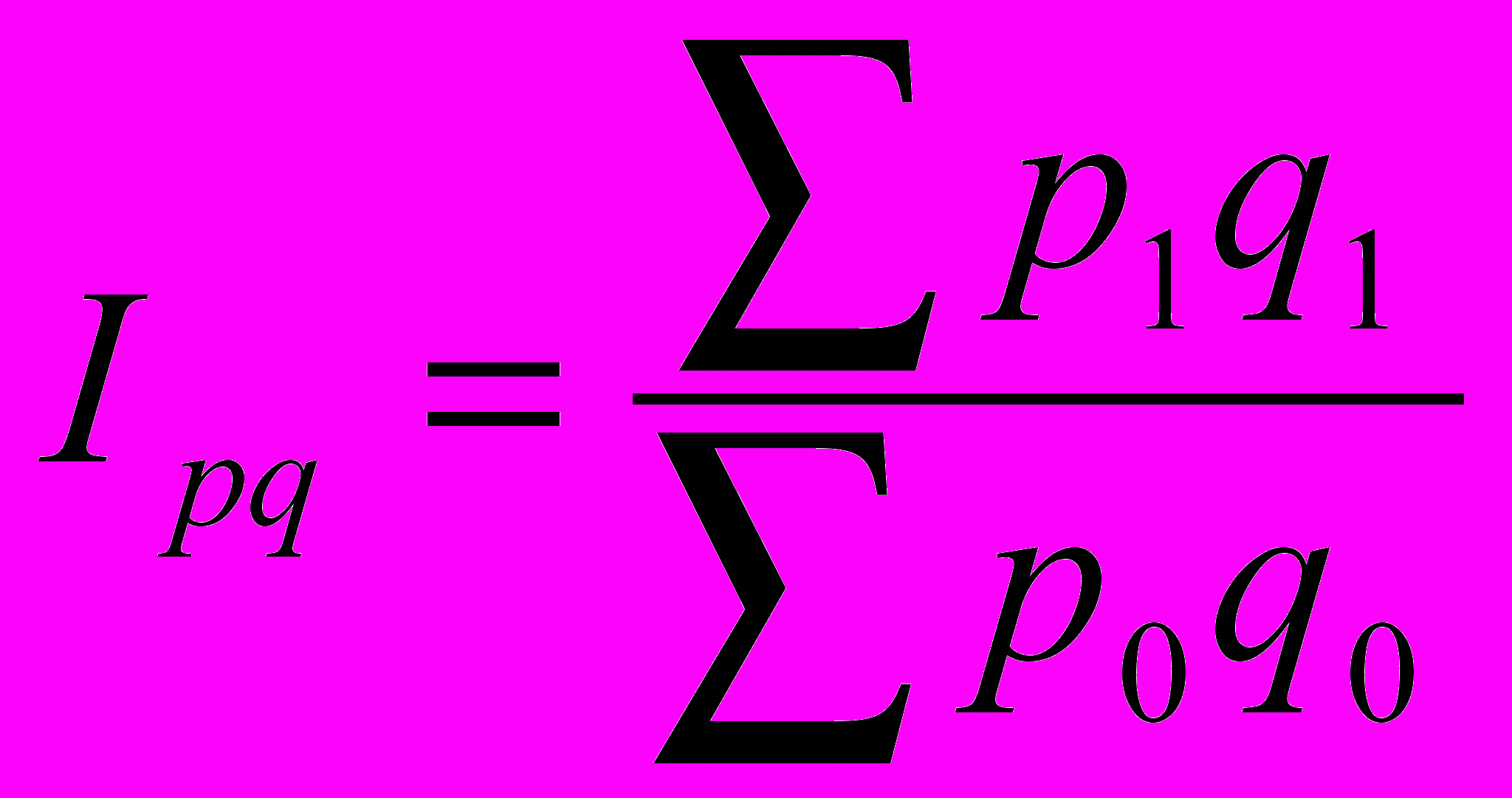
где I – общий индекс товарооборота
I = 3620 / 2500 = 1.45 раз – объем товарооборота во II квартале по сравнению с I увеличился в 1, 45 раз или на 45%.
Показатель изменения общей стоимости является функцией 2 величин: с 1 стороны изменения цен; со 2 стороны изменения количества.
Определим как меняется стоимость товарной массы под влиянием только одного фактора цены:
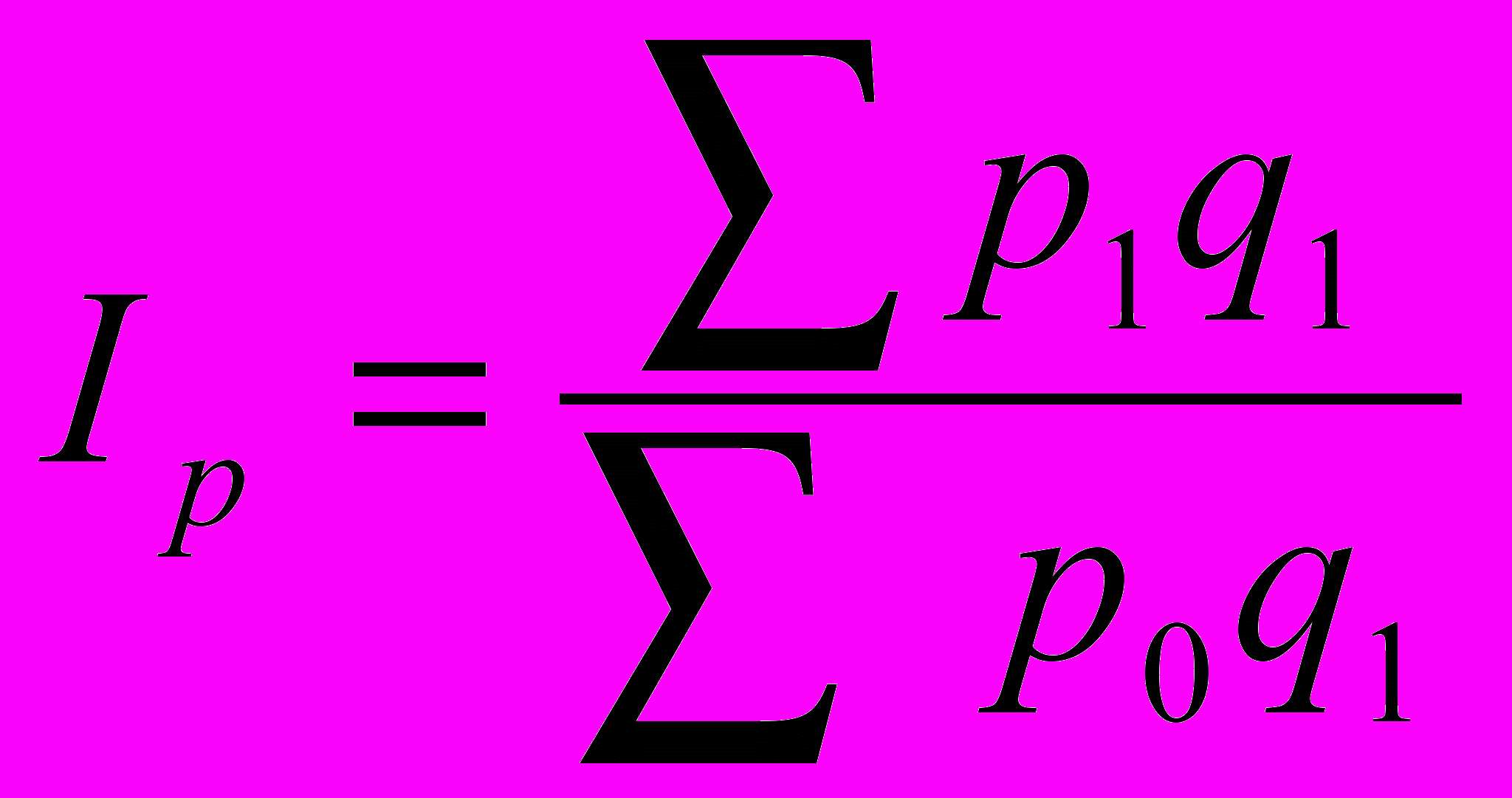
где Iр - агрегатный индекс цены.
Σ p0 q1 = 3,150 + 10,10 + 200,20 = 4550 тыс.грн.
Iр = 3620 / 4550 = 0, 79 или 79%
Цены в среднем понизились на 21%.
Влияние на прирост товарооборота изменения количества выражают следующей формулой:
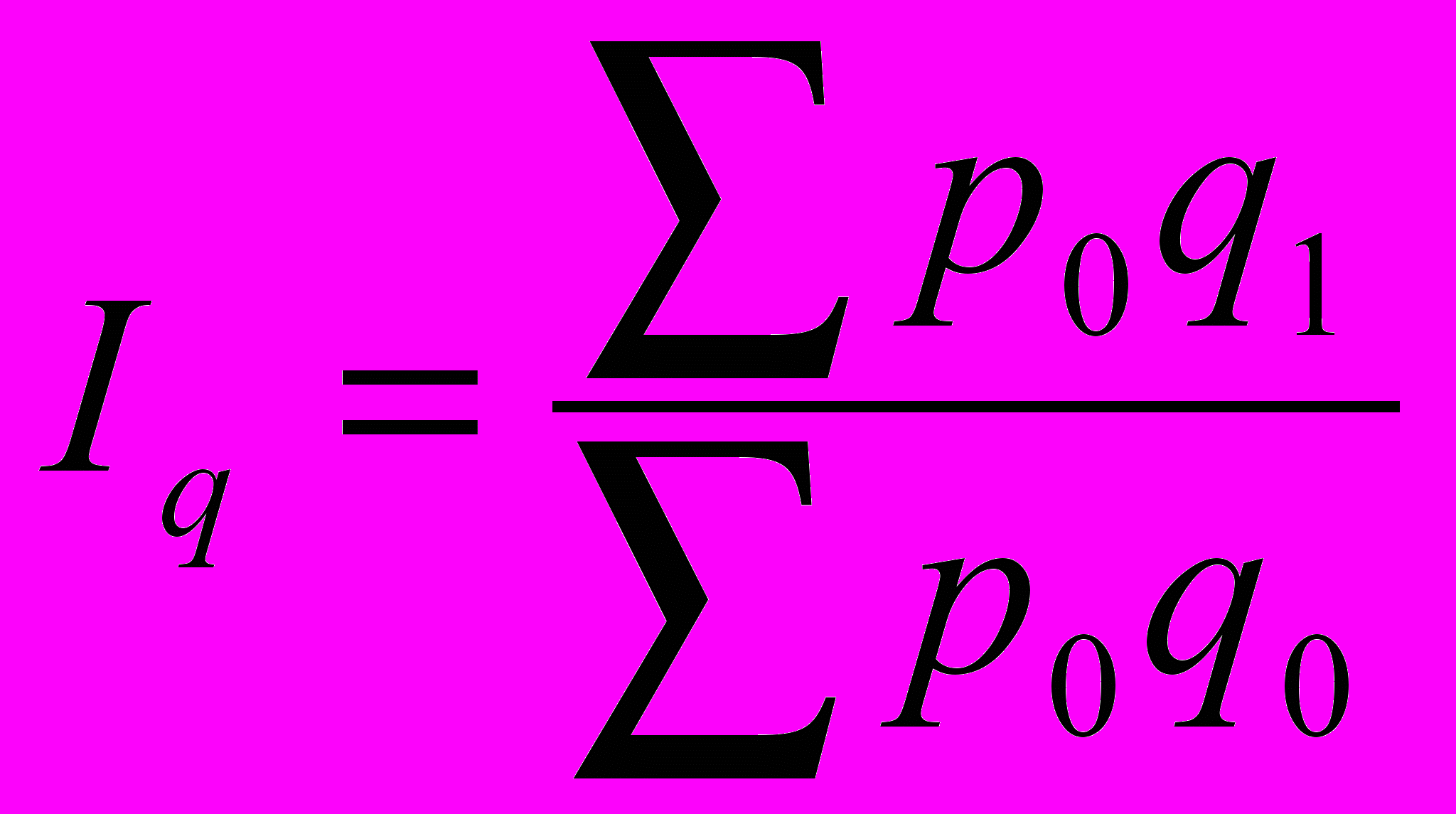 ,
,где Iq - агрегатный индекс количества
Iq = 4550 / 2500 = 1.8
Количество произведенной продукции в среднем увеличился в 1,8 раза или на 80%.
Поскольку числитель и знаменатель агрегатных индексов имеют экономический смысл, то в статистическом анализе нередко используются их разности (абсолютные приросты).
Абсолютный прирост исчисляется как разница между числителем и знаменателем соответствующих индексов:
∆ pq = Σ p1 q1 - Σ p0 q0
∆ р = Σ p1 q1 - Σ p0 q1
∆ q = Σ p0 q1 - Σ p0 q0
∆ pq = 3620 – 2500 = 1120 грн.
∆ р = 3620 – 4550 = - 930 грн
∆ q = 4550 – 2500 = 2050 грн.
Л. 1с. 206…219
