Развитие метода кинетической радиофлуорометрии для исследований ион-радикалов и их реакций в облученных неполярных растворах 01. 04. 17 химическая физика, в том числе физика горения и взрыва

Вид материала

Содержание

Глава 4 - Избыточные электроны в облученных алкановых растворах
TMPD C=1 мМ, E=4 кВ/см (кривые 1), C=20 мМ, E=24 кВ/см (2), C=1 мМ, E=24 кВ/см (3). R
L определяется характерным наклоном экспериментальной зависимости R

Подобный материал:

1 2 3 4 5

^а S- молекула растворителя, e^- - избыточный электрон. Реакция (1) инициируется ионизирующим облучением. Значения параметров получены экспериментально, либо взяты из литературы (см. текст и работу [22]).

Таким образом, моделирование показало, что влияние продуктов распада триплетных молекул алканов на кинетику радиофлуоресценции не очень велико. В то же время, вклад аннигиляции триплетных молекул, образованных в одной и той же шпоре может быть весьма значительным даже при сравнительно небольшом числе исходных ионных пар в шпоре.

Глава 4 - Избыточные электроны в облученных алкановых растворах

В 4-й главе описано исследование избыточных электронов, а также их реакций с акцепторами в алкановых растворах. Для изучения кинетики внутритрековой рекомбинации электронов с катионами описанная в предыдущем разделе модель была применена для описания кинетики радиофлуоресценции н-додекановых растворов TMPD. Молекулы этого соединения не захватывают избыточных электронов и являются акцепторами положительного заряда и энергии электронного возбуждения. Известно, что радиофлуоресценция алкановых растворов TMPD возникает в реакции рекомбинации

TMPD⁺^ + e^-  TMPD* (5)

Список основных реакций, определяющих кинетику радиофлуоресценции в этом случае приведен в табл. 1.

Одной из целей моделирования было определение усредненных пространственных характеристик шпоры и начального числа ионных пар в ней в случае додекановых растворов при облучении рентгеновскими квантами с энергией 20 кэВ. Характеристики типичной шпоры были определены, исходя из оптимального соответствия экспериментальных кинетик радиофлуоресценции исследованных растворов в диапазоне 0-250 нс и результатов компьютерного моделирования. Кроме этого, при тех же параметрах было промоделировано влияние на эту кинетику внешних магнитных и электрических полей.

Основными подбираемыми параметрами задачи были радиус шпоры и начальное число катион-электронных пар. Эти параметры варьировались от 1 нм до 20 нм и от 2 пар до 10 пар, соответственно. Лучшее и примерно одинаковое описание эксперимента было получено в случае шпор радиусом 5-5.5 нм, содержащей 4 ионных пары, и 9-10 нм, содержащей 5 ионных пар, при экспоненциальной функцией распределения исходных пар по расстояниям f(r>1 нм) ~exp(-r/b) при b=4.24.5 нм. Приведенные ниже расчетные кривые, если не указано иное, получены для случая 4 пар в шпоре радиусом 5 нм при b=4.3 нм.

Функция распределения первичных ион-электронных пар выбиралась такой, чтобы вероятность выхода ионов в объем в электрических полях 0 и 10 кВ/см составляла примерно 2.2 % и 3.5 %, соответственно, а вероятность геминальной рекомбинации пар S⁺^/e^- - примерно 0.5. При моделировании кривых ВМЭ дополнительными подбираемыми параметрами также были времена парамагнитной релаксации S⁺^ и TMPD⁺^, а также константа скорости вырожденного электронного обмена TMPD⁺^ в реакции (11, табл. 1) , которая является основной причиной фазовой релаксации во вторичных парах TMPD⁺^/e^-.

Коэффициенты диффузии D нейтральных частиц были определены с использованием литературных данных. Коэффициенты диффузии избыточных электронов, а также катион-радикалов растворителя S⁺^ и TMPD⁺^, определялись с применением метода ВЭЭ. Отметим, что неопределенность характеристик нейтральных радикалов – продуктов распада триплетно-возбужденных молекул алканов, не имеет большого значения, поскольку, согласно компьютерному моделированию, роль радикалов в исследуемых процессах незначительна.

Таблица 2. Значения коэффициентов диффузии активных частиц (D), подвижностей носителей заряда (), эффективных радиусов частиц R,^а времен фазовой и спин-решеточной релаксации в сильном магнитном поле T₂ и T₁, соответственно, а также эффективной скорости парамагнитной релаксации радикалов в нулевом магнитном поле T₀.

Частица	D/(см²/с)	/(см²/Вс)	R /нм	T₂=T₀, нс	T₁, нс
C₁₂H₂₆⁺^	6.510^-6	2.610^-4	0.5	3010	20050
e^-	2.110^-4	8.510^-3	0.5		
TMPD⁺^	3.810^-6	1.510^-4	0.38	(k₁₁C)^-1 ^c	22050
C₁₂H₂₆^*	8.910^-6 ^b	-	0.5	-	-
TMPD (TMPD^*)	8.210^-⁶^b	-	0.38	-	-
R^	810^-⁶^b	-	0.4	-	-

^а инкремент частицы в эффективный радиус R=k_s/4D бимолекулярной реакции с ее участием

^b приведены расчетные значения

^c скорость парамагнитной релаксации зависит от концентрации TMPD

Все использованные при моделировании характеристики частиц приведены в табл. 2. Величина радиуса переноса энергии (реакция 6) и вероятность образования синглетных состояний были определены, исходя из наилучшего описания эксперимента в диапазоне концентраций TMPD 120 мМ на начальном участке кинетики (0-50 нс). Для определения константы скорости k₃ образования TMPD⁺^ путем захвата первичных катион-радикалов растворителя был применен метод «дорекомбинационного» тушения (гл. 2) с использованием гексафторбензола в качестве акцептора электрона, аналогично работе [20].

Определение реакционного радиуса триплет-триплетной аннигиляции ³TMPD* было проведено с помощью измерений константы скорости этой реакции в условиях флеш-фотолиза по известной из литературы схеме. В проведении экспериментов с применением лазерного импульсного фотолиза большую помощь оказали д.х.н. В.Ф. Плюснин, к.ф.-м.н. И. Поздняков, Д. Воробьев (ИХКиГ СО РАН). Была измерена кинетика поглощения триплетных молекул TMPD при различных интенсивностях возбуждающего лазерного импульса с длиной волны 308 нм. Полученные характеристики спектра поглощения триплетных молекул TMPD близки к литературным данным. Время жизни ³TMPD* в процессе квазипервого порядка составляло около 50 мкс.

Спиновая динамика геминальных ион-радикальных пар. Расчет спиновой динамики производился в рамках квазиклассической модели (Schulten, K., Wolynes, P.G. J. Chem. Phys. 1978, 68, 3292.). Детали расчетов спиновой динамики могут быть найдены в работе [33].

На рис. 5 демонстрируется достигнутое согласие между расчетными и экспериментальными кинетиками радиофлуоресценции, кривыми ВЭЭ и ВМЭ при различных концентрациях TMPD. Показанные кривые соответствуют одной и той же поглощенной дозе или числу расчетных циклов.

В данной диссертации были впервые в рамках одной и той же модели описаны как кинетика радиофлуоресценции, так и влияние на нее внешних электрических и магнитных полей. Это позволило определить усредненные геометрические характеристики шпоры в треке, создаваемым рентгеновским квантом с энергией около 20 кэВ. Отметим, что такие детали взаимодействия ионизирующей частицы с конденсированной средой, как длина пробега ионизирующей частицы или средняя «порция» энергии, которую она отдает, хорошо известны, однако, экспериментально обоснованные данные о первичной структуре шпоры в алканах до последнего времени отсутствовали.

a b c

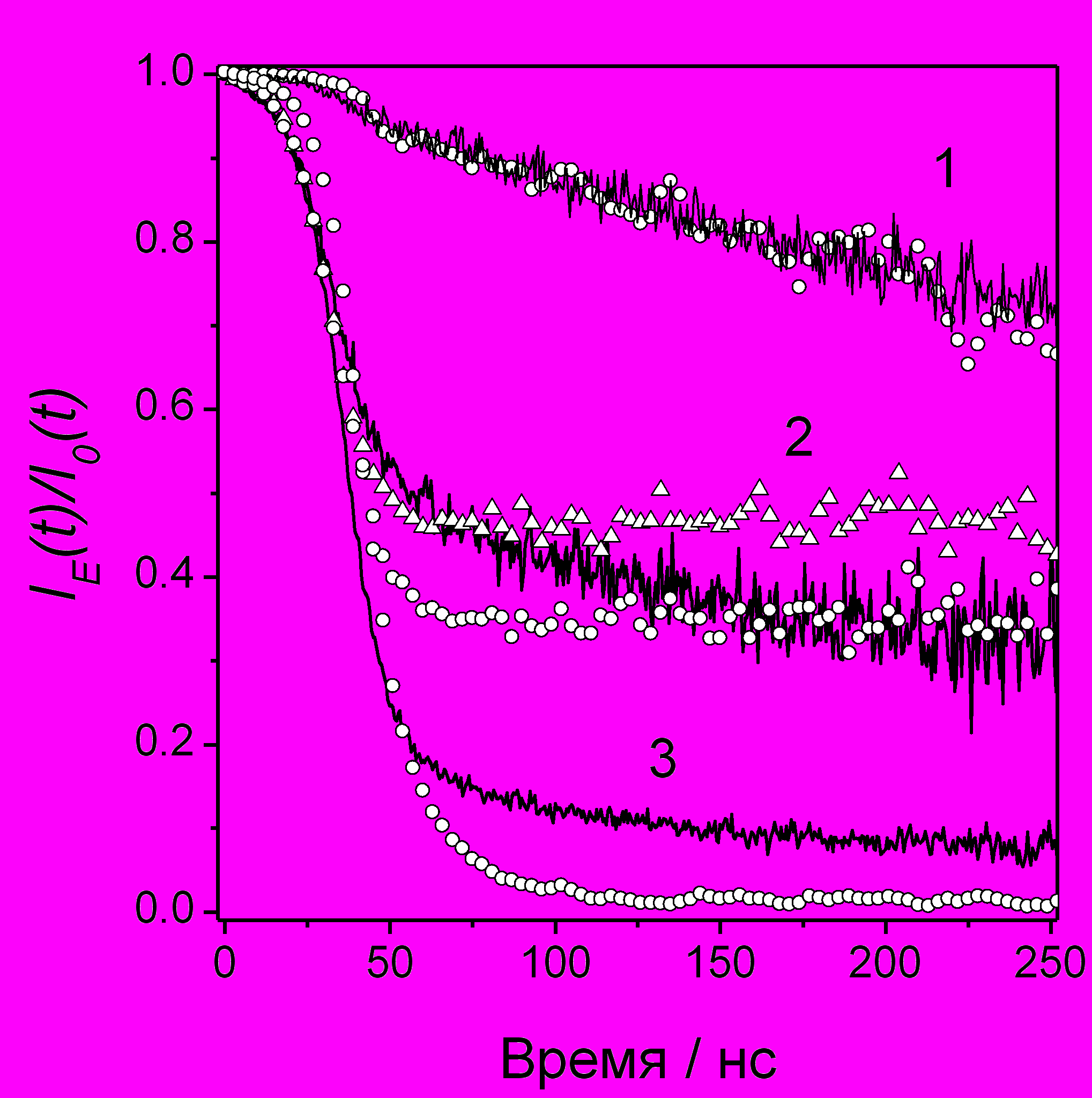
Рис. 5. а) Экспериментальные (линии) и расчетные () кинетики задержанной флуоресценции растворов TMPD при концентрации 20 мМ (кривые 1), 3 мМ (2), 1 мМ (3). Экспериментальные кривые нормированы на поглощенную дозу, а расчетные получены при одном и том же числе расчетных циклов;

b) Экспериментальные (линии) и расчетные (, ) кривые ВЭЭ при концентрации TMPD C=1 мМ, E=4 кВ/см (кривые 1), C=20 мМ, E=24 кВ/см (2), C=1 мМ, E=24 кВ/см (3). R_S=9 нм, N₀=5 ();R_S=5 нм, N₀=4 ();

с) Экспериментальные (линии) и расчетные () кривые ВМЭ для растворов TMPD в додекане при концентрации 20 мМ (кривые 1) и 1 мМ (2).

Реакции избыточных электронов с акцепторами.

Построение модели внутритрековой рекомбинации и определение основных факторов, определяющих интенсивность радиофлуоресценции в додекановых растворах, позволило получить обоснованные данные о реакциях избыточных электронов с акцепторами в этом растворителе:

e^- + A  Products (6)

Были определены подвижность электронов  и реакционные радиусы их захвата в диапазоне температур 265-343 К. Одной из целей исследований было получение информации о природе состояния, из которого происходит захват электрона на акцептор.

Реакция электрона с акцепторами исследовалась по влиянию последних на кинетику радиофлуоресценции додекановых растворов TMPD. Константа k скорости реакции реакции захвата (6) была измерена методом «дорекомбинационного» тушения (гл. 2). Подвижность избыточных электронов была определена методом ВЭЭ. Таким образом, были рассчитаны эффективные радиусы реакции захвата R_e=k/4D. Для анализа данных эксперимента были использованы известные результаты теоретических работ, посвященных описанию диффузионно-контролируемых реакций с дистанционным переносом электрона по обменному механизму. Фактически, проверялась гипотеза, что в н-додекане электрон захватывается на акцепторы только из локализованного.

В диффузионном пределе эффективный радиус рассчитывается как

R_e= a + L[1.15 + ln(w₀ L² /(4D))]/2 (7)

Здесь w₀ - скорость реакции в ситуации, когда реагенты находятся на расстоянии наибольшего сближения a. Зависимость скорости переноса от расстояния r описывается с использованием общепринятой зависимости:

w(r>a)=w₀exp[-2(r-a)/L]) (8)

Параметр L описывает затухание вероятности переноса и связан с затуханием волновой функции электронного состояния по мере удаления от реагента. Использование более точных выражений для R_e при прыжковом характере движения реагентов и произвольном соотношениях между параметрами, не изменяет основных выводов работы. В том случае, когда скорость переноса подчиняется закону Аррениуса

w₀(T)=₀exp(-E_a/k_BT), (9)

где ₀ - характерная частота движения, соответствующего координате реакции, k_B - постоянная Больцмана, E_a - энергия активации переноса, температурная зависимость эффективного радиуса R_e имеет вид

R_e = R₁ +L(E_D-E_a)/2k_BT, (10)

где R₁ - слабо зависит от температуры, а E_D - энергия активации диффузионного движения, которая примерно равна энергии активации подвижности. Поскольку E_D - независимо измеряемый параметр, из измерений температурной зависимости эффективного реакционного радиуса можно получить оценки для L и E_a.

Эксперимент. В качестве примеров экспериментально определенных зависимостей на рис. 6 приведены кривые относительного тушения I_C(t)/I₀(t) для додекановых растворов TMPD с добавлением гексафторбензола (а), а также зависимости скорости захвата электрона от концентрации для 1-бромогексана, тетрахлоруглерода, 1,12-дибромододекана (b). Из наклона прямых линий, являющихся линейной аппроксимацией экспериментальных точек, были определены константы скорости k реакции (6). Значения полученных констант скоростей при 293 К для исследованных акцепторов приведены в табл. 3. В этой же таблице приведены соответствующие значения R_e.

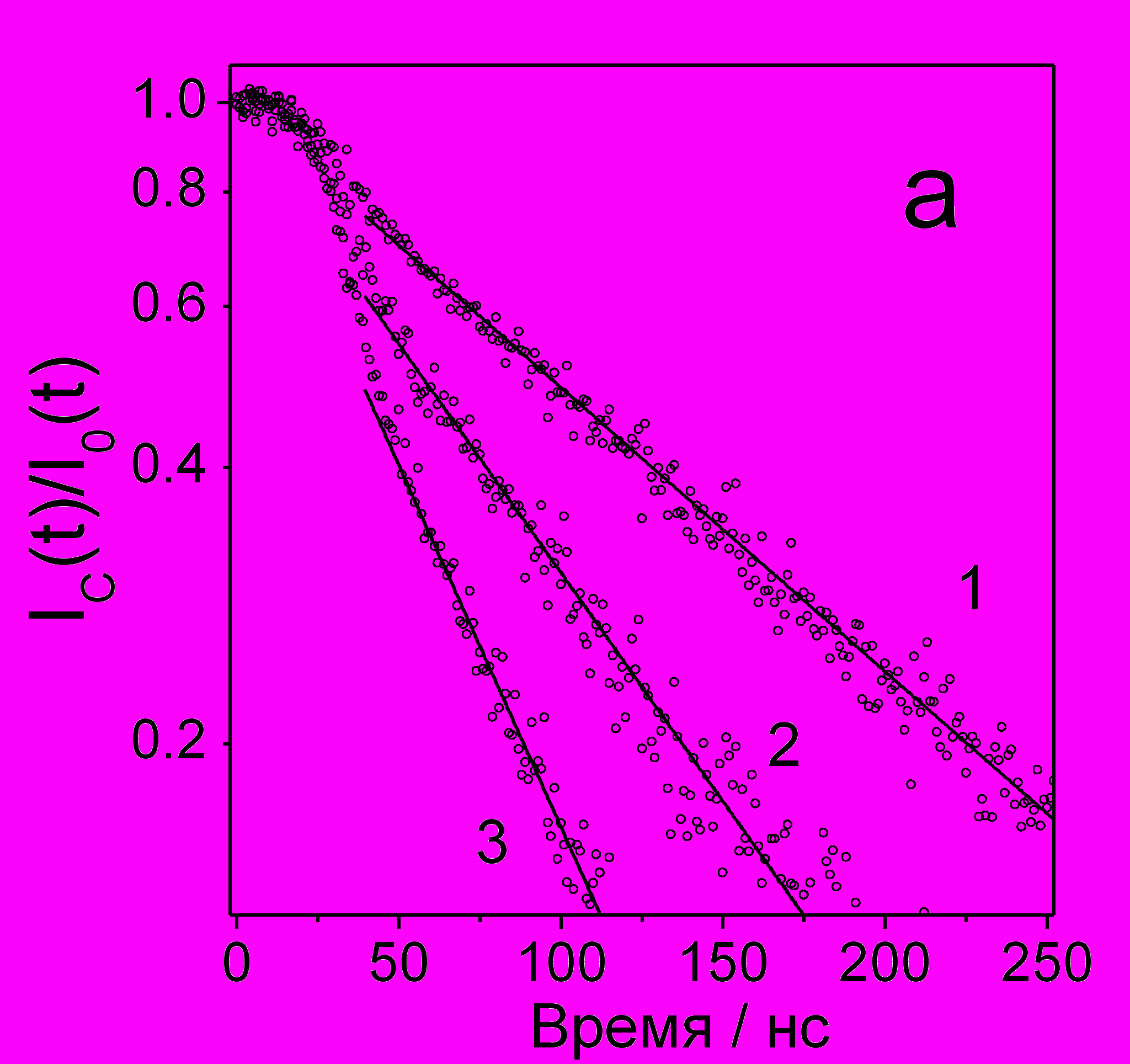
Рис. 6. а) Отношения I_C(t)/I₀(t) для додеканового раствора 1 мМ TMPD без добавления акцепторов (I₀(t)) и с добавлением C₆F₆ (I_C(t)) в концентрации C=0.06 мМ (кривая 1), C=0.09 мМ (2), C=0.12 мМ (3); b) Скорость захвата электрона при различных концентрациях 1-бромгексана (), тетрахлоруглерода (), 1,12-дибромдодекана (□) при 293 К в н-додекане. Прямые линии - линейная аппроксимация. Значения констант скоростей приведены в табл. 3.

Коэффициенты диффузии D_e для избыточных электронов в н-додекане в диапазоне температур 265-343 К были определены с применением метода ВЭЭ в тех же условиях, в которых были определены значения k. Результаты измерений подвижности показаны на рис. 6(а), где также приведена аппроксимация экспериментальных точек во всем исследованном температурном диапазоне аррениусовской зависимостью. Кроме этого, здесь же приведены литературные значения подвижности избыточных электронов в н-додекане.

Рис. 7. а) Подвижность избыточных электронов в н-додекане, определенная методом ВЭЭ в данной работе () и литературные значения (Gee, N., Freeman, G.R. J. Chem. Phys. 1987, 86, 5716). Прямая линия - аппроксимация экспериментальных точек аррениусовской зависимостью с предэкспонентом 130 см²/Вс и энергией активации 0.24 эВ; b) Зависимости эффективного радиуса реакции захвата (6) для антрахинона (), декафторбифенила () и дибромдодекана () от температуры. В случае антрахинона также приведена расчетная погрешность значений R_e. Сплошными линиями изображены зависимости R_e(Т^-1), вычисленные с помощью соотношений (7, 9). Значения параметров – в тексте.

При комнатной температуре измеренная в цитированной в подписи к рис. 7 работе подвижность электрона составила 2.010^-2 см²/Вс, что заметно выше, чем в данной работе. Причины такого различия остались невыясненными. В то же время, следует отметить, что в высокотемпературном пределе значения _e в обоих случаях близки к подвижности квазисвободного электрона в алканах (~10² см²/Вс), а энергия активации подвижности близка к опубликованным данным.

Таблица 3. Значения констант скорости и реакционные радиусы (R_e = k/4D) захвата избыточных электронов в н-додекане при Т=293 К.

Акцептор	k₁/10¹¹ М^-1с^-1 15 %	R_e/ нм , 20 %
(CH₃)₃SiCl	1.6	1.0
CCl₄	2.0	1.2
C₆F₆	1.9	1.2
1-BrC₆H₁₃	1.4	0.9
1,12-Br₂C₁₂H₂₅	2.6	1.6
3,4- Br₂C₆H₁₂	2.7	1.7
C₁₂F₁₀	2.9	1.8
C₁₄H₈O₂	3.2	2.0
(C₆H₅)₃CCl	2.2	1.4
(C₆H₅)₃GeBr	2.8	1.8
c-(C₆H₅)₈Ge₄	2.6	1.6

На рис. 7(b) приведены температурные зависимости эффективного радиуса реакции (6) в диапазоне 265-343 К для антрахинона, декафторбифенила, и 1,12-дибромдодекана. В случае антрахинона также приведена расчетная погрешность значений R_e. Сплошными линиями изображены зависимости R_e(T^-1), вычисленные с помощью соотношения (7) при a=0.8 нм, L=0.54 нм, E_D=0.24 эВ, E_a=0. Расчетные линии были получены при одних и тех же значениях параметров, исключая величину ₀. Она подбиралась для достижения согласия с экспериментом и в случаях антрахинона и декафторбифенила составляла 310¹³ и 10¹³ с^-1, соответственно.

Отметим, что величина L определяется характерным наклоном экспериментальной зависимости R_e(T^-1). При E_a=0 это приводит к тому, что приемлемые значения L лежат в диапазоне 0.45-0.65 нм. Практически такая же оценка для L получается из известного квантовомеханического выражения L~ħ/(2m_eE_b)^0.5 для характерного расстояния спада волновой функции в классически запрещенной области, если энергия связи электрона в растворителе E_b принять равной E_D.

В диссертации подробно обсуждается выбор конкретных значений параметров модели. Это важно для обоснования одного из основных выводов работы, посвященной захвату избыточных электронов: в пределах точности эксперимента перенос электрона происходит безактивационно. Аналогичный результат был ранее получен в случае водных растворов (Schmidt, K. H., Han, P., Bartels, D. M. J. Phys. Chem. 1995, 99, 10530). По-видимому, можно считать, что обнаруженные закономерности взаимодействия электронов и акцепторов характерны для всех алканов с невысоким значением .

Обратимый захват избыточных электронов в алканах. Известно, что взаимодействие избыточных электронов с некоторыми молекулами с небольшим или отрицательным газофазным сродством к электрону имеет характер обратимой реакции:

e^- + A  A^-^ (11)

Благодаря термической активации электрон может перейти в высокоподвижное состояние. При этом обратная реакция характеризуется значительной положительной энтропией активации, что позволяет наблюдать реакцию (11) в растворах даже при энтальпии реакции около 1 эВ (Holroyd, R. A. Ber. Bunsenges. Phys. Chem. 1977, 81, 298). Кроме величины сродства к электрону, энтальпия определяется энергией сольватации аниона и энергией избыточного электрона. Чем выше уровень дна зоны проводимости V₀ растворителя, тем более низкое сродство к электрону может быть у изучаемого акцептора.

Это явление может быть использовано для изучения анион-радикалов молекул с отрицательным газофазным сродством. В данной работе исследовано обратимое присоединение электрона к молекулам трифенилметана (TPM) и ряда фенилзамещенных силанов в н-додекане, который характеризуется практически наибольшей среди алканов величиной V₀ (при комнатной температуре - около 0.2 эВ).

На рис. 8(а) приведены измеренные с использованием метода ВЭЭ значения средней подвижности носителей отрицательного заряда в додекановых растворах трифенилметана с концентрацией от 0 до 1 мМ в диапазоне 265-343К. Гладкими линиями приведены результаты расчетов, выполненных в предположении, что в условиях эксперимента имеет место равновесие в реакции присоединения/отщепления избыточного электрона к молекуле TPM. Благодаря смещению равновесия в этой реакции имеет место переход от «электронной» подвижности _e при высоких температурах к «ионной» _A при низких.

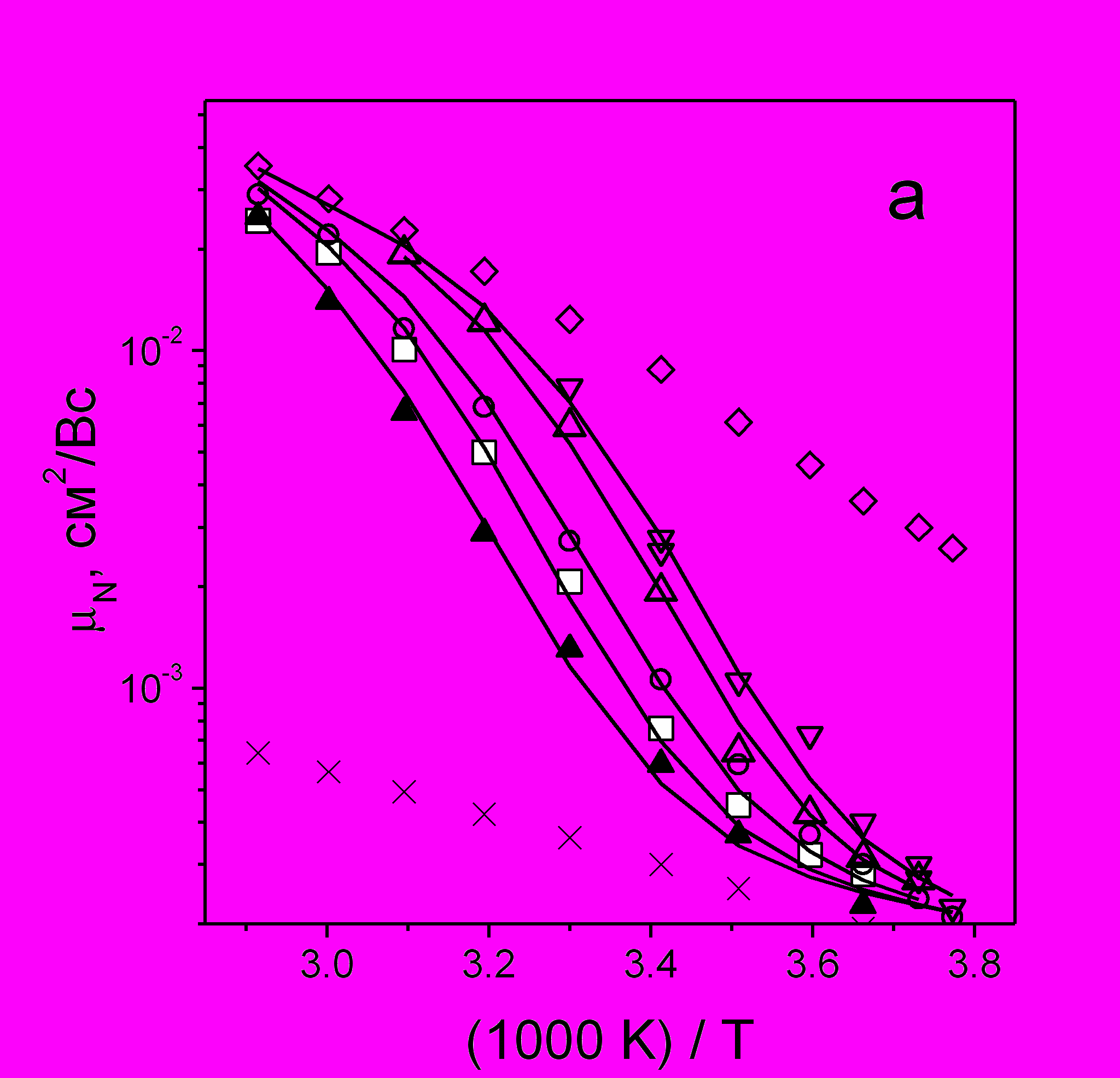
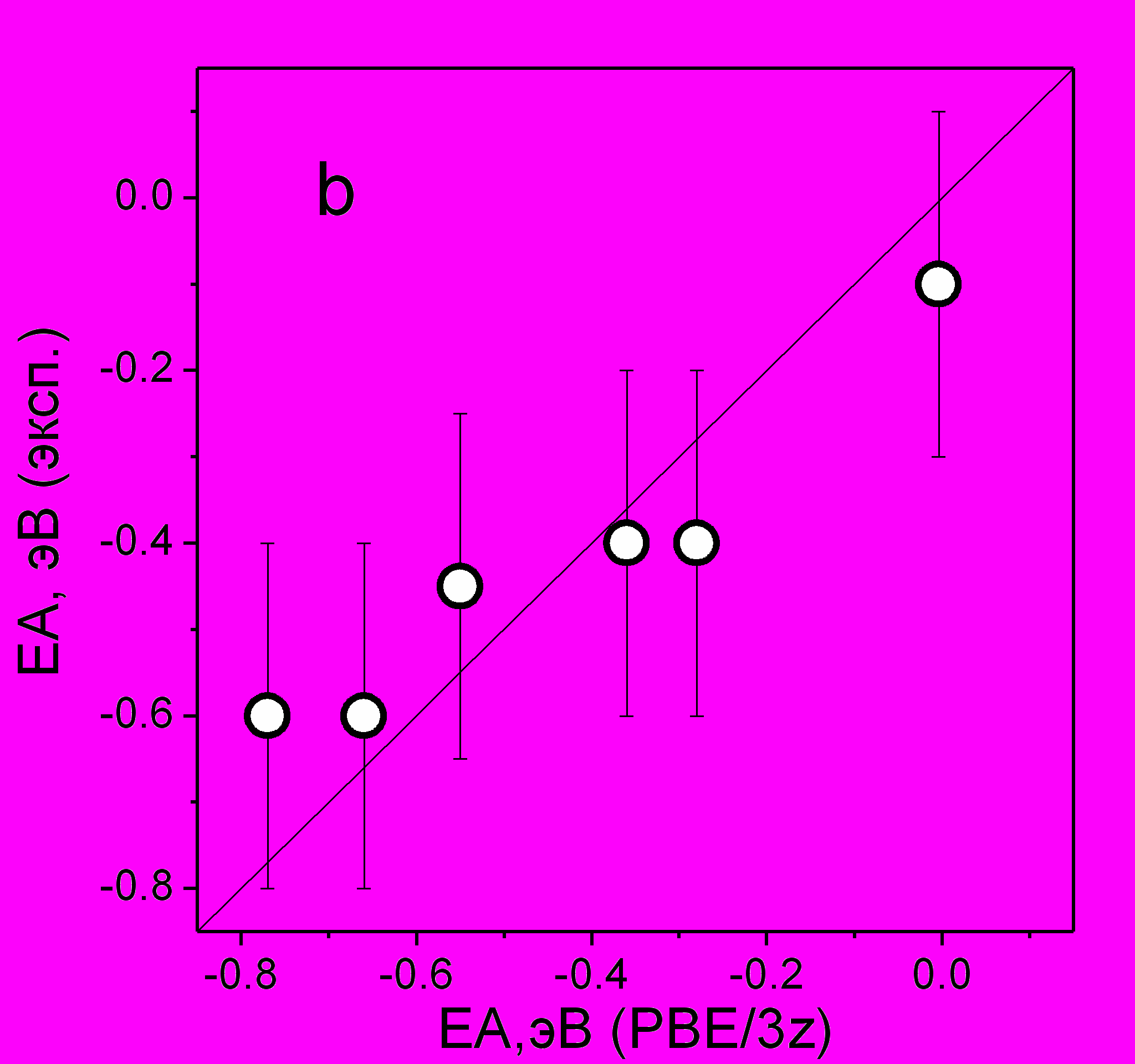
Рис. 8. а) Подвижность носителей отрицательного заряда в додекановом растворе TPM с концентрацией 0 (), 0.03 мМ (), 0.1 мМ (), 0.3 мМ (), 0.5 мМ (□), 1 мМ(▲), противоион - TMPD⁺^. Знаками () показаны расчетные значения подвижности TPM^-^. Гладкие линии - аппроксимация экспериментальных точек с помощью выражения (14), параметры приведены в тексте. b) Сравнение экспериментальных (приведены в скобках) и расчетных значений адиабатического сродства к электрону (в порядке возрастания ЕА) молекул фенилтриметилсилана ( -0.6 эВ), фенилдиметилсилана (-0.6 эВ), 2,3-диметилбутадиена-1,3 (-0.45 эВ), триптицена (-0.4 эВ), трифенилметана (-0.4 эВ), трифенилсилана (-0.1 эВ). Квантовохимические расчеты выполнены И.В. Береговой методом PBE/3z с помощью программы PRIRODA.

В диссертации, с использованием литературных данных, было показано, что в обсуждаемом случае необходим учет повторных контактов между e^- и A после отщепления. Были получены значения энтальпии активации (H=19.5 ккал/моль) и предэкспонента (А₀=610²² с^-1) для реакции отщепления. Константа скорости прямой реакции соответствует радиусу захвата около 1.5 нм.

Из полученных данных о термодинамическом равновесии в реакции (11), с помощью соотношения G₀= -EA_a + P^- -  G_sol(e^-) были получены оценки адиабатического сродства молекул к электрону в газовой фазе (ЕА_a) для ряда соединений (рис. 8(b)). Здесь P^- <0 - свободная энергия сольватации аниона, оцениваемая по формуле Борна, G_sol(e^-)=-0.2 эВ – свободная энергия растворения избыточного электрона.

В диссертации, на примере анион-радикала 2,3-диметилбутадиена в изооктане, также обсуждается способ оценки времени жизни анион-радикала с помощью измерения зависимости скорости спин-решеточной релаксации ион-радикальных пар от магнитного поля. Из такой зависимости было извлечено значение времени смены магнитного окружения электрона в результате вырожденного электронного обмена.

Blog

Содержание

Частица