Аннотации базовой части дисциплин циклов фгос
| Вид материала | Документы |
- Аннотации программ дисциплин, 1084.05kb.
- Материалы фгос впо по направлению подготовки 101100 гостиничное дело к разработке примерных, 195.61kb.
- Материалы фгос впо по направлению подготовки 100100 сервис к разработке примерных программ, 186.23kb.
- Материалы фгос впо по направлению подготовки 100400 туризм к разработке примерных программ, 147.92kb.
- Приложение 6 аннотации дисциплин базовой части учебного плана «производственный менеджмент», 758.32kb.
- Проект программ дисциплин учебного плана по направлению, 1776kb.
- Аннотации содержания дисциплин общие дисциплины Направление «Физика», 157.03kb.
- Программа 080200. 68. 10 Менеджмент по связям с общественностью Аннотации дисциплин, 428.99kb.
- Отчет о выполнении 1 этапа проекта кафедры «Инженерная графика и дизайн», 95.62kb.
- формирование систематизированных знаний об основных закономерностях и особенностях, 1579.89kb.
8. Уравнения математической физики
Дисциплина реализуется на ФММиПУ ТОГУ кафедрой Прикладная математика.
Содержание дисциплины:
Уравнения с частными производными первого порядка. Решение линейных уравнений в частных производных первого порядка методом характеристик. Уравнение Лиувилля и система Гамильтона. Стационарные решения уравнения Лиувилля. Уравнение переноса и его решение методом характеристик.
Уравнения диффузии (теплопроводности). Вывод уравнения диффузии (теплопроводности), а также задачи Коши и краевой задачи для него. Принцип максимума и его следствия. Метод разделения переменных для уравнения теплопроводности. Функции Бесселя. Поведение решения задачи Коши на больших временах.
Фундаментальное решение (функция Грина) и обобщенные функции. Общее понятие фундаментального решения и его физический смысл. Регулярные и обобщенные функции. Производные обобщенных функций. Преобразование Фурье обобщенных функций. Свойства
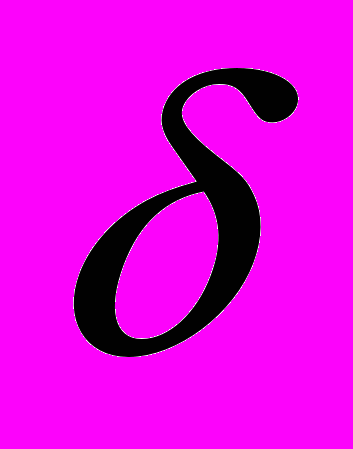- функции. Фундаментальное решение задачи Коши для уравнения теплопроводности.Уравнение Шредингера. Фундаментальное решение задачи Коши для свободного уравнения Шредингера. Представление решения общей задачи Коши с помощью разложения по собственным функциям. Решение задачи Коши для одномерного гармонического осциллятора.
Волновое уравнение. Вывод волнового уравнения из уравнений колебаний кристаллической решетки. Формула Даламбера на оси. Решение волнового уравнения на полуоси с краевыми условиями I , II и III рода. Решение задачи Коши для волнового уравнения в трехмерном и двумерном (метод спуска) пространствах.
Уравнения Лапласа и Гельмгольца. Фундаментальное решение уравнения Гельмгольца в трехмерном пространстве. Условие излучения, формула Кирхгофа. Решение уравнения Гельмгольца в полупространстве. Уравнение Пуассона в трехмерном и двумерном пространствах. Ньютонов потенциал. Решение краевых задач для уравнения Лапласа с помощью функции Грина. Задача Дирихле для полупространства и круга.
Дисциплина нацелена на формирование общекультурных компетенций ОК9,10,12,14, , профессиональных компетенций ПК10,11,14 выпускника.
Преподавание дисциплины предусматривает следующие формы организации учебного процесса: (лекции, лабораторные работы, практические занятия, коллоквиумы, самостоятельная работа студента, консультации, курсовая работа).
Программой дисциплины предусмотрены следующие виды контроля: текущий контроль успеваемости в форме курсовой работы, рубежный контроль в форме экзамена.
Общая трудоемкость освоения дисциплины составляет 5 зачетных единиц, 144 часов.
9. Методы оптимизации
Дисциплина реализуется на ФММиПУ ТОГУ кафедрой Прикладная математика.
Содержание дисциплины:
Экстремальные задачи и методы их решения. Классификация задач и методов оптимизации. Примеры задач оптимизации. Общая схема решения задач оптимизации.
Методы решения экстремальных задач. Методы одномерной минимизации нулевого порядка. Интерполяционный многочлен Лагранжа и процедура интерполяции с кратными узлами. Методы квадратичной и кубической аппроксимации. Методы одномерной глобальной оптимизации. Стандартные программы.
Элементы выпуклого анализа. Метод Лагранжа с выпуклой целевой функцией. Теорема Куна-Таккера и ее приложения. Достаточные условия условного минимума.
Вариационные методы. Задача Лагранжа. Простейшая задача классического вариационного исчисления. Задача Больца. Изопериметрическая задача. Задача со старшими производными. Уравнение Эйлера-Пуассона.
Численные методы математического программирования. Метод Ньютона и Левенберга-Маркварда для решения нелинейной задачи наименьших квадратов. Стандартные программы алгоритмов. Методы штрафных и барьерных функций и способы ускорения их сходимости. Симплекс метод. Линейное программирование.
Дисциплина нацелена на формирование общекультурных компетенций ОК9,10,12,14, , профессиональных компетенций ПК10,11,14 выпускника.
Преподавание дисциплины предусматривает следующие формы организации учебного процесса: (лекции, лабораторные работы, самостоятельная работа студента, консультации).
Программой дисциплины предусмотрены следующие виды контроля: текущий контроль успеваемости в форме отчетов по л.р., рубежный контроль в форме экзамена.
Общая трудоемкость освоения дисциплины составляет 5 зачетных единиц, 144 часов.
10. Физика
Физические основы механики. Классическая механика, состояние и уравнения движения, законы сохранения; кинематика и динамика твердого тела, жидкостей и газов, релятивистская механика, принцип относительности.
Физика колебаний и волн. Гармонический и ангармонический осциллятор, кинематика волновых процессов. Интерференция и дифракция.
Молекулярная физика и термодинамика. Статистическая физика и термодинамика, фазовые превращения.
Электричество и магнетизм. Электростатика и электродинамика. Уравнения Максвелла. Оптика. Волновая оптика.
Квантовая физика. Принцип неопределенности, квантовые операторы и уравнения.
Вариативная часть
1. Алгоритмы дискретной математики
Понятие алгоритма, основные требования, предъявляемые к алгоритму.
Вычислимые функции. Примитивно рекурсивные, частично рекурсивные и общерекурсивные функции.
Машина Тьюринга. Конфигурация машины Тьюринга. Композиция машин Тьюринга. Тезис Тьюринга.
Нормальные алгоритмы Маркова.
Неразрешимые алгоритмические проблемы.
Языки. Порождающие грамматики. Классификация грамматик и языков.
Конечные автоматы. Детерминизация и минимизация конечных автоматов.
Некоторые алгоритмы на графах. Алгоритм Прима и алгоритм Крускала нахождения дерева покрытия графа минимального веса.
Алгоритм Дейкстры для нахождения кратчайшего пути между двумя заданными вершинами.
Сети и потоки в сетях. Алгоритм Форда – Фалкерсона нахождения максимального потока в сети.
Задача планирования. Алгоритм нахождения критического пути в сети.
2. Дополнительные главы алгебры
Первая часть курса посвящена приложениям методов общей алгебры, которые в последние десятилетия широко проникают в многочисленные области технических и гуманитарных исследований. Курс включает начала теории чисел, теории групп и конечных полей, а также их приложения к построению кодов, исправляющих ошибки, и к криптографическим протоколам. Изложение начинается с повторения определений и простейших свойств основных алгебраических структур (знакомых слушателям по курсу «Геометрия и алгебра») и их обобщение на языке универсальной алгебры; в частности, вводится понятие морфизма алгебраических систем. Свойства колец вычетов и конечных групп используются в дальнейшем при описании криптографических протоколов, в частности, протокола RSA.
Вторая часть курса включает теорию решеток, которая предоставляет математические основы современных методов поиска зависимостей в данных – импликаций и ассоциативных правил на множествах признаков. Изложение начинается с повторения основных понятий теории отношений и теории графов. Важнейшим разделом современной прикладной теории решеток является анализ формальных понятий, исходным объектом которого служит бинарное отношение на множествах объектов и их свойств (признаков). На основе отношения определяется соответствие Галуа и оператор замыкания. Замкнутые множества объектов (признаков) образуют решетку (понятий), которая, с одной стороны, позволяет наглядно представлять иерархию классов объектов, а с другой – зависимости на признаках, определяемых в терминах импликаций и ассоциативных правил (частичных импликаций).
3. Численное решение задач математической физики
Решение краевых задач уравнения теплопроводности, уравнения гиперболического типа методом сеток. Дифференциальное уравнение и краевые условия. Построение сетки и введение сеточных функций. Явная, неявная схемы. Нахождение решения с помощью метода прогонки.Схемы с весами, Кранка-Николсона, «ромб». Методы повышения порядка аппроксимации начальных и краевых условий.
Устойчивость разностных схем для уравнений в частных производных. Понятие об устойчивости. Сходимость как следствие аппроксимации и устойчивости. Анализ устойчивости с помощью спектрального критерия Неймана.
Оценка погрешности конечно-разностного решения по правилу Рунге.
Решение краевых задач для двумерного уравнения теплопроводности методом конечных разностей. Явная схема. Чисто неявная схема. Экономичные разностные схемы.
Решение краевых задач для уравнений эллиптического типа методом конечных разностей. Разностная аппроксимация уравнения и краевых условий. Метод установления. Решение системы разностных уравнений универсальными итерационными методами (методы Якоби, Зейделя, итерации с параметром). Метод релаксации. Метод матричной прогонки.
Методы построения разностных схем для краевых задач математической физики. Метод разностных аппроксимаций. Метод неопределенных коэффициентов. Интегро-интерполяционный метод.
Метод конечных разностей при аппроксимациях специального вида. Случай переменного коэффициента. Случай неравномерной сетки. Случай разрывных коэффициентов.
Вариационно-разностные и проекционно-разностные методы. Вариационная постановка краевой задачи. Метод Ритца. Проекционная постановка краевой задачи. Метод Галеркина. Метод конечных элементов.
4. Вариационное исчисление
Введение в теорию вариационного исчисления. Линейное пространство. Линейное нормированное пространство
Функционал. Первая вариация функционала. Понятие минимума функционала. Необходимое условие минимума. Достаточные условия экстремума функционала
Уравнение Эйлера для функционала
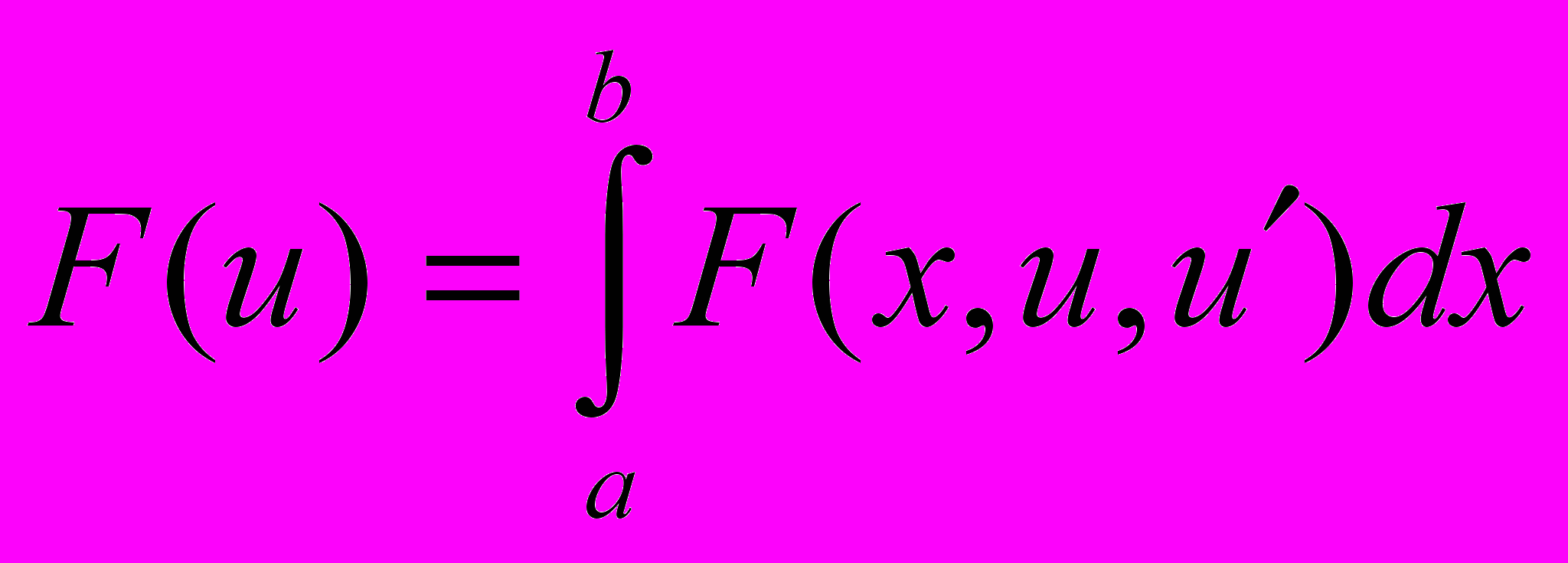. Лемма Дюбуа Раймонда.Вторая вариация для функционала
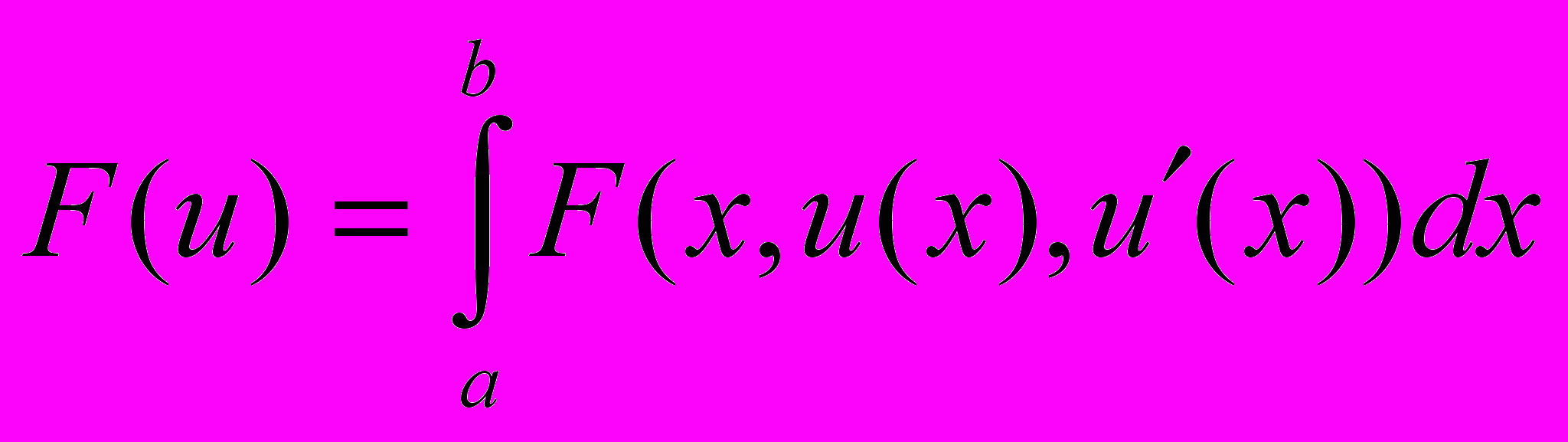. Условия Лежандра. Достаточное условие (Якоби) минимума функционала 
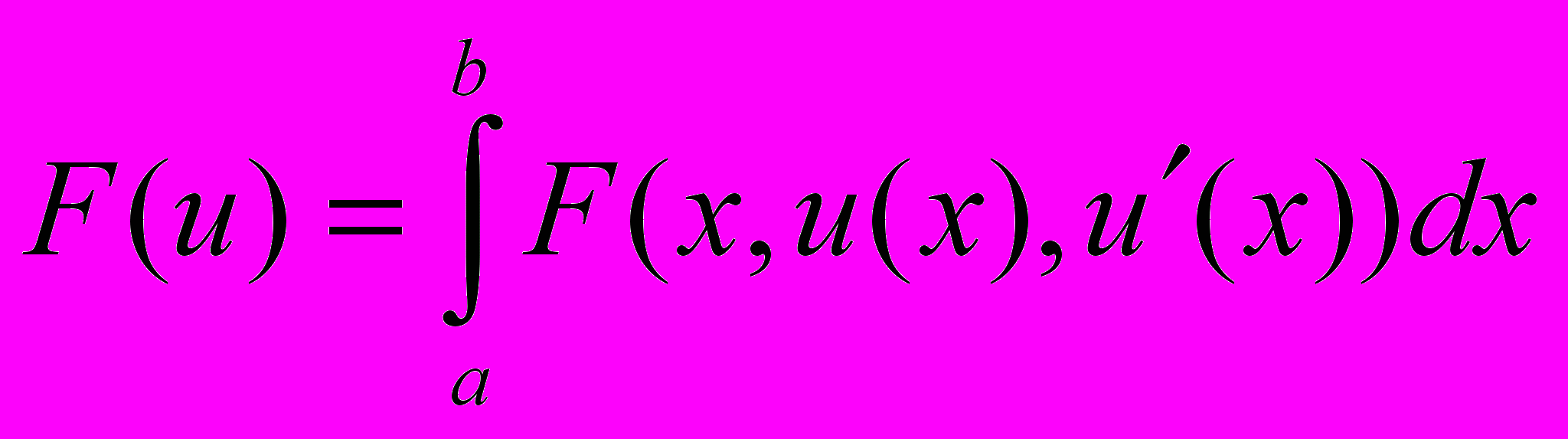, где u(a)=u(b)=0.. Необходимое условие экстремума функционала, заданного на выпуклом множестве. Выпуклый функционал на выпуклом множестве. Достаточное условие выпуклости. Теорема об экстремуме выпуклого функционала.
14. Динамическое программирование
Динамическое программирование – это метод оптимизации многошаговых процессов принятия решений, позволяющий указать пути исследования целого класса экстремальных задач.
Введение в динамическое программирование.
Задачи оптимального управления. Программное и позиционное управления. Подход динамического программирования. Принцип оптимальности. Уравнение Гамильтона-Якоби. Теорема о верификации. Множество достижимости, разрешимости. Их связь с функцией Беллмана. Уравнение Беллмана
Задачи с интегральными квадратичными функционалами для линейных управляемых систем.
Задачи на бесконечном интервале времени.
Постановка задачи поиска стабилизирующего управления. Задача со стабилизирующим функционалом. Задача для стационарной динамической системы (подынтегральный функционал с дисконтирующим множителем). Примеры.
Линейно-выпуклые задачи.
Понятие о линейно-выпуклой задаче. Множества достижимости и разрешимости. Синтез управления в задаче разрешимости. Задача быстродействия.
Линейно-выпуклые задачи с фазовыми ограничениями в конечном числе моментов времени.
Множество достижимости и разрешимости при фазовых ограничениях. Синтез управления при фазовых ограничениях.
Классические задачи динамического программирования.
Задача о наибольшей общей подпоследовательности: даны две последовательности, требуется найти самую длинную общую подпоследовательность.
Задача о порядке перемножения матриц: даны матрицы A1, ..., An, требуется минимизировать количество скалярных операций для их перемножения.
Задача о выборе траектории.
Задача последовательного принятия решения.
Задача об использовании рабочей силы.
Задача управления запасами.
Задача о ранце: из неограниченного множества предметов со свойствами «стоимость» и «вес», требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при ограниченном суммарном весе.
Алгоритм Флойда-Уоршелла: найти кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа.
Алгоритм Беллмана — Форда: найти кратчайший путь во взвешенном графе между двумя заданными вершинами.
Профессиональный цикл
- Математическое моделирование
Основные понятия механики сплошных сред. Переменные Лагранжа и Эйлера, уравнение несжимаемости и неразрывности. Теория малых деформаций, тензор деформаций, соотношение Коши. Теория напряжений, тензор напряжений, уравнение равновесия и движения сплошной среды.
Теория упругости. Идеально упругое тело, закон Гука, уравнение Ламэ. Краевые и вариационные задачи теории упругости, теория вычислительного эксперимента, оценка точности результатов моделирования. Равновесие, устойчивость и колебания упругого стержня. Упругие волны.
Основы физики жидкостей и газов. Идеальная жидкость, уравнение Эйлера, волны в газе.
Стационарные электромагнитные процессы. Уравнения Максвелла, законы сохранения, граничные условия. Постоянное электрическое поле, основные задачи электростатики, поляризация диэлектриков, энергия и силы в электростатике. Постоянное магнитное поле, магнетики, энергия постоянного магнитного поля.
Квазистационарные электромагнитные процессы. Уравнения квазистационарной теории, уравнения Кирхгофа, колебательный контур, анализ и интерпретация результатов моделирования. Энергия и силы в квазистационарном приближении
Быстропеременные электромагнитные процессы. Уравнения для потенциалов электромагнитного поля и запаздывающие потенциалы. Излучение, создаваемое электрическим и магнитным моментом, инструментальные средства и языки моделирования. Электромагнитные волны в однородных средах, отражение и преломление плоских электромагнитных волн на границе двух сред.
- Численные методы
Представление действительных чисел в вычислительной машине. Компьютерная система чисел с плавающей точкой. Абсолютная и относительная погрешности вычислений. Машинный эпсилон. Примеры неустойчивых алгоритмов. Примеры некорректных задач. Требования к вычислительным алгоритмам.
Прямые методы решения систем линейных алгебраических уравнений (СЛАУ). . Метод Гаусса для решения СЛАУ. Оценка количества умножений и делений, необходимых при решении системы из n уравнений методом Гаусса. Схема решения с частичным выбором ведущего элемента. LU- разложение матриц. Метод прогонки для решения СЛАУ с трехдиагональной матрицей. Метод Холецкого.
Погрешности решения и обусловленность систем уравнений. Невязка и погрешность решения СЛАУ прямыми методами. Число обусловленности матрицы. Зависимость относительной погрешности решения СЛАУ от погрешностей представления коэффициентов системы.
Итерационные методы решения СЛАУ. Метод простых итераций. Условия сходимости метода. Оценка погрешности решения. Оценка погрешности и скорости сходимости метода простых итераций. Приведение системы к виду, удобному для итераций. Метод Зейделя. Метод Якоби. Метод релаксации.
Методы численного решения нелинейных уравнений. Графический способ отделения корней нелинейных уравнений. Метод простых итераций (МПИ) для нелинейных уравнений с одним неизвестным. Задача о неподвижной точке. Метод простых итераций (МПИ) для систем нелинейных уравнений. Метод Ньютона (метод касательных) для решения скалярных нелинейных уравнений. Метод Ньютона для решения системы из двух нелинейных уравнений. Обобщение на систему с произвольным числом уравнений.
Интерполяция. Постановка задачи интерполяции. Интерполяционный многочлен Лагранжа. Априорная оценка остаточного члена интерполяционного полинома. Конечные и разделенные разности. Общая формула для разделенной разности n-го порядка. Формула для оценки погрешности интерполирования с использованием разделенной разности. Оценка производной с помощью разделенной разности. Первая и вторая интерполяционные формулы Ньютона с использованием разделенных разностей. Обратное интерполирование. Постановка задачи сплайновой интерполяции.
Методы вычисления собственных чисел и векторов. Прямой степенной метод. Обратный степенной метод со сдвигом. Приведение матрицы к форме Хессенберга. QR-алгоритм со сдвигом. Алгоритм решения полной спектральной задачи.
Решение задачи Коши одношаговыми численными методами. Метод Эйлера. Модификации метода Эйлера: неявный метод Эйлера, метод Хойна, усовершенствованный метод Эйлера с итерационной обработкой, уточнённый метод Эйлера. Построение методов Рунге-Кутты второго и четвертого порядков. Оценка главного члена погрешности решения методом пересчета с половинным шагом.
Приближенное вычисление определенных интегралов. Задача численного интегрирования. Квадратурные формулы Простые квадратурные формулы. Формулы прямоугольников и трапеций; оценка погрешности; порядок точности формул. Квадратурные формулы Ньютона-Котеса. Составные квадратурные формулы трапеций и Симпсона. Рекуррентные формулы интегрирования трапеций, Симпсона, Буля. Интегрирование по Ромбергу. Правило Рунге для оценивания погрешности.
Численное дифференцирование. Формулы численного дифференцирования для равномерных сеток; формулы второго порядка точности для первой и второй производных. Метод Рунге для повышения порядка точности численного дифференцирования. Некорректность операции численного дифференцирования. Выбор оптимального шага дискретизации при численном дифференцировании.
- Теория управления
Основные понятия теории управления. Понятие абстрактной временной системы. Описания систем типа «вход – выход». Задача управления системами. Программное управление и обратная связь. Типовые регуляторы. Модели линейных систем: импульсная переходная функция. Структурные схемы и их преобразования. Линеаризация нелинейных характеристик систем.
Стационарные системы: их передаточные функции и частотные характеристики. Аппарат преобразования Лапласа. Понятие передаточной функции. Нахождение реакции на типовые сигналы. Переходная характеристика системы. Передаточные функции и преобразования структурных схем. Преобразование Фурье и частотная передаточная функция. Частотные характеристики систем.
Типовые звенья систем и анализ качества. Стандартная форма передаточных функций. Типовые звенья, параметры типовых звеньев. Переходные и установившиеся режимы. Качество переходных процессов. Точность в установившемся режиме: коэффициенты ошибки и астатизм системы.
Устойчивость систем и частотные показатели качества. Понятие устойчивости и асимптотической устойчивости. Устойчивость линейных стационарных систем. Критерии Стодолы, Гурвица и Рауса. Критерий устойчивости Найквиста и запасы устойчивости. Применение ЛАЧХ для исследования устойчивости и качества систем.
Методы коррекции и синтеза стационарных систем. Интегральная и дифференциальная коррекция. Корневые оценки качества и корневой годограф. Частотные методы синтеза.
Методы пространства состояний. Понятие динамической системы. Уравнения линейных систем в пространстве состояний. Задача динамической реализации – жорданова форма, нормальная форма (форма Коши), управляемая и наблюдаемая формы. Преобразование структурных схем в пространство состояний. Преобразование координат состояния.
Решение уравнений состояния. Решение однородного и неоднородного уравнения систем в пространстве состояний: переходной оператор и матричная весовая функция. Случай стационарных систем – матричная экспонента. Методы нахождения матричной экспоненты – метод суммирования ряда, прямой интерполяционный метод – обращение матрицы Вандермонда, формула Сильвестра. Резольвентная матрица. Алгоритм Леверье-Фаддеева.
Дискретные модели систем. Переход от непрерывных моделей к дискретным. Z-преобразование и передаточные функции дискретных систем. Дискретные системы в пространстве состояний.
Системные свойства динамических моделей. Понятие управляемости и достижимости. Критерий Калмана. Грамианы матриц – управляемость и достижимость стационарных и нестационарных систем. Понятие наблюдаемости и восстанавливаемости. Критерии Калмана. Грамианы матриц – наблюдаемость и достижимость стационарных и нестационарных систем. Канонические формы управляемости и наблюдаемости и каноническая декомпозиция систем.
Обратная связь по состоянию. Постановка задачи об управлении системами в пространстве состояний. Существование регулятора. Нестационарные регуляторы. Стационарный регулятор. Задача наблюдения – нестационарные наблюдатели. Стационарный асимптотический наблюдатель. Наблюдатель пониженной размерности. Общая задача модального управления. Синтез наблюдателя и регулятора в системе с обратной связью.
- Исследование операций