Джеймс трефил

Вид материала

Закон

Содержание Дрейф генов Молекулярные часы Годфри харолд харди Вильгельм вайнберг Атомная теория отроения вещества Механическая теория теплоты Идеального газа Жак александр сезар шарль Майкл фарадей Отрезок прямой, соединяющий Солнце и планету, отсекает равные площади за равные промежутки времени Принцип коперника Закон сохранения момента импульса Первый закон Второй закон Третий закон Иоганн кеплер Закон сохранения Открытие электрона Густав роберт кирхгоф Открытие кирхгофа—бунзена). ... Полное содержание

Подобный материал:

• Джеймс А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон, 42.79kb.
• Джеймс блиш города в полете 1-4 триумф времени вернись домой, землянин жизнь ради звезд, 10495.38kb.
• Джеймс Н. Фрей. Как написать гениальный роман, 2872.12kb.
• Мюриел Джеймс, Дороти Джонгвард, 4810.7kb.
• Кен Арнольд Джеймс Гослинг, 5058.04kb.
• Джеймс Джодж Бойл. Секты-убийцы (Главы из книги) Перевод с английского Н. Усовой, 844.92kb.
• Джеймс Хэрриот, 3697.74kb.
• В. К. Мершавки Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 1972.4kb.
• В. К. Мершавки   Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 5237.48kb.
• Джеймс Боллард, 2244.23kb.

ЗАКОН


1920-е
ХАРДИ—ВАЙНБЕРГА


1953

ДРЕЙФ ГЕНОВ


нач. 1960-х

ДНК


1961

РОДСТВЕННЫЙ ОТБОР


1970-е
ГЕНЕТИЧЕСКИЙ КОД


2000

МОЛЕКУЛЯРНЫЕ ЧАСЫ


ПРОЕКТ ГЕНОМА

ЧЕЛОВЕКА


В научном мире нечасто случается, чтобы разные ученые независимо друг от друга наткнулись на одну и ту же закономерность, но все же таких примеров достаточно, чтобы заставить нас поверить в существование «духа времени». К их числу относится и закон Харди—Вайн-берга (известный также, как закон генетического равновесия) — одна из основ популяционной генетики. Закон описывает распределение генов в популяции. Представьте себе ген, имеющий два варианта, или, пользуясь научной терминологией, два аллеля. Например, это могут быть гены «низкорослости» и «высокорослости», как в случае мен-делевского гороха (см. законы менделя), или наличие/отсутствие предрасположенности к рождению двойни. Харди и Вайнберг показали, что при свободном скрещивании, отсутствии миграции особей и отсутствии мутаций относительная частота индивидуумов с каждым из этих аллелей будет оставаться в популяции постоянной из поколения в поколение. Другими словами, в популяции не будет дрейфа генов.

Рассмотрим этот закон на простом примере. Назовем два аллеля Х и х. Тогда у особей могут встречаться четыре следующие комбинации этих аллелей: ХХ, хх, хХ и Хх. Если обозначить через р и д частоту встречаемости индивидуумов с аллелями Х и х соответственно, то согласно закону Харди—Вайнберга

р² + 2рд + д² = 100%,

где р² — частота встречаемости индивидуумов с аллелями ХХ, 2рд — с аллелями Хх или хХ, а д² — частота встречаемости индивидуумов с аллелями хх. Эти частоты при соблюдении сформулированных выше условий будут оставаться постоянными из поколения в поколение, независимо от изменения количества индивидуумов и от того, насколько велики (или малы) р и д. Этот закон представляет собой модель, используя которую генетики могут количественно определять изменения в распределении генов в популяции, вызванные, например, мутациями или миграцией. Другими словами, этот закон является теоретическим критерием для измерения изменений в распределении генов.


ГОДФРИ ХАРОЛД ХАРДИ (Godfrey Harold Hardy, 1877-1947) — английский математик, родился в Кранли, графство Суррей. Сын учителя рисования. Изучал математику в Кембриджском и Оксфордском университете. Пожалуй, самую большую известность Харди принесли совместные работы с Джоном Идензором Литлвудом (John Edensor Littlewood, 1885-1977) и позднее с индийским математиком-самоучкой Сриниваса Рамануджаном (Srinivasa Aaiyangar Ramanujan, 1887-1920), который работал клерком в Мадрасе. В 1913 году Рамануджан послал Харди список доказанных им теорем. Признав гениальность юного клерка, Харди пригласил его в Оксфорд, и в

течение нескольких лет, предшествовавших безвременной смерти Рама-нуджана, они опубликовали серию блестящих совместных работ.

ВИЛЬГЕЛЬМ ВАЙНБЕРГ (Wilhelm Weinberg, 1862-1937) — немецкий врач, имевший большую частную практику в Штутгарте. По воспоминаниям современников, помог появиться на свет 3500 младенцам, в том числе по крайней мере 120 парам близнецов. На основании собственных наблюдений над рождением близнецов и переоткрытых генетических

ЗАКОНОВ МЕНДЕЛЯ пришел к выводу,

что предрасположенность к рождению двуяйцевых (неидентичных) близнецов передается по наследству.

ок. 420 до н.э.
Закон Шарля

При постоянном давлении объем газа пропорционален его температуре


•

АТОМНАЯ ТЕОРИЯ ОТРОЕНИЯ ВЕЩЕСТВА

1662 • ЗАКОН


•

1787
БОЙЛЯ—МАРИОТТА


1798

ЗАКОН ШАРЛЯ


1827

МЕХАНИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ


1834

БРОУНОВСКОЕ ДВИЖЕНИЕ


УРАВНЕНИЕ

СОСТОЯНИЯ


1849
ИДЕАЛЬНОГО ГАЗА


МОЛЕКУЛЯРНО-

КИНЕТИЧЕСКАЯ ТЕОРИЯ


Один из пионеров воздухоплавания Жак Александр Сезар Шарль пришел в науку в результате своего увлечения строительством монгольфьеров — больших воздушных шаров, заполненных разогретым воздухом, — которые тогда только-только появились. Я беседовал с современными пилотами воздушных шаров, и они утверждают, что их конструкция с использованием открытой газовой горелки, разработанная Шарлем более двух столетий назад, не претерпела принципиальных изменений и используется до наших дней. Ничего удивительного в том, что научные интересы Шарля лежали в области исследования свойств газов, стало быть, нет. Закон, носящий его имя, Шарль сформулировал в 1787 году после ряда опытов с кислородом, азотом, водородом и углекислым газом.

Чтобы понять смысл закона Шарля, представьте себе газ как скопление быстро движущихся и соударяющихся молекул. Давление газа определяется ударами молекул о стенки сосуда: чем больше ударов, тем выше давление. Например, молекулы воздуха в комнате, где вы находитесь, оказывают на поверхность вашего тела давление 101 325 паскалей (или 1 бар, если речь идет о метеорологии).

Чтобы понять закон Шарля, представьте себе воздух внутри воздушного шарика. При постоянной температуре воздух в шарике будет расширяться или сжиматься, пока давление, производимое его молекулами, не достигнет 101 325 паскалей и не сравняется с атмосферным давлением. Иными словами, пока на каждый удар молекулы воздуха извне, направленный внутрь шарика, не будет приходиться аналогичный удар молекулы воздуха, направленный изнутри шарика вовне. Если понизить температуру воздуха в шарике (например, положив его в большой холодильник), молекулы внутри шарика станут двигаться медленнее, менее энергично ударяя изнутри о стенки шарика. Молекулы наружного воздуха тогда будут сильнее давить на шарик, сжимая его, в результате объем газа внутри шарика будет уменьшаться. Это будет происходить до тех пор, пока увеличение плотности газа не компенсирует понизившуюся температуру, и тогда опять установится равновесие.

Закон Шарля, наряду с другими газовыми законами, лег в основу уравнения состояния идеального газа, описывающего соотношение давления, объема и температуры газа с количеством вещества.


ЖАК АЛЕКСАНДР СЕЗАР ШАРЛЬ

(Jacques Alexandre César Charles, 1746-1823) — французский физик, химик, инженер и воздухоплаватель. Родился в Божанси (Beaugency). В молодости служил чиновником в министерстве финансов в Париже. Заинтересовавшись воздухоплаванием,разработал монгольфьеры современной конструкции, подъемная сила которых обусловлена расширением нагретого

горелкой воздуха внутри шара. Он же одним из первых стал наполнять воздушные шары водородом (который во много раз легче воздуха и обеспечивает значительно большую подъемную силу, нежели горячий воздух), установив благодаря этому рекорды высоты подъема (более 3 000 м) и дальности полета (43 км). Именно занятия воздухоплаванием заставили Шарля заинтересоваться исследованиями свойств газов.



МАЙКЛ ФАРАДЕЙ (Michael Faraday, 1791-1867) — английский физик и химик. Родился в Лондоне в семье простого кузнеца, принадлежащего к маленькой протестантской секте. Возможностей для получения хорошего образования, учитывая происхождение и социальное устройство Англии начала XIX века, был лишен. Окончив всего лишь бесплатную начальную школу, с 12 лет работал посыльным в книжном магазине, с 14 лет стал подмастерьем переплетчика там же и неожиданно для себя заинтересовался содержанием умных книг, которые ему приходилось переплетать. Интерес к науке в юноше пробудили естественнонаучные разделы «Британской энциклопедии», попавшей в переплет к нему. В 1810 году Фарадею повезло — один из постоянных посетителей книжного магазина подарил любознательному молодому человеку абонемент на цикл из четырех публичных лекций с демонстрациями опытов одного из ведущих английских химиков того времени, профессора Королевского института, сэра Гемфри (Хамфри) Дэви (Humphry Davy,

1778-1829).

Фарадей, успев посетить лишь последние четыре лекции, так увлекся естественными науками, что свои подробные конспекты посещенных им четырех лекций переплел в кожу и... отправил сэру Дэви в

качестве подтверждения серьезности своих намерений вместе с письмом с просьбой помочь ему в реализации стремления заняться наукой. В 1813 году сэр Дэви сделал Фарадея своим ассистентом в Королевском институте, и тут молодой ученый проявил себя настолько блестяще, что теперь его считают самым выдающимся британским ученым Викторианской эпохи; сама королева Виктория регулярно удостаивала ученого личной аудиенции. Величайшие открытия Фарадея относятся к области выявления связей между электричеством и магнетизмом. Кроме того, он сформулировал законы электролиза, носящие его имя, разработал принципиальное техническое решение по генерации электроэнергии. Первоначально же, еще занимаясь преимущественно химией, Фарадей первым получил сжиженный хлор и ряд других газов, открыл формулу бензола. Столь выдающийся вклад в науку Фарадею удалось внести, прежде всего, благодаря тому, что он был изобретательным экспериментатором, не боявшимся проводить опыты, ставившие под сомнение устоявшиеся научные представления своей эпохи. Он был также выдающимся популяризатором науки: в 1826 году организовал при Королевском институте ежегодные циклы лекций для детей, которые читаются и сегодня.


Законы Кеплера

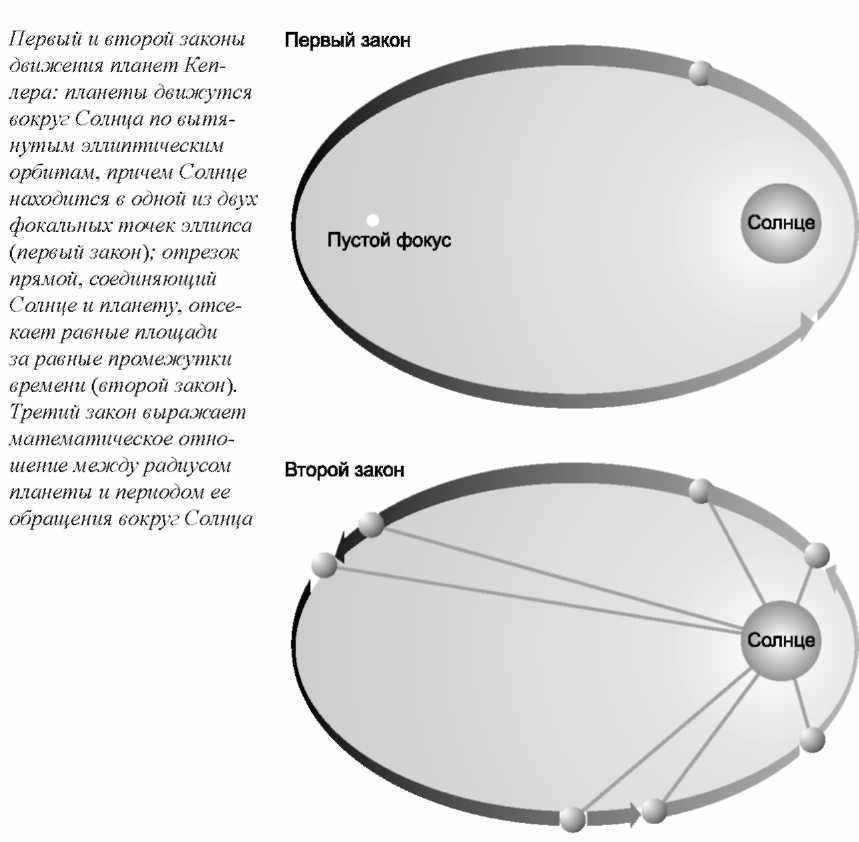
Планеты движутся вокруг Солнца по вытянутым эллиптическим орбитам, причем Солнце находится в одной из двух фокальных точек эллипса

Отрезок прямой, соединяющий Солнце и планету, отсекает равные площади за равные промежутки времени

Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит


XVI

1609, 1619

•

1687
ПРИНЦИП КОПЕРНИКА ЗАКОНЫ КЕПЛЕРА


1687
ЗАКОНЫ МЕХАНИКИ НЬЮТОНА


1736
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ НЬЮТОНА


* Между сферами Марса и Земли — додекаэдр (двенадцатигранник); между сферами Земли и Венеры — икосаэдр (двадцатигранник); между сферами Венеры и Меркурия — октаэдр (восьмигранник). Получившаяся конструкция была представлена Кеплером в разрезе на подробном объемном чертеже (см. рисунок) в его первой монографии «Космографическая тайна» (Муйегіа СсйшсгарЫса 1596 —Прим. переводчика?)

ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА


Иоганн Кеплер обладал чувством прекрасного. Всю свою сознательную жизнь он пытался доказать, что Солнечная система представляет собой некое мистическое произведение искусства. Сначала он пытался связать ее устройство с пятью правильными многогранниками классической древнегреческой геометрии. (Правильный многогранник — объемная фигура, все грани которой представляют собой равные между собой правильные многоугольники.) Во времена Кеплера было известно шесть планет, которые, как полагалось, помещались на вращающихся «хрустальных сферах». Кеплер утверждал, что эти сферы расположены таким образом, что между соседними сферами точно вписываются правильные многогранники. Между двумя внешними сферами — Сатурна и Юпитера — он поместил куб, вписанный во внешнюю сферу, в который, в свою очередь, вписана внутренняя сфера; между сферами Юпитера и Марса — тетраэдр (правильный четырехгранник) и т.д.* Шесть сфер планет, пять вписанных между ними правильных многогранников — казалось бы, само совершенство?

Увы, сравнив свою модель с наблюдаемыми орбитами планет, Кеплер вынужден был признать, что реальное поведение небесных тел не вписывается в очерченные им стройные рамки. По меткому замечанию современного британского биолога Дж. Холдейна (J. B. S. Haldane), «идея Вселенной как геометрически совершенного произведения искусства оказалась еще одной прекрасной гипотезой, разрушенной уродливыми фактами». Единственным пережившим века результатом того юношеского порыва Кеплера стала модель Солнечной системы, собственноручно изготовленная ученым и преподнесенная в дар его патрону герцогу Фредерику фон Вюртембургу. В этом прекрасно исполненном металлическом артефакте все орбитальные сферы планет и вписанные в них правильные многогранники представляют собой не сообщающиеся между собой полые емкости, которые по праздникам предполагалось заполнять различными напитками для угощения гостей герцога.

Лишь переехав в Прагу и став ассистентом знаменитого датского астронома Тихо Браге (Tycho Brahe, 1546-1601), Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки. Тихо Браге всю жизнь собирал данные астрономических наблюдений и накопил огромные объемы сведений о движении планет. После его смерти они перешли в распоряжение Кеплера. Эти записи, между прочим, имели большую коммерческую ценность по тем временам, поскольку их можно было использовать для составления уточненных астрологических гороскопов (сегодня об этом разделе ранней астрономии ученые предпочитают умалчивать).

Обрабатывая результаты наблюдений Тихо Браге, Кеплер столкнулся с проблемой, которая и при наличии современных компьютеров могла бы показаться кому-то трудноразрешимой, а у Кеплера не было иного выбора, кроме как проводить все расчеты вручную. Конечно же, как и большинство астрономов его времени, Кеплер уже был знаком с гелиоцентрической системой Коперника (см. принцип







** Исторически сложи­лось так, что законы Кеп­лера (подобно началам термодинамики) пронуме­рованы не по хронологии их открытия, а в порядке их осмысления в научных кругах. Реально же первый закон был открыт в 1605 году (опубликован в 1609 году), второй — в 1602 году (опубликован в 1609 году), третий — в 1618 году (опубликован в 1619 году). — Прим. переводчика.

Коперника) и знал, что Земля вращается вокруг Солнца, о чем свидетельствует и вышеописанная модель Солнечной системы. Но как именно вращается Земля и другие планеты? Представим проблему следующим образом: вы находитесь на планете, которая, во-первых, вращается вокруг своей оси, а во-вторых, вращается вокруг Солнца по неизвестной вам орбите. Глядя в небо, мы видим другие планеты, которые также движутся по неизвестным нам орбитам. Наша задача — определить по данным наблюдений, сделанных на нашем вращающемся вокруг своей оси и вокруг Солнца земном шаре, геометрию орбит и скорости движения других планет. Именно это в конечном итоге удалось сделать Кеплеру, после чего на основе полученных результатов он и вывел три своих закона!

Первый закон* * описывает геометрию траекторий планетарных орбит. Возможно, вы помните из школьного курса геометрии, что эллипс представляет собой множество точек плоскости, сумма расстояний от которых до двух фиксированных точек — фокусов — равна константе. Если это слишком сложно для вас, имеется другое определение: представьте себе сечение боковой поверхности конуса плоскостью под углом к его основанию, не проходящей через основание, — это тоже эллипс. Первый закон Кеплера как раз и утверждает, что орбиты планет представляют собой эллипсы, в одном из фокусов которых расположено Солнце. Эксцентриситеты (степень вытянутости) орбит и их удаления от Солнца в перигелии (бли-


ТЗчЗйшЕ* жайшей к Солнцу точке) и апогелии (самой удаленной точке) у всех

§планет разные, но все эллиптические орбиты роднит одно — Солнце расположено в одном из двух фокусов эллипса. Проанализировав данные наблюдений Тихо Браге, Кеплер сделал вывод, что плане-ДйУ тарные орбиты представляют собой набор вложенных эллипсов. До него это просто не приходило в голову никому из астрономов. щШФ* 'ЧЗрК Историческое значение первого закона Кеплера трудно переоце-ЧС" ;~р£? нить. До него астрономы считали, что планеты движутся исключи-I тельно по круговым орбитам, а если это не укладывалось в рамки р_{анняя геомет}р_{ическая} наблюдений — главное круговое движение дополнялось малыми модель Вселенной Кеп- кругами, которые планеты описывали вокруг точек основной кру-^{лера: шесть орбитальных} говой орбиты. Это было, я бы сказал, прежде всего философской

планетных сфер и пять

позицией, своего рода непреложным фактом, не подлежащим сом-

вписанных правильных многогранников между ними ^{нению и проверке.} Ф^ил°^с°^фЫ ^{утверждали,} что ^{небесное устройство}

в отличие от земного совершенно по своей гармонии, а поскольку совершеннейшими из геометрических фигур являются окружность и сфера, значит, планеты движутся по окружности (причем это заблуждение мне и сегодня приходится раз за разом развеивать среди своих студентов). Главное, что, получив доступ к обширным данным наблюдений Тихо Браге, Иоганн Кеплер сумел перешагнуть через этот философский предрассудок, увидев, что он не соответствует фактам — подобно тому как Коперник осмелился убрать Землю из центра мироздания, столкнувшись с противоречащими стойким геоцентрическим представлениям аргументами, которые также состояли в «неправильном поведении» планет на орбитах.

Второй закон описывает изменение скорости движения планет вокруг Солнца. В формальном виде я его формулировку уже приводил, а чтобы лучше понять его физический смысл, вспомните свое детство. Наверное, вам доводилось на детской площадке раскручиваться вокруг столба, ухватившись за него руками. Фактически, планеты кружатся вокруг Солнца аналогичным образом. Чем дальше от Солнца уводит планету эллиптическая орбита, тем медленнее движение, чем ближе к Солнцу — тем быстрее движется планета. Теперь представьте пару отрезков, соединяющих два положения планеты на орбите с фокусом эллипса, в котором расположено Солнце. Вместе с сегментом эллипса, лежащим между ними, они образуют сектор, площадь которого как раз и является той самой «площадью, которую отсекает отрезок прямой». Именно о ней говорится во втором законе. Чем ближе планета к Солнцу, тем короче отрезки. Но в этом случае, чтобы за равное время сектор покрыл равную площадь, планета должна пройти большее расстояние по орбите, а значит, скорость ее движения возрастает.

В первых двух законах речь идет о специфике орбитальных траекторий отдельно взятой планеты. Третий закон Кеплера позволяет сравнить орбиты планет между собой. В нем говорится, что, чем дальше от Солнца находится планета, тем больше времени занимает ее полный оборот при движении по орбите и тем дольше, соответственно, длится «год» на этой планете. Сегодня мы знаем, что это обусловлено двумя факторами. Во-первых, чем дальше планета находится






законы кеплера


ИОГАНН КЕПЛЕР

(Johannes Kepler, 1572-1630) — немецкий астроном. Родился в Вюртембурге. Начав с изучения богословия в Тюбингенской академии (позднее университет), увлекся математикой и астрономией и вскоре получил приглашение на должность преподавателя математики в гимназии австрийского города Грац. Там он снискал себе репутацию блестящего астролога благодаря ряду сбывшихся метеорологических прогнозов на 1595 год. Начиная с 1598 года Кеплер и другие протестанты стали подвергаться в католическом Граце жестоким религиозным гонениям, и в 1600 году ученый по приглашению датского астронома Тихо Браге переехал в Прагу. Работы Кеплера основывались на наблюдениях, сделанных Тихо Браге. Его дальнейшая жизнь сложилась трагично. Он жил в бедности и умер от лихорадки по дороге в Австрию, куда он отправился в надежде получить причитающееся ему жалованье.


от Солнца, тем длиннее периметр ее орбиты. Во-вторых, с ростом расстояния от Солнца снижается и линейная скорость движения планеты.

В своих законах Кеплер просто констатировал факты, изучив и обобщив результаты наблюдений. Если бы вы спросили его, чем обусловлена эллиптичность орбит или равенство площадей секторов, он бы вам не ответил. Это просто следовало из проведенного им анализа. Если бы вы спросили его об орбитальном движении планет в других звездных системах, он также не нашел бы, что вам ответить. Ему бы пришлось начинать все сначала — накапливать данные наблюдений, затем анализировать их и стараться выявить закономерности. То есть у него просто не было бы оснований полагать, что другая планетная система подчиняется тем же законам, что и Солнечная система.

Один из величайших триумфов классической механики Ньютона как раз и заключается в том, что она дает фундаментальное обоснование законам Кеплера и утверждает их универсальность. Оказывается, законы Кеплера можно вывести из законов механики ньютона, закона всемирного тяготения ньютона

и закона сохранения момента импульса путем строгих

математических выкладок. А раз так, мы можем быть уверены, что законы Кеплера в равной мере применимы к любой планетной системе в любой точке Вселенной. Астрономы, ищущие в мировом пространстве новые планетные системы (а открыто их уже довольно много), раз за разом, как само собой разумеющееся, применяют уравнения Кеплера для расчета параметров орбит далеких планет, хотя и не могут наблюдать их непосредственно.

Третий закон Кеплера играл и играет важную роль в современной космологии. Наблюдая за далекими галактиками, астрофизики регистрируют слабые сигналы, испускаемые атомами водорода, обращающимися по очень удаленным от галактического центра орбитам — гораздо дальше, чем обычно находятся звезды. По эффекту доплера в спектре этого излучения ученые определяют скорости вращения водородной периферии галактического диска, а по ним — и угловые скорости галактик в целом (см. также темная материя). Меня радует, что труды ученого, твердо поставившего нас на путь правильного понимания устройства нашей Солнечной системы, и сегодня, спустя века после его смерти, играют столь важную роль в изучении строения необъятной Вселенной.


Законы Кирхгофа

Алгебраическая сумма токов в любом узле электрической цепи равна нулю (то есть количество зарядов, выходящих через этот узел, должно быть равно количеству входящих зарядов)

Сумма напряжений в любом замкнутом контуре


•
электрической цепи равна нулю

1747

ЗАКОН СОХРАНЕНИЯ

ЭЛЕКТРИЧЕСКОГО


ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ВЕЩЕСТВА

ЗАКОНЫ КИРХГОФА
ЗАРЯДА


XIX


ОТКРЫТИЕ ЭЛЕКТРОНА

1845


ЭЛЕКТРОННАЯ ТЕОРИЯ

ПРОВОДИМОСТИ
1897

1900


Карьера Густава Кирхгофа во многом типична для немецкого физика XIX столетия. Германия позже своих западных соседей подошла к индустриальной революции и потому сильнее нуждалась в передовых технологиях, которые способствовали бы ускоренному развитию промышленности. В результате ученые, прежде всего естественники, ценились в Германии очень высоко. В год окончания университета Кирхгоф женился на дочери профессора, «соблюдя, тем самым, — как пишет один из его биографов, — два обязательных условия успешной академической карьеры». Но еще до этого, в возрасте двадцати одного года, он сформулировал основные законы для расчета токов и напряжений в электрических цепях, которые теперь носят его имя.

Середина XIX века как раз стала временем активных исследований свойств электрических цепей, и результаты этих исследований быстро находили практические применения. Базовые правила расчета простых цепей, такие, как закон ома, были уже достаточно хорошо проработаны. Проблема состояла в том, что из проводов и различных элементов электрических цепей технически уже можно было изготовлять весьма сложные и разветвленные сети — но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгофу удалось сформулировать правила, позволяющие достаточно просто анализировать самые сложные цепи, и законы Кирхгофа до сих пор остаются важным рабочим инструментом специалистов в области электронной инженерии и электротехники.

Оба закона Кирхгофа формулируются достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если рассмотреть любой узел цепи (то есть точку разветвления, где сходятся три или более проводов), то сумма поступающих в цепь электрических токов будет равна сумме исходящих, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если вы имеете Т-образный узел электрической цепи и по двум проводам к нему поступают электрические токи, то по третьему проводу ток потечет в направлении от этого узла, и равен он будет сумме двух поступающих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.

Второй закон не менее прост. Если мы имеем сложную разветвленную цепь, ее можно мысленно разбить на ряд простых замкнутых контуров. Ток в цепи может различным образом распределяться по этим контурам, и сложнее всего определить, по какому именно маршруту потекут токи в сложной цепи. В каждом из контуров электроны могут либо приобретать дополнительную энергию (например, от батареи), либо терять ее (например, на сопротивлении или ином элементе). Второй закон Кирхгофа гласит, что чистое приращение энергии электронов в любом замкнутом контуре цепи равно нулю. Этот закон также имеет простую физи-


ческую интерпретацию. Если бы это было не так, всякий раз, проходя через замкнутый контур, электроны приобретали или теряли бы энергию, и ток бы непрерывно возрастал или убывал. В первом случае можно было бы получить вечный двигатель, а это запрещено первым началом термодинамики; во втором — любые токи в электрических цепях неизбежно затухали бы, а этого мы не наблюдаем.

Самое распространенное применение законов Кирхгофа мы наблюдаем в так называемых последовательных и параллельных цепях. В последовательной цепи (яркий пример такой цепи — елочная гирлянда, состоящая из последовательно соединенных между собой лампочек) электроны от источника питания по серии проводов последовательно проходят через все лампочки, и на сопротивлении каждой из них напряжение падает согласно закону Ома.

В параллельной цепи провода, напротив, соединены таким образом, что на каждый элемент цепи подается равное напряжение от источника питания, а это означает, что в каждом элементе цепи сила тока своя в зависимости от его сопротивления. Примером параллельной цепи являются лампы «лесенкой»: напряжение подается на шины, а лампы смонтированы на поперечинах. Токи, проходящие через каждый узел такой цепи, определяются по второму закону Кирхгофа.



ГУСТАВ РОБЕРТ КИРХГОФ (Gustav Robert Kirchhof, 1824-77) — немецкий физик. Родился в Кенигсберге (современный Калининград). Законы расчета электрических цепей сформулировал еще будучи студентом Кёниг-сбергского университета. Продолжил свою блестящую карьеру в ряде германских университетов, последним из которых стал Берлинский, где он был профессором теоретической физики с 1875 года и до своей смерти. В период работы в университете г. Бреслау (на

территории современной Польши) совместно с Робертом Бунзеном разработал основы спектроскопии (см.

ОТКРЫТИЕ КИРХГОФА—БУНЗЕНА).

Кроме того, он открыл еще один цикл законов (названы его именем), описывающих тепловое поглощение и излучение. Хотя вторую половину своей жизни Кирхгоф в результате несчастного случая провел в инвалидной коляске, все современники отзывались о нем, как о приятнейшем человеке и убежденном оптимисте.

1920-е

нач. 1960-х

1970-е

Законы Менделя

Наследственные признаки передаются из поколения в поколение с помощью генов


1865
Потомки получают от каждого родителя по одному гену, кодирующему признак


1908