Джеймс трефил

Вид материала

Закон

Содержание Георг симон ом Закон отражения обета Массовые вымирания Закон сохранения Закон сохранения

Подобный материал:

• Джеймс А. Дискретная математика и комбинаторика [Текст] / Джеймс А. Андерсон, 42.79kb.
• Джеймс блиш города в полете 1-4 триумф времени вернись домой, землянин жизнь ради звезд, 10495.38kb.
• Джеймс Н. Фрей. Как написать гениальный роман, 2872.12kb.
• Мюриел Джеймс, Дороти Джонгвард, 4810.7kb.
• Кен Арнольд Джеймс Гослинг, 5058.04kb.
• Джеймс Джодж Бойл. Секты-убийцы (Главы из книги) Перевод с английского Н. Усовой, 844.92kb.
• Джеймс Хэрриот, 3697.74kb.
• В. К. Мершавки Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 1972.4kb.
• В. К. Мершавки   Доктор Джеймс Холлис известный юнгианский аналитик, директор Центра, 5237.48kb.
• Джеймс Боллард, 2244.23kb.

ГЕОРГ СИМОН ОМ (Georg Simon Ohm, 1789-1854) — немецкий физик. Родился в Эрлангене в 1789 году (по другим источникам — в 1787-м). Окончил местный университет. Преподавал математику и естественные науки. Признание в академических кругах получил достаточно поздно, лишь в 1849 году став профессором Мюнхенского университета, хотя уже в 1827 году сформулировал и опубликовал закон, который теперь носит его имя. Помимо электричества, занимался акустикой и изучением человеческого слуха.

ок. 100 н.э.
Закон

отражения

света

Отраженный и падающий лучи лежат в плоскости, содержащей перпендикуляр к отражающей поверхности в точке падения, и угол падения равен углу отражения


1621

ЗАКОН ОТРАЖЕНИЯ ОБЕТА


принцип ферма
закон снеллиуса

1650 _•

1690 принцип гюйгенса 1807 _•


1815
интерференция


1818

закон брюстера


дифракция


Представьте, что вы направили тонкий луч света на отражающую поверхность, — например, посветили лазерной указкой на зеркало или полированную металлическую поверхность. Луч отразится от такой поверхности и будет распространяться дальше в определенном направлении. Угол между перпендикуляром к поверхности (нормалью) и исходным лучом называется углом падения, а угол между нормалью и отраженным лучом — углом отражения. Закон отражения гласит, что угол падения равен углу отражения. Это полностью соответствует тому, что нам подсказывает интуиция. Луч, падающий почти параллельно поверхности, лишь слегка коснется ее и, отразившись под тупым углом, продолжит свой путь по низкой траектории, расположенной близко к поверхности. Луч, падающий почти отвесно, с другой стороны, отразится под острым углом, и направление отраженного луча будет близким к направлению падающего луча, как того и требует закон.

Закон отражения, как любой закон природы, был получен на основании наблюдений и опытов. Можно его вывести и теоретически — формально он является следствием принципа ферма (но это не отменяет значимости его экспериментального обоснования).

Ключевым моментом в этом законе является то, что углы отсчи-тываются от перпендикуляра к поверхности в точке падения луча. Для плоской поверхности, например, плоского зеркала, это не столь важно, поскольку перпендикуляр к ней направлен одинаково во всех точках. Параллельно сфокусированный световой сигнал — например, свет автомобильной фары или прожектора, — можно рассматривать как плотный пучок параллельных лучей света. Если такой пучок отразится от плоской поверхности, все отраженные лучи в пучке отразятся под одним углом и останутся параллельными. Вот почему прямое зеркало не искажает ваш визуальный образ.

Однако имеются и кривые зеркала. Различные геометрические конфигурации поверхностей зеркал по-разному изменяют отраженный образ и позволяют добиваться различных полезных эффектов. Главное вогнутое зеркало телескопа-рефлектора позволяет сфокусировать в окуляре свет от далеких космических объектов. Выгнутое зеркало заднего вида автомобиля позволяет расширить угол обзора. А кривые зеркала в комнате смеха позволяют от души повеселиться, разглядывая причудливо искаженные отражения самих себя.

Закону отражения подчиняется не только свет. Любые электромагнитные волны — радио, СВЧ, рентгеновские лучи и т. п. — ведут себя в точности так же. Вот почему, например, и огромные принимающие антенны радиотелескопов, и тарелки спутникового телевидения имеют форму вогнутого зеркала — в них используется все тот же принцип фокусировки поступающих параллельных лучей в точку.

1890, 1940-е

ок. 1930, 1980

1960-е
Закон последовательности напластования горных пород

В ненарушенных осадочных породах чем слой ниже, тем он древнее


1788

1666 закон последовательности напластования горных пород


кон. XVIII

униформизм


цикл преобразования горной породы


радиометрическое датирование

МАССОВЫЕ ВЫМИРАНИЯ

тектоника плит


Один из наиболее впечатляющих примеров осадочных пород

(см. цикл преобразования горной породы) можно увидеть

в Большом Каньоне в Аризоне, где яркие разноцветные горные породы располагаются одна над другой слой за слоем, а между ними — миллионы лет геологической истории. Осадочные породы образуются в виде горизонтальных слоев из ила и других отложений на дне океанов и озер. Естественно, новые слои откладываются поверх более старых. Рассматривая все более и более глубокие слои в Большом Каньоне (или другом подобном месте), мы увидим все более и более древние породы — по сути дела, мы будем двигаться назад во времени.

Этот закон напластования горных пород стал первым инструментом палеонтологов в процессе изучения истории жизни на нашей планете. Сегодня он кажется нам очевидным. Однако в XVII веке, когда он впервые был высказан, сама мысль о том, что у Земли есть долгое геологическое прошлое, в течение которого она значительно изменялась, была просто революционной. Позднее, в начале XIX века, пришла другая важная мысль: если нижние отложения древнее верхних, то те формы жизни, остатки которых найдены в нижних слоях, должны были появиться раньше тех, которые найдены в верхних слоях. Это — закон последовательной смены комплексов животных и растений во времени. (Напомним, что это было время, когда многие считали идею эволюции противоречащей религии, даже еретической.) История отдельного вида растений или животных начинается, когда находят самый ранний слой отложений, содержащий остатки этих растений (животных), а период исчезновения данного вида определятся по самому позднему слою, в котором еще есть эти остатки. Вооружившись данным законом и законом напластования горных пород, палеонтологи стали определять относительный возраст пластов горной породы по ископаемым остаткам, которые содержались в этих пластах.

Если последовательность отложений не нарушена и содержит достаточное количество окаменелостей, можно проследить превращение одного вида организма в другой — иными словами, проследить за ходом естественного отбора в процессе эволюции. Правда, ископаемые остатки обычно не слишком хорошо сохраняются (хотя во всем мире есть несколько мест с подходящими для этого условиями). Обычно же можно увидеть только отпечатки ископаемых организмов, да и то разрозненные, и палеонтологам приходится прибегать к теоретическим рассуждениям, чтобы связать свою находку с тем, что действительно происходило в прошлом. Например, довольно часто какой-нибудь вид находят в нескольких нижних пластах, затем в нескольких последующих пластах его не обнаруживают, а затем вновь находят в вышележащих пластах. Очевидно, что данный вид существовал в течение всего этого периода времени, но не сохранился в виде окаменелостей в промежуточных слоях. (Этот феномен был назван «эффектом Лазаря»


Верхний пласт глины в этой геологической формации в Норфолке (Англия) лежит поверх более ранних пластов песчаника. Это наглядно иллюстрирует принцип последовательности напластования горных пород, который гласит: чем ниже расположен слой, тем раньше он сформировался.


по аналогии с библейским преданием о воскрешении человека из мертвых.)

Несколько слов предостережения. Во-первых, закон напластования горных пород не позволяет точно указать момент времени, когда сформировались отложения — с его помощью можно определить только относительный возраст различных слоев. Чтобы определить абсолютный возраст, необходимо радиометрическое датирование. Во-вторых, слово «ненарушенный» в формулировке принципа чрезвычайно важно. Поскольку поверхность Земли постоянно меняется (см. т екто ника пл и т ), осадочные породы, сформировавшись, впоследствии могут образовать складку, а в месте складки более древние породы окажутся выше более молодых.






Закон Снеллиуса

Угол преломления луча при прохождении границы между двумя средами зависит от соотношения коэффициентов преломления этих сред


1621 ЗАКОН ОНЕЛЛИуОА


1650 принцип ферма


1864 спектр электромагнитного излучения


1864 уравнения максвелла


1924 дисперсия:

атомная теория


Виллеброрд Снеллиус открыл простой закон преломления лучей. Полное внутреннее отражение происходит, когда луч падает под критическим или более тупым углом к нормали


теория относительности заставила нас усвоить, что ничто не движется быстрее света, но при этом в данной формулировке имеется одна маленькая хитрость, о которой часто забывают. Теоретики, говоря «скорость света», имеют в виду скорость света в вакууме, которую принято обозначать латинской буквой с, и для них это настолько самоочевидно, что дополнение «в вакууме» они обычно не озвучивают. А ведь при распространении света в прозрачной среде, например, воде или стекле, он движется значительно медленнее скорости с из-за непрерывного взаимодействия с атомами материальной среды.

Так что же происходит с фронтом световой волны при ее прохождении через границу двух прозрачных сред? Ответ на это дает закон Снеллиуса (или «закон Снелля», если следовать не латинскому, а голландскому написанию. — Прим. переводчика), названный по имени голландского естествоиспытателя Вил-леброрда Снеллиуса, впервые сформулировавшего эту закономерность. Важнейший пример такого преломления мы наблюдаем при попадании светового луча из воздуха в стекло и затем снова в воздух — а именно это происходит (причем зачастую неоднократно) в любом оптическом приборе, будь то сложнейшее лабораторное оборудование или банальная пара очков. Представьте себе туристов, идущих гуськом по диагонали через квадратное поле, посередине которого, параллельно двум его сторонам, проходит граница, после которой начинается болото. Понятно, что по чистому полю туристы могут идти быстрее, а по болотной жиже — медленнее. И вот, когда первые туристы доходят до края болота и начинают вязнуть в грязи, скорость их продвижения падает, и они, как нормальные люди, отклоняются от курса, чтобы поскорее добраться до противоположного края болота, в то время как идущие следом движутся с прежней скоростью и в прежнем направлении. По мере залезания в болото все новых туристов они также сбрасывают скорость и начинают срезать угол. В итоге с высоты птичьего полета процессия туристов выглядит преломленной — по полю она идет в одном направлении, а по болоту — в другом. То






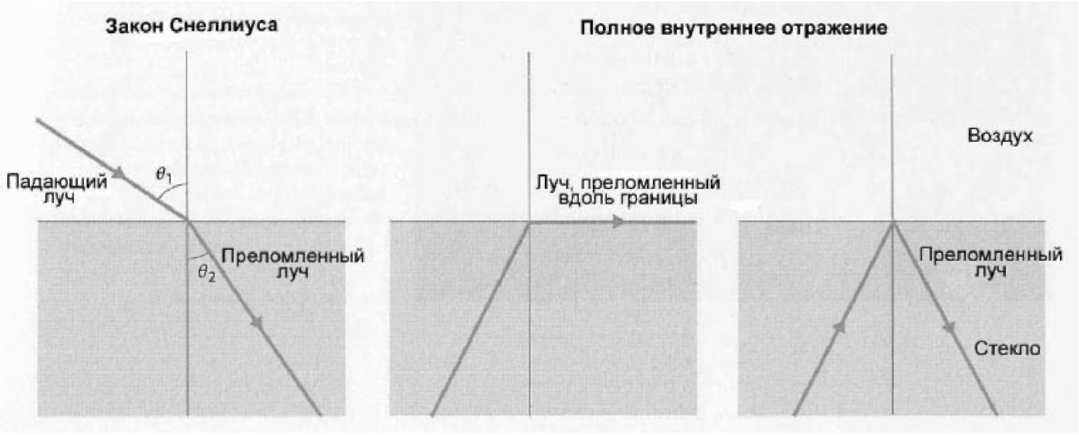
Полное внутреннее отражение

Представьте стеклянный параллелепипед, изнутри которого на одну из его граней падает луч света. При прохождении границы с воздухом луч преломляется и, поскольку коэффициент преломления света в воздухе (около 1) ниже, чем в стекле (около 1,5), луч отклоняется от перпендикуляра (нормали). По закону Снеллиуса, если луч падает на поверхность под углом, например, 30°, по ту сторону границы он выйдет под более тупым углом к нормали (около 49°). По мере увеличения отклонения угла падения от нормали угол преломления будет увеличиваться «опережающими темпами», пока, наконец, при угле падения примерно в 42° расчетный угол преломления не станет равен 90° к перпендикуляру — то есть, попав на поверхность, луч в этом случае не пройдет сквозь нее, а преломится строго вдоль границы между стеклом и воздухом.

Что же случится при дальнейшем увеличении угла падения луча? Угол преломления более 90° по сути означает, что луч не выйдет за пределы стекла и останется внутри стеклянного бруса, — то есть, он не преломится, а отразится от границы стекла с воздухом. Это явление называется полным внутренним отражением. Критический угол определяется из уравнения:

sin в > n₂/n₁.

При значениях в больше критического угла луч света изнутри стекла больше не проникает в воздух, а отражается обратно внутрь стекла, как от зеркала. Явление полного внутреннего отражения вы легко можете пронаблюдать и сами. В следующий раз, ужиная при свечах, возьмите бокал вина и поднимите его высоко над головой, и, рассматривая огонек свечи сквозь поверхность вина, начните его постепенно опускать. Сначала, пока бокал поднят достаточно высоко, пламя свечи будет проблескивать сквозь поверхность вина. Однако в какой-то момент, по мере того как вы опускаете бокал, вы достигнете точки, когда поверхность

вина вдруг сделается абсолютно темной. А все дело в том, что вы достигли критического угла падения луча и свет свечи теперь претерпевает полное внутреннее отражение, в результате чего никакой свет наружу не просачивается. Однако полное внутреннее отражение — это не просто любопытный фокус, а основа для целого ряда важных современных технологий; прежде всего — этот эффект лежит в основе оптоволоконной связи. Свет, поступая с одного конца в тончайшее стекловолокно под очень большим углом, в дальнейшем вынужден распространяться вдоль этого волокна, не покидая его пределов, раз за разом отражаясь от его стенок, поскольку угол его падения не достаточен, чтобы вырваться за его пределы, благодаря чему на противоположном конце выход оптического сигнала практически не теряет в интенсивности. Если связать множество таких оптических волокон в пучок, чередование импульсов света и затемненных промежутков на выходе из такого оптоволоконного кабеля будет строго соответствовать сигналу, поступившему в него на входе. Этот принцип сегодня широко используется в современных медицинских технологиях, в частности в артроскопии, когда тонкий пучок оптических волокон вводится в организм пациента сквозь крохотный надрез или естественное устье и доставляется буквально к самому органу, на котором производится микрохирургическая операция, позволяя хирургу в буквальном смысле видеть на экране монитора, что и как именно он оперирует.

Не менее широкое применение нашло полное внутреннее отражение и в области высокоскоростной передачи информации по оптоволоконным телефонным линиям связи. Посылая модулированные оптические сигналы вместо электромагнитных, мы получаем возможность на несколько порядков ускорить передачу информации по телекоммуникационным сетям. На самом деле во всех по-настоящему индустриально развитых странах мира вся телефония уже переведена на оптоволоконную связь.


же и со световым лучом: если при пересечении границы двух сред скорость света во второй среде ниже, чем скорость света в первой среде, луч отклоняется в сторону нормали (линии, перпендикулярной границе). Если же во второй среде скорость распространения света выше (как, например, при переходе света из стекла в воздух), луч, напротив, отклонится от нормали на больший угол (туристы ускорят шаг и спрямят направление).

Отношение скорости света в вакууме к скорости света в среде называется коэффициентом преломления среды. Так, коэффициент преломления стекла равен примерно 1,5 (зависит от сорта стекла), то есть свет в стекле замедляется примерно на треть по сравнению со скоростью его распространения в вакууме. У каждого прозрачного материала — собственный коэффициент преломления (совпадения, конечно же, возможны, но они ни о чем не говорят).

Закон Снеллиуса устанавливает числовое соотношение между углами падения и преломления луча при переходе из одной среды в другую. Если в₁ и в₂ — углы, соответственно, падения и преломления относительно нормали (см. рисунок) при переходе луча из одной среды в другую, а n₁ и n₂ — коэффициенты преломления этих сред, то имеет место соотношение:

n₁ sin 6_l = n₂ sin в₂.

Смысл этого закона в том, что, если известны коэффициенты преломления света в двух граничащих средах и угол падения луча, можно рассчитать, насколько отклонится луч после пересечения границы между средами.

Доводилось ли вам когда-либо стоять у бортика бассейна и удивляться, отчего это у вашей подруги, стоящей по пояс в воде, ноги кажутся непропорционально короткими? А все дело в том, что световые лучи, которые вы воспринимаете и которые доносят до вас зрительный образ, выйдя из воды и попав в воздух, преломились и достигают ваших глаз под более тупым углом, чем если бы бассейн стоял без воды. Мозг же верит глазам, и вам кажется, что ступни вашей подруги ближе, чем они есть на самом деле.


биллеброрд сиеллиус

(СНЕЯЛЬ) (Willebrord Van Roijen Snell, 1580-1626) — голландский математик и физик. Родился в Лейдене в семье профессора математики местного университета. Изучал математику и юриспруденцию в различных университетах Европы, много путешествовал, познакомился со многими видными учеными своего времени, включая Иоганна Кеплера. В 1613 году стал преемником отца на должности профессора Лейденского университета. Стоял

у истоков новой науки геодезии, первым усмотрев важность использования метода подобия треугольников при проведении геодезических измерений. В 1621 году, после многочисленных экспериментов по оптике, открыл закон преломления лучей, позже названный его именем. Своих результатов Снеллиус не публиковал, — они пылились в архивах, пока не были обнаружены Рене Декартом епй Descartes), который включил их в свой фундаментальный труд «Начала философии».


Закон

сохранения

линейного

импульса


•
Линейный импульс замкнутой системы сохраняется

1668

ЗАКОН СОХРАНЕНИЯ

ЛИНЕЙНОГО


1687
ИМПУЛЬСА


1736

ЗАКОНЫ МЕХАНИКИ НЬЮТОНА


ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА


Начав двигаться, тело имеет тенденцию продолжать движение. Первый закон механики ньютона гласит: если тело движется, то при отсутствии внешних воздействий оно так и будет двигаться дальше прямолинейно и равномерно до тех пор, пока не подвергнется воздействию внешней силы. Эту тенденцию называют линейным импульсом. С ней часто сталкиваемся в повседневной жизни. Бильярдный шар катится по столу с той скоростью, которая придана ему кием, копье летит с той скоростью, с которой его метнули.

Физики определяют линейный импульс телар как его массу т, умноженную на его скорость у:

р = ту.

Буквы р и у выделены полужирным шрифтом, чтобы показать, что эти величины характеризуются не только абсолютным значением, но и направлением. Так, применительно к скорости, мы не просто говорим, что машина движется со скоростью 40 км/ч, а что она движется со скоростью 40 км/ч, например, на север. Величина, которая кроме абсолютного значения имеет направление, называется вектором.

Понятно, что, согласно первому закону Ньютона, количество движения отдельно взятого тела в отсутствии внешних сил сохраняется. Закон же сохранения импульса гласит, что при соблюдении этого условия сохраняется векторная сумма импульсов всех тел, входящих в замкнутую механическую систему. В таком представлении система из двух бильярдных шаров массой т, пущенных друг навстречу другу с одинаковыми скоростями у, будет иметь нулевой момент импульса, хотя каждый из шаров по отдельности и обладает импульсом ту. Однако импульсы шаров взаимно пога-сятся вследствие их векторной природы (поскольку их скорости противоположно направлены).

Вообще, любая величина, характеризующая систему и не изменяющаяся в результате взаимодействия внутри нее, называется консервативной, и для нее имеется свой закон сохранения. В частности, в механических системах, помимо закона сохранения импульса действует еще и закон сохранения момента импульса или количества вращения — величины, которая описывает количество движения тел вокруг собственной оси и по изогнутым траекториям.

Что же происходит при прямолинейном соударении двух бильярдных шаров на встречных курсах? Происходит сразу несколько явлений. Во-первых, в момент столкновения шары слегка деформируются и часть их кинетической энергии переходит в тепловую. Во-вторых, мы знаем, что совокупный импульс системы из двух шаров не изменяется и остается равным нулю. Значит, видя, что один шар откатывается после лобового столкновения в обратном направлении с определенной скоростью, мы можем с уверенностью сказать, что второй шар в данный момент времени катится в обратном направлении ровно с той же скоростью.


Второй закон механики ньютона, кстати, можно легко интерпретировать и как формулу, согласно которой скорость изменения импульса равна силе, приложенной к замкнутой системе. Таким образом, чтобы изменить импульс системы, требуется внешняя сила. В молекулярно-кинетической теории, например, это наглядно просматривается: давление объясняется импульсами ударов молекул о стенки сосуда, содержащего газ. Поскольку молекулы газа упруго отскакивают в обратном направлении, их импульсы меняются на противоположные, а значит, стенка оказывает силовое воздействие на ударяющиеся об нее молекулы. но это означает, что и молекулы, в силу третьего закона ньютона, оказывают силовое воздействие на стенку, которое и воспринимается нами как давление.


Закон

сохранения

момента

импульса

В замкнутой системе

выполняется закон сохранения момента импульса


1668

ЗАКОН СОХРАНЕНИЯ

ЛИНЕЙНОГО


1687
ИМПУЛЬСА


1736

ЗАКОНЫ МЕХАНИКИ НЬЮТОНА