Викторина по математике для 9-х классов к "Неделе математики"

Вид материала

Викторина

Содержание IV тур. Творчество участников (участвуют 6 человек) Члены жюри Члены жюр V тур. Финал (участвуют 3 человека) Члены жюри определяют победителя.

Подобный материал:

• Отчет о проведении недели математики, 26.03kb.
• Программа элективного курса по математике для учащихся 9 11 классов «Клуб знатоков, 51.57kb.
• Викторина по истории математики, 16.14kb.
• Программа составлена на основе программы элективного курса для учащихся 9-х классов, 200.18kb.
• Татьяна Владимировна Никулина Эта игра-викторина, 178.83kb.
• Программа математического кружка «Юные математики» для учащихся 5 8 классов, 146.39kb.
• Викторина для учащихся младших классов Квитко Л. А викторина «Портреты героев сказок», 30.59kb.
• «Золотая пропорция», 166.35kb.
• Внеклассное мероприятие по математике для классов гуманитарного профиля Подготовили, 222.95kb.
• Решение нестандартных задач по математике, 54.73kb.

IV тур. Творчество участников (участвуют 6 человек)

1) Участникам предлагается рисунок. <Рисунок 6>. К данному рисунку придумать задание (участникам отводится 2 минуты).
Члены жюри должны будут определить самый интересный вопрос, который оценивается 3 баллами; менее интересный – 2 баллами и участники, которые справились с заданием, получают по 1 баллу.
2) «Ты - мне, я – тебе» (домашняя работа участников).
Каждый участник задаёт по одному вопросу другому участнику по указанию ведущего.

Члены жюри определяют самый интересный вопрос и ставят за него 3 балла, за правильный ответ участники получают по 1 баллу.

Подведение итогов IV тура. Из конкурса выбывают 3 человека.

V тур. Финал (участвуют 3 человека)

1) Блиц - турнир (на вопрос отвечает участник, первым поднявшим руку. Участник, ответивший на меньшее количество вопросов покидает конкурс. Время на обдумывание не даётся.)

1. Число, делящееся на два нацело - (чётное).
   
2. Математик, доказавший, что 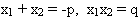- (Виет).
   
3. Не самая большая из сторон прямоугольного треугольника - (катет).
   
4. Математик, доказавший, что квадрат гипотенузы равен сумме квадратов катетов (Пифагор).
   
5. Меньшая сторона прямоугольника - (ширина).
   
6. Большая из сторон прямоугольного треугольника - (гипотенуза).
   
7. Геометрическая фигура, все точки которой равноудалены от некоторой точки плоскости - (окружность).
   

2) Вопросы-софизмы

Участникам раздаются карточки с решёнными заданиями. Нужно найти ошибку.

А. 5 = 6

Для доказательства возьмём числовое тождество 35 + 10 - 45 = 42 + 12 – 54.
Вынесем общие множители левой и правой частей за скобки: 5 · (7 + 2 – 9) = 6 · (7 + 2 – 9).
Разделим обе части на общий множитель, получим 5 = 6. Где ошибка?

Б. 2 · 2 = 5

Имеем числовое тождество 4 : 4 = 5 : 5. Вынесем за скобки в каждой части общий множитель: 4(1 : 1) = 5(1 : 1). Числа в скобках равны, значит, 4 = 5, или 2 · 2 = 5. Где ошибка?

Ведущие.

Софизм – это доказательство ложного утверждения, причём ошибка в доказательстве искусно замаскирована. Софистами называли группу древнегреческих философов IV – V вв. до н.э., достигших большого искусства в логике.

Проверка выполнения задания. Члены жюри определяют победителя.

Внеклассное мероприятие по математике "Слабое звено"

Цели игры:

1. Формирование интереса к математике, показать необходимость знаний по математике в других науках.
2. Развитие внимания, сообразительности, находчивости.
3. Воспитание стремления к непрерывному совершенствованию своих знаний; формирование дружеских отношений, умения работать командой.

Оформление кабинета.

На доске нарисовано табло, таблички с именами участников, формат А4, фломастеры.

500000
400000
300000
200000
150000
100000
50000
20000
10000
БАНК

Правила игры:

В каждом раунде вы должны ответить на достаточное количество вопросов. Чтобы достичь максимально возможной суммы, 500 000 рублей, в ограниченный период времени, самый быстрый способ состоит из 9 правильных ответов в каждом раунде, но если вы успеете сказать слово банк до того, как я задам вопрос, вы положите в банк эту сумму, если не знаете ответы на вопросы, то у вас капитал не увеличится.

Мы начинаем игру с того игрока, у кого имя первое. Итак, начинаем игру «Слабое звено».

Вопросы:

1. Знак математического действия из четырех букв (плюс).

2. Записать из одной или нескольких цифр (число).

3. Часть прямой, которая ограничивается двумя точками (отрезок).

4. Многоугольник, в котором имеется четыре вершины (четырехугольник).

5. Старинная мера длины из четырех букв (пядь).

6. Часть прямой, которая ограничивается с одной точкой (луч).

7. Упражнения, выполняемые с помощью рассуждений (задачи).

8. Число разрядов в классе (три).

9. Как называют числа, которые перемножают? (множители).

10. Чему равно произведение m 1? (m).

11. Отрезок координатного луча (единичный).

12. как называют результат умножения? (произведение).

13. Сколько сантиметров в одном квадратном дециметре (100).

14. Что означает, решить уравнение? (найти все его корни).

15. Какой доле килограмма равен 1 грамм? (1).

16. Что называют процентом? (одну сотую часть).

17. Какой угол называют развернутым? (180).

18. Место, занимаемое цифрой в записи число (разряд).

19. Натуральный корень уравнения Х² = Х (единица).

20. Как называют сотку? (ар).

21. Отрезок, который соединяет точку окружности с центром (радиус).

22. Единица массы драгоценных камней (карат).

23. Как называют равенство двух отношений? (пропорция).

24. Как называют первое число при делении? (делимое).

25. Чёртова дюжина в квадрате (169).

26. Наименьшее четырёхзначное число, составленное из цифр 6, 1, 4, 3. Цифры не должны повторяться (1346).

27. Соотношение между числами? (неравенство).

28. Результат действия (ответ)

29. Фигура, которая состоит из трёх точек и трёх отрезков, их соединяющих (треугольник).

30. Единица массы, равная 1000 кг (тонна).

31. Счётный прибор, которым пользовались древние греки и египтяне (абак).

32. Прямоугольник, все стороны которого равны (квадрат).

33. Наименьшее четырёхзначное число(1000).

34. Мера длины в прежней России – это расстояние от плеча до конца среднего пальца вытянутой руки (аршин).

35. Что записывает ученик в тетради перед примером или задачей? (номер).

36. Нахождение всех корней уравнения (решение).

37. Самое маленькое натуральное число (единица).

38. Английский учёный – путешественник, который в 1120 году ввёл в Европе десятичную систему записи чисел (Аделард).

39. Единица длины, равная длине первой фаланги большего пальца руки (дюйм).

40. 30 – 31 дней (месяц).

41. Единица массы, равная 100 кг (центнер).

42. Сторона грани прямоугольного параллелепипеда (ребро).

43. Одна из основных величин, характеризующих геометрическое тело, например, куб, параллелепипед (объем).

44. Единица площади многих западных стран (акр).

45. Число, которое иногда получается при делении (остаток).

46. Площадь квадрата со стороной 10 м (сотка).

47. Совокупность символов для обозначения математических объектов (алфавит).

48. Часть круга, ограниченная двумя его радиусами и дугой окружности (сектор).

49. Центральный угол, длина дуги которого равна радиусу (радиан).

50. Одна из характеристик вектора (направление).

51. Выдающийся древнегреческий математик (III в. до н. э. ), автор сочинений «Начала» (Евклид).

52. Наука о числах и операциях над ними ( арифметика).

53. Вертикальная, горизонтальная или наклонная прямая, к которой неограниченно приближается график функции (асимптота).

54. Утверждение, не требующее доказательства (аксиома).

55. То, что приходится делать в уме, если нет калькулятора (вычисление).

56. Учебник, напичканный задачами (учебник математики).

57. Ученый, прозревший после удара по голове (Ньютон).

58. Математическое действие, воспетое в песне Шаинского (умножение).

59. Близкий родственник квадрата (прямоугольник).

60. Школьная крыса (биссектриса).

61. Богатый родственник квадрата. Богаче в шесть раз (куб).

62. «Если долго мучаться, что-нибудь получится. . . » (ответ).

63. «А ну-ка, отними!» наоборот (сложение).

64. Зловещее место в Бермудах (треугольник).

65. Проблеск света в темном царстве (луч).

66. Что бывает даже у простого ученика, если очень постараться (пять).

67. Ученый, который любил купаться в ванной (Архимед).

68. Связь между числителем и знаменателем (отношение).

69. Дырка от бублика (ноль).

70. Забор для математических действий (скобки).

71. Привычное место непослушного ребёнка (угол).

72. Постоянная величина в данной задаче (параметр).

73. Среднеазиатский философ, врач, математик, астроном конца Х - Х?????I веков (Авиценна).

74. Соразмерность, пропорциональность в расположении частей чего – либо по обе стороны от середины центра (симметрия).

75. Русская мера длины, равная 2 м 13 см (сажень).

76. Произвольная линия (кривая).

77. Научно-популярный физико-математический журнал (Квант).

78. Старинная русская денежная единица, равная 1 копейки (грош).

79. Один из видов уравнений (алгебраическое).

80. Местоположение точки на прямой (координата).

81. Стоимость одного изделия или единицы товара (цена).

82. Французский математик Х в. , который ввел координаты точки на плоскости (Декарт).

83. Число богатырей на известной картине В. М. Васнецова (три).

84. Автор четырехзначных математических таблиц (Брадис).

85. Прибор для измерения углов на местности (угломер).

86. Часть круга, отсекающаяся хордой (сегмент).

87. Четная тригонометрическая функция (косинус).

88. Сторона прямоугольного треугольника, лежащая против прямого угла (гипотенуза).

89. Точное предписание о выполнении в определенном порядке некоторой системы предписаний (операций).

90. Точное предписание о выполнении в определенном порядке некоторой системы предписаний (операций).

91. Отношение длины линий на плане или карте к длине линии на местности (масштаб).

92. Вторая буква греческого алфавита (бета).

93. Монета достоинства в 3 копейки (алтын).

94. Один из видов афиного преобразования плоскости в себя (сдвиг).

95. Денежная единица Франции, Бельгии, Швеции и некоторых других сторон (франк).

96. Необходимая часть текста задачи (вопрос).

97. Утверждение, требующее доказательства (теорема).

98. Результат сложения однородных величин (сумма).

99. Числовой, буквенный или иной символ, которым снабжается обозначение математической величины (индекс).

100. Многочлен, содержащий в точности три члена (трёчлен).

101. Автор учебника «Алгебра и начала анализа» (Колмогоров).

102. Конечная область вместе с границей (тело).

103. Единичный вектор (Орт).

104. Вторая степень числа (квадрат).

105. Связь между величинами, выражения условными знаками (формула).

106. Первая русская женщина-математик (Ковалевская).

107. Метка, предмет, условное изображение чего-нибудь (знак).

108. Древнегреческий ученый, известна формула площади треугольника его имени (Герон).

109. Единица языка, служащая для названия отдельного понятия (слово).

110. Прибор для измерения и построения углов (транспортир).

111. Знак корня (радикал).

112. Получени6е образования, усвоение каких-либо знаний, навыков (учеба).

113. Как называется в геометрии, длина замкнутого контура (периметр).

114. Мера бумаги, прежде равная 480 листам, а в метрической системе 1000 листам

(стопа).

115. Чему равен диаметр окружности, если радиус равен 50? (100).

116. Угол разбивает плоскость на две части. Как называется каждая часть? (плоский угол).

117. Как называется отношение противолежащего катета к гипотенузе в прямоугольном треугольнике? (синус).

118. Как называется ломаная, если у нее концы совпадают? (замкнутая).

119. Чему равна площадь прямоугольника? (S = a*b).

120. Что больше пять третьих или три вторых? (пять третьих).

121. Чему равна десять в третьей степени (1000).

122. Как называется зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у? (функция).

123. Как называется уравнение вида ах⁴ + вх² + с = 0, где а = 0? биквадратными).

124. Как называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом?

(арифметическая прогрессия).

125. Чему равно пять минус второй степени? (одна двадцать пятая).

126. Как называется угол поворота по часовой стрелке? (отрицательным).

127. Чему равен синус тридцать градусов? (одна вторая).

128. Какой знак имеет синус в третьей четверти (минус).

129. Чему равен приближенно один радиан? (57 градусов).

130. Что означает приставка «Би»? (два).

131. Чему равен угол в квадрате? (90⁰).

132. Сколько земли в дыре глубиной 2м, шириной 2м, длиной 2м? (нисколько).

133. Кто в году четыре раза переодевается? (Земля).

134. На руках 10 пальцев. Сколько пальцев на 10 руках? (50).

135. Один человек купил трех коз и заплатил 3 руб. Спрашивается: почему пошла каждая коза? (Козы по деньгам не ходят).

136. Линия, соединяющая центры оснований цилиндров (ось).

137. Как называется абсолютная величина числа? (модуль).

138. График квадратной функции (парабола).

139. Как называется все значения независимость переменной?

(область определения функции).

140. Как называют сотую часть рубля? (копейка).

141. Чему равен объем куба с ребром 2см? (8 куб. см).

142. Что найдем, если расстояние разделим на скорость? (Время).

143. Сколько ребер у куба? (12).

144. Шоколадка стоит 10 рублей и еще половина шоколадки? Сколько стоит шоколадка?

(20 руб. )

145. Когда заходим в школу мы поднимаемся по лестнице. Сколько ступенек на лестнице?

146. Почему штативы к фотоаппаратам и рояли имеют три ноги, а не четыре?

(Из стереометрии известно, что три точки определяют единственную плоскость).

147. Какое число делится на все числа без остатка? (ноль).

148. Как называется точка Д луча ДЕ? (начало).

149. Единица массы, равная 10 центнерам (тонна).

150. Проживают в трудной книжке

Хитроумные братишки.

10 их, но братья эти

Сосчитают все насвете. (Цифры).

151. Когда исполнится козе 7 лет, что будет дальше (8-ой пойдет).

152. Какие три числа, если сложить или перемножить дают и тот же результат? (1,2,3).

153. Как называются прямые, если при пересечении двух прямых секущей накрест лежащие углы равны? (Параллельные).

154. В каком году родился А. С. Пушкин? (1799).

155. Первый космическая скорость. (8 км/с).

156. Самая длинная река в мире – это Нил. Чему равна ее длина? (6671).

157. Чему равняется число Авогадро? (N_A = 6*10²³ моль^-1).

158. Сколько глав в романе «Евгений Онегин»? (8 глав).

159. Какой год был следующим за 74-ом годом до нашей эры? (73).

160. Сколько ног у пауков? (8 ног).

161. Сколько граммов составляет 1 моль этиловый спирт? (46).

162. Ускорение свободного падения чему равняется? (9,8 м/с²).

163. Сколько положений эволюционной теории развития органического мира? (4).

164. Сколько видов животных существует на земле? (не менее 2 млн. ).

165. Сколько строк в строфах в романе «Евгений Онегин» (14).

166. Самая высокая гора – это Гималаи (пик Джомолунгма или Эверест? Чему равна высота этой вершины? (8848м).

167. Чему равна молекулярная масса воды?) (18 г/моль).

168. Чему равен 1 пуд? (146 кг).

169. Шла старуха в Москву. Навстречу ей 3 старика. Сколько человек шло в Москву?

(одна старуха).

170. Сколько метров глубина озера Байкал? (1620м).

171. К натуральному числу справа приписали три нуля. Во сколько раз увеличилось число?

(в 1000 раз).

172. Какую часть часа составляет 20 мин? (1/3 часть).

173. Периметр прямоугольника равен 64 см. чему равна сторона с тем же периметром? (16 см).

174. Какого года рождение наш президент – Владимир Владимирович Путин? (1952 г. ).

175. Какой знак надо поставить между двойкой и тройкой, чтобы получилось число больше 2 и меньше 3? (запятая).

176. Как называется треугольник со сторонами 3,4,5? (египетским).

177. Как называется угол с вершиной в центре окружности? (центральным).

178. Разделите сто на половину, сколько будет? (200).

179. В каком году Христофор Колумб открыл Америку? (1492 г. ).

180. Чему равняется произведение чисел 7,8,125? (7000).

181. Какой буквой записывалось число 50 в Древнем Риме? (L).

182. Чему равно произведение: 13*15*0*0,1? (ноль).

183. Что легче: 1кг ваты или 1кг железа? (одинаково).

184. Бежала тройка лошадей. Каждая лошадь пробежала 5 км. Сколько километров проехал ямщик? (5 км).

185. Что больше: 34*54 или 43*55? (43*55).

186. Чему равняется 1% метра? (1 см).

187. Прибор для измерения углов? (транспортир).

188. Специфическая единица измерения объема нефти? (баррель, 159л).

189. Наука, изучающая свойства фигур в пространстве? (стереометрия).

190. Что такое экер? (прибор для построения прямых углов на местности).

191. Чему равен один фунт? (400 г).

192. Может ли угол параллелограмма быть равным 200⁰? (нет).

193. Фигура, состоящая из всех точек плоскости, равноудаленных от одной точки?

(окружность).

194. Переведите на древнегреческий язык слова «натянутая тетива» (гипотенуза).

195. Что больше: 5 или корень из 28 (корень из 28).

196. Площадь квадрата 49 см². Чему равен его периметр? (28 см).

197. Единица измерения скорости на море? (узел).

198. Может ли при умножении получиться ноль? (да).

199. Зачем нужна рейсшина? (для построения параллельных прямых).

200. Мог ли Омар Хайям быть учеником Евклида? (нет).


Внеклассное мероприятие по математике в 6-м классе

"Старая сказка на новый лад"

Воспитательные цели: 

• создать условия для воспитания навыков самостоятельной деятельности учащихся;
  
• воспитывать эстетические качества, умение общаться.
  

Развивающие цели:  

• способствовать развитию интереса к математике, активации мыслительной деятельности,
  
• развитие творческого мышления, математической речи учащихся.
  

Обучающие цели:   

• повторение теоретического материала по данному разделу;
  
• способствовать формированию знаний по пройденной теме;
  
• закрепление навыков решения уравнений.
  

 Тип урока: урок-сказка

Сегодня, ребята я вам расскажу сказку. Сказку добрую, сказку волшебную. Сказку с намеком, добрым людям для урока. Слайд 1

Итак, в 101 царстве-государстве жила-была царица (в её роли буду я) и было у неё три сына (вызвать к доске трех учеников).

Пришло время женить сыновей, дала им царица по стреле и сказала:

“На чей двор упадет стрела, оттуда и невесту брать будите”

А стрелы то не простые, а с секретом, не каждый и выстрелить сможет, но на то они и царевичи.

Слайд 2

(ребята вместе с царевичами записывают уравнения, написанные на стрелах, и находят их корни) Слайд 3

Итак, упала стрела первого царевича на царский двор (Слайд 4), второго на купеческий (Слайд 5),

а третьего царевича взмыла и улетела неведомо куда (Слайд 6)

Нечего делать третьему царевичу, собрался он в путь-дорожку искать своё стрелу. Долго ли коротко ли шел царевич, но добрался он до трех дорог и задумался, по какой идти.

Давайте, ребята поможем нашему царевичу найти верную дорогу.

Устная работа

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Помогли определить добрые люди дорогу, и зашагал он дальше.

А дорога привела его в лес. Деревья кругом высокие, верхушек не видно.

Идет царевич оглядывается, жутко ему. Вдруг откуда не возьмись чудовище страшное, невиданное выкатывается. (слайд 11) Идет по лесу и все вокруг стонет.

Испугался царевич, не знает, что и делать. Тут лесная фея ему на помощь пришла, подсказала: “ поговори с чудовищем и ответь на его вопросы ”

Кто поможет царевичу с чудовищем справиться? Как хорошо, что на свете не перевелись добрые люди, готовые прийти на помощь в трудную минуту! Выполнили задание, и исчезло чудовище.

Пошел царевич дальше и попал в царство кромешной тьмы. (Слайд 12) Потихоньку идет царевич, по шажку, по два – как получается. А вот как получается у царевича, на это вы сейчас и ответите.

(игра “темная” - ученики закрывают глаза и на пальцах показывают ответы на предлагаемые задания)

1/2 * 2 =1

0,5 + 0,5 = 1

5,4 - 0,4 = 5

3/4 + 5/4 = 2

10/2 : 5 = 1

15/3 - 4/2=3

34/68 – 1/2 = 0

13/8 – 5/8 = 1

6/7 * 7/6 = 1

12/6 + 12/6 = 4

36/18 + 72/36 = 4

0 * 15,67 = 0

13,89 : 0 = ?

Вот вышел наш царевич, из царства тьмы, а впереди река. А моста нет.

Строить надо, да разве под силу такая работа одному? Давайте, ребята поможем нашему царевичу. (Слайд 13)

(выполняется задание)

Помогли добрые люди царевичу – построили мост. Перебрался он на другую сторону, а перед ним болото. (Слайд 14) А посреди болота лягушка сидит и стрелу его держит. (Слайд 15) Чтобы добраться до неё, по кочкам идти надо. А кочки то разные, есть хорошие, а есть мнимые, сразу не отличишь.

(если пример решен правильно, то кочка хорошая, если нет – мнимая)

Ответы на вопросы дает царевич, а класс помогает. (Слайд 16)

В грязи весь извалялся, вымок, но добрался царевич до лягушки, а она стрелу просто так не отдаёт, тоже задание предлагает.

Вот тебе 5 карточек, назови элементы изображенные на них. (Слайд 17)

Выполнил царевич задание лягушки, получил свою стрелу, взял лягушку и отправился домой. Возвращаться пришлось через лес, а за это время деревья повырастали, кусты завалы образовали. Расчищать надо.

(задание выполнить)

(Слайд 18)

(Слайд 19)

(Слайд 20)

(Слайд 21)

Многое понял царевич за время своего путешествия. Вернулся он домой, рассказал о добрых людях, которых встречал на своем пути. Время шло.

И стал задумываться наш царевич, что нашли братья его свои половинки, а у него только лягушка. Думал, думал и надумал, решил обратиться к колдунье.

Может она поможет.

Но до неё дойти легко, но попасть очень трудно к ней. Имя её знать нужно, чтобы дверь в её пещеру открылась. А имя её зашифровано, одному не под силу отгадать.

2х -7/2 = 7/2 - Т

1 + 7/3х = 7/5 - Ь

0,5х – 2,5 = 3/2 - М

2 – 7/4х = 4/3 - А

(задание: из отгаданных букв складывается слово “тьма” ) (Слайд 22)

Помогли, выполнили задание, узнали имя колдуньи, произнесли его вслух, и открылся вход в пещеру. А колдунья на встречу идет и говорит:

“Знаю, знаю, зачем ты потревожил меня, царевич. Суженую ты от меня ждешь, да нашел ты её и без меня. Лягушка это твоя. Расколдовать ты её должен. А это дело не простое. Должен ты отправиться в царство Кощея и победить его. Но путь этот не легкий, трудно тебе будет ” - сказала колдунья и открыла секрет дороги в Кощеево Царство.

Подумал царевич, да уж делать не чего, чем с лягушкой жить, уж лучше её попробовать расколдовать. Собрался в путь дорогу, позвал с собой друзей.

Долго ли коротко ли ехал царевич, но вместе с друзьями преодолели они преграды, миновали болота и вышли ко дворцу Кощея. А он на встречу идет.

(Слайд 22)

(Слайд 23)

(Слайд 24)

Победили Кощея Бессмертного. Разрушили царство Кощея, и с победой вернулись, наш царевич с друзьями домой. А дома встретила его прекрасная царевна, увидел её Иван царевич и влюбился. И стали они жить поживать, да добра наживать.

(Слайд 25)


Внеклассное мероприятие по математике для учащихся 5-го класса по теме: "Авторалли по городам Математики"

Цель:

• Расширение кругозора учащихся, развитие математических способностей, мыслительной деятельности учащихся.
  
• Укрепление интереса к математике, воспитание внимания.
  

Ход игры

Ведущий: На участие в соревновании авторалли по городам Математики поступили две командные заявки. Чтобы принять участие в соревновании, нужно каждой команде назвать 1-2 высказывания о математике.

Право на участие в соревновании получили обе команды: команда “Плюсик” и команда “Юный математик”. Маршрут, по которому будет проходить авторалли, начерчен на доске. Задания для команд в конвертах на доске у каждого города. (Команды знакомятся с маршрутом соревнования).



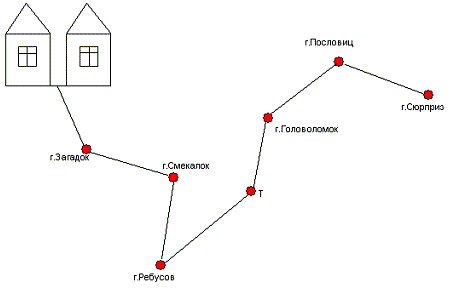
Ведущий: Внимание! Начинаем наше соревнование – авторалли по городам Математики. Команды в сборе? Участникам занять свои места! Внимание! В путь!

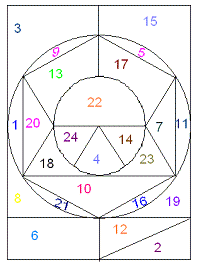
По пути следования играем в игру “Веселый счет”. От каждой команды представить по одному участнику. Команда, участник которой затратит меньше времени, получат жетон. (Необходимо найти все числа от 1 до 24.)



Ведущий: Первый город на пути нашего маршрута – это город Загадок. Необходимо отгадать три загадки.

На десятерых братьев двух шуб хватит. (рукавицы) Семьсот ворот да один вход (сеть, невод) Есть три брата родные: один ест – не наестся, другой пьет – не напьется, третий гуляет – не нагуляется. (огонь, вода, земля)

Четыре в избе, пятый возле. (рукавицы) У маленькой скотинки сто серебряных монеток на спинке. (рыба) Один пастух тысячи овец пасет. (месяц, звезды)

За каждую правильно отгаданную загадку, команда получает жетон.

Ведущий: А сейчас продолжаем путь. В пути проведем игру “Шагай – соображай!”. От каждой команды представить по одному участнику (Участники стоят рядом с ведущим. Все делают первые шаги, и в это время ведущий называет какое-нибудь число, например 7. При следующих шагах участники должны называть числа, кратные 7: 14, 21, 28 и т.д. На каждый шаг по числу. Ведущий идет с ними в ногу, не давая замедлить шаг. Как кто-то ошибется, он остается на месте до конца движения. Команда-победительница получает жетон.)

Ведущий: Подъезжаем к другому городу – городу Смекалок. Тут мы долго не задержимся, а лишь поможем жителям города вернуть на свои места сбежавшие цифры. Вместо звездочек поставьте соответствующие цифры:



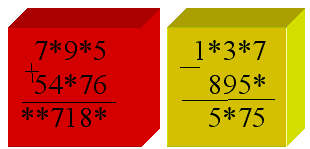
За правильно решенный пример, команда получает жетон.

Ведущий: Продолжаем путь. В пути проведем игру “Не ошибись!”. От каждой команды по 2 участника. (Участники выстраиваются в ширину перед зрителями. Ведущий становится лицом к участникам игры и показывает подряд (с небольшими паузами) одно за другим различные числа. Если число делится на 3, играющие поднимают вверх руку, ели не делится, не поднимают. Тот, кто ошибется, выходит из игры. Игра заканчивается, когда в шеренге останется 1 участник. Он объявляется победителем. Команда получает жетон.)

Ведущий: Новый город на нашем пути – это город Ребусов. Расшифровать по три ребуса. За каждый правильно расшифрованный ребус команда получает жетон.



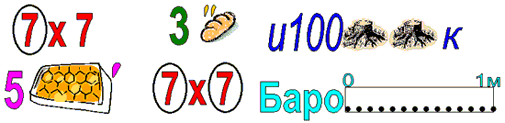
Ведущий: Мы продолжаем путь дальше.

Проехали половину пути, а впереди стоянка Т – это техосмотр своих машин. Вам нужно найти поломки, т.е. ошибки в примерах и устранить их. Расставьте скобки так, чтобы равенства были верны.

 

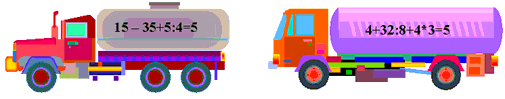
За каждый правильно решенный пример, команда получает жетон.

Ведущий: Поломки устранены – можно двигаться дальше. Впереди город Головоломок. За каждую правильно решенную головоломку команда получает жетон.

• Из 10 спичек построен “дом”. Переложите 2 спички так, чтобы он повернулся другой стороной.
  

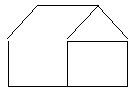
• Расставьте в зале 10 стульев так, чтобы около каждой стены стояло поровну стульев.
  

Ведущий: Отправляемся в путь. В пути следования поиграем в игру “Слушай одновременно нескольких”. Трое участников одной команды одновременно говорят по одному (разных) слову, а участник другой команды должен различить, кто какие слова сказал. Выигрывает та команда, участник которой различил большее количество слов. Команда получает жетон.

Ведущий: Следующий город на пути – город Пословиц. Нужно назвать как можно больше пословиц, чтобы в них встречались какие-либо числа. Команда – победитель получает жетон.

Ведущий: Мы опять отправляемся в путь. В пути следования проведем игру “Не ошибись!”. От каждой команды по 2 участника. Если названное число делится на 2, участник поднимает вверх правую руку, если на 3 – то левую, а если и на 2 и на 3 то сразу обе. Тот, кто ошибется, выходит из игры. Игра заканчивается, когда остается 1 участник. Он объявляется победителем. Команда получает жетон.

Ведущий: мы прибываем к городу Сюрприз. Пока подводятся итоги, мы побываем в этом замечательном городе. (Открывается запись на доске возле этого города. Там записано: “Аплодисменты!”).