Geum.ru

С. Н. Бобылев, А. Л. Новоселов, Н. В. Чепурных экология и экономика природопользования

Вид материалаДокументы

Содержание


17.2. Формирование плана реализации природоохранной программы
Критерий минимизации времени выполнения программы
Ограничение по объему складируемых ресурсов
Таблица 17.1 Алгоритмы реализации метода сдвига мероприятий в пределах заданного горизонта планирования
Подобный материал:
1   ...   58   59   60   61   62   63   64   65   ...   68

17.2. Формирование плана реализации

природоохранной программы



В настоящее время разработан достаточно широкий набор различных экономико-математических моделей и методов, позволяющих сформировать программу реализации комплекса мероприятий. Обычно в моделях такого рода используются:

Критерий минимизации времени выполнения программы:



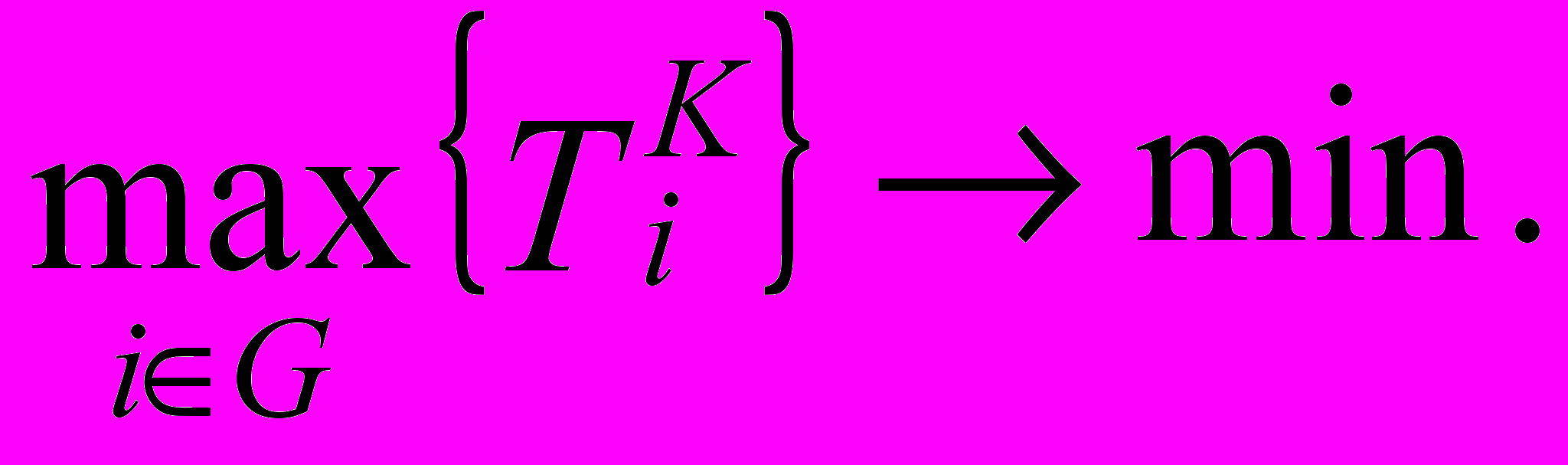
Ограничение на технологическую последовательность выполнения работ:



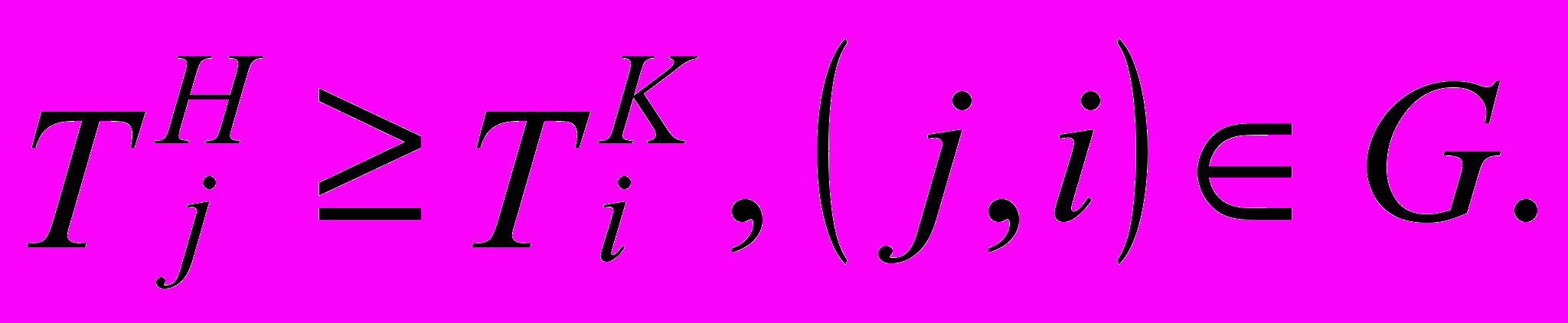
Зависимость между началом и окончанием реализации мероприятия с учетом требования непрерывности:



Ограничение по объему нескладируемых ресурсов:



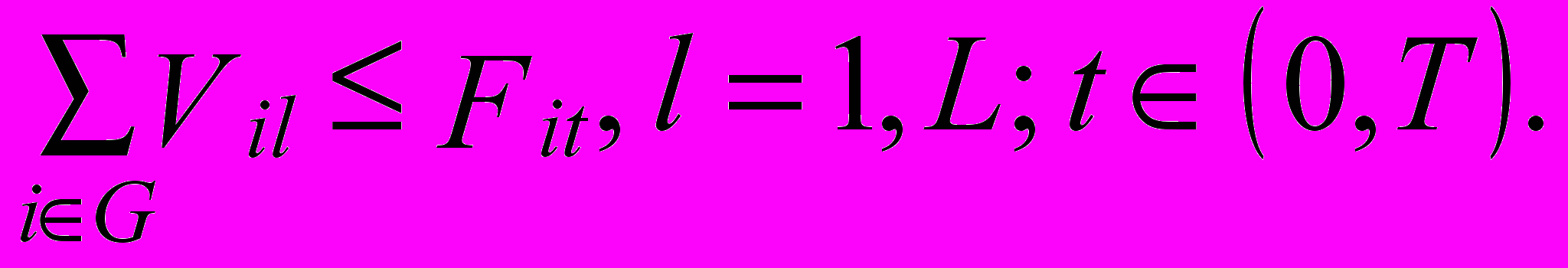
Ограничение по объему складируемых ресурсов:



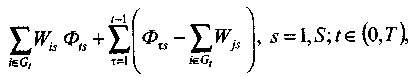
где G — сетевой граф, регламентирующий технологическую последовательность реализации мероприятий;

Gt — множество программных мероприятий, выполняемых в момент времени t :

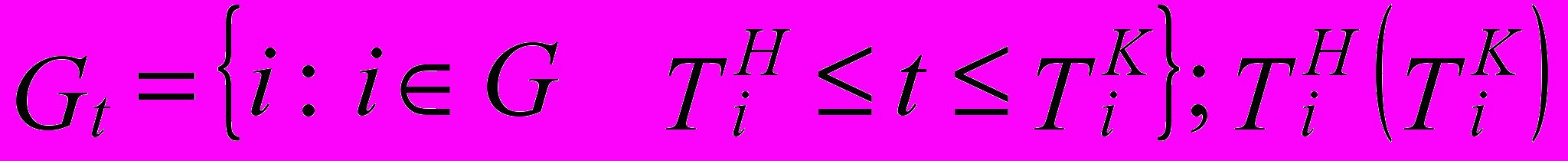— время начала (окончания) реализации мероприятий i;

ti — продолжительность реализации мероприятия i;

Vit — потребность i-го мероприятия в j-м виде нескладируемых ресурсов в единицу времени;

Ftl — поступление l-го вида нескладируемого ресурса в момент времени;

Wis — потребность i-го мероприятия в s-том виде складируемого ресурса в единицу времени;

Фts — поступление складируемого ресурса s-го вида в момент t.


Обычно такие модели ориентированы на критерий минимизации времени или минимизации затрат. При планировании природоохранных мероприятий целесообразно максимизировать показатель эффективности программы:



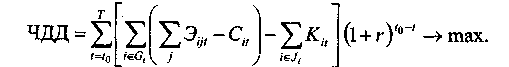
Изучение созданных ранее программ и опыт подобных разработок показывает, что горизонт планирования должен быть заранее ограничен, а потребность в ресурсах желательно выровнять (хотя бы в части финансирования из федерального бюджета).

Рассмотренная выше модель и метод решения задачи построения программы применимы в ограниченных случаях. Необходимо создание модели и специального метода, которые позволили бы укладываться в заранее заданный горизонт планирования и выравнивать потребности в ресурсах вокруг заданной величины. При равномерном вложении и освоении средств, величина ежегодного объема инвестиций рассчитывается по формуле:



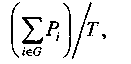
где Т — горизонт планирования.

Увеличение горизонта планирования позволяет уменьшить ежегодный объем инвестиций. С целью получения программы реализации мероприятий с потребностью в инвестициях, близкой или равной указанной величине, необходимо потребовать удовлетворения критерия минимального отклонения от равномерной потребности в ресурсах:



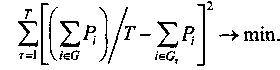
Наряду с этим критерием сохраняют актуальность и экономические критерии. Искомые сроки начала и окончания мероприятий должны подчиняться традиционным ограничениям:



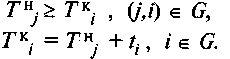
При этом оказывается актуальным вопрос об оптимизации перечисленных экономических показателей, которые могут быть максимизированы в условиях равномерного потребления инвестиций на заданном горизонте планирования. Значения этих показателей зависят от расписания реализации мероприятий программы, поэтому необходим специальный инструментарий, позволяющий решить поставленную задачу.

Данная задача относится к теории расписаний, точнее распределению ресурсов. Методы решения такого рода задач делятся натри основные группы:

1) методы математического программирования;

2) комбинированные методы;

3) эвристические методы.

Первые две группы методов довольно сложно использовать в практических расчетах в силу того, что большая размерность не позволяет использовать современную вычислительную технику. Этим объясняется широкое использование именно эвристических методов для решения реальных задач планирования. Среди эвристических методов известны метод логического ранжирования, методы распределения по фронту работ, методы последовательного растяжения, методы последовательного назначения и другие. Среди этого разнообразия методов группа методов последовательного назначения наиболее часто применяется для решения задач формирования программ, что обусловлено по крайней мере двумя причинами:

• простотой алгоритма, что дает возможность при небольшой трудоемкости расчетов решать задачи большой размерности;

• возможностью использования и разработки различных правил выбора мероприятий, что позволяет модифицировать алгоритм метода последовательного назначения для решения конкретной поставленной задачи.

В большинстве случаев используются правила предпочтения, которые основываются на временных характеристиках: минимальном или максимальном времен выполнения мероприятий, принадлежности работы наиболее длительному пути от альтернативной работы до конечного события сетевого графа и т.д. В ряде случаев выбор работы базируется на потребности в ресурсах — наибольший или наименьший. Есть правила, которые позволяет учитывать топологию сетевого графа, например, выбор работы, открывающей доступ к наибольшему числу работ. Эти правила обычно рассматриваются как правила второго порядка, применяемые для снятия неопределенности выбора в том случае, когда правила, основанные на временных параметрах, не позволяют однозначно выбрать мероприятия для включения в календарное расписание.

В случае применения критерия максимизации ЧДЦ для выбора мероприятия, включаемого в план в момент времени, используется формула:



Иногда для простоты расчетов можно использовать правило выбора мероприятий по максимуму рентабельности инвестиций.

Результаты расчетов на базе разработанной модели приводят к формированию природоохранной программы, которая обеспечивается ресурсами, в каждый момент времени, учитывает поступление и накопление ресурсов, а также максимизирует принятый критерий оптимальности.

Поскольку жестко заданный горизонт планирования не должен быть нарушен, необходимо применить принципиально иную логику формирования программы. Для критерия ЧДД наилучший вариант программы достигается при начале всех мероприятий с положительными значениями ЧДД в самые ранние сроки. При этом потребность в ресурсах в начале рассматриваемого временного периода наибольшая, постепенно снижается к концу периода. Для выравнивания потребности в ресурсах следует сдвинуть сроки реализации части мероприятий вправо. Для минимального ухудшения значения ЧДД целесообразно сдвигать мероприятия с минимальными значениями ЧДД. Для оценки качества полученного выравнивания потребности в ресурсах следует использовать среднеквадратичное отклонение от заданного (среднего) значения потребности в ресурсах:



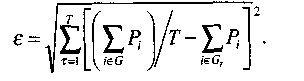
Известны пять вариантов реализации метода сдвига. Особенности этих алгоритмов представлены в табл. 17.1.

Таблица 17.1

Алгоритмы реализации метода сдвига мероприятий в пределах заданного горизонта планирования





Данная модель применяется и для более общего случая — выравнивания под заданную неравномерность потребления инвестиций. Если задаются объемы потребления инвестиций при фиксированном горизонте планирования Т: Zt, t = l, Т, то следует проверить достаточность этих средств, поскольку в этом случае должно выполняться равенство



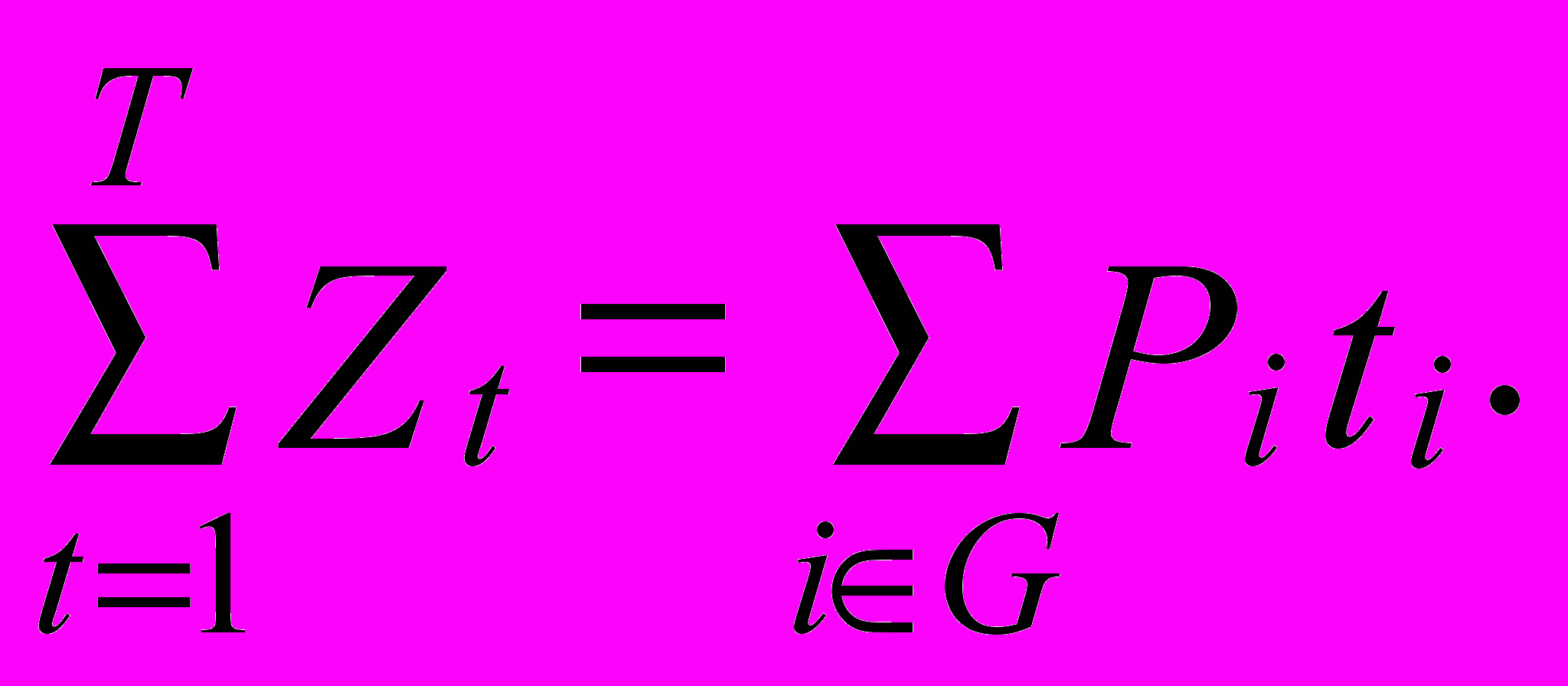
При выполнении данного равенства критерий выравнивания потребления инвестиций под заданную закономерность можно записать следующим образом:



Еще одно существенное дополнение позволяет расширить возможности модели. Осуществление некоторых мероприятий, прежде всего относящихся к социальной сфере, здравоохранению, должны начаться в предельно ранние сроки. Сдвиг вправо по оси времени таких мероприятий недопустим независимо от их экономической эффективности. В этих случаях следует фиксировать сроки выполнения таких мероприятий и запретить их перемещение внутри расписания. Метод сдвига мероприятий и предложенные алгоритмы останутся без изменения.


Пример. В регионе предполагается реализовать природоохранную программу из десяти мероприятий. Капитальные затраты на реализацию мероприятий предполагаются быть равномерными. Исходные данные, характеризующие эти мероприятия, приведены в нижеследующей таблице. Объем ежегодно выделяемых капиталовложений равен в среднем 48 млн руб.


Номер

меро-

приятия
Продолжи-

тельность

реализации,

лет
Потребность

в капитало-

вложениях

на реализацию

мероприятии,

млн руб./год
Величина

предотвра-

щаемого

ущерба

от реализа-

ции меро-

приятия,

млн руб./год
Рентабель-

ность меро-

приятия

1

2
30
10
0,17

2

1
20
4
0,20

3

3
20
20
0,33

4

4
10
10
0,25

5

2
30
18
0,30

6

3
20
16
0,27

7

2
20
15
0,38

8

2
10
8
0,40

9

1
30
7
0,23

10

3
20
17
0,28


Для решения задачи воспользуемся методом последовательного назначения мероприятий в расписание при жестко заданном ограничении на объем выделяемых ресурсов. В качестве приоритетов используем значения рентабельности мероприятий. Первый вариант расписания построим по правилу: если в текущий момент на реализацию приоритетного мероприятия не хватает ресурсов, то проводится попытка включения менее приоритетных мероприятий (до полного исчерпания списка). Затем происходит переход к следующему моменту времени. В результате будет получено расписание реализации мероприятий, представленное на рис. 17.2, 17.3.




Как видно из полученного расписания реализации природоохранных мероприятий, срок реализации программы оказался равным 13 годам. Если провести расчет среднеквадратичного отклонения потребности в инвестициях от среднего ежегодного объема инвестиций, то окажется, что е = V 2652/13 = 14,28 млн руб., что составляет 28,56% от средней величины ежегодных инвестиций.

Если же изменить алгоритм и назначать мероприятия строго в соответствии с приоритетностью на первый момент времени от начала числовой оси, когда достаточно финансовых средств, то расписание изменится.





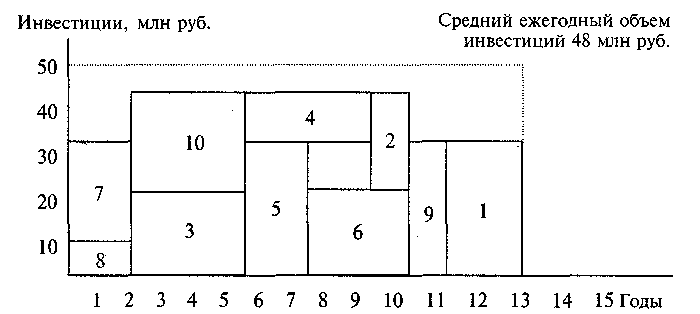
Рис. 17.3


Однако при этом срок реализации всей программы остался прежним, не изменилась и величина среднеквадратичного отклонения от среднегодового объема инвестирования.

Воспользовавшись алгоритмом выравнивания потребности в инвестициях при горизонте планирования, равном 9 годам, получим следующее расписание реализации природоохранных мероприятий (рис. 17.4).





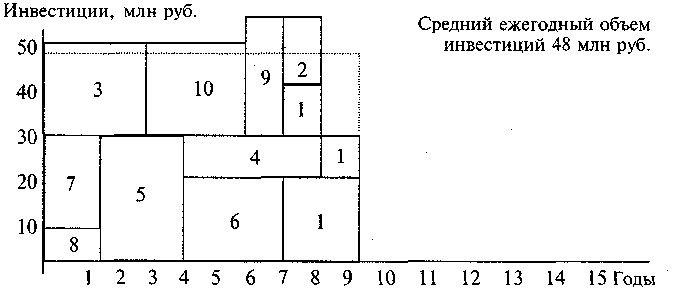
Рис. 17.4


При уменьшении срока реализации программы на 4 года (или на 30,7%) получена среднеквадратичная ошибка потребности в инвестициях отклонения от среднегодового объема инвестирования вдвое меньшая, чем в первых двух вариантах расчетов: 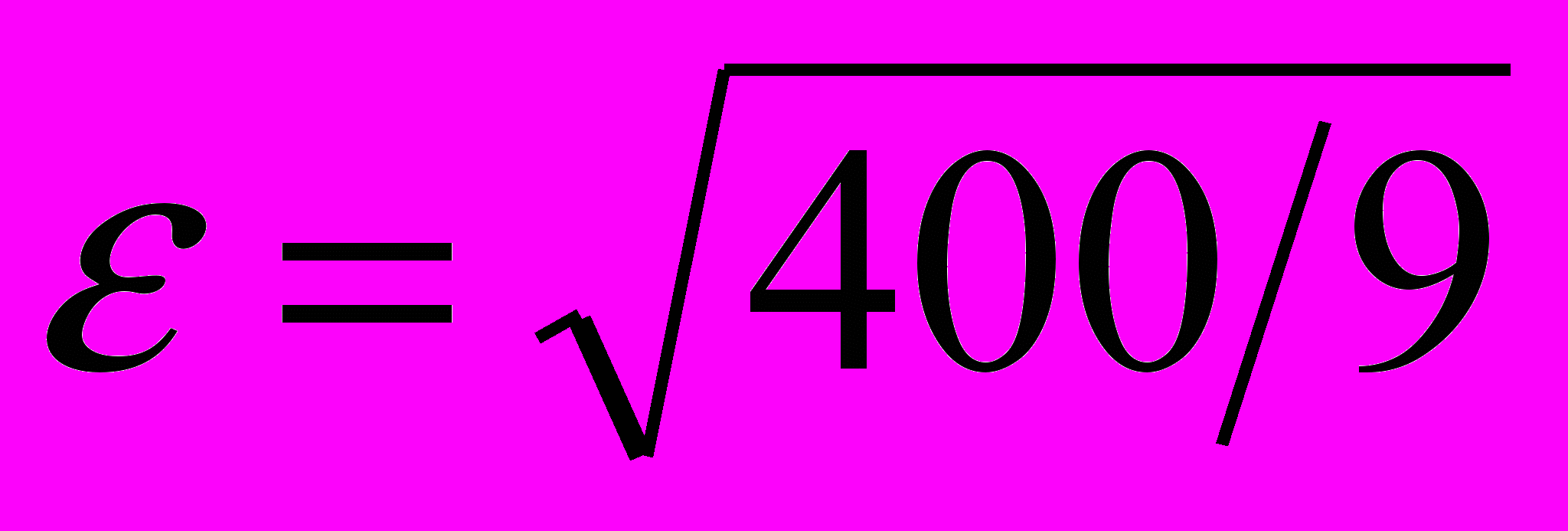= 6,67 млн руб , что составляет 13,3% от среднегодового объема инвестирования.