Тишкиной Ниной Тимофеевной Рецензируемая программа
| Вид материала | Программа |
- Турганововой Ниной Васильевной 14 разряд Томск 2010 год пояснительная записка, 179.2kb.
- Турганововой Ниной Васильевной 14 разряд Томск 2010 год пояснительная записка, 222.07kb.
- Турганововой Ниной Васильевной 14 разряд Томск 2010 год пояснительная записка, 228.15kb.
- Бусыгиной Ниной Александровной Саратов 2009 Тема урок, 132.25kb.
- Владимир Высоцкий, 146.89kb.
- Реферат на тему: " Мне не стало хватать его " (о творчестве В. С. Высоцкого), 81.5kb.
- Обелюнас Ниной Владимировной. На экспертизу представлена запись телепередачи от 9 октября, 261.01kb.
- Программа конституционно-демократической партии Программа Союза 17 октября Воззвание, 1341.78kb.
- Литература 8 класс Программа: базовый уровень. Программа, 302.33kb.
- Программа формирования ууд программа отдельных предметов, курсов и внеурочной деятельности., 10807.27kb.
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №6 г. Ноябрьска
ПРОГРАММА по математике
10, 11 класс,
профильное математическое направление
Составлена учителем математики
МОУ СОШ №6 Тишкиной Н.Т. в 1996 г.,
исправлена и дополнена в 2006 г.
Рецензент: профессор Новосибирского
Государственного Университета
кандидат физико-математических наук
ведущий сотрудник Института
математики СО РАН
Чуркин Валерий Авдеевич
2006 – 2007 учебный год
Рецензия на рабочую программу предметов
«Алгебра и начала анализа» и «Геометрия»,
составленную учителем математики МОУ СОШ №6
г. Ноябрьска ЯНАО Тишкиной Ниной Тимофеевной
Рецензируемая программа предметов «Алгебра и начала анализа» и «Геометрия» составлены в соответствии с Государственными требованиями к обязательному минимуму содержания образования, а также Концепции модернизации школьного образования: целям и задачам предпрофильной подготовки в основной школе и профильного обучения в старшей школе, принципу уровневой дифференциации. Примерная программа рассчитана на 340 часов из расчета 5 часов в неделю по алгебре и началам анализа и 204 часа в неделю из расчета 3 часа в неделю по геометрии. В ней предусмотрен резерв свободного времени в объеме 42 учебных часов по алгебре и началам анализа и 51 учебного часа по геометрии для реализации авторских подходов, внедрения современных методов обучения и педагогических технологий, использования разнообразных форм организации учебного процесса.
В рецензируемой программе определена основная задача предмета как обеспечение полного и сознательного овладения учащимися системой математических знаний, достаточных для изучения смежных дисциплин и продолжения образования. Целью является обучение математике в десятых, одиннадцатых классах, направленное на обеспечение подготовки учащихся к поступлению в ВУЗ и продолжению самообразования при подготовке к профессиональной деятельности, требующей высокой математической культуры.
При изучении математики по данной программе учащимся предъявляются более высокие требования к теоретическим знаниям по сравнению с обязательным уровнем. Большое внимание уделяется различным способам решения задач. Так как в классы с математическим направлением приходят учащиеся с различным уровнем подготовки, то в данной программе уделено внимание повторению, обобщению и систематизации знаний.
Следует отметить, что программой предусмотрено формирование представлений об идеях и методах математики, о математике, как об универсальном языке науки, средстве моделирования явлений и процессов. Также программой предусмотрено развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.
Для реализации данной программы используются различные технологии обучения, которые позволяют развить у учащихся интерес к предмету и организации самостоятельной работы, продолжить образование и освоить избранную специальность на современном уровне, понять значимость математики для научно-технического прогресса.
Рецензируемая рабочая программа предметов «Алгебра и начала анализа» и «Геометрия» рассчитана на учащихся общеобразовательных школ и может использоваться при профильном обучении и подготовке в технические ВУЗы.
Пояснительная записка
Данная программа составлена для изучения математики в 10 – 11 классах и рассчитана на учащихся, имеющих устойчивый интерес к математике и решивших после окончания школы выбрать профессию, связанную с дальнейшим изучением математики. Обучение математике в 10 – 11 классах направлено на обеспечение подготовки к поступлению в ВУЗ и продолжению образования, а также подготовке к профессиональной деятельности, требующей высокой математической культуры.
Изучение математики по данной программе на профильном уровне направлено на достижение следующих целей:
- формирование представления об идеях и методах математики, о математике как универсальном языке науки, средстве моделирования явлений и процессов;
- овладение языком математики в устной и письменной формах, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, продолжения образования и освоения избранной специальности на современном уровне;
- развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
- воспитание средствами математики культуры личности через знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для научно-технического процесса.
Данная программа учитывает также разрыв между школьной программой и программой вступительных экзаменов в ВУЗы. В программу вступительных экзаменов в ВУЗы включаются вопросы, которые по обычной программе школьного курса не изучаются совсем или изучаются в ознакомительном плане, такие как «решение уравнений, неравенств, систем уравнений и неравенств, содержащих параметры или знак модуля», «решение тригонометрических уравнений, неравенств, систем, при решении которых используются специальные подстановки, введение вспомогательного аргумента и т.п.», «построение графиков уравнений, содержащих знак модуля», «планиметрические задачи», «решение показательных, логарифмических уравнений, содержащих иррациональность», «иррациональные неравенства» и т.д.
Программа рассчитана на более длительное изучение элементарной математики и практического применения некоторых вопросов математического анализа, знакомство с элементами комбинаторики, математической статистики и теории вероятностей. Длительное изучение темы «Применение производной и интеграла в физике» способствует более глубокому усвоению предмете физики. В программу по алгебре также включена тема «Объёмы тел» из геометрии: объёмы призмы, цилиндра, конуса и шара вычисляются при помощи интегрального исчисления.
При изучении математики по данной программе к учащимся предъявляются более высокие требования к теоретическим знаниям по сравнению с обязательным уровнем: они должны уметь свободно пользоваться математическими терминами, уметь грамотно и точно излагать свои мысли. Большое внимание уделяется различным способам решения задач и выбору среди этих способов более рационального.
Так как в классы с математическим направлением приходят учащиеся с различным уровнем подготовки, то в данной программе уделено большое внимание повторению, обобщению и систематизации знаний, так, например, первая половина 10 класса отведена повторению, обобщению, систематизации знаний по темам «Действительные числа», «Уравнения, неравенства», «Многочлены», «Свойства функций». Заканчивается изучение программы в 11 классе также обобщением и систематизацией знаний по теме «Уравнения, неравенства, системы», где предусмотрено обобщение различных приёмов и методов решения уравнений, неравенств и их систем, изученных в 10 – 11 классах. В этой же теме отведено время для изучения некоторых специальных приёмов решения, а также приближенных методов решения. Изучение данной темы способствует более осмысленному усвоению программы по математике.
Программа по геометрии соответствует программе общеобразовательного уровня, дополнительное время отводится на решение конкурсных планиметрических и стереометрических задач, подготовке к ЕГЭ.
При изучении этой программы очень важно организовать дифференцированный подход к учащимся, который позволяет избежать перегрузки и способствует развитию способностей каждого ученика в зависимости от его учебных возможностей. При реализации данной программы рекомендуется использование технологии модульного обучения, которая позволяет осуществить поуровневую индивидуализацию учебной деятельности, создает ситуацию выбора для учителя и ученика, способствует глубоким и прочным знаниям предмете, воспитывает такие качества личности, как самостоятельность, целеустремленность, учит общению, умению отстаивать свое мнение, воспитывает интерес к предмету. При обучении по этой технологии используются различные формы проведения уроков: урок-лекция, урок-практикум, урок-семинар, урок развивающего, дифференцированного обучения, урок контроля, урок коррекции знаний. При обучении широко используются групповые методы работы. Группы не являются постоянными, их состав меняется в зависимости от целей урока. Большое внимание уделяется контролю: это может быть самостоятельная работа, зачет по теории или практике, тестирование, отчет участника группы перед классом или учителем, контрольная работа.
При обучении по данной программе рекомендуется домашнее задание давать на продолжительное время, это могут быть домашняя контрольная работа по какой-либо теме, реферат, тест и т.д.
Одним из способов достижения целей этой программы является создание классов математического профиля, в которых на изучение математики количество часов увеличено со 154 до 288 в год в 10 классе и со 136 до 282 часов в 11 классе, из них 5 часов в неделю отводится на изучение алгебры и начал анализа и 3 часа на изучение геометрии. При этом достижение обязательного уровня подготовки необходимо. Программа полностью содержит стандарт среднего (полного) общего образования по математике, рекомендованного Министерством образования для изучения математики на профильном уровне.
Алгебра и начала анализа
10 класс
(5 часов в неделю, всего 170 часов)
Действительные и комплексные числа (14 часов)
Натуральные числа, целые, рациональные числа, иррациональные числа. Обращение бесконечной периодической дроби в обыкновенную. Операции над действительными числами. Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая части, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в различных формах записи. Комплексно сопряжённые числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры*.
Основная цель: систематизировать сведения о числах, проследить исторический путь развития понятия числа, повторить правила действий с числами.
Учащиеся должны знать идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических и внутренних задач математики. Уметь обращать периодическую десятичную дробь в обыкновенную, выполнять действия над действительным числами, где встречаются периодические дроби; выполнять действия над комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнения с действительными коэффициентами.
Уравнения, системы, неравенства (28 часов)
Уравнения высших степеней, решение уравнений, сводящихся к квадратным. Замена переменных, возвратные уравнения. Решение уравнений, содержащих знак модуля. Системы уравнений, однородные уравнения. Решение систем уравнений методами замены переменных, подстановки, сложения, с помощью теоремы, обратной теореме Виета. Решение систем уравнений, содержащих знак модуля. Графический способ решения систем уравнений. Решение уравнений и систем уравнений с параметрами. Неравенства, решение и доказательство неравенств. Метод интервалов, решение неравенств, содержащих знак модуля и параметры.
Основная цель: повторить способы решения уравнений, неравенств, систем, изученных в курсе алгебры 7-9 классов. Повторить основные способы решения уравнений: разложение на множители, введение новой переменной, графический метод решения уравнений. Познакомить учащихся с возвратными, однородными уравнениями, с решением уравнений, неравенств ,их систем, содержащих знак модуля и параметры.
Учащиеся должны уметь решать неравенства методом интервалов, уравнения вида |f(x)|=|g(x)|, |f(x)|=g(x), неравенства вида |f(x)|>|g(x)|, |f(x)|
Многочлены (20 часов)
Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными.
Тождественные преобразования целых рациональных выражений. Многочлен от одной переменной. Деление многочлена на многочлен, корни многочлена. Схема Горнера. Теорема Безу, теорема о нахождении рациональных корней многочлена.
Решение рациональных уравнений высших степеней. Многочлены от двух переменных. Формулы сокращённого умножения для старших степеней. Бином Ньютона. Многочлены от нескольких переменных, симметрические многочлены.
Учащиеся должны знать: определение многочлена и его корня, схему Горнера, теорему Безу, теорему о рациональных корнях.
Учащиеся должны уметь: выполнять деление многочлена на многочлен с остатком, уметь отыскивать корни многочленов третьей и четвёртой степеней с помощью теоремы о рациональных корнях и теоремы Безу.
Функции (19 часов)
Определение функции, способы задания функций. Область определения и область значений функции. Сложная функция (композиция функций). График функции. Линейная, квадратичная, дробно-рациональная функции, их графики. Построение графиков функций с помощью преобразований: параллельного переноса, симметрии относительно осей координат и начала координат, относительно прямой y = x, растяжения и сжатия вдоль осей координат. Графики уравнений, содержащих знак модуля. Чётные, нечётные функции, возрастание и убывание функций. Наибольшее и наименьшее значения функции. Экстремум функции. Выпуклость функции. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной.
Основная цель: повторить все сведения о функциях, изученные в курсе алгебры 7-9 классов, познакомить учащихся с построением графиков функций с помощью преобразований.
Учащиеся должны знать: определения функции, её области значения, области определения, определения графика функции, экстремальной точки и экстремума функции.
Уметь: строить графики линейной, квадратичной, дробно-линейной функций с помощью преобразований (сдвиг влево, вправо, вверх, вниз, растяжение, сжатие), графики уравнений 1-ой и 2-ой степеней, содержащих знак модуля, описывать свойства функций, пользуясь их графиками..
Тригонометрические функции (40 часов)
Длина дуги, радианные измерения дуг и углов. Синус, косинус, тангенс, котангенс произвольного угла. Синус, косинус, тангенс и котангенс числа. Единичная окружность. Определение тригонометрических функций. Периодичность, четность, нечетность тригонометрических функций. Формулы приведения, основные тригонометрические тождества, формулы сложения. Тригонометрические функции двойного, тройного, половинного аргумента. Преобразование разности и суммы одноименных тригонометрических функций в произведение и обратно. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование тригонометрических выражений. Решение простейших тригонометрических уравнений. Основные методы решения тригонометрических уравнений. Графики тригонометрических функций. Решение и доказательство тригонометрических неравенств. Обратные тригонометрические функции, их свойства и графики.
Основная цель: обобщить все знания о тригонометрических функциях, полученные в 9 классе, познакомить с графиками тригонометрических функций и обратными тригонометрическими функциями, с основными методами решения тригонометрических уравнений и неравенств.
Учащиеся должны знать определения тригонометрических функций и их свойства, основные формулы, значения тригонометрических функций для
, 
, 
, 
, 
, 
, 
, 
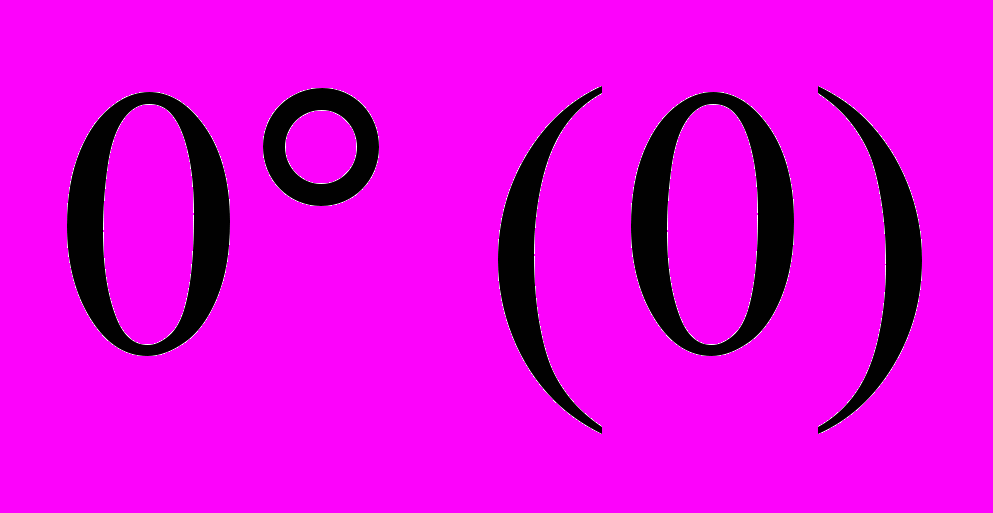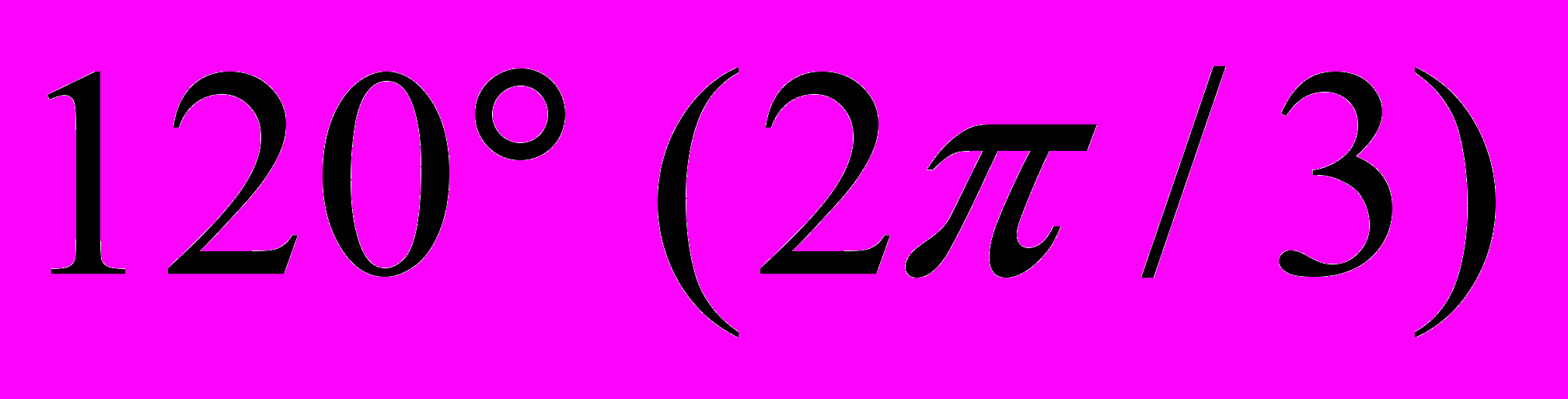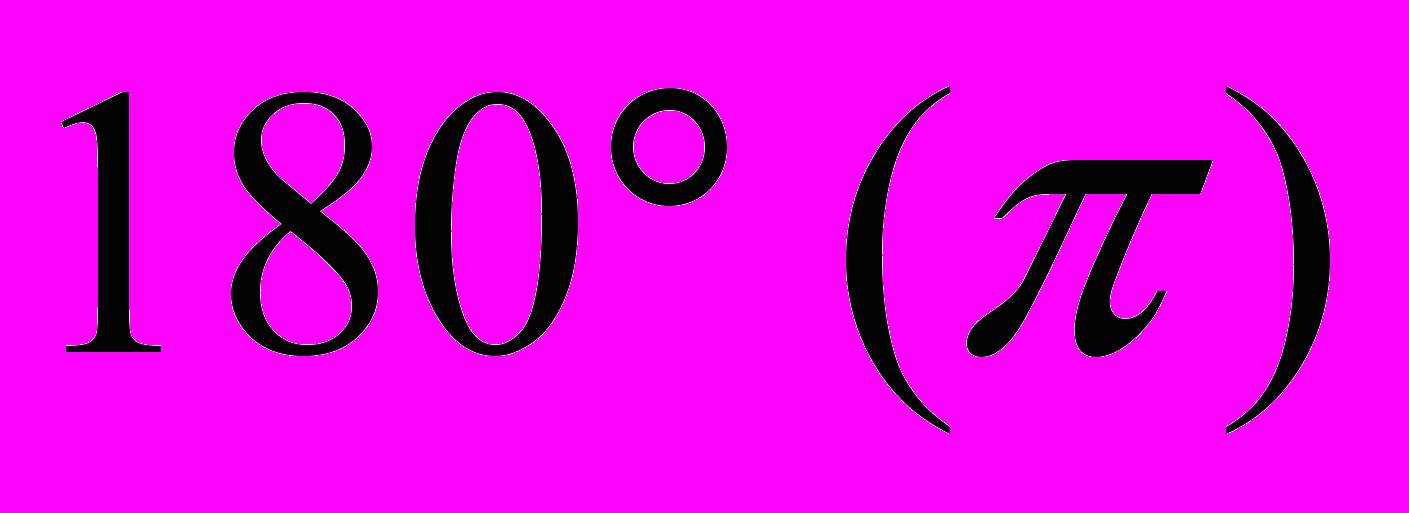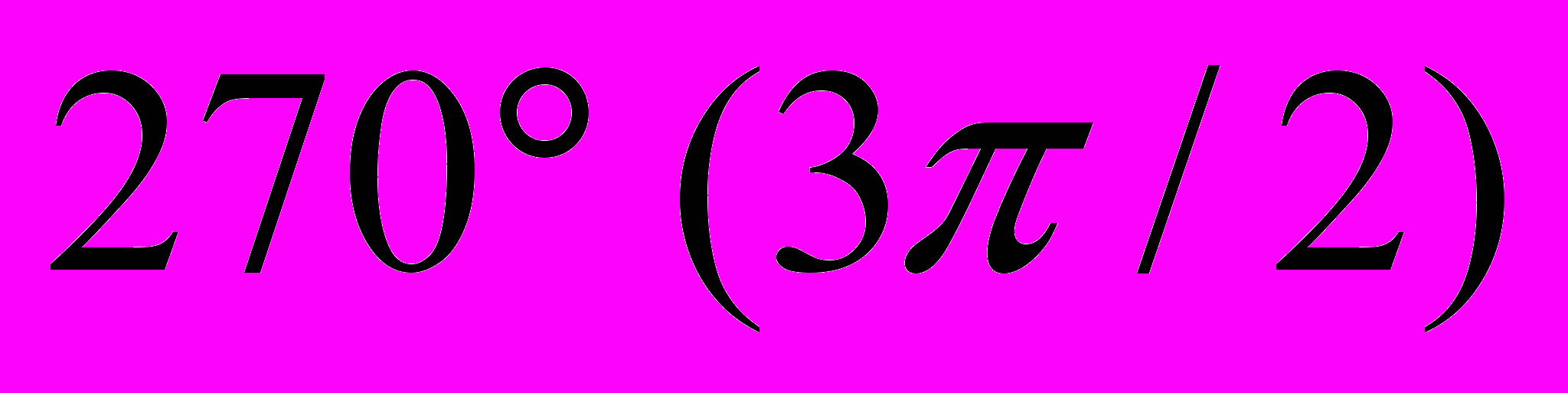. Учащиеся должны уметь преобразовывать тригонометрические выражения, находить значения остальных тригонометрических функций по известному значению одной тригонометрической функции, решать простейшие тригонометрические уравнения и неравенства, уравнения, сводящиеся к квадратным и однородные уравнения, знать некоторые специальные приемы решения уравнений, такие как понижение степени уравнения, введение вспомогательного аргумента и другие, уметь строить графики тригонометрических функций с помощью преобразований, выполнять действия с обратными тригонометрическими функциями.Предел и непрерывность (7 часов)
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Теоремы о пределах последовательностей. Переход к пределам в неравенствах. Понятие о непрерывности функции. Основные теоремы о непрерывных функциях. Понятие о пределе функции в точке. Поведение функции на бесконечности. Асимптоты.
Основная цель: познакомить учащихся с понятием предела функции на интуитивном уровне с помощью геометрической иллюстрации, с понятием непрерывной функции.
Учащиеся должны знать геометрическую иллюстрацию предела функции в точке, определение непрерывной функции. Учащиеся должны уметь находить пределы функций в простейших случаях, сумму бесконечно убывающей геометрической прогрессии.
Производная и ее применение (36 часов)
Приращение функции, производная, ее геометрический и физический смысл. Касательная к графику функции. Дифференцируемые функции, связь непрерывности и дифференцируемости функций. Техника дифференцирования. Производные линейной, степенной функций. Производная суммы, произведения, дроби. Производная сложной и обратной функций. Производная тригонометрических функций. Вторая производная. Необходимые условия экстремума функции. Отыскание наибольших и наименьших значений функции на отрезке. Исследование функции на возрастание и убывание. Исследование графика функции на выпуклость, вогнутость, точки перегиба. Исследование функций и построение графиков. Использование производных при решении уравнений и неравенств, текстовых, физических и геометрических задач. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного функцией или графиком.
Основная цель: познакомить учащихся с производной, ее геометрическим и физическим смыслом, показать ее применение для исследования функций и решения физических задач. Выпуклость, вогнутость, точки перегиба даются в ознакомительной форме.
Учащиеся должны знать определение производной, ее физический и геометрический смыслы, правила вычисления производных, таблицу производных, определение критической точки, теоремы о достаточном и необходимом условиях существования экстремума, признаки возрастания и убывания функции. Учащиеся должны уметь вычислять производные элементарных функций, применяя правила вычисления производных и справочные материалы; исследовать функции и строить их графики с помощью производной; решать задачи с применением уравнения касательной к графику функции; задачи на нахождение наибольшего и наименьшего значения функции на отрезке.
Повторение (6 часов)
Алгебра и начала анализа
11 класс
(5 часов в неделю, всего 170 часов)
Первообразная и интеграл (20 часов)
Повторение: производная, правила вычисления производных. Определение первообразной, общий вид первообразных, правила вычисления первообразной, неопределенный интеграл и его свойства. Криволинейная трапеция и ее площадь, определенный интеграл и его свойства. Формула Ньютона-Лейбница. Вычисление площади криволинейной трапеции и площадей фигур. Применение интеграла в физике и геометрии (вычисление объемов).
Основная цель: познакомить учащихся с понятием первообразной, ее вычислением и применением в физике и геометрии.
Учащиеся должны знать определение первообразной, ее свойства, правила вычисления первообразной, доказательства теорем о вычислении объемов призмы, пирамиды, конуса, цилиндра, шара. Учащиеся должны уметь находить общий вид первообразных, неопределенный интеграл в простейших случаях, применять формулу Ньютона-Лейбница, находить площадь криволинейной трапеции, уметь пользоваться формулой «интеграл разности» для вычисления площадей фигур.
Корень n-ой степени, иррациональные уравнения и неравенства (14 часов)
Определение корня степени n>1 и его свойства, иррациональные уравнения, иррациональные неравенства.
Основная цель: повторить и обобщить знания по теме «Корень n-ой степени», полученные в курсе алгебры 9 класса, познакомить с различными методами решения иррациональных уравнений, в том числе уравнений, связанных с применением формул «куб суммы» и «куб разности», познакомить учащихся с решением иррациональных неравенств.
Учащиеся должны знать определения корня n-ой степени, арифметического корня n-ой степени, свойства арифметического корня n-ой степени. Учащиеся должны уметь выполнять преобразования выражений, содержащих корень n-ой степени, решать иррациональные уравнения различной степени сложности, иррациональные неравенства, содержащие один знак радикала.
Показательная и логарифмическая функции (50 часов) .
Обобщение понятия степени, степень с рациональным показателем и ее свойства, понятие о степени с действительным показателем, свойства степени с действительным показателем. Преобразование выражений, содержащих степени. Степенная функция с натуральным показателем, ее свойства и график. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций*. Показательная функция (экспонента), ее свойства и график. Решение показательных уравнений и неравенств. Логарифм числа, свойства логарифма. Логарифмическая функция, ее свойства и график. Решение логарифмических уравнений и неравенств. Производная показательной функции. Число e, натуральные и десятичные логарифмы. Производная логарифмической функции. Исследование и построение графиков функций.
Основная цель: повторить и обобщить определение степени с различным показателем и ее свойства, познакомить учащихся со степенью с иррациональным показателем,. определением логарифма и его свойствами, обратить внимание на свойства логарифмов, не изучаемые по обычной программе. Познакомить учащихся с различными методами решений показательных и логарифмических уравнений и неравенств. Познакомить учащихся с числом e, вывести формулы для вычисления производных функций
, 
, 
, 
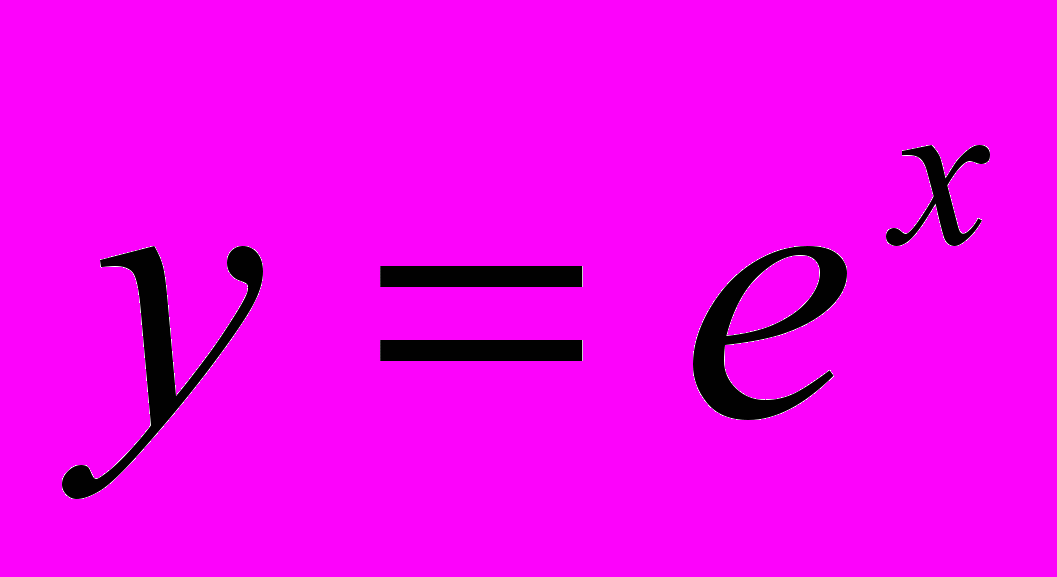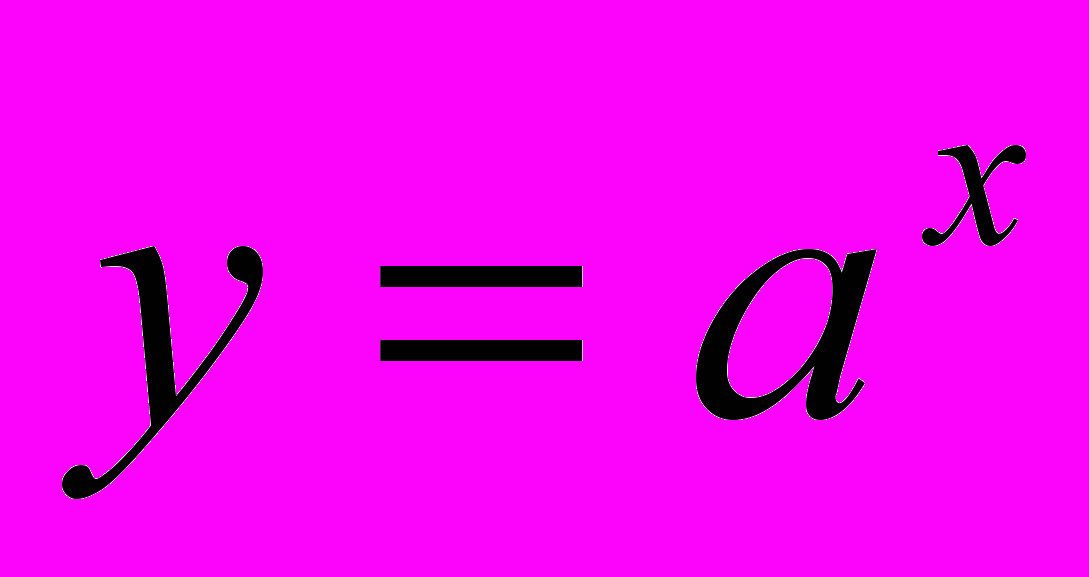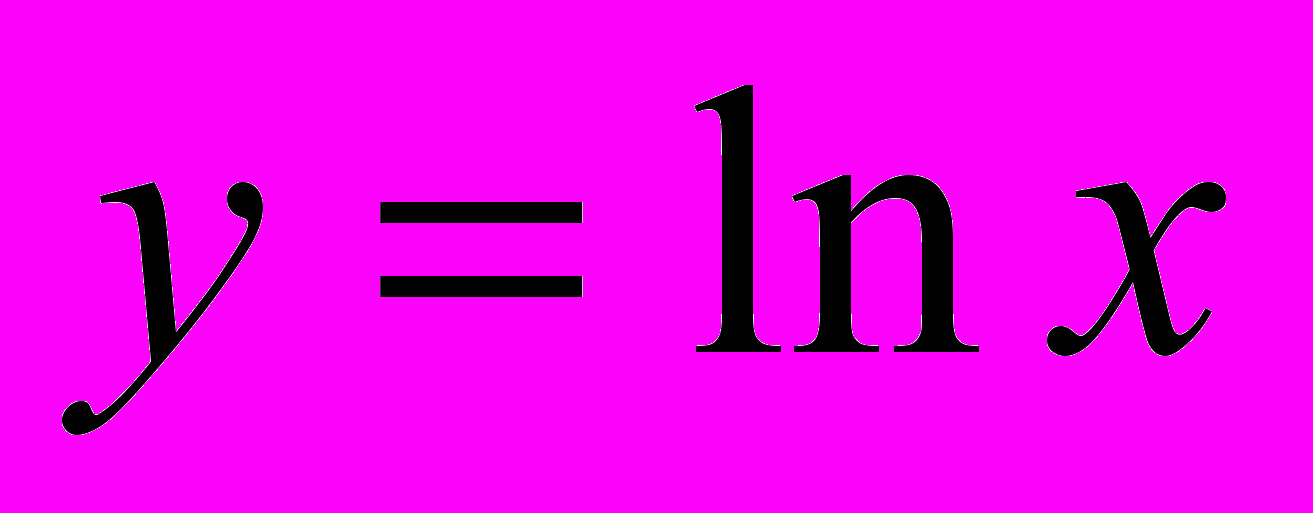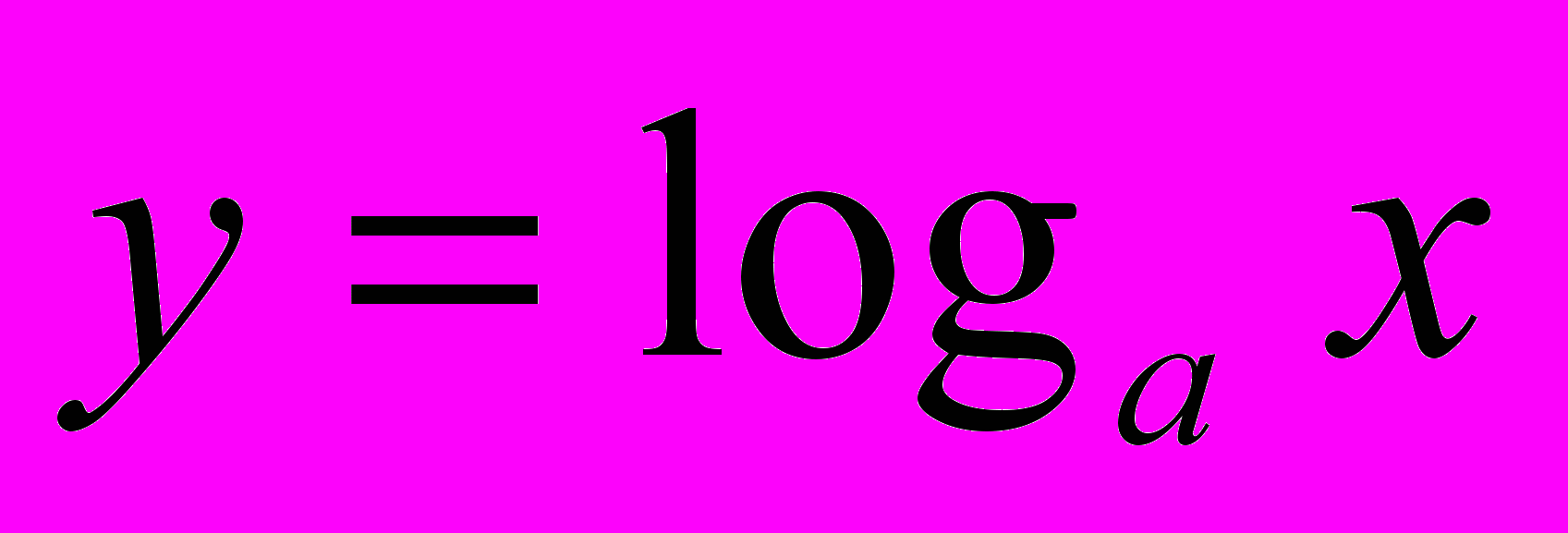, первообразных функций , , 
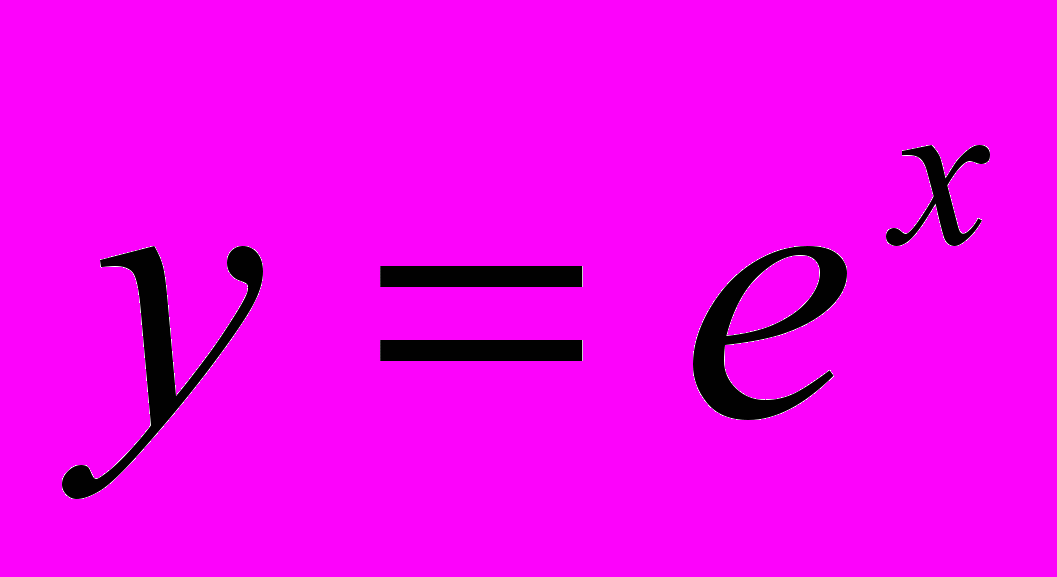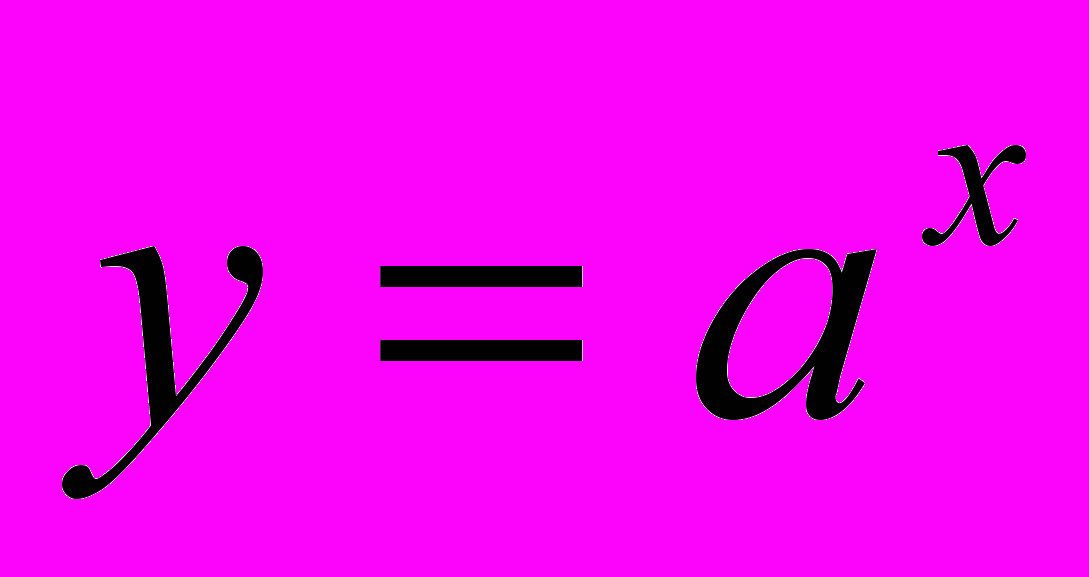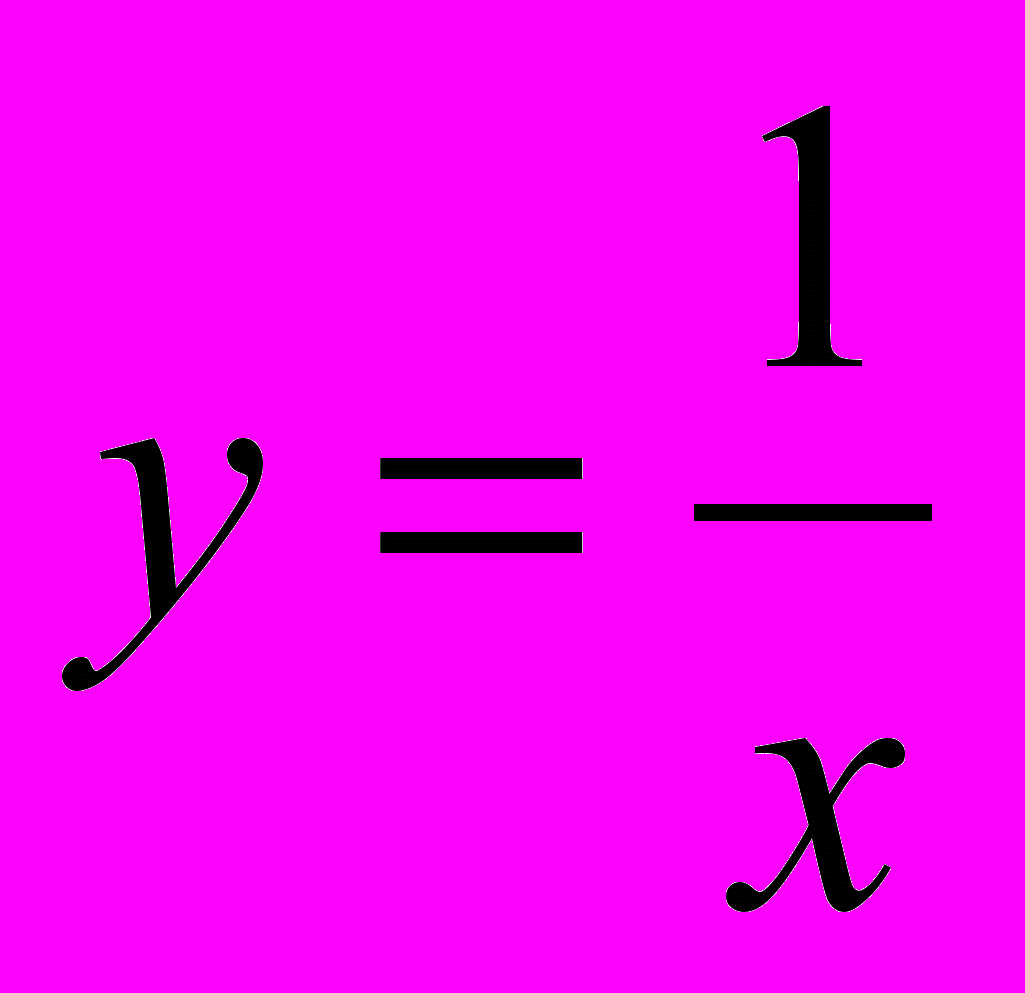, повторить всю теорию по теме «Применение производной к исследованию функции» и познакомить с ее применением к исследованию функций вида 
, 
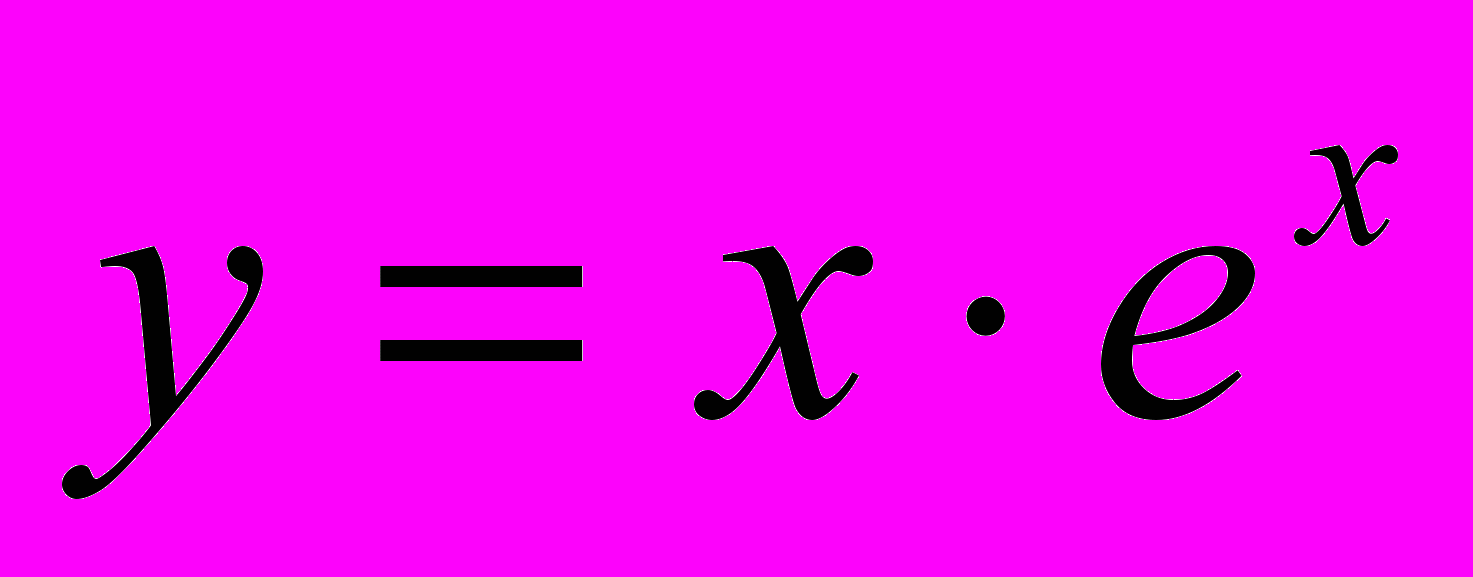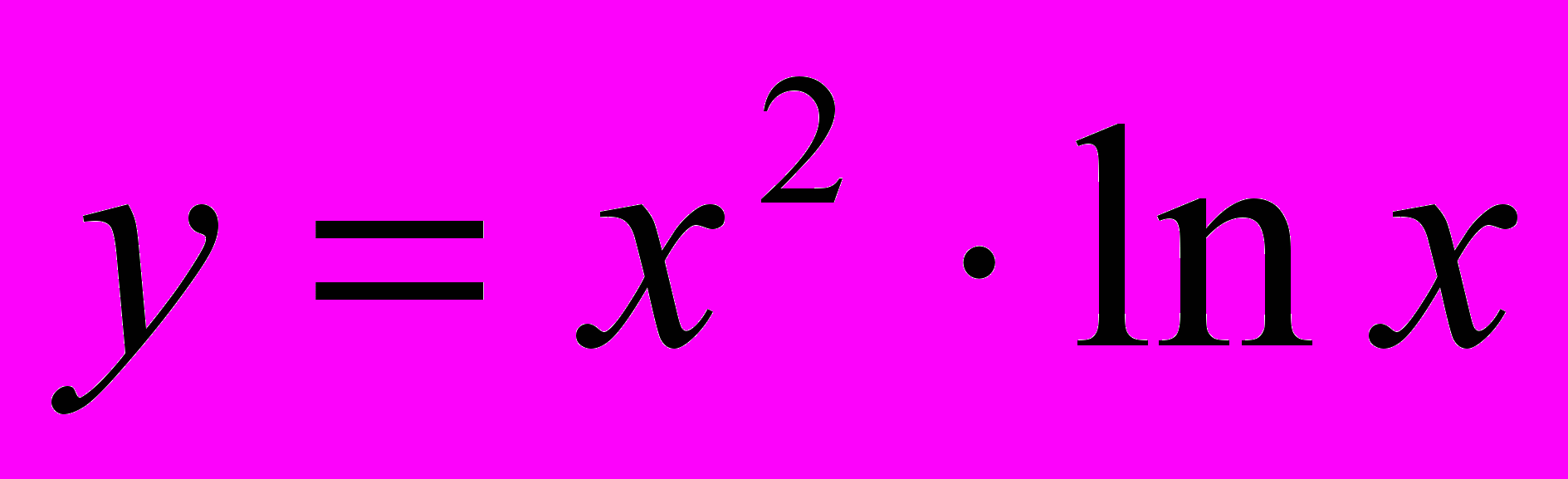и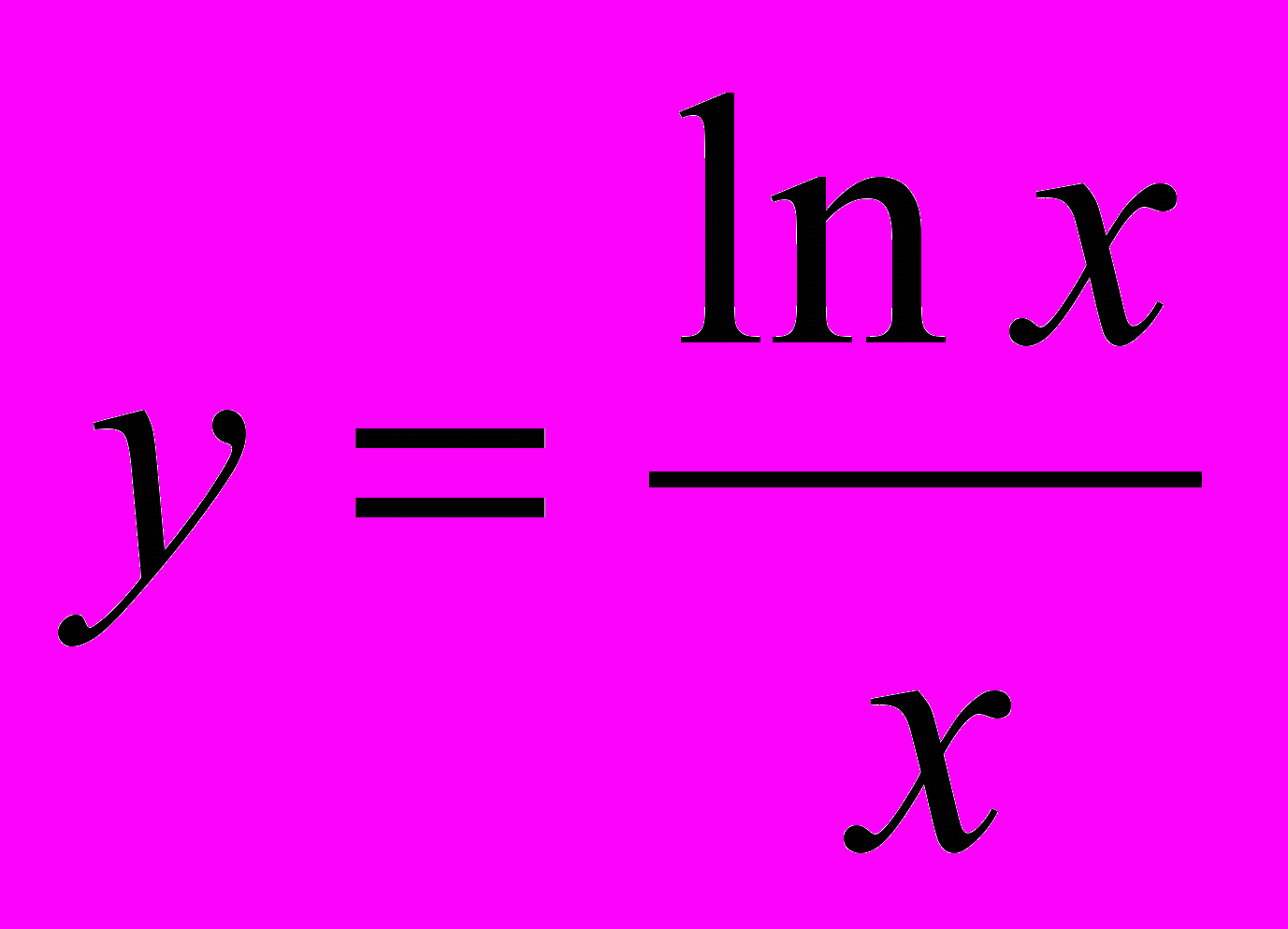 
и т.д. При изучении этой темы большое внимание уделяется решению задач для вступительных экзаменов в ВУЗы.Учащиеся должны знать все теоретические положения данной темы, особенно определение логарифма и показательной функции, свойства логарифмов и показательной функции. Учащиеся должны уметь строить графики показательной и логарифмической функций, решать показательные и логарифмические уравнения, предусмотренные обычной программой, кроме того, знать некоторые специальные приемы решения показательных и логарифмических уравнений (например, однородных показательных уравнений, решение показательных уравнений методом логарифмирования, решение показательных и логарифмических уравнений, содержащих параметр, модуль и т.д.).
Уравнения, неравенства, системы (34 часа)
Равносильные уравнения и уравнения-следствия. Общие методы решения уравнений, переход к равносильным уравнениям, переход к уравнению-следствию, посторонние корни, потеря корней. Различные приемы решения уравнений: разложение на множители, замена переменной, возведение в степень, функционально-графический метод, некоторые нестандартные приемы решения уравнений. Системы уравнений и способы их решения: подстановка, сложение, введение новых переменных, графический способ. Решение неравенств, доказательство неравенств, изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Уравнения, неравенства, системы с параметрами и модулями. Применение математических методов для решения содержательных задач из различных областей науки и практики, интерпретация результата, учет реальных ограничений.
Основная цель: обобщение различных приемов решения уравнений, неравенств, систем различного вида: логарифмических, показательных, иррациональных, тригонометрических.
Учащиеся должны знать перечень преобразований, которые приводят к появлению посторонних решений или потере корней. Учащиеся должны уметь применять различные способы решений уравнений, неравенств, систем, знать недостатки и достоинства каждого способа, уметь выбирать рациональные способы решений.
Элементы комбинаторики, статистики и теории вероятностей. (16 часов)
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
Основная цель: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Учащиеся должны уметь :
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля, вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
- вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи).
Повторение (36 часов)
Основная цель: обобщение и систематизация полученных знаний. Значительное место при повторении должно быть уделено решению задач, отвечающих требованиям для поступающих в ВУЗы, где математика является профилирующим предметом. Необходимо повторить некоторые темы из 9 класса, такие как «Арифметическая и геометрическая прогрессии», «Решение текстовых задач». Обучение алгебре на данном этапе должно быть направлено также на подготовку к Единому Государственному экзамену.
* Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
Геометрия
10 класс
(3 часа в неделю, всего 102 часа)
Геометрия на плоскости (24 часа)
Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей.Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей.
Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной.
Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма.
Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.
Геометрические места точек. Решение задач с помощью геометрических преобразований и геометрических мест.
Теоремы Чевы и Менелая*.
Эллипс, гипербола и парабола как геометрические места точек.
Неразрешимость классических задач на построение.
Прямые на плоскости и в пространстве (30 часов)
Основные понятия стереометрии (точка, прямая, плоскость, пространство). Понятие об аксиоматическом способе построения геометрии.
Пересекающиеся, параллельные и скрещивающиеся прямые. Угол межу прямыми в пространстве. Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная к плоскости. Угол между прямой и плоскостью.
Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла.
Расстояние от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Параллельное проектирование. Ортогональное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур. Центральное проектирование.
Координаты и векторы (21 час)
Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным векторам.
Повторение (27 часов)
Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
Геометрия
11 класс
(3 часа в неделю, всего 102 часа)
Многогранники (21 час)
Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера.*
Призма, ее основание, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед, куб.
Призма, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усечённая пирамида.
Симметрии в кубе, параллелепипеде, призме и пирамиде.
Понятие о симметрии в пространстве (центральная, осевая, зеркальная cимметрии).
Сечения многогранников. Построение сечений.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Тела и поверхности вращения (27 часов)
Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения, параллельные основанию.
Шар и сфера, их сечения. Эллипс, гипербола, парабола как сечения конуса. Касательная плоскость к сфере. Сфера, вписанная в многогранник и описанная около него.
Цилиндрические и конические поверхности.
Объемы тел и площади их поверхностей (30 часов)
Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, параллелепипеда, призмы, цилиндра, пирамиды и конуса. Формулы площадей поверхности цилиндра и конуса. Формулы объема шара и площади сферы.
Повторение (24 часов)
* Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
ЛИТЕРАТУРА.
Основная.
- Алгебра и начала анализа: Учебник для 10-11 кл. общеобразовательных учреждений / А.Н.Колмогоров и др.; под ред. А.Н.Колмогорова. – М.:Просвещение, 2004.
- Алгебра: Учебное пособие для учащихся 8 кл. с углубленным изучением математики/ Н.Я. Виленкин и др.; под ред. Н.Я. Виленкина. – М.:Просвещение, 2001.
- Алгебра: Учебное пособие для учащихся 9 кл. с углубленным изучением математики/ Н.Я. Виленкин и др.; под ред. Н.Я. Виленкина. – М.:Просвещение, 2001.
- Алгебра и математический анализ. Учебное пособие для учащихся 10 кл. с углубленным изучением математики/ Н.Я. Виленкин и др.; под ред. Н.Я. Виленкина. – М.:Просвещение, 1995.
- Алгебра и математический анализ. Учебное пособие для учащихся 11 кл. с углубленным изучением математики/ Н.Я. Виленкин и др.; под ред. Н.Я. Виленкина. – М.:Просвещение, 1995.
- Алгебра: элементы статистики и теории вероятностей.: Учебное пособие для учащихся 7-9 кл. общеобразовательных учреждений/ Ю.Н.Макарычев, Н.Г.Миндюк; под ред. С.А.Теляковского. – М.:Просвещение, 2005.
- Геометрия.: Учебник для 10-11 кл. общеобразовательных учреждений/Л.С.Атанасян и др. – М.:Просвещение, 2003.
Дополнительная.
1. Сборник задач по алгебре для 8-9 кл.: Учебное пособие с углубленным изучением математики/ М.Л. Галицкий и др. . – М.:Просвещение, 1995.
- Математика ЕГЭ: методическое пособие для подготовки/ Ю.А.Глазков и др.- М.: Издательство «Экзамен», 2006.
- Вероятность и статистика. 5-9 кл.: Пособие для общеобразовательных учебных учреждений. -М.: Дрофа, 2002.
- Факультативный курс по математике.: Теория вероятностей: Учебное пособие для 9-11 классов средней школы. – М.:Просвещение, 1990.
- Геометрия. 11 кл.: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики/ Е.В.Потоскуев, Л.И.Звавич. -М.: Дрофа, 2003.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
Основной.
- Дидактические материалы по алгебре и началам анализа для 10 кл./ Б.М. Ивлев и др. –М.: Просвещение, 2004.
- Дидактические материалы по алгебре и началам анализа для 11 кл./ Б.М. Ивлев и др. –М.: Просвещение, 2004.
- Дидактические материалы по алгебредля 9 кл. с углубленным изучением математики. – М.: Просвещение, 1999.
- Сборник заданий для проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс/ Г.В.Дорофеев и др. -М.: Дрофа, 2004.
- Единый государственный экзамен: математика: контрольные измерительные материалы: 2005-2006/ под общей ред. Л.О.Денищевой; Министерство образования и науки РФ, Федеральная служба по надзору в сфере образования и науки, Федеральный институт педагогических измерений. - М.: Просвещение, 2006.
- Единственные реальные варианты заданий для подготовки к единому государственному экзамену. ЕГЭ-2006. Математика/ А.Г.Клово.- М.: Федеральный центр тестирования, 2006.
- Дидактические материалы по геометрии для 10 кл./Б.Г.Зив. –М.: Просвещение, 2003.
- Дидактические материалы по геометрии для 11 кл./Б.Г.Зив. –М.: Просвещение, 2003.
Дополнительный.
- Самостоятельные и контрольные работы по алгебре и началам анализа для 10 -11 кл./ А.П.Ершова, В.В.Голобородько. – М.: Илекса, 2003.
- Тесты по алгебре и началам анализа для 10 -11 кл./ Б.Г.Зив. – СП(б):СМИО Пресс, 2002.
- Сборник задач по алгебре и началам анализа: Учебное пособие для учащихся 10-11 кл.с углубленным изучением математики/ А.П.Карп. –М.: Просвещение, 1995.
- Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов .с углубленным изучением математики/Л.И.Звавич и др. -М.: Дрофа, 2002.
- Самостоятельные и контрольные работы по геометрии для 10 кл. – М.: Илекса, 2005.
- Самостоятельные и контрольные работы по геометрии для 11 кл. – М.: Илекса, 2005.
- Дидактические материалы по геометрии для 10 кл. с углубленным изучением математики.–М.: Просвещение, 2002.
- Дидактические материалы по геометрии для 11 кл. с углубленным изучением математики.–М.: Просвещение, 2002.
* Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
* Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
*.
*