Преподаватель: доц. Глущенко И. А. Вопросы к зачету по дисциплине
| Вид материала | Документы |
- Курс специальности «Математика», 7 семестр, 2011-2012 уч г., Одо требования к зачету, 39.3kb.
- Вопросы к зачету (экзамену) по дисциплине: «Управленческий учет» преподаватель: Трофимова, 25.56kb.
- Учебно-методическое пособие по самостоятельной работе для студентов всех специальностей, 913.38kb.
- Учебно-методическое пособие по самостоятельной работе для студентов всех специальностей, 879.94kb.
- Вопросы к зачету по дисциплине «Налогообложение банков» преподаватель: к э. н., доцент,, 21.5kb.
- Преподаватель: к э. н. Танина А. В. Вопросы к зачету, 66.95kb.
- Вопросы к зачету по дисциплине «Учет затрат, калькулирование и бюджетирование в отраслях, 15.03kb.
- Вопросы к дифференцированному зачету II этапа аттестации, 36.22kb.
- Методические рекомендации Издание второе, переработанное и дополненное Минск 2006 удк, 270.38kb.
- Преподаватель Сухарев А. Н. Вопросы к зачету, 33.29kb.
Относительные показатели вариации
Относительные показатели вариации включают:
- Коэффициент осцилляции
- Относительное линейное отклонение (линейный коэффициент варианции)
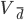
- Коэффициент вариации (относительное отклонение)
Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:
| Коэффициент осцилляции |  |
| Относительное линейное отклонение |  |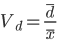
| Коэффициент вариации |  |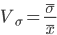
Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан
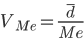,так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.
В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение
, где 
— средний квартиль полусуммы разности третьего (или верхнего) квартиля (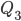
) и первого (или нижнего) квартиля (
).
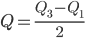.На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).
Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии
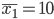при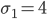 
, а по другой — 
при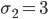
. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (
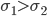. Относительная мера вариации (
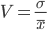позволяет сделать противоположный вывод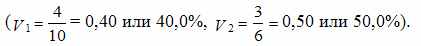
- Средние величины, их назначение и виды, порядок расчёта и область применения
Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.
Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака
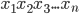некоторой уравновешенной средней величиной 
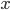.Например, индивидуальная выработка у 5 операционистов коммерческого банка за день составила 136, 140, 154 и 162 операции. Чтобы получить среднее число операций за день, выполненных одним операционистом, необходимо сложить эти индивидуальные показатели и полученную сумму разделить на количество операционистов:
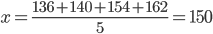операций.Как видно из приведенного примера, среднее число операций не совпадает ни с одним из индивидуальных, так как ни один операционист не сделал 150 операций. Но если мы представим себе, что каждый операционист сделал по 150 операций, то их общая сумма не изменится, а будет также равна 750. Таким образом, мы пришли к основному свойству средних величин: сумма индивидуальных значений признака равна сумме средних величин.
Это свойство еще раз подчеркивает, что средняя величина является обобщающей характеристикой всей статистической совокупности.
Средние величины широко применяются в различных отраслях знаний. Особо важную роль они играют в экономике и статистике: при анализе, планировании, прогнозировании, при расчете нормативов и при оценке достигнутого уровня. Средняя всегда именованная величина и имеет ту же размерность, что и отдельная единица совокупности.
Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие:
- В каждом конкретном случае необходимо исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и имеющиеся для расчета данные.
- Индивидуальные значения, из которых вычисляются средние, должны относиться к однородной совокупности, а число их должно быть значительным.
Виды средних величин
Средние величины делятся на два больших класса: степенные средние и структурные средние
Степенные средние:
Структурные средние:
Выбор формы средней величины зависит от исходной базы расчета средней и от имеющейся экономической информации для ее расчета.
Исходной базой расчета и ориентиром правильности выбора формы средней величины являются экономические соотношения, выражающие смысл средних величин и взаимосвязь между показателями.
Расчет некоторых средних величин:
- Средняя заработная плата 1 работника = Фонд заработной платы / Число работников
- Средняя цена 1 продукции = Стоимость производства / Количество единиц продукции
- Средняя себестоимость 1 изделия = Стоимость производства / Количество единиц продукции
- Средняя урожайность = Валовый сбор / посевная площадь
- Средняя производительность труда = объем продукции, работ, услуг / Отработанное время
- Средняя трудоемкость = отработанное время / объем продукции, работ, услуг
- Средняя фондоемкость = Средняя стоимость основных фондов / объем продукции, работ и услуг
- Средняя фондоотдача = объем продукции, работ и услуг / средняя стоимость основных фондов
- Средняя фондовооруженность = средняя величина основных производственных фондов / среднесписочная численность производственного персонала
- Средний процент брака = ( стоимость бракованной продукции / Стоимость всей произведенной продукции ) * 100%