Кинематический анализ и синтез механизмов с шестизвенной четырёхповодковой структурной группой и выстоями выходных звеньев

Вид материала

Автореферат диссертации

Содержание Научный руководитель Ведущая организация Общая характеристика работы Актуальность темы. Цель работы Для достижения поставленной цели должны быть решены следующие задачи Методы исследования. Научная новизна На защиту выносятся следующие положения Практическая значимость. Апробация работы. Структура и объём диссертации. Основное содержание работы В первой главе Во второй главе В в шестизвенной четырёхповодковой структурной группе, задачу о положении её звеньев можно свести к определению точек пересечени D в принятой системе координат. Угловая координата φ А и шатунной точкой В Третья глава ОАВ таким образом, чтобы одно её предельное положение соответствовало движению шатунной точки Е ... Полное содержание

Подобный материал:

• Оптимизационный кинематический синтез плоских рычажных механизмов IV класса с приближенным, 314.16kb.
• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.
• Темы курсового проекта по дисциплине «Теория механизмов и машин», 69.21kb.
• Анализа и синтеза у дошкольников с нарушениями речи. Нарушение речи является распространенным, 68.85kb.
• Курс Семестр Трудоемкость (в зачетных единицах), 33.22kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Волков Глеб Юрьевич систематика и структурно-параметрический синтез механизмов на базе, 545.92kb.
• Решение задачи оптимизационного кинематического синтеза плоских рычажных механизмов, 72.84kb.
• Рабочая программа дисциплины государственный экзамен по направлению подготовки бакалавров, 75.18kb.

На правах рукописи


Осипова Ольга Ивановна


КИНЕМАТИЧЕСКИЙ АНАЛИЗ И СИНТЕЗ МЕХАНИЗМОВ

С ШЕСТИЗВЕННОЙ ЧЕТЫРЁХПОВОДКОВОЙ СТРУКТУРНОЙ ГРУППОЙ

И ВЫСТОЯМИ ВЫХОДНЫХ ЗВЕНЬЕВ


Специальность 05.02.18 - Теория механизмов и машин


Автореферат

диссертации на соискание учёной степени

кандидата технических наук


Омск 2012

Работа выполнена в Омском государственном техническом университете

на кафедре «Автоматизация и робототехника» и Новосибирском государственном аграрном университете на кафедре «Теоретическая и прикладная механика»


Научный руководитель: ХОМЧЕНКО Василий Герасимович

доктор технических наук, профессор


Официальные оппоненты: ХОРУНЖИН Владимир Степанович

доктор технических наук, профессор


РЕДРЕЕВ Григорий Васильевич

кандидат технических наук, доцент


Ведущая организация: ФГБОУ ВПО «Алтайский государственный технический университет им. И.И. Ползунова», г. Барнаул


Защита состоится: 2 марта 2012 г. в 14⁰⁰ часов на заседании

диссертационного совета Д 212.178.06 при ФГБОУ ВПО «Омский государственный технический университет» по адресу: 644050, г. Омск, пр. Мира, 11

С диссертацией можно ознакомиться в библиотеке ФГБОУ ВПО «Омский государственный технический университет»


Автореферат разослан «___»___________ 2012 г.


Учёный секретарь диссертационного совета,

кандидат технических наук, профессор В.Н. Бельков

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Для экономического развития государства необходимым условием является развитие машиностроительной отрасли, что требует создания новых машин и механизмов, наиболее полно удовлетворяющих нужды современного производства. Проектирование новых машин и механизмов возможно на основе серьёзного научного фундамента, позволяющего обеспечить высокую эффективность машин уже на ранней стадии их проектирования.

Актуальность темы. В ряде отраслей промышленности широко используются цикловые технологические машины-автоматы и манипуляторы, рабочие органы которых совершают возвратно-поступательные или возвратно-вращательные движения с выстоями в крайних положениях. В последние десятилетия в мировой практике произошёл качественный сдвиг в структуре и техническом уровне машин и оборудования в сторону применения лазерных, оптических, компьютерных и других устройств для управления движением и остановкой рабочих органов. Однако их применение, приводящее к усложнению и повышению стоимости машин, не всегда оправдано. Закон движения рабочих органов с выстоем выходного звена может быть обеспечен с помощью кулачковых механизмов, применение которых сдерживает ряд недостатков, в их числе малая износоустойчивость кулачков и склонность к размыканию при высоких угловых скоростях ведущего вала. Рычажные механизмы отличаются высокой надёжностью, долговечностью, высокой нагрузочной способностью и могут успешно применяться в быстроходных машинах-автоматах. Плоские рычажные механизмы, содержащие в своём составе шестизвенную четырёхповодковую структурную группу, обладают широкими кинематическими возможностями для получения различных законов движения одного или двух выходных звеньев, в том числе их выстоев. Однако их применение в практике ограничено в силу малой изученности, относительной сложности кинематического анализа и синтеза механизмов высоких классов и, как следствие, отсутствия научной базы для проектирования. В связи с этим становится актуальной задача исследования всего многообразия модификаций шестизвенной группы Ассура, разработка алгоритмов кинематического анализа механизмов, в состав которых она входит, и создание на этой основе системы алгоритмов кинематического синтеза плоских рычажных механизмов с выстоями одного и двух выходных звеньев.

Цель работы. Расширение технологических возможностей механизмов цикловых машин-автоматов с выстоями выходных звеньев на основе использования плоских рычажных механизмов с шестизвенной четырёхповодковой структурной группой.

Для достижения поставленной цели должны быть решены следующие задачи:

• определение числа модификаций шестизвенной четырёхповодковой структурной группы, их систематизация и классификация по виду кинематических пар;
  
• определение критерия для выбора метода решения задачи о положениях звеньев шестизвенной группы Ассура различных модификаций;
  
• разработка методов определения положений звеньев шестизвенных четырёхповодковых структурных групп различных модификаций с определением фактического числа сборок группы;
  
• составление алгоритмов решения задачи о положениях механизмов с различными способами присоединения шестизвенной четырёхповодковой структурной группы к входным звеньям;
  
• разработка алгоритмов синтеза восьмизвенных механизмов с выстоями одного и двух выходных звеньев;
  
• разработка методики оценки работоспособности механизма со структурной группой третьего класса четвёртого порядка по условиям качества передачи движения.
  

Методы исследования. В работе использованы методы теории механизмов и машин, теоретической механики, аналитической геометрии, синтеза и анализа плоских рычажных механизмов высоких классов, приближённые итеративные методы решения параметрических уравнений.

Научная новизна работы состоит в следующем:

• определено число модификаций шестизвенной четырёхповодковой структурной группы, проведена их систематизация и классификация по виду кинематических пар;
  
• составлены алгоритмы решения задачи о положениях механизмов при различных способах присоединения шестизвенных четырёхповодковых структурных групп различных модификаций к входному звену;
  
• разработаны алгоритмы синтеза восьмизвенных механизмов третьего класса с возвратно-вращательным и возвратно-поступательным движением выходных звеньев с выстоями одного выходного звена и двух выходных звеньев, происходящими одновременно или в противофазах;
  
• предложены методы определения условий собираемости, существования кривошипа и углов давления, решения задач статического силового анализа в механизмах с шестизвенной четырёхповодковой структурной группой.
  

Достоверность научных положений подтверждается применением апробированных методов теории механизмов и машин. При решении задач кинематического анализа и синтеза механизмов использованы принципы, разработанные в трудах ведущих учёных в области теории механизмов и машин, плоских рычажных механизмов высоких классов, итеративные математические методы решения параметрических уравнений. Полученные в диссертационной работе результаты не противоречат положениям вышеперечисленных теорий.

На защиту выносятся следующие положения:

• систематизация и классификация шестизвенных четырёхповодковых структурных групп по виду кинематических пар;
  
• алгоритмы кинематического анализа плоских рычажных механизмов с шестизвенной четырёхповодковой структурной группой различных видов;
  
• алгоритмы синтеза восьмизвенных плоских рычажных механизмов третьего класса с выстоем одного выходного звена, выстоями двух выходных звеньев одновременными и в противофазах;
  
• синтезированные кинематические схемы кривошипно-коромысловых и кривошипно-ползунных рычажных механизмов с шестизвенной группой Ассура с приближённым выстоем одного и двух выходных звеньев.
  

Практическая значимость. Разработанные теоретические положения доведены до алгоритмов и конкретных практических рекомендаций, направленных на проектирование механизмов с шестизвенной четырёхповодковой структурной группой. Получен ряд кинематических схем восьмизвенных механизмов третьего класса с выстоями одного и двух выходных звеньев. Результаты диссертационной работы используются в качестве методических материалов в конструкторской практике предприятия ФГУП «СибНИА им. С.А. Чаплыгина» при разработке специализированного экспериментального оборудования и внедрены в учебный процесс ФГБОУ ВПО Новосибирский государственный аграрный университет на кафедре «Теоретическая и прикладная механика».

Апробация работы. Основные результаты работы докладывались на:

• десятой Международной конференции по научному обеспечению азиатских территорий «Научное обеспечение АПК Сибири, Монголии и Казахстана» 3-6 июля 2007 г., г. Улан-Батор;
  
• ежегодной научно-практической конференции студентов и аспирантов Инженерного Института НГАУ 2 апреля 2008г., г. Новосибирск;
  
• Международной научно-практической конференции «Машино-технологическое, энергетическое и сервисное обеспечение сельхозтоваропроизводителей Сибири», посв. 100-летию со дня рождения академика ВАСХНИЛ А.И. Селиванова 9–11 июня 2008 г., п.г.т. Краснообск ;
  
• Международного научно-практического форума «Инновации в агропромышленном комплексе» 3-4 июня 2009 г., г. Новосибирск;
  
• VII Международной научно-технической конференции «Динамика систем, механизмов и машин» 10-12 ноября 2009 г., г. Омск;
  
• I Международной научно-технической интернет-конференции молодых учёных «Автоматизация, мехатроника, информационные технологии» 18-20 мая 2010 г., г. Омск.
  

Публикации. Основное содержание диссертационной работы отражено в 15 научных работах автора, из которых три работы опубликованы в журналах, входящих в перечень изданий, рекомендованных ВАК РФ, две – в ведущих научных журналах, шесть – в сборниках трудов Международных научно-технических конференций, одна – в материалах ежегодной научно-практической конференции студентов и аспирантов Инженерного Института НГАУ, три патента на полезную модель.

Структура и объём диссертации. Диссертационная работа состоит из введения, пяти глав, заключения, списка литературы (167 наименований), приложений. Объём работы 199 страниц основного текста, в том числе 88 рисунков и 4 таблицы.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ


Во введении обоснована актуальность исследуемой проблемы, сформулированы основные положения, выносимые на защиту, научная новизна и практическая ценность.

В первой главе диссертационной работы представлен обзор литературы, освещающей методы решения основной задачи кинематического анализа - задачи о положениях плоских рычажных механизмов третьего класса, а также вопросы возможности получения остановки конечной продолжительности в многозвенных рычажных механизмах, сформулированы цели и задачи работы.

Объектом исследования в диссертационной работе являются плоские рычажные механизмы, в состав которых входит шестизвенная четырёхповодковая структурная группа.

Среди научных трудов, посвящённых изучению рычажных механизмов высоких классов, следует выделить работы И.И. Артоболевского, В.М. Абрамова, У.А. Джолдасбекова, Л.Т. Дворникова, К.С. Иванова, В. Име, Н.И. Левитского, С.А. Черкудинова, О.Г. Озола, Э.Е. Пейсаха, В.Г. Хомченко, В.С. Хорунжина, Л.Т. Дворникова, Н.Г. Скабкина, В.Ю. Соломина, Е.С. Гебель, Ю.И. Евдокимова, С.П. Старикова и других учёных.

На основе проведённого обзора литературных источников отмечено, что в литературе рассматривались вопросы кинематического анализа механизмов с шестизвенной четырёхповодковой структурной группой ограниченно, лишь для варианта с вращательными кинематическими парами. Вопросы о модификациях четырёхповодковой структурной группы, кинематическом анализе механизмов с различными видами группы Ассура и разными способами присоединения к входному звену, не поднимались. Применяемые в промышленности и сельскохозяйственном машиностроении механизмы, содержащие шестизвенную группу Ассура, спроектированы эмпирическим путём, который не позволяет оптимизировать их параметры.

На основании выводов, сделанных по результатам анализа литературных источников, сформулированы цели и задачи диссертационной работы.

Во второй главе диссертации определено число возможных модификаций шестизвенной четырёхповодковой структурной группы, проведена их систематизация и классификация, предложены варианты решения задачи о положениях звеньев структурной группы. Установлено, что выбор метода решения задачи о положениях зависит от наибольшего числа вариантов сборки структурной группы, которое определено для каждой её модификации. Разработаны алгоритмы решения задачи о положениях механизмов при разных способах присоединения структурной группы к входному звену.

Шестизвенная четырёхповодковая структурная группа содержит два трёхпарных звена, образующих между собой центральную кинематическую пару и четыре поводка – по два на каждое трёхпарное звено (Рис.1). В основе предложенной систематизации таких структурных групп лежит деление поводков на четыре вида (Рис.2) в зависимости от вида внешней А и внутренней В кинематической пары. Предложено обозначать вид структурной группы двумя парами цифр и буквой между ними В или П по виду поводков и центральной кинематической пары, соответственно.

В
работе установлено, что шестизвенная четырёхповодковая структурная группа по виду поводков может иметь 110 модификаций (Табл.1). В первой строке и первой колонке таблицы 1 указаны виды поводков, в остальных клетках – обозначения модификаций группы.

Таблица 1.

Модификации шестизвенной четырёхповодковой структурной группы

	11	12	13	14	22	23	24	33	34	44
11	11П11 11В11	-	-	-	-	-	-	-	-	-
12	11П12 11В12	12П12 12В12	-	-	-	-	-	-	-	-
13	11П13 11В13	12П13 12В13	13П13 13В13	-	-	-	-	-	-	-
14	11П14 11В14	12П14 12В14	13П14 13В14	14П14 14В14	-	-	-	-	-	-
22	11П22 11В22	12П22 12В22	13П22 13В22	14П22 14В22	22П22 22В22	-	-	-	-	-
23	11П23 11В23	12П23 12В23	13П23 13В23	14П23 14В23	22П23 22В23	23П23 23В23	-	-	-	-
24	11П24 11В24	12П24 12В24	13П24 13В24	14П24 14В24	22П24 22В24	23П24 23В24	24П24 24В24	-	-	-
33	11П33 11В33	12П33 12В33	13П33 13В33	14П33 14В33	22П33 22В33	23П33 23В33	24П33 24В33	33П33 33В33	-	-
34	11П34 11В34	12П34 12В34	13П34 13В34	14П34 14В34	22П34 22В34	23П34 23В34	24П34 24В34	33П34 33В34	34П34 34В34	-
44	11П44 11В44	12П44 12В44	13П44 13В44	14П44 14В44	22П44 22В44	23П44 23В44	24П44 24В44	33П44 33В44	34П44 34В44	44П44 44В44

После исключения 26 модификаций с лишними степенями свободы (в таблице 1 они выделены жирным шрифтом) остаются 45 видов структурной группы с вращательной и 39 с поступательной центральной кинематической парой.

Решение основной задачи кинематического анализа – задачи о положениях звеньев для четырёхповодковой структурной группы третьего класса сводится к определению действительных точек пересечения шатунных кривых m и n двух четырёхзвенных механизмов, полученных из группы путём размыкания центральной кинематической пары Е и изменения условно-обобщённых координат φ₁ и φ₆ (Рис. 3). Число решений задачи о положениях звеньев группы соответствует числу вариантов её сборки. Наибольшее число N вариантов сборки четырёхповодковой структурной группы может служить критерием сложности решения задачи и определять выбор метода решения. Исследуя шатунные кривые на их порядок и циркулярность, определено число N для каждой из сорока пяти модификаций четырёхповодковой структурной группы с вращательной кинематической парой между трёхпарными звеньями (Табл. 2) по формуле:

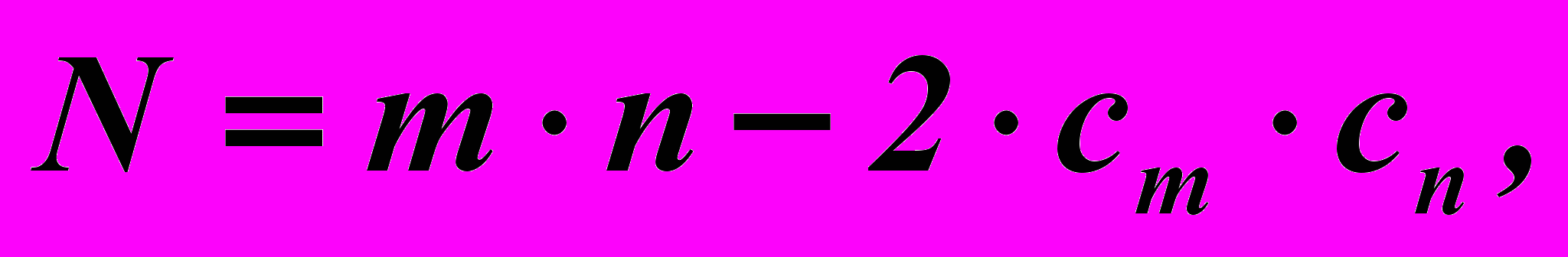
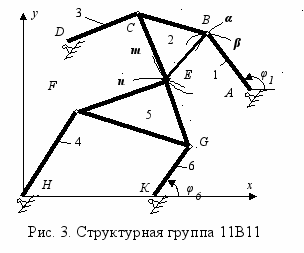(1)

где m, n – порядок шатунных кривых как алгебраических линий,

с_m, и c_n – их циркулярность, т.е. число пар бесконечно удалённых мнимых точек, через которые проходит каждая из кривых.

Так, шатунная кривая шарнирного четырёхзвенника имеет шестой порядок и является трициркулярной. Структурная группа основного вида с вращательными кинематическими парами, таким образом, может иметь в общем случае максимально восемнадцать вариантов сборки. В первой строке и первой колонке таблицы 2 указаны виды поводков, в остальных клетках помещены наибольшие числа вариантов сборки для каждой модификации группы с вращательной центральной кинематической парой.

Таблица 2.

Наибольшее число вариантов сборки модификаций структурной группы

	11	12	13	14	22	23	24	33	34
11	18
12	18	18
13	18	18	14
14	6	6	6	2
22	12	12	12	4	8
23	18	18	14	6	12	14
24	6	6	4	2	4	4	1
33	12	12	8	4	8	8	2	4
34	6	6	4	2	4	4	1	2	1

Для восьми видов структурной группы с N=1 или N=2 задача о положениях её звеньев решается в принципиальном отношении точно и сводится в геометрическом смысле к определению точки пересечения двух прямых, либо двух окружностей, либо окружности или эллипса с прямой. В этих случаях аналитически задача о положениях звеньев структурной группы сводится к решению системы двух линейных уравнений, либо системы двух уравнений, одно из которых линейное, а другое имеет второй порядок. Двадцать восемь видов структурной группы имеет максимальное число сборок не менее шести, задача о положениях её звеньев сводится к определению точек пересечения двух шатунных кривых, либо шатунной кривой с прямой линией, окружностью или эллипсом. Поскольку шатунная кривая как алгебраическая линия в общем случае имеет высокий порядок, решение задачи может быть получено приближёнными итеративными методами. Девять видов структурной группы могут иметь максимально четыре сборки, для них задачу о положениях звеньев в общем случае можно свести к решению уравнения четвёртого порядка, т.е. к определению корней полинома четвёртой степени. Существующие точные методы решения таких уравнений громоздки, поэтому целесообразно решение этой задачи производить также приближённым итеративным способом.

Р
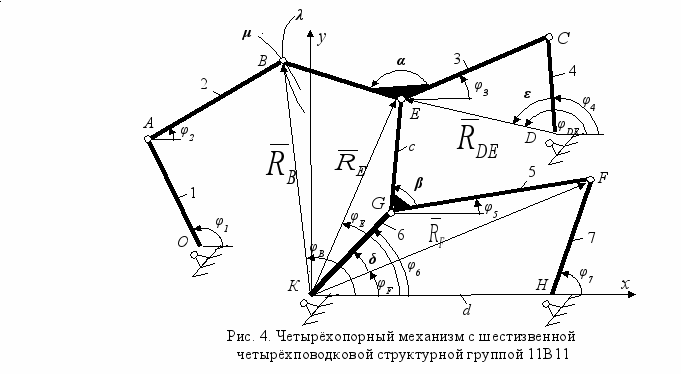
азомкнув шарнир В в шестизвенной четырёхповодковой структурной группе, задачу о положении её звеньев можно свести к определению точек пересечения шатунной кривой λ и окружности μ с центром в точке А и радиусом АВ. Составим параметрические уравнения шатунной кривой λ, приняв в качестве условно-обобщённой координаты угловую координату φ₇. При этом используем экспоненциальную форму комплексных чисел, что делает записи краткими и удобными для программирования. Например, для структурной группы основного вида 11В11 (Рис. 4) обозначим размеры звеньев АВ=l₂, ВС=l₃, СD=l₄, HF=l₇, KG=l₆, GF=l₅, углы трёхпарных звеньев α и β.

В системе координат, связанной с центрами шарнирных опор К и Н, положение центра шарнира F при заданном значении угловой координаты φ₇ выражается вектором

, (2)

где d – расстояние между центрами шарнирных опор K и H.

Угловая координата звена 6 определяется соотношением

, (3)

в котором

. (4)

Здесь k₁=1, если обход по контуру GFK направлен против хода часовой стрелки и k₁=-1 в противном случае.

Положение отрезка GF шатуна 5 определяется разностью векторов

, (5)

откуда можно определить его угловую координату φ₅.

Координаты шатунной точки Е выражаются комплексным числом

. (6)

В уравнении (6) с – размер отрезка GE трёхпарного звена 5.

Угол φ_DE вектора R_DE, определяющего положение точки Е, можно определить как разность комплексных чисел

, (7)

где последнее определяет заданное положение центра шарнира D в принятой системе координат.

Угловая координата φ₄ звена 4 определяется суммой углов

. (8)

Угол ε, входящий в (8), определяется соотношением

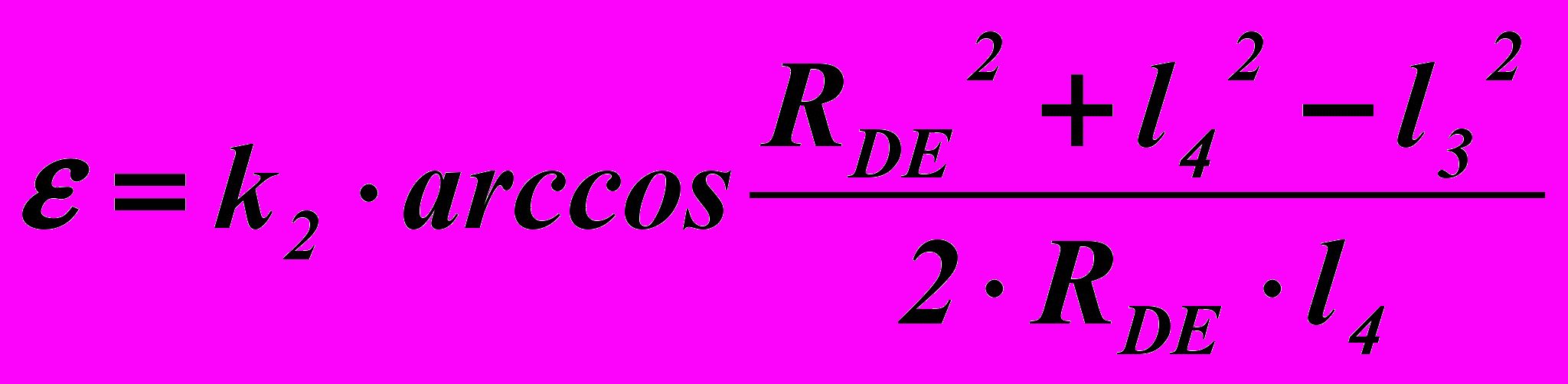. (9)

Здесь k₂=1, если обход по контуру DEC направлен против хода часовой стрелки и k₁=-1 в противном случае.

Угловая координата φ₃ отрезка ЕС трёхпарного звена 3 может быть определена как аргумент комплексного числа

. (10)

Положение точки В трёхпарного звена 3 можно выразить вектором

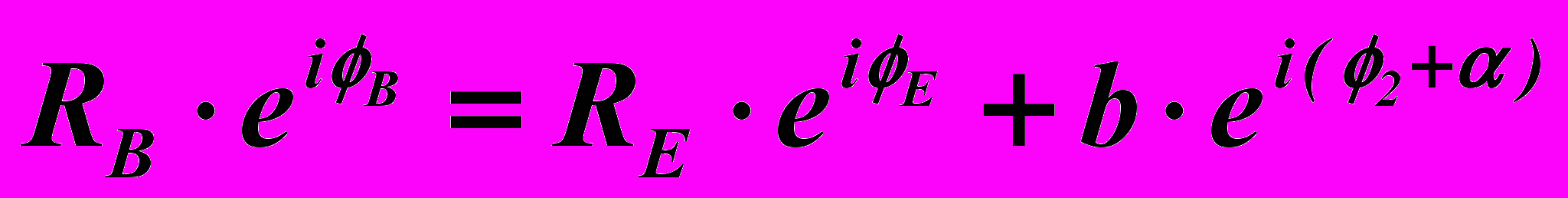, (11)

где b – размер отрезка ЕВ.

Решение задачи о положениях звеньев структурной группы сводится к определению точек пересечения шатунной кривой λ точки В звена 3 с окружностью, которую описывает при движении точка В поводка 2, итеративными методами, т.е. к решению неравенства

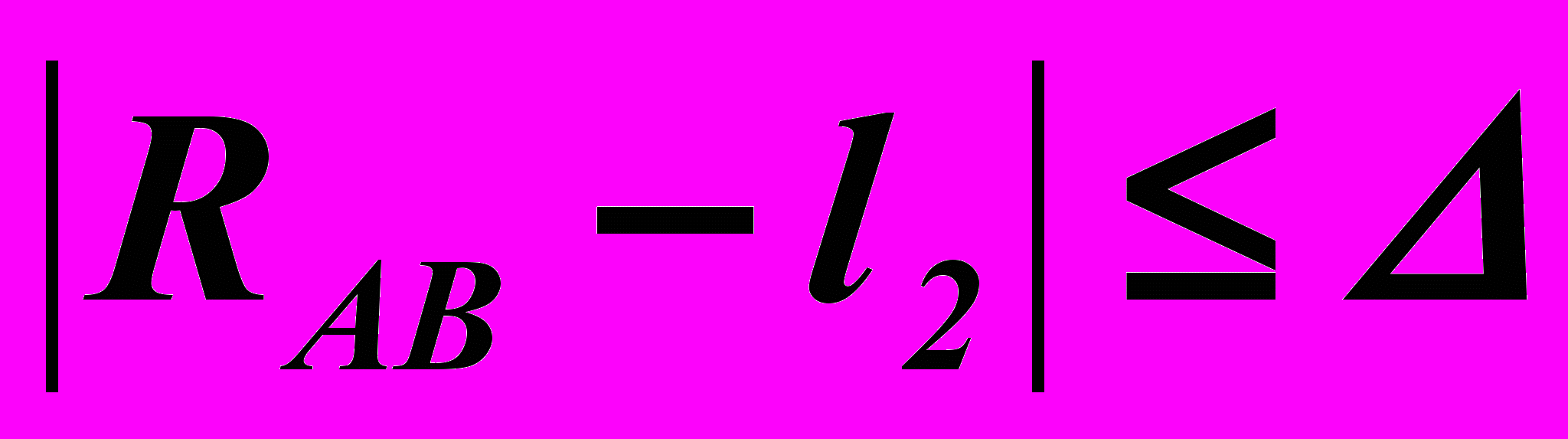, (12)

где Δ – заданная точность вычислений,

R_AB – модуль комплексного числа, определяющего расстояние между центром шарнира А и шатунной точкой В звена 3

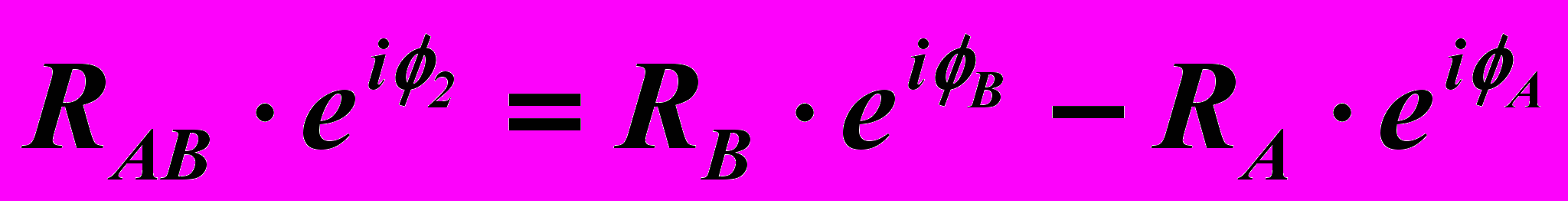. (13)

Разработаны алгоритмы определения положений механизмов при различных способах присоединения структурной группы к входному звену. Например, для четырёхопорного механизма с вращательными кинематическими парами (Рис. 4) алгоритм решения задачи о положениях представлен последовательностью (Рис. 5), где приняты обозначения:

1. Ввод исходных данных.
   
2. Формирование массива с параметрами точек шатунной кривой λ в зависимости от изменения условно-обобщённой координаты φ₇.
   
3. Задание начального значения угла поворота кривошипа φ₁ .
   
4. Определение положения звеньев механизма для текущего значения φ₁.
   
5. Задание следующего значения угла поворота начального звена φ₁=φ₁+Δφ₁, где Δφ₁ – принятый шаг вычислений.
   
6. В
   ыход. Вывод результатов расчётов в печать.
   

Третья глава посвящена разработке алгоритмов кинематического синтеза восьмизвенных механизмов третьего класса с выстоем выходных звеньев.

П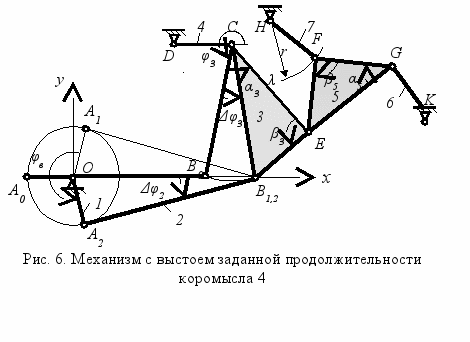редложен алгоритм кинематического синтеза плоских рычажных восьмизвенных механизмов третьего класса с возвратно-вращательным и возвратно-поступательным движением выходного звена с выстоем заданной продолжительности в крайнем положении, сочетающий метод предельных положений В.Г. Хомченко с методом использования участка шатунной кривой, приближенного к дуге окружности. Синтез механизма с выстоем (Рис. 6) предложено выполнить прямым способом, т.е. от входного звена к выходному. Выстой заданной продолжительности выходного звена 4 обеспечивается тем, что положение входной диады ОАВ на фазе выстоя φ_в совмещено с движением шатунной точки E по траектории, приближенной к дуге окружности. Для получения траектории необходимой кривизны используем способ остановки выходного звена и построения траектории λ центра шарнира F при изменении угловой координаты φ₃ на величину Δφ₃, соответствующую фазе выстоя начального звена ОА. Определив радиус r и положение центра кривизны шатунной кривой λ, поместим в него центр шарнирной опоры Н. Получим механизм, в котором на фазе выстоя центр шарнира Е движется по траектории, приближенной к дуге окружности, что обеспечивает приближённый выстой звена 4. Изменяя задаваемые параметры (размеры звеньев, фазу выстоя, углы трёхпарных звеньев, коэффициенты вариантов сборки контуров), можно получить различные механизмы с выстоем заданной продолжительности звена 4. Точность позиционирования выходного звена и его угол размаха (ход) можно при этом варьировать.

Д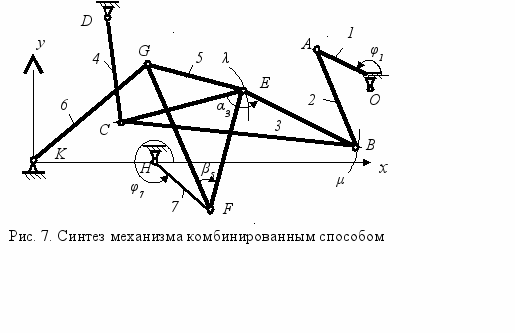ля синтеза механизма с шестизвенной четырёхповодковой структурной группой комбинированным способом предлагается сочетать метод замены начального звена с методом использования участка шатунной кривой, приближенного к дуге окружности и методом предельных положений. Синтез механизма комбинированным способом предполагает обратный способ синтеза (от выходного звена к входному). Вначале целесообразно выбрать вид и параметры кинематической цепи HFGK (Рис. 7). Обозначим размеры звеньев HF=l₇, FG=l₅, KG=l₆, FE=с₅, угол трёхпарного звена β₅, расстояние между центрами шарнирных опор КН=d. В системе координат, связанной с центрами опорных шарниров К и Н положение точки Е определяется параметрическими уравнениями (2…6). При изменении условно-обобщённой координаты φ₇ точка Е описывает шатунную кривую λ. Выберем на шатунной кривой участок, приближенный к дуге окружности. Значение угловой координаты, соответствующее средней точке выбранного участка, обозначим t, крайние точки участка отличаются от него на ±Δφ_7. После нахождения по трём точкам центра кривизны траектории λ поместим в него центр шарнира С. Поводок 4 размером l₄ расположим под прямым углом к ЕС для создания оптимальных условий передачи движения. Построим шатунную кривую μ, которую описывает точка В звена 3 при изменении угловой координаты φ₇. Входную диаду ОАВ в её предельном положении присоединим к точке В, соответствующей значению угла φ₇ в начале, либо в конце выбранного участка траектории и располагая так, чтобы обеспечить минимальный угол давления в шарнире В. Назначив размеры ОА=l₁ и АВ=l₂, найдём положение центра шарнирной опоры О следующим образом:

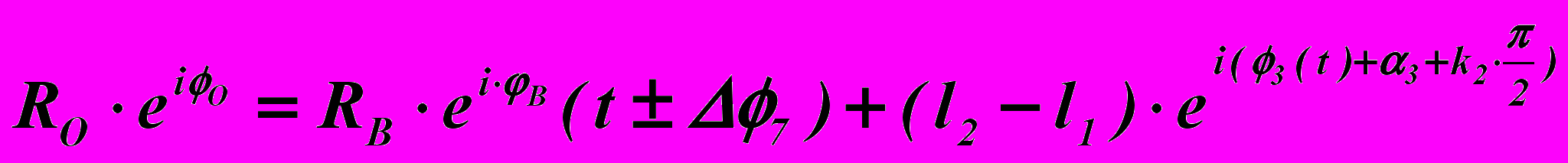, (14)

где k₂ – коэффициент компоновки, который может принимать значения 1 или -1 в зависимости от направления обхода контура СВА.

В синтезированном таким образом механизме околопредельному положению входной диады соответствует положение четырёхзвенника, обеспечивающее движение точки Е по дуге окружности, чем и достигается приближённый выстой выходного звена 4.

Для синтеза механизма с промежуточным выстоем выходного звена 4 следует, применяя изложенную методику, присоединить находящуюся в предельном положении входную диаду механизма в ином, промежуточном положении точки В на её траектории.

Кинематическая цепь HFGK с размерами звеньев l₅, l₆, l₇ и расстоянием между опорными шарнирами d имеет предельные положения, в которых возникает эффект поглощения движения. Значения угловой координаты φ₇, соответствующие предельным положениям шарнирного четырёхзвенника HFGK, обозначим s₁ и s₂:

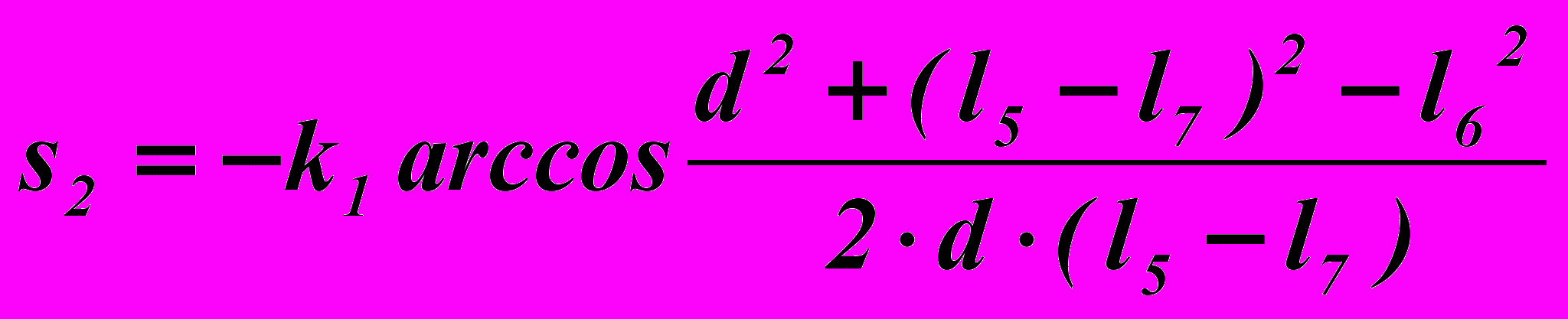, . (15)

Применяя комбинированный способ синтеза механизма, присоединим входную диаду ОАВ таким образом, чтобы одно её предельное положение соответствовало движению шатунной точки Е по участку траектории, приближенном к дуге окружности, а второе - предельному положению шарнирного четырёхзвенника HFGK. В механизме, синтезированном таким методом, звено 4 совершает выстой в одном из предельных положений входной диады, а звено 6 – в другом.

Используя этот же способ, можно синтезировать механизм с одновременными выстоями двух выходных звеньев. Для этого следует в качестве средней точки дуги шатунной кривой λ принять точку, соответствующую предельному положению четырёхзвенника (t=s₁ или t=s₂).

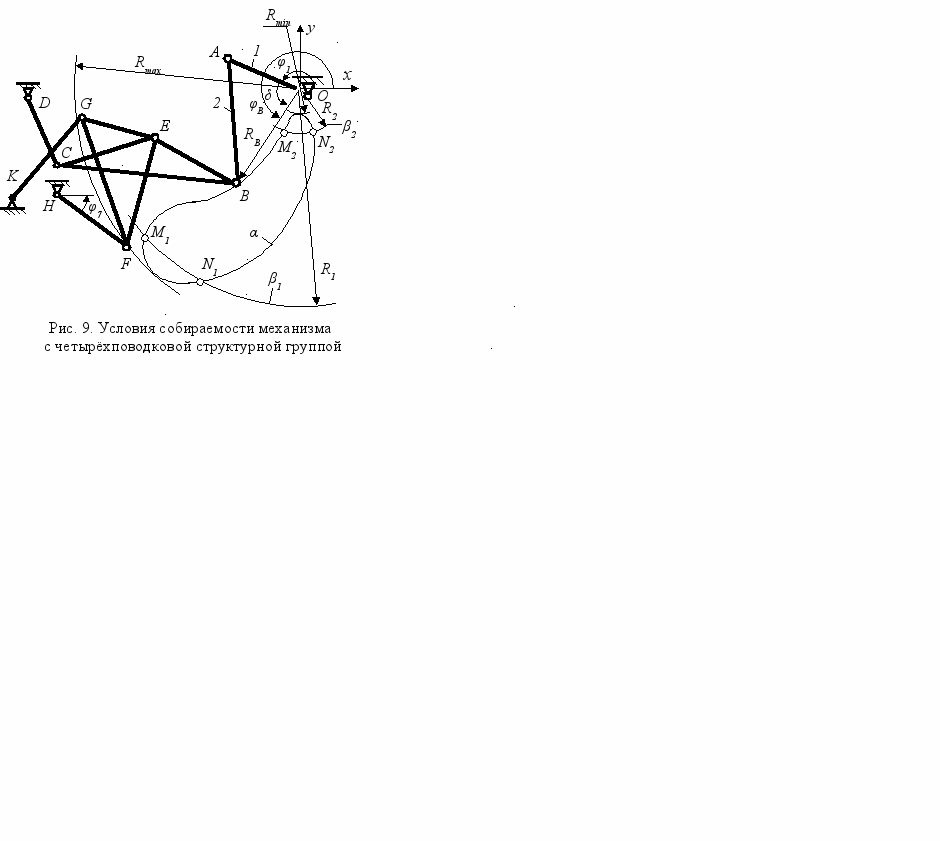
Для синтеза механизма с одновременными выстоями двух выходных звеньев предложен также метод предельных положений. Предельное положение входной диады ОАВ (Рис. 8) предлагается совместить с предельным положением одного из коромысел четырёхзвенной кинематической цепи HFGK, например HF. Мгновенный центр скоростей трёхпарного звена 5 расположен в непосредственной близости к центру шарнира G. Поместив в него центр шарнира С, можно достигнуть одновременного выстоя коромысел CD и GK.

В четвёртой главе рассмотрены кинематические и статические особенности механизмов с шестизвенной четырёхповодковой структурной группой основного вида, определены условия собираемости и существования кривошипа.

При изменении условно-обобщённой координаты φ₇ механизма с вращательными кинематическими парами (Рис. 9) точка В описывает шатунную кривую . Положение точки В относительно шарнирной опоры О определяется радиус- вектором 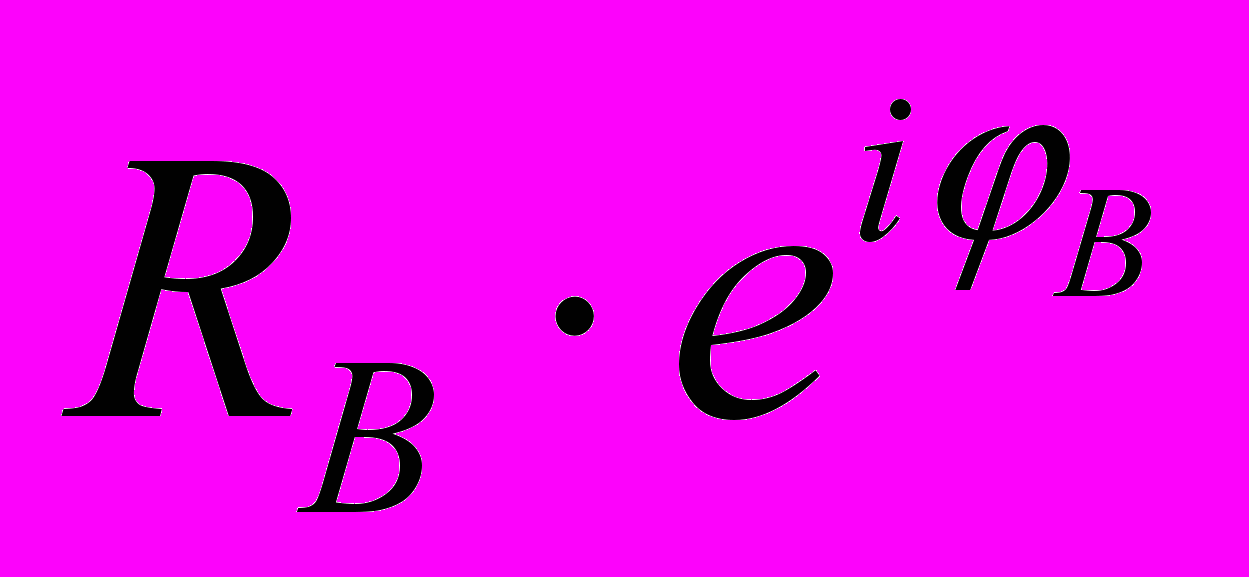. Из рисунка 9 следует, что угловая координата φ₁ звена ОА может быть определена соотношением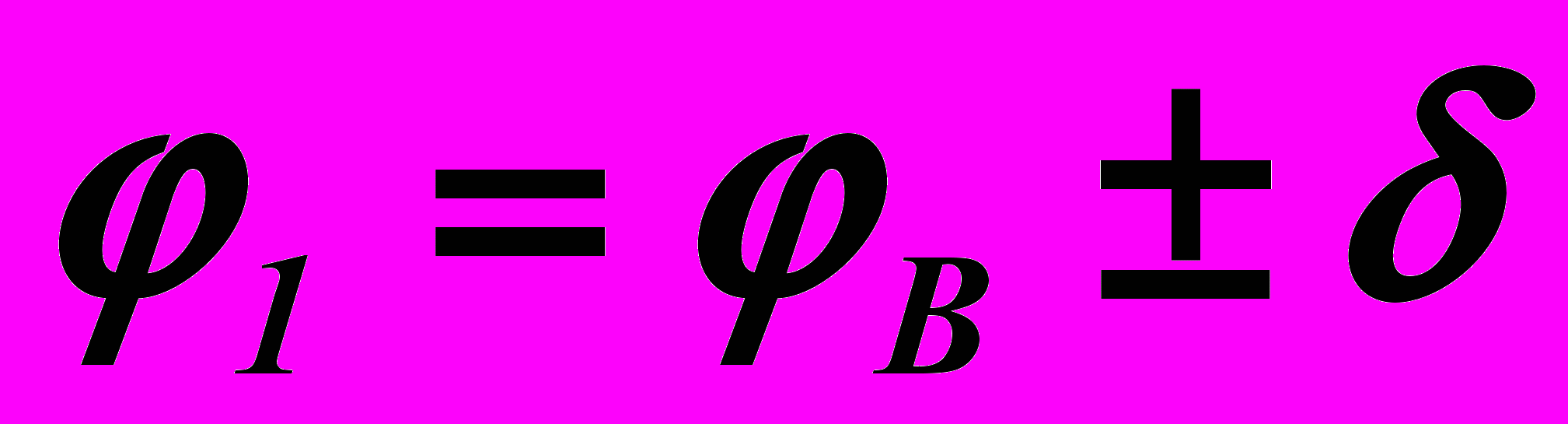

. (16)

Угол φ_В определён для любой точки В на шатунной кривой α. Угол 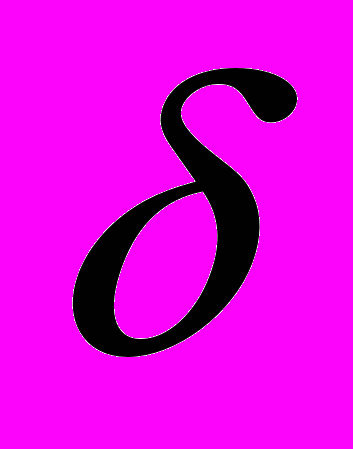определён только для тех точек шатунной кривой, для которых может быть построен треугольник ОАВ со сторонами ОА=r, АВ=l и R_B=R. Построение такого треугольника возможно при выполнении условий ,

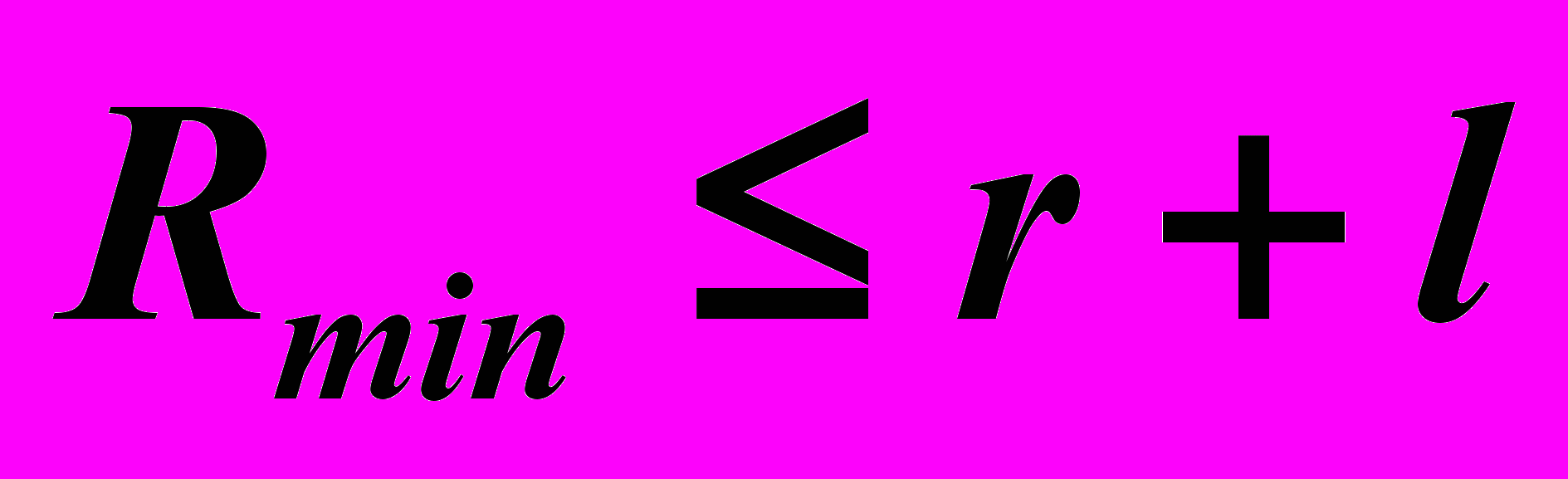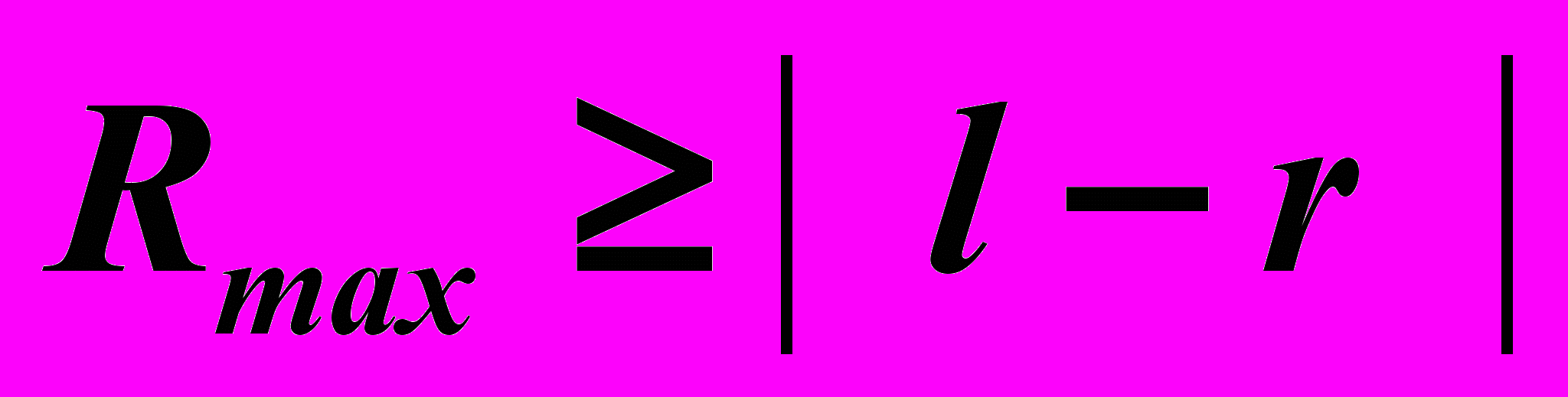, (17)

которые и являются необходимыми условиями собираемости механизма.

В том случае, если участок шатунной кривой ограничен двумя точками, одна из которых лежит на окружности β₁ радиуса 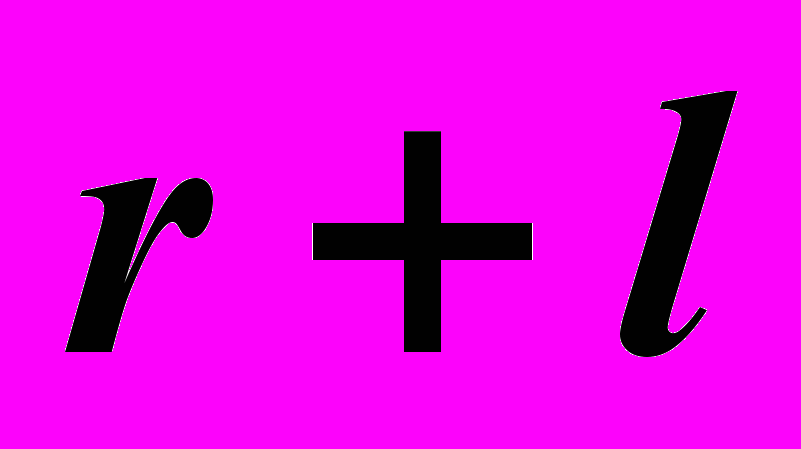а другая – на окружности β₂. радиуса , механизм будет кривошипным при соблюдения условия, что функция R_В(₁) не имеет внутри интервала относительных экстремумов. Соотношения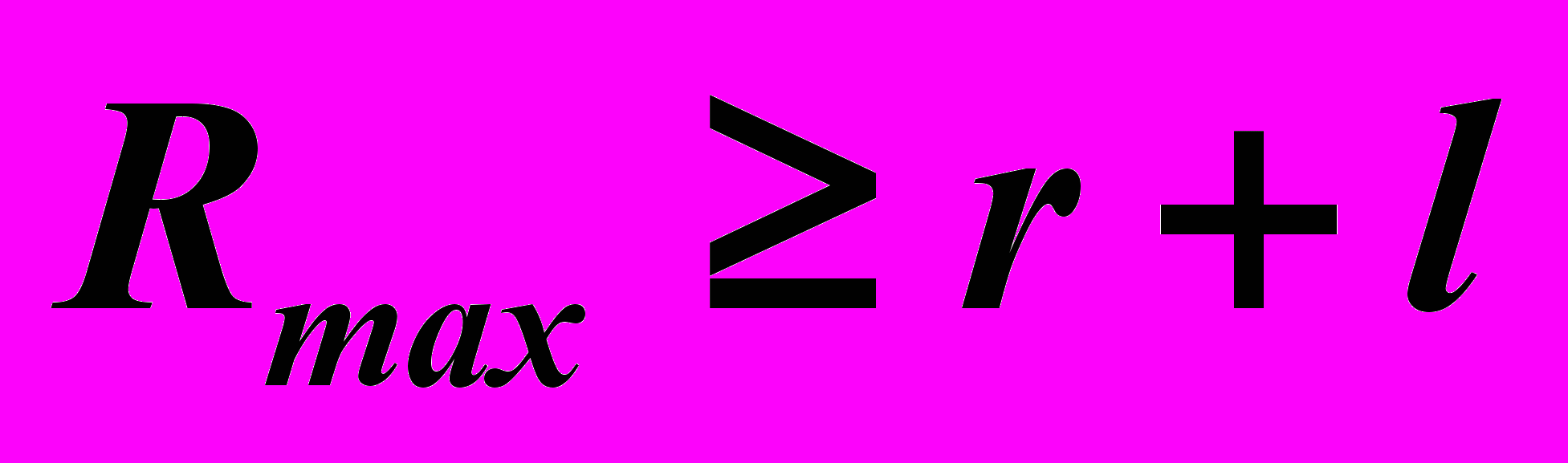

, (18)

являются геометрическими условиями существования кривошипа в механизмах с четырёхповодковой структурной группой при соотношениях размеров кривошипа и входящего с ним во вращательную кинематическую пару поводка r/l ≤ 1.

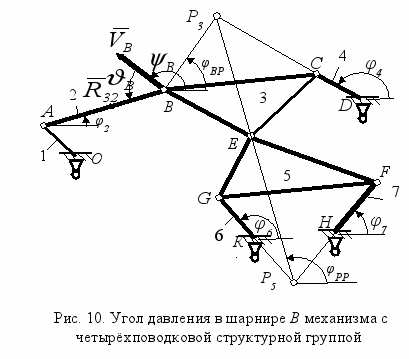
Важным показателем качества передачи движения является угол давления в кинематических парах. Для получения угла давления в кинематической паре В определим направления скоростей центров шарниров механизма (Рис. 10). В точке пересечения продолжений отрезка Р₅Е и поводка 4 находится мгновенный центр скоростей Р₃ шатуна 3. Его положение в принятой системе координат можно выразить комплексным числом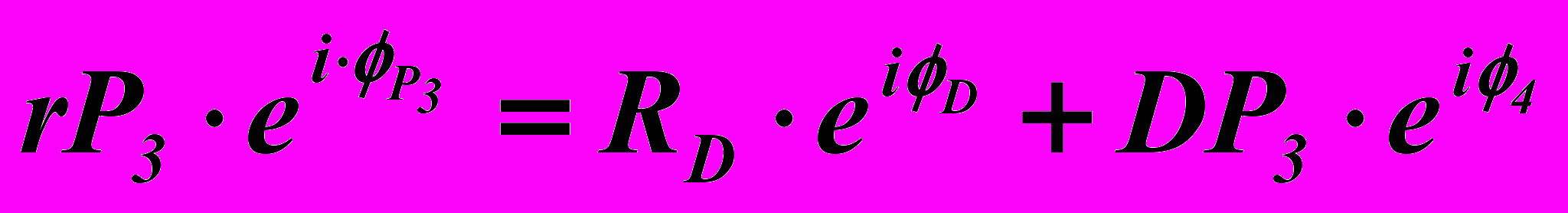

, (19)

в котором модуль DP₃ второго слагаемого определяется равенством

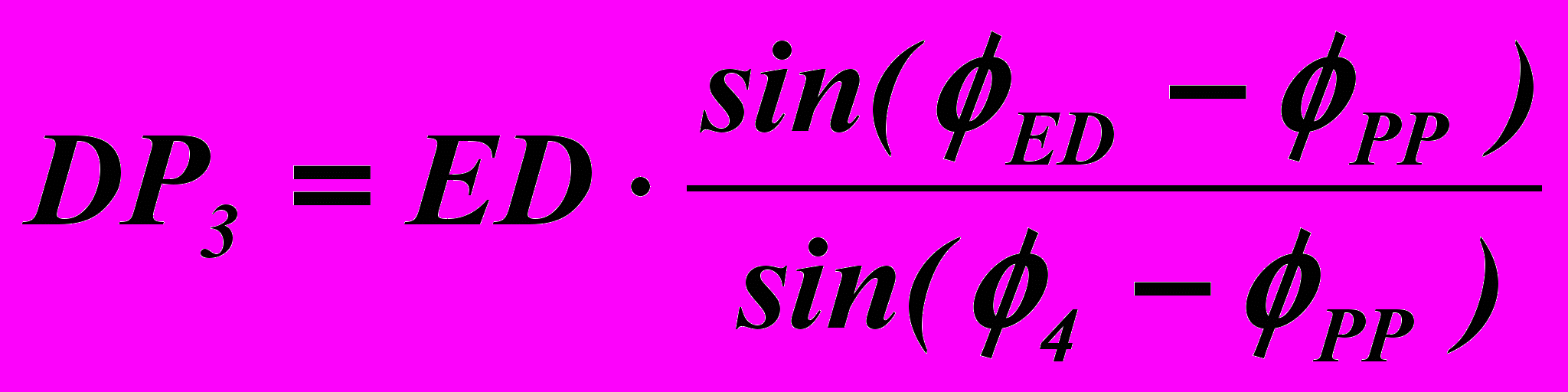. (20)

Положение отрезка ВР₃ может быть выражено комплексным числом

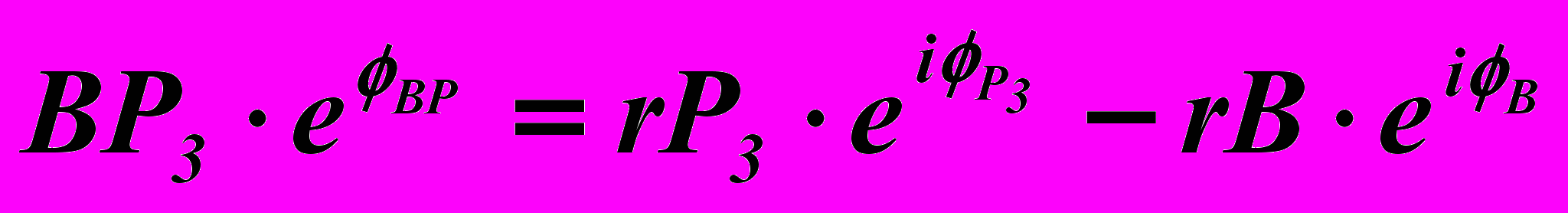. (21)

откуда определяется аргумент φ_ВР комплексного числа.

Реакция 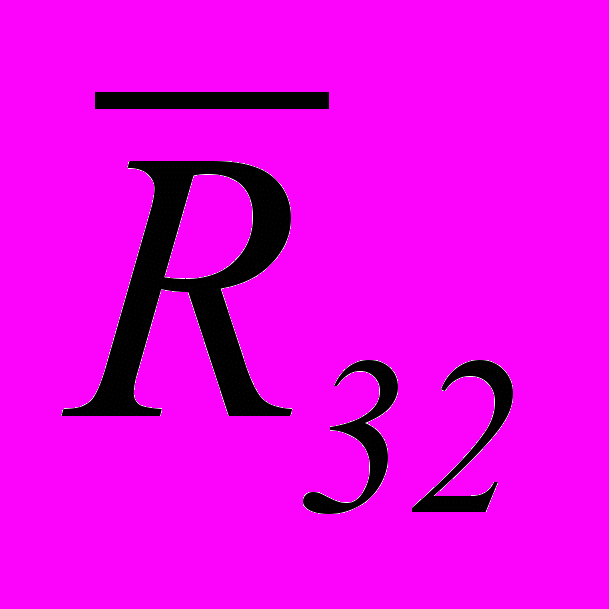в шарнире В направлена вдоль линии АВ поводка 2. Угол передачи движения ν_В и угол давления в шарнире В определим соответственно по формулам:

,

. (22)

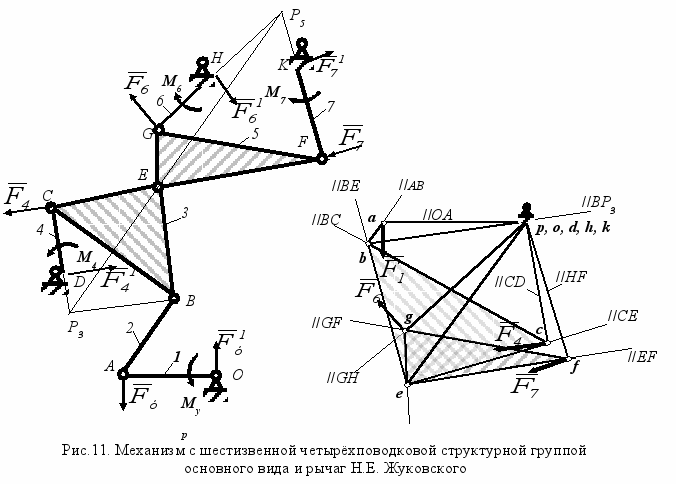
Определяя таким образом для любого значения обобщённой координаты в пределах интервала её изменения угол давления и сравнивая с его допускаемым значением, можно на этапе кинематического синтеза механизма судить о степени удалённости параметров механизма от опасной зоны, в которой условия передачи движения неблагоприятны.

Разработана схема анализа действия статических силовых факторов в кинематических парах шестизвенной четырёхповодковой структурной группы основного вида, последовательность и расчётные формулы для определения реакций во внешних шарнирах шестизвенной четырёхповодковой структурной группы и определения уравновешивающего момента. Для определения уравновешивающего момента с помощью рычага Н.Е. Жуковского построен план скоростей четырёхопорного механизма со структурной группой основного вида (Рис. 11). Из условия равновесия рычага Жуковского следует:

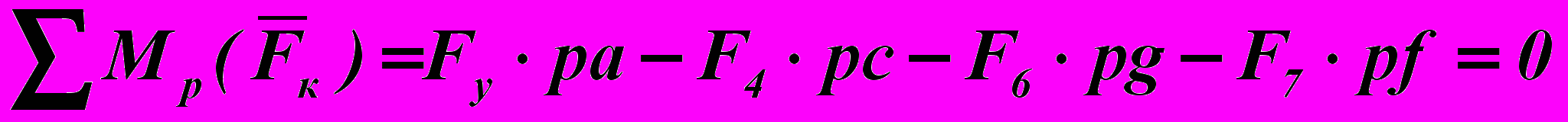, (23)

где pa, pc, pg, pf – плечи соответствующих сил на рычаге Жуковского.

Уравновешивающий момент находится из (23) по формуле:

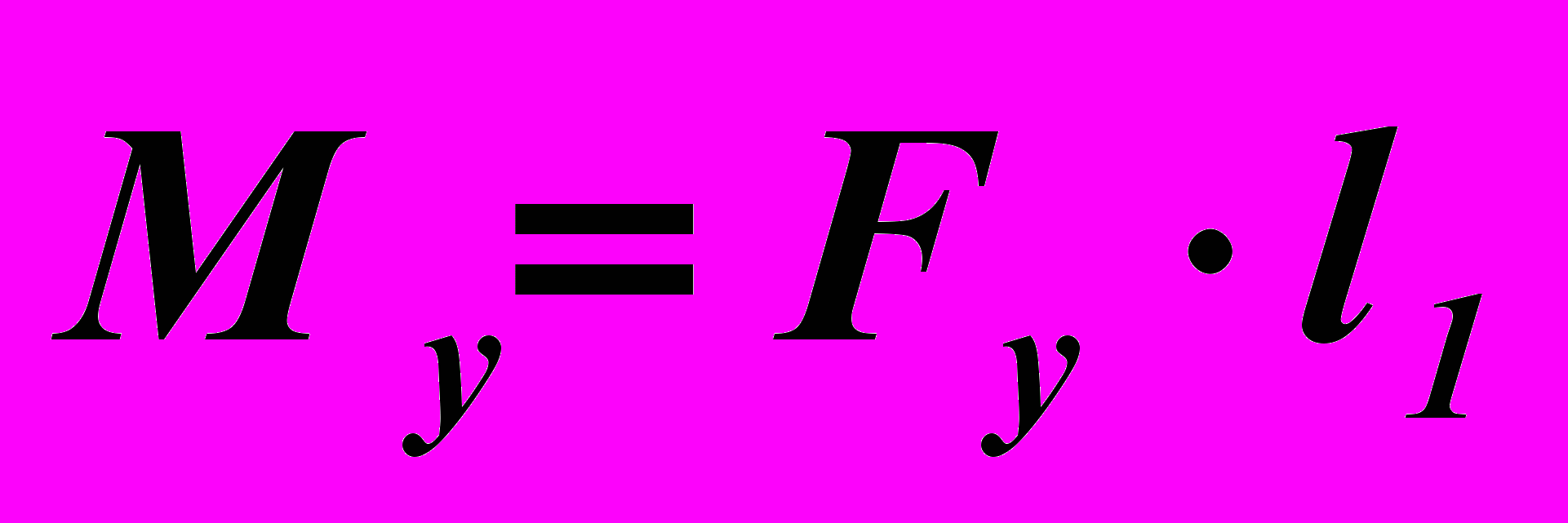, (24)

В (23), (24) каждый из моментов сил сопротивления и уравновешивающий момент представлены в виде пар сил, величины которых равны

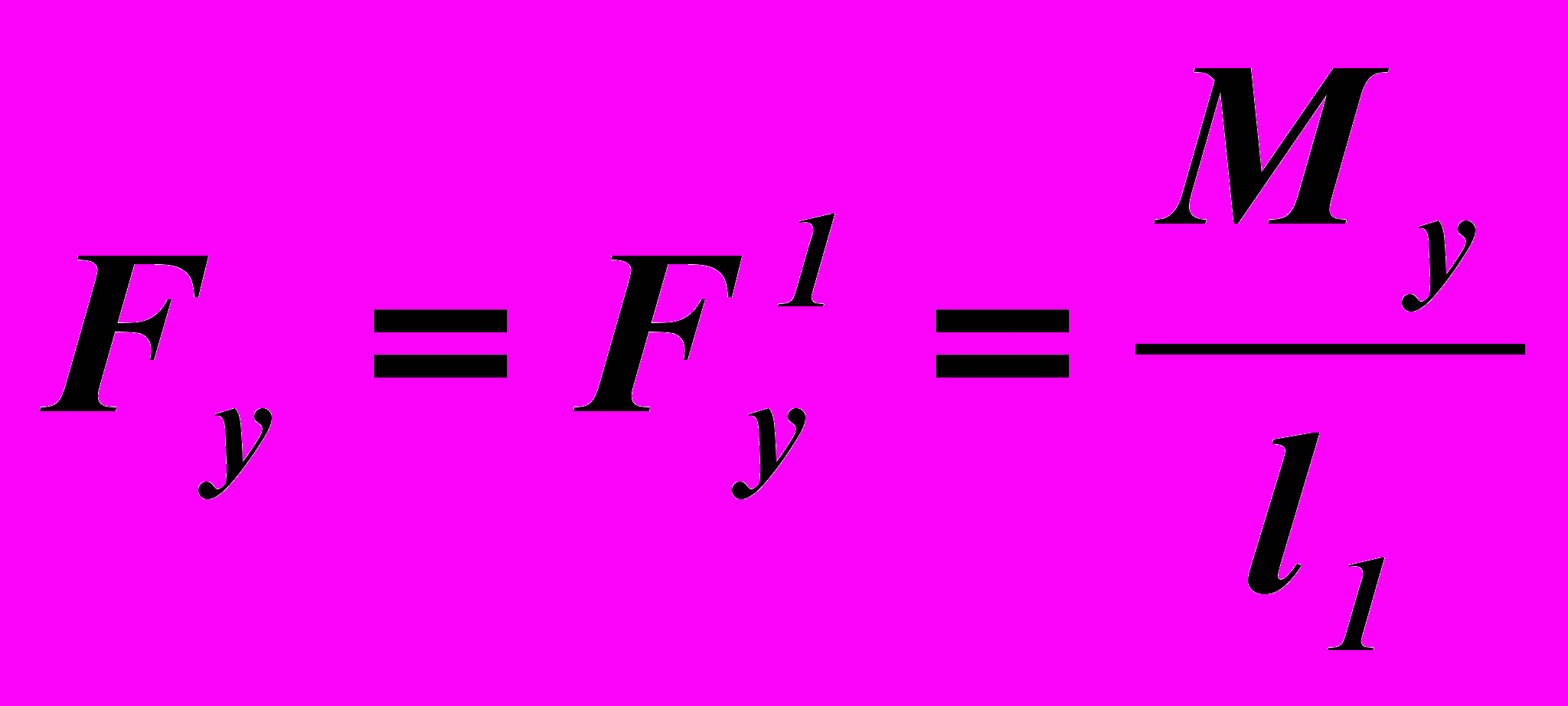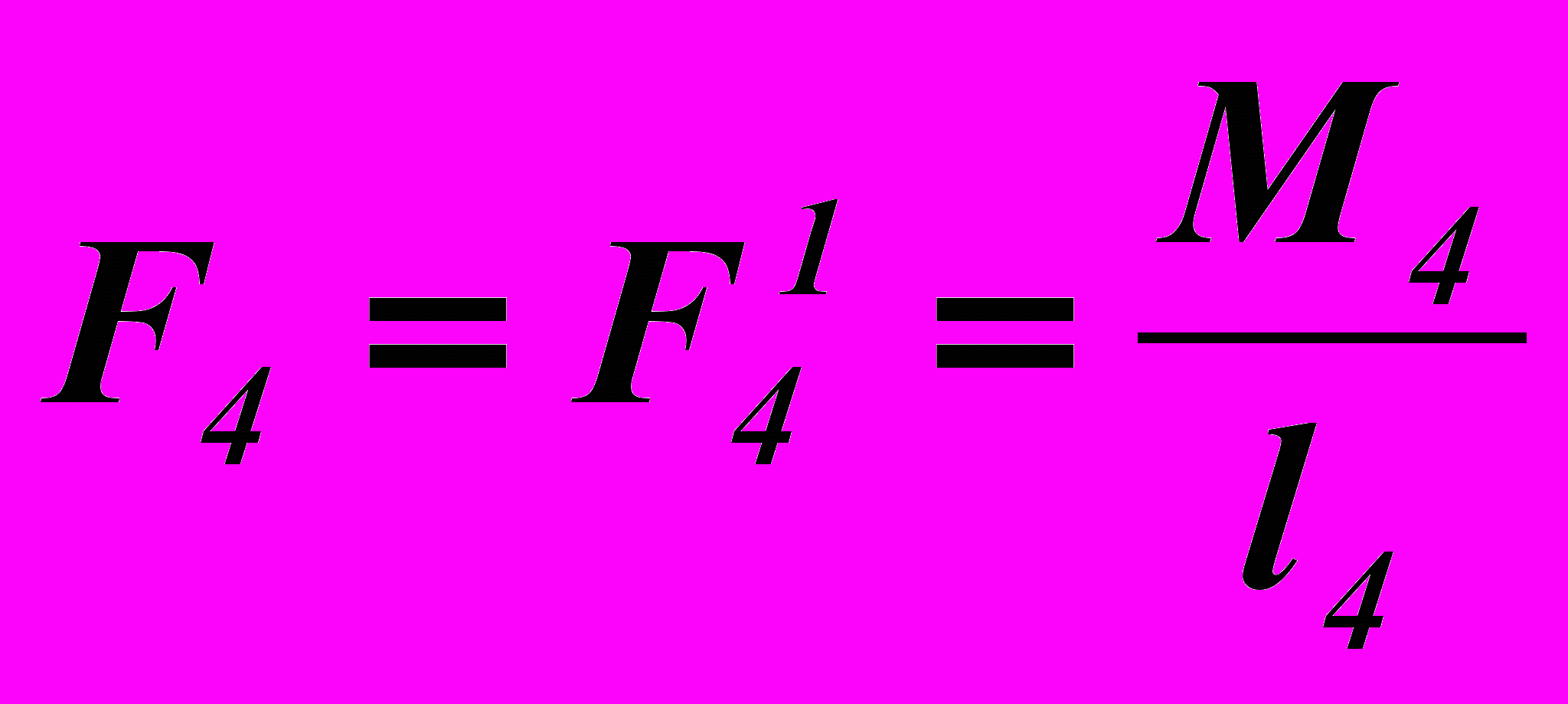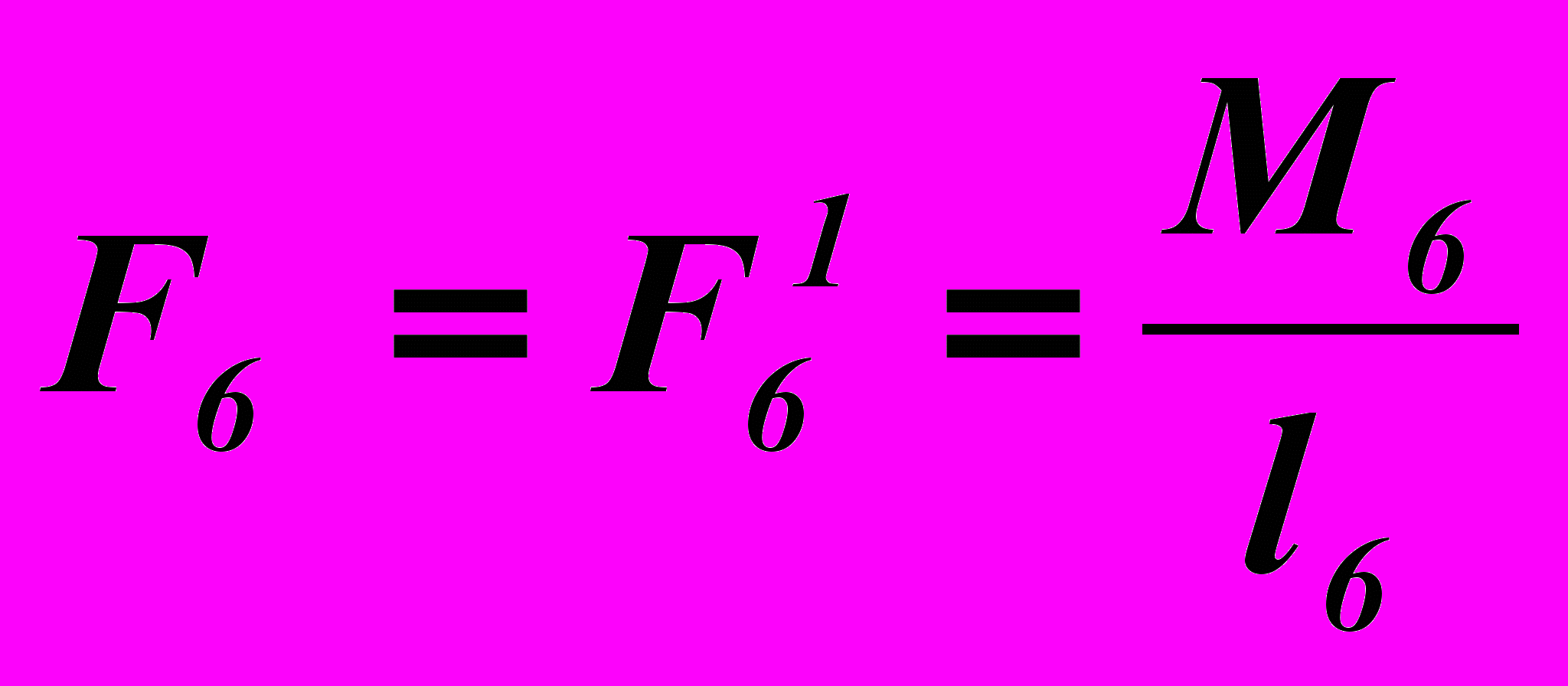, , , , (25)

где l₁ – длина входного звена ОА, l₄, l₆, l₇ – размеры соответствующих поводков.

П
ятая глава работы посвящена практической реализации применения шестизвенной четырёхповодковой структурной группы в механизмах и устройствах.

Р
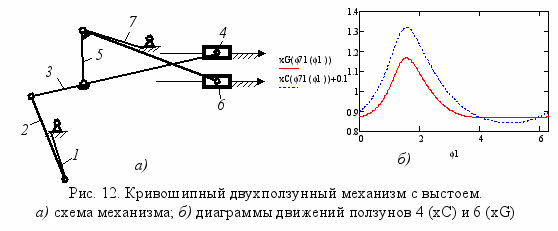
азработанные в настоящем исследовании алгоритмы позволили синтезировать ряд новых схем механизмов с двумя выходными звеньями и выстоями, пригодных для использования в промышленности. На рисунках 12-15 приведены кинематические схемы и диаграммы движений выходных звеньев 4 и 6 разработанных новых механизмов, защищённых патентами РФ на полезную модель, в их числе кривошипный двухползунный механизм с выстоем патент № 109251 (Рис.12),

кривошипный двухползунный механизм с выстоями ползунов в противофазах патент № 110157 (Рис.13),

к
ривошипный двухкоромысловый механизм с выстоями в противофазах патент № 112311 (Рис.14), механизм с одновременными выстоями двух коромысел (Рис.15).

Проведённые в настоящей диссертации кинематические исследования и разработанные алгоритмы синтеза позволяют на ранних стадиях проектирования производить расчёты механизмов, содержащих в своём составе шестизвенную четырёхповодковую структурную группу, что значительно снижает время на их разработку и даёт возможность создавать цикловые машины-автоматы с выстоями рабочих органов.

Основные выводы

1. Установлено, что шестизвенная четырёхповодковая структурная группа имеет 84 модификации по виду кинематических пар.
   
2. Принято в качестве критерия выбора метода решения задачи о положениях звеньев шестизвенной группы Ассура максимально возможное число вариантов сборки, которое определяется с использованием результатов исследований на порядок и циркулярность шатунных кривых четырёхзвенников.
   
3. Разработаны с учётом максимально возможного числа вариантов сборки методы определения положений звеньев шестизвенных четырёхповодковых структурных групп различных модификаций. Выявлены модификации структурной группы, задача о положениях звеньев которых имеет точное решение, допускающее геометрическую интерпретацию. Для решения задачи о положениях звеньев других модификаций структурной группы предложены итеративные методы.
   
4. Составлены алгоритмы решения задачи о положениях для механизмов с различными способами присоединения четырёхповодковой структурной группы к входному звену. Решения задачи о положениях механизмов представлены в форме неравенств с использованием параметрических уравнений шатунных кривых, составленных с применением экспоненциальной формы записи комплексных чисел.
   
5. Разработаны алгоритмы синтеза восьмизвенных механизмов третьего класса с возвратно-вращательным и возвратно-поступательным движением выходных звеньев, обеспечивающих выстой одного выходного звена заданной продолжительности или выстои двух выходных звеньев, происходящие одновременно или в противофазах.
   
6. Получены аналитические описания дополнительных условий синтеза: условий собираемости и существования кривошипа, критериев качества передачи движения и углов давления.
   
7. Синтезированы новые схемы восьмизвенных плоских рычажных механизмов с выстоями одного и двух выходных звеньев, происходящими одновременно и в противофазах, применение которых в цикловых машинах-автоматах позволит расширить их технологические возможности.
   

Список опубликованных работ по теме диссертации

Публикации в изданиях, рекомендованных ВАК:

1. Евдокимов Ю.И., Осипова О.И. Условия собираемости механизмов с шестизвенной четырёхповодковой структурной группой/ Ю.И. Евдокимов, О.И. Осипова // Сибирский вестник сельскохозяйственной науки. – 2007. - №8 - С. 102-109.
   
2. Хомченко В.Г., Осипова О.И. Синтез механизма с шестизвенной четырёхповодковой структурной группой с заданной длительностью выстоя выходного звена/ В.Г. Хомченко, О.И. Осипова // Омский научный вестник. – 2010. - № 3. - С. 71-73.
   
3. Осипова О.И. Синтез механизма с одновременным выстоем двух выходных звеньев / О.И. Осипова // Вестник НГАУ. – 2011. -№1 – С. 134-138.
   

Публикации в других изданиях:

4. Осипова О.И. Определение положений звеньев шестизвенной четырёхповодковой структурной группы / О.И. Осипова // Научное обеспечение АПК Сибири, Монголии и Казахстана: материалы 10-й Междунар. конф. по научному обеспечению азиатских территорий (г. Улан-Батор, 3-6 июля 2007 г.). - Новосибирск, 2007. - С. 460-461.
   
5. Евдокимов Ю.И., Осипова О.И. Видоизменения шестизвенной четырёхповодковой структурной группы / Ю.И. Евдокимов, О.И. Осипова // Научное обеспечение АПК Сибири, Монголии и Казахстана: материалы 10-й Междунар. конф. по научному обеспечению азиатских территорий (г. Улан-Батор, 3-6 июля 2007 г.). - Новосибирск, 2007. - С. 442-444.
   
6. Осипова О.И. Геометрическая модель для определения положений механизмов с шестизвенной четырёхповодковой структурной группой / О.И. Осипова // Материалы ежегодной научно-практ. конф. студентов и аспирантов Инженерного Института (Новосибирск, 2 апреля 2008г.) / Новосиб. гос. аграр. ун-т. Инженер. ин-т. – Новосибирск, 2008. - С. 92-94.
   
7. Осипова О.И. Определение центра и радиуса кривизны шатунной кривой / О.И. Осипова // Машинно—технологическое, энергетическое и сервисное обеспечение сельхозтоваропроизводителей Сибири: материалы Междунар. научно-практ. конф., посв. 100-летию со дня рождения академика ВАСХНИЛ А.И. Селиванова (9–11 июня 2008 г., п.г.т. Краснообск). - Новосибирск, 2008. - С. 625-627.
   
8. Осипова О.И. Алгоритм кинематического анализа механизма очистки зерноуборочного комбайна с двумя решетами/ О.И. Осипова // Вестник НГАУ. – 2009. - №4. - С. 38-40.
   
9. Осипова О.И. Определение уравновешивающего момента в механизмах с шестизвенной четырёхповодковой структурной группой с помощью рычага Н.Е.Жуковского / О.И. Осипова // Инновации в агропромышленном комплексе: материалы Междунар. научно-практ. форума (3-4 июня 2009 г.). - Новосибирск, 2009. - С. 187-190.
   
10. Осипова О.И. Алгоритм определения положений восьмизвенного механизма третьего класса / О.И. Осипова // Вестник НГАУ. – 2009. - №2. - С. 52-55.
    
11. Осипова О.И. Систематизация и основные задачи кинематики механизмов с шестизвенными четырёхповодковыми структурными группами / О.И. Осипова // Динамика систем, механизмов и машин: материалы VII Междунар. научно-техн. конф. 10-12 ноября 2009 г..– Омск: Изд.ОмГТУ, 2009. Кн. 4. - С. 471-475.
    
12. Осипова О.И. Синтез восьмизвенного механизма третьего класса с выстоем выходного звена / О.И. Осипова // Автоматизация, мехатроника, информационные технологии: материалы I Междунар. научно-техн. интернет-конф. молодых учёных 18-20 мая 2010 г. – Омск: Изд.ОмГТУ, 2010. - С. 86-89.
    
13. Пат. 109251 Российская Федерация, МПК F16Н21/00 Кривошипный двухползунный механизм с выстоем / Осипова О.И; заявитель и патентообладатель Новосиб. гос. аграрн. ун-т. - № 2011112407; заявл.31.03.11; опубл. 10.10.11, Бюл. № 28 – 1 с., 1 ил.
    
14. Пат. 110157 Российская Федерация, МПК F16Н21/00 Кривошипный двухползунный механизм с выстоями ползунов в противофазах / Осипова О.И., заявитель и патентообладатель Новосиб. гос. аграрн. ун-т. - № 2011127738/11; заявл. 06.07.11; опубл. 10.11.11, Бюл. № 31 – 1 с., 1 ил.
    
15. Пат. 112311 Российская Федерация, МПК F16Н21/00 Кривошипно-коромысловый механизм с выстоями в противофазах / Осипова О.И., заявитель и патентообладатель Новосиб. гос. аграрн. ун-т. - № 2011126972/11; заявл. 30.06.11; опубл. 10.01.12, Бюл. № 1 -1 с., 1 ил.