Волков Глеб Юрьевич систематика и структурно-параметрический синтез механизмов на базе замкнутых систем тел качения специальность: 05. 02. 18 «Теория механизмов и машин» автореферат

Вид материала

Автореферат

Содержание Плеханов Фёдор Иванович Анфёров Валерий Николаевич. Общая характеристика работы Цель исследования Задачи исследования Объектом исследования являются Методы исследования Научную новизну На защиту выносятся Апробация работы Структура и объем работы Содержание работы В первой главе Н», материальные оси «О Структурная формула Уровень структурных чисел Уровень структурных формул Уровень анализа реализуемости схем Третья глава Четвертая глава ... Полное содержание

Подобный материал:

• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Памятка для студентов группы пкм- по изучению дисциплины " Теория механизмов и машин, 72.92kb.
• Димитрюк Сергей Олегович, доцент кафедры «Теория механизмов и машин» к т. н., доцент, 37.69kb.
• Рабочая программа по дисциплине опд. Ф. 04 Теория механизмов и машин для направления, 252.07kb.
• «Теория машин и механизмов и проектирование текстильных машин», 240.94kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Учебная программа дисциплины теория механизмов и машин (Наименование дисциплины в соответствии, 241.34kb.
• Примерная программа дисциплины теория механизмов и машин Рекомендуется Минобразованием, 326.52kb.
• Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.

на правах рукописи

УДК 621.01


Волков Глеб Юрьевич


СИСТЕМАТИКА И СТРУКТУРНО-ПАРАМЕТРИЧЕСКИЙ СИНТЕЗ МЕХАНИЗМОВ на базе ЗАМКНУТЫХ СИСТЕМ ТЕЛ КАЧЕНИЯ


Специальность: 05. 02.18 – «Теория механизмов и машин»


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора технических наук


Курган – 2011

Работа выполнена в Курганском государственном университете


Официальные оппоненты: заслуженный деятель науки УР,

доктор технических наук, профессор

Плеханов Фёдор Иванович;


доктор технических наук, профессор

Лопатин Борис Александрович;


доктор технических наук, профессор

Анфёров Валерий Николаевич.


Ведущая организация: Институт Машиноведения

УРО РАН, г. Екатеринбург.


Защита состоится 27 марта 2012 года в 14⁰⁰ часов на заседании диссертационного совета Д 212.065.01 ФГБОУ ВПО

«Ижевский государственный технический университет» по адресу:

426069, Удмуртия, г. Ижевск, ул. Студенческая, д. 7, ИжГТУ, корп. 5.


С диссертацией можно ознакомиться в научной библиотеке ФГБОУ ВПО «Ижевский государственный технический университет».


Отзыв на автореферат, заверенный гербовой печатью, просим направлять по указанному адресу на имя ученого секретаря диссертационного совета.


Автореферат разослан _____________ февраля 2012 г.


Ученый секретарь диссертационного совета,

Доктор технических наук, профессор Щенятский А. В.

Общая характеристика работы


Актуальность проблемы. Одним из направлений совершенствования механизмов, улучшения их массогабаритных, энергетических и многих других технических характеристик является замена трения скольжения трением качения. Это, на первый взгляд, очевидное направление не исчерпывается только использованием подшипников качения во вращательных кинематических парах. Существует целый класс устройств, которые не содержат (или почти не содержат) никаких кинематических пар, кроме центроидных кинематических пар (пар качения). Это концентричные и эксцентричные бессепараторные подшипники, фрикционные и зубчатые планетарные передачи и другие механизмы. Они представляют собой или содержат в качестве основной составной части замкнутую систему тел качения (ЗСТК). Помимо снижения трения конкретные механизмы, построенные на базе ЗСТК, могут иметь достоинства, связанные с упрощением конструкции, возникающим благодаря совмещению функций, устранению нетехнологичных деталей, повышением общей нагрузочной способности и т.д. Решение этих задач особенно остро стоит в условиях жесткой конкуренции машиностроительной продукции, как на отечественном, так и мировом рынках.

В настоящее время известны сотни разнообразных устройств, которые следует отнести к классу ЗСТК. Большинство из них появились как изобретения в различных предметных областях при решении конкретных инженерных задач. Однако направленному, комплексному научному исследованию этот класс механизмов до сих пор не подвергся – не построено стройной теории, позволяющей систематизировать эти механизмы и решать задачи их структурного и параметрического синтеза. Следовательно, глубокое изучение, совершенствование и широкое практическое использование механизмов, построенных на базе ЗСТК, систематизация и синтез новых схем ЗСТК, приводящих к повышению технических характеристик многих машин, является актуальной проблемой.

Цель исследования: Повышение технических характеристик машин на основе разработанной систематики и методологии синтеза новых схем фрикционных и зубчатых механизмов, содержащих замкнутые системы тел качения.

Задачи исследования.

В первой части работы решаются общие теоретические задачи, относящиеся ко всему многообразию плоских замкнутых систем с круглыми телами качения:

• анализ структурных и параметрических свойств, присущих всем ЗСТК, в том числе: условий кинематической и геометрической совместимости звеньев, условий замкнутости кинематических пар ЗСТК;
  
• разработка единого подхода к формализации структуры механизмов, содержащих ЗСТК, и соответствующего метода ее компактного отображения;
  
• разработка принципиального алгоритма структурного синтеза ЗСТК.
  
• систематизация известных механических систем, являющихся разновидностями ЗСТК, в соответствии с принятой формализацией их структуры.
  

Во второй части работы стереотипные задачи структурного синтеза, параметрического анализа и синтеза, разработки конструкций и проверки их работоспособности решаются для конкретных структурно-функциональных групп (семейств) механизмов:

• бессепараторных подшипников;
  
• эксцентриковых подшипников и механизмов, построенных на их базе;
  
• фрикционных и зубчато-фрикционных планетарных передач;
  
• безводильных зубчатых планетарных передач;
  
• рабочих механизмов объемных гидромашин, строящихся на базе планетарной системы с двумя плавающими сателлитами.
  

Объектом исследования являются фрикционные и зубчатые механизмы, построенные на базе замкнутых систем тел качения (ЗСТК).

Предмет исследования – общие структурные свойства и условия существования ЗСТК, принцип формализации структуры механизмов на базе ЗСТК, систематизация и методы их структурно-параметрического анализа и синтеза.

Методы исследования базируются на основных положениях классической теории механизмов и машин, а также теории зубчатых зацеплений, системного анализа, методах дискретной математики, аналитических методах кинематического и силового анализа механизмов. При проведении экспериментальных исследований использовалось стендовое оборудование предприятий, на которых внедрялись результаты работы.

Достоверность результатов работы подтверждается корректностью постановки задач и применяемых методов теории механизмов и машин и теории зубчатых зацеплений, адекватностью построения формальных моделей реальным механизмам, соответствием синтезируемых структур известным техническим решениям, экспериментальной проверкой работоспособности и практическим внедрениям разработанных механизмов.

Научную новизну представляют:

• объединение многообразия замкнутых механических систем тел качения (ЗСТК) в особый класс механизмов на основании выявленных общих структурных свойств и параметрических условий существования;
  
• принцип формализации, составляющий теоретическую основу систематики и структурного синтеза зубчатых и фрикционных механизмов на базе ЗСТК, и метод компактного отображения их структуры с использованием свойства структурной симметрии объектов;
  
• метод структурного синтеза механизмов на базе ЗСТК, включающий в себя этапы генерации структурных формул и структурных чисел;
  
• новые структурные схемы механизмов различного функционального назначения, полученные с помощью предложенного метода;
  
• критерии оценки работоспособности фрикционных механизмов, построенных на базе ЗСТК с «гладкими» звеньями;
  
• метод геометрического расчета зубчатых ЗСТК по условиям сборки, основанный на решении систем уравнений, соответствующих замкнутым контурам;
  
• теорема о полюсе заменяющего механизма зубчатого эксцентрикового подшипника;
  
• способ модификации закона движения ведомого звена механизмов, содержащих ЗСТК, по принципу сложения двух гармоник.
  

Практическую ценность работы составляют:

• алгоритмы структурного синтеза ЗСТК, относящихся к конкретным структурно-функциональным семействам;
  
• упорядоченные массивы структур механизмов, содержащих ЗСТК;
  
• конструкции механизмов, содержащих ЗСТК, защищенные авторскими свидетельствами СССР, патентами РФ на изобретения и полезные модели, в том числе:
  

• рациональные конструкции бессепараторных подшипников с «гладкими» телами качения;
  
• конструкции фрикционных планетарных механизмов, обладающих повышенной тяговой способностью;
  
• конструкции безводильных зубчатых планетарных передач, отличающиеся от аналогов повышенной нагрузочной способностью, компактностью и др. компоновочными и технологическими достоинствами;
  
• ряд конструкций зубчатых эксцентриковых подшипников (ЗЭП), обладающих различными передаточными отношениями и обеспечивающими максимальный эксцентриситет;
  
• конструкции рычажных механизмов, содержащих ЗЭП, обеспечивающие модификацию закона движения ведомого звена сложением двух гармоник;
  
• принципиальное устройство и конструкции многорядного планетарного редуктора для скважинного оборудования;
  
• конструкции рабочих механизмов шестеренных гидрообъемных машин, обладающих увеличенным полезным объемом и улучшенной герметичностью рабочих полостей;
  

• разработанные методики геометрического, кинематического, силового, прочностного расчетов упомянутых выше механизмов.
  

На защиту выносятся:

• предложение выделить устройства, содержащие ЗСТК, в единый класс механизмов. Систематизация и результаты комплексного изучения структурных особенностей, условий существования и критериев работоспособности ЗСТК с «гладкими» и зубчатыми телами;
  
• метод формализованного отображения структуры механизмов, представляющих собой ЗСТК. Сформированные на базе этого метода массивы схем ЗСТК, относящиеся к различным структурно-функциональным семействам механизмов;
  
• наиболее перспективные новые схемы ЗСТК и конструкции механизмов, построенных на их основе.
  
• методы параметрического анализа и синтеза ЗСТК, относящиеся к конкретным семействам механизмов.
  

Апробация работы. Основные положения работ докладывались на Всесоюзном (1988 г.) и межгосударственных (1993, 1997г.г.) симпозиумах по теории реальных передач зацеплением в Кургане; на Всесоюзном семинаре по ТММ им. академика И.И. Артболевского (Ленинград, 1989 г.); на Всероссийской научно-технической конференции с участием зарубежных представителей «Машиноведение и детали машин» (Москва, МГТУ им. Н.Э. Баумана – 2008 г.), на научно-технических конференциях с участием зарубежных представителей «Теория и практика зубчатых передач и редукторостроения» (Ижевск, ИжГТУ–1998, 2008 гг.); на международной научно-технической конференции «Инновационные технологии в автоматизированном машиностроении и арматуростроении» (Курган, 2010г.).

Публикации. По теме диссертации опубликовано 59 научных работ, в том числе 32 в изданиях, рекомендуемых ВАК (из них 10 – статьи в рецензируемых журналах, 10 – авторские свидетельства СССР, 12 – патенты РФ на изобретения).

Структура и объем работы. Диссертация состоит из введения, семи глав, заключения, списка литературы (270 наименований) и приложения; включает 151 рисунок, 19 таблиц; общий объем – 300 страниц.


Содержание работы


Во введении обоснована актуальность диссертационной работы, сформулированы ее цель и основные задачи, представлены научная новизна и практическая ценность выполненных исследований.

В первой главе вносится и обосновывается предложение выделить устройства, содержащие ЗСТК, в особый класс механизмов и решаются общие задачи, относящиеся к механизмам этого класса.

История вопроса и уточнение объекта исследования

Первыми устройствами, в которых присутствуют исключительно центроидные пары (пары качения), по-видимому, следует считать: бессепараторный подшипник (Беккер, 1871 г.); безводильную планетарную передачу (Вебстер, 1873 г.); зубчатый подшипник (один их первых патентов – Стилсон, Бредфорд 1902 г.). Десятки схем бессепараторных подшипников и планетарных передач разработаны А. Насвайтисом в 60-70 г.г. 20 века. Многие новые схемы и обзорные статьи принадлежат Е. Трауту (80-е г.г.).

Большой вклад в изучение зубчатых центроидных механизмов неэлементарной структуры внесли отечественные ученые: И.И. Артоболевский, Э.Л. Айрапетов, Ан И-Кан, А.Е. Беляев, В.И. Гольдфарб, Л.Т. Дворников, М.Л. Ерихов, Х.И. Кетов, Н.И. Колчин, В.Н. Кудрявцев, Ф.Л. Литвин, М.Л. Новиков, Ф.И. Плеханов, Л.Н. Решетов, и др. Среди исследователей фрикционных центроидных механизмов необходимо упомянуть Р.В. Вирабова, В.Н. Борисова и И.Г. Левицкого. Направленное изучение механических систем, содержащих только кинематические пары качения, в России началось в 80-е г.г. 20 века – П.Д. Балакин, А.В. Бородин, Г.Ю. Волков, Н.Н. Крохмаль, позднее – В.Н. Сызранцев, Н.М. Федченко, Д.А. Курасов.

Термин «ЗСТК» впервые использован в статье Волкова, Крохмаля (1988 г.) в отношении систем, состоящих из «гладких» звеньев (тел качения). Не возникает противоречия и при использовании этого термина применительно к системам с зубчатыми звеньями, в особенности к тем, кинематические пары которых являются центроидными, т.е., помимо тангенциальных воспринимают и радиальные силы.

В данной работе изучаются «плоские» ЗСТК с «круглыми» телами качения, но, помимо «чистых» ЗСТК, состоящих исключительно из тел качения (в том числе зубчатых), рассматриваются и системы, содержащие некоторое количество рычажных звеньев – «дополненные» ЗСТК. По функциональному назначению «гладкие» ЗСТК могут быть подшипниками (концентрическими и эксцентриковыми) и фрикционными передачами (с постоянным натяжением и самонатяжением). «Зубчатые» ЗСТК используются в подшипниках (концентрических и эксцентриковых), в планетарных передачах (с водилом и безводильных), в рабочих механизмах гидромашин.

Структурные и параметрические особенности и формализация ЗСТК

Рассматривая объект в качестве системы, важно рационально выбрать принцип его структурирования. В случае «чистых» плоских ЗСТК целесообразно принять в качестве элементов системы части звеньев (рис.1.1), а именно: охватываемую начальную окружность – ролик (Р) и охватывающую начальную окружность – кольцо (К). Единственная связь, которая может существовать между такими элементами в ЗСТК – это «тангенциальная» связь «Т», означающая качение без скольжения (т.е. центроидная кинематическая пара). При этом возможны внешнее взаимодействие двух роликов и внутреннее взаимодействие кольца и ролика. Жесткое концентричное соединение «С» кольца и ролика в одно звено предлагается рассматривать как предельный параметрический случай их внутреннего взаимодействия.




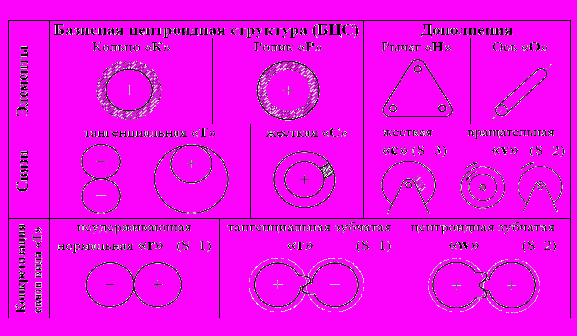
Рис.1.1. Формализация структуры ЗСТК


В дополненных ЗСТК могут присутствовать рычажные звенья « Н», материальные оси «О» и вращательные пары «v». Однако основу дополненной ЗСТК составляет ее «базисная центроидная структура» (БЦС), которая включает только кольца и ролики.

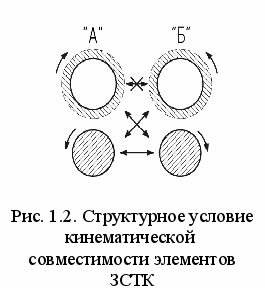
Анализ условий кинематической совместимости элементов в БЦС ЗСТК показывает, что связи в них могут существовать только между элементами, принадлежащими к двум различным группам («А» и «Б»), в одну из которых входят кольца (К), вращающиеся (в системе остановленных осей) по ч.с., и ролики (Р), вращающиеся против ч.с., в другую – кольца и ролики противоположных направлений вращения (рис.1.2).

Отмеченное свойство БЦС ЗСТК позволяет существенно упростить матрицу связей, используемую для отображения структуры механизма. Вместо «традиционной» квадратной (или «треугольной») матрицы смежностей, имеющей размерность m×m, где m – общее число звеньев системы, можно использовать сокращенную, прямоугольную матрицу связей. (рис.1.3). Индексы столбцов такой «сжатой» матрицы соответствуют элементам группы «A», индексы строк – элементам группы «Б», а размерность: m_Am_Б, где m_A,m_Б – числа элементов, принадлежащих группам «А, Б».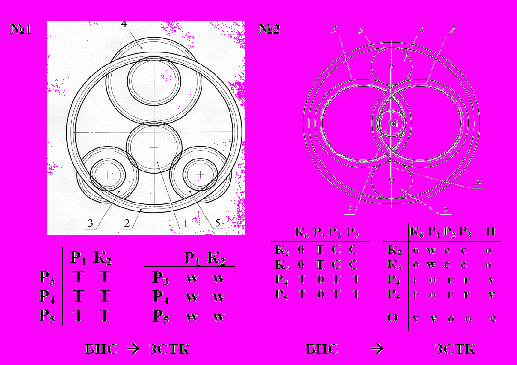



Рис. 1.3. Построение прямоугольных матриц связей ЗСТК


При переходе от описания БЦС к описанию конкретной ЗСТК, уточняется вид связей «Т»: неудерживающая нормальная «r» (S=1), тангенциальная зубчатая «т» (S=1) или центроидная зубчатая «w» (S=2). Символом «0» (или «о») обозначается отсутствие связи. При наличии в системе «дополнительных» звеньев «Н» или «О» они также отображаются в матрице связей.

Описание ЗСТК дополнительно упрощается, если учитывать их структурную симметрию. Неповторяющиеся («центральные») элементы обозначаем символами К, Р; повторяющиеся элементы – К^о, Р^о в случае зеркальной (осевой) симметрии; Кⁿ, Рⁿ или К², Р², К³, Р³ – при наличии симметрии вращения n-го порядка. Символы связей между элементами повторяющихся структурных фрагментов снабжаются надстрочным индексом «1» или «2». Обозначение вида «Т¹» показывает, что данная связь существует не внутри фрагмента, а между соседними фрагментами; обозначение «Т²» говорит о том, что связь присутствует как внутри фрагмента, так и между элементами соседних фрагментов (см. рис.1.4).





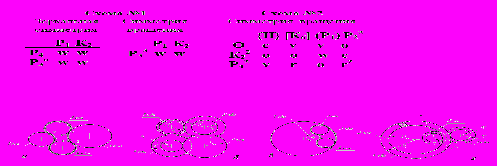
Рис. 1.4. Структурная симметрия ЗСТК

Системы с «крупными» повторяющимися фрагментами можно упрощенно обозначить с указанием различных чисел n, k кратности повторений.

Для того, чтобы «зашифрованная» в матрице кинематическая цепь получила признаки механизма, выделяем звенья с помощью различных скобок: (ведущее), [опорное], {ведомое}.

Обозначения строк и столбцов матрицы связей – ее «титульная структура».

Для отбора неизоморфных структур вводится цифровое кодирование:

К => «1», Р => «2», Кⁿ => «3», Рⁿ => «4».

Титульные строка и столбец, записанные подряд, дают «структурное число» БЦС. Правила выбора «учетного» структурного числа: 1) числа, записанные в строке и столбце, выбираются минимальными; 2) число в строке больше числа в столбце. При перечислении ЗСТК приоритет отдается меньшим структурным числам, прочитанным без учета разделительного знака (а при полном совпадении – с учетом). Примеры: «структурное число» схемы №1– «12.4»; схемы №2 – «124.34».

Структурное число не только показывает состав элементов БЦС, но (с учетом того, что элементы уже разделены на две группы) и предопределяет возможные связи между ними – это некоторая обобщенная структура целой группы ЗСТК.

Для лаконичного описания структуры конкретных ЗСТК вводим понятие

« Структурная формула» ЗСТК – ее матрица связи, записанная «в строку».

Символы неповторяющихся (центральных) дополнительных элементов Н и О ставим впереди элементов, составляющих БЦС, а повторяющихся дополнительных элементов – позади них.

Окончательно структурные числа и структурные формулы механизмов, показанных на рис.1.3, будут выглядеть следующим образом:

№ 1 – «12.4» – КР×Рⁿ : ww;

№ 2 – «124.34» – {H}[K](P)P² × ОK²P² : cvvo, oowc, vror².

Предложенная формализация описаний ЗСТК позволяет решать задачи упорядочения многообразия их структур и структурного синтеза.

Для выполнения оценки схем ЗСТК нужно исследовать основные условия их работоспособности. Наиболее общее свойство ЗСТК – условие кинематической совместимости их элементов на структурном уровне (см. рис.1.2) уже легло в основу их формализованного описания. Следствием этого условия является, в частности, обязательно четное число тел качения в каждом замкнутом контуре ими образуемом. Данное условие накладывает ограничения и на диаметры центроид (начальных окружностей) тел качения: передаточное отношение i₁₁ по контуру всегда равно единице. В случае «зубчатых» тел качения дополнительно возникает требование соблюдения «условий сборки» (т.е. целочисленности количества зубьев в контурах).

Не менее важным является условие гарантированной замкнутости кинематических пар, т.е. устойчивости ЗСТК. Сложности возникают в случае «чистых» ЗСТК, когда связи между элементами неудерживающие (односторонние).

На уровне математической модели – это условие эквивалентности системы неравенств (1), описывающей связи ЗСТК, соответствующей системе уравнений:


F₁(q₁,q₂..q_h) 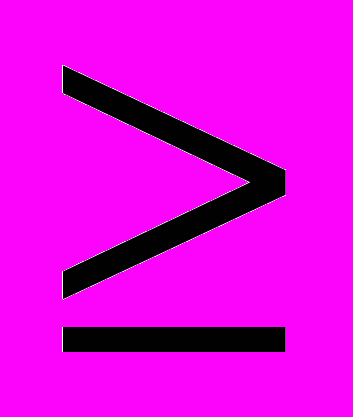(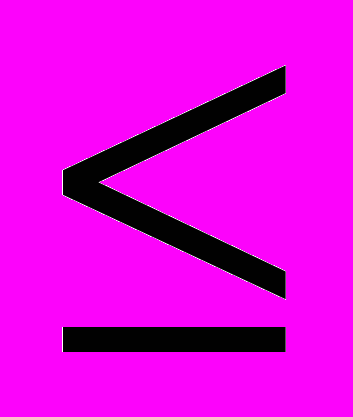) 0; а₁₁δq₁ + а₁₂δq₂…+ a_1hδq_h 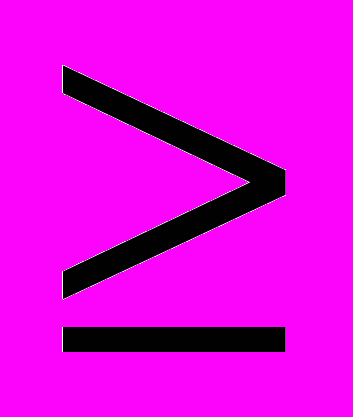0; a₁₁ U₁ + a₂₁ U₂ …+ a_s1 U_s = 0;

F₂(q₁,q₂..q_h) 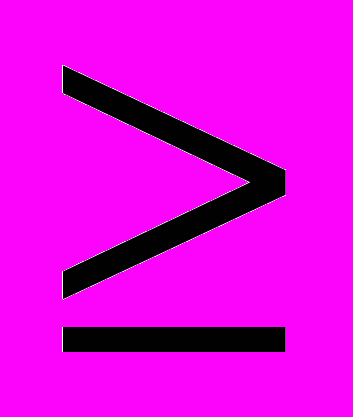(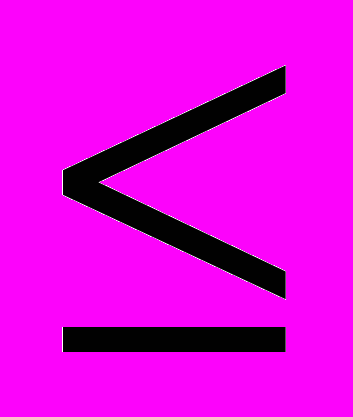) 0; а₂₁δq₁ + а₂₂δq₂…+ a_2hδq_h 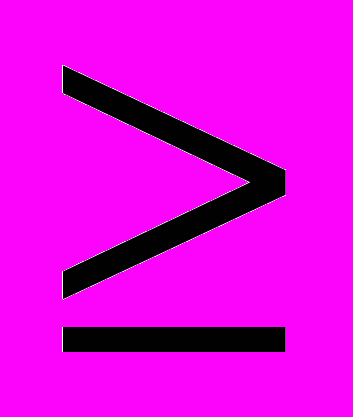0; a₁₂ U₁ + a₂₂ U₂ …+ a_s2 U_s = 0;

··················································· ··········································································· ···········································································

F_s(q₁,q₂..q_h) 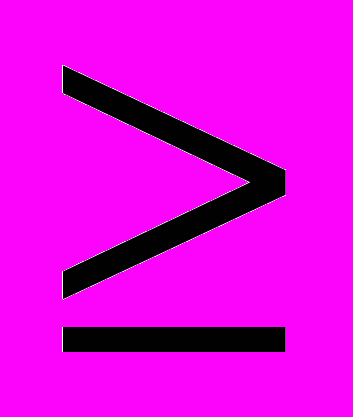(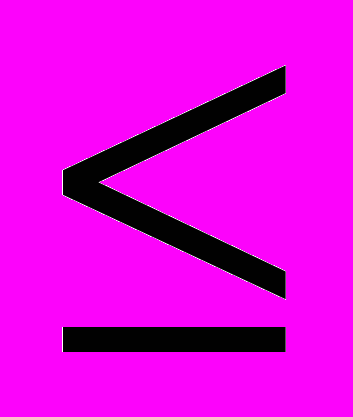) 0. a_s1δq₁ + а_m2δq₂…+ a_shδq_h 0, a_1h U₁ + a_2h U₂ …+ a_sh U_s = 0.

1. (2) (3)
   

При этом, согласно теории неравенств, вариации δq обобщенных координат (возможные перемещения узловых точек) в системе (2) должны равняться нулю (δq = 0), а неопределенные множители Лагранжа U в системе (3) иметь строгоположительные значения (U>0).

Необходимое (предварительное) условие устойчивости: s > h - число s неравенств связи больше числа h неизвестных обобщенных координат. Другими словами, устойчивая система с неудерживающими связями всегда статически неопределима, т.е. расчетное число степеней ее свободы меньше нуля W_р ≤ -1.

На уровне экспресс-анализа структурных свойств ЗСТК методами ТММ применима модифицированная формула Чебышева:

W_р = 3∙(m – 1) – 2∙p₅ – p₄ - L_п ,

где m – общее число элементов; p₅, p₄ – числа пар 5 и 4 кл.

L_п – число «лишних» степеней свободы: L_п = L_с+ L;

L_с - число независимых вращений тел относительно собственных осей;

L - число линейных вырождений системы;

В ЗСТК с «гладкими» звеньями L_с = m, поэтому: