Geum.ru

Волков Глеб Юрьевич систематика и структурно-параметрический синтез механизмов на базе замкнутых систем тел качения специальность: 05. 02. 18 «Теория механизмов и машин» автореферат

Вид материалаАвтореферат

Содержание


Четвертая глава
Подобный материал:
1   2   3   4   5

Рис.3.1. Синтез простейших ЗСТКО с «гладкими» телами качения




«23.44» – P1K62×P102P82:rr, rr2


Рис. 3.2. Преобразователь движения (А.с. 1610156)


Дальнейшее повышение ранга матрицы связей приводит к резкому возрастанию количества структур, прошедших тест предварительного отбора. Чтобы уменьшить объем работы на этапе анализа полученных схем, целесообразно сузить область поиска, введя дополнительные ограничения, вытекающие из условий применения ЗСТК в конкретных структурно-функциональных семействах механизмах.

Применительно к бессепараторным подшипникам была поставлена задача генерации «чистых» ЗСТК, обладающих структурной симметрией вращения. Дополнительное условие – «наличие центральных кольца и ролика, не взаимодействующих между собой». Тест предварительного отбора прошли (считая по структурным числам) одна 4-элементная и двадцать одна 5-элементная схемы. Анализ этих схем показал, что часть из них не реализуемы по «достаточному» условию, часть – имеют очевидные недостатки компоновочного характера, а наиболее удачные схемы уже известны. Далее были введены более жесткие ограничения поиска, формулируемые в виде некоторых «эвристических гипотез». Например: «Подшипник должен иметь только одно кольцо и один центральный ролик». Проведенный структурный синтез показал, что такому условию отвечают ранее не известные двухслойный (рис.3.3) и трехслойный (рис.3.4) бессепараторные подшипники качения с параллельными рядами роликов. Помимо отсутствия сепаратора, их достоинствами является повышенная радиальная податливость и стойкость к ударам. Другая «поисковая гипотеза»: «Модернизация лучшей из известных систем «124.124» с целью устранения ступенек на роликах» привела к схеме – рис.3.5.




«244.14» – PPkPn × КРn : o r r, r r2kr2n; или PPnPn KPnPn: orrr, rrro, rr1rr2.

W = 2М – 3 – S – L = 2(2 + 5n) – 3 – 11 n = 1 – n,

Рис.3.3. «Двухслойный» бессепараторный подшипник (А.с 1581896)


«124.444» – КPРn × PkPnPn:

r r r2k, o r r2n , r o r2n или

К2 P1 Р5n Р7n × Р3n Р4n Р6n P8n P9n:

r r r2о, orrr, r o r r, r o r1r, o r r1r.
«1244.1444» – К1P2Р7nР8n × К3Р5nР6nP4n:

oоrr, orrr, rorr, rrr1r. (W = 3 – 2n).

Рис.3.4. «Трёхслойный»

бессепараторный подшипник
Рис.3.5. Подшипник (А.с. 1432297)


В целом, приходится констатировать, что ни известные концентрические бессепараторные подшипники, ни те несколько новых схем, которые удалось выявить, пока не представляют серьезной альтернативы обычным подшипникам качения, освоенным промышленностью. Мотивация применения бессепараторных схем повышается применительно к эксцентриковым подшипникам, которые совмещают в себе функции кривошипа, опоры качения и фрикционной передачи. В таких подшипниках трение тел качения о сепаратор и, в особенности, его износ недопустимы.

Поиск схем эксцентриковых бессепараторных подшипников проводился в нескольких направлениях.

Во-первых, преобразование к эксцентричному виду концентричных схем. Примечательно, что при этом устойчивость некоторых схем (например, показанной на рис.1.5) повышается. По оценке автора, одна из лучших схем бессепараторного эксцентрикового подшипника – рис.3.5.

Во-вторых, синтез схем, заведомо не обладающих структурной симметрией вращения, в частности, путем развития (т.е. дополнения) условно-симметричной структуры: «КРn…× PРn…: r …». Одна из синтезированных таким путем схем эксцентриковых подшипников показана на рис.3.6.




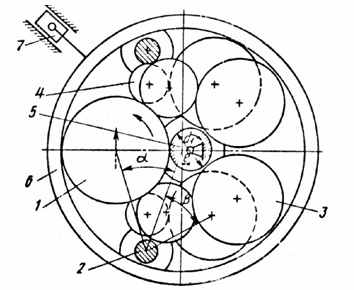
«144.244» – КРnРn × PРnРn или

К1 Р3 Р40 Р50 × Р2 Р60 Р70 Р80 : r r r r, r r r o, r r o r, r o r r.

Рис.3.6. Эксцентриковый подшипник (А.с. 1719749)


В работе также проанализированы возможности эксцентриковых подшипников, содержащих рычажные элементы, и предложены рациональные конструкции: патент РФ 2315212, полезная модель (П.м.) 59174.

Бессепараторный подшипник с «гладкими» телами качения является фрикционным механизмом, поэтому его эксцентриситет еmax ограничен расчетной величиной fр коэффициента трения (еmax = dср ∙ fр) и при использовании жидких машинных масел не превышает 0,05 от среднего диаметра dср подшипника. Существует возможность увеличить эксцентриситет за счет использования плавающего наибольшего ролика (например, см. рис.3.2). Недостатком таких конструкций является «люфт» при реверсе нагрузки. Другой способ увеличения эксцентриситета (вдвое) состоит в «спаривании» двух- или трехслойных подшипников общим слоем роликов А.с. 1370350.

ЗСТК с «гладкими» телами составляют основу фрикционных передач с самонатяжением в плоском контуре. Такие передачи известны с начала 20-го века, но до настоящего времени недостаточно изучены с теоретических позиций. В основе любой из них лежит контур, содержащий два «закрепленных» Э1,Э2 и один плавающий Эп элемент: Э1Э2 × Эп. – рис. 3.7. Конкретизируя вид этих элементов (кольцо К или ролик Р), получим всего четыре варианта:

а)РР×Р; б)РР×К; в)КР×Р; г)КК×Р.

Три из них (а,б,в) заложены в известных фрикционных передачах (рис.3.8), а один – (г) КК×Р – нигде прежде не использовался. На основании его нами предложены две новые схемы планетарных передач А.с. 1477967 (рис. 3.9) и А.с. 1733770. Эти передачи были изготовлены, испытаны и применены в редукторе пневмодрели (рис.3.10).






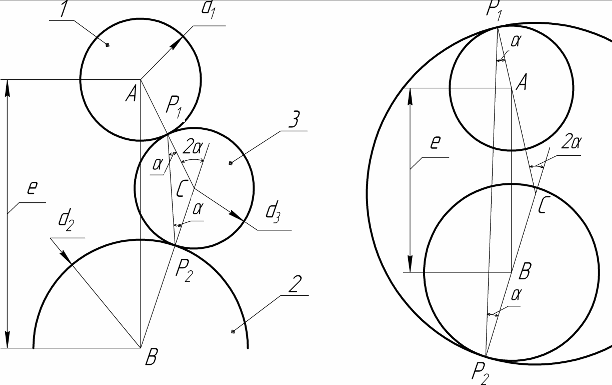а б в г – новая

Рис 3.7. Контуры звеньев, обеспечивающие самонатяжение



а (hD= 0,2) б (hD= 0,25) в (hD= 4)


Рис. 3.8. Известные схемы передач с самонатяжением




«1234. 44» – [К3] (Р5) K7n P2n × {H1} P7n P8n: voou, orcr, roro


Рис 3.9. Фрикционная планетарная передача (А.с. 1477967) hD = 0,22



Рис.3.10. Пневмодрель с фрикционным редуктором


На основании анализа схем самонатяжения в плоском контуре (рис.3.7) предложен геометрический критерий относительной оценки долговечности соответствующих фрикционных передач. Допустимое изменение h размеров звеньев (вследствие износа или упругой деформации), приведенное к диаметру плавающего тела:

h = ,

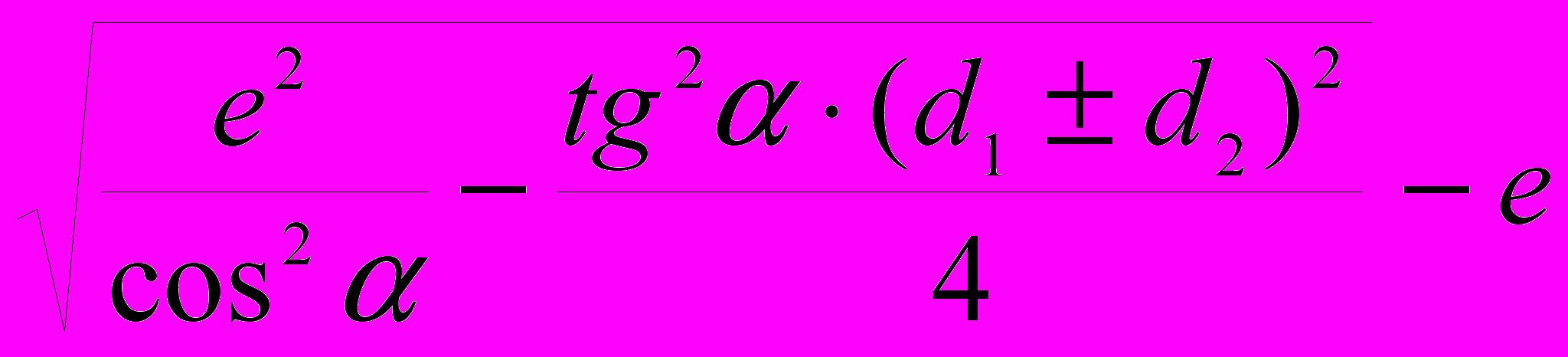где е – эксцентриситет; α – угол трения;

d1, d2 – диаметры «закрепленных» тел качения.

Знаки: «–» - для схем «а», «б» и «г»; «+» - для схемы «в» (см. рис. 3.7.)

Пренебрегая малыми величинами приближенно получаем:

для схем «а,б,г» – h = fp2 ∙ e /2 ;

для схемы «в» – h = fp2 ∙ dср 2 /2e.

Введем безразмерный критерий: hD = h / fp2 ∙D,

где D – характерный габаритный размер (диаметр) механизма.

Таким образом, безразмерный геометрический критерий оценки долговечности фрикционных передач с самонатяжением:

hD = e / 2∙D, для схем «а ,б, г»;

hD = dср 2 / 2∙e∙D, для схемы «в»;

Согласно оценке по данному критерию, долговечность передач, построенных по схеме «в» на порядок выше других (см. рис.3.8). Недостатком известной передачи, основанной на схеме «в», является эксцентриситет ее центральных звеньев. В работе предложены две новые передачи (А.с.1626024, А.с.1770646), лишенные этого недостатка.


Четвертая глава посвящена зубчатым эксцентриковым подшипникам (ЗЭП). В связи с тем, что ранее ЗЭП не применялись и не изучались, исследование касалось самого широкого круга вопросов.

Работу начали с синтеза схем без учета их структурной симметрии. Простейшая из устойчивых «зубчатых» ЗСТКО (рис.4.1) состоит всего их 4-х элементов-звеньев. Она не является геометрически неизменяемой: центральная шестерня может двигаться в радиальном направлении, увлекая за собой сателлиты. При этом сохраняется возможность согласованного вращения всех звеньев. На рис.4.1 также показаны 5-и и 6-и элементные схемы «зубчатых» ЗСТКО.

Для использования в зубчатом эксцентриковом подшипнике (ЗЭП) наиболее подходят схемы б, г (рис.4.1), обладающие структурной симметрией вращения порядка n = 3 и n = 4. Их максимальный эксцентриситет многократно превышает эксцентриситет фрикционных эксцентриковых подшипников.


М
КР × РР:

ww, ww

атрица связей 2×2



а
Матрица связей 2×3.



б в

Матрицы 2×4
Матрицы 3×3



г д е



ж з и к

Рис. 4.1. Структурные схемы простейших «зубчатых» ЗСТКО


Эксцентриситет может быть еще несколько увеличен. Для этого предлагается использовать дополнительное «подвешенное» кольцо – П.м.73045, РФ 2345256, РФ 2341698. Соответствующие схемы получаем на базе структурных чисел: «14.14» и «124.14».

В другом структурно-кинематическом варианте эксцентрикового подшипника (ЗЭПн) центральная шестерня Р непосредственно взаимодействует с венцом К. Схемы такого механизма получаем путем «развития» несимметричной структуры: К…× P…: w… – см. рис. 4.2.



а б в г д

Рис.4.2. Рациональные схемы ЗЭПН (РФ 2341697):


а) [K1] P3 × (P2) P4o : ww, ww; б) [K1] P3o × (P2) P4 P5o : ww, ww, ww;

в) [K1] P3 P5o × (P2) P4o P6o : wrw, wow, rrr; г) [K1]P3o × (P2)P4 H5 : ww, ww, ov;

д) [K1]P3P5oH7 × (P2)P4oP6o : wrro, rrro, rorv.

Расчеты ЗЭП потребовали разработки не только новых алгоритмов, но и методов их параметрического анализа и синтеза.

Существенные особенности имеет геометрический расчет ЗЭП. В частности, условие сборки (см. рис.4.3) содержит уравнения вида:



или ,

где ,

составленные для нескольких замкнутых контуров, образуемых разновеликими сателлитами.

Вместо «традиционного» условия соосности возникает условие (см. рис.4.4) соответствия начальных диаметров колес их расположению, например, в виде системы уравнений:


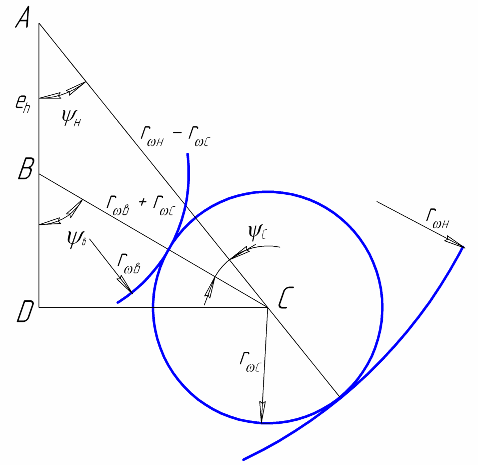Рис. 4.3. К условию сборки
Рис.4.4. К условию соответствия начальных диаметров колёс их расположению

.

.

.

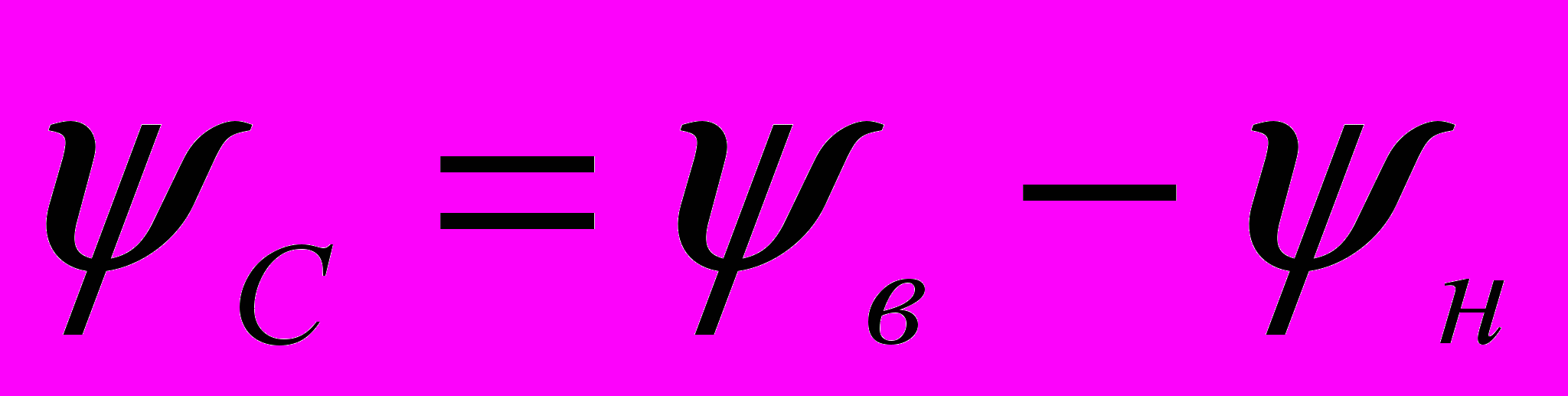и- целочисленные величины; - монотонно варьируются.

При решении задачи силового анализа системы, содержащей ЗЭП, использовался заменяющий механизм (рис.4.5).

Сформулирована теорема «О полюсе ЗЭП»:

В механизме, заменяющем ЗЭП, линии всех поводков пересекаются в одной точке, расположенной на межосевом отрезке и делящей его на части пропорционально числам зубьев и .

Рассмотрено несколько конструктивных вариантов реализации центроидной пары ЗЭП: 1)беззазорное эвольвентное зацепление; 2)зацепление Новикова; 3)сочетание зубчатых венцов с дорожками качения. Предпочтение отдано последнему варианту. Для упрощения изготовления деталей предложено использовать внеполюсное зацепление (патент РФ 2331000). При этом дорожки качения центральных элементов совпадают с их начальной поверхностью и лежат на уровне поверхности впадин зубчатых венцов.

Расчетная нагрузочная способность ЗЭП соизмерима с нагрузочной способностью роликового подшипника качения тех же габаритов. Испытания опытных образцов (см. рис.4.7) подтвердили работоспособность ЗЭП.



Рис. 4.7. Опытные образцы ЗЭП

Зубчатые подшипники не только превосходят фрикционные по величине эксцентриситета, но, что не менее важно, обеспечивают постоянное передаточное отношение от центральной шестерни к мнимому водилу. Это расширяет возможности применения ЗЭП. Так, например, можно блокировать несколько ЗЭП на общем валу. Поставив ЗЭП на ведущий вал, выполненный в виде эксцентрика (см. рис.4.8), можно модифицировать закон движения ведомого звена (например, ползуна) по принципу сложения двух гармоник.



Рис. 4.8. Преобразователь движения (РФ 2352839)

Соответствующие расчетные зависимости получены с использованием методов, используемых при исследовании зубчато-рычажных механизмов:









В результате, получается движение с выстоями, подъем и опускание с разными скоростями и др. циклические кривые (рис.4.9).

Применение ЗЭП целесообразно и в других зубчато-рычажных механизмах – РФ 2365799, П.м. 69178. Последовательное соединение двух эксцентриковых подшипников в одном механизме (А.с.1237833) сообщает ему дополнительные кинематические возможности.


Рис.4.9. Модификация закона движения ползуна кривошипно-ползунного механизма за

счёт применения ЗЭП