Волков Глеб Юрьевич систематика и структурно-параметрический синтез механизмов на базе замкнутых систем тел качения специальность: 05. 02. 18 «Теория механизмов и машин» автореферат

Вид материала

Автореферат

Содержание Уровень структурных чисел Уровень структурных формул Уровень анализа реализуемости схем Третья глава

Подобный материал:

• Рабочей программы дисциплины Теория механизмов и машин по направлению подготовки 190100, 33.66kb.
• Памятка для студентов группы пкм- по изучению дисциплины " Теория механизмов и машин, 72.92kb.
• Димитрюк Сергей Олегович, доцент кафедры «Теория механизмов и машин» к т. н., доцент, 37.69kb.
• Рабочая программа по дисциплине опд. Ф. 04 Теория механизмов и машин для направления, 252.07kb.
• «Теория машин и механизмов и проектирование текстильных машин», 240.94kb.
• Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
• Учебная программа дисциплины теория механизмов и машин (Наименование дисциплины в соответствии, 241.34kb.
• Примерная программа дисциплины теория механизмов и машин Рекомендуется Минобразованием, 326.52kb.
• Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
• Задачи кинематического анализа и синтеза механизмов. Передаточные функции и отношения., 55.01kb.

W_р =2∙m – 3 – p₄ - L 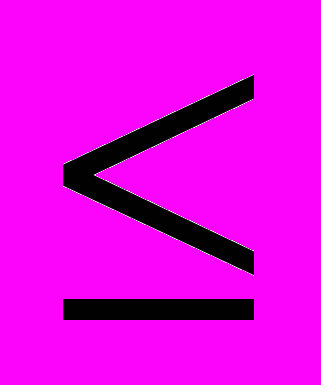-1


или (для заменяющей стержневой системы):


W_р =2 ∙М – 3 – S - L 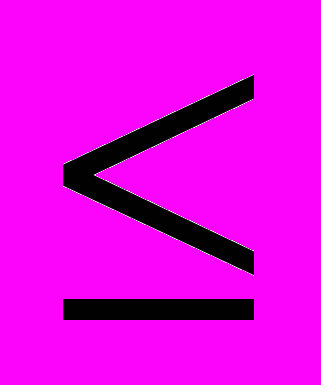-1.


В «зубчатых» ЗСТК L_с = 1 – согласованное вращение всех звеньев, поэтому:


W_р = 3∙(m – 1) – 2∙p₅ – L 0.


Достаточное условие устойчивости ЗСТК – это параметрическая задача, связанная с анализом решений системы неравенств. При этом важно, чтобы система обладала «запасом устойчивости». В случае «гладких» ЗСТК этот запас выражается в допустимом уменьшении диаметров тел качения (вследствие их износа или упругой деформации).

Заметим, что ранее, в том числе в работах автора, требование, аналогичное условию устойчивости, называлось условием геометрической неизменяемости системы. Действительно, «чистые» ЗСТК с «гладкими» телами качения и фрикционными связями, должны иметь оси звеньев, положение которых относительно некоторой системы отсчета является неизменным. Для них потеря геометрической неизменяемости означает одновременно потерю устойчивости и размыкание кинематических пар. Среди зубчатых ЗСТК существуют «чистые» ЗСТК, расстояния, между осями круглых зубчатых звеньев которых изменяются в процессе работы механизма.

Возможные подходы к поиску структурных решений в области ЗСТК

Предложенный принцип описания ЗСТК позволяет выполнять формализованный структурный синтез механизмов.

Наиболее универсальным является алгоритм структурного синтеза ЗСТК (таблица 1), основанный на комбинировании простейших (базисных) элементов и связей.

В таблице 3, в качестве примера синтеза на первом уровне, показан массив структурных чисел ЗСТК сложностью до 5 элементов, сформированный с учетом структурной симметрии вращения.

Предварительный отбор структурных чисел происходит в соответствии с тестом (см. таблицу 2). Абсолютный запрет на существование ЗСТК накладывает только невозможность контакта кольца с кольцом (п.5) – черный цвет. Структурные числа, не реализуемые в любых «чистых ЗСТК» (п.п. 1,4), отмечены штриховкой. В массивах также указаны структурные числа, которые уже использованы в известных «гладких» (Г), зубчатых (З) или дополненных (Н) системах. Действует правило: структурные числа, осуществимые в варианте (Г), заведомо реализуемы в исполнении (З) и, тем более, (Н).

Таблица 1. Алгоритм структурного синтеза ЗСТК

№	Выполняемые операции
Уровень структурных чисел
1.	Выбор параметров и формирование массива структурных чисел, соответствующего заданному полю поиска. Устранение изоморфизмов.
2.	Отбраковка вариантов структурных чисел по тесту предварительного отбора (см. таблицу 2).
Уровень структурных формул
3.	Назначение между элементами связей, виды которых соответствуют принятым ограничениям синтеза. Устранение изоморфизмов.
4.	Отбраковка вариантов структурных формул по тесту предварительного отбора (см. таблицу 2).
5.	Проверка вариантов по необходимому условию замкнутости кинематических пар системы с учетом ее линейных вырождений.
6.	Назначение ведущего «()», опорного «[]» и ведомого «{}» элементов ЗСТК (звеньев механизма).
Уровень анализа реализуемости схем
7.	Проверка по достаточному (параметрическому) условию замкнутости кинематических пар. Оценка запаса устойчивости системы.
8.	Неформализованный анализ систем с точки зрения их работоспособности, компактности, технологичности и т.д.

Таблица 2. Формальные признаки (тест) предварительного отбора ЗСТК




Таблица 3. Массив структурных чисел ЗСТК






В качестве примера синтеза «чистых» ЗСТК на этапе структурных форму возьмем конкретное структурное число «124.14». Связи, разрешенные тестом на уровне БЦС, указаны в таблице 4; результаты оценки структур по W – в таблице 5. Возможные варианты конкретизации функций звеньев в механизме:

для подшипника: [1][2]4.14, [1]24.[1]4, 1[2]4.[1]4.

для передачи: (1)[2]4.{1}4, [1](2)4.{1}4, [1]{2}4.(1)4,

(1){2}4.[1]4, {1}(2)4.[1]4, {1}[2]4.(1)4.

Таблица 4. Связи, разрешенные тестом (уровень БЦС)	Таблица 5. Результаты оценки структур по W
1 (К) 2 (Р) 4 (Рn) 1 (К) 0 С, Т, 0 Т 4 (Рn) Т Т Т, Т2	«124.14», т.е. КРРn × КРn: «зуб» «гл» Структурно-симметричные 0СТ,ТТТ2 0СТ,ТТТ 00Т,ТТТ2 00Т,ТТТ + − + − + − + − Условно-симметричные 0ТТ,ТТТ2 0ТТ,ТТТ + − − −

В результате оценки выполнения параметрических условий замкнутости кинематических пар, кинематических, конструктивных и технологических свойств механизмов работоспособными признаны устройства, показанные на рис. 1.5 – 1.8. Из них две схемы имеют новизну на уровне изобретений.

Помимо рассмотренного выше основного алгоритма синтеза ЗСТК «из базисных элементов» в работе применялся структурный синтез новых ЗСТК путем интегрирования модулей (подсистем), присутствующих в известных ЗСТК и рычажных механизмах.

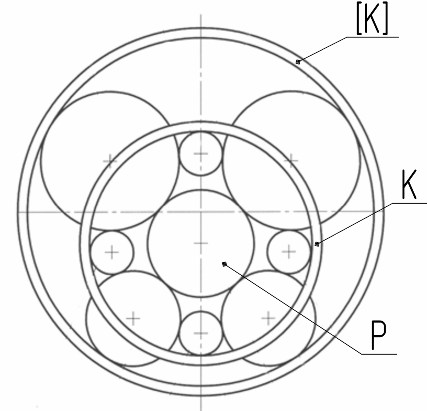[К][Р]Рn × КРn: oor, rrr2	[К][Р]Рn × КРn: ocr, rrr2
Рис. 1.5. Бессепараторный подшипник (только эксцентриковый)	Рис. 1.6. Бессепараторный подшипник

	(К)[Р]Рn × {К}Рn: oow, www2
К[Р]Рn × [К]Рn: oow, rww2	(К){Р}Рn × [К]Рn: oow, www2
Рис.1.7.Зубчатый эксцентриковый подшипник (патент РФ 2341698)	Рис. 1.8. Безводильная передача (патент РФ 2423634)

Во второй главе разработанный принцип формализованного описания ЗСТК и критерии предварительной оценки их работоспособности использованы при анализе существующих схем и конструкций механизмов.

В ходе патентного поиска обнаружены десятки существенно различных структурных схем ЗСТК и сотни конструкций, соответствующих им механизмов. Наиболее многочисленным оказалось семейство известных структурных схем бессепараторных подшипников с «гладкими» телами качения (см. табл.6). Анализ показал, что большая часть этих схем имеет серьезные недостатки. Встречаются запатентованные конструкции, которые не работоспособны (оценка «–») по достаточному и даже необходимому условиям геометрической неизменяемости. Наиболее удачны решения (оценка «+++»), соответствующие структурному числу «124.124» – по ним запатентованы десятки конструкций.

Эксцентриковых подшипников (ни «гладких», ни зубчатых) в патентно-технической литературе почти нет. Особенно тщательно был проведен поиск фрикционных планетарных передач с самонатяжением в плоском контуре, зубчатых безводильных передач и различных типов передач, сочетающих зубчатые и фрикционные элементы. Интерес представляют схемы насосов, построенные на базе планетарной системы с аномальной подвижностью звеньев.

Таблица 6 – Известные схемы «гладкотельных» бессепараторных подшипников

Стр. число	Структурная формула	Оценка
12.4	КР×Рn : rr	+++
123.4	КРКn×Рn : rrr2	+
14.14	КРn×КРn : оr, rr2	+
14.24	КРn×РРn : оr, rr2	–
123.44	КРКn ×Рn Рn : rос, оrr2 КРКn × Рn Рn : rrс, оor2	+ ++
124.14	КРРn×КРn : ооr, rrr2 КРРn×КРn : осr, rrr2	– ++
124.24	КРРn×РРn : ооr, rrr2 КРРn×РРn : осr, rrr2	– ++
124.34	КРРn×КnРn : оrс, rоr2	+
124.44	КРРn×РnРn : rrr2, оrr2	+
224.14	РРРn×КРn : соr, rrr2	+
1233.44	КРКnКn×РnР2n : rrсr, ооrr	++
124.124	[К]РРn× К(P)Рn : осr, ооr, rrr2 [К](Р)Рn × КPРn : осr, ооr, rrr2 [К](Р)Рn× КPРn : ооr, соr, rrr2 [К](Р)Рn× КPРn : ооr, ооr, rrr2	++ +++ +++ –
124.134	[К](Р)Рn× ККnРn : ооr, оrс, rоr2	+
124.144	[К](Р)Рn× КРnРn : ооr, rоr2,оrr2	–
124.244	[К](Р)Рn× РРnРn : ооr, rоr2, оrr2	–
1244.34	[К](Р)РnРn × КnРn : ооrr, rrr2r2	+
144.234	[К]РnРn× (Р)КnРn : оrо,осr2,rr2о	+
1244.124	[К]Р(Р) Рn × КРРn: ооrо, ооr, rrr2r2	–
1244.144	[К]Р(Р)Рn × КРnРn: осоr,rrоr2,ооrr2	++

Третья глава посвящена синтезу систем с «гладкими» телами качения.

Вначале была поставлена задача синтеза «гладкотельных» структур ЗСТКО (т.е. систем с одной рабочей поверхностью каждого звена) без учета их структурной симметрии и без предопределения функционального назначения. Генерировалась матрица связей и выполнялась оценка реализуемости соответствующей ЗСТКО по тесту предварительного отбора (таблица 2). Две простейшие схемы, прошедшие тест, состояли из 6 элементов (рис.3.1). 7-и элементных схем оказалось 8, но две из них «г, и» не имели параметрической области, удовлетворяющей достаточному условию геометрической неизменяемости. Схемы «б», «ж» оказались известными ранее, остальные – новыми. Преобразователь движения (рис.3.2), построенный по схеме «д», признан изобретением. Достоинством этого механизма является совмещение функций двуплечего кривошипа и редуктора.

6 эл.		Структурная формула а КРК × РРР: rrr, rrr, rro б РРК × РРК: rrr, rrr, rro в РККК×РРР: rrrr, rrro, rror г РРРР × КРР: rrrr, rrro, rror д РРРР × РКК: rrrr, rrro, rror е РРРР × РКР: rrrr, rrro, rror ж РККК × РРР: rorr, rrro, rror з РРРР × РКК: rorr, rrro, rror и РРРР × ККК: rorr, rrro, rror к РРРК × РРК: rorr, rrro, rror
	а б
7 эл.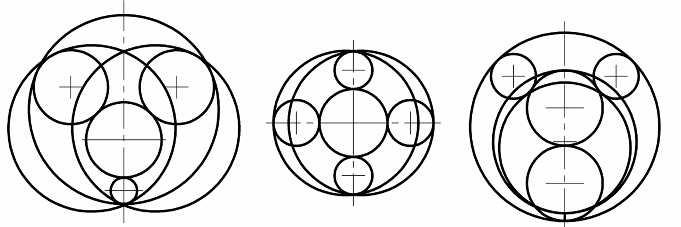
	в д е
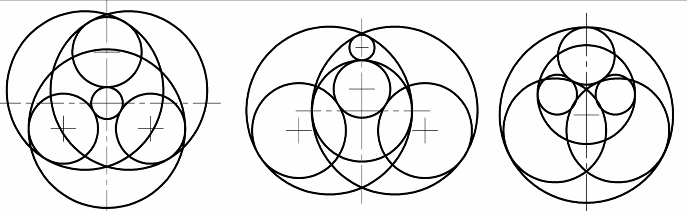	ж з к