Geum.ru

Решение задачи оптимизационного кинематического синтеза плоских рычажных механизмов IV класса с выстоем выходного звена с учетом их возможных модификаций по

Вид материалаРешение
Подобный материал:

Компьютерное моделирование рычажных механизмов высоких классов

Gebel Е.S., Solonin Е.V.


В настоящее время в России и за рубежом уделяется большое внимание созданию автоматизированных технических средств: промышленных роботов, машин-автоматов, манипуляторов, автоматизированных складов, автоматизированных транспортных средств. Рабочие органы исполнительных механизмов при выполнении своих функций совершают в составе таких средств автоматизации строго установленные движения. К наиболее характерным можно отнести возвратно-вращательные и возвратно-поступательные с одним или двумя выстоями выходного звена в крайних положениях.

Такой характер движения рабочих органов может быть обеспечен различными механизмами, в частности, рычажными механизмами высоких классов. Исходными данными на стадии разработки принципиальной схемы механизма с выстоем могут служить критерии, определяющие назначение механизма, требуемый тип производимых перемещений и их величину, степень нагружения механизма и др.

Решение задачи оптимизационного кинематического синтеза плоских рычажных механизмов IV класса с выстоем выходного звена с учетом их возможных модификаций по критерию точности позиционирования на интервале выстоя и обеспечением требуемого качества передачи движения на сегодняшний день не существует методики получения свободных параметров синтеза аналитическим способом. К тому же в виду разнообразных технологический и конструктивных требований, в каждом конкретном случае решение инженерных вопросов кинематического синтеза схемы рычажного механизма IV класса требует индивидуального подхода. Таким образом, в практике проектирования подобных сложных систем мощным, удобным и зачастую единственно приемлемым решением является математическое моделирование, в связи с чем развитие методов автоматизации проектирования и анализа оптимальных схем рычажных механизмов высоких классов является актуальным вопросом.

В общем случае процесс математического моделирования условно можно разделить на два этапа. Первым этапом является создание модели реального объекта, отображающей с необходимой точностью связи между свободными и рассчитываемыми кинематическими параметрами, описывающими схему проектируемого механизма, разработка моделирующего алгоритма и его реализация в пакете имитационного моделирования. Для определения необходимого состава компонентов математической модели оптимизационного синтеза рычажного механизма IV класса по критерию точности позиционирования рабочего органа с учетом дополнительных условий, характеризующих качество передачи сил и движения необходимо выявить ее структурные элементы. При решении поставленной задачи были выделены следующие блоки: подпрограммы кинематического синтеза и анализа, блок, в котором рассчитываются качественные характеристики проектируемой схемы механизма, и непосредственно блок, реализующий один из известных методов оптимизации. Целевой функцией в данном случае выступает кинематическая точность позиционирования выходного звена на интервале выстоя, поскольку одним из основных технологических требований, предъявляемых к данным механизмам, – это минимальное значение отклонения от заданного значения угла размаха рабочего органа. Математическая модель рычажного механизма IV класса с учетом его возможных модификаций должна быть комплексной, позволяющей автоматическую идентификацию выявленных схем на основе предложенных признаков. Представляется целесообразным создание библиотеки отлаженных и верифицированных моделей схем механизма.

Вторым этапом математического моделирования является постановка вычислительных экспериментов на ЭВМ с целью оптимизации кинематических параметров рычажного механизма IV класса для обеспечения требуемого функционирования разрабатываемой системы. Оптимизация по параметру подразумевает итерационное нахождение условий, при которых критерии качества передачи сил и движения находятся в допустимых пределах и целевая функция достигает минимального значения. Проектируя оптимальную схему механизма, приходиться проводить большое количесво однотипных расчетов, отличающихся значениями, как правило, одного свободного кинематического параметра при фиксированных значениях остальных. В связи с тем, что проведение одного вычислительного эксперимента может занимать продолжительное время, необходимо стремиться к получению максимальной информации при анализе результатов проведения небольшого числа экспериментов. Для этого необходимо их соответствующее планирование. Также, посредством проведения серии вычислительных экспериментов, осуществляется анализ чувствительности, т.е. выявление тех параметров, которые в наибольшей степени оказывают влияние на значение целевой функции и критерии качества передачи движения, т.е. на поведение механизма. Результатом проделанной работы являются ограничения, устанавливающие пределы изменения значений свободных параметров синтеза.

На рис. 1 представлены кинематическая схема одной из возможных модификаций плоского рычажного механизма IV класса с выстоем выходного звена и список свободных параметров синтеза [1].


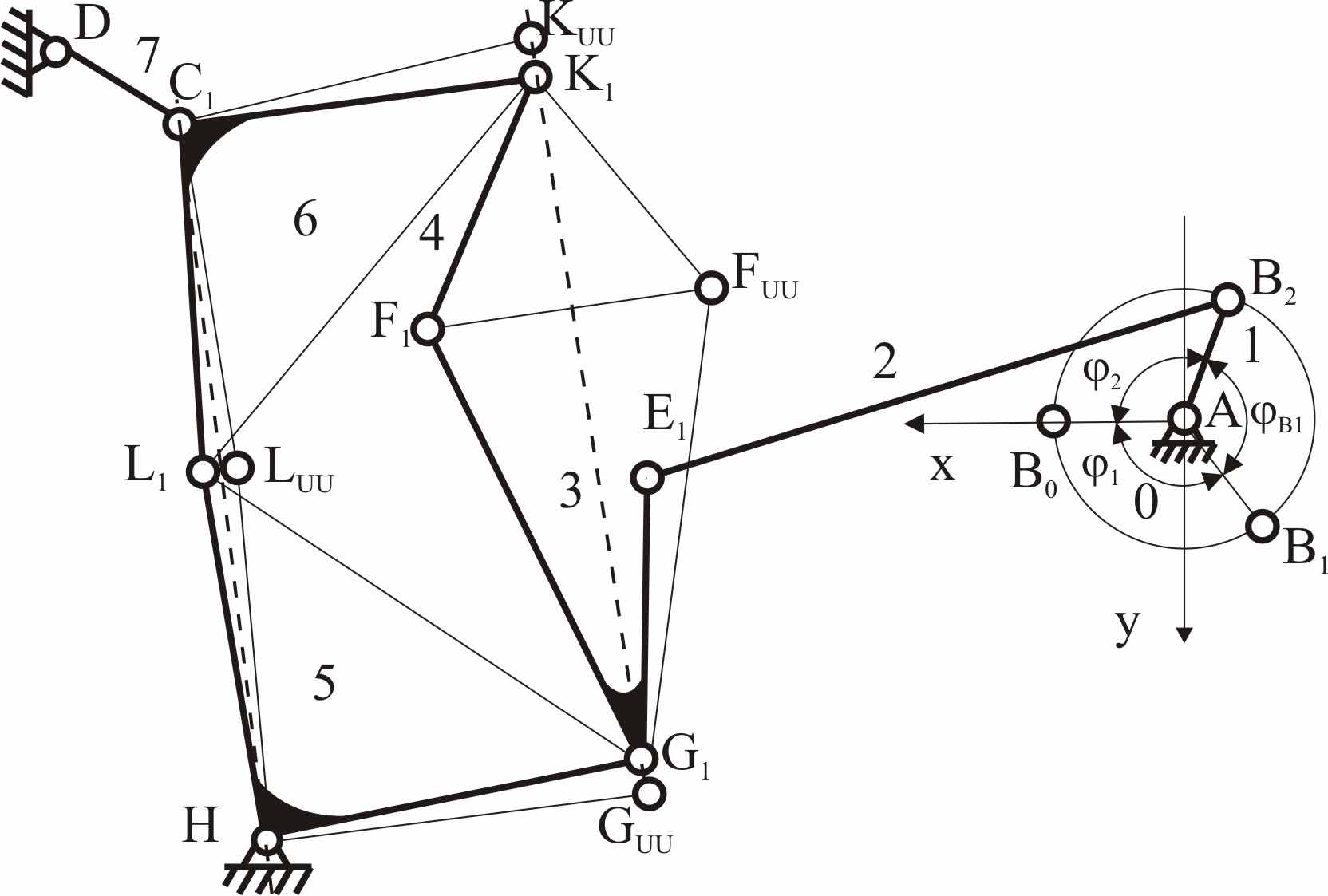Рис. 1. Кинематическая схема механизма и список свободных параметров синтеза

Общая структура математической модели оптимизационного синтеза механизма, реализованная в MVS (рис. 2), представлена тремя блоками: «Синтез» - подпрограмма синтеза механизма; «Начальное положение» - установка начальных координат характерных точек модели; «Моделирование» - кинематический анализ механизма.



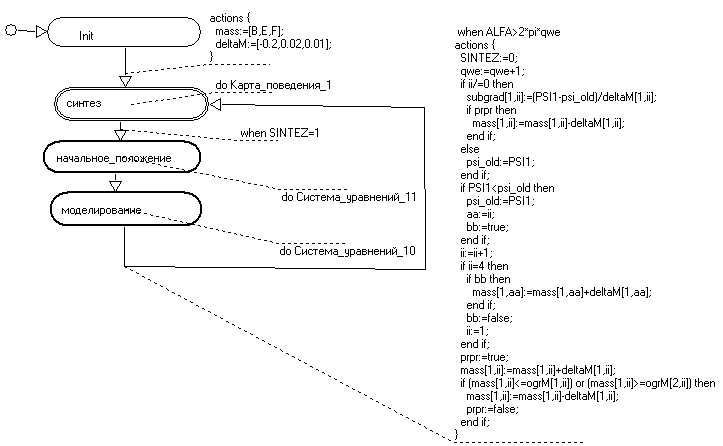
Рис. 2. Карта поведения

Переходы на карте поведения блока «Синтез» (рис. 3) отражают возможные модификации рычажного механизма IV класса с выстоем. «Успешность» кинематического синтеза контролируется логической переменной SINTEZ.



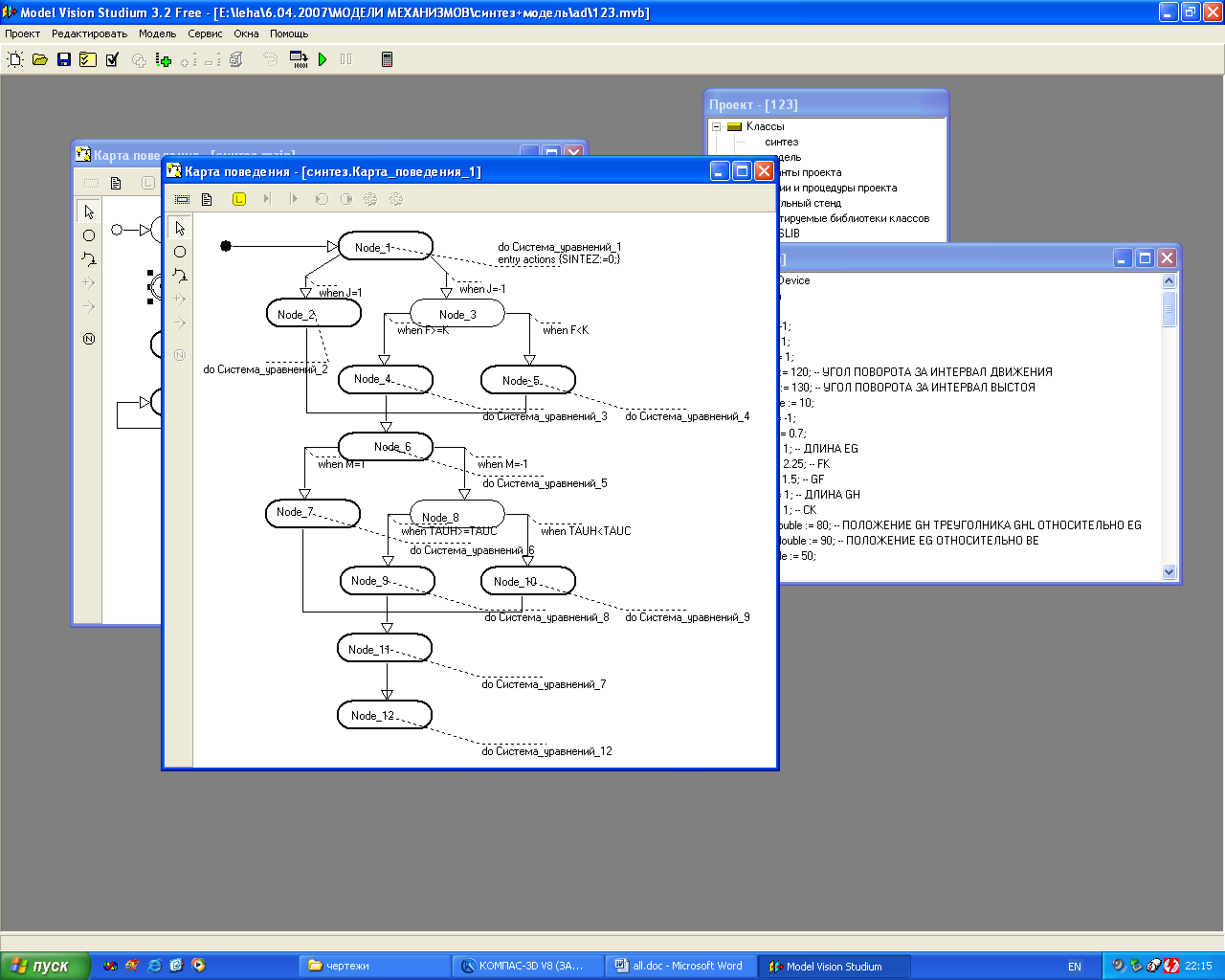
Рис. 3. Карта поведения блока «Синтез»

В соответствии с методом кинематического синтеза рычажных механизмов IV класса в блоке «Синтез» (рис. 3) рассчитываются линейные и угловые параметры схемы, а также положение неподвижных шарниров и значение кинематической погрешности выстоя. Для проверки адекватности математической модели кинематического синтеза в программе построены две виртуальные модели, отражающие положение звеньев механизма в момент начала/конца интервала выстоя и в момент мгновенного выстоя. В блоке «Начальное положение» (рис. 2) вычисляются начальные значения углов alfa0, delta0, gamma, epsilon поворота звеньев относительно друг друга с использованием вложенных операторов ветвления, учитывающих возможное взаимное расположение шарниров звеньев механизма.

При переходе карты поведения в состояние «Моделирование» (рис. 2) запускается процесс решения задачи кинематического и качественного анализа механизма, результаты которых отображаются на визуальной модели (рис.4) и диаграмме (рис.5) соответственно. Многозвенные шарнирные механизмы характеризуются сложными функциями перемещениями, описываемыми системой нелинейных уравнений. Метод составления системы уравнений, используемый в блоке «Моделирование» для кинематического анализа механизма, основан на применении геометрических связей между шарнирами треугольных звеньев и функций невязок, что позволяет получить минимальный набор уравнений [2]. В качестве характеристик качества передачи сил и движения для механизма IV класса с выстоем приняты критерии, предложенные профессором Э.Е. Пейсахом, и углы давления.



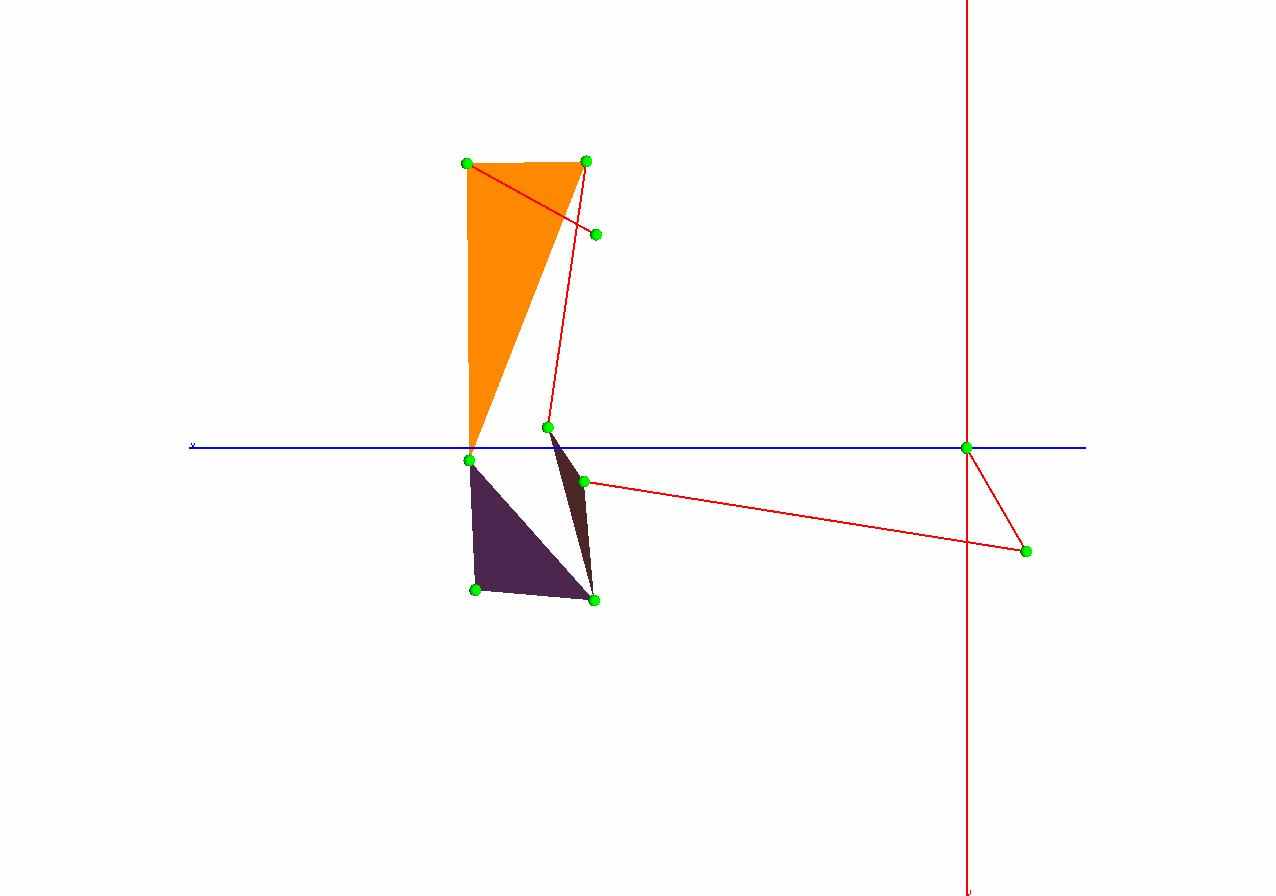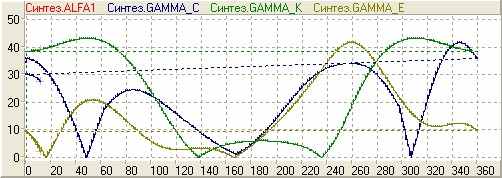Рис. 4. Визуальная модель механизма IV класса с выстоем
Рис. 5. Графики изменения критериев качества передачи сил и движения в механизме

Сканированием области свободных параметров определены границы работоспособности и существования кривошипной сборки механизма в определенной модификации в виде замкнутой кинематической цепи на всем диапазоне положений звеньев. На рис. 7 в прямоугольной системе координат изменения величин b и е относительных длин шатуна ВЕ и стороны EG треугольного звена GEF соответственно изображены линии уровня, отражающие характер изменения одной из составляющих погрешности останова выходного звена механизма.



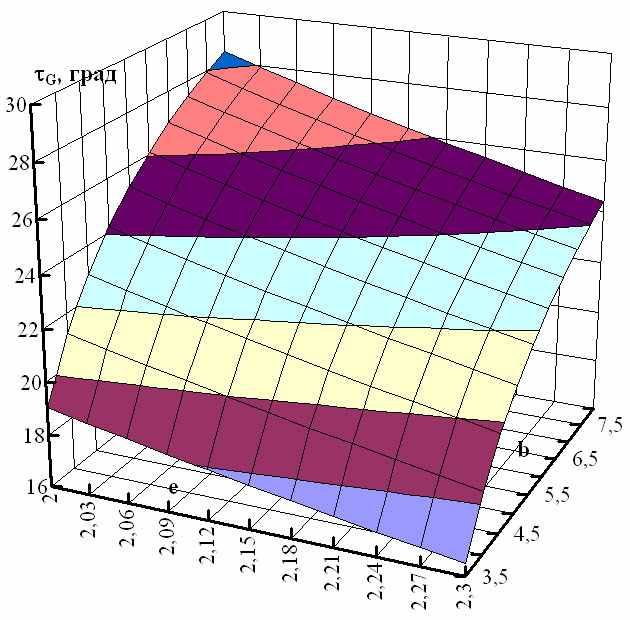
Рис. 7. Линии уровня

На этапе оптимизации в качестве целевой функции используется значение кинематической точности выстоя рабочего органа механизма IV класса, значение которой рассчитывается в блоке «Синтез» и выражается через малый угол 1 поворота выходного звена CD на интервале выстоя. В работе использовался направленный метод поиска экстремума главного критерия качества, а именно градиентный метод.

При срабатывании перехода между узлами «Моделирование» и «Синтез» выполняются операции, при которых происходит экстремума главного критерия оптимизации в направлении антиградиента, соответствующем быстрейшему уменьшению целевой функции, что максимально ускоряет процесс поиска. Величина шага по каждому свободному параметру синтеза механизма IV класса первоначально различная, назначенная в соответствии с проведенным предварительным сканированием области изменения параметров, и варьируется в широких пределах, но при приближении к оптимуму, как правило, уменьшается.

В результате найдено такое сочетание свободных параметров синтеза, при котором выполнялось условие существования кривошипа, кинематическая погрешность выстоя выходного звена была минимальна, а значения критериев качества передачи сил и движения находились в допустимых пределах. Применение формальных оценок математической статистики позволит оценить влияние изменения варьируемых параметров и их парных сочетаний на анализируемые свойства рассматриваемого механизма. Таким образом, следующим этапом оптимизации является классификация всех параметров по степени их влияния на значение функции цели и выделение среди них существенных, что потребует анализа многомерной области свободных параметров синтеза.

Технологии компьютерного моделирования при решении задач оптимизационного кинематического синтеза плоских рычажных механизмов высоких классов применяются сложности или невозможности получения результатов аналитическими методами. При этом использование базы данных отлаженных и верифицированных библиотек математических моделей схем рассматриваемых механизмов, в совокупности с развитием методологии проведения серии вычислительных экспериментов помогает добиваться резкого сокращения сроков проектирования.


Литература

1. Гебель Е.С. Моделирование и оптимизация работы рычажного механизма IV класса с выстоем. / Е.С. Гебель, Е.В.Солонин// Труды международной научно-технической конференции «Компьютерное моделирование 2008» 24-25 июня 2008г. – СПб.: Изд-во Политехн. Ун-та, 2008. – с. 151 – 155.

2. Гебель Е.С. Моделирование как инструмент изучения дисциплины «Терия механизмов и машин» / Е.С. Гебель, Е.В. Солонин // Компьютерные инструменты в образовании. - № 5. – 2008. – с. 37 – 44.