Geum.ru

М. А. Кремень психология управления курс лекций

Вид материалаКурс лекций

Содержание


ТЕМА 4. ИНФОРМАЦИЯ В ДЕЯТЕЛЬНОСТИ РУКОВОДИТЕЛЯ Лекция 4. Информация в деятельности руководителя
Информация и знание
Н – среднее количество информации; р
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   24

ТЕМА 4. ИНФОРМАЦИЯ В ДЕЯТЕЛЬНОСТИ РУКОВОДИТЕЛЯ

Лекция 4. Информация в деятельности руководителя


Основные понятия:

информация и знание; вероятность события в сообщении; информационная емкость; энтропия; информационная пропускная способность; информационная перегрузка; информационная недогрузка; избыточность информации; тезаурус.

Информация и знание


С помощью понятия информации наука пытается объективизировать и сделать доступной измерению категорию знания. Само слово «знаю» мало характеризует степень и объем знания. Оно применимо и к таблице умножения, и к сведениям типа «Волга впадает в Каспийское море», и к сложнейшим научным теориям. Мы часто говорим «знаю», когда следовало бы сказать «имею представление», и с большим трудом научаемся оценивать меру нашего незнания. Оказывается, что во многих ситуациях можно не просто говорить о знании, но измерять числом количество информации, содержащееся в этом знании или необходимое, чтобы получить нужное знание.

Наибольший интерес для нас представляет такое обобщение теории информации, которое позволяет приложить ее к психологии управления. Важным аспектом здесь является определение способности человека принимать, перерабатывать, сохранять и передавать информацию, поступающую на его «сенсорный вход».

Прежде чем поставить вопрос о том, что способна принести теория информации для психологии управления, следует выяснить сущность основного в этой теории понятия информации и способов измерения количества информации. Для элементарного уяснения данного вопроса обратимся к фактам обыденной жизни.

Представим себе, что кто-то в полдень в условиях естественного освещения сообщает находящемуся рядом с ним зрячему собеседнику: сейчас день. Ясно, что в таком сообщении для принимающего нет ровно никакой информации. Но если тот же человек примет сообщение от 5 октября 1957 г. о запуске первого в мире искусственного спутника Земли, то в этом высказывании, если оно истинно, будет содержаться громадная информация, так как до получения такого сообщения вероятность запуска спутника Земли 5 октября 1957 г. была еще очень мала. Такая информация перестраивает все наличные знания по данному вопросу, значительно их расширяет.

В основе приведенного примера о величине информации лежит установление вероятности события, о котором сообщалось, теория вероятности и дает ключ к определению величины информации. По определению, принятому в теории информации, полученная информация (Н) равна:



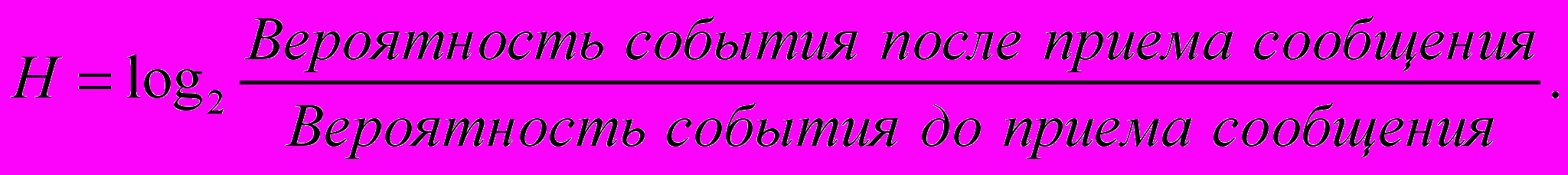
Простейшим случаем, разбираемым в теории вероятности, является выбор из двух независимых и равновероятных возможностей. Допустим, что в ящике находятся два шара – черный и белый. После изъятия какого-либо из них мы сообщаем о выборе одним из двух слов: «черный», «белый». Вероятность выбора каждого из шаров равна 1/2. Условимся, что всякий раз, когда мы сообщаем о выборе одного из двух независимых и равновероятных событий, мы передаем одну единицу информации. Иначе говоря, за наиболее простой случай принимается такой, в котором вероятность события до приема сообщения ранга 1/2. В случае отсутствия помех вероятность события после приема сообщения равна единице.

Полученная информация здесь при двоичном основании log22 = 1. Эта величина и является единицей численного измерения информации. Она получила название «бит» (от английского binary digit двоичная единица).

Таким образом, одна двоичная единица информации соответствует сообщению о том, что произошло одно из двух равновероятных событий. По сути, передача информации является процессом ни бора из определенного ряда альтернатив. Один бит соответствует выбору из двух равновероятных альтернатив. Чем шире ряд альтернатив, тем больше требуется информации для того, чтобы сделать выбор.

Пример 1.

Пусть в ящик вложено 16 предметов разной фирмы и цвета. Спрашивается: сколько двоичных единиц информации будет содержаться в сообщении, когда мы выбираем только один из 16 предметов, например, красный кубик? Метод вычисления прост. Вначале разобьем 16 предметов на две подгруппы по 8 предметов в каждой. В таком бинарном делении уже содержится одна двоичная единица информации, так как необходимо знать, в какой из групп находится красный кубик. Возьмем нужную подгруппу и снова разделим ее на две части, содержащие по 4 предмета, выбрав ту из них, в которой находится предмет сообщения. В этот момент мы затратили вторую двоичную единицу информации. И, наконец, выбрав из последней подгруппы красный кубик, мы дополним информацию четвертой двоичной единицей.

Таким образом, при сообщении о красном кубике, находившемся в группе из 16 предметов, мы должны были сделать 4 выбора, каждый из которых соответствовал одной двоичной единице информации.

Следовательно, в нашем сообщении об этом кубике содержались четыре двоичные единицы. Количество предметов в группе и подгруппах в процессе двоичного деления информации было следующим:

16; .

Отсюда видно, что степень числа 2 в последнем, четвертом, выборе является мерой информации в двоичных единицах и соответствует числу выборов.

Переходя от единичного примера к обобщенной формулировке и обозначая через n число предметов выбора, через Н – число выборов (т.е. количество двоичных единиц), можно записать: п = 2*. Отсюда следует:

Н = log2n.

Иначе говоря, величина информации Н может быть определена как логарифм с основанием 2 от числа возможных выборов. Двоичный логарифм наиболее удобен, так как при этом в конечном выборе мы доходим до последней единицы отбора.

Разобранный пример относится к случаю отбора из равновероятных независимых событий. Указанную выше формулу можно распространить и на явления, встречающиеся с разной вероятностью.

В общем случае вышеизложенное можно представить следующим образом. Величина информации о любом из равновероятных событий определяется по формуле

,

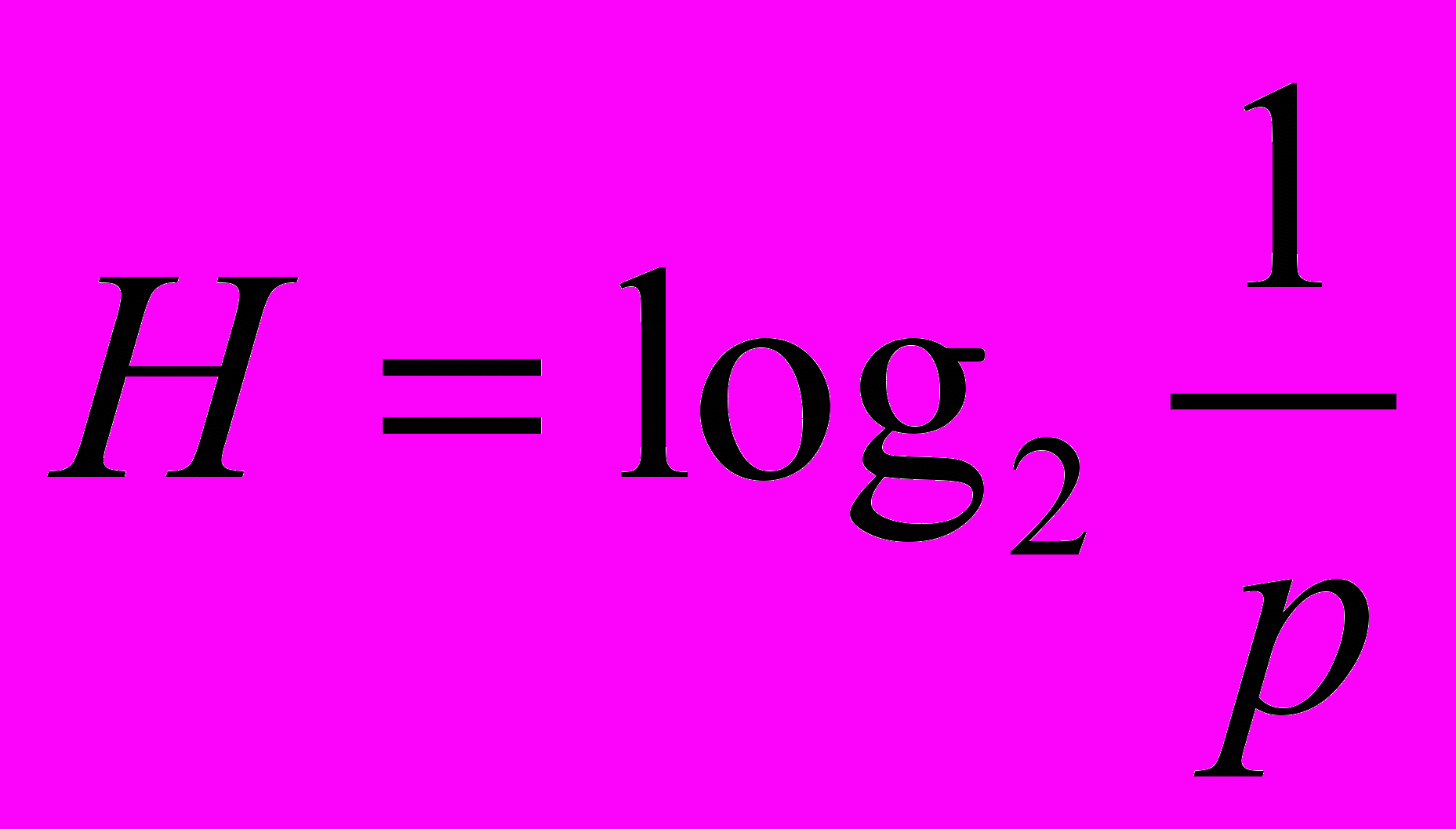где Н – информация о событии;

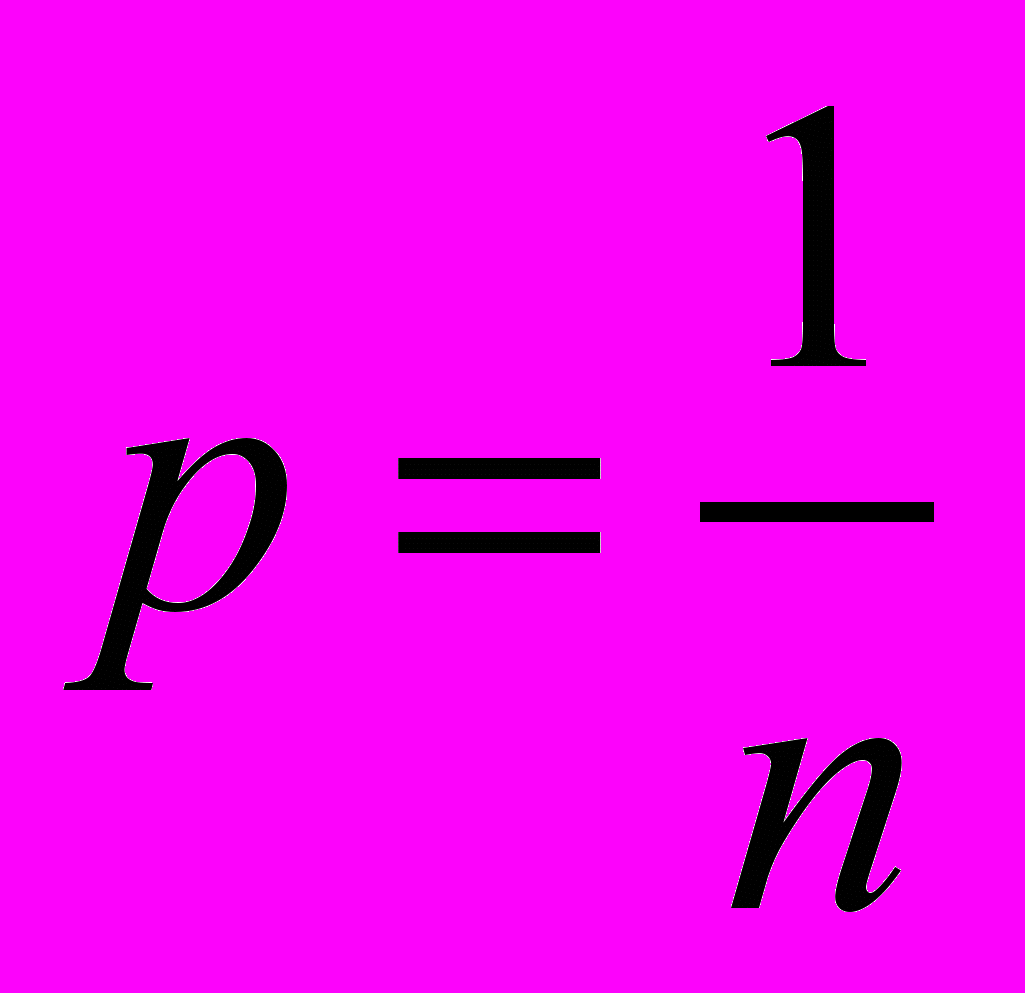– вероятность события.

В том случае, если события (альтернативы) имеют разную вероятность, информация о каждом из них (индивидуальная информация) может быть найдена по аналогичной формуле:

,

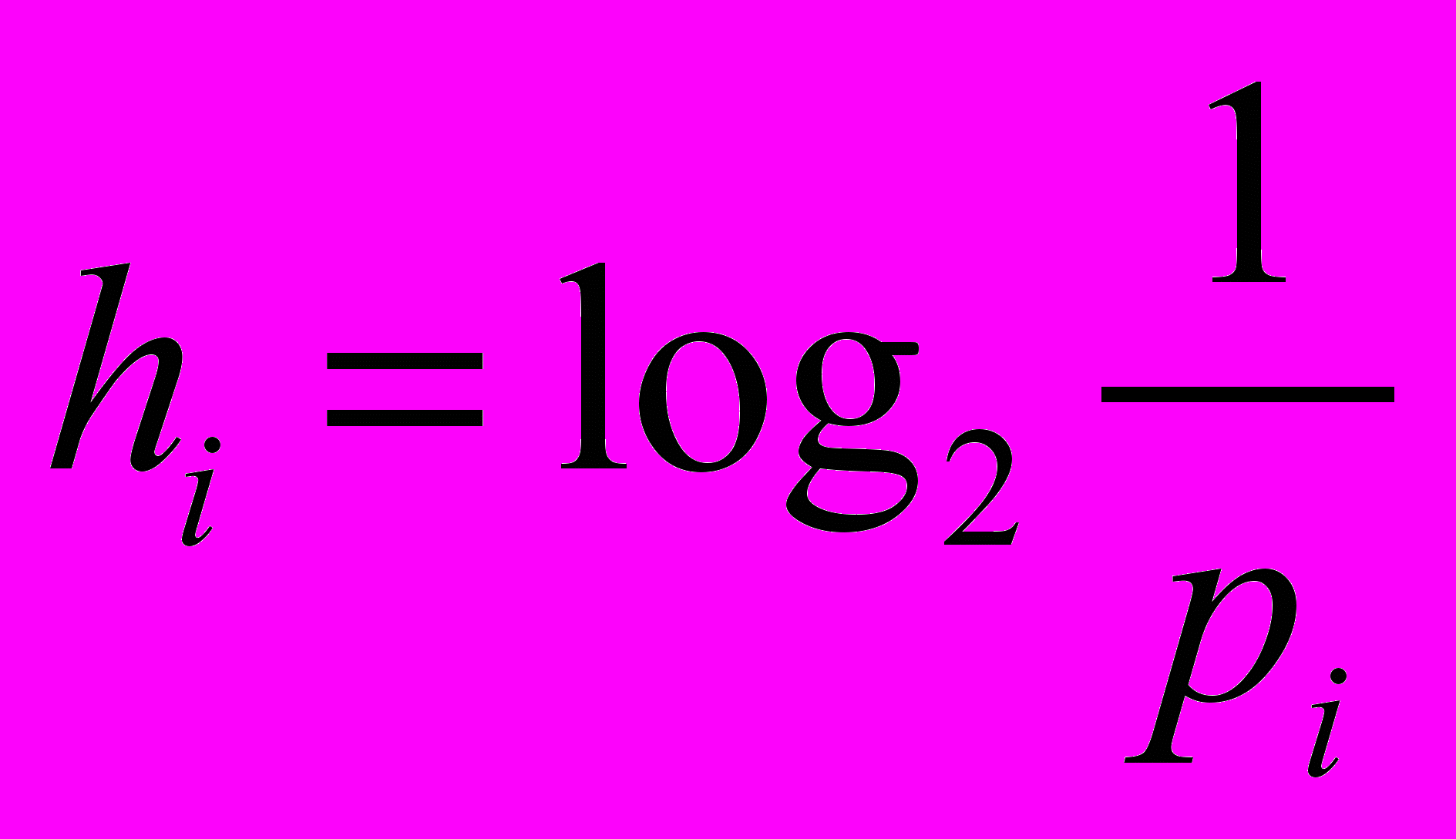где hi – информация об i-ом событии;

pi – вероятность i-го события.

Однако для решения многих задач знания об индивидуальной информации недостаточно. В этом случае пользуются формулой Шеннона:

,

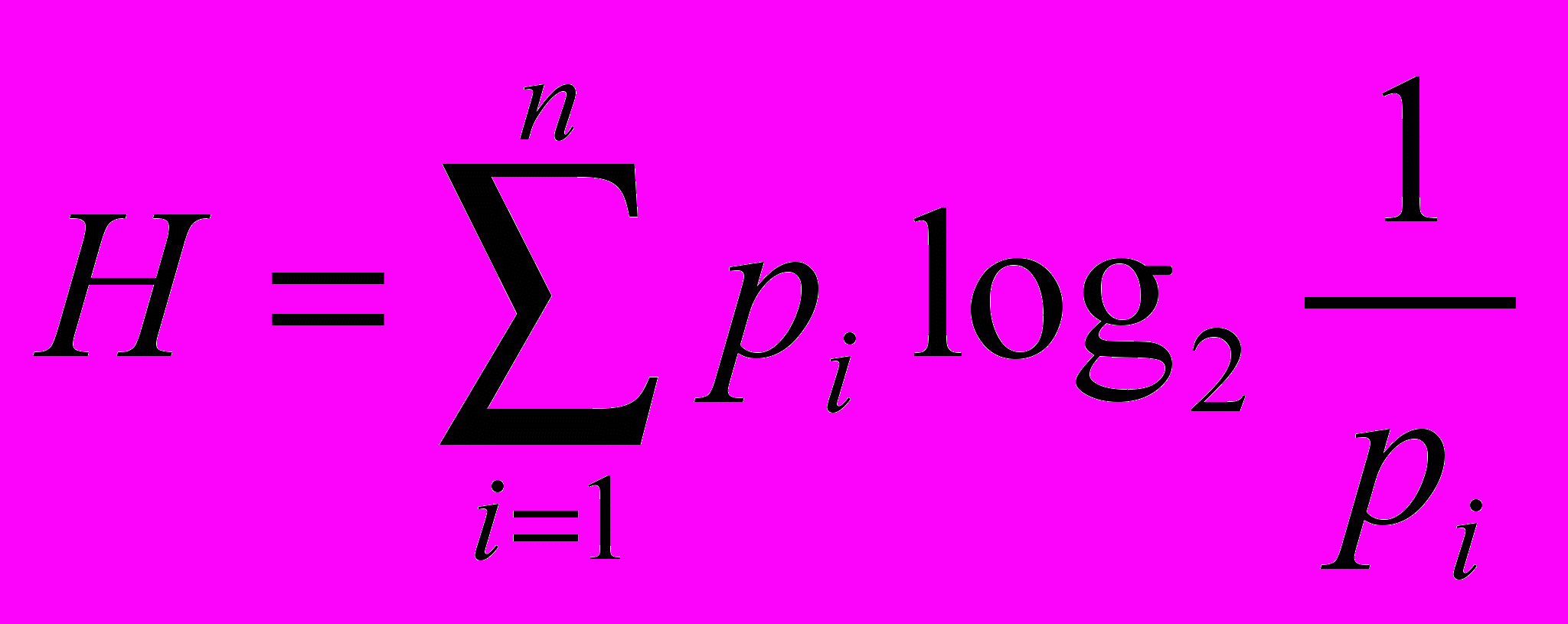где Н – среднее количество информации;

рi – вероятность i -го события.

При этом следует заметить, что при равной вероятности событий h (индивидуальная информация) и H (средняя информация) совпадают.