Фізичної величини (гост 16263-70)

Вид материала

Документы

Подобный материал:

• Додаток використання комп’ютера для графічного оформлення результатів вимірювань, 42.39kb.
• Метрологія, стандартизація та сертифікація. Сутність та взаємозв'язок дис­циплін. Необхідність, 128.07kb.
• 1 липня 2007 року, 155.8kb.
• Дсту гост 1-2006 держспоживстандарт україни, 498.5kb.
• Додаток елементи теорії похибок наукове пізнання людиною оточуючого світу стало можливим, 263.8kb.
• Закон великих чисел. Збіжність майже напевно та посилений закон великих чисел. Збіжність, 32.18kb.
• Що вивчала статистика як сфера практичної діяльності у стародавні часи (Китай, Греція,, 519.67kb.
• Курс лекцій Розділ 2: тема 5 Тема Оборотні кошти підприємства, 193.19kb.
• Методические указания для курсового проекта по курсу, 337.36kb.
• Описание типа средств измерений для государственного реестра, 83.78kb.

1

ЗАГАЛЬНІ ПИТАННЯ ЕЛЕКТРИЧНИХ ВИМІРЮВАНЬ

Розділ 1 ФІЗИЧНІ ВЕЛИЧИНИ І ВИМІРЮВАННЯ

1.1. Основні поняття і визначення

Поняття фізичної величини і види величин. Об'єкти навколишнього матеріального світу — фізичні системи, їх стани і процеси —мають різноманітні .властивості. Якісно однакові властивості можуть відріз­нятися між собою кількісним вмістом, який далі будемо називати розміром. Звідси випливає визначення поняття фізичної величини (ГОСТ 16263—70).

Фізична величина — властивість, спільна в якісному відношенні для багатьох фізичних об'єктів (фізичних систем, їх станів {процесів, що в них відбуваються), але в кількісному відношенні індивідуальна для кожного об'єкта.

Приклади фізичних величин: довжина, маса, швидкість, прискорення, електричний опір, напруга, струм, магнітний потік, світловий потік та ін.

Розмір фізичної величини існує об'єктивно, незалежно від того, що ми про нього знаємо. Завдяки розміру фізична величина, будучи якісно однаковою властивістю багатьох об'єктів, у одного об'єкта може бути більша, однакова або менша, ніж у іншого.

Фізичні величини, які мають тільки розмір, називають­ся скалярними (довжина, площа, маса, температура), а ве­личини, які крім розміру мають і напрямок, називаються векторними (сила, швидкість, прискорення, напруженість електричного поля тощо).

Фізичні величини, як і об'єкти, яким вони притаманні, існують у часі і просторі. Тому загалом їх розміри, а у век­торних величин і напрямки, є функціями часу і координат простору. Якщо розміри скалярних або розміри і напрямки векторних величин не змінюються, то вони називаються сталими (незмінними), а якщо змінюються, то —змінними величинами. Можна розглядати сталість і змінність величин в часі і просторі, а також залежно від інших

Величини, всі можливі розміри яких (або розміри і на­прямки) при їх зміні в часі чи просторі (або в часі і просторі) на скінченному проміжку утворюють незліченну множину (континуум), називаються безперервними (континуальними) величинами. Якщо ця множина зліченна, то величини ди­скретні. Проте коли зміни фізичних величин, зумовлені дискретністю, незначні порівняно з їх розмірами, то вони сприймаються як безперервні.

Поняття одиниці фізичної величини і види значень величин. Розмір фізичної величини, який треба визначити, позначимо через X. Виберемо певний розмір х₀ цієї величини і порівняємо з ним розмір X, їх відношення Х/х₀ = М назвемо істинним числовим значен­ням величини.

Якщо X = х₀, то М = 1. Тому х₀—одиниця даної фі­зичної величини, а добуток Мх₀= X — істинне значення ве­личини, тотожне її розміру.

Розмір одиниці величини може бути вибраний довільно, але для порівняння результатів вимірювань в різних оди­ницях треба знати співвідношення між розмірами цих одиниць.

Усі попередні вирази теоретичні. Через неминучість похибок вимірювань не можна знайти істинного значення величини, і тому замість числа М знаходять наближене його значення N, яке називається числовим значенням величини, а замість істинного дістають значення величини х = Nx₀.

Значення фізичної величини, яке настільки близьке до істинного, що його можна використати замість істинного, називається дійсним:




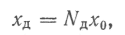
де N_Д — дійсне числове значення величини.

Детерміновані і випадкові вели­чини і процеси. Фізична величина, перебуваючи у причинно-наслідкових зв'язках з іншими величинами, є їх функцією, в тому числі функцією часу. Функція часу — це процес, тобто послідовна в часі зміна розміру величини, а стала величина — окремий випадок процесу.

Величина детермінована, якщо її значення можна зазда­легідь точно передбачити на підставі причинно-наслідко­вих зв'язків з іншими величинами. Коли ж значення вели­чини ніякому передбаченню не піддаються, то вона індетермінована. Проміжне місце займають випадкові величини, частина причинно-наслідкових зв'язків яких з іншими ве­личинами відома, а частина не відома. Тому випадкова величина має дві складові —детерміновану й індетерміновану. Апріорне ставлення суб'єкта (спостерігача) до певної конкретної фізичної величини (детермінованої, індетермі-нованої, випадкової) залежить від того, наскільки йому ві­домі її причинно-наслідкові зв'язки з іншими величинами і наскільки точно йому треба знати значення цієї величини.

Щодо вимірювань, теоретично всі величини можна трак­тувати як випадкові з різним співвідношенням між детермі­нованою й індетермінованою складовими. Практично, якщо детермінована складова велика, а індетермінована менша від допустимої похибки, з якою треба знайти значення даної величини, то ця величина трактується як детермінована. Якщо індетермінована складова велика, а детермінована менша від допустимої похибки, то, навпаки, величина трак­тується як індетермінована. Таким чином, чим менша до­пустима похибка визначення значення величини, тим більш треба враховувати ЇЇ характер — поділ на детерміновану та індетерміновану складові, тобто розглядати величину як випадкову.

На підставі викладеного видно, що вимірювана вели­чина і тим більше результат вимірювань, одержаний з по­хибкою, і самі похибки повинні трактуватися як випадкові величини. Зв'язок між можливими значеннями випадкової величини X і їх імовірностями описується її законом роз­поділу — функцією розподілу Р(х) або густиною розподілу імовірностей




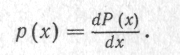
Подібно можна розглядати питання про детерміновані, індетерміновані та випадкові функції і процеси. Функція, яка для кожного значення аргументу (значень аргументів) набуває заздалегідь точно передбачуваних значень, є де­термінованою. Аналогічно визначається детермінований процес, як детермінована функція часу. Випадковою нази­вається функція, яка в кожному окремому досліді може на­бути певного конкретного вигляду, але заздалегідь невідо­мо, якого саме. Випадковим процесом називається випадкова функція часу, причому розрізняють безперервні випадкові процеси (функції безперервного часу) і дискретні випадкові процеси або випадкові послідовності — випадкові функції дискретного часу (дискретних моментів часу).

Поняття вимірювання і вимірю­вальної інформації. В літературі зустрічає­ться визначення поняття вимірювання як пізнавального процесу, який полягає у порівнянні шляхом фізичного екс­перименту даної величини з певним ЇЇ значенням, прийнятим за одиницю порівняння.

ГОСТ 16263—70 визначає поняття вимірювання як «зна­ходження значень фізичних величин дослідним шляхом за допомогою спеціальних технічних засобів». Там же даються визначення поняття вимірювальної інформації, яка трактує­ться як інформація про значення вимірюваних фізичних величин.

Значення вимірюваної величини дістають множенням її числового значення на розмір її одиниці, а числове зна­чення •— порівнянням розміру вимірюваної величини з роз­міром її одиниці. Якщо операцію порівняння неможливо або важко виконати безпосередньо, то вимірювану величину та її одиницю «перетворюють» на іншу величину, придатну для безпосереднього порівняння і одержання числового значення. В цьому полягає основна мета вимірювальних перетворень.

Вимірювальною інформацією є числові значення вимірю­ваних величин.

1.2. Класифікація вимірювань

Класифікаційні ознаки. Повної устале­ної і загальновизнаної класифікації вимірювань немає. Практично використовується певний варіант неповної кла­сифікації, яка базується на класифікаційних ознаках, що відповідають її призначенню.

Розглянемо класифікаційні ознаки, потрібні для пояс­нення термінів, які використовуються нижче у викладі матеріалу і за якими вимірювання поділяються на електрич­ні і неелектричні, аналогові і цифрові, однократні і багато­кратні, рівноточні і нерівноточні, прямі, непрямі, сумісні та сукупні.

Ознакою поділу вимірювань на електричні і неелектрич­ні є відповідно наявність або відсутність у вимірювальному колі перетворення сигналу на електричний.

Поділ вимірювань на аналогові і цифрові визначається видом вимірювальних приладів (аналогових чи цифрових), з допомогою яких здійснюються вимірювання.

Поділ вимірювань на одно- і багатократні визначається кількістю повторень вимірювань даної сталої величини.

Багатократні вимірювання (незмінної величини) поді­ляються.: на рівноточні і нерівноточні. Вимірювання рівно-точні, якщо вони виконуються в тих самих умовах, тими самими засобами і експериментатором. В інших випадках вимірювання нерівноточні.

Ознакою поділу вимірювань на прямі, непрямі, сукупні та сумісні є вид математичної залежності між вимірюваною величиною і результатом вимірювання, а також залежний від цього шлях знаходження результату. Цією класифіка­ційною ознакою визначаються види вимірювань, кожний з яких розглянемо окремо.

Прямі вимірювання. Прямим називається вимірювання, при якому значення вимірюваної величини знаходять безпосередньо з дослідних даних. Результат пря­мих вимірювань дістають порівнянням розміру вимірюваної величини з розміром, що відтворюється мірою, або у ви­гляді показів вимірювального приладу. Приклади: вимірю­вання довжини здопомогоюлінійки з поділками; вимірюван­ня струму амперметром, напруги вольтметром, потужності ватметром тощо.

Непрямі вимірювання. Непрямим називається вимірювання, при якому значення х вимірюваної
величини знаходять за результатами x_lt х_г, ..., х_п прямих
вимірювань інших величин, пов'язаних з х відомою явною
функціональною залежністю х = F(x_lt х_г х_п).

Н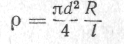априклад, питомий опір


матеріалу знаходять за результатами вимірювань опору R, довжини l і діаметра d круглого проводу; значення по­тужності постійного струму Р = UI або опору R — U/I знаходять за результатами прямих вимірювань напруги U вольтметром і струму I амперметром.

Непрямі вимірювання найбільш поширені і використо­вуються переважно у тих випадках, коли величину немож­ливо або складно виміряти прямо, або тоді, коли вони дають більш точний результат, ніж прямі вимірювання.

Сукупні вимірювання. Сукупними називають вимірювання n > 2 однойменних величин Х_ь Х₂, ... , Х_п, значення яких знаходять розв'язуванням системи рівнянь

я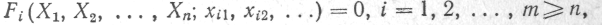ку дістають при прямих вимірюваннях різних комбіна­цій Хп, Хі2, . . . цих величин.

Наприклад, для визначення опорів R_lt R₂, R₃ резисто­рів, з'єднаних трикутником, вимірюють опори кожної пари вершин трикутника і дістають систему рівнянь (при m = п = 3)




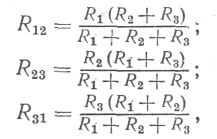
розв’язки якої дають значення опорів R_±, R₂ і R₃.

Сумісні вимірювання. Сумісними нази­вають вимірювання, при яких значення різнойменних ве­личин xl Х₂, .... Х_п, де п> 2, знаходять розв'язуванням системи рівнянь




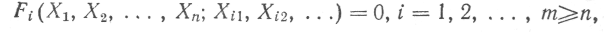
що пов’язують їх з величинами Хі1, Хі₂, ..., які піддають­ся прямим (або навіть непрямим) вимірюванням. Для під­вищення точності, як і при сукупних вимірюваннях, забез­печують умову т > п і систему рівнянь розв'язують мето­дом найменших квадратів.

Наприклад, індуктивність котушки




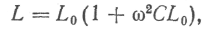
де L₀—індуктивність на частоті ω = 2f→ 0; С —міжвиткова ємність котушки.

Значення L₀ і С не можна знайти прямими або непря­мими вимірюваннями. Тому в найпростішому випадку, коли т = 2, вимірюють індуктивність котушки l1 == X_u на частоті w₁= Х₁₂ і L.₂= Х₂₁ при w₂= Х22 і складають систему рівнянь




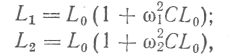
розв'язуючи яку, знаходять




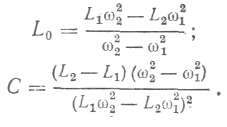
Іншим прикладом сумісних вимірювань може бути ви­значення температурних коефіцієнтів опору за результа­тами прямих вимірювань опору резистора і його темпера­тури.


1.3. Одиниці фізичних величин

Принципи побудови систем оди­ниць і види одиниць. Одиниця фізичної ве­личини — це фізична величина, розмір якої умовно дорів­нює 1.

У природі фізичні величини пов'язані між собою за­лежностями, що виражають фізичні закони. Сукупність величин, серед яких одні умовно прийняті як незалежні, а інші виражаються через них, називається системою ве­личин. Незалежні величини системи називаються основ­ними, а всі інші — похідними.

Наприклад, у запропонованій ще в 1832 р. К- Ф. Гауссом системі LM.T довжина l, маса m і час t — основні вели­чини, а площа S = l, швидкість v = dlldt, прискорення а = dv/dt і інші величини —похідні.

Одиниця основної величини називається основною, а по­хідної— похідною. Сукупність основних і похідних одиниць певної системи величин становить систему одиниць.

Вибір основних величин і розміру їх одиниць теоретич­но довільний, але він диктується певними вимогами прак­тики:

_а) кількість основних величин має бути невеликою;

б) за основні мають бути вибрані величини, одиниці
яких легко відтворити з високою точністю;

в) розміри основних одиниць мають бути такими, щоб
на практиці значення всіх величин системи не виражались
ні надто малими, ні надто великими числами;

г) похідні одиниці мають бути когерентними, тобто
входити в рівняння, що пов'язують їх з іншими одиницями
системи, з коефіцієнтом 1.

Одиниці системи, які не належать ні до основних, ні до похідних, називаються додатковими одиницями (радіан — рад, стерадіан —ср).

Одиниці, що не входять ні в одну із систем, називаються позасистемними одиницями (літр — л, калорія —кал., рентген — Р та ін.). Позасистемні одиниці, що визначають­ся із відношення двох значень величини, називаються логарифмічними, наприклад, непер —Нп, бел —Б, деци­бел — дБ.

У випадку відношення значень струму чи напруги




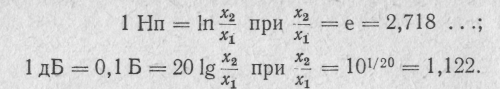
Якщо значення відношень струму чи напруги порівняно малі, то




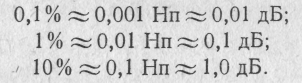
У випадку відношення значень потужності




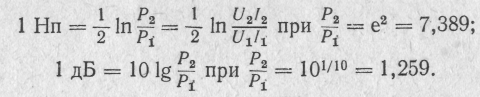
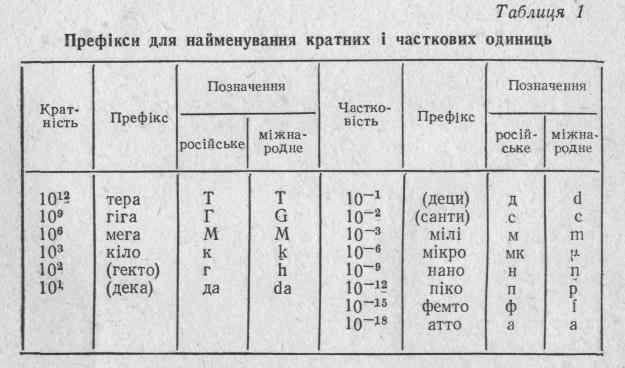
Одиниця, що в ціле число разів більша системної або по­засистемної одиниці, називається кратною. Наприклад, кілометр —1000 м, мегават —10 Вт, хвилина —60 с, гектолітр — 100 л. Одиниця, що в ціле число разів менша від системної або позасистемної одиниці, називається част­ковою. Наприклад, міліметр — 10³ м, мікросекунда —· 10⁶с, мілілітр — 10³л.

Префікси для найменування кратних і часткових оди­ниць наведені в табл. 1.

Види систем одиниць. Запропонована Гаус-сом система LMT була названа ним абсолютною. Основні одиниці цієї системи є одиницями величин, які відобра­жають найбільш загальні властивості матерії — масу і форму існування (простір і час).

Проте система LMT не є абсолютною у повному розу­мінні цього слова. В кінці минулого століття В. Томсон за­пропонував систему LT, тобто побудовану на двох основних величинах. Відомі також системи з однією основною вели­чиною, а також так звані натуральні системи одиниць, що ґрунтуються на універсальних фізичних сталих.





Теоретично, користуючись поняттям чотиривимірного евклідового простору, всі фізичні явища —теплові, елек­тричні, оптичні —можна звести до механічних і обійтися системою LMT, але це не завжди доцільно. У зв'язку з цим 1901 р. італійський фізик Джорджі запропонував для від­повідних розділів фізики ввести четверту основну одиницю —теплову, електричну або оптичну.

Залежно від форми запису рівнянь електромагнітного поля, які використовуються для утворення похідних оди­ниць, системи одиниць електричних і магнітних величин можуть бути нераціоналізовані або раціоналізовані. Раціо­налізація цих рівнянь запропонована в кінці минулого століття англійським фізиком Хевісайдом і полягає в тому, що множник 4л залишається тільки в рівняннях, пов'яза­них із сферичною симетрією (закони Гауса і Кулона), а в більшості інших рівнянь відсутній. Тому при однакових розмірах основних одиниць розміри окремих похідних оди­ниць нераціоналізованої і раціоналізованої систем різні.

Наприклад, напруженість магнітного поля у кільце­вому осерді завдовжки l при проходженні струму I по обмотці з числом витків w буде: в нераціоналізованій системі H = 4Iw/l, а в раціоналізованій — Η = Iw/l. Отже, одиниця напруженості магнітного поля в раціона­лізованій системі у 4л разів більша, ніж у нераціона­лізованій.

Розмірності. Розмірністю основної величини є саме її позначення, наприклад, L, Μ, Τ, І, а розмірністю похідної величини —вираз, що описує її зв'язок з основ­ними величинами системи, наприклад,




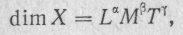
де α, β, γ —показники розмірності.

Величина, в розмірності якої хоча б один показник роз­мірності відмінний від нуля, називається розмірною вели­чиною, а величина, в розмірності якої всі показники роз­мірності дорівнюють нулю,— безрозмірною. Величина, яка є безрозмірною в одній системі одиниць, може бути розмір­ною в іншій системі. В даній системі одиниць розмірність кожної величини однозначна, але є різні за природою вели­чини, які мають однакову розмірність.

Поняття розмірності дає можливість контролювати пра­вильність математичних операцій над величинами. На до­вільній стадії виконання цих операцій права і ліва сторони рівності повинні мати однакові розмірності. Методом пере­вірки розмірностей контролюють правильність і відповід­ність математичних виразів їх фізичній суті.

Міжнародна система одиниць (СІ). Одинадцятою Генеральною конференцією по мірах і вагах в 1960 р. прийнято Міжнародну систему одиниць (Система Інтернаціональна, або СІ), основні одиниці якої метр, кіло­грам, секунда, ампер, кельвін, кандела, моль, а додаткові — радіан та стерадіан.

Метр—довжина, що дорівнює 1650763,73 довжин хвиль у вакуумі випромінювання, яке відповідає переходові між рівнями 2р10

і 5d₅ атома криптону-86.

Кілограм—одиниця маси—дорівнює масі міжнарод­ного прототипу кілограма.

Секунда —9 192 631 770 періодів випромінювання, яке відповідає переходу між двома надтонкими рівнями основ­ного стану атома цезію-133.

Ампер —сила незмінного струму, який, проходячи по двох паралельних прямолінійних провідниках нескінченної довжини і дуже малого колового перерізу, розміщених на відстані 1 м один від одного у вакуумі, викликав би між цими провідниками силу, що дорівнює 2 · 10 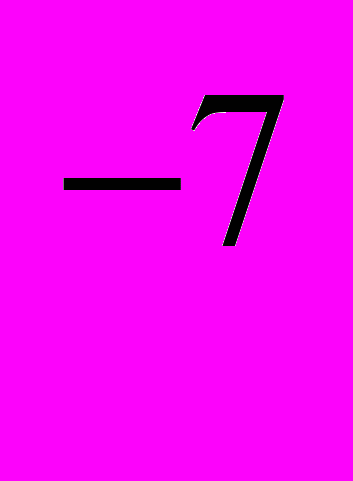Η на кожний метр довжини.

Кельвін—одиниця термодинамічної температури — 1/273,16 частина термодинамічної температури потрійної точки води.

Кандела—сила світла, що випромінюється з площі 1/600 000 м² перерізу повного випромінювача в перпенди­кулярному до цього перерізу напрямку, при температурі випромінювача, яка дорівнює температурі тверднення пла­тини при тиску 101 325 Па.

Моль — кількість речовини, яка містить стільки ж структурних елементів (атомів, молекул або інших частинок), скільки міститься атомів у вуглеці-12 масою 0,012 кг.

Радіан — кут між двома радіусами кола, довжина дуги між якими дорівнює радіусу.

Стерадіан —тілесний кут з вершиною у центрі сфери, який вирізає на поверхні сфери площу, що дорівнює площі квадрата, довжина сторони якого дорівнює радіусу сфери.

Міжнародна система одиниць — практична, когерентна, раціоналізована.