Решение, если мы не проводим над ней дальнейших процедур калибровочного характера

Вид материала

Решение

Содержание 1. Градиентная (калибровочная) инвариантность A и  - старые электромагнитные потенциалы; A 2. Безинерциальные заряды и токи 3. Уравнения квазистатической электродинамики 4. Законы сохранения для волновой электродинамики А и плотность тока безинерциальных зарядов j Таблица 1. Энергетические компоненты волновых полей 4. Законы сохранения для квазистатической электродинамики 5. Предельный переход 6. О причинности

Подобный материал:

• Методика определений акцентуаций характера К. Леонгарда, 171.17kb.
• Уроков литературы по теме: «Условия и факторы формирования характера и нравственных, 50.05kb.
• I I. Действия над многочленами. III. Комплексные числа >IV. Разложение многочленов, 201.14kb.
• А. Л. Городенцев 1 курс Лемма Барта : если ранг коммутатора двух линейных операторов, 77.76kb.
• Информация на республиканское совещание по Феодосийскому «Разрешительному центру», 129.47kb.
• Доклад министра труда и социального развития, 167.74kb.
• Доклад на Втором съезде работников, 167.31kb.
• Святое может признать только святой, 5768.83kb.
• Победа над болью – 2, 1932.81kb.
• «римский нос», 16.97kb.

А хорошо ли мы знаем и понимаем электродинамику?

Часть 2.Электродинамика против теории относительности А.Эйнштейна.

Введение

Процедура поиска других решений, которые мы назвали параллельными решениями волнового уравнения, непосредственно связана с введением в новое решение дополнительной функции, которая обладает иными, отличными от волновых, пространственными и временными свойствами. Эту процедуру мы будем называть математической калибровкой волнового уравнения. Она имеет следующие особенности:

Каждая математическая калибровка имеет единственное решение, если мы не проводим над ней дальнейших процедур калибровочного характера.

Решения, соответствующие различным математическим калибровкам исходного волнового уравнения, отличаются друг от друга, т.е. не являются, вообще говоря, взаимозависимыми. Калибровочная инвариантность решений, т.е. независимость решения от выбора калибровки, в общем случае не имеет места.

Это очень важный и принципиальный результат, который требует переоценки многих положений физических теорий, опирающихся на мнение о градиентной инвариантности. Градиентная (калибровочная) инвариантность уже превратилось в предрассудок или догму. Ниже мы рассмотрим этот вопрос и некоторые другие, непосредственно относящиеся к проблемам специальной теории относительности.

1. Градиентная (калибровочная) инвариантность

Считается, что кулоновская калибровка и калибровка Лоренца равноправны (эквивалентны). Это заблуждение с одной стороны подпитывалось теоремой о существовании и единственности уравнений Максвелла (решения уравнений электродинамики не зависят от выбора калибровки), с другой – доказательством, так называемой, градиентной инвариантности.

Теперь мы покажем, что, как и первое, последнее заключение неверно. Запишем уравнения Максвелла в кулоновской калибровке. Для удобства мы будем помечать поля запаздывающих потенциалов индексом «w» (wave), а мгновенно действующие потенциалы индексом «ins» (instantaneous). Очевидно, что потенциал А в этой калибровке является запаздывающим (уравнение для векторного потенциала), а скалярный потенциал  - мгновенно действующий.

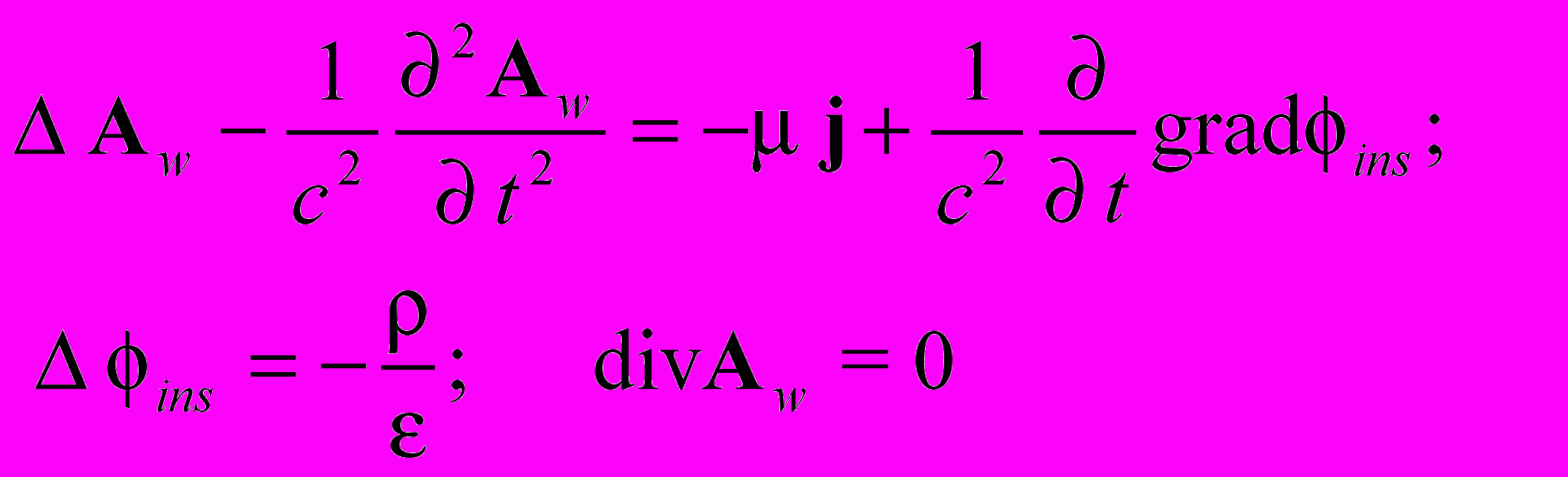(1.1)

Утверждается также, что мгновенно действующее электрическое поле скалярного потенциала Е₁ = - grad_ins компенсируется соответствующим компонентом поля векторного потенциала Е₂ = 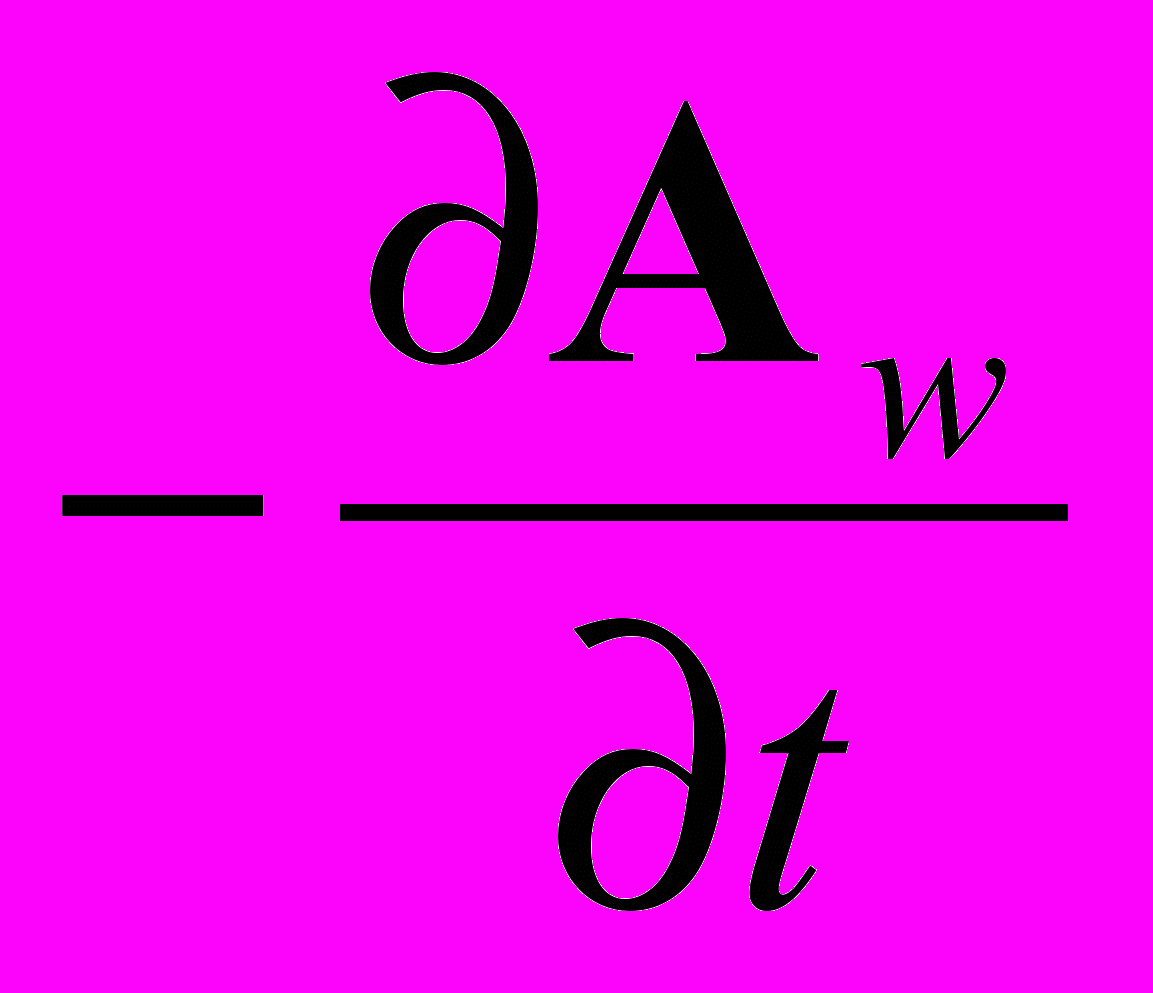во всем свободном пространстве. Иными словами, мгновенно действующая суммарная составляющая электрического поля оказывается равной нулю.

Чтобы показать ошибочность подобного заключения, мы преобразуем векторное уравнение, используя уравнение непрерывности для скалярного потенциала _ins (см. [1])

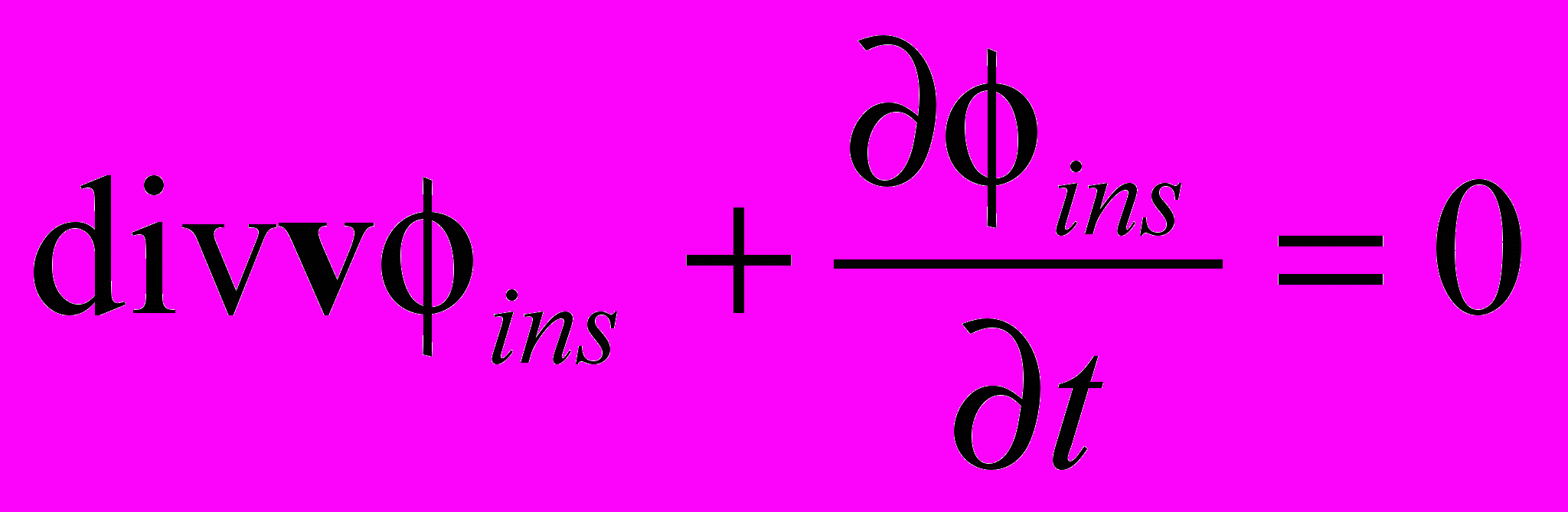(1.2)

Для простоты будем считать вектор скорости v заряда постоянным.

Преобразуем теперь правую часть уравнения (1.1) 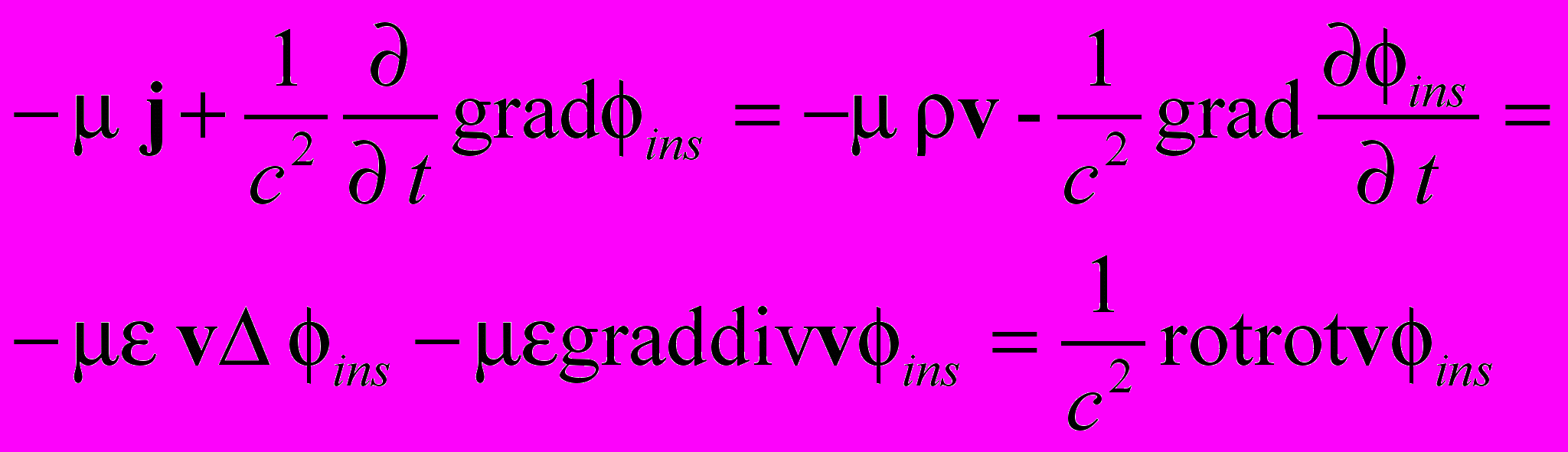(1.3)

Компенсация электрического поля - grad_ins частью вихревого поля 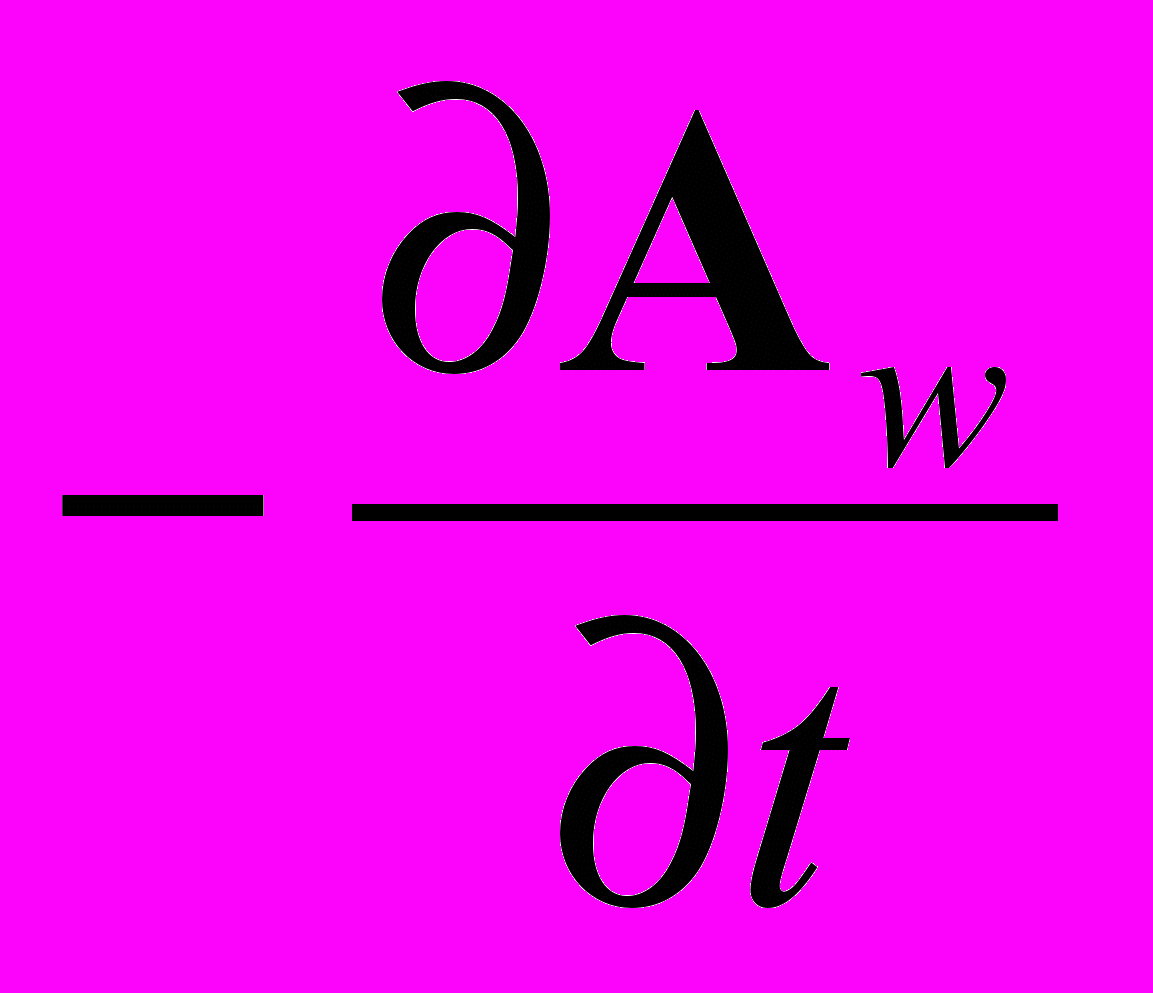невозможна по следующим причинам.

1. Во-первых, правая часть уравнения для векторного потенциала пропорциональна v/c. В частности, когда v/c очень мало или стремится к нулю, поле 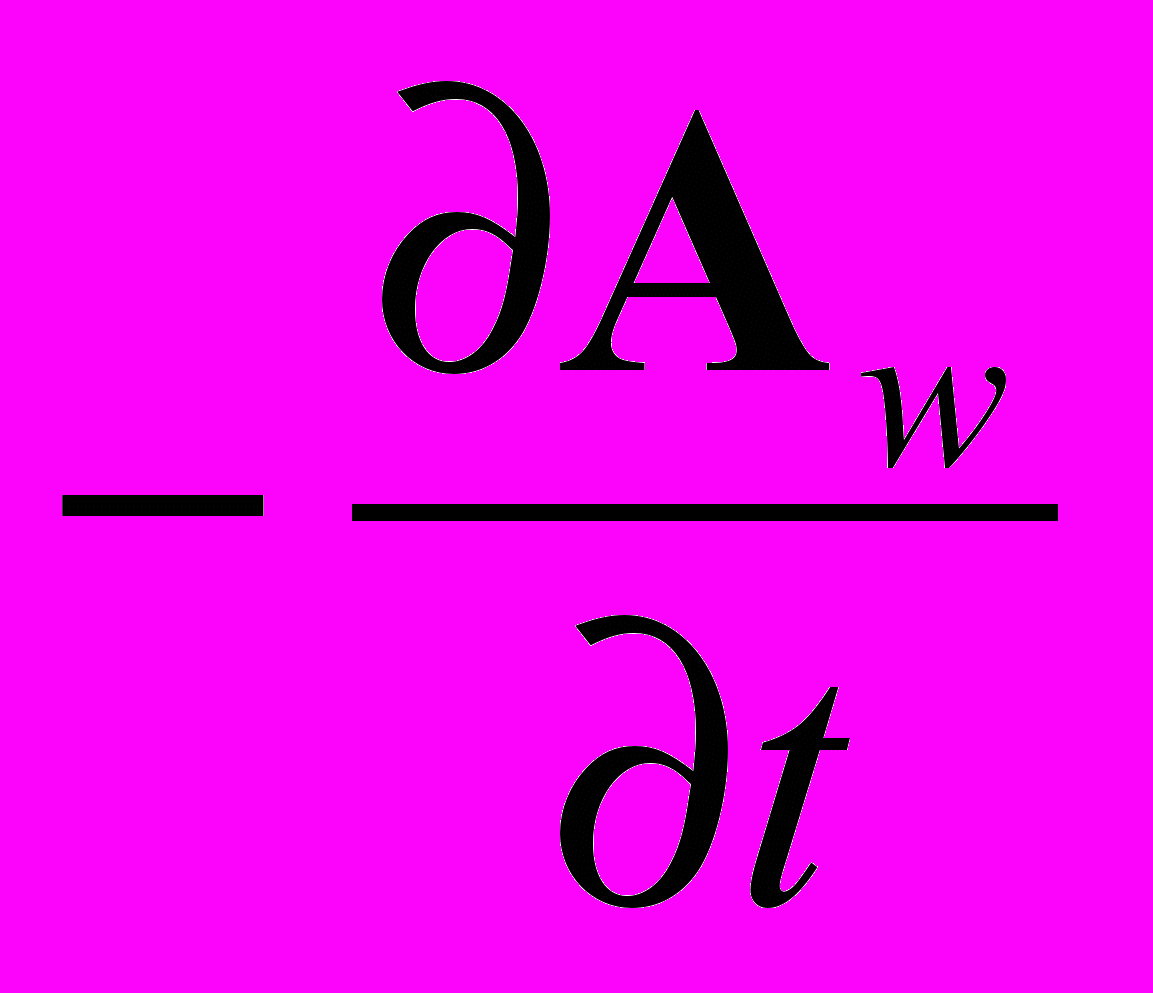тоже стремится к нулю и не может компенсировать - grad_ins во всем свободном пространстве.
   
2. Во вторых, источник поля векторного потенциала соленоидальный (правая часть (1.3)). Он может создавать только соленоидальные векторные поля векторного потенциала A. Создать компенсирующее поле полярного вектора, используя только соленоидальный, в общем случае невозможно.
   

Однако утверждается, что компенсация безвихревого поля полем векторного потенциала прямо следует из градиентной инвариантности, связывающей кулоновскую калибровку с калибровкой Лоренца. Рассмотрим теперь этот вопрос более подробно.

Хорошо известно, что электрическое поле E и магнитное поле H сохраняются при следующем преобразовании.

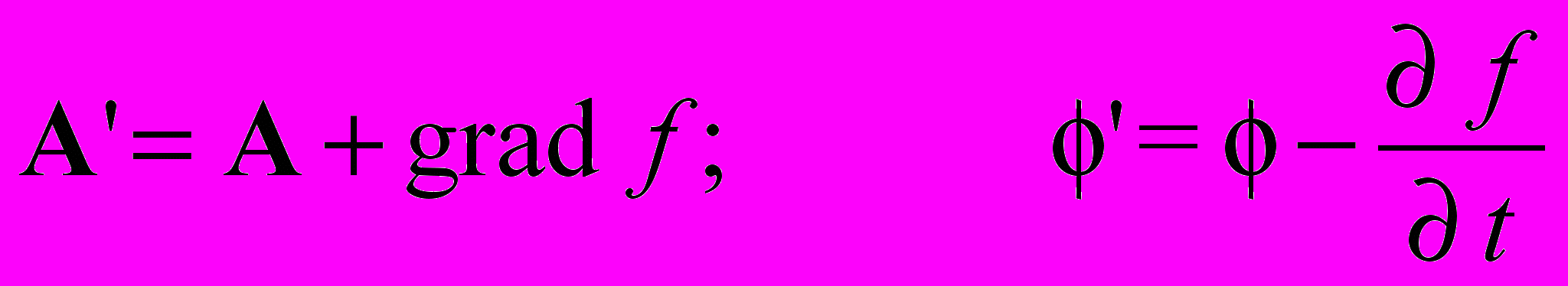(1.4)

где: A и  - старые электромагнитные потенциалы; A' и ' – новые электромагнитные потенциалы; f есть некоторая функция (градиентный или калибровочный потенциал), которая удовлетворяет однородному волновому уравнению.

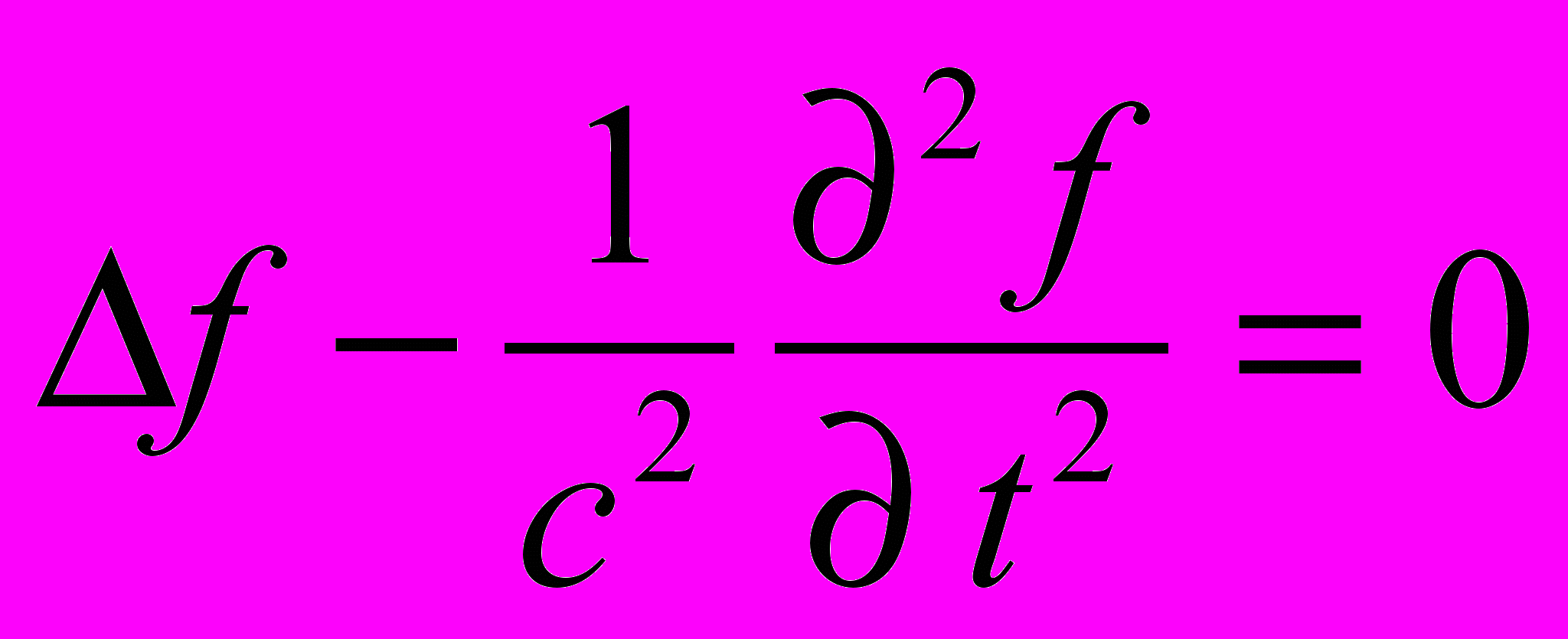(1.5)

Очевидно, в (1.5) потенциал f не является мгновенно действующим.

Запишем уравнения Максвелла в калибровке Лоренца и будем, как условились ранее, помечать индексами запаздывающие и мгновенно действующие потенциалы.

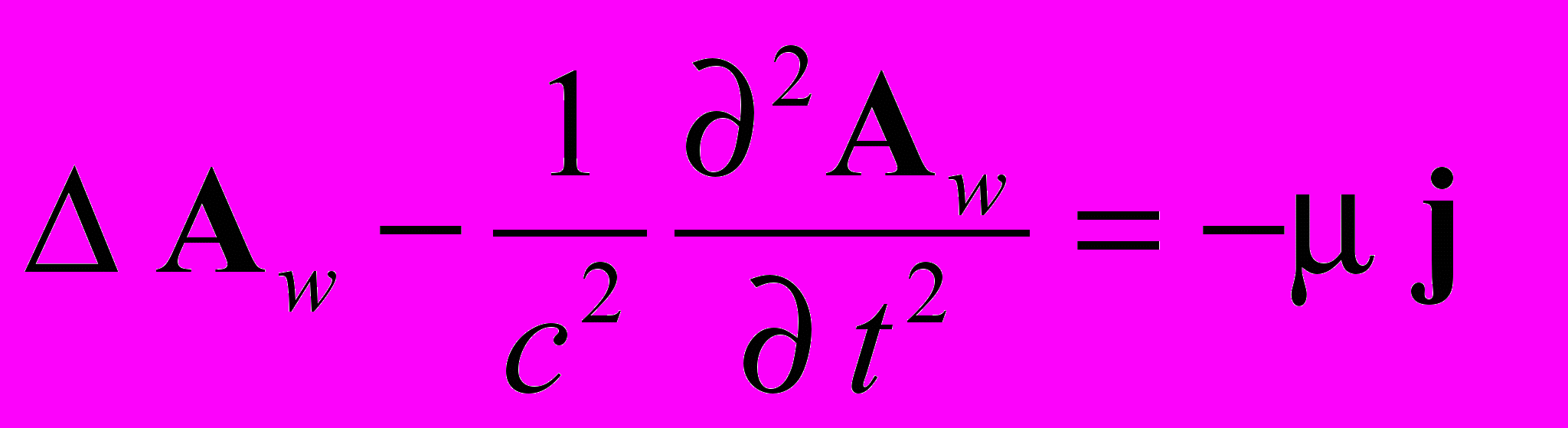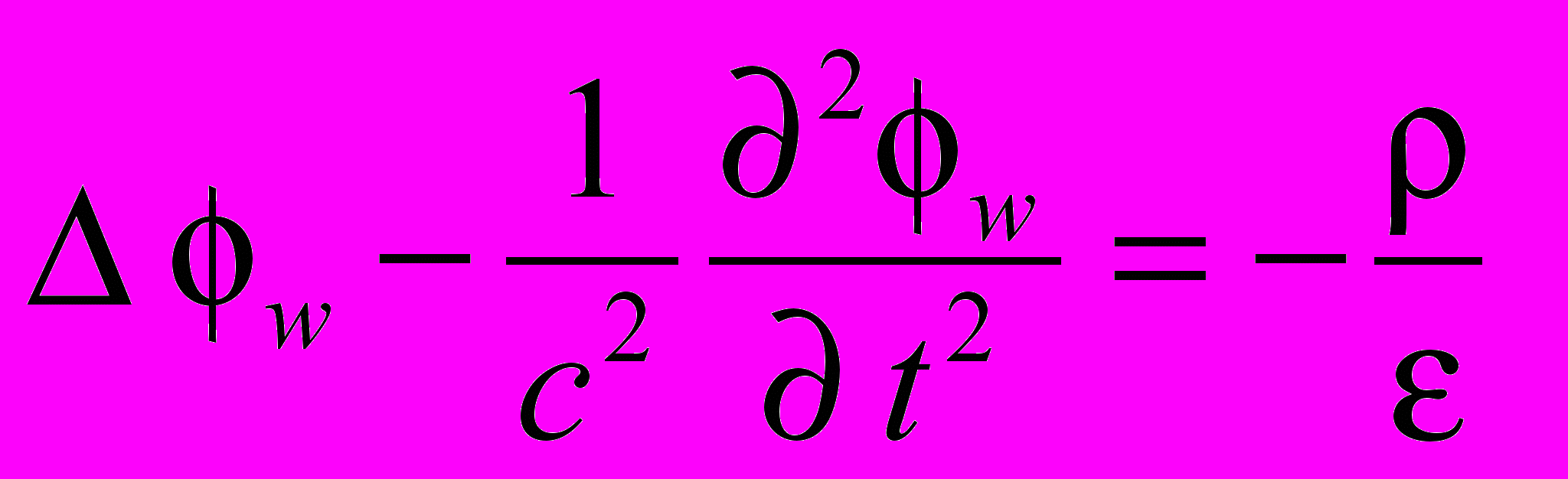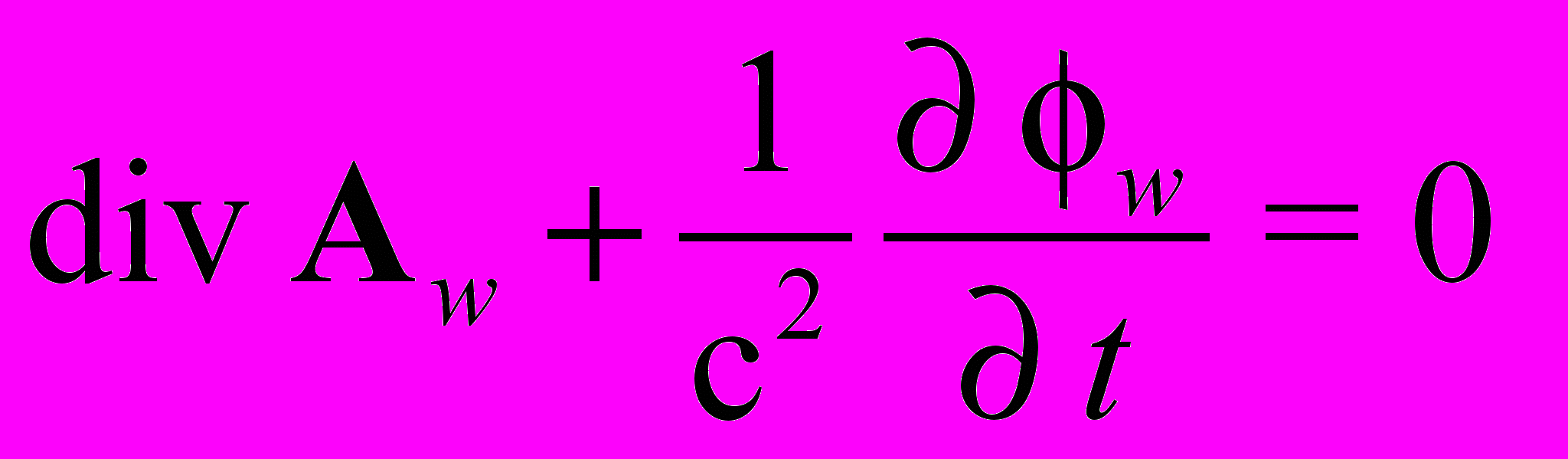; ; (1.6)

Чтобы получить из этих уравнений Максвелла в калибровке Лоренца уравнения в кулоновской калибровке на функцию f накладывается условие: 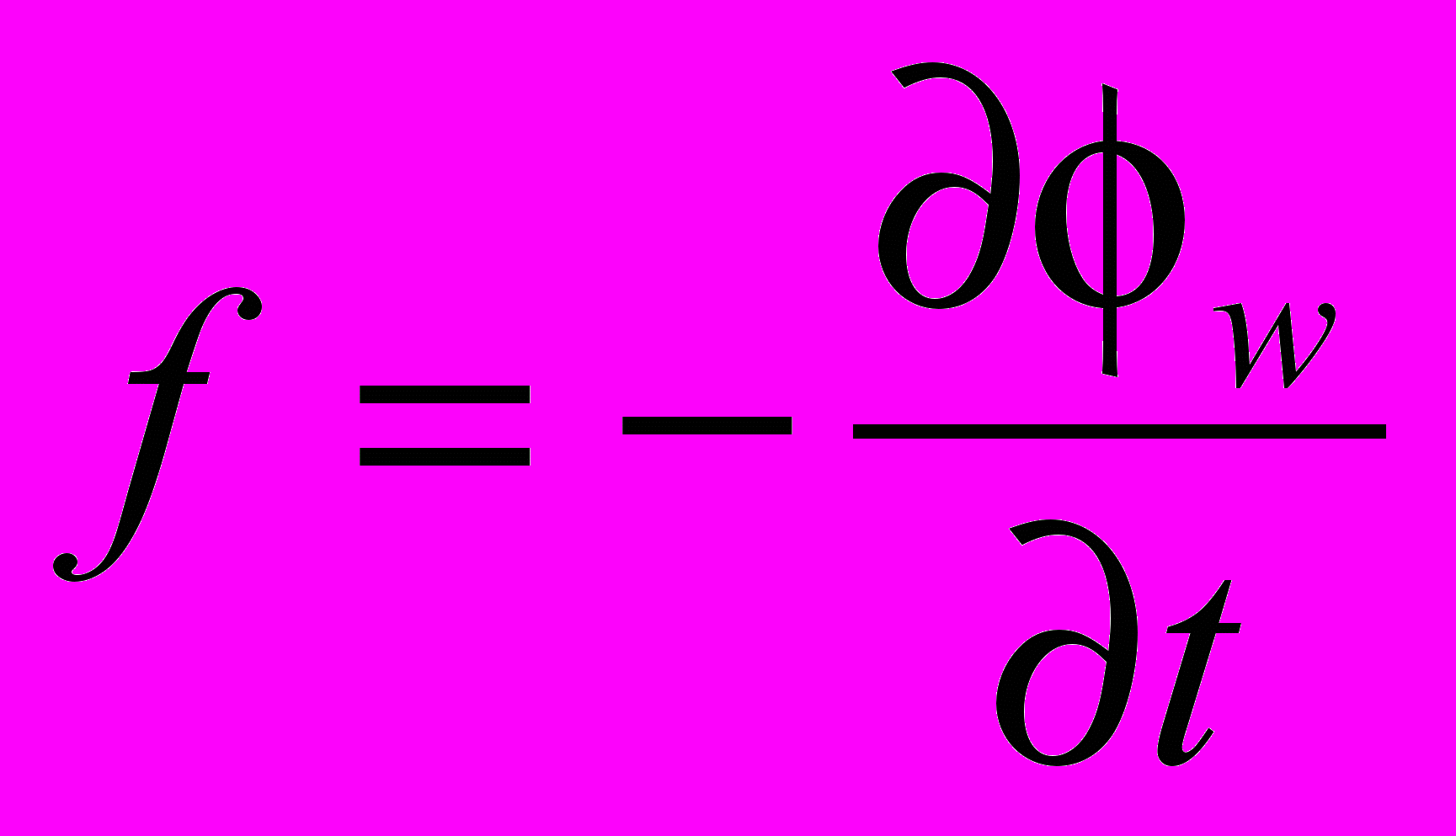(1.7).

Используя это условие и выражение (1.4), выразим в выражении (1.6) потенциалы A и  через A' и '. Мы получаем:

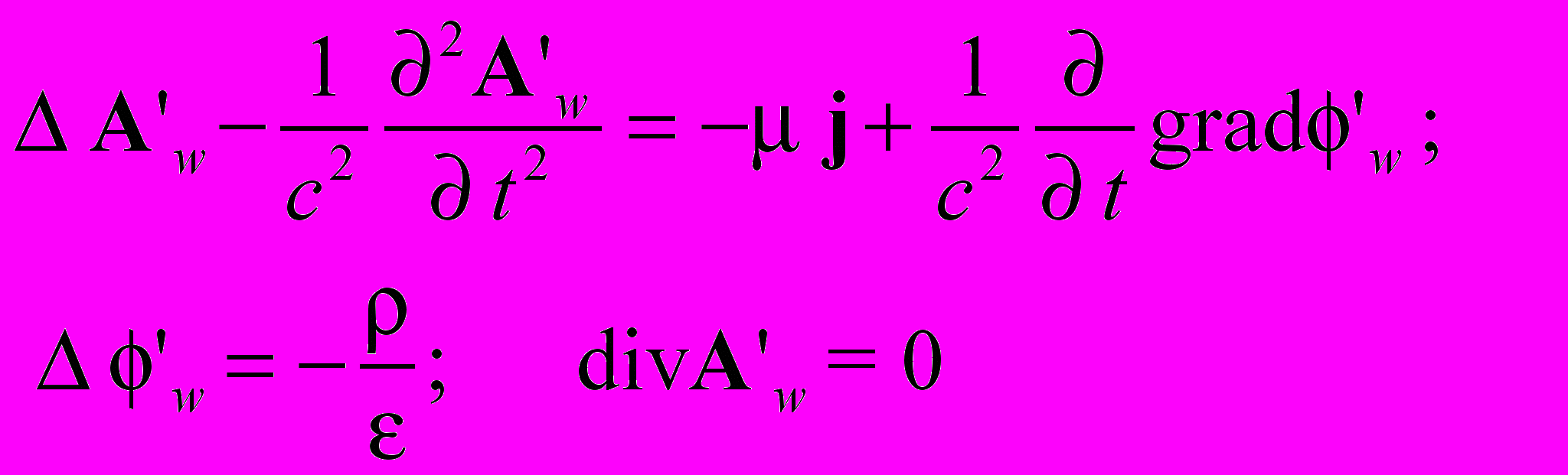(1.8)

Кажется, что мы действительно имеем дело с кулоновской калибровкой. Однако выражение для скалярного потенциала в (1.8) и соответствующее выражение в (1.1), находятся в противоречии. Потенциал ’_w в выражении (1.8) обязан быть запаздывающим, а в уравнении (1.1) ’_ins - мгновенно действующий.

Рассмотрим этот аспект. Условие (1.5), наложенное на f (см. (1.7)), приводит к следующему соотношению:

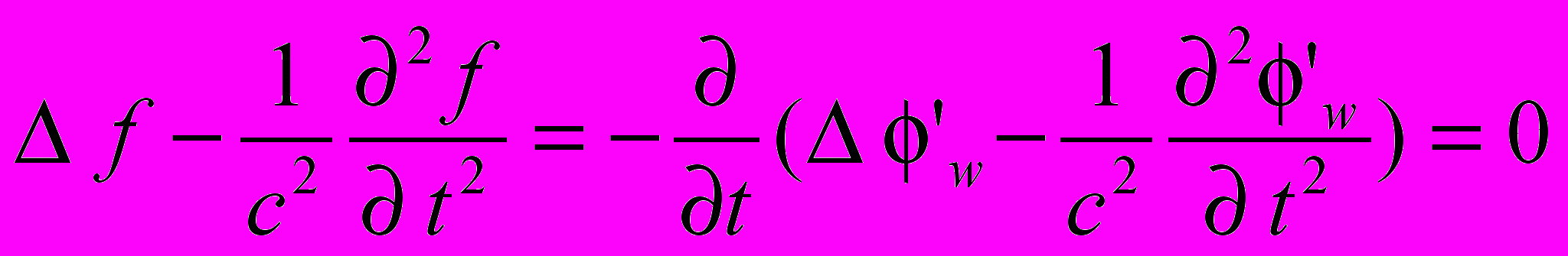(1.9)

Из (1.9) следует, что

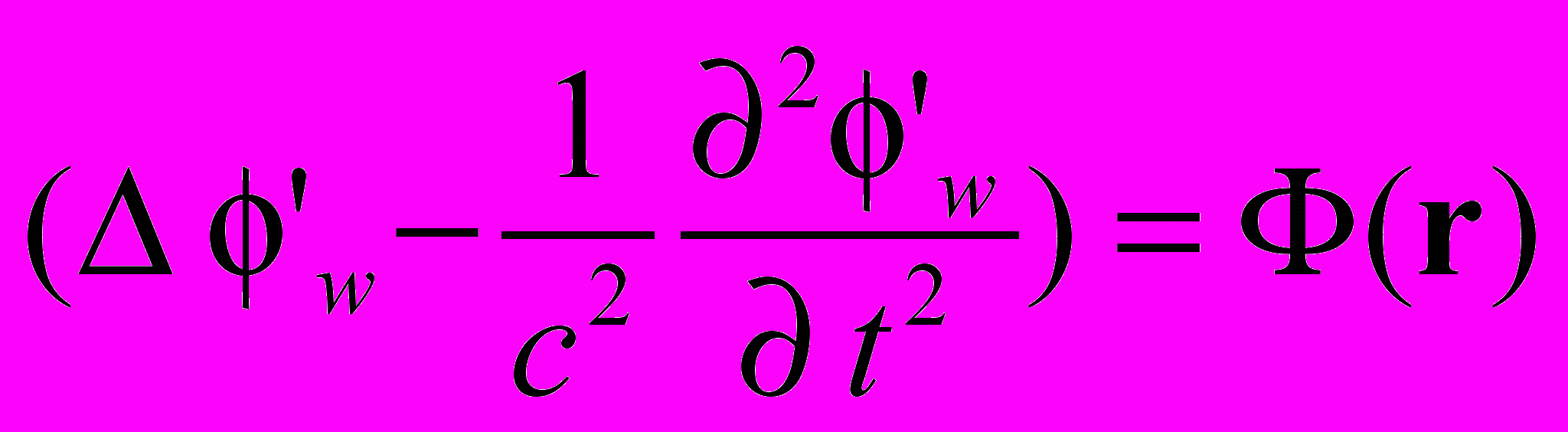(1.10)

где функция  не должна зависеть от времени.

Этого требует математика. Из физики явлений следует, что соотношение (1.10) не должно зависеть от выбора инерциальной системы отсчета (v постоянна). Иными словами, функция (r-vt) не должна зависеть от времени при любых скоростях v.

Вернемся к (1.9) и (1.10) и запишем производную по времени 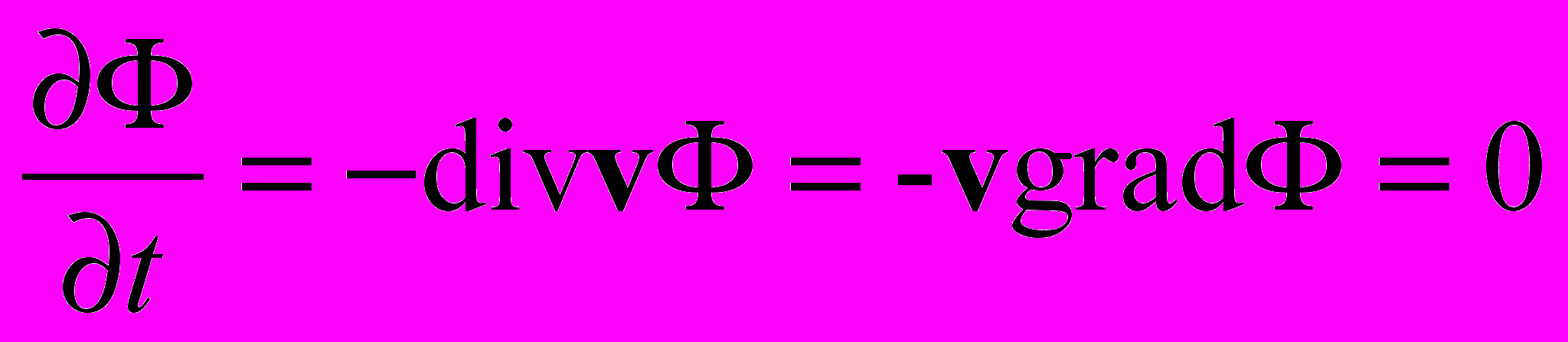. Поскольку v произвольна, grad = 0. Отсюда вытекает, что функция  должна быть константой. Подобно, тому, как в электростатике потенциал определен с точностью до произвольной постоянной, правая часть (1.10) также определена до аналогичной постоянной. Мы ее можем положить равной нулю, т.к. ей нельзя приписать какой-либо физический смысл.

Итак, два выражения (индексы мы опускаем)

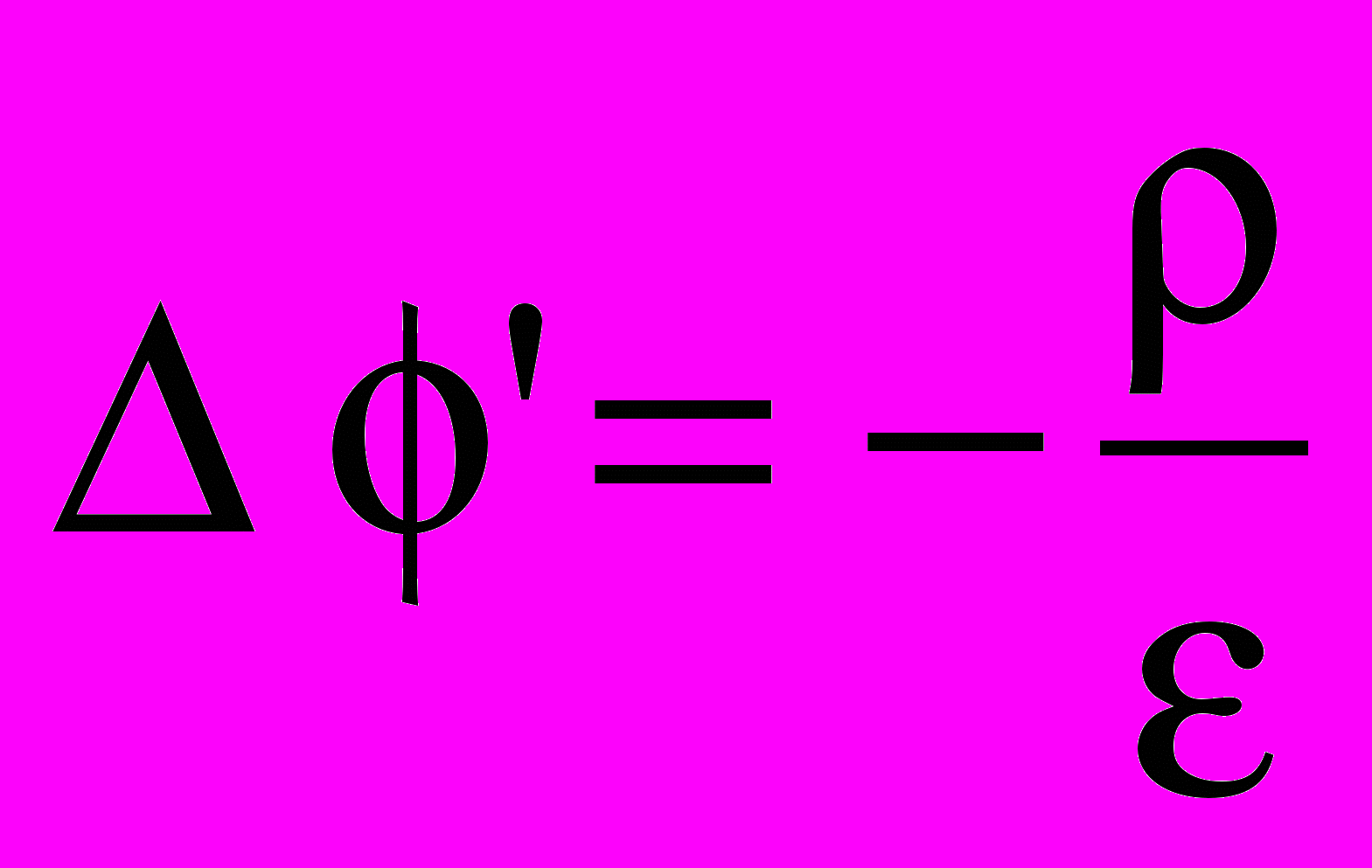и 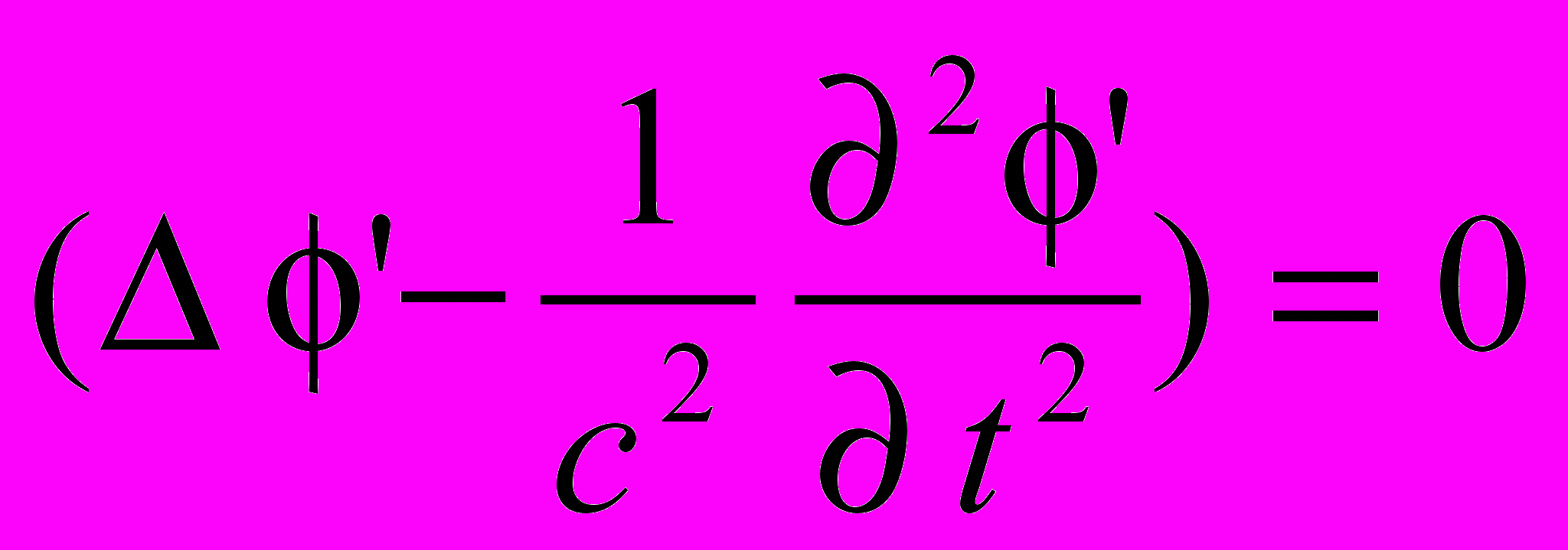(1.11)

являются в общем случае несовместными, а кулоновская калибровка и калибровка Лоренца различны.

2. Безинерциальные заряды и токи

Результат, полученный выше, имеет важное значение для квантовой электродинамики. Что делать: постулировать ли новые уравнения электродинамики (ввести новые гипотезы) или же попытаться найти условие, при котором эти калибровки эквивалентны и, тем самым, сохранить многие важные соотношения, полученные в квантовой электродинамике?

Условия совместности двух уравнений кажутся на первый взгляд невыполнимыми. С одной стороны, потенциал должен быть запаздывающим, с другой – мгновенно действующим.

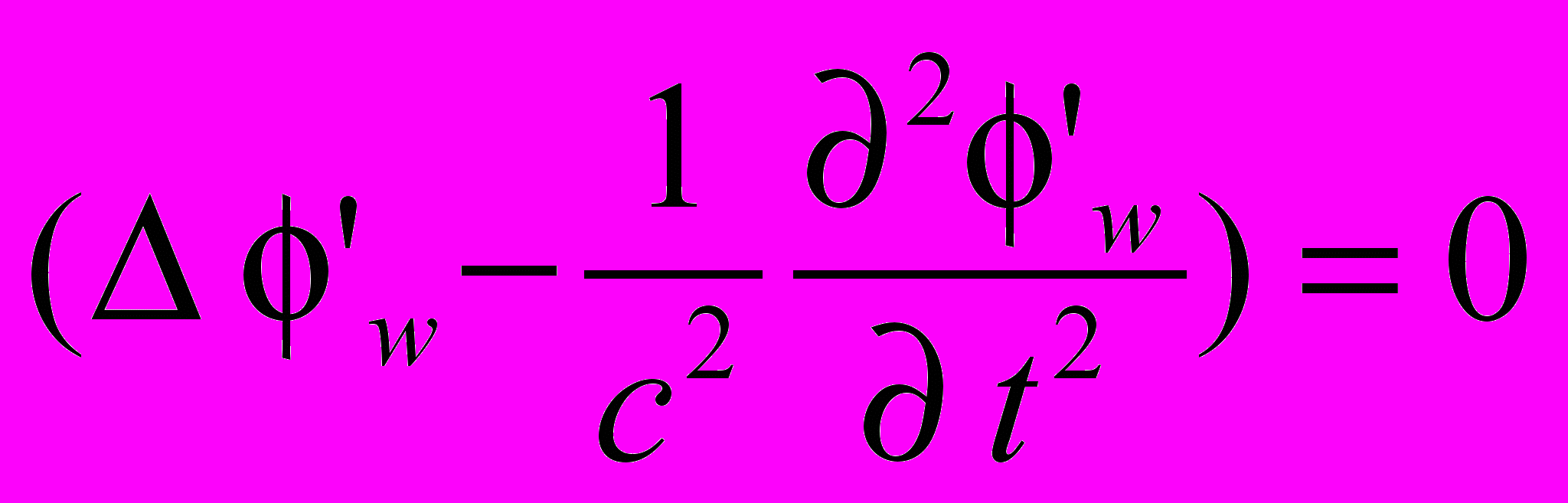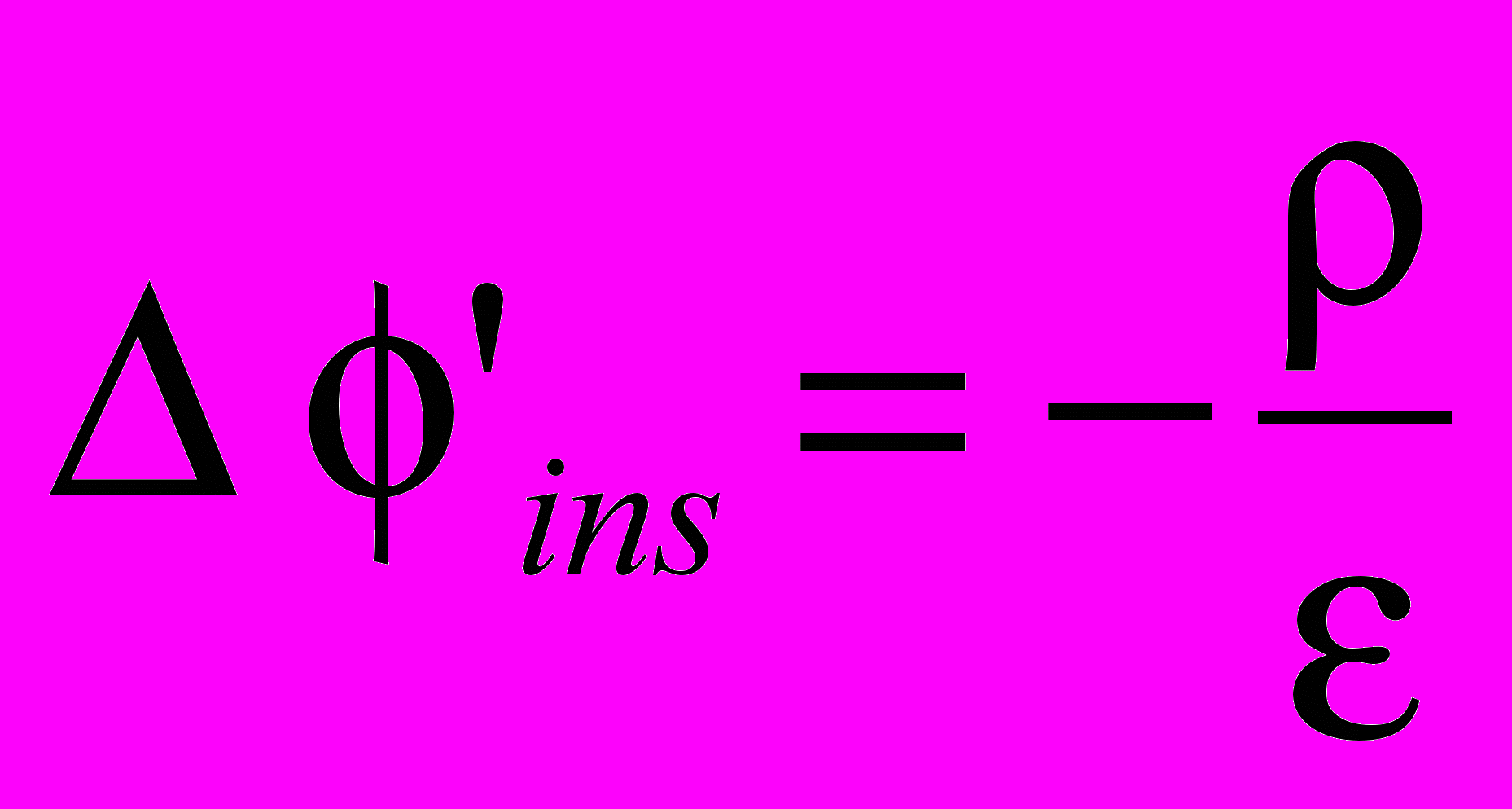и (2.1)

Однако выход все же имеется. Действительно, если предположить, что плотность заряда  удовлетворяет однородному волновому уравнению

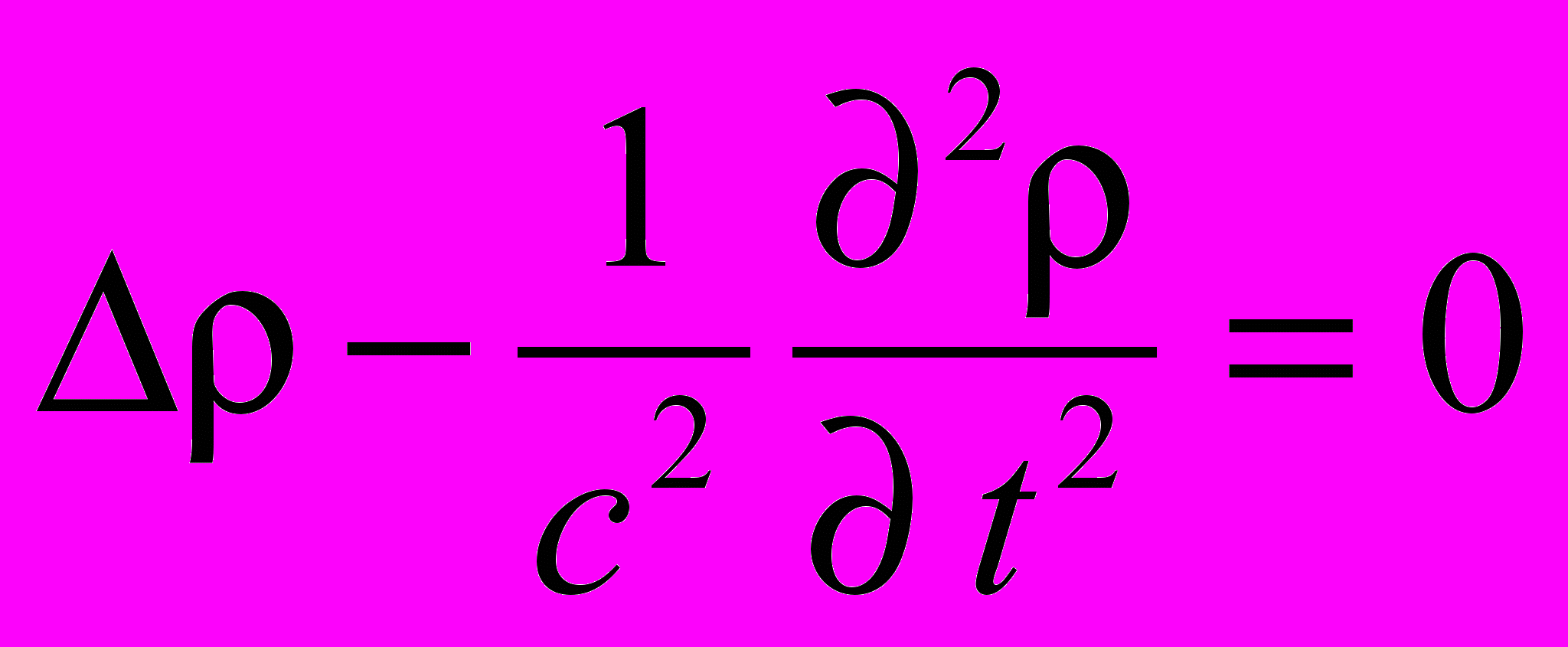(2.2)

тогда потенциал в (2.1) (второе уравнение) автоматически становится «запаздывающим».

Действительно, действуя на второе уравнение (2.1) оператором Даламбера, получим



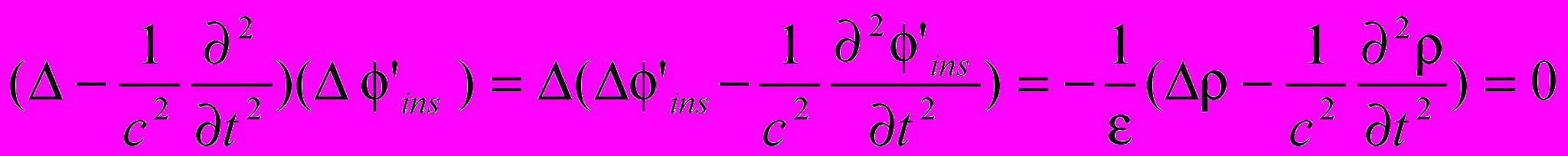
Коль скоро плотность заряда удовлетворяет волновому уравнению (такие заряды всегда движутся со скоростью света!) инерциальная масса (масса покоя) таких зарядов должна быть равна нулю. Таким образом, мы приходим к заключению, что помимо заряженных частиц (электронов, протонов и др.) должны существовать так называемые «безинерциальные» заряды [2].

Соответственно этому должны появиться и «безинерциальные» токи 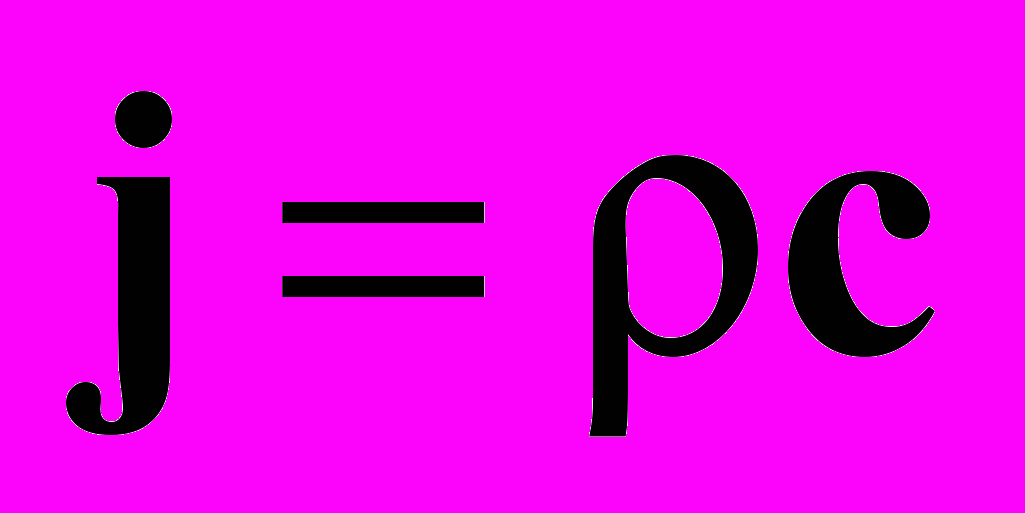(2.3)

Такова цена, заплаченная за эквивалентность кулоновской калибровки и калибровки Лоренца [2]. Запишем уравнения Максвелла для этих безинерциальных зарядов и токов.

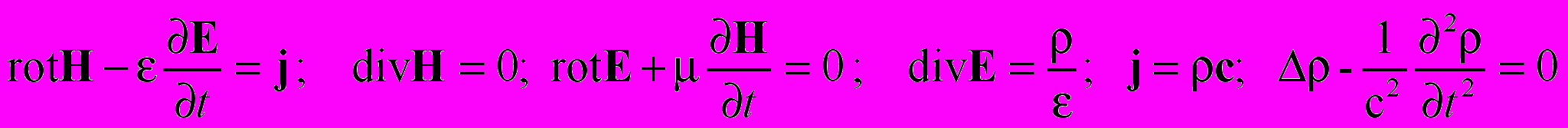(2.3)

Итак, мы записали уравнения «волновой» электродинамики [1]. Но есть ли подтверждение гипотезе о существовании безинерциальных зарядов? Да.

1. 
   Во-первых, вся теория антенно-фидерных устройств свидетельствует об этом. Просмотрите соответствующие учебники, и вы увидите, что при прохождении электромагнитной волны в волноводах, коаксиальных и полосковых линиях возникают поверхностные заряды и токи, которые могут распространяться с фазовой скоростью, превышающей скорость света [2]. Инерциальным электронам такая задача «не под силу». Таким образом, новый подход не только не затрагивает хорошо разработанную и многократно экспериментально подтвержденную теорию антенно-фидерных систем, но дает обоснование и объяснение поверхностным токам.
   
2. Во вторых, Эксперименты Авраменко, на наш взгляд, также служат подтверждением существования безинерциальных токов и зарядов в проводниках даже на очень низких частотах [2].
   
   Как видно из уравнений (2.5), они вполне вписываются в преобразование Лоренца или родственные ему преобразования.
   
   Замечание. Уже с самого своего создания Специальная теория относительности выдвинула неограниченные претензии. Преобразование Лоренца и постулат о существовании «предельной скорости распространения взаимодействий» были объявлены обязательными для всех без исключения физических процессов (если можно так выразиться: «для всех времен и народов»). В физике появилось жесткое требование к физическим уравнениям: они должны быть обязательно «релятивистски ковариантными».
   
   Теория относительности, по сути, превратилась в абсолютную истину.
   
   Однако с материалистической точки зрения подобные претензии не могут быть обоснованными. В физике нет абсолютных истин. Любая физическая теория всегда имеет границы применимости, за которыми она теряет свою объективность и превращается в заблуждение. Такие границы должны существовать и у преобразования Лоренца (если оно правильно отражает объективную реальность). Такие границы должна иметь Специальная теория относительности (как одна из многих возможных интерпретаций сущности преобразования Лоренца). Уже один только этот признак заставляет усомниться во «всеобщей применимости» теории А.Эйнштейна. А таких признаков мы встретим много.
   

3. Уравнения квазистатической электродинамики

А как быть с инерциальными зарядами?

Для них должны существовать свои уравнения. Это обусловлено тем, что свойства полей таких зарядов существенно отличаются от свойств полей электромагнитных волн. Электромагнитная волна после излучения распространяется и ее «судьба» уже не зависит от «судьбы» источника, породившего эту волну. Волна может дифрагировать, отражаться от объектов и т.д. И всегда вместе с электрическим полем неизменно «путешествует» магнитное поле. Напротив, поле заряда всегда жестко связано с зарядом. Если заряд покоится, то он всегда имеет одно и то же электрическое поле (магнитное равно нулю!). Это поле не зависит от того, что происходило с зарядом ранее, и что произойдет с ним потом. Покоящийся заряд имеет свое «стандартное» электрическое поле.

Запишем теперь уравнения для полей инерциальных зарядов. Это уравнения «квазистатической» электродинамики [4].

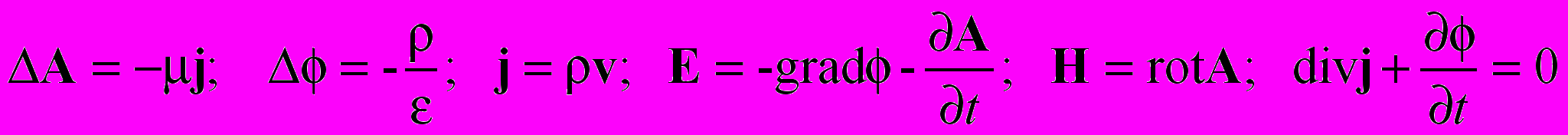(2.4)

Поля и потенциалы инерциальных зарядов всегда мгновенно действующие. В проводниках такие заряды могут существовать одновременно с безинерциальными зарядами. Заметим также, что ускоренный инерциальный заряд при данном подходе не может излучать электромагнитную волну, будучи ускоренным. Он может тогда и только тогда переизлучать или рассеивать электромагнитную волну, когда он взаимодействует с этой волной. Другие источники, вызывающие ускорение инерциального заряда, не приводят к появлению электромагнитной волны.

Замечание. Постулат о ковариантности уравнений квазистатической электродинамики здесь не имеет ни силы, ни места. Квазистатические проблемы находятся вне рамок преобразования Лоренца. Они подвластны только преобразованиям Галилея.

4. Законы сохранения для волновой электродинамики

Теперь рассмотрим некоторые энергетические соотношения, характерные для волновой электродинамики.

Запишем уравнения Максвелла (2.3) в калибровке Лоренца. Но сделаем одно преобразование. Мы представим векторный потенциал А и плотность тока безинерциальных зарядов j в виде суммы соленоидальной и безвихревой частей [1].

A = A₁ + A₂; j = j₁ + j₂ (3.1)

где: div A₁ = 0; div j₁ = 0; rot A₂ = 0; rot j₂ = 0.

Это не новая калибровка, а новое представление калибровки Лоренца. С учетом выражения (3.1) калибровка Лоренца принимает следующий вид:

;

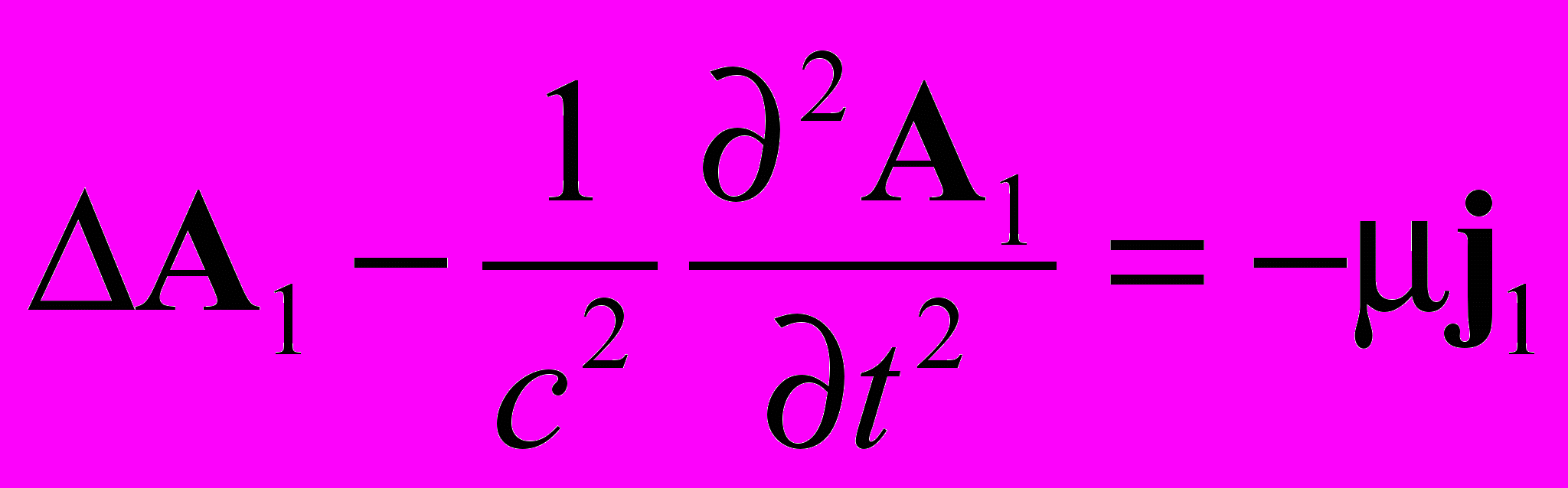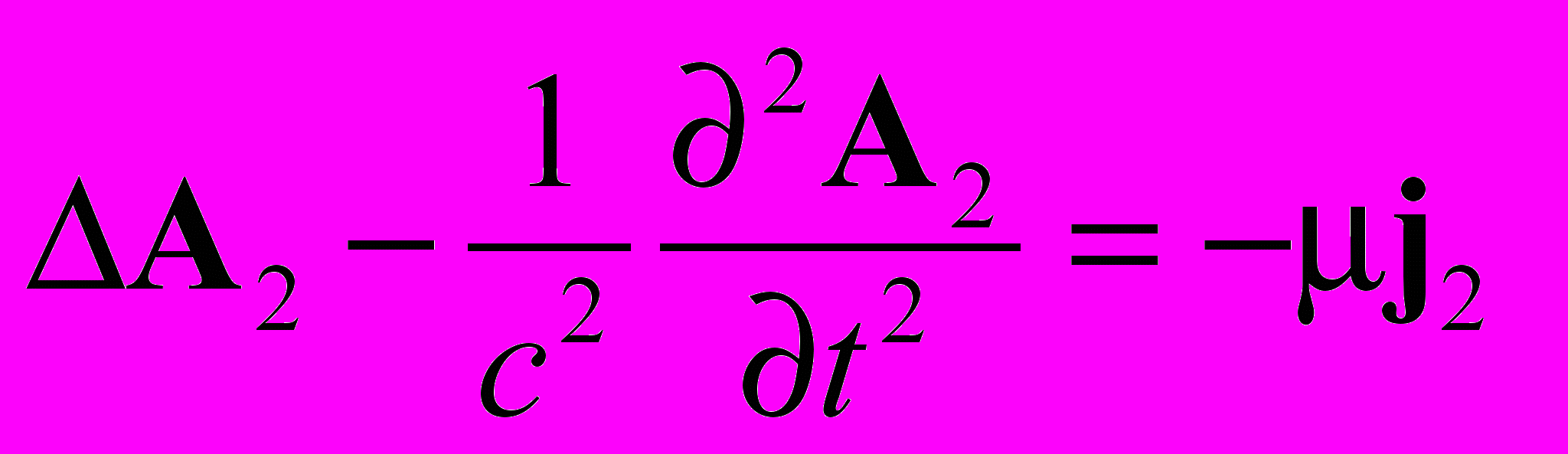
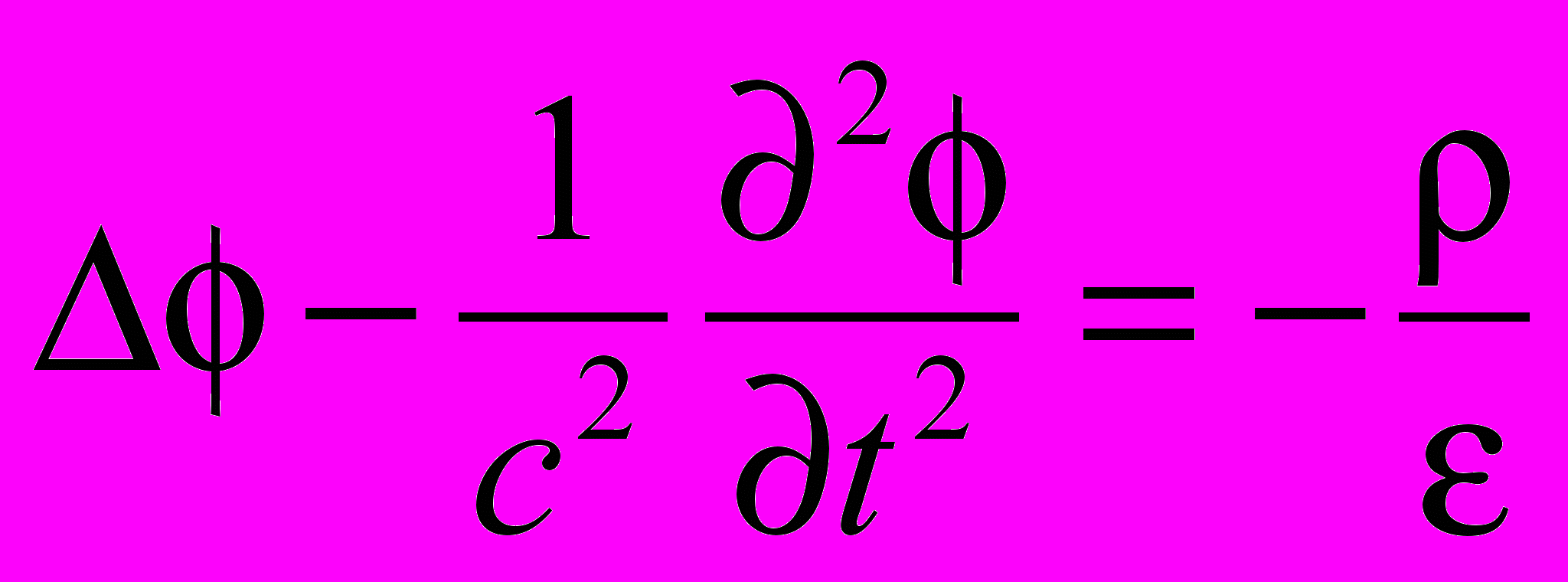
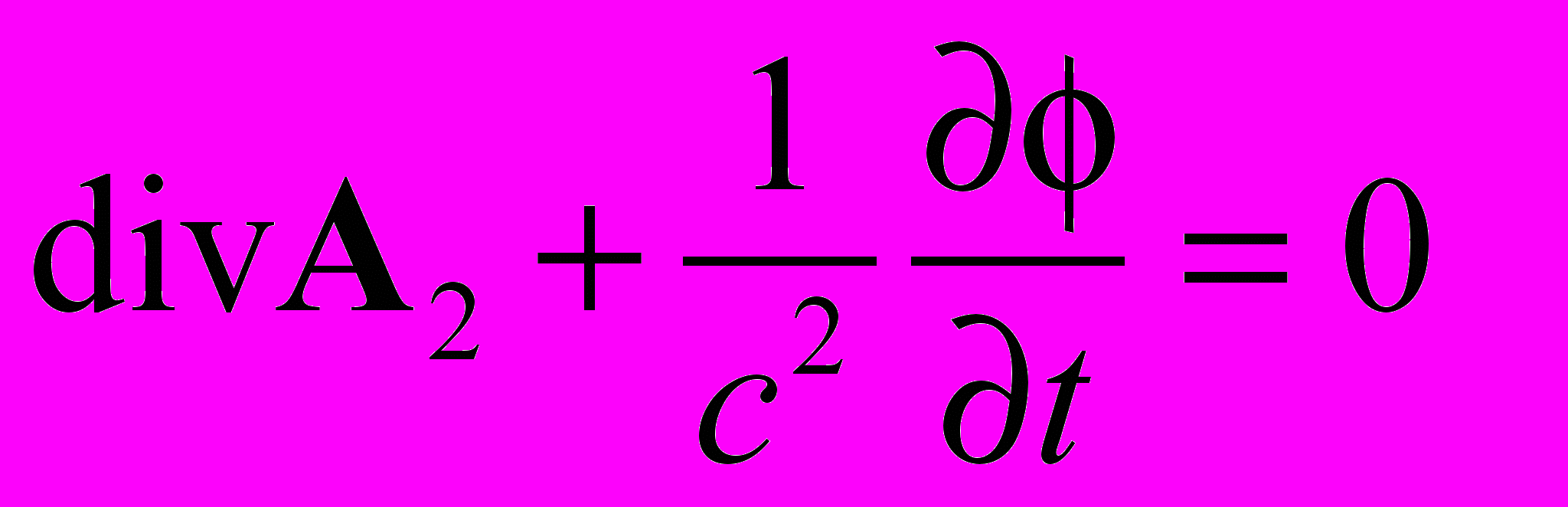(3.2)

Как показано в [1], каждое из трех волновых уравнений имеет плотность энергии и создает свой поток энергии. Закон сохранения энергии имеет пойнтинговский вид:

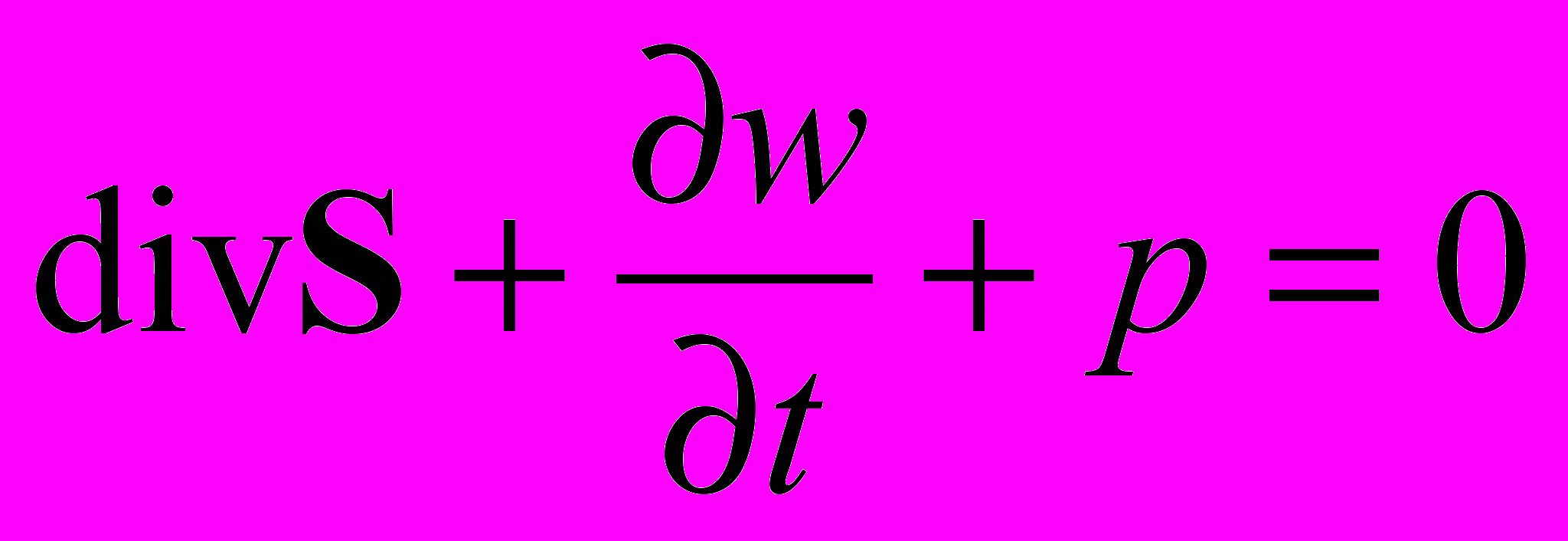(3.3)

где: S – плотность потока энергии; w – плотность энергии волны; p – плотность мощности сторонних сил. Значения этих величин приведены в таблице 1.


Таблица 1.

Энергетические компоненты волновых полей

Поперечные волны векторного потенциала
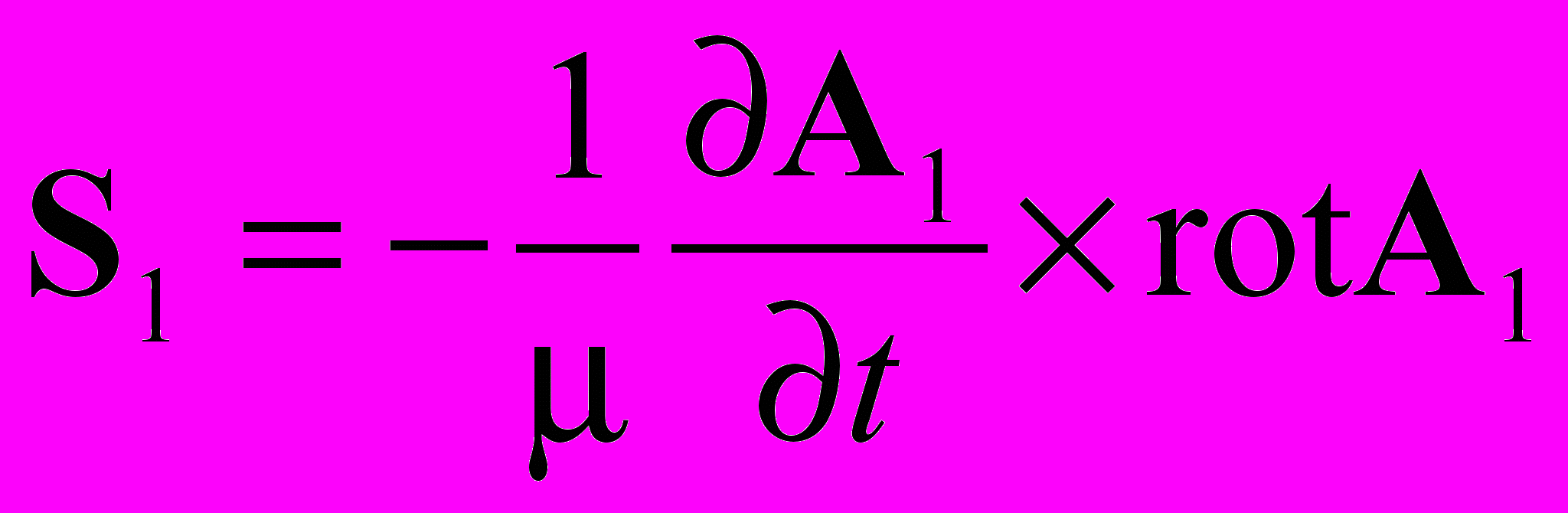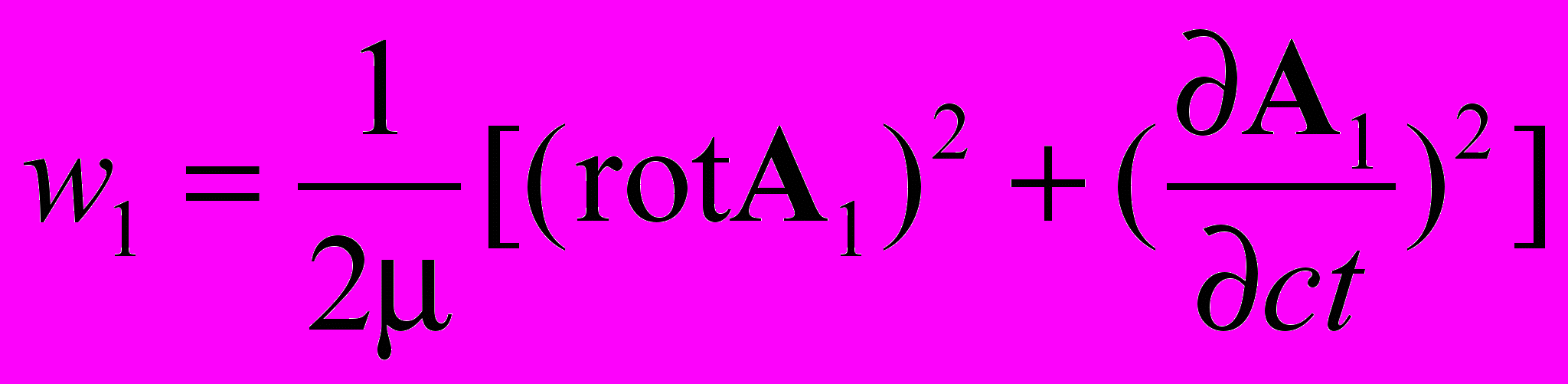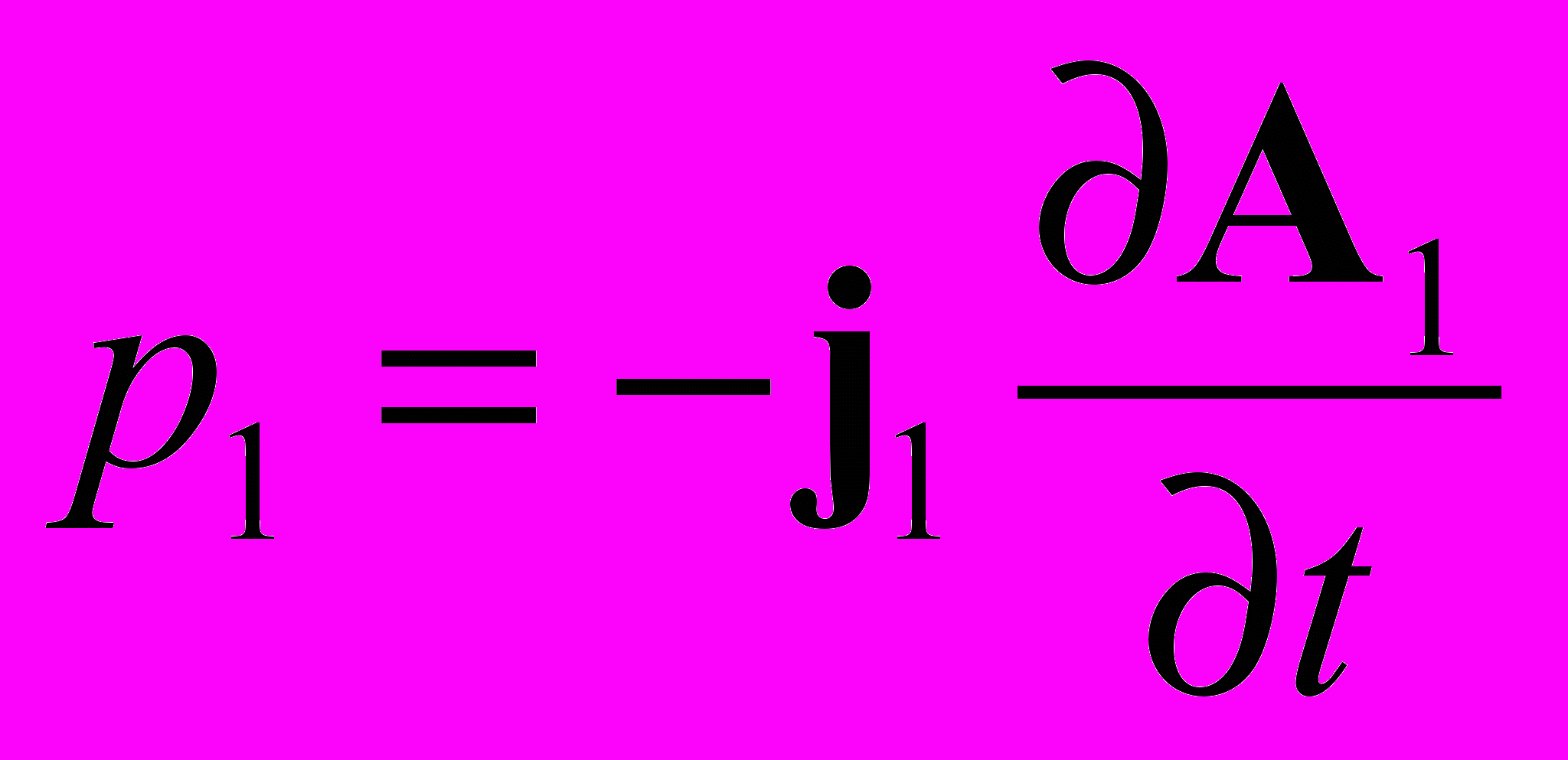Продольные волны векторного потенциала
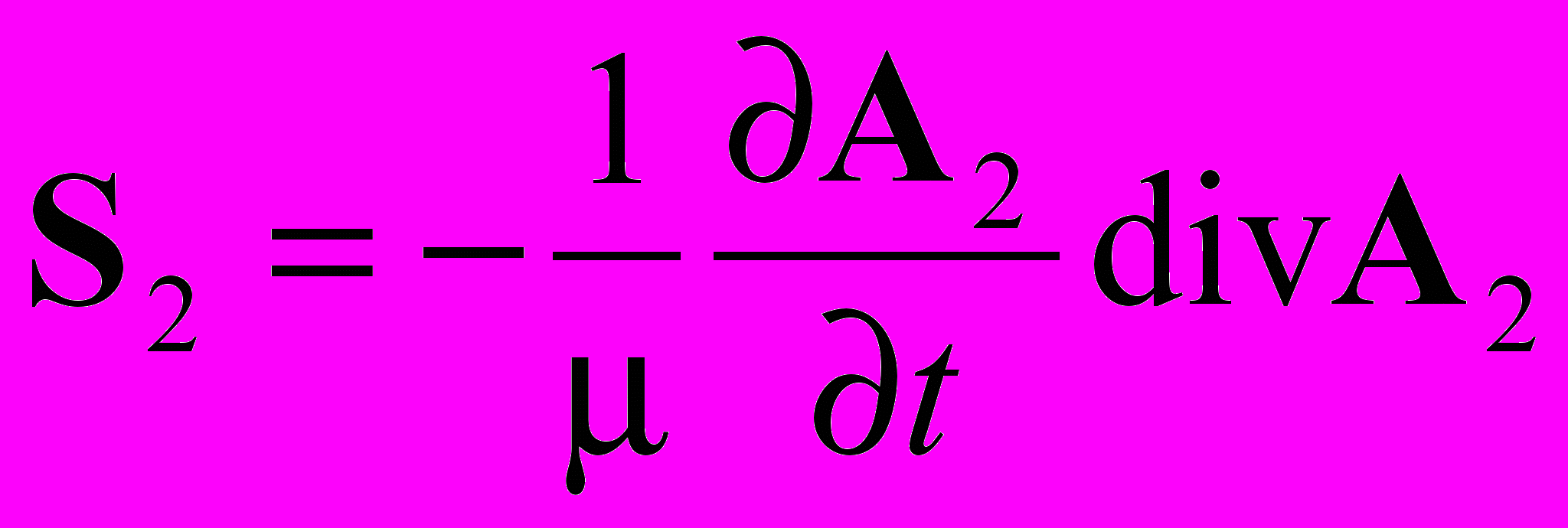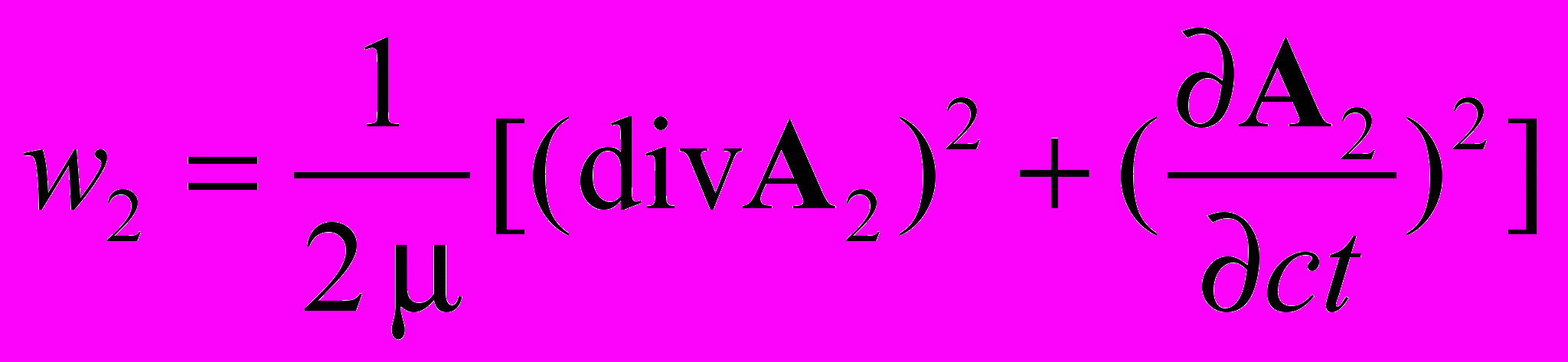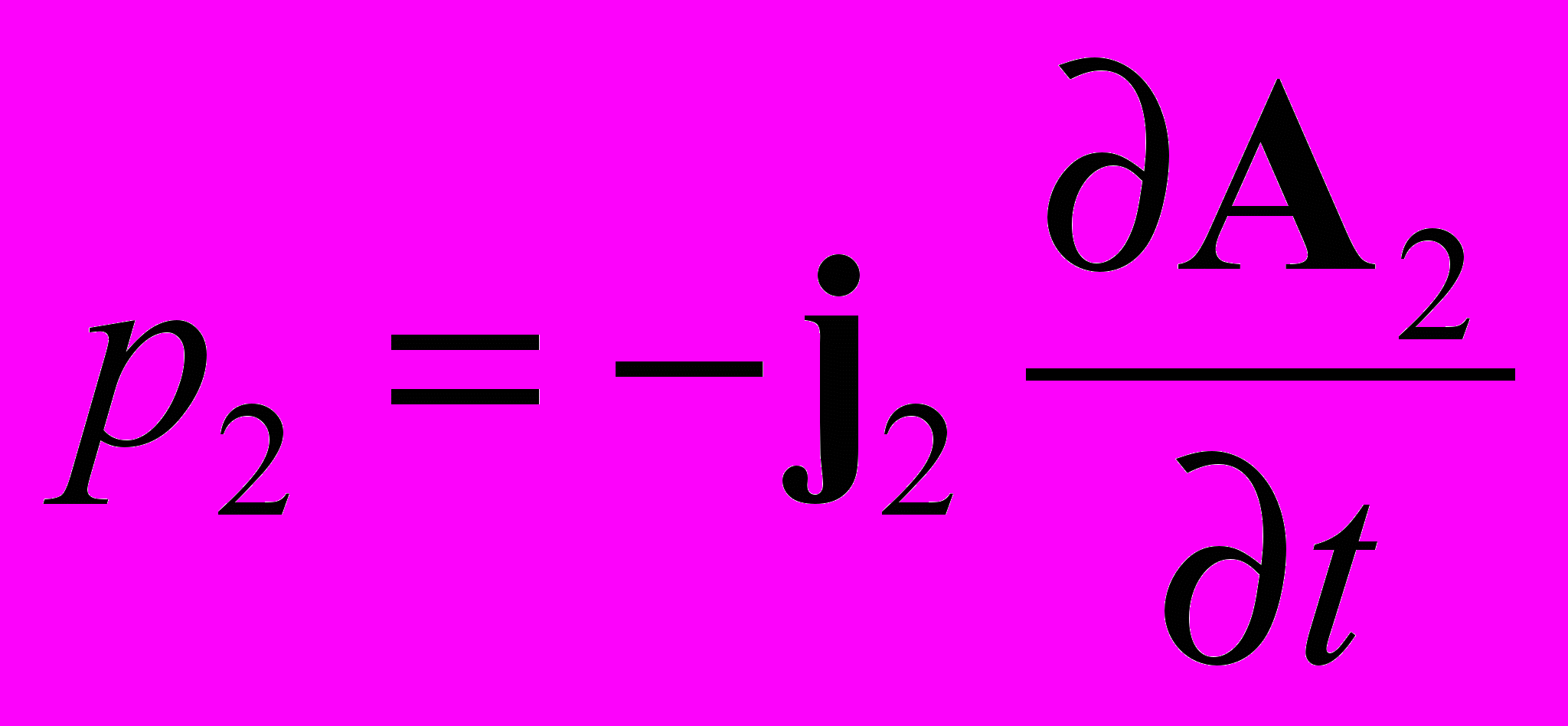Продольные волны скалярного потенциала

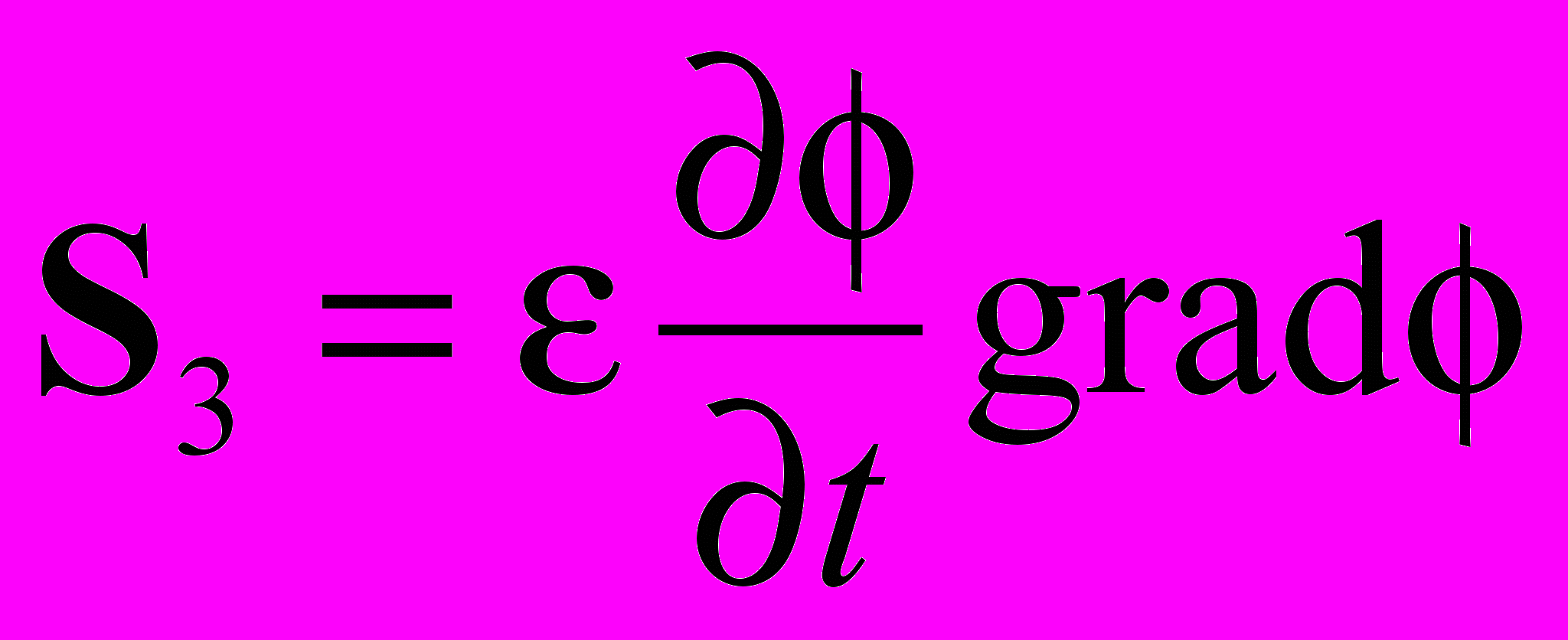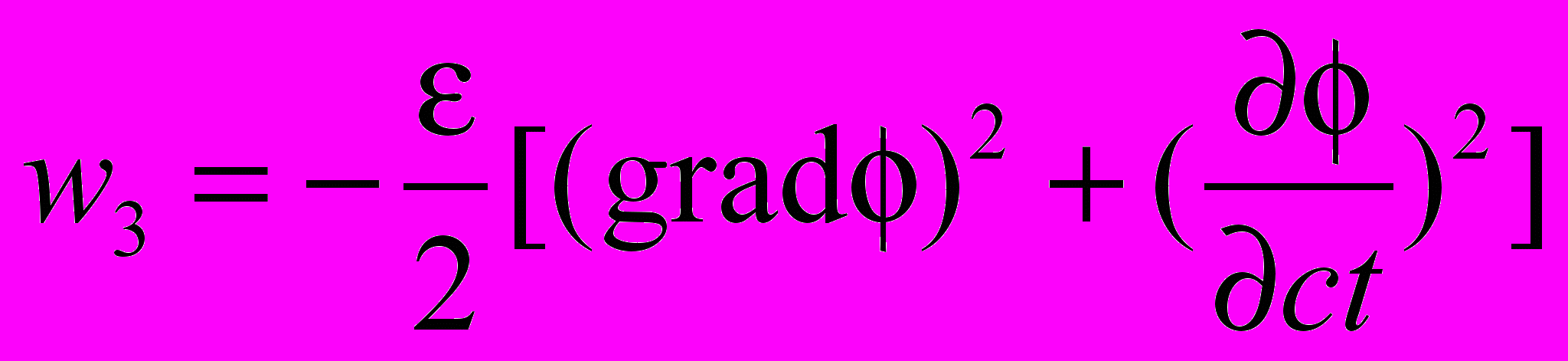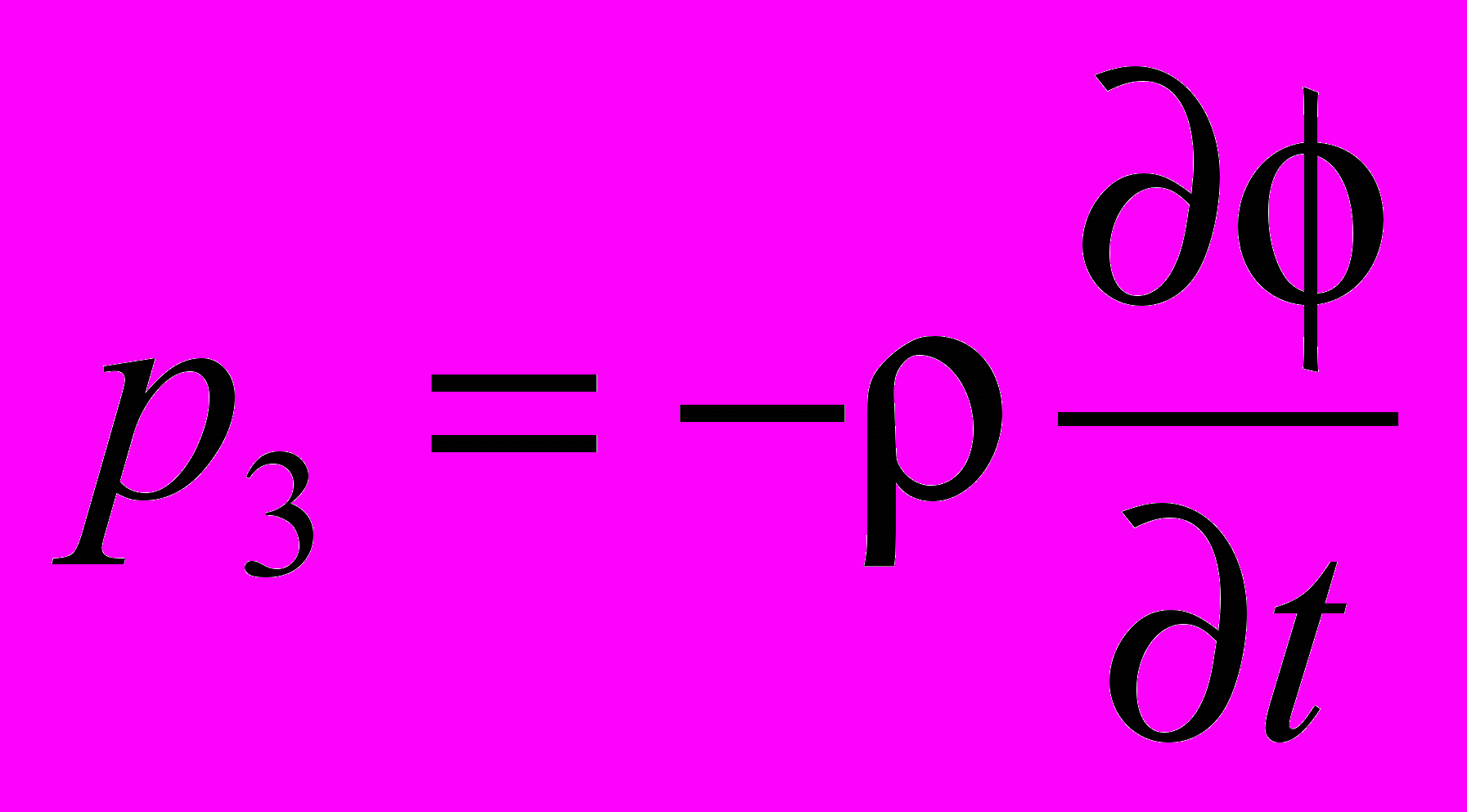Как видно из таблицы в рамках волновой электродинамики существуют два потока продольных волн и один поперечной волны. Здесь мы не будем детально рассматривать проблему продольных волн. Она решается просто. Если суммарное продольное электрическое поле равно нулю, т.е. 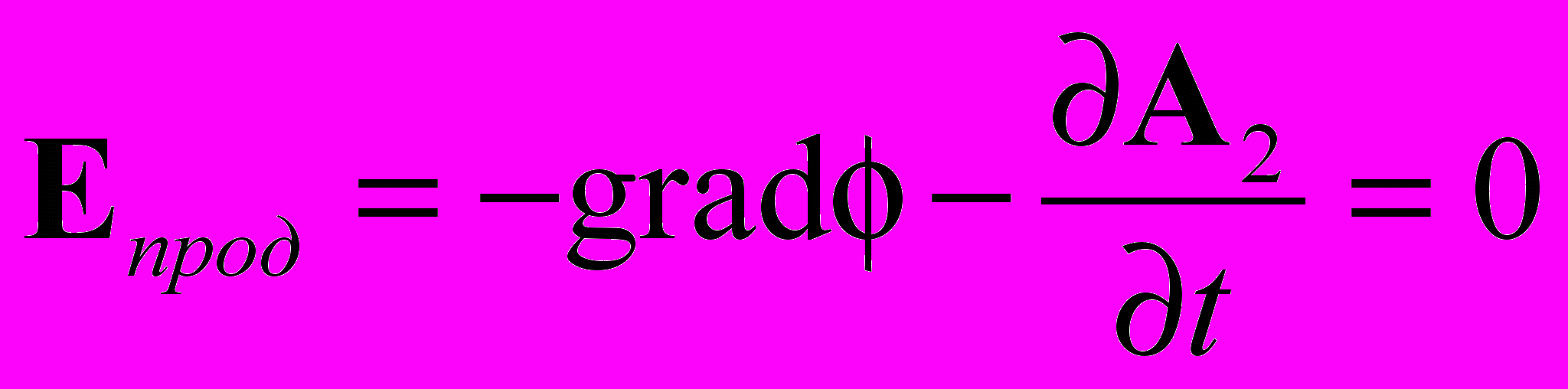, тогда суммарный поток энергии продольных волн будет отсутствовать.

Учитывая условие 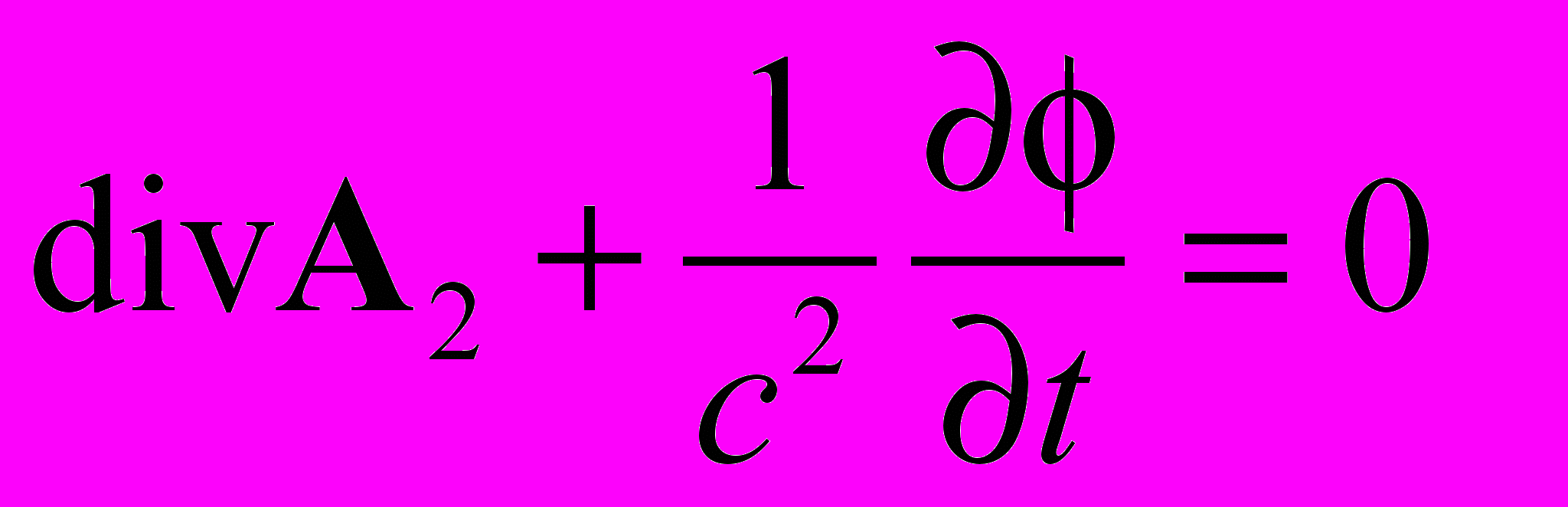нетрудно показать, что для выполнения записанного условия оба потенциала должны удовлетворять однородным волновым уравнениям

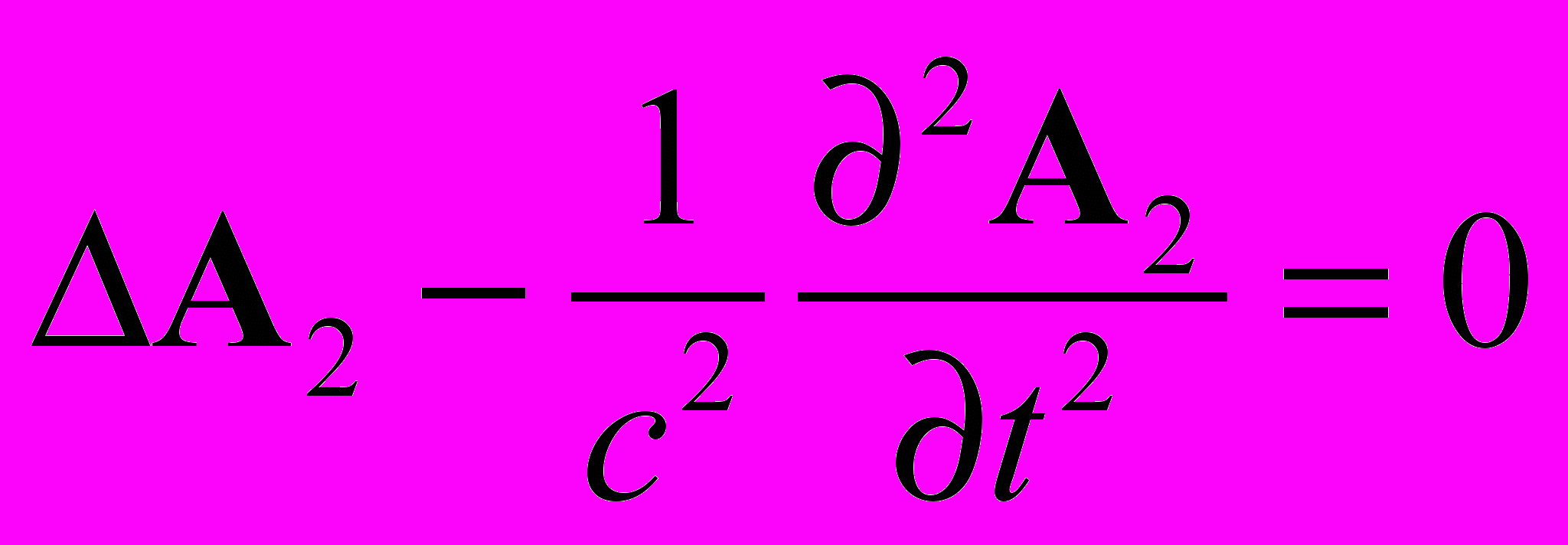и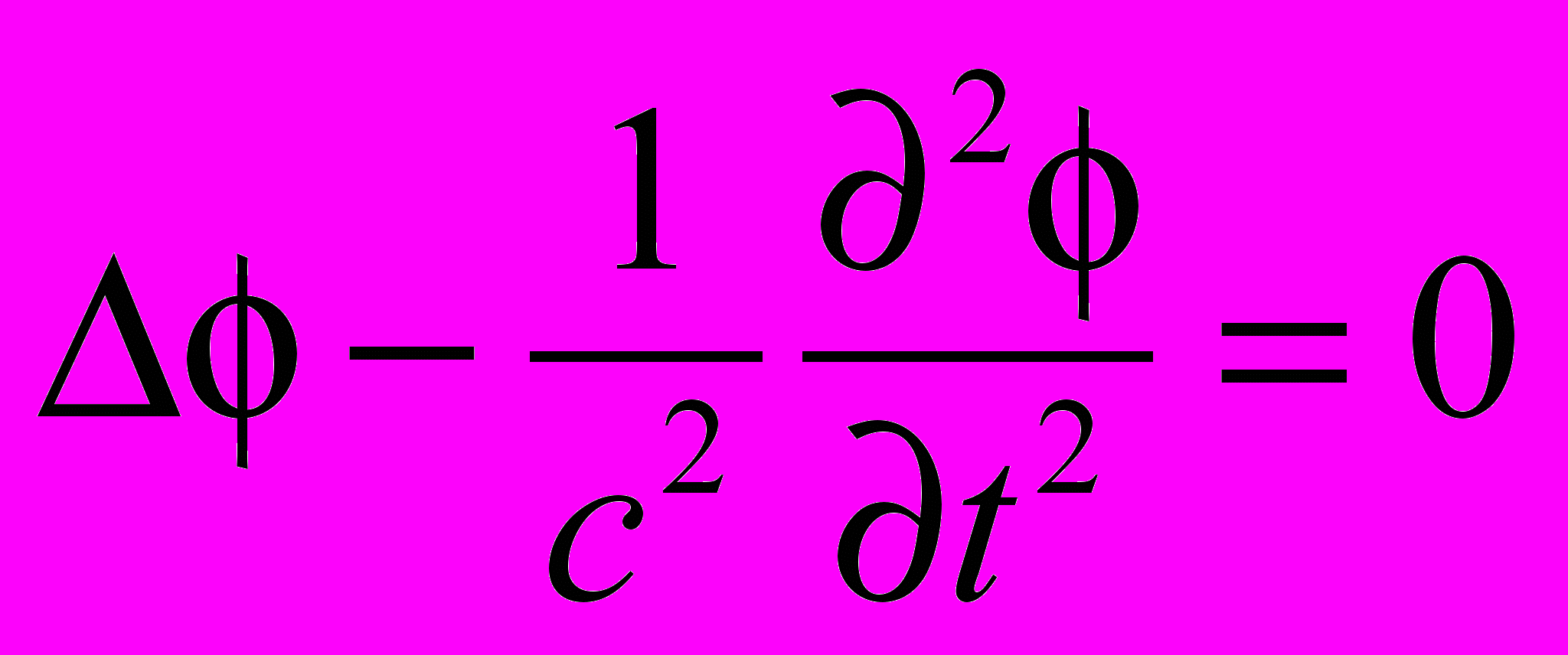

Итак, продольные волны «гасят» друг друга, когда вне источников (в свободном пространстве) они удовлетворяют однородному волновому уравнению. Что касается потока поперечных волн, то они уносят энергию от источника со скоростью света в бесконечность. Однако это доказательство не выявляет всех особенностей взаимной компенсации продольных волн. Доказательство с энергетических позиций позволяет выявить интересные явления [1], о которых мы упомянем ниже.

Теперь мы можем сделать промежуточные выводы.

Во-первых, как мы видим, закон сохранения энергии Пойнтинга не является уникальным и универсальным для электродинамики. Закон пойнтинговского типа имеет место для любых волновых уравнений.

Во вторых, мы обращаем внимание на то, что энергия поля скалярного потенциала, как установлено в [1], отрицательна (!). Мы специально обращаем внимание на этот важный факт. Только благодаря этому возможна полная компенсация, т.е. полное «обнуление» суммарной плотности энергии и суммарной плотности потока продольных волн. Более того, отрицательность энергии поля скалярного потенциала следует непосредственно из общепринятого тензора энергии-импульса электромагнитного поля [1].

Отрицательность энергии поля скалярного потенциала принципиально не согласуется с современными представлениями о взаимодействии инерциальных зарядов (электронов, например). Если бы мы могли совершить предельный переход, то столкнулись бы со следующим явлением. Закон Кулона должен был бы иметь другую формулировку: одноименные заряды должны были бы притягиваться, а разноименные – отталкиваться (?!).

Пока нет ответа на многие вопросы. Какова природа безинерциальных зарядов? Почему энергия поля этих зарядов отрицательна, если исходить из калибровки Лоренца? Почему только они способны излучать электромагнитную энергию, а инерциальные заряды не способны этого делать непосредственно? Проблема природы безинерциальных зарядов еще ждет своего решения.

Итак, разделение электродинамики на волновую и квазистатическую имеет под собой серьезное и глубокое основание.

4. Законы сохранения для квазистатической электродинамики

Перейдем теперь к уравнениям квазистатической электродинамики. В свое время возникла проблема электромагнитной массы, которая до настоящего времени не имеет решения в официальной науке. Опираясь на идею корпускулярно-волнового дуализма, предпринимались и сейчас имеют место попытки «сконструировать» заряженную частицу в виде суммы волн. Очевидно, что они заведомо обречены на провал. Причины следующие:

1. 
   Масса покоя любой волны, распространяющейся со скоростью света, всегда равна нулю. Можно, конечно, складывать до бесконечности нулевые массы покоя, но получить ненулевую массу как сумму нулевых масс – абсурд.
   
2. «Частица», т.е. «волновой пакет» (даже, если бы удалось обойти первый пункт) в среде с дисперсией неминуемо бы «расползалась».
   
3. Такая «частица» должна была бы перемещаться в пространстве, «перенося» свой волновой пакет с групповой скоростью. Однако групповая скорость вообще не имеет отношения к переносу энергии любой из волн, образующей волновой пакет. Как показано в [3] групповая скорость есть скорость перемещения интерференционной картинки второго рода. Такая интерференционная картинка образуется не в плоскости, перпендикулярной направлению движения группы волн, а вдоль направления движения волн. Скорость движения волнового пакета и скорость переноса энергии любой волной, создающей этот пакет, в общем случае не равны и могут иметь даже противоположные направления.
   
4. Волны, образующие волновой пакет, должны иметь свои источники, хотя бы на бесконечности.
   

Как показано в [5], для квазистатических уравнений электродинамики (2.4) существует свой закон сохранения энергии. Форма этого закона напоминает форму закона (3.3), но имеет иное содержание. Запишем его в интегральной и в дифференциальной формах

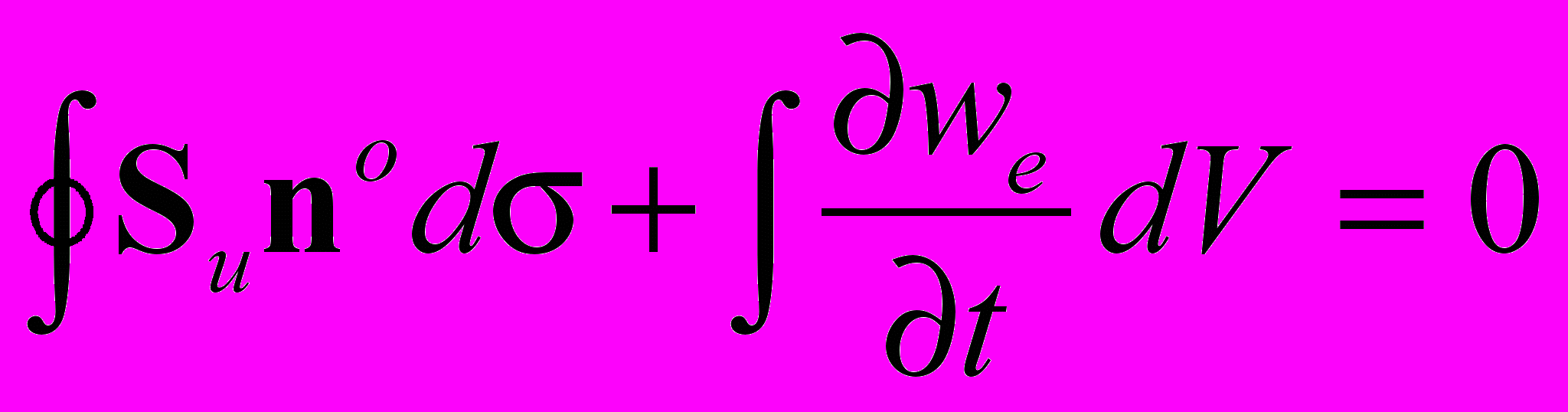
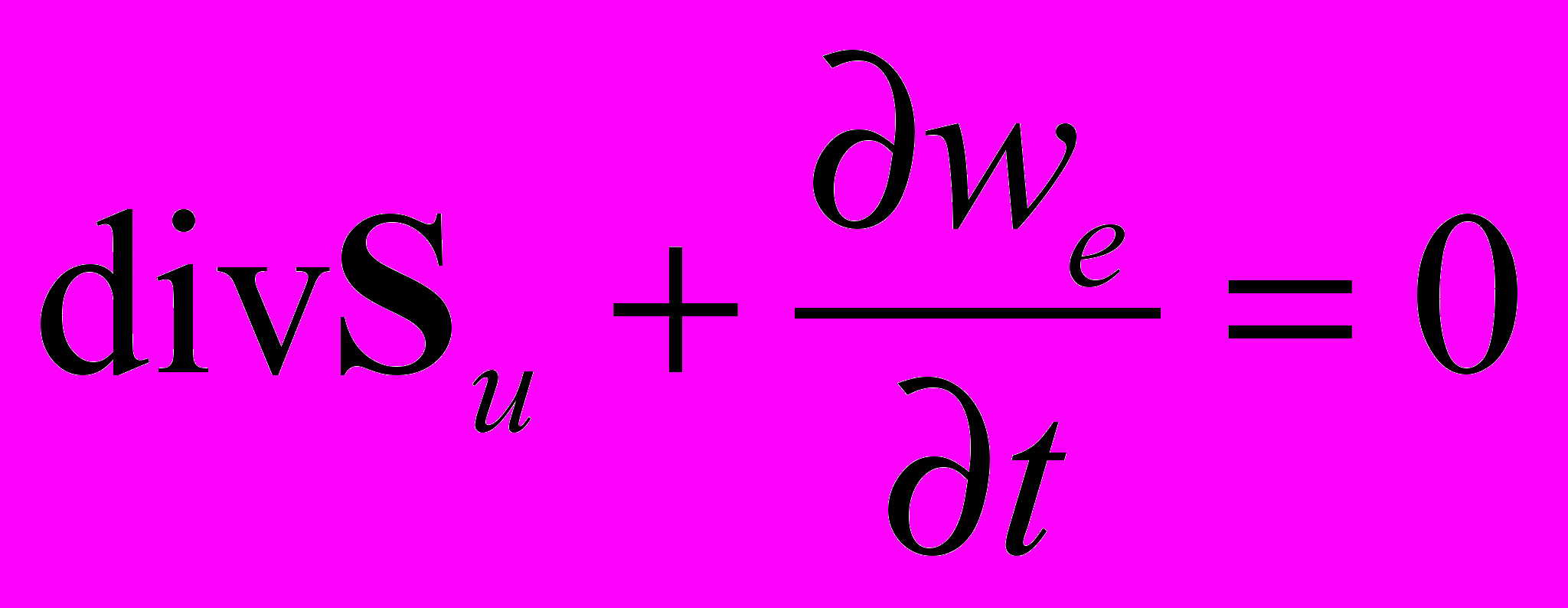(3.4)

где: S_u - плотность потока поля заряда (вектор Умова)

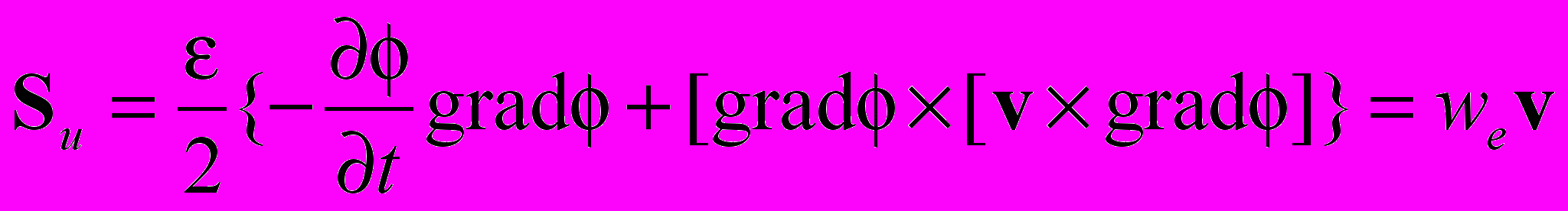(3.5);

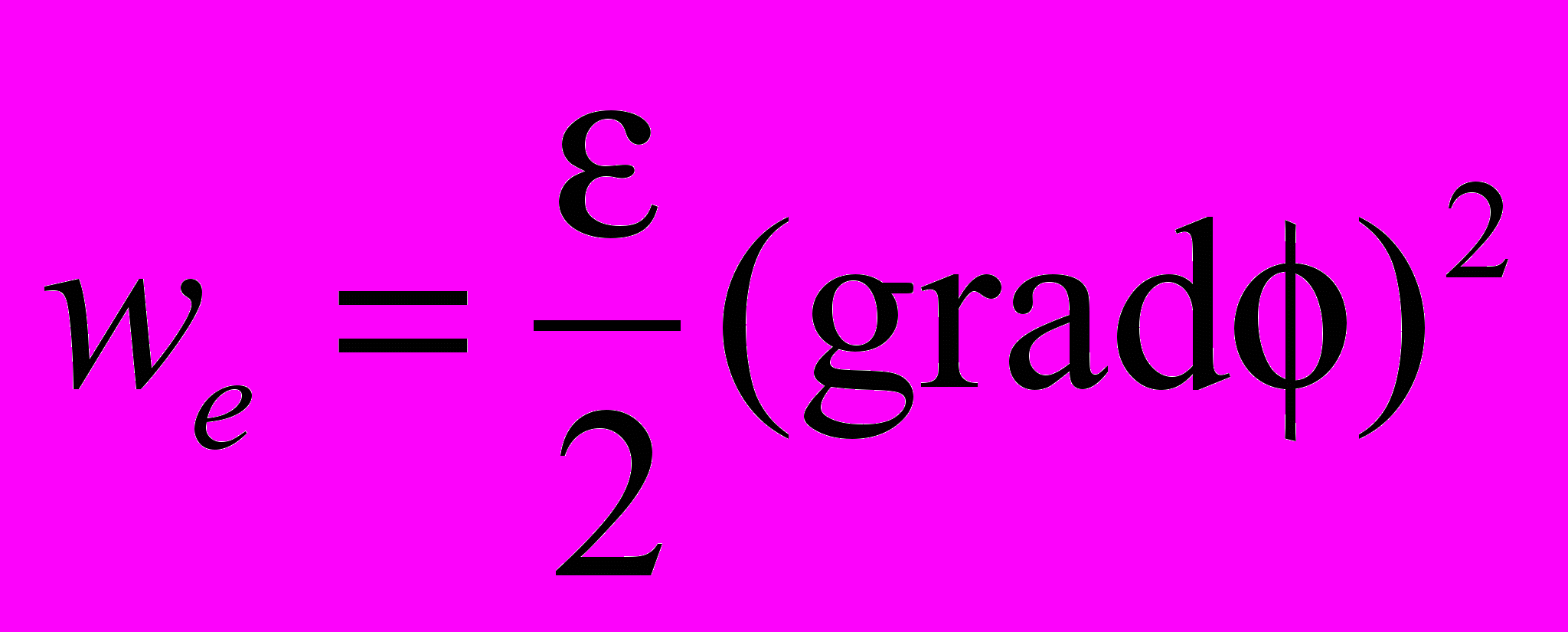- плотность энергии поля заряда (3.6)

Уравнение (3.4) есть закон сохранения энергии Умова для мгновенно действующих электростатических полей квазистатической электродинамики.

Теорема Умова справедлива для полей, описываемых уравнениями только эллиптического типа, т.е. только для мгновенно действующих потенциалов. Более того, вектор Пойнтинга и вектор Умова независимы и не выводимы один из другого. Называть выражение (3.3) теоремой Умова-Пойнтинга – означает демонстрировать принципиальное непонимание сути физических процессов в электродинамике. Принципиальное отличие закона сохранения Умова от законов сохранения пойнтинговского типа в том, что закон Умова описывает конвективный перенос энергии со скоростью движения источника поля v, а не перенос энергии излученной электромагнитной волной со скоростью света.

Вектор Умова, например, превосходно описывает поток энергии движущегося заряда. Вектор же Пойнтинга принципиально не способен описывать конвективный перенос энергии. Использование вектора Пойнтинга для вычисления электромагнитной массы заряда приводит к известной проблеме «4/3» и другим проблемам.

Очевидно уравнения (3.5) и (3.6) прекрасно соответствуют механике Ньютона. Используя их, мы можем дать корректное описание электромагнитной массы через потенциал поля заряда. Приведенные ниже соотношения (электромагнитная масса заряда, электромагнитный импульс) справедливы для зарядов произвольной формы.

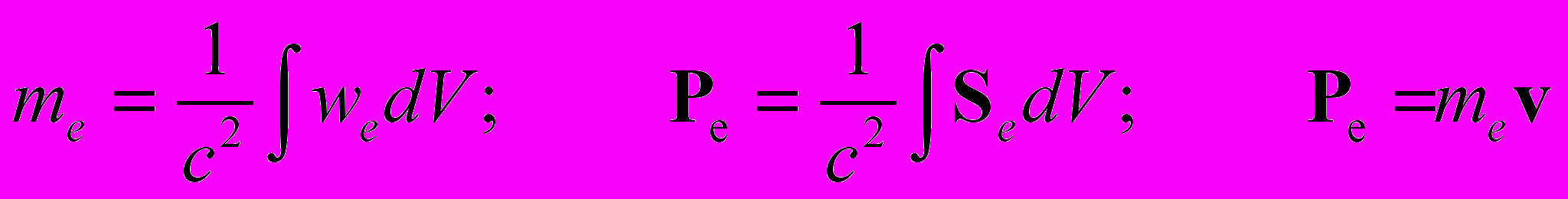(3.7)

Из соотношений (3.7) следует, что электромагнитная масса заряда обладает всеми стандартными свойствами обычной инерциальной массы. Как следствие, неэлектромагнитная масса заряда, отвечающая за его устойчивость, также должна иметь те же стандартные свойства (удовлетворять соотношениям вида (3.7)).

5. Предельный переход

Рассмотрим еще одно важное следствие, вытекающее из нарушения единственности решения задачи Коши для волнового уравнения. Мы поясним это на примере, оставив в стороне доказательство. Напомним только, что использование уравнений для получения параллельного решения можно связать определенным образом с операцией калибровки.

Вернемся к волновому уравнению, описывающему некоторый скалярный потенциал.

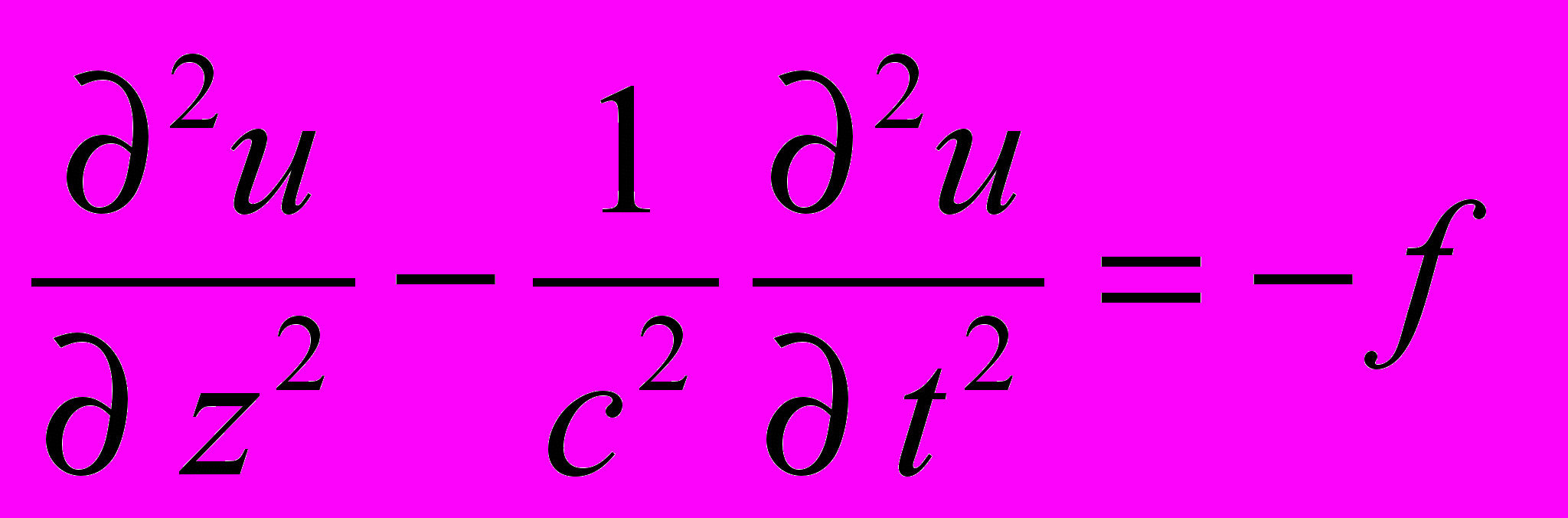(4.1)

где f есть обильность источника поля скалярного потенциала. Пусть источник локализован вблизи начала координат.

Частное решение неоднородного уравнения (4.1), удовлетворяющее принципу причинности, есть запаздывающий потенциал, который вне источника f для z > 0 имеет вид: u(z-ct).

Запишем уравнения для получения параллельного решения, полагая u₁ = v + w. Потенциал v есть мгновенно действующий, w – запаздывающий. Пусть

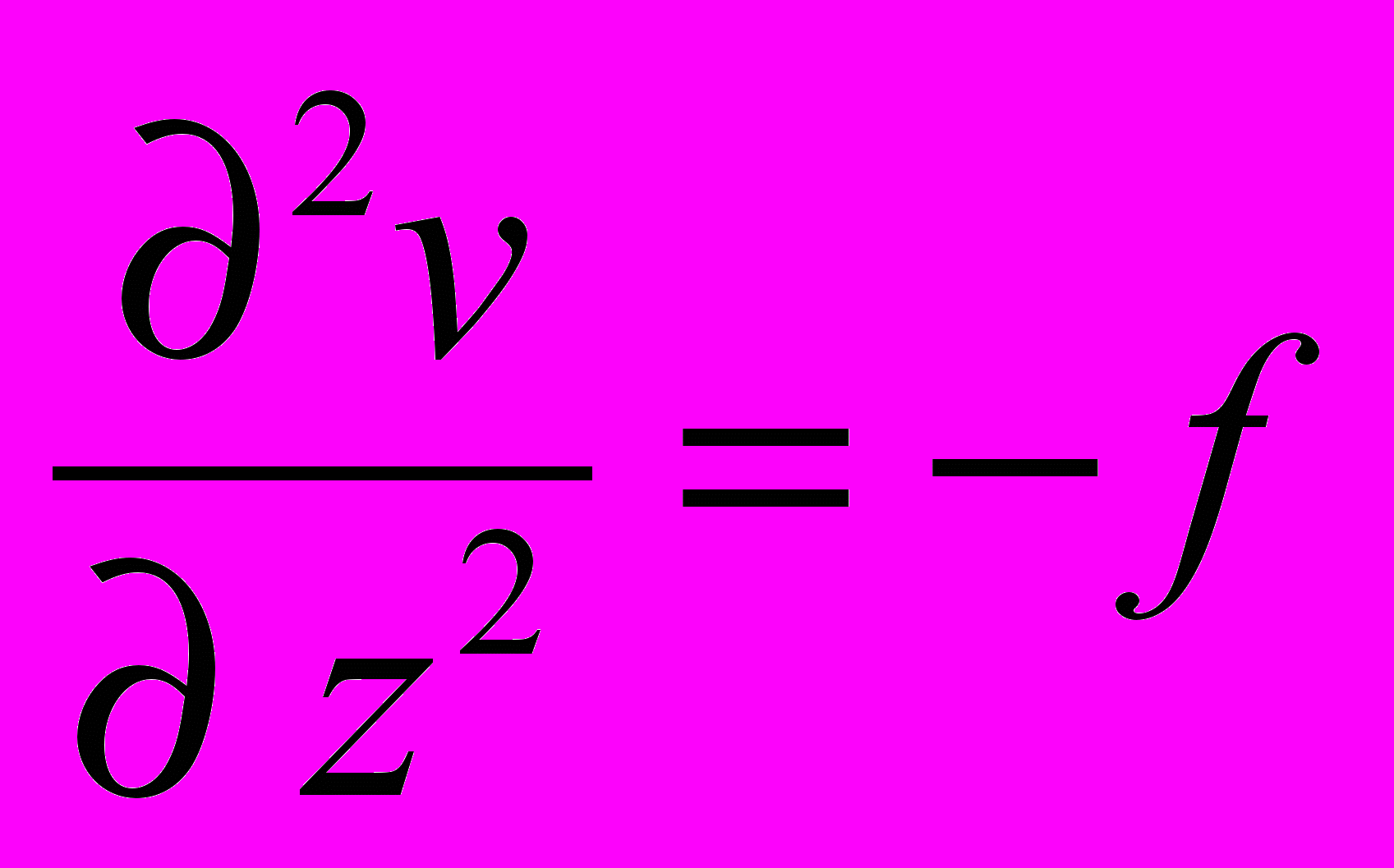(4.2) тогда 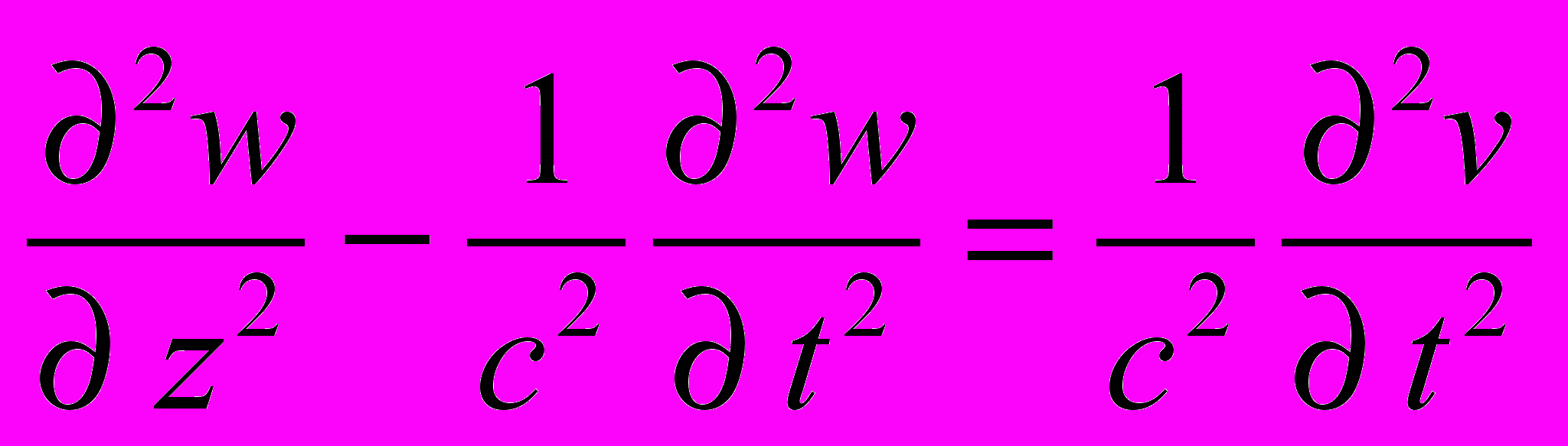(4.3)

Допустим, что параллельное решение существует.

Рассмотрим теперь предельный переход уравнений и их решений при с  .

1. 
   Начнем с анализа параллельного решения. Очевидно, что уравнение (4.2) сохраняется без изменений, а правая часть уравнения (4.3) стремится к нулю. Таким образом, потенциал u₁  v . Остается только мгновенно действующая часть решения.
   
2. Предельный переход применительно к уравнению (4.1) приводит его к виду (4.2), т.е. 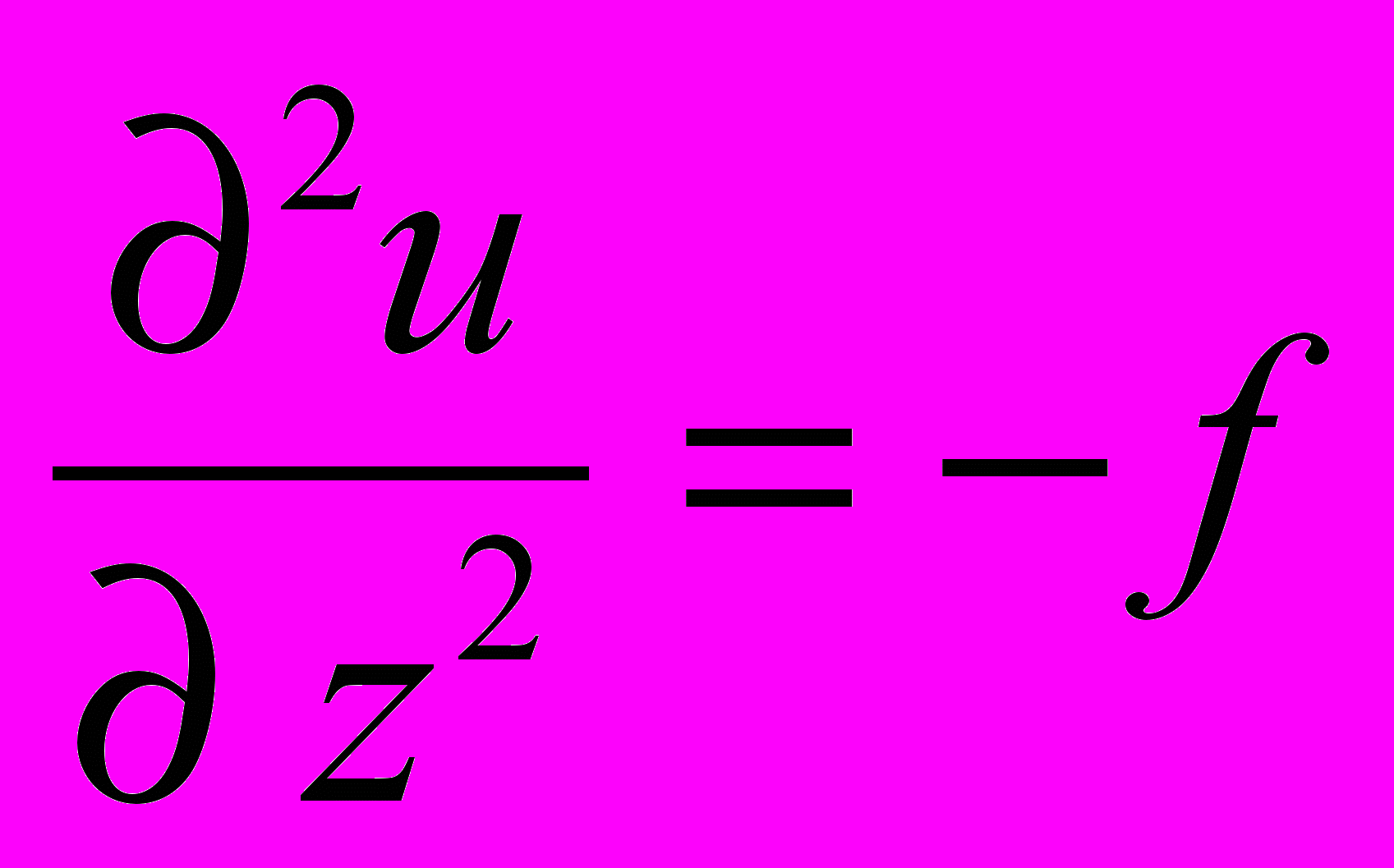. Соответственно запаздывающий потенциал u превращается в мгновенно действующий.
   

Подобное «превращение» некорректно с физической и математической точек зрения. Запаздывающий потенциал уносит энергию поля от источника со скоростью с. Мгновенно действующий потенциал такими свойствами не обладает. Мы продемонстрировали это на законе сохранения Умова для уравнения Пуассона (квазистатическая электродинамика) и на законах сохранения пойнтинговского типа для волновых уравнений (волновая электродинамика).

Таким образом, в общем случае, предельный переход с   не является законным. Он переводит решение из одной калибровки в другую, т.е. «незаконно подменяет» решение одной группы уравнений решением, принадлежащим другой группе уравнений.

Опираясь на аналогию, выскажем предложение, что процедура «получения» из преобразования Лоренца преобразование Галилея при с   также есть незаконная процедура.

6. О причинности

В связи с тем, что в электродинамике восстанавливаются мгновенные взаимодействия, актуальной становится проблема причинности. Не возникает ли здесь проблемы в связи с тем, что такие взаимодействия противоречат постулату о «конечной скорости распространения взаимодействий»? Нет.

Во-первых, как было показано в работе [6] мгновенное взаимодействие не противоречит диалектической модели причинности.

Во вторых, в специальной теории относительности не определены понятия «взаимодействие» и «скорость распространения взаимодействия». Взаимодействие между материальными телами, на наш взгляд, это процесс, который сводится к изменению (перераспределению) энергии, импульса и других характеристик взаимодействующих объектов. В английском языке существует понятие, родственное интенсивности процесса. Это rate. Именно оно наилучшим образом подходит к взаимодействию. Но говорить о распространении взаимодействия в пространстве, как какого-то материального объекта, движущегося с какой-то скоростью (в английском velocity или speed), равной или меньшей скорости света, которая независима от выбора инерциальной системы отсчета, есть абсурд или нонсенс. Именно поэтому многие исследователи предлагают другую формулировку постулата: постулат о существовании предельной скорости распространения информации. Но информация и взаимодействие не тождественные понятия.

Тех, кто интересуется проблемами причинности в физике, отсылаем к работам [6], [7].

Заключение

Подведем предварительные итоги.

1. Опираясь на установленное нарушение единственности решения волнового уравнения, мы сделали в Части 1 заключение об отсутствии эквивалентности калибровки Лоренца и кулоновской калибровки.
   
2. В Части 2 эта проблема была проанализирована. Оказалось, что существует важный частный случай, когда эти калибровки равноправны.
   
3. Равноправие калибровок достигается тем, что появляются безинерциальные заряды и токи.
   
4. Это приводит к необходимости разделения уравнений электродинамики на две самостоятельные группы: уравнения волновой электродинамики и уравнения квазистатической электродинамики.
   
5. Подобное разделение обосновано с нескольких точек зрения. Например, законы сохранения для уравнений двух этих групп различны. Это позволяет дать корректное решение проблемы электромагнитной массы, устраняет трудности, связанные с проблемой излучения ускоренного заряда, снимает проблему продольных волн и т.д.
   
6. Из сопоставления решений различных математических калибровок следует, что в общем случае предельный переход (с  ) не является корректным, и любое его использование требует специального обоснования. Это имеет отношение не только к уравнениям электродинамики, но и к переходу от преобразования Лоренца к преобразованию Галилея.
   
7. Мы пришли к выводу о существовании границ применимости для преобразования Лоренца, и о возможности параллельного существования мгновенных взаимодействий в рамках преобразования Галилея.
   

Теперь мы можем вновь вернуться к анализу преобразования Лоренца. В первой статье (kuligin-alex.narod.ru/k1) мы показали, опираясь на теорию познания, что пространство является общим и евклидовым для всех инерциальных систем отсчета, а время единым. В следующем обзоре мы продолжим анализ преобразования Лоренца.


Литература.

1. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева Кризис релятивистских теорий, часть 2. (Анализ основ электродинамики). НиТ, 2001. (www.n-t.ru/tp/ns/krt.htm)
   
2. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. Безинерциальные заряды и токи. НиТ, 2002. (www.n-t.org/tp/ns/bzt1.htm и www.n-t.org/tp/ns/bzt2.htm)
   
3. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. Фазовая скорость, групповая скорость и скорость переноса энергии . НиТ, 2002. (www.n-t.org/tp/ns/fs.htm)
   
4. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. Кризис релятивистских теорий, часть 6. (Магнитные взаимодействия движущихся зарядов). НиТ, 2001. (www.n-t.ru/tp/ns/krt.htm)
   
5. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. Кризис релятивистских теорий, часть 5. (Электромагнитная масса). НиТ, 2001. (www.n-t.ru/tp/ns/krt.htm)
   
6. В.А. Кулигин. Причинность и взаимодействие в физике // Детерминизм в современной науке. Воронеж, 1987. (www.n-t.ru/tp/ns/pvf.htm)
   
7. В.А. Кулигин, Г.А. Кулигина, М.В. Корнева. К столетнему юбилею СТО. НиТ, 2001 (www.n-t.ru/tp/ns/sto.htm)