Алгебраическая алгоритмика
| Вид материала | Документы |
СодержаниеУметь: строить алгоритмы для решения алгебраических задач, исследовать их сложность.Владеть |
- Алгебраическая алгоритмика, 79.05kb.
- Календарно-тематическое планирование пооивт "алгоритмика 5-6", 67.48kb.
- Программа дисциплины Алгебраическая геометрия для направления 010100. 62 «Математика», 205.57kb.
- Алгебраическая геометрия и теория, 22.22kb.
- Направление: теоретическое и системное программирование, 13.45kb.
- Вопросы по предмету цифровая и микропроцессорная техника для учащихся заочной формы, 90.48kb.
- Ф-рабочая программа по дисциплине утверждено ученым советом факультета математики, 49.58kb.
- 1. Нейроподобный элемент (нейрон), 130.75kb.
- Арифметика комплексных чисел, 21.1kb.
- Методика изучения векторов в средней школе., 20.73kb.
Наименование дисциплины: Алгебраическая алгоритмика
Направление подготовки: 010200 Математика и компьютерные науки
Профильная направленность: Математика и компьютерные науки
Квалификация (степень) выпускника: магистр
Форма обучения: очная
Автор: к.ф.-м.н., доцент, доцент кафедры алгебры и математической логики С.И.Яблокова.
1. Целями освоения дисциплины (модуля) "Алгебраическая алгоритмика" являются:
Обеспечение подготовки в одной из важных областей, находящихся на границе алгебры и информатики; овладение основными алгоритмическими вопросами классической и современной алгебры; освоение основных методов разработки эффективных алгоритмов для решения задач, возникающих как в самой алгебре, так и в ее приложениях.
2. Дисциплина «Алгебраическая алгоритмика» входит в цикл вариативных профессиональных дисциплин. Для ее успешного изучения необходимы знания и умения и навыки, приобретенные в ходе изучения таких базовых курсов, как «Алгебра» и «Теория чисел», а также курсы, связанные с изучением основ программирования. Эта дисциплина закладывает основы алгебраического и алгоритмического образования будущего специалиста.
3. В результате освоения дисциплины обучающийся должен:
Знать:
основные методы решения алгоритмических проблем, возникающих в алгебре и в ее приложениях к решению практических задач; формировать алгоритмическое мировоззрение, творческое мышление и навыки в проведении самостоятельных научных исследований.
Уметь:
строить алгоритмы для решения алгебраических задач, исследовать их сложность.
Владеть:
основными понятиями и методами алгебры в кольце целых чисел и в кольце многочленов от одной переменной.
4. Общая трудоемкость дисциплины составляет 3 зачетные единицы, 108 часов.
5. Содержание дисциплины:
| № п/п | Раздел дисциплины |
| 1 | Наибольший общий делитель (НОД) целых чисел. Теорема о представлении НОД. Многочлены. Евклидово деление. НОД многочленов. |
| 2 | Алгоритм Евклида и теорема Ламе. Леммы о числе итераций алгоритма Евклида для чисел. Двоичная оценка сложности алгоритма для чисел. Количество делений для многочленов. Теорема Лазара. |
| 3 | Расширенный алгоритм Евклида для чисел и для многочленов. Вычисление коэффициентов Безу. Оценки коэффициентов Безу. |
| 4 | Алгоритм Евклида и цепные дроби. Свойства цепных дробей. Теорема единственности для рациональных чисел. Теорема единственности для иррациональных чисел. Теорема о представлении рациональных чисел цепными дробями. Периодические цепные дроби. Теорема о представлении иррациональных чисел цепными дробями. |
| 5 | Неразложимые и простые числа. Основная теорема арифметики. Факториальные кольца. Теорема о простых числах. Функция Эйлера и ее основные свойства. |
| 6 | Классы вычетов по модулю m. Целостное кольцо. Кольцо и поле вычетов по модулю m . Евклидовы кольца. Разложение на множители в евклидовом кольце. |
| 7 | Простые и неприводимые многочлены. Классы эквивалентности по модулю m(x). Факторкольцо 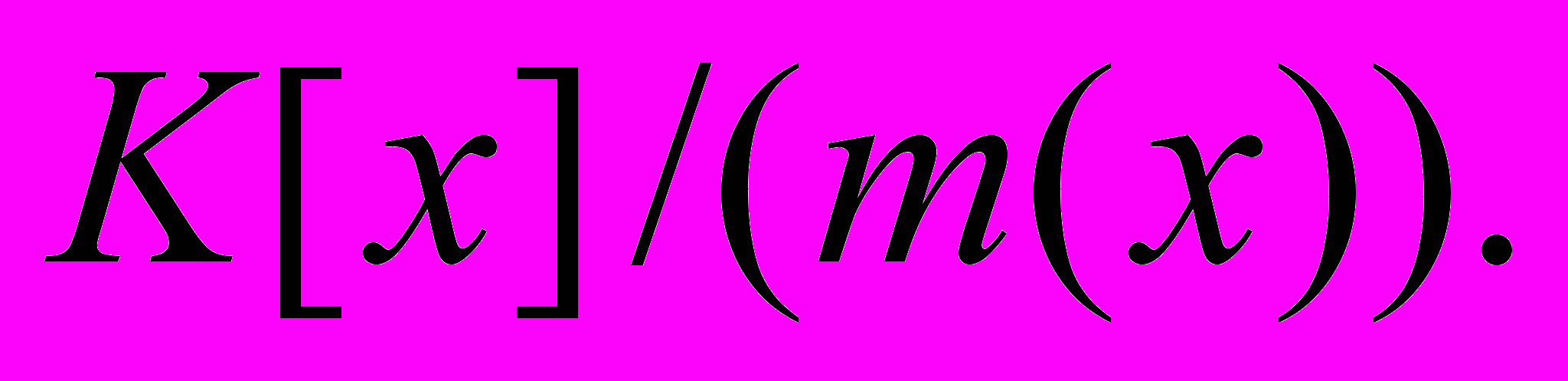 Поле Поле 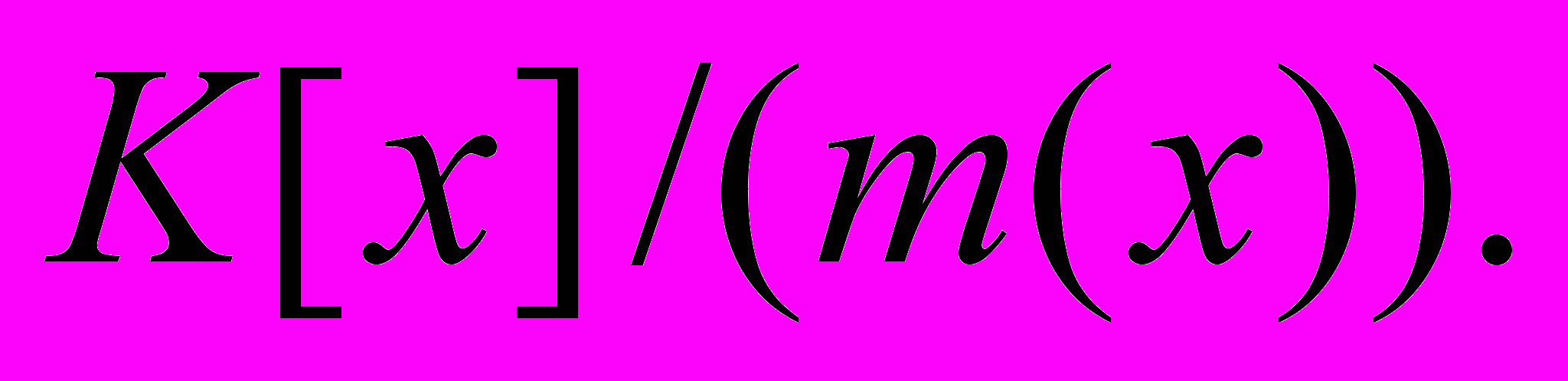 |
| 8 | Малая теорема Ферма. Теорема Эйлера. Дихотомический алгоритм. Псевдопростые числа по данному основанию. Теоремы о существовании бесконечного числа псевдопростых чисел по основанию 2, по основанию a. Числа Кармайкла. Теорема Вильсона. Свойства чисел Кармайкла. |
| 9 | Мультипликативная группа кольца 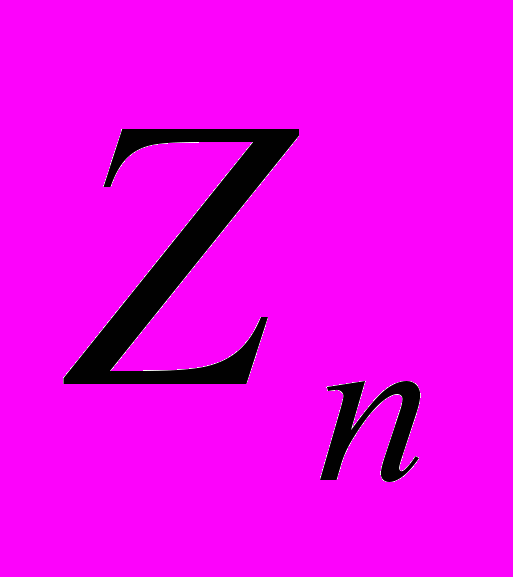 . Циклические группы. Примитивный корень по модулю m . Порядок элемента группы. Цикличность группы . Циклические группы. Примитивный корень по модулю m . Порядок элемента группы. Цикличность группы 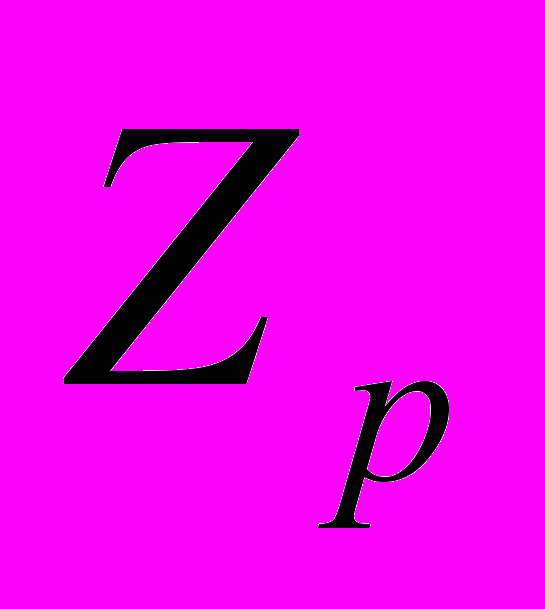 при простом p. Лемма Гаусса. Теорема Гаусса (необходимое и достаточное условие цикличности группы при простом p. Лемма Гаусса. Теорема Гаусса (необходимое и достаточное условие цикличности группы 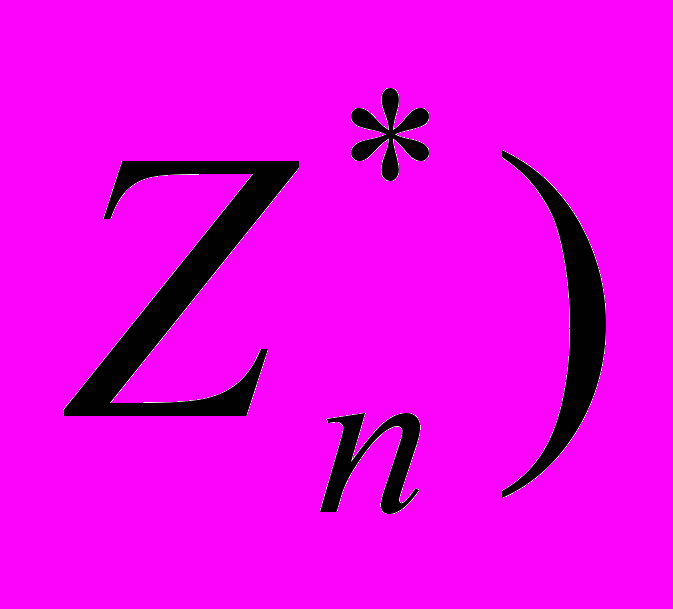 . . |
| 10 | Китайская теорема об остатках для чисел. Китайские теоремы об остатках для систем сравнений. Китайская теорема об остатках для многочленов. |
| 11 | Интерполяция над полем. Формула Лагранжа. Интерполяция с помощью китайской теоремы об остатках. |
| 12 | Неприводимые многочлены. Факториальные и евклидовы кольца. Разложение на множители. Теорема Гаусса. Примитивные многочлены. Рациональные корни многочленов из 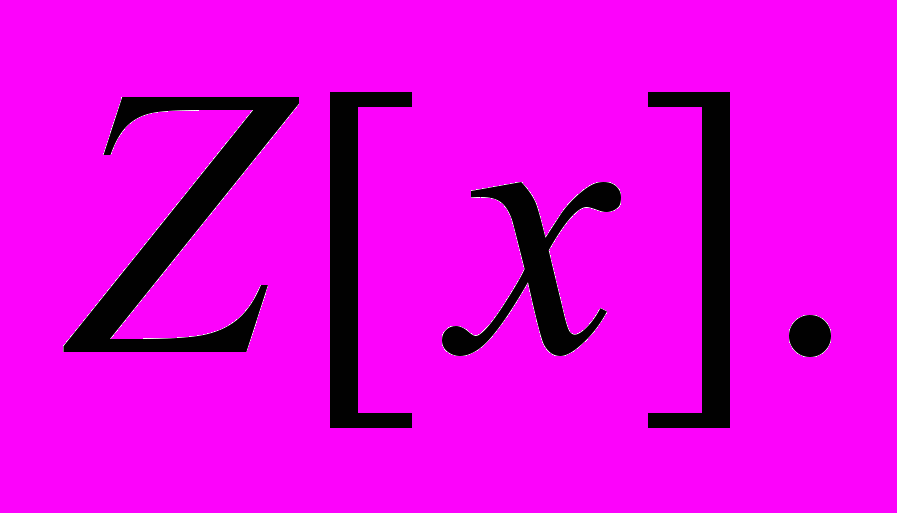 Критерий неприводимости многочлена над Z. Критерий неприводимости многочлена над Z. |
| 13 | Неприводимые многочлены с коэффициентами из 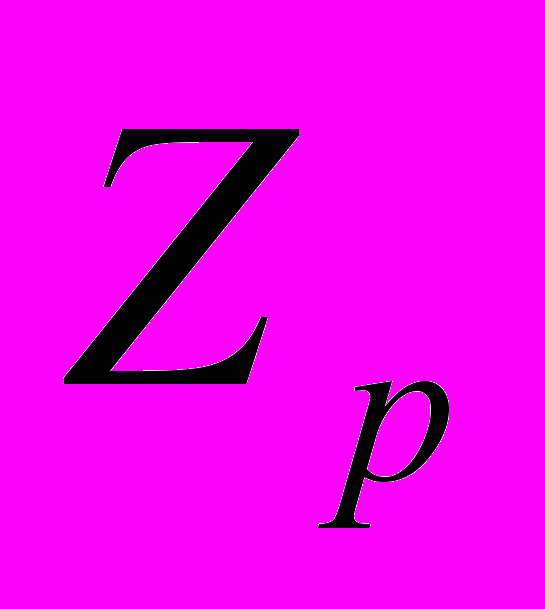 . Число неприводимых многочленов степени n в . Число неприводимых многочленов степени n в 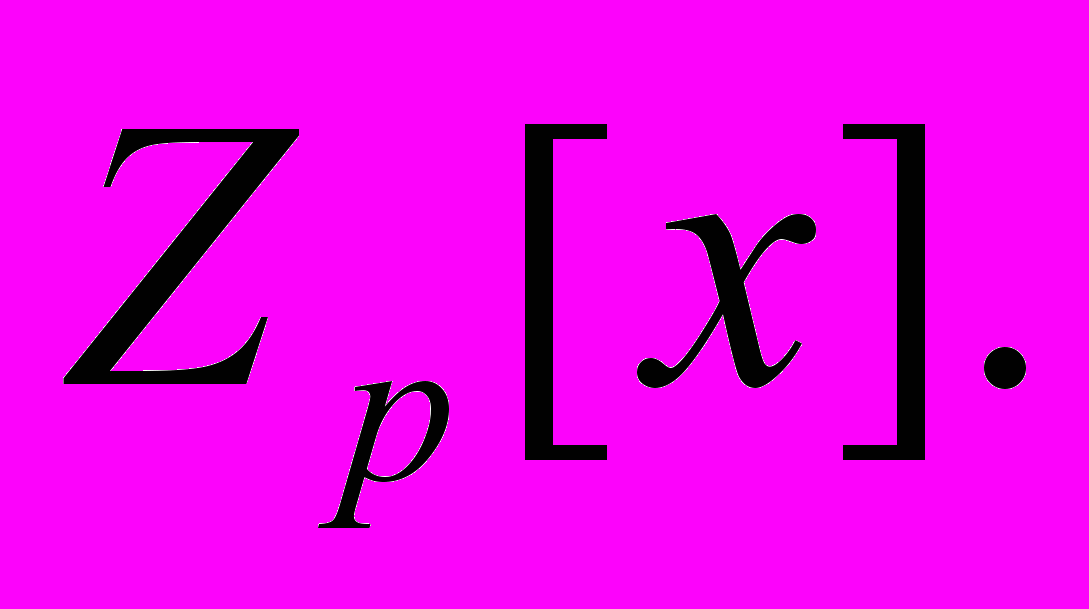 Критерий неприводимости многочлена над Критерий неприводимости многочлена над 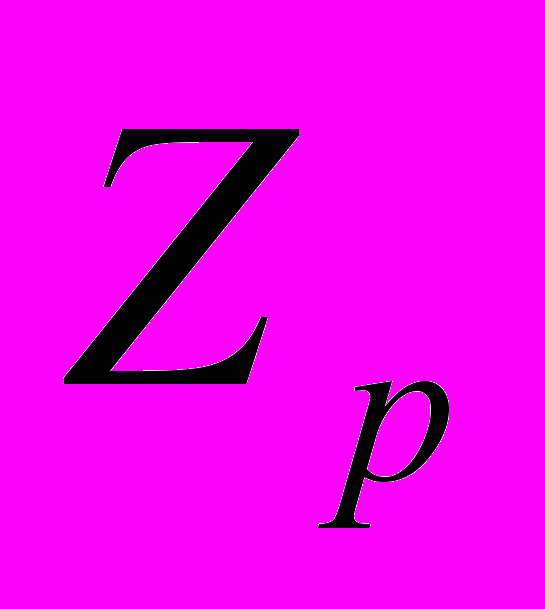 . «Решето Эратосфена» для многочленов над . «Решето Эратосфена» для многочленов над 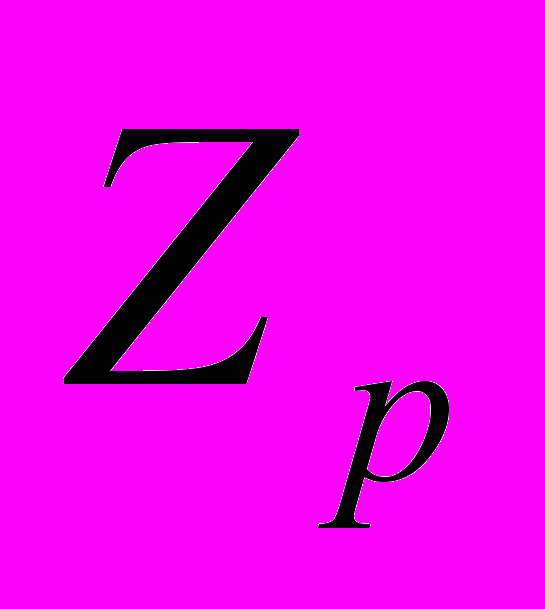 . . |
| 14 | Конечное поле. Свойства его элементов. Основные теоремы. Факторкольцо 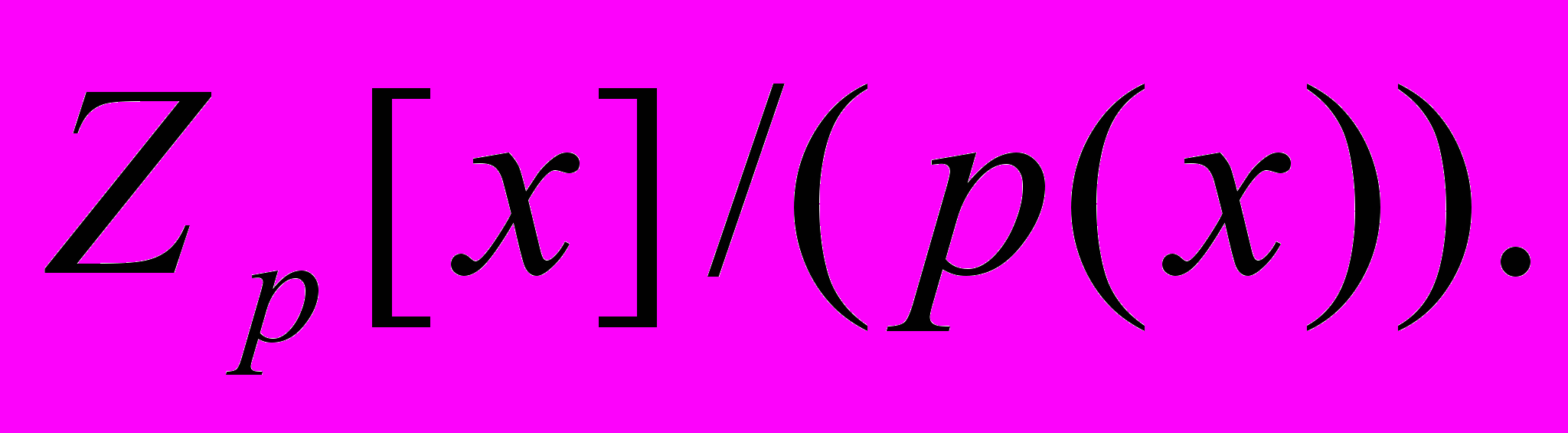 Характеристика поля. Мультипликативная группа конечного поля. Характеристика поля. Мультипликативная группа конечного поля. |
| 15 | Примитивный элемент поля. Нахождение примитивного элемента в конечном поле. Поле разложения многочлена. Минимальный многочлен алгебраического над полем элемента. Правило возведения в степень p в поле с характеристикой p. |
| 16 | Корни неприводимого многочлена в 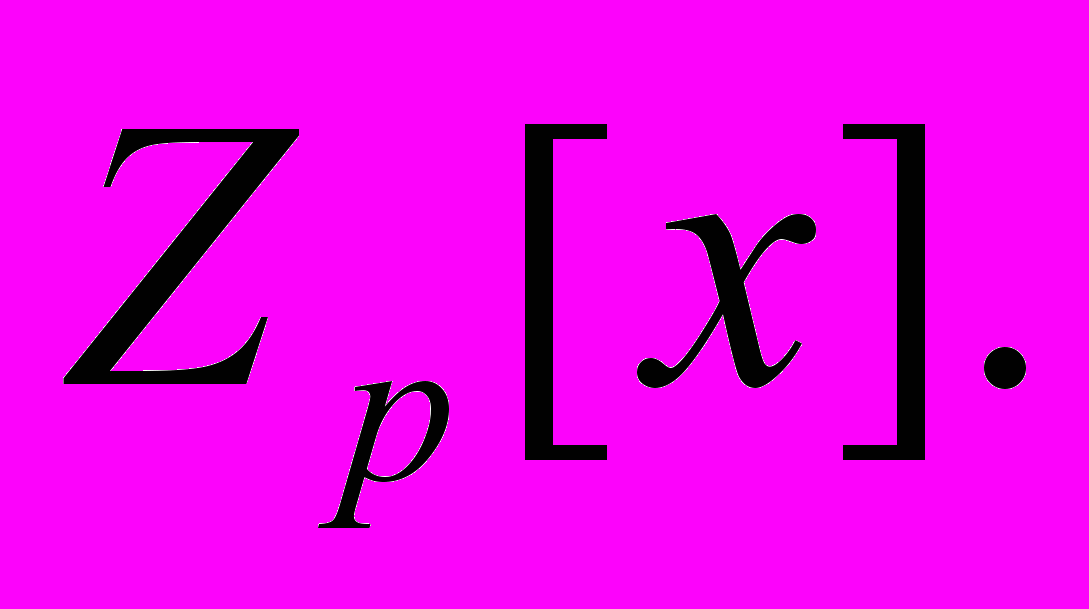 Существование конечного поля из Существование конечного поля из 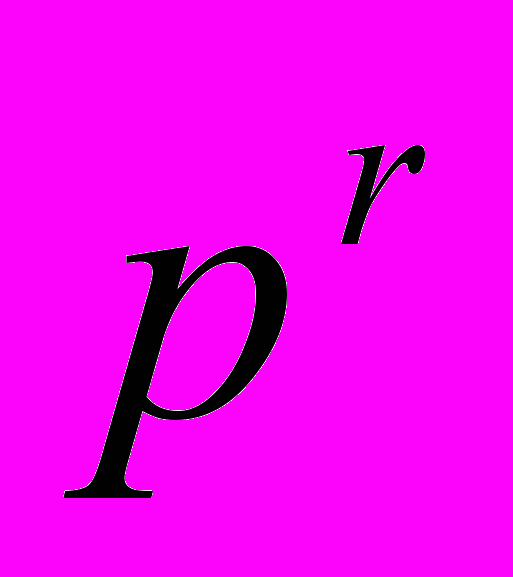 элементов. Неприводимые многочлены в конечном поле. Разложение многочлена на неприводимые в конечном поле. Построение полей Галуа элементов. Неприводимые многочлены в конечном поле. Разложение многочлена на неприводимые в конечном поле. Построение полей Галуа  Круговые многочлены. Круговые многочлены. |
| 17 | Метод Кронекера – Шуберта разложения многочлена на множители над кольцом 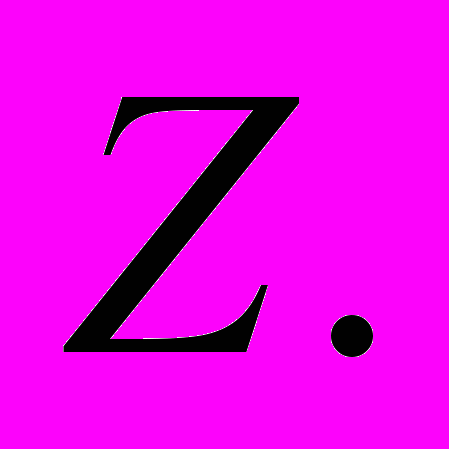 Разложение на свободные от квадратов множители над конечными полями. Разложение на свободные от квадратов множители над конечными полями. |
| 18 | Разложение многочлена на множители разных степеней над конечными полями. Алгоритм Берлекэмпа разложения многочлена на множители над конечным полем. |
6. Учебно-методическое и информационное обеспечение дисциплины:
а) основная литература:
- Ноден П., Китте К. Алгебраическая алгоритмика. – М.: Мир, 1999. – 720с.
- Яблокова С.И. Основы алгебраической алгоритмики. Часть 1: учебное пособие. – Ярославль:ЯрГУ, 2008. – 127с.
3. Яблокова С.И. Основы алгебраической алгоритмики. Часть 2: учебное пособие. – Яро-
славль: ЯрГУ, 2009. – 120с.
б) дополнительная литература:
1. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976.
2. Берлекэмп Э. Алгебраическая теория кодирования. – М.: Мир, 1971.
3. Акритас А. Основы компьютерной алгебры с приложениями. – М.: Мир, 1994. – 554с.
