Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания
| Вид материала | Документы |
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2306.3kb.
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2307.28kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 6750.33kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 5892.74kb.
- В. М. Найдыш Концепции современного естествознания, 8133.34kb.
- Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
- Концепции Современного Естествознания, 274.86kb.
- Программа курса «Концепции современного естествознания», 168.05kb.
- Программа дисциплины Концепции современного естествознания Специальность/направление, 456.85kb.
- Бюллетень новых поступлений в нб согу за период с 05. 2011 по 10. 2011гг, 975.89kb.
Эволюционный этап развития химии, начавшийся с 60-х гг. XX в., связан с синтезом новых сложных, высокоорганизованных соединений без участия человека. Необходимость решать эволюционные задачи у химиков возникла по следующим причинам. Во-первых, это мечта овладеть опытом «лаборатории живого организма». Во-вторых, ввести в химию идею истории, чтобы объяснить самопроизвольное восхождение от низших химических материальных систем к высшим. В-третьих, появились работы, указывающие на установленные опытным путем факты прогрессивной эволюции химических объектов через естественный отбор.
Эволюционный катализ, приведший к понятию эволюционной химии, связан с теорией А.П.Руденко. Самосовершенствование катализаторов в реакциях было открыто в работах А. Гуотми и Р. Каннингема в 1958 —1960 гг. Обычно катализаторы в ходе реакции стареют, и их деятельность ослабевает, а здесь они перестраивались в сторону повышения активности и селективности. В 1964— 1969 гг. А. П. Руденко, развивая идеи своего учителя А. А. Баландина о перестройке поверхности гетерогенных катализаторов под влиянием основной реакции, обобщил опыт действия катализаторов в различных реакциях и сформулировал теорию саморазвития каталитических систем. Процессы саморазвития химических систем, подводящие к биогенезу, тогда представлялись в русле идей А. И. Опарина. Саморазвитие систем происходит за счет постоянного поглощения катализаторами потока энергии, выделяющейся в ходе реакции. Таким образом, система является открытой, в ходе реакции происходит отбор каталитических центров с наибольшей активностью.
Освоение опыта живой природы — давняя мечта химиков. Еще Берцеллиус называл биокатализ основой основ лаборатории живого организма. Ориентацию на опыт живой природы проводили Либих, Пастер, Бертолле, Н. Н. Семенов и др. Н. Н. Семенов открыл разветвленные цепные реакции, что послужило сближению
539

 химии и физики, подтолкнуло к изучению неравновесных систем. Но биокатализаторы очень быстро портятся и теряют свою активность. Встала проблема стабилизации ферментов и создания иммобилизованных ферментов — выделенных из живого организма и прикрепленных к твердой поверхности путем адсорбции. Они устойчивы, их можно использовать многократно. Эти работы были начаты И.В.Березиным.
химии и физики, подтолкнуло к изучению неравновесных систем. Но биокатализаторы очень быстро портятся и теряют свою активность. Встала проблема стабилизации ферментов и создания иммобилизованных ферментов — выделенных из живого организма и прикрепленных к твердой поверхности путем адсорбции. Они устойчивы, их можно использовать многократно. Эти работы были начаты И.В.Березиным.Реакция Белоусова—Жаботинского — один из наиболее впечатляющих примеров возникновения самоорганизации в химических реакциях. В 1951 г. Б. П. Белоусов установил, что в растворе серной и малоновой кислот, сульфата церия и бромида калия при добавлении в качестве индикатора ферроина можно следить за ходом окислительно-восстановительных реакций по изменению цвета или по спектральному поглощению. Как только все эти вещества сливают в пробирку, раствор начинает менять цвет с красного, означающего избыток Се3+, на голубой, соответствующий избытку Се4+. В зависимости от концентрации раствора цвет менялся периодически, и этот период четко сохранялся, поэтому такие реакции стали называть «химическими часами». Кривая изменения поглощения света показывала, что колебания отличаются от синусоидальных, а начиная с некоторого числа колебаний, определяемого концентрацией, спонтанно возникают неоднородности концентрации и образуются устойчивые красные и синие слои, сохраняющиеся в течение получаса. Поскольку реакция идет в замкнутой системе, она приходит в конце концов к состоянию равновесия.
Как выразился А.И.Осипов (МГУ), «можно сказать, что химический организм умирает, задушенный избытком энтропии, которую нет возможности выбрасывать в окружающую среду». Белоусов писал (1957): «В реакционной смеси возникает ряд скрытых, упорядоченных в определенной последовательности окислительно-восстановительных процессов, один из которых периодически выявляется отчетливым временным изменением цвета взятой реакционной смеси». В начале 50-х гг. это казалось невозможным. Понимание механизма происходящей реакции связано с работами А.М.Жаботинского, который с 1964 г. исследовал много сходных химических реакций. Сейчас реакция Белоусова—Жаботинского изучается, вошла в учебники и явилась толчком к развитию новой области науки, меняющей мировоззрение эпохи.
Образование структуры в жидкостях в этих химических реакциях заинтересовало И. Р. Пригожина с сотрудниками в начале 70-х гг. В ряде опытов картина изменения цвета как бы замирала, а затем возникали окрашенные слои или устойчивые пространственные структуры типа тех, которые получались в теоретической модели Тьюринга. Английский математик А. Тьюринг сформулировал задачу о возможности образования в реакторе в усло-
540
виях химической реакции устойчивых конфигураций промежуточных продуктов и построил теорию их образования (1952). Фигуры сохранялись до тех пор, пока не иссякал запас начальных веществ-реагентов. Это свойство роднило их с диссипативными структурами, которые должны непрерывно «подпитываться» энергией и веществом от внешней среды. В обеих ситуациях структуры возникали в открытой системе, находящейся в неравновесном состоянии, и при наличии внешней подпитки, а эффект достигался после преодоления некоего порогового значения меняющегося параметра. И группа Пригожина, переформулировав модель Тьюринга, создала свою, названную брюсселятором в честь города, где работали.
Они рассмотрели протекание реакции между двумя сортами непрерывно поступающих в реактор продуктов, причем количество этих веществ поддерживалось постоянным. После реакции продукты реакции выпадали в осадок, но все время в объеме присутствовали два промежуточных вещества. В реакции Белоусова промежуточные вещества периодически мерцали, создавая эффект изменения цвета раствора. Расчет дал колебательный режим при определенном соотношении реагентов, изменение соотношений между реагентами менял характеристики колебаний концентраций промежуточных продуктов реакции.
Уравнения, описывающие этот процесс, совпали с уравнениями автоколебательных систем (электрических или механических).
Автоколебательные химические реакции нескольких типов были открыты в 70 —80-е гг. XX в. Выход таких реакций меняется с течением времени; такие реакции были обнаружены и в живой природе. Изучение автоколебательных реакций составляет часть нестационарной кинетики. Автоволновые процессы — аналоги автоколебаний для распределенных систем — исследовались советскими учеными. Сам термин «автоволны» был введен одним из создателей нелинейной оптики академиком Р. В. Хохловым. Советская школа подошла к изучению явлений самоорганизации со стороны развитой теории колебаний и волн. В конце 50-х гг. в научной школе, созданной академиком Л.И.Мандельштамом, сложилось направление по теории автоколебаний. Эти работы продолжил академик А. А. Андронов, сформировавший Горьковскую научную школу. После того как работы Андронова получили известность, автоколебания стали обнаруживать всюду—в механике, радиотехнике, теории автоматического регулирования, химии, биологии, экологии. В это время в МГУ теорию волн развивали Хохлов и С. А.Ахманов, создавший к 70-м гг. свою школу нелинейной оптики.
Автоволны — это самоподдерживающиеся волны, которые распространяются в активных средах или средах, поддерживаемых энергетически. За счет внутренних источников среды автоволны способны поддерживать свои характеристики, поэтому автоволны были открыты при химических реакциях, реакциях горения, при пере-
541

 даче возбуждения по нервным волокнам, мышцам, сетчатке глаза, при анализе численности популяций и т.д. Волна возбуждения движется по возбудимой среде без затухания, потери на диссипацию полностью поддерживаются подводом энергии извне.
даче возбуждения по нервным волокнам, мышцам, сетчатке глаза, при анализе численности популяций и т.д. Волна возбуждения движется по возбудимой среде без затухания, потери на диссипацию полностью поддерживаются подводом энергии извне.Пример распространения автоволны — распространение фронта горения. В 1938 г. Зельдович и Франк-Каменецкий установили, что в однородной среде фронт горения движется с постоянной скоростью, определяемой параметрами среды и не зависящей от начальных условий, кроме того, остается неизменной и форма профиля этой волны. Для полной аналогии с биологической задачей нужно было наделить среду способностью к восстановлению. Оно имеет место при сгорании травы в степи — после сгорания (третьей стадии) трава вновь отрастает, так что степь может гореть вновь. Сегодня процессы типа горения с восстановлением лежат в основе исследования почти всех возбудимых сред. В реакции Белоусова— Жаботинского осуществляется процесс окисления с последующим подавлением его за счет выделения ингибитора. При горении вместе с повышением теплоты тоже может выделяться какое-то вещество, подавляющее горение. Если выделение ингибитора произойдет быстро, то он может прервать процесс горения, и для продолжения процесса нужно будет запускать новую волну и продолжать это до тех пор, пока не будет израсходовано все горючее. Длительность рефракторного состояния определяется временем, которое необходимо для рассасывания ингибитора (например, дыма).
При хорошем перемешивании продуктов в объеме модель сильно усложняется (ее называют точечной), но устойчивые во времени и пространстве структуры промежуточных продуктов сохраняются. Эти структуры спонтанно возникают под действием термодинамических сил в далекой от равновесия системе, когда ее параметры превышают критические значения, т.е. происходит перестройка в системе, называемая самоорганизацией. Группа Приго-жина создала модель для изучения волновых явлений реакции Белоусова—Жаботинского, названную ими реакцией в системе БМФ (аббревиатура от слов: бромид — броммалоновая кислота — ферроин). В ней могут быть самовозбуждающиеся волны, или говорят об образовании волнообразных пространственно-временных диссипативных структур. Волна концентрации возникает в начале реакции, отражаясь от стенок реактора, ее источник — мелкие неоднородности среды или небольшие повышения концентрации кислоты, т.е. случайные неоднородности или флуктуации, которые до некоторых пор гасятся силами внутренней инерции. Помещая мелкие неоднородности в раствор, можно управлять этими волнами, делать их сферическими или спиральными.
Открытие Белоусовым колебательной реакции И.Пригожин назвал «одним их важнейших экспериментов нашего века». Колебательная реакция имеет в своей основе два типа молекул,
542
способных превращаться друг в друга. При хаотических столкновениях молекул был бы получен усредненный цвет, что и наблюдается вблизи равновесия. Вдали от него происходит иное — раствор меняет окраску синхронно. Получается, что молекулы как бы устанавливают связь между собой на больших расстояниях через большие промежутки времени, т.е. есть сигнал, на который молекулы действуют разом, система реагирует как целое. Раньше такое поведение считали присущим только живому. Пригожин рисует картину поведения систем с большим числом взаимодействующих субъединиц как вблизи равновесия, так и в удалении от него. При удалении от равновесия система «теряет иммунитет к возмущениям», становится неустойчивой, и если эти возмущения (автокатализ) достаточно сильны, система достигает точки бифуркации, в которой ее отклик на внешнее воздействие становится неоднозначным, возврат к начальным состояниям необязательным. Происходит необратимый переход в новое, когерентное, состояние: система приобретает новую диссипативную структуру (образованную за счет рассеяния—диссипации —энергии). Суть когерентности — в «коллективной стратегии поведения» субъединиц системы. Затем система может пройти и следующие точки бифуркации, приобретая черты историзма. Так начался новый уровень познания природы — эволюционный.
Подходы к проблеме химической эволюцииу И.Пригожина и А. П. Руденко основаны на неравновесной термодинамике, но отличаются по самоорганизующимся объектам. Пригожин исследует макросистемы с целью доказательства возможности самоорганизации. Поэтому он не описывает химическую эволюцию с естественным отбором. Руденко исследует самоорганизацию макросистем с целью воссоздания хода химической эволюции через отбор для выяснения биогенеза.
13.7. Возникновение самоорганизации в морфогенезе
Разрывный характер образования видов следует из анализа уравнений популяционной генетики, и этот процесс подобен фазовому переходу (М. В. Волькенштейн, Б. Н. Белинцев). Время существования вида гораздо более продолжительно, чем время его образования. На каждом скачке возникают новые признаки, часть из которых становится объектами отбора на той или другой стадии адаптации. Нуклеиновые кислоты и белки меняются постепенно, путем точечных замещений. В процессе образования видов и макроэволюции меняются качество белка, место и время его работы в организме. Поэтому и важна регуляция работы генов, о которой пока мало известно, поскольку регуляторные вещества функционируют в очень малых количествах.
543
 Существует связь между историческим развитием (филогенезом) и индивидуальным развитием организма (онтогенезом). Образование структур в онтогенезе означает изменения в пространственном использовании основных клеточных механизмов, но не самих механизмов. Так, главные типы клеток позвоночных почти не изменились за 500 млн лет, менялись условия существования клеток от вида к виду. При этом важна позиционная информация (ПИ) — этот термин введен Л.Вольпертом (1969). Каждая клетка воспринимает информацию в соответствии со своей генетической программой, и различия в строении организмов определяются уже не самими клетками, а их относительным расположением. Позиционная информация предполагает наличие некоторого физического свойства, которое диктует выбор режима функционирования и пространственной ориентации, после чего начинается стадия трансляции ПИ. Такой подход позволяет разобраться в механизмах становления пространственной упорядоченности клеток, отвлекшись от деталей процессов внутри них.
Существует связь между историческим развитием (филогенезом) и индивидуальным развитием организма (онтогенезом). Образование структур в онтогенезе означает изменения в пространственном использовании основных клеточных механизмов, но не самих механизмов. Так, главные типы клеток позвоночных почти не изменились за 500 млн лет, менялись условия существования клеток от вида к виду. При этом важна позиционная информация (ПИ) — этот термин введен Л.Вольпертом (1969). Каждая клетка воспринимает информацию в соответствии со своей генетической программой, и различия в строении организмов определяются уже не самими клетками, а их относительным расположением. Позиционная информация предполагает наличие некоторого физического свойства, которое диктует выбор режима функционирования и пространственной ориентации, после чего начинается стадия трансляции ПИ. Такой подход позволяет разобраться в механизмах становления пространственной упорядоченности клеток, отвлекшись от деталей процессов внутри них.Морфогены — специальные белковые молекулы — сообщают ПИ. Они могут подавлять или активизировать работу регуляторных генов. Морфогены образуют и морфополя — совокупности физико-химических процессов, протекающих в далеких от равновесия открытых системах. Математические модели таких процессов дают решение, которое показывает, что в первоначально однородной системе неоднородности (пространственные и временные) порождают упорядоченность. При этом неоднородности являются продуктом диффузии и автокаталитических реакций, происходящих с разными скоростями для разных веществ.
Механизм формирования пространственной упорядоченности в онтогенезе многоклеточных организмов принципиально по-новому объяснял почти 50 лет назад английский математик А. Тьюринг, когда почти ничего не знали о молекулярных процессах в клетке. Тьюринг показал, что однородное распределение химических реагентов по объему химического реактора при определенных условиях становится неустойчивым, и у системы появляются новые, коллективные черты поведения — в ответ на сколь угодно малые возмущения она покидает исходное состояние и эволюционирует в новое. Тьюринг выделил условия возникновения самоорганизации. Клетки могут свободно перемещаться и взаимодействовать друг с другом. При гидролитическом расщеплении АТФ выделяется энергия, которая служит источником работы. Малые изменения в поле морфогенов, изменения времени и места действия регуляторных генов приводят к существенным изменениям строения целого организма. Пример тому — человек и шимпанзе. Их белки и клетки почти одинаковы, отличия в последовательности аминокислот в 44 белках составляют не более 1 %. Итак, регуляция синтеза белков определяет вид, а не
544
сами белки. Поэтому и направленная эволюция требует меньшего времени, чем потребовалось бы при простом переборе изменений в геномах.
Гены не постоянны, они могут изменяться не только замещениями нуклеотидов в геномах вследствие мутаций, но и из-за переноса генов внутри хромосом, от одной хромосомы к другой, от одного организма к другому. Это «непостоянство генома» ускоряет эволюцию и говорит о единстве всего живого. Генетические элементы могут перемещаться «по горизонтали», что используется в генной инженерии. Например, кишечную палочку «научили» синтезировать инсулин и интерферон. Все функции клетки и организма определяются белками, т.е. цепями из 20 типов аминокислотных остатков. Эти цепи могут сворачиваться в глобулы, достаточно плотные образования, похожие на несимметричные кристаллы. Для синтеза белков необходимы РНК и ДНК, служащие матрицами для сборки цепей. Нуклеиновые кислоты состоят из четырех сортов нуклеотидов. Структурный ген — участок цепи ДНК, ответственный за синтез одной белковой цепи. Нуклеиновые кислоты представляют законодательную власть клетки, белки — исполнительную. В процессе эволюции меняются гены и соответствующие белки.
Эволюцию на молекулярном уровне позволяет проследить сопоставление однотипных белков разных видов организмов, можно построить и эволюционное древо на основе состава белка. Различие может быть связано с естественным отбором, но отбор определяется биологическими функциями белков, фенотипами. Однако не всегда однозначна связь «текста» первичной структуры цепи и пространственного строения белковой глобулы с биологической функцией белка. Не все мутации белков ведут к изменению их функций, часть их оказывается нейтральной. По теории нейтралистской молекулярной эволюции японского генетика М.Кимуры (1968) скорость эволюции белка не зависит от размера популяции, причем активная часть цепи эволюционировала медленнее, чем ее «каркас». Скорость эволюции белка за год он выражал отношением числа замещенных аминокислотных остатков к одному остатку. Она оказалась постоянной для разных линий эволюции при сохранении функций и пространственной структуры молекулы. Величины скоростей замещений были меньше 10-9. Значит, время существования Вселенной недостаточно для построения макромолекул, если бы положение каждого звена фиксировалось отбором.
Выводы Кимуры об эволюции белков и нуклеиновых кислот не следует распространять на естественный отбор, относящийся к организмам. Нейтральность мутаций в «каркасе» белка во многом предопределена его строением и кодированием. Эволюция макромолекул отличается от эволюционного поведения организмов. Гомеостаз ведет к тому, что многие вредные мутации ведут себя
545

 как нейтральные. Например, одна из мутаций ухудшила свойства белка-фермента, и он стал перерабатывать субстрат медленней. Тогда организм исправит ситуацию каким-то способом, может быть, увеличит количество этого ослабленного фермента.
как нейтральные. Например, одна из мутаций ухудшила свойства белка-фермента, и он стал перерабатывать субстрат медленней. Тогда организм исправит ситуацию каким-то способом, может быть, увеличит количество этого ослабленного фермента.Математические модели могут изменить представление биологов об истоках упорядоченности в эволюции. Ведь все живые организмы являются строго упорядоченными системами. Они обладают сложными структурами, которые поддерживали и воспроизводили себя благодаря слабо выраженному взаимодействию химических и поведенческих процессов. Со времен Дарвина биологи рассматривали естественную эволюцию как основной источник порядка.
13.8. Моделирование отношений между трофическими уровнями в биоценозах
Между видами существует связь, основанная на конкуренции за места обитания, за пищу и на «сожительстве» (например, лишайники как симбиоз грибов и водорослей). Широко распространена связь «паразит—хозяин», а также передача наследственных признаков через вирусы и бактериофаги (у бактерий).
В современной биологии одно из центральных мест занимают проблемы кооперативных эффектов и самоорганизации, соотношения «случая» и «необходимости». С появлением понятий биоценоза и биогеоценоза в биологических исследованиях стали применять методы математического моделирования, а использование ЭВМ для анализа процессов в сложных системах существенно обогатило науку о биосфере и экологию.
По распределению и численности видов имеется огромная информация, но ее нужно перевести на математический язык. Вводят «макроскопические характеристики», описывающие популяцию. Это число особей, соответствующее параметру порядка сложной системы. Оно «управляет» судьбой особей «в среднем». Если п — число особей (их плотность), то изменение п от скорости (числа) рождений g и числа смертей d можно записать как
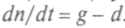 . В простейшем случае
. В простейшем случае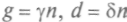 , где
, гдекоэффициенты не зависят от общей численности, а определяются доступностью пищи, климатическими условиями и т. п. Если эти внешние условия поддерживаются постоянными, то уравнение
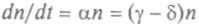 описывает растущую или убывающую по экспоненте популяцию. Значит, стационарного решения у этого уравнения нет, и рост не зависит от плотности, поэтому внешние условия должны зависеть от плотности. Наиболее важным из всех факторов, которые мы проигнорировали, вероятно, является истощение источников питания, который можно учесть введением
описывает растущую или убывающую по экспоненте популяцию. Значит, стационарного решения у этого уравнения нет, и рост не зависит от плотности, поэтому внешние условия должны зависеть от плотности. Наиболее важным из всех факторов, которые мы проигнорировали, вероятно, является истощение источников питания, который можно учесть введением546
в уравнения члена
 (здесь предполагается, что пища поступа-
(здесь предполагается, что пища поступа-ет с постоянной скоростью). Тогда получается уравнение Ферхюльста:

При этом могут встретиться ситуации: «конкуренция—сосуществование»; «хищник—жертва»; «симбиоз». При сосуществовании различные виды не питаются одной и той же пищей, не поедают друг друга, размножаются в разных местах. Тогда уравнения для численности записываются как
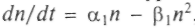 ,
, 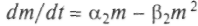 . Ситуация усложняется, если виды живут или пытаются жить за счет одного и того же источника пищи или зависят от одних и тех же жизненных условий. Пример: растения, извлекающие фосфор из почвы. При этом одни растения закрывают листьями другие, лишая их солнечного света, или другой пример — птицы, которые строят гнезда в одних и тех же дуплах, и т.п. Математически это соответствует установлению генерации в лазере или автокаталитической реакции между двумя группами молекул. Решение показывает, что выживет только один тип, наиболее приспособленный. Это выживание может быть достигнуто улучшением индивидуальных констант и адаптацией. Если перекрываются источники пищи N, М:
. Ситуация усложняется, если виды живут или пытаются жить за счет одного и того же источника пищи или зависят от одних и тех же жизненных условий. Пример: растения, извлекающие фосфор из почвы. При этом одни растения закрывают листьями другие, лишая их солнечного света, или другой пример — птицы, которые строят гнезда в одних и тех же дуплах, и т.п. Математически это соответствует установлению генерации в лазере или автокаталитической реакции между двумя группами молекул. Решение показывает, что выживет только один тип, наиболее приспособленный. Это выживание может быть достигнуто улучшением индивидуальных констант и адаптацией. Если перекрываются источники пищи N, М: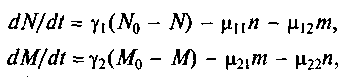
|где
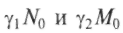 — скорости поступления пищи;
— скорости поступления пищи;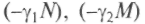 —
—547
убыль пищи за счет внутренних причин типа гниения. Рассматривая правые части уравнений («силы») в плоскости п, т, можно найти условия, при которых возможно сосуществование. Обобщение на случай многих видов и источников пищи производится аналогично. Поэтому понятно, какую важную роль играют экологические ниши для выживания видов и почему виды так приспособлены к ним. Примером такого сосуществования служит распределение растительности по высоте, что изучается специально в биогеографии. Эта модель проста, но позволяет сделать оценки относительно динамики популяций при введении еще одного параметра, отвечающего за появление новых видев. Гены могут претерпевать мутации, образуя аллели. Мутации происходят случайно, но частота их может меняться под воздействием внешних факторов (повышение температуры, добавление химических агентов, ультрафиолетовое облучение и т.п.), поэтому можно считать, что мутации оказывают «мутационное давление», благодаря которому возникают особи новых типов. Новые свойства сначала будут рецессивными и только через несколько поколений станут доминантными. Пусть число особей новых типов, возникших из-за случайной мутации, равно и. Их показатели рождения и гибели иные, и но-

 вая популяция возникнет только при наличии флуктуации, которые будем описывать некой флуктуирующей силой и введем ее в уравнения роста популяций:
вая популяция возникнет только при наличии флуктуации, которые будем описывать некой флуктуирующей силой и введем ее в уравнения роста популяций: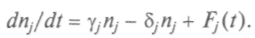
Пусть функция Fj(t) зависит от прежней популяции и факторов окружающей среды. Такие уравнения можно записать для разных типов, возникающих в системе. Так, система «подвидов» подвергается «давлению отбора», и это можно учесть, используя вышеприведенные уравнения, если считать, что условия окружающей среды (пища, например) остались прежними. Тогда для любого из подвидов, пользующихся тем же источником пищи, получим уравнение:

Если скорость мутаций у определенных видов мутантов мала, то выживут только наиболее приспособленные. Как отмечал Ха-кен, размножение видов можно заменить циклом А—В —С—..., который постулировался при описании эволюции макромолекул. Итак, возникновение новых видов благодаря мутациям (флуктуирующей силе) и отбору (вынуждающей силе) можно рассматривать как аналог неравновесного фазового перехода второго рода, т. е. аналогично процессам в лазере.
Модель Вольтерра—Лотки была одной из первых экологических моделей. В любом биоценозе происходит взаимодействие между всеми его элементами: особи одного вида взаимодействуют с особями и своего вида, и других видов. Эти взаимодействия могут быть мирными, а могут иметь связь типа «хищник-жертва». Было замечено, что численность хищных рыб колеблется в обратной пропорции относительно колебаний численности мелких рыбешек, которые служат им пищей. Анализ этих колебаний позволил математику Вито Вольтерра вывести (1926) уравнения, описывающие этот процесс. Если бы в биоценозе было только два вида (очень большое упрощение), то и в этом случае динамика численности каждого из видов сильно отличалась бы от картины их независимого существования.
Примером анализа таких структур может служить эволюция численности зайцев и волков, которая характеризуется колебаниями во времени. Изменение численности животных установлено по числу заготовленных шкурок. Абстрагируясь от различных обстоятельств, так или иначе влияющих на численность зверей, можно проанализировать важнейшую зависимость: зайцы едят траву, а волки — зайцев. Если бы жили одни зайцы и корма было достаточно, то их численность росла бы по экспоненциальному закону, а если бы жили только волки, то они вымирали бы. При их совместном существовании скорость изменения численности зайцев и волков связа-
548
 на с частотой их столкновений, т. е. пропорциональна количеству тех и других с некоторым коэффициентом. Уже эти соображения приведут к системе уравнений, и при определенных условиях система «хищник—жертва» придет в равновесие.
на с частотой их столкновений, т. е. пропорциональна количеству тех и других с некоторым коэффициентом. Уже эти соображения приведут к системе уравнений, и при определенных условиях система «хищник—жертва» придет в равновесие.В случае неожиданной флуктуации (смерть волка или зайца, отстрел во время охоты и т.д.) равновесие нарушается и система приходит в движение. Она ведет себя как колебательная система, численности «хищников» и «жертв» начинают колебаться синфазно, с отставанием. Объяснение простое: рост численности зайцев приводит к увеличению питания для волков, но уменьшает количество травы, так что вскоре численность волков вырастает, а зайцев — уменьшается. Количество травы увеличивается, но запасы пищи для волков уменьшаются, и их численность падает. Тогда поголовье зайцев снова растет, и процесс повторяется. Режим колебаний с определенным периодом оказывается устойчивым. Такая система описывается уравнениями:
 , где первое уравнение описывает количество жертв п, второе — количество хищников т. Эти уравнения имеют периодическое решение. Стационарное решение соответствует полному вымиранию, и оно единственное устойчивое. В природе такое может случиться, но биологи указывают на возможность животных-жертв найти убежище, не доступное хищникам, так что некоторая часть их выживет. Модель может усложняться введением нескольких типов жертв, которыми может питаться один хищник, и другими вариантами.
, где первое уравнение описывает количество жертв п, второе — количество хищников т. Эти уравнения имеют периодическое решение. Стационарное решение соответствует полному вымиранию, и оно единственное устойчивое. В природе такое может случиться, но биологи указывают на возможность животных-жертв найти убежище, не доступное хищникам, так что некоторая часть их выживет. Модель может усложняться введением нескольких типов жертв, которыми может питаться один хищник, и другими вариантами.Ситуация «симбиоз» тоже моделируется, как и ситуации «хищник—жертва» и «конкуренция—сосуществование». Симбиоз отражает кооперацию отдельных видов в борьбе за существование, когда один вид помогает или покровительствует другому (как, например, кооперация пчел или деревьев). Поскольку скорость размножения одного вида зависит от наличия другого, то, пренебрегая внутривидовым подавлением
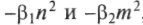 , имеем:
, имеем:
Здесь стационарный случай соответствует и = т = 0. В этих простых схемах не хватает очень многих факторов — смены климата и погоды, связи возраста особи и смертности, колебаний запасов пищи в разное время года и на разных территориях и т.д. Но использование даже простых моделей при разных, эмпирически учтенных тех или других параметрах дает интересные результаты.
Строя математические модели и проводя полевые испытания, ученые пытаются понять, каким образом паразиты и их хозяева коэволюционировали в тесные сообщества. Компьютерные модели этих процессов соответствуют «гонке вооружений» в ходе эво-
549


 люции. Паразиты должны все время приспосабливаться, чтобы получить от хозяина больше ресурсов для роста своей популяции, а хозяин всячески старается этого не допустить. Биологи-эволюционисты считают, что существование полов с эволюционной точки зрения неудачно, и половые различия должны бы постепенно исчезнуть, но этого не происходит. Вероятно, потому, что пол является неким «секретным оружием», сохраняющим большую устойчивость хозяина: ведь паразит приспосабливается обычно к определенному его типу. Как только хозяева становятся жертвами, численность менее распространенных типов хозяев увеличивается, и наоборот. Исследования 90-х гг. XX в. показали, что бесполые рыбы чаще поражаются паразитами, чем разнополые. Те же результаты получены и на птицах — наличие паразитов наносит ущерб яркому оперению, и самки не выбирают таких самцов.
люции. Паразиты должны все время приспосабливаться, чтобы получить от хозяина больше ресурсов для роста своей популяции, а хозяин всячески старается этого не допустить. Биологи-эволюционисты считают, что существование полов с эволюционной точки зрения неудачно, и половые различия должны бы постепенно исчезнуть, но этого не происходит. Вероятно, потому, что пол является неким «секретным оружием», сохраняющим большую устойчивость хозяина: ведь паразит приспосабливается обычно к определенному его типу. Как только хозяева становятся жертвами, численность менее распространенных типов хозяев увеличивается, и наоборот. Исследования 90-х гг. XX в. показали, что бесполые рыбы чаще поражаются паразитами, чем разнополые. Те же результаты получены и на птицах — наличие паразитов наносит ущерб яркому оперению, и самки не выбирают таких самцов.Созидательный характер симбиоза показала Л.Маргулис, исследуя роль естественного отбора в эволюции. Она предположила, что эукарио-тические клетки, имеющие внутренние органеллы, произошли от симбиоза более простых безъядерных клеток. Митохондрии и хлоропласты содержат иные гены, чем ядра клеток эукариот, но похожи на гены некоторых бактерий. Возможно, им не нужно было изобретать дыхание и фотосинтез методом «проб и ошибок». Большинство травоядных животных зависят от микроорганизмов, живущих в их кишечнике и переваривающих потребляемую животными клетчатку. Эволюционную схему, показывающую, как травоядные животные могли развиться от симбиоза их предков и микроскопических паразитов растений, очертил П. Прайс. Паразит приобрел способность производить ферменты для переваривания веществ, составляющих организм его хозяина-растения. Животное, вступив в симбиоз с паразитом, смогло использовать для себя продукты ферментации растительной массы. Успех в освоении новых пищевых ресурсов обеспечил преимущества в естественном отборе таких животных.
Жизнь даже небольшого озера невероятно сложна и многообразна, так что описать и «проверить алгеброй» эту достаточно простую систему почти невозможно, хотя такие попытки имеют место. Во многих странах разработаны системы моделирования гидробиоценозов — акватроны, соединенные напрямую с ЭВМ, которые сами ведут наблюдения и подсчитывают объекты, т. е. система сама корректирует модель. Например, для учета химико-биологических превращений нужно знать интенсивность роста водорослей, фотосинтеза, смертность каждого вида, скорость разложения органического вещества. Конечно, такие разработки очень дороги, но в конечном счете обещают значительный экономический результат.
Химическое равновесие в биосфере опирается на биотический круговорот. Хотя отдельные циклы изучены недостаточно, ясно, что система находится на грани порядка и хаоса и может быть выведена из этого состояния неустойчивого равновесия даже малым воздействием. Ряд ученых (Л. Маршалл, М. И. Буды-ко, Л.Беркнер и др.) считают, что резкое уменьшение углекис-
550
лоты в атмосфере с появлением фотосинтеза приводило к похолоданию и оледенению Земли и, естественно, к нарушению существовавших циклов. Собственно, это сейчас и делает индустриально вооруженный человек. Биосфера сформировалась по своему плану, без участия человека, и биогеоценозы пока еще находят резервы, чтобы справиться с вмешательством человека, но неизвестно, насколько их хватит.
Качественно новый этап развития биосферы начался с появлением человека в конце третичного периода, хотя сначала его деятельность мало отличалась от деятельности других существ. Беря у биосферы все необходимое, человек отдавал ей то, что могли использовать другие, т.е. включился в биотический круговорот. Добывание огня вьщелило человека из ряда других животных. При этом человек не только сумел расселиться в районы холодного климата, пережить оледенения и защититься от хищников, но и научился уничтожать органические остатки, заменив в чем-то микроорганизмы. Так с малых шагов началось ускоряющееся изменение равновесия в биосфере.
13.9. Элементы теории самоорганизованной критичности
Системы, состоящие из многих взаимодействующих элементов, постоянно самоорганизуются и могут достичь некоторого критического состояния, в котором даже малое событие вызывает цепную реакцию, могущую привести к катастрофе. Когда происходит что-то непредвиденное или катастрофа, то всегда ищут причину. Например, когда узнали о гибели динозавров по отпечаткам на окаменелостях, одни палеонтологи приписали их исчезновение падению крупного метеорита, другие — извержению вулкана. Землетрясение геологи связывают с неустойчивостью вдоль разлома земной коры. Когда рушится рынок акций, находят где-то неконтролируемую продажу товара.
При исследовании сложных систем часто пользуются теми же методами, что и при исследовании простых систем, так как они хорошо разработаны и проверены. Большую систему делят на малые подсистемы, изучают каждую из них по отдельности и считают, что реакция или отклик в каждой из них пропорционален внешнему возмущению. Описывают динамику больших систем в терминах равновесного состояния, которое изредка нарушается внешним воздействием. Но оказалось, что многие хаотические системы не поддаются такому анализу. П. Баком, К.Визенфельдом и Ч.Тангом (США) была разработана теория самоорганизованной критичности.
Согласно этой теории, многие составные части системы эволюционируют естественным образом к критическому состоянию,
551


 в котором малое возмущение может вызвать цепную реакцию, способную повлиять на любое число элементов системы. И хотя в составных частях происходит больше незначительных событий, чем катастроф, цепные реакции разных масштабов вошли в динамику системы, т. е. малые события вызывает тот же механизм, что и крупные. Кроме того, составные части системы не достигают равновесия, а эволюционируют от одного метастабильного состояния к другому. Считается, что глобальные характеристики не зависят от микроскопических механизмов, поэтому их нельзя понять, разбивая систему на подсистемы и анализируя их отдельно. Эта модель исследовалась и улучшила понимание процессов в эволюции земной коры, на рынке акций, в экосистемах и других больших системах, которые ранее анализировали по частям.
в котором малое возмущение может вызвать цепную реакцию, способную повлиять на любое число элементов системы. И хотя в составных частях происходит больше незначительных событий, чем катастроф, цепные реакции разных масштабов вошли в динамику системы, т. е. малые события вызывает тот же механизм, что и крупные. Кроме того, составные части системы не достигают равновесия, а эволюционируют от одного метастабильного состояния к другому. Считается, что глобальные характеристики не зависят от микроскопических механизмов, поэтому их нельзя понять, разбивая систему на подсистемы и анализируя их отдельно. Эта модель исследовалась и улучшила понимание процессов в эволюции земной коры, на рынке акций, в экосистемах и других больших системах, которые ранее анализировали по частям.Идея теории самоорганизованной критичности началась с наблюдений и опытов с кучей песка. Г.Хелд, проводивший эксперименты по компьютерному моделированию, разработал устройство, которое медленно и равномерно — по одной песчинке — насыпало песок на круглую подложку. Песчинки сначала оставались в месте падения, потом громоздились в кучу, а когда склон становился очень крутым и достигалось критическое состояние, одна песчинка вызывала катастрофу. Песчинка падала сначала спокойно, но, достигнув неустойчивых песчинок, вызывала лавину — разновидность цепной реакции или ветвящегося процесса. Как только «активные» песчинки скатывались с кучи, процесс прекращался. Куча сохраняла свою крутизну и высоту, потому что вероятности прекращения активности и ее ветвления в среднем равны. Если крутизна будет меньше критической, то лавины будут слабее, а при большей кривизне — значительно возрастут.
Эксперименты с мокрым песком показали, что сначала лавины будут меньшего размера, чем в сухой куче, и крутизна превзойдет критическую, но затем резко произойдут обвалы и падения. Такая система неустойчива по многим параметрам, а ее критическое состояние весьма

устойчиво («суб- и суперкритические» крутизны стремятся стать «критическими», сбрасывая лишние песчинки). Хотя песок сыплется с постоянной скоростью, его количество меняется со временем, и график этой величины — хаотический сигнал разных длительностей. Возникающие при этом структуры, полученные при различных типах деформации мокрого песка в Институте горного дела СО РАН (Новосибирск, 1984), упорядочены (рис. 13.9).
Сигнал называют фликкер-шумом или шумом мерцания типа
552
1/f, если прошлые события в памяти сохраняются. «Белый», или «случайный», шум означает отсутствие корректировки динамики с прошлыми событиями. Шум мерцания широко распространен в природе: в активности Солнца и излучении галактик, в протекающем через резистор токе, в потоке воды в реке. Шум мерцания содержит наборы всех длительностей и всех амплитуд сигналов, возникающих, когда система, находящаяся в критическом состоянии, порождает цепные реакции всех амплитуд и длительностей.
Построенная в то же время математическая модель помогла понять динамику землетрясений, экосистем и турбулентности в жидкости. Еще в 1956 г. геологи Бено Гутенберг и Чарлз Рихтер (введший шкалу Рихтера) установили закон связи числа сильных и слабых землетрясений, который носит их имена. Согласно этому закону, число землетрясений, высвобождающих за год определенное количество энергии Е, пропорционально Е-b, где b
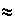 1,5, и не зависит от географического района. Следовательно, сильные землетрясения происходят реже слабых, и все они связаны с одним и тем же процессом. В качестве последнего обычно называют механизм проскальзывания: блоки коры слипаются, а затем скользят относительно других блоков, образуя разломы. При скольжении блоков возникшее напряжение снимается и распространяется на соседние районы.
1,5, и не зависит от географического района. Следовательно, сильные землетрясения происходят реже слабых, и все они связаны с одним и тем же процессом. В качестве последнего обычно называют механизм проскальзывания: блоки коры слипаются, а затем скользят относительно других блоков, образуя разломы. При скольжении блоков возникшее напряжение снимается и распространяется на соседние районы.Этот механизм был проверен на опытах, поставленных В.Бобровым и М.Лебедкиным, наблюдавшими «землетрясения», амплитуда и частота которых были связаны степенным законом. Они провели опыты с алюминиевым и ниобиевым стержнями и получили близкие результаты, хотя механизмы процессов в земной коре и модели отличались. Потом была создана компьютерная модель земной коры, состоящая из двух плит, — упругой и жесткой, взаимодействующих посредством трения. На этой модели результаты проверялись несколько раз, при этом записывались распределения сил до и после взаимодействия, а не детали динамики. Сначала регистрировались слабые «землетрясения», потом система эволюционировала к критическому состоянию, в котором регистрируются как слабые, так и сильные «землетрясения». Равномерное увеличение силы в целом уравновешивалось высвобождением ее на границе. Энергия, выделяемая во время землетрясения, связана в модели с числом событий проскальзывания, происходящих после возникновения одиночной неустойчивости в каком-то «эпицентре». Если подсчитать число землетрясений каждой величины за длительный период, то получается закон Гутенберга—Рихтера (рис. 13.10). Катастрофические землетрясения представлены частью графика, относящейся к более высоким значениям энергии, а слабые — к низким. С.Обухов показал, что в четырех и более измерениях отдельные ветвящиеся процессы не-
553




зависимы и b = 1,5. Это подтверждает предположение о том, что земная кора находится в критическом состоянии.
Эта модель не только объясняет эволюцию землетрясений, но и описывает распределение их эпицентров. Степенные законы и ранее применяли для анализа распределений таких объектов, как горы, облака, галактики, вихри в турбулентных потоках. Показатель степени числа r вычисляется по числу объектов внутри сферы радиуса r. Такое распределение называют фракталом, и число фракталов в природе велико. Авторы описываемой теории считают фракталы мгновенными «срезами» самоорганизующихся критических процессов. Фрактальные структуры и шум мерцания — пространственные и временные «отпечатки» самоорганизованной критичности.
Задача прогнозирования землетрясений осложнена зависимостью от начальных условий; кроме того, иногда сказывается влияние событий, далеких от эпицентра. Численные эксперименты показали, что неопределенность начальных условий растет со временем по степенному, а не по экспоненциальному закону, как в системах с развитым хаосом, т.е. соответствует эволюции на грани хаоса или состоянию «слабого хаоса». В этом проявляется самоорганизованная критичность, и поэтому некоторые
554
прогнозы возможны. Например, если погода есть явление хаотическое и 100 обсерваторий собирают достаточно информации на двухдневный прогноз, то 1000 обсерваторий могли бы обеспечить прогноз на четыре дня. Если погода — явление слабохаотическое, то 1000 обсерваторий обеспечили бы прогноз на 20 дней вперед. Вместо погоды можно говорить о куче песка или землетрясениях. Например, если известно, что распределение автомобилей на дорогах описывается шумом мерцания, то движения с попеременными остановками и троганием с места можно рассматривать как критические лавины, которые распространяются по потоку автомобилей.
В рассмотренных выше случаях теория самоорганизованной критичности применялась к системам с сохраняющимся числом частиц. Анализируя игру Конуэя «Жизнь», имитирующую возрастание сложности в биосистеме, авторы данной теории установили, что распределение живых ячеек является фракталом, который можно описать степенным законом с показателем степени 1,7. Таким образом, число живых ячеек колебалось со временем так же, как размеры лавин в куче песка, и система самоорганизовалась в критическое состояние.
Флуктуации в экономике, как заключили Ф.Андерсон и Б.Артур, также могут быть вызваны лавинами в самоорганизованном критическом состоянии системы. Б. Мандельброд из корпорации IBM проанализировал такие показатели, как индекс Доу-Джонса, и обнаружил флуктуации, соответствующие шуму мерцания. Различные метастабильные состояния экономики могут быть рассмотрены как метастабильные состояния кучи песка или земной коры. В других экономических моделях состояния более устойчивы, и большие агрегатные флуктуации могут возникать только от внешних ударов, влияющих на разные секции одинаково. Но причины их отыскать трудно, пример тому — депрессия 30-х гг. XX в. в США. В модели самоорганизованной критичности причины могут быть и при отсутствии таких «толчков». Большие флуктуации являются внутренним и неизбежным свойством динамики этой модели экономики. Такая проверка была проделана, и оказалось, что при изменении спроса на продукт нескольких компаний случайным образом на малую величину может возникнуть «лавина» в продаже и производстве.
Вопросы для самопроверки и повторения
- В чем заключается явление самоорганизации? Приведите примеры из области химии и физики. Почему они не могут быть описаны с позиций классической науки?
- Как строится термодинамика открытых систем? Что такое устойчивые и неустойчивые равновесные состояния? Поясните понятия простой и сложной системы.
- Как возникают структуры из хаоса в неорганической и живой материях? Каковы условия их образования? Приведите примеры из разных областей естествознания.
555
-
 Что такое синергетика и каково ее значение для современной картины мира? Каков механизм эволюции в соответствии с представлениями синергетики?
Что такое синергетика и каково ее значение для современной картины мира? Каков механизм эволюции в соответствии с представлениями синергетики?
- Какие этапы можно выделить в развитии самоорганизующихся систем? Что такое фазовое пространство и как оно используется в моделировании сложных систем?
- Поясните понятие диссипативной структуры по И.Пригожину.
- Каково соотношение случайного и закономерного в концепции развития? Какую роль сыграл принцип элементарного беспорядка в естествознании?
- Поясните понятия «хаос», «бифуркация», «катастрофа». Как теория катастроф связана с синергетикой?
- Какие системы могут находиться в высокоупорядоченном состоянии? Каковы необходимые условия возникновения «самоорганизации» и существуют ли достаточные?
10. Дайте представление о прямой и обратной связях в сложной систе
ме. Поясните связь процессов в земной коре с теорией самоорганизован
ной критичности. Дайте примеры использования этой теории.
