Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания
| Вид материала | Документы |
Содержание13.4. Математические закономерности эволюции. Понятие бифуркации 13.5. Синергетика — новый научный метод Коллективные процессы |
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2306.3kb.
- Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2307.28kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 6750.33kb.
- С. Г. Хорошавина концепции современного естествознания курс лекций, 5892.74kb.
- В. М. Найдыш Концепции современного естествознания, 8133.34kb.
- Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
- Концепции Современного Естествознания, 274.86kb.
- Программа курса «Концепции современного естествознания», 168.05kb.
- Программа дисциплины Концепции современного естествознания Специальность/направление, 456.85kb.
- Бюллетень новых поступлений в нб согу за период с 05. 2011 по 10. 2011гг, 975.89kb.
Пороговый характер самоорганизующихся процессов термодинамика связала с неустойчивостью: новая структура есть результат неустойчивости и возникает из флуктуаций. В «допороговом» состоянии флуктуации затухают и макроскопически не проявляются (например, в конвекционном потоке при малых температурах они рассасываются за счет сил вязкого трения). В состоянии выше порога флуктуации уже не рассасываются, а усиливаются, достигают макроскопических значений и выводят систему на устойчивый режим, создают новую структуру, возникающую после неустойчивости. Математически это связано с нелинейностью уравнений, описывающих систему вдали от равновесия. Если линейное уравнение имеет одно стационарное решение, то нелинейное — несколько. Система может принимать любое из этих состояний, и переход из одного в другое стационарное состояние соответствует преодолению порога.
Катастрофой называют скачкообразное изменение, которое может возникнуть в ответ на плавное изменение внешних условий. Для систем это означает потерю устойчивости. Область математики, занимающаяся катастрофами, названа теорией катастроф. Она является в некотором роде обобщением исследования функций на экстремум на случай многих переменных и опирается на теорию особенностей гладких отображений. Отображение поверхности на плоскость есть сопоставление каждой точки поверхности с точкой плоскости.
Исследования особенностей таких отображений начал в 1955 г. Г. Уитни, ознакомившись с работами Пуанкаре и Ляпунова, а также советских ученых — Андронова, развившего теорию бифуркаций, и Понтрягина, который ввел понятие грубости — структурной устойчивости системы. Важность исследований в направлении, названном К.Зиманом теорией катастроф, оценил французский математик Р. Тома. Он сформировал эту теорию и ее приложения. Сразу появились работы по применению теории катастроф к разным объектам (исследования биения сердца, физическая и геометрическая оптика, лингвистика, геология, эмбриология, гидродинамика, моделирование деятельности мозга и психических расстройств, восстаний в тюрьмах, поведения биржевых игроков и т.д.). Первые публикации по теории катастроф появились в 1970 г. Видный советский математик академик В. И.Ар-
528
нольд так писал о них: «В журналах типа «Ньюс уик» сообщалось о перевороте в математике, сравнимом разве что с изобретением Ньютоном дифференциального и интегрального исчислений. Утверждалось, что новая наука — теория катастроф — для человечества гораздо ценнее, чем математический анализ: в то время как ньютоновская теория позволяет исследовать лишь плавные, непрерывные процессы, теория катастроф дает универсальный метод исследования всех скачкообразных переходов, разрывов, внезапных качественных изменений».
Большинство окружающих нас тел ограничено гладкими поверхностями, но видимые контуры тел — это проекции ограничивающих поверхностей на сетчатку глаза. При этом могут возникать некоторые особенности: при проецировании сферы на плоскость в точках экватора образуется складка. На горизонтальной плоскости-проекции выделяется окружность, разделяющая сферу на внутреннюю и внешнюю, при этом точки внутренней сферы имеют по два прообраза (от двух точек сферы), а точки внешней — ни одной, точки окружности — один прообраз. При подходе с внутренней стороны к окружности два прообраза сливаются в один — это и есть особенность складки (рис. 13.4, а). Кроме того, Уитни нашел и другую особенность — сборку (рис. 13.4, б). Представление о ней можно получить, рассматривая устойчивость бутылки из-под молока. Уитни показал, что сборка и складка — устойчивы.
Точке экстремума соответствует равенство нулю производной при второй производной, отличной от нуля. В многомерном случае производные от функции U будут браться частные, и они должны быть равны нулю, а смешанные, т.е. вторые производные, отличны от нуля и det
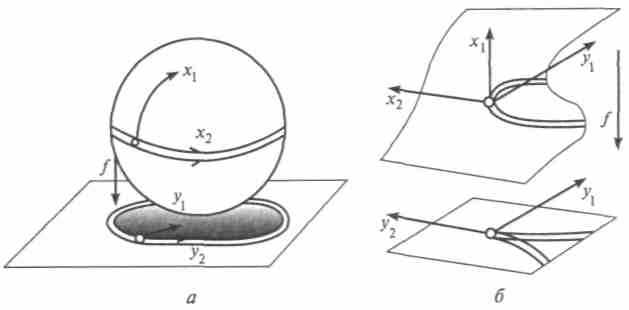
Рис. 13.4. Примеры проецирования поверхностей на плоскость:
а — складка проецирования сферы на плоскость; б — сборка проецирования поверхности на плоскость
529

 = 0; если потенциальная функция представлена в квадратичной форме, и в случае, например, двух переменных,
= 0; если потенциальная функция представлена в квадратичной форме, и в случае, например, двух переменных,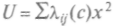 функция будет напоминать рельефную карту: вершины гор и седла связаны хребтами, имеются озерные впадины и седлообразные долины. При диагонализа-ции функции выделяются направления главных осей линий максимального градиента. Если представить рельеф заполненным водой, то она соберется в озера, расположенные в низких частях долин. Минимум, притягивающий воду, получил название аттрактора, причем аттракторы разделяются хребтами, седлами, вершинами на различные бассейны притяжения.
функция будет напоминать рельефную карту: вершины гор и седла связаны хребтами, имеются озерные впадины и седлообразные долины. При диагонализа-ции функции выделяются направления главных осей линий максимального градиента. Если представить рельеф заполненным водой, то она соберется в озера, расположенные в низких частях долин. Минимум, притягивающий воду, получил название аттрактора, причем аттракторы разделяются хребтами, седлами, вершинами на различные бассейны притяжения.Такая качественная рельефная картина изменится при наличии вырожденных точек, для которых одно или несколько значений det
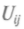 = 0. Это условие получается при некоторых значениях управляющих параметров са. Если при изменении са система проходит через вырожденную точку, меняется вся топология, поэтому и говорят о катастрофе. При приближении к этой точке — границе перехода — критические точки рельефа начинают сближаться, а потом и вовсе сливаются. Множество точек са, отвечающих функции с det
= 0. Это условие получается при некоторых значениях управляющих параметров са. Если при изменении са система проходит через вырожденную точку, меняется вся топология, поэтому и говорят о катастрофе. При приближении к этой точке — границе перехода — критические точки рельефа начинают сближаться, а потом и вовсе сливаются. Множество точек са, отвечающих функции с det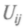 = 0, разбивают пространство управляющих параметров на области с разными рельефами.
= 0, разбивают пространство управляющих параметров на области с разными рельефами.При пересечении границы областей, являющихся геометрическим местом особенностей, происходят катастрофы состояний системы. Поэтому математики искали эти области и исследовали системы на устойчивость в их окрестностях. Арнольд провел классификацию таких особенностей катастроф и получил удивительное совпадение с классификацией точечных групп, описывающих симметрию молекул, а также с правильными многогранниками в евклидовом пространстве (которыми представлял мир Платон) и простыми группами Ли. Пока причины этих взаимосвязей до конца не выяснены.
Приведем для наглядности примеры катастрофы сборки и складки. Для каждого типа катастроф рассматривается поверхность, зависящая от числа переменных и числа управляющих параметров. Обратимся к простейшей катастрофе складки (она похожа на складку на ткани) с одним управляющим параметром. Функция катастрофы задана Cat(t, с) = х3/3 + сх. В области с < 0 все кривые подобны и имеют две критические точки; при с > 0 — кривые также подобны, но критических точек нет; точка с, равная нулю, в пространстве управляющих параметров является сепаратрисой. Катастрофы типа складки появляются в моделях нагруженных арок, триггеров, диссипативных структур, моделях релаксации.
Функция катастрофы сборки Cat(x, а, b) = (1/4) х4 + (1/2) ах2 + + bх зависит от одной переменной состояния и двух управляющих параметров. Сепаратриса сборки разделяет плоскость управляющих параметров на две области с одной и тремя критическими точками, ее линии имеют дважды вырожденные точки, а точка пересечения вырождена трижды. Потенциальные функции соответствуют некоторым точкам плоскости управляющих параметров. Модели с функцией сборки встречаются в механике конструк-
530
ций, при описании многих колебательных режимов, в динамике квантовых систем.
Теория катастроф позволяет свести огромное многообразие сложных ситуаций к небольшому числу точно изученных схем. Математические образы теории катастроф реализуются в волновых полях. Известны геометрические места точек, в которых происходит фокусировка волнового поля, называемые в оптике каустиками. При пересечении каустик происходит скачкообразное изменение состояния — меняется число лучей, приходящих в данную точку пространства. Для одной-двух переменных и не более пяти управляющих параметров существует семь типов элементарных катастроф. Все семь канонических катастроф имеют в каустиках свои образы. Теория катастроф, широко используемая в метеорологии, аэро- и гидродинамике, оптике, теории кооперативных явлений, квантовой динамике и др., подводит стандартную и эффективную базу под описание качественных изменений в нелинейных уравнениях, описывающих далекие от равновесия системы.
13.4. Математические закономерности эволюции. Понятие бифуркации
Если теория катастроф описывает области устойчивости структур, то развитие этой статической картины во времени дается теорией бифуркаций. Нелинейная система имеет целый спектр решений, и нужно определить, какие из них «ответвляются» от известного решения при изменении параметра. Изменения управляющих параметров способны вызывать катастрофические (большие) скачки переменных состояний, и эти переходы осуществляются почти мгновенно (скачком). Состояние системы, описываемой потенциалом U(xi, са), задается точкой хi в которой потенциал имеет минимум. При изменении внешних условий меняются управляющие параметры с, которые в свою очередь, влияют на изменения U(х, с). Глобальный минимум может стать метастабильным или исчезнуть, а система перейдет из одного локального минимума в другой.
Момент перехода определяется свойствами системы и уровнем флуктуаций в ней. Выделяют два принципа: принцип максимального промедления, определяемый существованием устойчивого уровня, и принцип Максвелла, определяющий состояние системы глобальным минимумом. Каждому из принципов соответствует множество точек в пространстве управляющих параметров, в котором происходит переход из одного локального минимума в другой. Последовательность бифуркаций, возникающая с ростом неравновесности в системе, меняется, и процесс пойдет по разным
531
сценариям. Выше описано развитие турбулентности при движении жидкости по трубе в зависимости от числа Re (пропорционального скорости потока). Движение становится неустойчивым и при больших Re характеризуется набором N колебаний с несоизмеримыми частотами
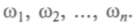 Это квазипериодическое движение называют динамическим хаосом.
Это квазипериодическое движение называют динамическим хаосом.Приведем данную Л. П. Кадановым наглядную иллюстрацию перехода к хаосу, которую используют при рассмотрении биологических проблем. Пусть на изолированном острове выводятся летом насекомые численностью
 и откладывают яйца. Потомство их появится на следующее лето численностью
и откладывают яйца. Потомство их появится на следующее лето численностью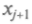 . Рост популяции насекомых описывается первым членом в правой части уравнения
. Рост популяции насекомых описывается первым членом в правой части уравнения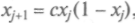 , а убыль — вторым. При
, а убыль — вторым. Прис < 1 популяция с ростом / вымирает и исчезает, в области 1 < с < 3 — приближается к значению х = 1 - 1/с, которое получается при подстановке в уравнение вместо
 и
и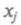 их предельных значений; это область стационарного состояния. В диапазоне 3 < с < 3,4 — две ветви решения, и численность колеблется между ними. Она растет резко от малого значения (откладывается много яиц). Перенаселенность, возникающая на следующий год, вновь резко снижает численность в последующем году, так что период колебаний численности — 2 года. Далее, при 3,4 < с < 3,54 имеем уже 4 ветви, и возникает четырехстадийный цикл колебаний. Так период начинает удваиваться, и далее появляются 8, 16, 32, 64, ... ветвей.
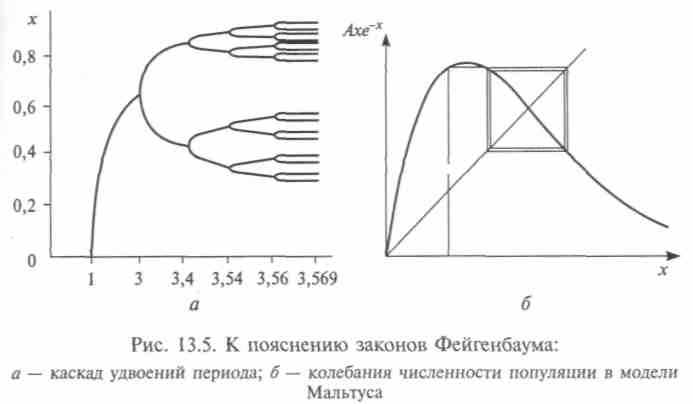
их предельных значений; это область стационарного состояния. В диапазоне 3 < с < 3,4 — две ветви решения, и численность колеблется между ними. Она растет резко от малого значения (откладывается много яиц). Перенаселенность, возникающая на следующий год, вновь резко снижает численность в последующем году, так что период колебаний численности — 2 года. Далее, при 3,4 < с < 3,54 имеем уже 4 ветви, и возникает четырехстадийный цикл колебаний. Так период начинает удваиваться, и далее появляются 8, 16, 32, 64, ... ветвей.Итак, существует диапазон значений параметра с, когда поведение системы упорядочение и периодично; происходит последовательное удвоение периода. Такие решения имеют место для широкого класса систем — химических, электрических, гидродинамических, механических и т.д. В 1978 г. М.Фейгенбаум нашел универсальные законы перехода к хаотическому состоянию при удвоении периода. Если выбрать соседние значения
 цикле,
цикле,где п = 4,66 для всех систем, то разность между ними убывает с ростом п как аn, где а = 2,5 и тоже является универсальным. Законы Фейгенбаума подтверждены на опытах в совершенно различных по своей природе системах. Иногда их называют (из-за удвоения) законами каскадов Фейгенбаума (рис. 13.5). При с = 3,57 период уже стремится к бесконечности, движение становится апериодическим, поведение системы — хаотическим, происходит перекрытие различных решений. Все расчеты на ЭВМ делаются некорректными, зависящими от случайных процессов в самой вычислительной машине, решения для близких начальных условий оказываются далекими.
Сценарии перехода к хаосу могут быть и другими. Исследования сценариев связаны с анализом свойств странных аттракторов, к которым притягиваются точки (состояния системы) в многомерном фазовом пространстве. Введение понятия аттрактора — несомненная заслуга теории катастроф, как и пропаганда знаний об их бифуркациях. Сейчас к этим
532
терминам привыкли и фонемы речи, к примеру, называют аттракторами звукообразующей динамической системы.
Если популяция растет так, что отношение прироста численности к общей численности остается постоянным, то говорят, что закон роста линейный, а рост — экспотенциальный. При приросте 5 % популяция увеличивает свою численность вдвое за 14 лет. Но для роста есть пределы, на что обратил внимание П. Ферхюльст еще в середине XIX в. Он заключил, что прирост должен быть нелинейным. Уравнение Ферхюльста используют и для описания свойств турбулентного потока при приростах около 200%. В этой области происходят колебания, и становится невозможным достижение оптимальной численности. Когда прирост превысит 245 %, происходит такое усложнение поведения систем, что возникает хаос. Это и обнаружил Э.Лоренц для явлений в атмосфере.
Свойства аттракторов задаются набором траекторий в пространстве п переменных состояния, зависящих от времени как от параметра. В обычном аттракторе эти траектории простые, среди них есть замкнутые, называемые предельными циклами. В странном аттракторе траектории запутанные, не похожи ни на точки, ни на кривые, ни на поверхности; их представляют многослойными поверхностями. Странность состоит в том, что, попав в область странного аттрактора, точка (выбранное наугад решение) будет «блуждать» там и только через большой промежуток времени приблизится к какой-то его точке. И поведение системы, отвечающее такой точке, будет сильно зависеть от начальных условий. Итак, при медленном изменении параметра наблюдается качественно новое явление затягивания потери устойчиво-
533







сти, описанное в 1973 г. М. А. Шишковой (рис. 13.6). В 1985 г. было показано, что это свойство имеет место во всех системах с медленно меняющимся параметром.
После прохождения параметра через бифуркационное значение, соответствующее рождению цикла или мягкому возникновению автоколебаний, система некоторое время остается в окрестности неустойчивого состояния, за которое параметр меняется на конечную величину. После этого система скачком переходит в момент бифуркации в автоколебательный режим (уже ставший жестким). Существование аттракторов с экспоненциально расходящимися фазовыми кривыми на них и устойчивость явлений установлены в начале 60-х гг. XX в. в работах С. Смейла, Д.А.Аносова, Я. Г.Синая. Независимо от этих работ Лоренц в 1963 г. описал наблюдавшийся им в численных экспериментах по моделированию конвекции в атмосфере аттрактор с разбегающимися фазовыми кривыми и указал на связь его с турбулентностью. Перепутывание частот при таком режиме оказывается принципиальным, получается, что частоты определены закона-
534
ми динамики и, следовательно, детерминированы. Поэтому и хаос назван детерминированным.
В 1975 г. американские ученые Т. Ли и Дж. Йорк опубликовали статью «Период три дает хаос», где доказали, что при некоторых условиях самопроизвольное появление моды с утроенной частотой возможно только вместе со всем остальным турбулентным спектром. Поэтому хаотический турбулентный режим имеет более сложную структуру, чем упорядоченный ламинарный. Принципиальным в теориях динамического хаоса является признание роли начальных условий, того обстоятельства, что в ходе эволюции система занимает не все точки «фазового пространства». В нем есть определенные места, «цепочки» их концентрации, статистические «аномалии», влияющие на всю микроструктуру. Исследования диалектики случайностей и регулярностей облегчаются возможностями моделирования этих процессов на ЭВМ. Исследования динамического хаоса показывают, что он способен породить не только «унылое равновесие», возникает «вторичная динамика», которую исследуют в синергетике.
Итак, в точке бифуркации поведение системы «разветвляется», становится неоднозначным. При достижении третьей бифуркации наступает состояние динамического хаоса, который скрывает внутреннюю упорядоченность. Проблема выяснения условий возникновения порядка из хаоса, по словам известного физика-теоретика Уилера, — задача номер один современной науки.
13.5. Синергетика — новый научный метод
Аналогию процессов, происходящих в сложных нелинейных системах, с фазовыми переходами отметили несколько ученых, работавших в квантовой электронике: немецкие ученые Грэхем и Хакен и итальянские — де Джиржио и Скулли в 1970 г. Если рассматривать излучение лазера и лампы накачки, то можно сказать, что оно претерпело фазовый переход и изменило свои свойства — свет стал когерентным, более узким в спектральном отношении и усиленным по направлению испускания. Сначала такая аналогия казалась поверхностной, но с каждым параметром фазового перехода в парамагнетике удалось сопоставить соответствующий параметр квантовой генерации. Возражение, касающееся искусственности создания самого прибора, творящего эти превращения со светом, были сняты, когда открыли мазеры в космическом пространстве, где генерация происходила естественным путем.
Коллективные процессы Г. Хакен выделил во всех самоорганизующихся системах: коллективно организуются молекулы в узлах кристаллической решетки, элементарные магнитные моменты (спины) в ферромагнетике, вихри внутри жидкости, порождая види-
535

 мую на макроскопическом уровне структуру. Возбуждаясь в рабочем веществе лазера, атомы самосогласованно и коллективно испускают когерентное излучение. Итак, кооперативность — общая черта процессов самоорганизации. Кроме того, инверсная населенность, как и неравновесное состояние в жидкостях, должна поддерживаться внешней средой, только в этом случае возникающие структуры будут устойчивы. Система должна быть открытой. Устойчивые структуры возникают при обмене с внешней средой энергией (или веществом — для биологических систем), которые могут поддержать отклонение от равновесия. Этот внешний поток не только гасит рост энтропии, но может привести к ее понижению. И еще: для самоорганизующихся систем непременными атрибутами являются сложное движение, описываемое нелинейными уравнениями, и пороговый характер возникновения.
мую на макроскопическом уровне структуру. Возбуждаясь в рабочем веществе лазера, атомы самосогласованно и коллективно испускают когерентное излучение. Итак, кооперативность — общая черта процессов самоорганизации. Кроме того, инверсная населенность, как и неравновесное состояние в жидкостях, должна поддерживаться внешней средой, только в этом случае возникающие структуры будут устойчивы. Система должна быть открытой. Устойчивые структуры возникают при обмене с внешней средой энергией (или веществом — для биологических систем), которые могут поддержать отклонение от равновесия. Этот внешний поток не только гасит рост энтропии, но может привести к ее понижению. И еще: для самоорганизующихся систем непременными атрибутами являются сложное движение, описываемое нелинейными уравнениями, и пороговый характер возникновения.Эти самоорганизующиеся системы и процесс самоорганизации математически оформили следующим образом: сначала просто записали связь эффекта с его причиной в зависимости от времени, а потом исключили внешнее воздействие, предоставив систему самой себе. Хакен расширил систему так, чтобы включенные в уравнения внешние силы стали силами внутренними, и описал механизм нарастания внутренних флуктуаций с помощью введения стохастического члена. Так самоорганизация определяется характером взаимодействия случайных и необходимых факторов системы и ее среды. В дальнейшем он разработал теорию лазерной генерации как фазового перехода, а потом теорию гидродинамических неустойчивостей как фазовых переходов. Для них удалось получить не только теоретическое подтверждение факта существования ячеек Бенара, но и описание положения шестиугольных цилиндров и их диаметров. И каждый раз в этой аналогии открывались более глубинные черты. Развиваемый метод дал интересные результаты при рассмотрении фазового перехода — разрушения упругой конструкции (моста, например). Так стал работать новый метод — синергетический, основанный на идее синтеза.
Самоорганизация происходит при генерации в атомной системе. В кристалле твердотельного лазера имеются активные, возбужденные накачкой от внешнего источника атомы, которые работают как антенна и испускают цуг волн. При малой мощности накачки световые цуги испускаются независимо друг от друга, и лазер работает как обычная лампа, испуская некогерентный свет. Начиная с некоторого значения мощности накачки (порогового) все антенны начинают работать согласованно, атомы испускают свет в одной фазе, возникает гигантский цуг когерентного лазерного излучения, интенсивность излучения резко возрастает (на торцах кристалла — зеркала, отбирающие цуги). Переход лазера в режим генерации соответствует образованию ячеек Бенара. В сверхкритической области устанавливается стабильный режим лазера,
536
тогда как у простой лампы — неустойчивый. Очевидно, что лазер является системой, находящейся вдали от равновесия. Наблюдается кооперативное поведение атомов и излучения.
К основным свойствам самоорганизующихся систем относятся открытость, нелинейность, диссипативность. Система должна находиться в состоянии, далеком от равновесия.
Открытость системы обеспечивается непрерывным потоком вещества, энергии или информации, получаемым из внешней среды на поддержание определенного состояния. В таких системах флуктуации играют определяющую роль, могут привести к необратимому макроскопическому изменению состояния системы, разрушить созданный в ней порядок.
На нелинейные системы не распространяется принцип суперпозиции, т.е. возможно, чтобы совместные действия двух причин привели к результату, совершенно отличному от того, который был бы, если эти причины действовали по отдельности. Процессы в нелинейных системах носят пороговый характер — в состояниях, далеких от равновесия, слабые возмущения могут усиливаться и радикально перестроить систему. Нелинейные системы, открытые и неравновесные, сами создают в среде неоднородности. Между средой и системой может установиться положительная обратная связь (так, в реакции может вырабатываться фермент, присутствие которого стимулирует выработку его же самого). Важно найти эту петлю положительной обратной связи, и в системе начнется режим самоорганизации. В химии — это автокатализ, в молекулярной биологии — основа жизни. Системы неравновесные необычно и «чутко» реагируют на внешнее воздействие и «учитывают» их в своем функционировании. Поэтому некоторые слабые воздействия могут оказать на эволюцию системы большее влияние, чем сильные, но не адекватные собственным тенденциям системы.
Диссипативность — качественно своеобразное макроскопическое проявление процессов, происходящих на микроуровне. Она проявляется в разных формах: в способности «забывать» детали некоторых внешних воздействий; в «естественном отборе» среди многих микропроцессов для обеспечения основной тенденции развития; в когерентности микропроцессов, устанавливающей темп развития, и пр. С диссипативностью связано понятие «параметр порядка», который выделяет только ведущие степени свободы из всех возможных для системы. Уравнения для параметров порядка намного проще, и основная задача — найти параметры порядка системы при моделировании поведения системы.
Примером возникающей самоорганизации являются вихревые структуры в виде двойной спирали, впервые обнаруженной в закрученных газовых потоках в трубке Ранка—Хилша (рис. 13.7, а, б) в Институте теплофизики СО РАН группой исследователей (Ю.Н.Дубнищев, В. А. Арбузов, П. П. и П.Я.Белоусовы). Интерес
537


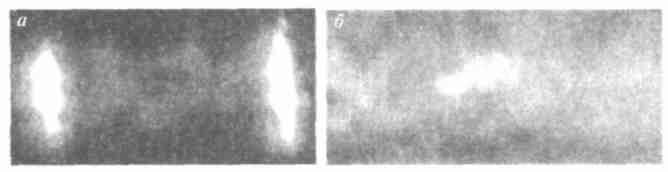
Рис. 13.7. Биспиральные вихревые структуры в закрученных потоках,
проявляющиеся посредством визуализации поля оптической фазовой
плотности (а) и поля скоростей в заданном сечении (б)

к таким системам связан с попытками построить адекватную физическую модель энергоразделения в закрученных потоках, где структуры возникают при определенных угловых скоростях. Еще один пример упорядоченных волновых структур, имеющих синер-гетическую природу и возникающих на поверхности вращающихся жидкостей и тонких пластин, показан на рис. 13.8.
Итак, переход от хаоса к порядку поддается математическому моделированию, причем универсальных моделей такого перехода оказалось не так много. Они пригодны в разных областях естествознания, в истории, экономике, экологии и пр. История развития природы — история образования все более сложных форм, которые обеспечивают эволюцию природы на всех уровнях организации — вплоть до самых высших. Э. Ферми и Д. Нейман в 50-е гг.
538
XX в. решали на ЭВМ задачи о возникновении теплового хаоса в цепочке грузов с нелинейными пружинками. Ферми, Паста и Улам (ФПУ) получили неожиданный результат: такая система описывается уравнением КдФ. Так солитоны обрели второе рождение (см. гл. 3). Они ведут себя как частицы, и были найдены в разных средах. Ярким приложением солитонной теории стало явление самоиндукцированной прозрачности, которое привело к идее «оптического телеграфа» — передачи светового солитона по стекловолокну.
