Geum.ru

Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания

Вид материалаДокументы

Содержание


Концепции взаимодействий
Волновая механика
Матричная механика
Квантовая механика
6.2. Принципы соответствия и неопределенности. Роль прибора и процесса измерения в квантовой механике
Подобный материал:
1   ...   17   18   19   20   21   22   23   24   ...   53
Глава 6

КОНЦЕПЦИИ ВЗАИМОДЕЙСТВИЙ

И СТРУКТУР В МИКРОМИРЕ

6.1. Описание движения микрочастиц. Принципы дополнительности и причинности

Микромир — невидимый мир микрообъектов: атомов, электронов, нейтронов, протонов и пр. Он не может быть описан понятиями и принципами классической физики, которые в некоторой мере соответствуют наглядным представлениям (как в гл. 5). Классическая физика признает наличие материи как в виде вещества, так и поля. Но она не допускает объектов, обладающих свойствами и поля, и вещества. Подчеркивая кажущуюся противоречивость свойств микрообъектов, у которых эти свойства дополняют друг друга, Н.Бор выдвинул принцип дополнительности (1927).

При одном описании или наблюдении за поведением микрочастицы удобнее представлять ее волной, а при другом — частицей. Единая картина синтезирует эти описания. После доказательства волновых свойств электрона и «полного успеха» корпускулярно-волнового дуализма вещества необходимо было подвести теорию к объяснению явлений. Идея о волновых свойствах электронов оказалась очень плодотворной. Для создания механики микрочастиц нужно было сформулировать ее основной закон (в классической науке таков закон динамики Ньютона). Для макрообъектов длина волны де Бройля, равнаямала, и их движения можно описать законами классической механики как волновые процессы, характеризующиеся волновой функцией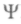. Но когда длиной волны де Бройля нельзя пренебречь, закон движения микрообъектов должен быть аналогичен волновому уравнению в оптике: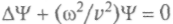. Австрийский физик Э. Шредингер, опираясь на аналогию оптико-лучевого и оптико-волнового описаний, обобщил гипотезу де Бройля для случая, когда электрон движется не в свободном пространстве, а во внешнем поле. Английский математик У. Гамильтон, ранее выразивший идею об оптико-механической аналогии, показал, что задачу классической механики можно формально записать как задачу геометрической оптики. Тогда в приведенном выше уравнении для фазы вместо 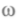надо поставить циклическую частоту волн де Бройля 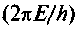, а вместо скорости v — скорость распространения поверхности равного действия 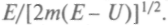Тогда уравнение для частицы примет вид: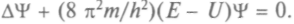

208

Здесь введен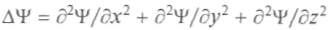— оператор Лап-

ласа; (Е - U) — функция координат и времени, которая характеризует силовое поле, в котором движется микрочастица.

Волновая механика — вариант механики микромира, разработанный Шредингером. Уравнение Шредингера в микромире играет такую же роль, как уравнения Ньютона в классической механике. Его решение в отсутствие внешнего поля дает волны де Брой-ля. Уравнение Шредингера для волновой функции не может быть выведено из других соотношений, т.е. это — исходное предположение, справедливость которого доказывается тем, что вытекающие из него следствия согласуются с экспериментальными данными.

Дифференциальные уравнения с частными производными второго порядка имеют бесконечное множество решений. Необходимое частное решение находят при определенных условиях, соответствующих данной конкретной задаче. Шредингер решил уравнение для простейших квантовых систем — осциллятора, ротатора и т. п. При движении свободного электрона уравнение не накладывало никаких ограничений на его энергию — она может принимать любые значения, не квантуется. Шредингер трактовал 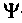-функцию как величину, описывающую плотность частиц в реальном пространстве, и считал, что она отражает только волновые свойства частиц.

Для атома водорода Шредингер получил ряд дискретных значений энергии, что и соответствовало теории Бора. Он определил вид волновых функций и возможные значения энергии, сумев уйти от постулатов Бора в строении атома водорода. Целочисленность значений энергии получилась сама собой, как получается целое число узлов при рассмотрении колебаний струны. Из условия стремления к нулю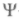-функции на больших расстояниях (быстрое ослабление удерживающего поля) можно найти решения уравнения Шредингера для связанных состояний. Для кулонов-ского потенциала атома водорода решение получается не для всех энергий, а для определенных дискретных значений, совпадающих с теми, что давала теория Бора. Тем самым прояснялся смысл правил квантования Бора— Зоммерфельда: допустимые значения энергии соответствуют требованию, чтобы в области движения частицы уложилось целое число волн де Бройля.

Хотя смысл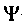-функции был еще не понятен, волновой формализм теории Шредингера приняли, поскольку он позволял решать сложные задачи разработанными методами математической физики, основанными на непрерывных функциях. Интересно высказывание Планка по поводу уравнения Шредингера и введения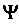-функции: «уравнению придает основополагающее значение... новая методика, позволяющая с помощью математики преодолеть трудную квантово-теоретическую проблему. Это первый случай, когда квант действия, который до сих пор не поддавался

209

никаким попыткам подойти к нему с точки зрения физики непрерывного, удалось включить в дифференциальные уравнения». Смысл -функции был осознан лишь в 1926 г. М. Борном, и «волны материи» получили вероятностную интерпретацию. Об этом чуть ниже.

Но свойства 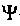-функции не сводились только к «волновым пакетам», что экспериментально доказали советские ученые Л. М. Биберман, Н. Г. Сушков и В. А. Фабрикант (1948). Пропуская пучок электронов чрезвычайно малой интенсивности через кристалл (фактически по одному), они получили на фотопластинке за кристаллом отдельные пятнышки, плотность распределения которых соответствовала распределению интенсивностей в дифракционной картине, которая была бы при большой плотности пучка электронов. Эти «пятнышки» демонстрировали дискретность электронов, а их распределение свидетельствовало о подчиненности их статистическим законам.

М. Борн с 1922 г. начал работать над теорией строения атома Бора, собрав в Геттингене одаренных молодых физиков-теоретиков из разных стран и воодушевив их на разработку новой, квантовой физики. По воспоминаниям Гейзенберга, благодаря Борну Геттинген, славившийся своей математической школой (традиции Гаусса, Римана, Вебера продолжали Клейн и Гильберт), стал центром атомной физики. Борн в книге «Физика в жизни моего поколения» писал: «Развитие квантовой механики показывает, что совокупность наблюдений и измерений медленно создает абстрактные формулы для их сжатого описания и что понимание их значения приходит впоследствии».

Матричная механика — другой вариант механики микромира, созданный В.Гейзенбергом, М.Борном, П.Дираком и П.Иорданом. В своей первой работе Гейзенберг пытался выработать основы атомной механики, построенной на связях между принципиально наблюдаемыми величинами без привлечения моделей. Он считал, что теория явлений микромира должна устанавливать соотношения между величинами, которые непосредственно наблюдаются в эксперименте (частота спектральных линий, поляризация и др.), а «ненаблюдаемые» (скорость, масса, ускорение, положение частицы) не должны быть в ней. Гейзенберг отказался от «представлений об электронных орбитах с определенными радиусами и периодами обращения, потому что эти величины не могли быть наблюдаемы».

Это достижение Гейзенберга и стало основой матричного варианта квантовой механики, для которой Борн разработал математический аппарат. Гейзенберг представил физические величины как совокупность всех возможных амплитуд перехода из одного квантового состояния в другие, так как при изучении спектральных закономерностей атом представлялся совокупностью вир-

210

туальных гармонических осцилляторов. Сама вероятность перехода пропорциональна квадрату модуля амплитуды, наблюдаемому в экспериментах. Тогда каждая величина должна иметь два индекса, соответствующих верхнему и нижнему состояниям. Эти величины называются матрицами. Гейзенберг получил и уравнения для наблюдаемых величин, но в первоначальном виде они были сложными. В 1926 г. он сумел объяснить отличие двух систем термов для пара- и ортогелия как соответствующих симметричным и антисимметричным решениям его уравнения.

Квантовая механика — теория движений в микромире, основанная на единстве матричной и волновой механики. Шредингер вскоре доказал их математическую эквивалентность. В квантовой механике нет разницы между описаниями частицы с помощью волновых и корпускулярных представлений. Вращающийся вокруг ядра электрон можно представлять в виде волны, длина которой определяется его скоростью. И там, где укладывается целое число длин волн электрона, они складываются, образуя разрешенную орбиту в планетарной модели строения атома Бора. Если же в орбиту не укладывается целое число волн, гребни их станут компенсировать впадины, такая орбита не будет разрешена. Уравнение Шредингера позволяет однозначно определить волновую функцию в любой момент времени, если известно ее значение в данный момент. Поэтому само уравнение вполне динамично. Но оно было написано еще до того, как стал понятен смысл этой функции.

Верную трактовку смысла волновой функции дал М.Борн в 1926 г. Обратившись к работам Эйнштейна по теории фотонов и проанализировав задачу о рассеянии частиц, он подошел к созданию формализма квантовой механики с позиции статистических методов. Он показал, что интенсивность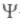-волн есть мера вероятности положения частицы в определенном месте.

Квадрат модуля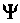-функции определяет вероятность dW того, что частица будет обнаружена в объеме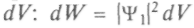

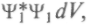при этом полная вероятность обнаружения частицы во всем объеме, определяемая интегралом по объему, должна равняться (как достоверного события) единице:. Значит, квантовая механика носит статистический характер.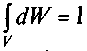Она позволяет найти лишь вероятность того, что координаты лежат внутри определенного интервала,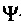-функция позволяет только предсказать вероятность обнаружения частицы В различных точках пространства. Как выразился Р.Фейнман, «приходится признать, что мы изменили нашим прежним идеалам понимания природы. Может быть, это шаг назад, но никто не научил нас, как избежать его».

Итак, микропроцессам свойственны не динамические, а статистические закономерности, тем самым в области микромира

211

причинность реализуется через многообразие случайностей и характер причинной связи в микромире отличается от детерминизма классической науки. Классическая наука, стремясь к объективности законов, фактически игнорировала случайность. В ней фигурировали только средние данные, но в реальных процессах всегда происходят случайные флуктуации (отклонения от средних), которыми можно пренебречь лишь в некоторых ситуациях. Динамические теории не могут описывать явления с большими флуктуа-циями, связь со случайностью сглажена, огрублена. Поэтому статистические законы глубже, чем динамические, а вероятностная причинность оказывается глубже, чем динамическая.

Положение о первичности статистических законов выдвинули создатели квантовой механики. Сначала многие связывали его с индетерминизмом, поскольку детерминизм в привычном понимании в микромире оказался недостижим. Большая часть ученых воспринимала статистические законы как недостаточность наших знаний о микрообъектах, т. е. как промежуточный этап развития знаний. Но когда оказалось, что вероятностная теория подтверждается многими экспериментами, стали говорить, что эти законы дополняют друг друга и в то же время не могут быть сведены друг к другу. Статистические закономерности — объективные законы природы, отражающие реальные связи в микромире. В макромире поведение индивидуальных объектов подчинено динамическим законам, а совокупности объектов — статистическим. В микромире и объекты, и их совокупности описываются как динамическими, так и статистическими законами. История науки показывает, что динамические законы постепенно сменяются законами статистическими, представляющими более глубокий уровень понимания сущности и более широкий охват явлений природы. Статистические закономерности приводят к более хорошему согласию с экспериментом. Ее результаты при определенных условиях согласуются с результатами динамических теорий, что и предполагает принцип соответствия Бора.

До создания квантовой механики Борн вместе с учениками получил выдающиеся результаты по объяснению явлений в твердых телах и кристаллах, используя понятие кристаллической решетки и применяя теорию групп. Поэтому он сразу же применил этот подход к различным проблемам строения атома, физики твердого тела и молекулярной физики. В 1926 г. Борн предложил способ расчета электронных оболочек атома и методы решений для задач столкновения частиц по теории возмущений, которые известны как борновское приближение, и вместе с Н. Винером ввел в квантовую механику понятие оператора. В отличие от ситуации в классической механике некоторые величины (момент импульса, энергия при движении в замкнутой области пространства и др.) могут принимать лишь дискретный ряд значений. Возможные значения

212

физических величин являются собственными значениями операторов, сопоставляемых в квантовой механике с каждой физической величиной. Эта величина может принимать определенные значения с вероятностью, равной единице, только в случае, если система находится в состоянии, изображаемом собственной функцией этого оператора. Тогда вероятность превращается в достоверность.

Зная 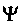-функцию, можно вычислить среднее значение любой физической величины и ее отклонение от среднего значения — дисперсию. В отличие от классической механики поведение отдельной частицы имеет статистический характер, т. е. это уже не связано с наличием очень большого числа частиц. Но при формулировке квантовой механики пришлось ввести еще один принцип — фундаментальный принцип неотличимости или тождественности частиц. В классической механике частицы можно отличить по их состояниям, в этом смысле они не теряют индивидуальности. В квантовой механике это невозможно, так как микрочастица не имеет траектории. Если волновые функции двух частиц перекрываются, то в области перекрытия нет возможности отличить одну частицу от другой. Поэтому получается, что тождественными оказываются и свойства частиц, и их состояния. В природе реализуются лишь те состояния совокупности одинаковых частиц, которые не меняются при обмене местами одинаковых частиц. Поэтому и состояния описываются лишь симметричными или антисимметричными волновыми функциями, а характер симметрии определяется собственным моментом импульса частицы (ее спином). Сформулированный на этой основе принцип Паули позволил сформировать статистические правила для частиц с целым и полуцелым спином и понять построение Периодической системы химических элементов.

В 1927 г. Борн разработал, при участии американского физика Р. Оппенгеймера, теорию строения двухатомных молекул. Квантовая механика явилась теоретической основой химии. С ее помощью удалось построить теорию твердого тела, многих его свойств в различных полях. На ней базируются квантовые статистика, электродинамика, теория излучения и др. Она легла в основу теории радиоактивного распада и стала базой атомной и ядерной физики.

6.2. Принципы соответствия и неопределенности. Роль прибора и процесса измерения в квантовой механике

Границы применимости существуют у каждой теории. Так, классическая механика описывает движение макроскопических тел при скоростях, существенно меньших скорости света. Эти границы выяснились только после создания СТО — релятивистская меха-

213

ника расширила классическую на случай больших скоростей. Ценность механики Ньютона при этом не уменьшилась — для малых скоростей тел (по сравнению со скоростью света) поправки малы. При создании квантовой механики было важно строить новую теорию так, чтобы соотношения между величинами были аналогичны классическим, т. е. каждой классической величине нужно было поставить в соответствие квантовую, а потом найти соотношение между квантовыми величинами, пользуясь классическими законами. Такие соответствия можно было найти только из операций измерения.

Принцип соответствия — новая теория не может быть справедливой, если не будет содержать в качестве предельного случая старую теорию, относящуюся к тем же явлениям, если она уже подтверждена опытом в этой области. Этот принцип построения новых теорий в других областях, сформулированный Н. Бором (1923), отражает диалектику соотношения абсолютной и относительной истин. Смена теорий (относительных истин) есть шаг на пути приближения к абсолютной истине, тем самым принцип соответствия отражает объективную ценность физических теорий — новые теории не отрицают старых именно потому, что старые теории с определенной степенью приближения отражают объективные закономерности природы.

В 1927 г. В. Гейзенберг при поддержке Бора и его школы предложил устранить противоречие «волна — частица», которое он понимал как аналогию. Он шел от наглядных феноменологических моделей. Считая, что «совокупность атомных явлений невозможно непосредственно выразить нашим языком», он предложил отказаться от представления о материальной точке, точно локализованной во времени и пространстве. Либо точное положение в пространстве при полной неопределенности во времени, либо наоборот — таково требование квантовых скачков.

Принцип неопределенности Гейзенберга — это фундаментальное положение квантовой теории, отражающее ограничение информации о микрообъектах самими средствами наблюдения.

Пусть в какой-то момент нам нужно узнать положение и скорость электрона. Самый точный метод — осветить электрон пучком фотонов. Электрон столкнется с фотоном, и его положение будет определено с точностью до длины волны фотона. Для большей точности нужно использовать фотоны наименьшей длины (или большей частоты, или обладающие большими энергией Е и импульсом hv/c). Но чем больше импульс фотона, тем сильнее он исказит импульс электрона. Для точного знания положения электрона нужно использовать фотоны бесконечной частоты, но тогда и импульс его будет бесконечным, совершенно неопределенным. И, наоборот, желая определить точно импульс электрона,

214

из аналогичных рассуждении придем к неопределенности положения. Выразив ее как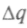, а неопределенность импульса как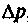, получим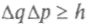. Для других сопряженных величин — энергии Е

и времени t — квантово-механическое соотношение неопределенности будет

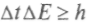
Значит, чем точнее фиксирован импульс, тем большая неопределенность в значении координаты. Аналогично связаны энергия и время — точность измерения энергии пропорциональна длительности процесса измерения. И это не неточность определения величин, которая может быть улучшена более точным прибором, это принципиальная неточность определения физических величин в атомной физике. Причина этого — взаимодействие с макроскопическим прибором. Принцип дает ограничения, которые нельзя устранить никакими усовершенствованиями прибора. В классической науке приборы и наблюдения тоже искажали измерения, но эти искажения можно было уменьшать. Разница в том, что соприкасаются и взаимодействуют объекты разных миров: для изучения микромира используются приборы и наблюдатели из макромира. Они-то и вносят искажения в состояния микрообъектов, которые не устранимы. Поэтому будущее состояние микрочастицы не может быть достоверно и точно предсказано. Повышение точности знания одного параметра увеличивает неточность в знании сопряженного ему параметра. Отсюда — дискуссии о непредсказуемости явлений микромира, о «свободе воли» электрона, о победе случайности над детерминизмом, нарушении принципа причинности в микромире и др. Принцип неопределенности иногда называют следствием принципа дополнительности, что до сих пор вызывает дискуссии.

Основа интерпретации квантовой механики — принцип Гейзенберга — устанавливает границы применимости классической физики и считается общепризнанным.

Применим соотношения Гейзенберга, например, к электрону в атоме. Так как скорость электронов при движении вокруг ядра порядка 106 м/с, то максимально допустимая неопределенность скорости не должна превышать самой скорости. Пусть они равны, тогда из соотношения неопределенностей для координат и импульсов 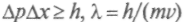. Иливчислах: 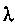= 6,62 10-34Дж с/(9,1 10-31 кг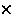 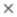106 м/с) = 7 • 10-10 м, т. е. неопределенность в координате порядка размеров самого атома. Отсюда вывод: электрон размазан по всему объему атома в виде пульсирующего облачка, и его боров-ская орбита — геометрическое место точек, в которых корпускулярные свойства электрона наиболее выражены.

Понятие вероятности становится первичным, и вокруг него строится наука XX в., формируя новую, неклассическую стратегию познания. Опыты дают набор возможных значений величин с распределением их вероятности, и это может быть предвычисле-

215

но! Исследуя специфику взаимодействия микрообъекта с классическим средством наблюдения, Гейзенберг в работе «О наглядном содержании квантовой кинематики и механики» (1927) рассмотрел основные положения квантовой механики, ориентируясь на возможности измерения величин, характеризующих состояние микрообъекта. Он заключил, что в микромире «чем точнее определяется местоположение, тем менее точными становятся сведения об импульсе». Или, в отличие от «лапласовского детерминизма», поскольку мы не можем знать настоящего во всех деталях, то не можем достоверно предсказать будущее. Природа накладывает на понятия координаты и импульса принципиальные ограничения, которых не было в классической науке, возможно, из-за малой величины h.

«Бог не играет в кости» — считал Эйнштейн. Связь принципа неопределенности с принципом дополнительности Бора — основа так называемый «копенгагенской» трактовки квантовой механики. Эйнштейн долгое время оппонировал Бору. Он писал: «Существует нечто вроде «реального» состояния физической системы, существующего объективно, независимо от какого-то ни было наблюдения или измерения». Споры Бора с Эйнштейном проясняют многое в истолковании смысла квантовой механики, фактически они отражают продолжавшуюся более двух десятилетий борьбу двух мировоззрений, двух теорий познания. Вероятностное толкование волновой функции было подготовлено работами Бора, который применял идею вероятности к переходам электронов, но еще раньше Эйнштейн ввел понятие вероятностей для спонтанного и индуцированного излучений. От них вероятностные представления вошли в науку XX в.

Дирак отмечал: «Бор считал, что высшая мудрость должна быть выражена обязательно такими словами, смысл которых не может быть определен однозначно. Следовательно, истинность высшей мудрости является не абсолютной, а только относительной в соответствии с одним из значений двухзначных слов: поэтому противоположное высказывание также правомерно и мудро». Принцип дополнительности как вершину диалектики Бора относят к копенгагенской школе.

К Бору постепенно примкнули Гейзенберг, Борн, Иордан, Паули, а в некоторых вопросах и Дирак. Паули даже предложил (1932) назвать квантовую механику «теорией дополнительности». Иордан в книге «Наглядная квантовая теория» (1937) тоже свел все существо квантовой механики к идее дополнительности и утверждал, что «представление об объективной картине процессов теряет свою справедливость». Представители копенгагенской школы не признавали реальности микрообъектов и микропроцессов, отрицая причинность в элементарных процессах. Эти вопросы обсуждались на Сольвеевских конгрессах, где «копенгагенцам» рез-

216

ко возражали Лоренц, Эйнштейн, Ланжевен, Планк, Лауэ и др. Ланжевен, например, писал: «Я уверен, что, отказываясь от детерминизма, мы лишим науку ее основного движущего начала — того, что до сих пор составляло ее силу и залог ее успеха: веры в конечную познаваемость Вселенной. Ничто в переживаемых нами трудностях не оправдывает и не требует изменения наших установок, что, по моему глубокому убеждению, было бы равносильно отречению». Они были «детерминистами», а новый, неклассический образ природы завоевывал молодые умы.

Мысленный эксперимент А.Эйнштейна, Б.Подольского и Н. Розена был задуман для доказательства ошибочности толкования квантовой механики. Они задались вопросом, что случится, если состоящая из двух протонов частица распадется так, что протоны разлетятся в противоположных направлениях. По квантовой механике при отсутствии наблюдателя свойства протонов остаются неопределенными и могут быть представлены как суперпозиция всех возможных состояний. Означает ли это, что каждый протон движется во всех возможных направлениях? Из-за общности происхождения их свойства связаны (коррелируют) друг с другом. Так, по закону сохранения импульса, если один протон полетит вверх, то второй — обязательно вниз. Поэтому, измерив импульс одного, мы узнаем импульс и второго даже в том случае, если он уже улетел на другой конец Вселенной. Эйнштейн назвал это «действием призраков на расстоянии», которое нельзя сопоставить ни с какой реалистической моделью из обыденного опыта: все свойства каждого из протонов должны быть зафиксированы с того момента, когда они только начали свой разлет.

Допустим, неопределенность в поведении электрона зависит не только от импульса, координаты и спина, но и от каких-то других скрытых параметров, которые нам удалось познать. Можно ли в этом случае достичь полного описания, как в классической механике? Это можно осуществить для единичного измерения, но оно так ограничит область значений скрытых параметров, что уже ко второму измерению их будет недостаточно для согласия с квантовой механикой. Гейзенберг и Бор проанализировали возможности одновременного измерения двух сопряженных величин (Е, t и д, р) и провели мысленные эксперименты, подтверждающие принцип неопределенности. Получалось, что микрообъект при использовании одних приборов представляется локализованной во времени (t) и в пространстве (х) материальной точкой, не обладающей определенными импульсом (р) и энергией (Е), а при использовании других приборов — как нечто, обладающее Е и р, но не локализованное по х и t. Бор и его «копенгагенская школа» обобщили принцип Гейзенберга, утверждая, что в естественных науках можно пользоваться только теми величинами, для измерения которых существует опре-

217

деленная измерительная процедура и созданы соответствующие приборы. Но результат измерения получается всегда в классических величинах и понятиях, поэтому все объекты уже не существуют сами по себе, как в классической науке, а связаны с экспериментальной установкой вместе с наблюдателем и как бы теряют свою самостоятельную реальность. Впоследствии известный советский физик-теоретик В.А.Фок назвал это свойство «относительностью к средствам наблюдения».

Г.Гейзенберг активно участвовал в обсуждении философских проблем, связанных с квантовой физикой и теорией познания. Вместе с П.Дираком он выдвинул идею обменного взаимодействия, позволившую (независимо от Я. И. Френкеля) разработать первую квантово-механическую теорию ферромагнетизма, основанную на обменном взаимодействии. В начале 30-х гг. они создали теорию дырок Дирака и постулировали эффект поляризации вакуума.

В 50-е гг. Хью Эверетт предложил гипотезу «множественности миров», в которой считается, что каждое проведение измерения заставляет частицу сделать выбор, например пойти в правую или левую щель. При каждом таком выборе вся Вселенная как бы расщепляется на две. Но есть и иное мнение. Возможно, квантовая теория требует большей перестройки нашего мышления, нашей логики. Булева логика, основанная на бинарности мышления, на утверждениях типа «или—или» не дает нам возможности понять свойств частицы, проходящей через две щели, и квантовая теория может изменить наши представления о мире в большей степени, чем изменились наши понятия пространства и времени с появлением теории относительности.