Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания

Вид материала

Документы

Содержание D меняется в соответствии с уравнением dN/dt D. В кинетической теории среднеквадратичная скорость молекул пропорциональна Т/т 8.5. Понятия фазы и фазового перехода. Фазовые переходы первого и второго рода Фазовыми переходами первого рода Фазовые переходы второго рода

Подобный материал:

• Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2306.3kb.
• Учебно-методический комплекс концепции современного естествознания высшее профессиональное, 2307.28kb.
• С. Г. Хорошавина концепции современного естествознания курс лекций, 6750.33kb.
• С. Г. Хорошавина концепции современного естествознания курс лекций, 5892.74kb.
• В. М. Найдыш Концепции современного естествознания, 8133.34kb.
• Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
• Концепции Современного Естествознания, 274.86kb.
• Программа курса «Концепции современного естествознания», 168.05kb.
• Программа дисциплины Концепции современного естествознания Специальность/направление, 456.85kb.
• Бюллетень новых поступлений в нб согу за период с 05. 2011 по 10. 2011гг, 975.89kb.

8.4. Процессы диффузии и осмоса, их роль в клеточных мембранах

Л. Больцман стремился дать интерпретацию термодинамики в рамках атомистической концепции с помощью статистической механики. Его идеи обрели реальность и значимость, когда было доказано, что материя состоит из атомов. Формулу Больцмана для энтропии проверили экспериментально, а статистический метод обрел предсказательную силу. Больцман считал, что с течением времени система побывает во всех энергетически возможных конфигурациях, т.е. будет возвращаться снова и снова к любой такой конфигурации. После его смерти эта идея вечного возврата была сформулирована в эргодическую гипотезу. Смысл ее в следующем. Состояние системы в классической физике изображается точкой в фазовом пространстве, поэтому при движении в фазовом пространстве точка проведет в каждой его области долю времени,

299

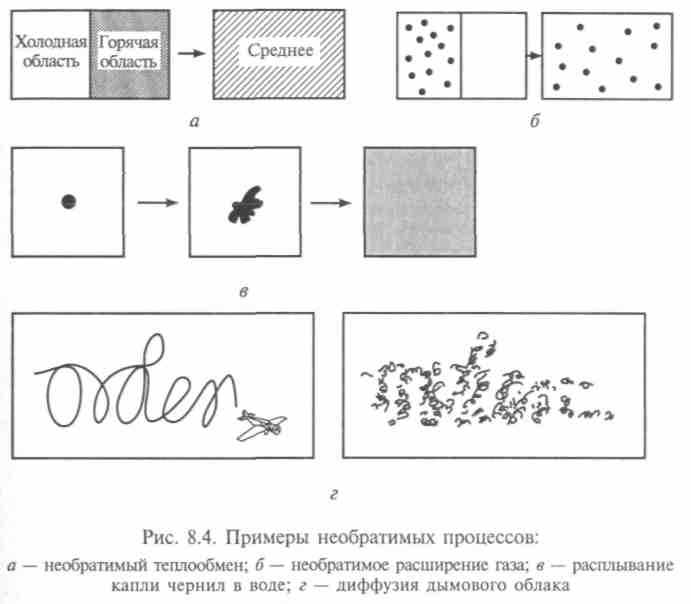
пропорциональную объему этой области. В квантовой механике объему фазового пространства соответствует число состояний. Исходя из эргодической гипотезы можно понять возникновение необратимых процессов.

В качестве примера рассмотрим процесс смешивания двух равных объемов воды при разных температурах. В результате процесса мы не получим отдельных слоев (горячего и холодного) в одном сосуде, т.е. энтропия полученной теплой воды окажется больше, чем сумма энтропии объемов воды до смешивания в соответствии со вторым началом термодинамики. Это означает, что и количество состояний при смешивании увеличилось. С позиции эргодической гипотезы точка проведет большую часть времени в области фазового пространства, соответствующей теплой воде, а в областях, соответствующих горячему и холодному слоям, — малое время. Опыт показывает, что возврата к отдельным слоям после смешивания можно ждать неограниченно долгое время. Введя необратимости, Больцман считал, что это соответствует тому, что исходное состояние очень невероятно, оно отвечает малому объему фазового пространства (или малой энтропии).

К необратимым процессам п е р е н о с а массы, энергии, импульса, заряда, количества движения и пр. относят явления, происходящие из-за перемешивания молекул. Такими процессами являются диффузия, термодиффузия, теплопроводность, вязкое течение, электропроводность, явления термоэлектричества, расширения газов в пустоту, осмос и др. (рис. 8.4). Из-за непрерывных столкновений друг с другом ни одна из молекул (или их групп) газа или жидкости не перемещается из одного участка сосуда в другой с большой скоростью. Если небольшой кристаллик йода поместить в сосуд с воздухом, то очень медленно начнут распространяться пары рыжего цвета. Этот процесс называется диффузией, т. е. пары йода диффундируют сквозь молекулы воздуха. Даже внешне процесс диффузии аналогичен процессу распространения теплоты в стержне, условием которого служит наличие градиента температуры. Для диффузии необходим градиент концентрации с, и его наличие позволяет рассчитать скорость изменения числа молекул в объеме dN/dt, которая пропорциональна площади поверхности S, через которую будет происходить диффузия.

Коэффициент диффузии D меняется в соответствии с уравнением dN/dt = -DS (dc/dx).

Это уравнение, похожее на уравнение распространения теплоты (знак минус показывает, что диффузия происходит противоположно росту концентрации), получил немецкий физиолог А.Фик (1855). В 1822 г. французский инженер Л. Навье математически описал движение вязкой жидкости. Через 100 лет выяснилось, что уравнения Фурье, Навье и Фика являются частными случаями общего уравнения, описывающего неравновесные процессы.

300



Скорость диффузии зависит от скоростей диффундирующих молекул с учетом коэффициента диффузии D. В кинетической теории среднеквадратичная скорость молекул пропорциональна Т/т, поэтому можно ожидать, что и коэффициент D будет также зависеть от температуры и массы. Опыты подтвердили это с высокой точностью. Можно проверить зависимость D от т по данным для некоторых небольших молекул в воздухе при атмосферном давлении: для водорода при T= О D = 6,34; для воды при Т= 8 D = 2,39; для кислорода при T= О D= 1,78; для углекислого газа при Т= 0 D = 1,39; для дисульфида углерода при Т= 20 D = = 1,02 (здесь T—°C, D — 0,00001 м²/с).

Диффузия в растворах, особенно в воде, важна для биосистем. Здесь также подходит закон Фика, но коэффициент диффузии 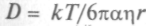, и из-за того, что масса m пропорциональна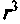, , 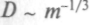в жидкостях коэффициент диффузии сильно зависит от массы частиц.

Используя связь коэффициентов диффузии отдельных молекул в воде и измеряя их, можно найти размеры молекул. Так как плотность р многих больших биологических молекул в сухом виде примерно равна 1,27 г/см³, а при погружении в воду к их поверх-

301

ности налипают молекулы воды, увеличивая их эффективный объем, то масса увеличивается почти в 1,5 раза. С учетом этого можно найти массы молекул по их размерам и средней плотности: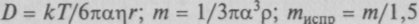

Диффузия молекулярных ионов через мембраны, образующие клеточные стенки, осуществляется при наличии определенного электрического потенциала внутри клетки. Кроме того, определенные химические процессы, происходящие внутри мембраны, меняют направление скорости диффузии различных ионов так, что по нервным волокнам распространяются электрические сигналы, представляющие нервный импульс. В биофизике распространен термин — транспорт частиц, являющийся синонимом диффузии. Процесс диффузии ответствен за 98 % необходимого кислорода, поглощаемого легкими. Стенки небольших емкостей внутри легких (альвеол), в которых происходит диффузия, имеют у взрослого человека площадь порядка 70 м², а толщину всего 0,5 мкм. Эти стенки плотно обвиты капиллярами, поэтому кровь циркулирует через мембраны легких только тоненькими струйками, причем ее общее количество около 100 мл. Так как площадь поверхности, через которую кислород диффундирует в кровь, а углекислый газ — обратно, очень велика, а толщина мембран мала, становится понятна эффективность процесса диффузии.

Диффузия через полупроницаемую перегородку названа осмосом. Мембрана полупроницаема, если она пористая и через нее возможна избирательная диффузия. Биологические мембраны часто проницаемы для воды, но непроницаемы для других веществ, растворенных в воде. Например, молекулы воды, имеющие диаметр 0,38 нм, проходят сквозь поры, а молекулы глюкозы диаметром 0,88 нм задерживаются. Но молекулы глюкозы не позволяют молекулам воды свободно подходить к мембране, замедляя скорость ее прохождения. Возникает разное осмотическое давление по разные стороны мембраны, а общее давление раствора равно сумме парциальных давлений разных составляющих. В 1887 г. Я. Вант-Гофф установил, что осмотическое давление пропорционально концентрации растворенного вещества с_в и температуре Т. Осмотическое давление раствора зависит от концентрации частиц, которые не могут пройти через мембрану, при этом ионизированные вещества создают большее давление, чем неионизирован-ные. Например, если при растворении в воде поваренной соли происходит разделение на две осмотические частицы, принято считать, что 1 моль NaCl соответствует 2 осмолям. Осмолярность, равная 1, отвечает 1 осмолю растворенного вещества в 1 л воды. Нормальная осмолярность клеточной жидкости 300 осмоль/м³, поэтому при нормальной температуре тела (Т = 310 К) осмотическое давление равно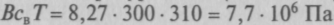. Получи-

302

лось огромное значение давления, и оно останется таким, если вокруг клетки будет чистая вода. На самом деле это не так: окружение имеет концентрацию, близкую к той, что внутри клетки, и если поместить клетку в чистую воду, разность осмотических давлений будет столь высока, что вода с большим напором устремится внутрь клетки и разорвет ее.

Осмос не обязательно связан с наличием мембран. Набухание — тоже осмотический эффект.

8.5. Понятия фазы и фазового перехода. Фазовые переходы первого и второго рода

Фазы — это различные однородные части физико-химических систем. Вещество однородно, когда все параметры состояния вещества одинаковы во всех его элементарных объемах, размеры которых велики по сравнению с межатомными состояниями. Смеси различных газов всегда составляют одну фазу, если во всем объеме они находятся в одинаковых концентрациях. Одно и то же вещество в зависимости от внешних условий может быть в одном из трех агрегатных состояний — жидком, твердом или газообразном. Фазы — это устойчивые состояния определенного агрегатного состояния. Понятие фазы более широкое, чем понятие агрегатного состояния.

В зависимости от внешних условий система может находиться в равновесии либо в одной фазе, либо сразу в нескольких фазах. Их равновесное существование называется фазовым равновесием.

Испарение и конденсация — часто наблюдаемые фазовые переходы воды в окружающей природе. При переходе воды в пар происходит сначала испарение — переход поверхностного слоя жидкости в пар, при этом в пар переходят только самые быстрые молекулы: они должны преодолеть притяжение окружающих молекул, поэтому уменьшаются их средняя кинетическая энергия и соответственно температура жидкости. Наблюдается в быту и обратный процесс — конденсация. Оба эти процесса зависят от внешних условий. В некоторых случаях между ними устанавливается динамическое равновесие, когда число молекул, покидающих жидкость, становится равным числу молекул, возвращающихся в нее. Молекулы в жидкости связаны силами притяжения, которые удерживают их внутри жидкости. Если молекулы, имеющие скорости, которые превышают среднюю, находятся вблизи поверхности, они могут ее покинуть. Тогда средняя скорость оставшихся молекул понизится и температура жидкости уменьшится. Для испарения при постоянной температуре нужно сообщить жидкости некоторое количество теплоты: Q = rт, где r — удельная теплота парообразования, которая уменьшается с ростом температуры. При комнатной температуре для одной молекулы воды теплота парообразования составляет 10^-20 Дж, тогда как средняя энергия теплового движения равна 6,06 • 10^-21 Дж. Это значит, что в пар переходят

303

молекулы с энергией, которая в 10 раз больше энергии теплового движения. При переходе через поверхность жидкости потенциальная энергия быстрой молекулы растет, а кинетическая уменьшается. Поэтому средние кинетические энергии молекул пара и жидкости при тепловом равновесии равны.

Насыщенный пар — это пар, находящийся в динамическом равновесии, соответствующем данной температуре, со своей жидкостью. Опыт показывает, что он не подчиняется закону Бойля—Мариотта, поскольку его давление не зависит от объема. Давление насыщенного пара — наибольшее давление, которое может иметь пар при данной температуре. Процессы испарения и конденсации воды обусловливают сложные взаимодействия атмосферы и гидросферы, важные для формирования погоды и климата. Между атмосферой и гидросферой происходит непрерывный обмен веществом (круговорот воды) и энергией.

Исследования показали, что с поверхности Мирового океана, составляющего 94 % земной гидросферы, за сутки испаряется около 7 000 км³ воды и примерно столько же выпадает в виде осадков. Водяной пар, увлекаемый конвекционным движением воздуха, поднимается вверх и попадает в холодные слои тропосферы. По мере подъема пар становится все более насыщенным, затем конденсируется, образуя дождевые капли. В процессе конденсации пара в тропосфере за сутки выделяется около 1,6-10²² Дж теплоты, что в десятки тысяч раз превосходит вырабатываемую человечеством энергию за то же время.

Кипение — процесс перехода жидкости в пар в результате всплывания пузырьков, наполненных паром. Кипение происходит во всем объеме. Разрыв пузырьков у поверхности кипящей жидкости свидетельствует о том, что давление пара в них превышает давление над поверхностью жидкости. При температуре 100 °С давление насыщенных паров равно давлению воздуха над поверхностью жидкости (так была выбрана эта точка на шкале). На высоте 5 км давление воздуха вдвое меньше и вода закипает там при 82 °С, а на границе тропосферы (17 км) — приблизительно при 65 °С. Поэтому точка кипения жидкости соответствует той температуре, при которой давление ее насыщенных паров равно внешнему. Слабое поле тяготения Луны (ускорение свободного падения у ее поверхности равно всего 1,7 м/с²) не способно удержать атмосферу, а при отсутствии атмосферного давления жидкость мгновенно выкипает, поэтому лунные «моря» безводны и образованы застывшей лавой. По той же причине безводны и марсианские «каналы».

Вещество может находиться в равновесии и в разных фазах. Так, при сжижении газа в состоянии равновесия фаз объем может быть каким угодно, а температура перехода связана с давлением насыщенного пара. Кривая равновесия фаз может быть получена при проекции на плоскость (р, Т) области перехода в жидкое состояние. Аналитически кривая равновесия двух фаз определяется из решения дифференциального уравнения Клаузиуса—Клапейрона. Аналогично можно получить кривые плавления и возгонки, которые соединяются в одной точке плоскости (р, Г), в тройной точке (см. рис. 7.1), где в определенных пропорциях находятся в равно-

304

весии все три фазы. Тройной точке воды соответствует давление 569,24 Па и температура -0,0075 °С; углекислоты — 5,18 • 10⁵ Па и 56,6 °С соответственно. Поэтому при атмосферном давлении р, равном 101,3 кПа, углекислота может быть в твердом или газообразном состоянии. При критической температуре физические свойства жидкости и пара становятся одинаковыми. При температурах выше критической вещество может быть только в газообразном состоянии. Для воды — Т= 374,2 °С, р = 22,12 МПа; для хлора — 144 °С и 7,71 МПа соответственно.

Температурами перехода называют температуры, при которых происходят переходы из одной фазы в другую. Они зависят от давления, хотя и в различной степени: температура плавления — слабее, температуры парообразования и сублимации — сильнее. При нормальном и постоянном давлениях переход происходит при определенном значении температуры, и здесь имеют место точки плавления, кипения и сублимации (или возгонки).

Переход вещества из твердого состояния непосредственно в газообразное можно наблюдать, например, в оболочках кометных хвостов. Когда комета находится далеко от Солнца, почти вся ее масса сосредоточена в ее ядре, имеющем размеры 10—12 км. Ядро окружено небольшой оболочкой газа — это голова кометы. При приближении к Солнцу ядро и оболочка кометы начинают нагреваться, вероятность сублимации растет, а десублимации (обратного ей процесса) — уменьшается. Вырывающиеся из ядра кометы газы увлекают за собой твердые частицы, голова кометы увеличивается в объеме и становится газопылевой по составу. Давление околокометного ядра очень низкое, поэтому жидкая фаза не возникает. Вместе с головой растет и хвост кометы, который вытягивается в сторону от Солнца. У некоторых комет он достигает в перигелии сотен миллионов километров, но плотности в кометном веществе ничтожны малы. При каждом подходе к Солнцу кометы теряют большую часть своей массы, в ядре сублимируют все более летучие вещества, и постепенно оно рассыпается на метеорные тела, образующие метеорные потоки. За 5 млрд лет существования Солнечной системы так закончили свое существование множество комет.

Весной 1986 г. в космос для исследования кометы Галлея были направлены автоматические советские станции «Вега-1» и «Вега-2», которые прошли на расстоянии от нее 9000 и 8200 км соответственно, а станция НАСА «Джотто» — на расстоянии всего 600 км от ядра кометы. Ядро имело размеры 14 х 7,5 км, темный цвет и температуру около 400 К. Когда космические станции прошли через голову кометы, сублимировало около 40 000 кг ледяного вещества за 1 с.

Поздней осенью, когда после сырой погоды наступает резкое похолодание, на ветвях деревьев и на проводах можно наблюдать

305

иней — это десублимировавшиеся кристаллики льда. Подобное явление используют при хранении мороженого, когда углекислота охлаждается, так как переходящие в пар молекулы уносят энергию. На Марсе явления сублимации и десублимации углекислоты в полярных шапках играют такую же роль, что и испарение — конденсация в атмосфере и гидросфере Земли.

Теплоемкость стремится к нулю при сверхнизких температурах, как установил Нернст. Отсюда Планк показал, что вблизи абсолютного нуля все процессы протекают без изменения энтропии. Построенная Эйнштейном теория теплоемкости твердых тел при низких температурах позволила сформулировать результат Нернста как третье начало термодинамики. Наблюдаемые при низких температурах необычные свойства веществ — сверхтекучесть и сверхпроводимость — нашли объяснение в современной теории как макроскопические квантовые эффекты.

Фазовые переходы бывают нескольких родов. Во время фазового перехода температура не меняется, но меняется объем системы.

Фазовыми переходами первого рода называют изменения агрегатных состояний вещества, если: температура постоянна во время всего перехода; меняется объем системы; меняется энтропия системы. Чтобы произошел такой фазовый переход, нужно данной массе вещества сообщить определенное количество теплоты, соответствующее скрытой теплоте превращения.

В самом деле, при переходе из более конденсированной фазы в фазу с меньшей плотностью нужно сообщить некоторое количество энергии в форме теплоты, которое пойдет на разрушение кристаллической решетки (при плавлении) или на удаление молекул жидкости друг от друга (при парообразовании). Во время преобразования скрытая теплота расходуется на преодоление сил сцепления, интенсивность теплового движения не изменяется, в результате температура остается постоянной. При таком переходе степень беспорядка, а следовательно, и энтропия возрастают. Если процесс идет в обратном направлении, то скрытая теплота выделяется.

Фазовые переходы второго рода связаны с изменением симметрии системы: выше точки перехода система, как правило, обладает более высокой симметрией, как показал в 1937 г. Л.Д.Ландау. Например, в магнетике спиновые моменты выше точки перехода ориентированы хаотически, и одновременное вращение всех спинов вокруг одной оси на одинаковый угол не изменяет свойств системы. Ниже точки перехода спины имеют некоторую преимущественную ориентацию, и одновременный их поворот меняет направление магнитного момента системы. Ландау ввел коэффициент упорядочения и разложил термодинамический потенциал в точке перехода по степеням этого коэффициента, на основе чего построил классификацию всех возможных типов перехо-

306

дов, а также теорию явлений сверхтекучести и сверхпроводимости. На этой основе Ландау и Лифшиц рассмотрели много важных задач — переход сегнетоэлектрика в параэлектрик, ферромагнетика — в парамагнетик, поглощение звука в точке перехода, переход металлов и сплавов в сверхпроводящее состояние и др.

Расчет термодинамических свойств системы на основе статистической механики предполагает выбор определенной модели системы, и чем сложнее система, тем проще должна быть модель. Е. Изинг предложил модель ферромагнетика (1925) и решил задачу об одномерной цепочке с учетом взаимодействия с ближайшими соседями для любых полей и температур. При математическом описании таких систем частиц с интенсивным взаимодействием выбирается упрощенная модель, когда происходит взаимодействие только парного типа (такая двумерная модель названа решеткой Изинга). Но фазовые переходы не всегда удавалось рассчитать, вероятно, из-за каких-то неучтенных явлений, общих для систем многих частиц, причем не имеет значения природа самих частиц (частицы жидкости или магниты). Л.Онсагер дал точное решение для двумерной модели Изинга (1944). Он поместил в узлах решетки диполи, которые могут ориентироваться только двумя способами, а каждый такой диполь может взаимодействовать только с соседом. Получилось, что в точке перехода теплоемкость обращается в бесконечность по логарифмическому закону симметрично по обе стороны точки перехода. В дальнейшем оказалось, что этот вывод весьма важен для всех фазовых переходов второго рода. Работа Онсагера показала, что метод статистической механики позволяет получить новые результаты для фазовых превращений.

Фазовые переходы второго, третьего и т.д. родов связаны с порядком тех производных термодинамического потенциала Ф, которые испытывают конечные изменения в точке перехода. Такая классификация фазовых превращений связана с работами физика-теоретика П. Эренфеста. В случае фазового перехода второго рода в точке перехода испытывают скачки производные второго порядка: теплоемкость при постоянном давлении С_р = 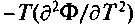, сжимаемость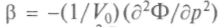, коэффици-

ент теплового расширения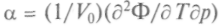, тогда как пер-

вые производные остаются непрерывными. Это означает отсутствие выделения (поглощения) теплоты и изменения удельного объема.

Квантовую теорию поля начали использовать для расчетов систем частиц только в 70-е гг. XX в. Система рассматривалась как решетка с меняющимся шагом, что позволяло менять точность вычислений и приближаться к описанию реальной системы и использовать ЭВМ. Американский физик-теоретик К. Вильсон, применив новую методику расчетов, получил качественный скачок в понимании фазовых переходов второго рода, связанных с перестройкой симметрии системы. Фактически он связал квантовую механику со статистической, и его работы получили фунда-

307

ментальное значение. Они применимы и в процессах горения, и в электронике, и в описании космических явлений и ядерных взаимодействий. Вильсон исследовал широкий класс критических явлений и создал общую теорию фазовых переходов второго рода.