В. Н. Каразіна 25-річному Ювілеєві першої в Україні природоохоронної кафедри

Вид материала

Документы

Содержание 1.4.4.Топологічні структури ФГМС 1.5. Ієрархія флювіальної мережі 1.5.1. Мережа тальвегів 1.5.2. Ієрархії мережі тальвегів L – розрахунковим значенням довжини русла даного порядку, S A – розрахункова площа водозбору до замикаючого створу русла даного порядку i A. Симетрія щодо осі, що збігається з кінцевим (тобто низхідним у системі флювіальної мережі) елементом дуги і вершиною трійника М. Кут між бісектрисою кута В и віссю симетрії (показник асиметрії). Д. 1.5.3. Ієрархія вододілів 1.5.4. Лінії перегину схилів 1.5.5. Формалізація двовимірних структурних мереж тальвегів 1.5.6. Тривимірні мережі ФГМС

Подобный материал:

• Харківський національний університет імені В. Н. Каразіна назва роботи, 8.52kb.
• Українське/національне в радянській офіційній політиці пам’яті про примусову працю, 342.65kb.
• М.І. Пирогова «затверджено» на методичній нараді кафедри Завідувач кафедри 200 р. Методичні, 265.61kb.
• Г. О. Кулєшова, аспірантка кафедри соціально-економічної географії І регіонознавства, 113.14kb.
• Міністерство освіти І науки, молоді та спорту україни харківський національний університет, 200.57kb.
• Розпорядження, 501.27kb.
• України Суми "Видавництво СумДУ", 1850.09kb.
• Р І шенн я, 1135.29kb.
• Затверджено наказом ректора Харківського національного університету імені В. Н. Каразіна, 88.61kb.
• Р І шенн я про Програму розвитку туризму у Володарському районі на 2008-2010 роки Відповідно, 259.78kb.

1.4.4.Топологічні структури ФГМС

Топологічні структури відрізняються від елементів тим, що вони здатні до саморозвитку.

Характерні поєднання елементів 1,2,3-го порядків створюють топологічні структури ФГМС. Кожна топологічна структура самовідтворюється у флювіальному рельєфі будь-якого порядку. Саме через це формування наступного порядку флювіальної мережі не спотворює попередній рельєф, але ж підвищує на одиницю ранг усіх його елементів 2- та 3-го порядків (тобто ліній і граней). У сучасній світовій літературі існує потік праць з аналізу флювіальних мереж, але практично не звертається уваги на мережу вододілів. Зокрема, в роботі В. Ньюмена та Д. Таркотта ⁵⁵ досліджено й фізично описано каскадні флювіальні мережі двох регіонів Заходу США (за схемою А. Шейдеггера, що викладається нижче) з огляду на визначення енергетичної потужності флювіального процесу засобами спектрального аналізу. Фрактальному моделюванню водозбору присвячено одну з робіт С.В. Кострікова ¹⁴.

Нагадаємо деякі положення щодо значення топологічної структури флювіального рельєфу, що були викладені нами раніше.

Дерево тальвегів має дві інваріантні властивості: орієнтованість й упорядкованість. Перша проявляється в тому, що водний потік та твердий стік відбуваються лише в одному фіксованому напрямку. Друга властивість полягає в тому, що відрізки мережі і вузли мережі природно супідрядні, тому що вони творяться злиттям тих відрізків флювіальної мережі,, що розташовані вище за течією. Причому, кожне злиття двох тальвегів нижчого порядку, що творять тальвег більш високого порядку, утворює трійник. Трійник є основним структурним елементом ерозійної мережі флювіального рельєфу. Він є інваріантним утворенням щодо розміру й рангу системи, самоподібним сам до себе (тобто саме він має фрактальні властивості).

Досить часто структурний та функціональний аналіз зливаються в спряжений структурно-функціональний аналіз через те, що вони органічно взаємопов‘язані і самозалежні: структура визначає функцію рельєфу, а функція (тобто процес рельєфоутворення) створює структуру.

Топологічна структура ФГМС інваріантна. Вона зберігається незмінною незалежно від того, яким способом виражена чи в якій системі координат відображається. Завдяки властивості інваріантості, топологічна структура рельєфу проглядає "крізь" інші геофізичні чи геохімічні поля, задаючи їхню структуру, що є вторинною до структури рельєфу.

Ця обставина має зрозуміле фізичне пояснення: рельєф є організуючим, ведучим компонентом ландшафту, бо він перерозподіляє прямо чи модифікує побічно всі залежні від нього, більш слабкі, за термінологією ландшафтознавців, компоненти ландшафту: сонячну радіацію, поверхневий і внутрігрунтовий стік, мезо- і мікроклімат, а через них - біотичні компоненти.

Топологія рельєфу відносно стійка в часі. У процесі розвитку зберігаються колишні структурні елементи і відбувається нарощування нових структурних ярусів тальвегів і вододілів, що призводить до ускладнення структури і зростання на один порядок усіх попередніх структурних елементів. Зростання складності поліпшує властивості рельєфу як дисипативної структури.


1.4.5. Геоморфологічне значення топологічної структури ФГМС

І.С. Щукін у "Морфології суші" одним з перших геоморфологів підкреслив значення долин в устрої ерозійно-денудаційного рельєфу, де вони виконують роль організуючої ланки у його функціонуванні. Дійсно, долинна мережа - це свого роду кровоносна система геоморфологічного ландшафту, причому подібність між системами стоку і кровоносних судин настільки тісна, що навіть закони організації долинних мереж, з одного боку, і кровоносних мереж, з іншого, є одними й тими самими, що уже відзначалося в науковій літературі. Значення топологічної структури і в рельєфі, і в інших системах полягає в тому, що вона детермінує процес функціонування. Для флювіального рельєфу особливе значення має його інваріантна структура. Взаємне положення тальвегів і вододілів визначає напрямок і траєкторії потоків речовини, а тривимірність їхнього положення - швидкість і енергію її переміщення.

Кожен етап розвитку рельєфу запам'ятовується в структурі рельєфу, створюючи свій "структурний шар", тобто визначений порядок в інваріантній структурі. Це пов'язане з тим, що кожний певний етап розвитку додає нову генерацію тальвегів нижчого порядку, отже разом із ним, похідну від них мережу вододілів, а також схилів між тальвегами і вододілами, тобто ще на один структурний "крок" ускладнює рельєф. З цього погляду структура - свого роду літопис рельєфу, який за потреби можна прочитати засобами структурного аналізу.

Процеси енерго-масопереносу, що відбуваються в кожній точці рельєфу, визначаються її структурним положенням. Інтенсивність цих процесів у цілому характеризується, як відомо, глибиною розчленовування місцевості, ухилами поверхні, складністю розчленовування. Усі ці параметри залежні від топологічної структури рельєфу.


Глибина розчленовування - це, за вдалим виразом М.О. Флоренсова, "робочий" інтервал висот, у межах якого відбувається формоутворення. Він визначається вертикальною різницею поміж вершинною і базисною поверхнями. "Воображаемая поверхность, которая соединяет тальвеги местной овражной сети – прогрессивный уровень относительно поверхности плато, которое регрессирует", - писав він (див.[³⁹, с. 67). Описуючи процес розчленовування плато ярами, М.О. Флоренсов прийшов до принципових більш широких, ніж того допускав об’єкт вивчення, висновків:

— рельєф істотно змінюється (розвивається) при незмінному субстраті, сталості клімату і невтручанні ендогенних факторів;

— еволюція рельєфу протікає шляхом саморозвитку, забезпечуваного протиріччями двох рівнів (гіпсометричних – І.Ч.) у полі сили ваги, а також потенційною можливістю необмеженого розвитку ярів через їх подовження і розгалуження в умовах обмеженості простору (території плато).

Далі М.О. Флоренсов підкреслював, що розвиток і саморозвиток рельєфу забезпечуються існуванням контрастів і геоморфологічно зводиться до подолання протиріччя між високим і низьким, до постійної, через ізостазію, тенденції до згладжування і вирівнювання.


Якщо, наприклад, точка рельєфу знаходиться на схилі між вододілом 1-го і тальвегом 4-го порядків, то рельєфотворний процес буде більш інтенсивним, тому що він тепер визначається різницею між вершинною поверхнею 1-го порядку і базисною 4-го порядку, що значно більша, аніж між однопорядковими поверхнями різних типів.

Необхідно відзначити, що, крім найближчого тальвегу, на геоморфологічний процес у даній точці рельєфу впливає положення тальвегів вищих порядків. Цей вплив опосередкований через ухили в тальвегах, швидкість наростання порядків, довжину шляху і перепад висот, що їх повинен здолати у процесі руху потік наносів - складова літодинамічного потоку. Тому можна вважати, що кожний із цих впливів зводиться до взаємодії базисних поверхонь у даній точці, по "сходинках" якої спадає динамічний потік.

Менш очевидною є роль вершинних поверхонь, хоча формально ланцюг міркувань і тут може залишатися таким же. Процеси в даній точці залежать від потужності потоку води і транзиту твердого матеріалу, розгону, що його може набрати водний потік і т.д., а ці параметри, у свою чергу, визначаються положенням точки щодо верхнього базису денудації. Тут також очевидна залежність від того, які структурні елементи сусідять з даною точкою, тобто від горизонтальної структури рельєфу.

Структурний підхід дозволяє пояснити природними відмінами ряд явищ, що часто відносяться дослідниками до числа аномальних. Концентрація ярів, посилений змив ґрунту, аномально короткі чи, навпаки, протяжні тальвеги визначеного порядку, збільшені ухили та інші морфологічні, морфометричні і динамічні відмінності, що зазвичай пояснюються, як правило, тектонічними причинами, можуть одержати і нетектонічне тлумачення - як результат певного незвичайного структурно-топологічного положення ділянок. Цю обставину необхідно враховувати в ході структурно-геоморфологічних досліджень у прикладних цілях, що дає можливість надати їхнім результатам більшої визначеності і у певній мірі сприятиме підвищенню результативності структурно-геоморфологічного аналізу в цілому.


1.5. ІЄРАРХІЯ ФЛЮВІАЛЬНОЇ МЕРЕЖІ

Як зазначалось, ієрархія флювіальної мережі набула популярності переважно з класичної роботи англійського гідролога Р. Хортона 53, що надалі захопила увагу переважно західних гідрологів, геоморфологів і геофізиків.

Через півтора десятиліття російський геолог-геоморфолог В.П. Філософов у невеличкій і непоказній книжці навів блискучий спосіб ієрархічного аналізу просторового положення мереж тальвегів (карти базисних поверхонь) для виявлення за особливостями такого положення ділянок локальних тектонічних рухів.

Приблизно через такий самий час український геоморфолог М.Г. Волков розробив ще один спосіб просторового аналізу тальвегів (метод ізодеф), теж застосувавши його для аналізу локальної тектоніки. Відсутність посилань на роботи названих авторів свідчить про те, що вони залишились поза увагою світової геоморфологічної спільноти.

Водночас, В.П.Філософов першим запропонував аналіз мережі вододілів (карти вершинних поверхонь), співставивши їх із тальвегами. Дещо пізніше І.Г. Черваньов запропонував спільний аналіз тальвегів і вододілів для тривимірного топологічного аналізу рельєфу.


1.5.1. Мережа тальвегів


Головна структурна особливість ФГМС, що відрізняє її від устрою інших поверхонь, - підпорядкованість її структури і функцій мережі тальвегів (флювіальній мережі у функціональному відношенні). Ця властивість є найбільш вираженою.

Флювіальна мережа являє собою утворення, котре дивує досконалістю упорядкованості і погодженості її структурних елементів. Досить нагадати, що неодноразово встановлювалася аналогія між структурою і функціонуванням цієї мережі і системою кровоносних судин високоорганізованої живої істоти.

Повсякденний досвід і спеціальні дослідження цього феномену переконують, між іншим, що явища неживої природи за своєю структурною організацією можуть зрівнятися в чомусь з живим організмом.


1.5.2. Ієрархії мережі тальвегів


Існує кілька підходів до опису структури річкової мережі ФГМС. Вони належать Р.Хортону, В.Філософову, А.Стралеру, Н.Ржаницину, А. Шейдеггеру й ін. Найбільш відомі три традиційні схеми порядкового бонітування елементів мережі (рис. 1.1).




Рис. 1.1. Моделі ієрархії структури річкової мережі ФГМС: а - за Хортоном; б - за Філософовим-Стралером; в - за Шейдеггером.


Р.Хортон [⁵³] запропонував першу схему упорядкування річкової мережі. Він розглядав структуру мережі від гирла вгору проти течії. Нижній відрізок брався за головний. У кожного розгалуження визначалося, яке саме з річищ є головним. Використовувались дві ознаки: 1) якщо водотік вище точки розгалуження сильніше відхиляється від напрямку загального русла, то він вважається другорядним; 2) якщо обидва водотоки вище точки розгалуження однаково відхиляються від напрямку загального русла (тобто є симетричними відносно осі трійника - І.Ч.), то другорядним є той, котрий коротший. Потім, за цією схемою, позначаються порядки, починаючи від елементарного, котрий одержує індекс 1, і т.д.

Таким чином, була вперше впроваджена схема порядкового бонітування флювіальної мережі фактично подавала просторове поєднання елементів різного порядку на реальному рельєфі, що у свою чергу давало можливість визначити певні закономірності, які уперше і були кількісно доведені Р. Хортоном. Це стало початковим прикладом формального опису мереж флювіального рельєфу. “Закони Хортона”, про які йдеться (див. частину другу книжки), стверджують, що розрахункові значення чисел русел, їх довжин та схилів суттєво різняться по елементах різного порядку. Визначені закономірності у подальшому неодноразово зазначалися у певній мірі присутніми не тільки у мережах постійних водотоків, але і у всьому морфологічному різноманітті водно-ерозійного рельєфу.

Незважаючи на те, що “закони Хортона” записуються в певною мірою різних редакціях, просторово-територіальна структура даного водозбору може бути досить повно визначена лише кількома наступними дескриптивними показниками:


коефіцієнтом біфуркації R_B  ( N_i ) ^{1 / (  - i)} , (1.1)


коефіцієнтом довжин R_L  ( L_i / L_ ) , (1.2)

та

коефіцієнтом схилів R_S  ( S_i / S_ ) ^{1 / (  - i)} , (1.3)


де N є числом русел даного порядку i,  - порядком головного русла водозбору (порядком усієї руслової мережі), L – розрахунковим значенням довжини русла даного порядку, S – розрахунковим значенням схилу русла даного порядку. Пізніше С. Шумом був запропонований аналогічний додатковий дескриптивний показник – коефіцієнт площин (див. [⁵⁸]):

R_A  ( A_i / A_ ) ^{1 / (  - i)} , (1.4)


де A – розрахункова площа водозбору до замикаючого створу русла даного порядку i.

С. Костріков довів (див.[¹⁴]), що із точки зору чисельного моделювання вказані коефіцієнти (R_B , R_{L ,} R_S , R_A) є величинами, що визначаються нахилом ліній регресії відповідних значень log (N_i , L_i , S_i , A_i) по i. Тобто можливо переписати, наприклад (1.1) і (1.2) як

N_i  R_B ^{ - i} i = 1, 2, …,  (1.5)

та

L_i  L₁ R_L ^{i – 1}, (1.6)


використовуючи дескриптивні показники R_B і R_L при модельних розрахунках топологічних і метричних властивостей мережі флювіального рельєфу на підставі виразів (1.5) і (1.6), відповідно. Подібним чином можна подавати (1.3) і (1.4).

Схема Хортона зручна тим, що дозволяє простежити стовбур дерева й гілки різних порядків на протязі усієї їхньої довжини. Але, зі структурного боку, цю схему не можна вважати досконалою. Її недоліки:

• морфометрична непорівнянність різних відрізків структурного елемента одного порядку, що знаходяться між суміжними точками злиття водотоків. На рис. 1.1, а видно, що водотік 3 порядку в нижній течії найбільший, натомість на самому верхньому відрізку він відносно менший, ніж водотоки нижчих, тобто 2 і 1-го порядків.
  
• однакові за метричними показниками елементи дерева тальвегів набувають різного порядку.
  

Через такі особливості схеми Хортона, вона видається нам неприйнятною з огляду на задачі структурного аналізу, тому що не забезпечує порівнянності однопорядкових елементів мережі. Натомість, її автор призвів до революції у флювіальній геоморфології та гідрології, бо завдяки цій схемі йому вдалося установити закони гідравлічної геометрії (див. , що нагадують закони розгалуження кровоносних судин, і залежності між структурними параметрами і функціональними характеристиками. На нашу думку, цю схему можна назвати функціонально-геометричною.

В.П.Філософов [³⁷,³⁸] і А.Стралер (Strahler) ⁶¹,⁶² незалежно один від одного розробили однакові схеми упорядкування річкової мережі на іншому, топологічному принципі. У цих схемах не враховується довжина елементів - лише їхня топологічна ієрархія. Тут (у обох авторів незалежно) була прийнята наступна нумерація дихотомічного дерева: два потоки одного порядку, що зливаються, дають потік наступного порядку і т.д. Такого роду схема зручна тим, що забезпечує топологічну порівнянність однопорядкових елементів одного басейну і навіть декількох басейнів, якщо вони охарактеризовані з однаковим ступенем детальності; обчислений порядок структуроутворення відповідає аналогічному в теорії графів. Недолік схеми - ігнорування нею непорядкоутворюючих елементів, що не підвищують порядок. Наприклад, впадання у водотік 4-го порядку двох водотоків 3-го порядку за збільшенням водності потоку порівнянне з ефектом від злиття двох водотоків 4-го порядку. Однак у першому випадку порядок головного водотоку зберігається незмінним, а в другому - підвищується. Ця особливість схеми призводить до похибок у оцінюванні водотоків за їх водністю.

Саме через це, схеми Філософова-Стралера варто відносити до топологічних моделей. Завдяки математичній строгості принципу визначення порядків у такій схемі, вони отримали найбільш широке поширення, водночас удосконалювалися далі.

Однак також, суттєвою відміною схеми В.П. Філософова від схеми А. Стралера є те, що тальвеги (долини, за цим автором) зберігають висотні відмітки, тобто не розглядаються як плоскі утворення, у той час як у А. Стралера й усіх його західних послідовників вони є плоскими. Це дало можливість В.П. Філософову будувати на топологічній мережі тальвегів карти базисних поверхонь, досліджуючи за ними аномалії ухилів тальвегів одного й того ж порядку у різних місцях досліджуваної території.

А.Шейдеггер (Scheidegger) ⁵⁷ розробив схему, що у більшій мірі відображує гідрологічний фактор – вирішальний у флювіальному процесі. Він врахував потенційну водність елементів різного порядку, котра забезпечується, за Шайдеггером, числом тальвегів першого порядку. Тобто вважається, що кожен із них є однорідною за потужністю елементарною одиницею, що створює потік рівної потужності. Оскільки елементарні водотоки близькі за своїми гідрологічними параметрами, можна оцінювати потужність потоку на будь-якому відрізку мережі через його індекс. А. Шайдеггер надав кожному елементарному потокові незалежно від його структурної позиції індексу 2. При злитті чи впадінні водотоків додаються їхні індекси, що має відображувати зростання потужності похідного водотоку: наприклад, злиття двох елементарних водотоків, що дає за схемою Філософова-Стралера 2-й порядок потоку, за схемою Шейдеггера позначається індексом 4.

За величиною індексу будь-якого відрізка мережі легко встановити, скільки елементарних водотоків знаходиться вище за течією. Наприклад, якщо ділянка мережі має індекс 24, отже, вище впадає 12 елементарних водотоків. Однак за схемою Шейдеггера не можна підрахувати числа водотоків порядків більш високих, аніж 1-й, тому що вони не фіксуються. Таку схему варто називати функціонально-топологічною. На рис. 1.1, в показана схема того ж дерева, індексована за А. Шейдеггером.

Найбільш прийнятна для наших подальших побудов схема В.П. Філософова (з урахуванням того, що тальвеги і вододіли зберігають висотні відношення), тому що вона забезпечує порівнянність однопорядкових елементів, що знаходяться навіть у різних басейнах, і допускає морфометричний аналіз рельєфу по інваріантних лініях. Крім того, Філософов уперше увів поняття «порядку вододілу», застосував свою схему для узгодження порядків водотоків і вододілів по "залежній" схемі (див. нижче) і забезпечив порівнянність порядків суміжних елементів двох мереж, що надалі необхідне нам для структурної декомпозиції рельєфу.

Один із найновітніших варіантів упорядкування топологічної (двовимірної, плоскої) мережі водотоків запропонували К. Куденнік та ін. (див. ⁵⁴). Ці автори ввели поняття гідравлічного шляху (ГШ) в мережі флювіального рельєфу, відрізняючи, таким чином, ГШ по руслах флювіальної мережі від схилового шляху, який проходять обсяги немаршрутизованого гідрологічного стоку. Загальна схема цього новітнього порядкового бонітування пояснена згаданими авторами на прикладах, схожих на рис. 112 (рис. 1.2).

В рамках порядкового бонітування концепції ГШ елементом, або компонентом системи i-го порядку буде послідовність русел або їх відрізків того ж саме (i-го) порядку. За думкою вказаних авторів, порядкове бонітування елементів-компонентів ГШ може бути відмінною від класичних схем (рис. 1.2), хоча насправді практично повертається до найпершої з них – схеми Р.Хортона (рис. 1.1, а). Запропоновані поняття гідрологічного шляху, гідравлічної довжини, (яку розглядають в якості репрезентативної змінної, що адекватно характеризує руслову мережу як фрактальний об’єкт в рамках плоскої двовимірної моделі водозбірного басейну (рис. 1.2). Підкреслюється, що для кожної точки русла у водозбірному басейні ГД може визначатися наступна сума:

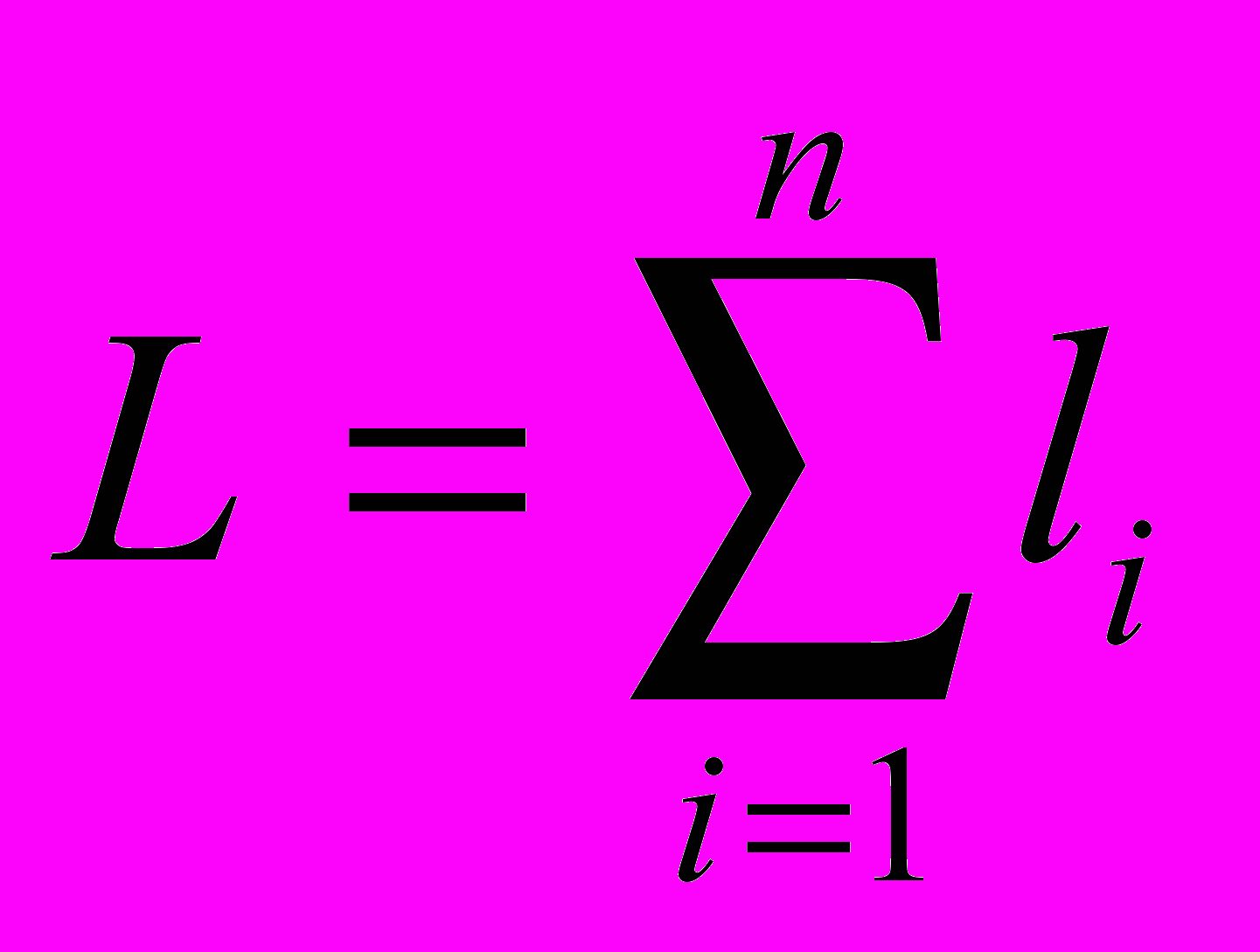, (1.7)


де n – порядок руслової мережі даного водозбору, l _i – довжина компонента i- го порядку в даному ГШ (рис. 1.2).

Подібно до базового відношення Р. Хортона щодо довжин русел (1.2) автори, на яких ми посилаємося, вводять поняття відношення довжин компонентів ГШ:







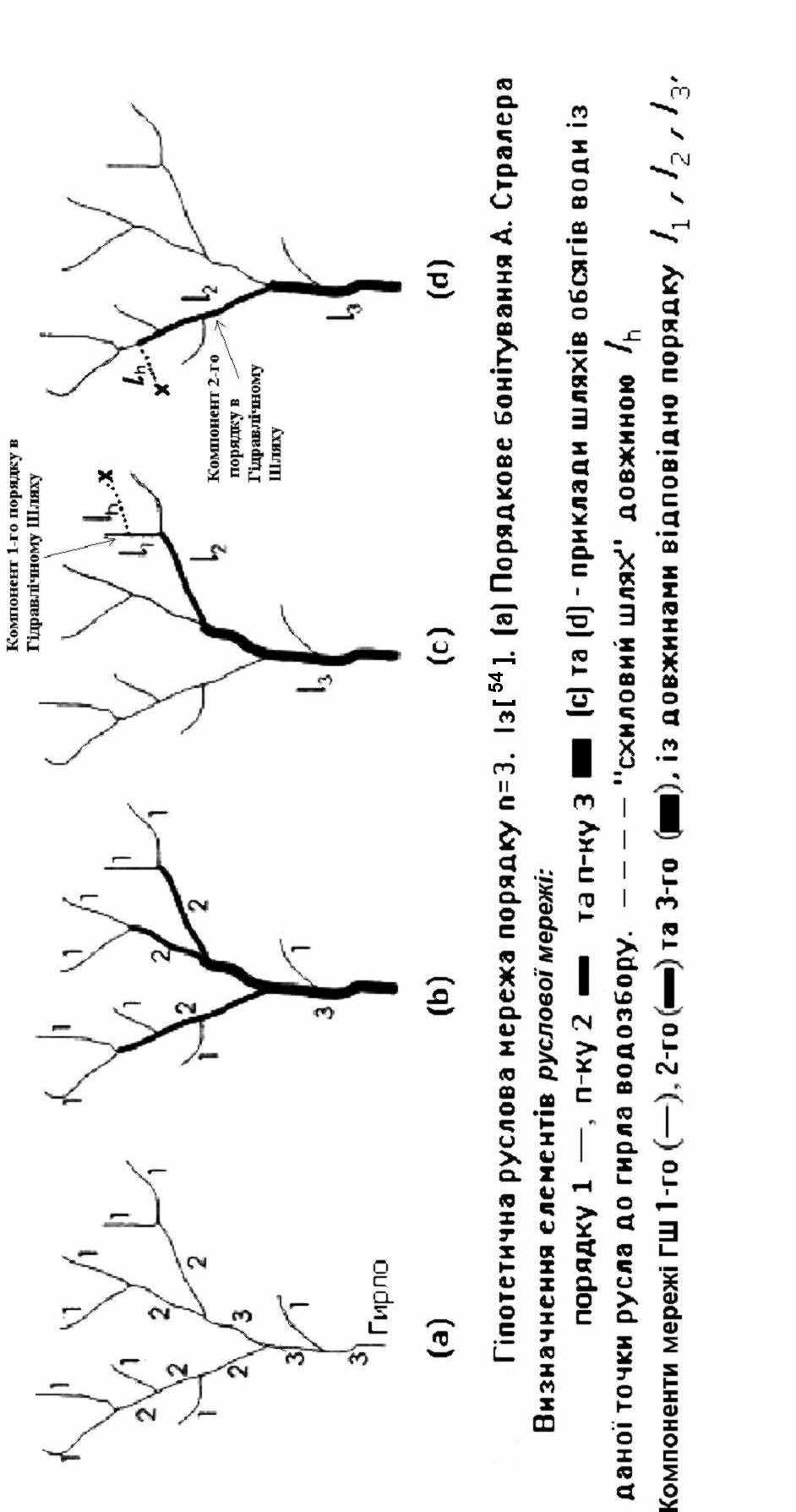
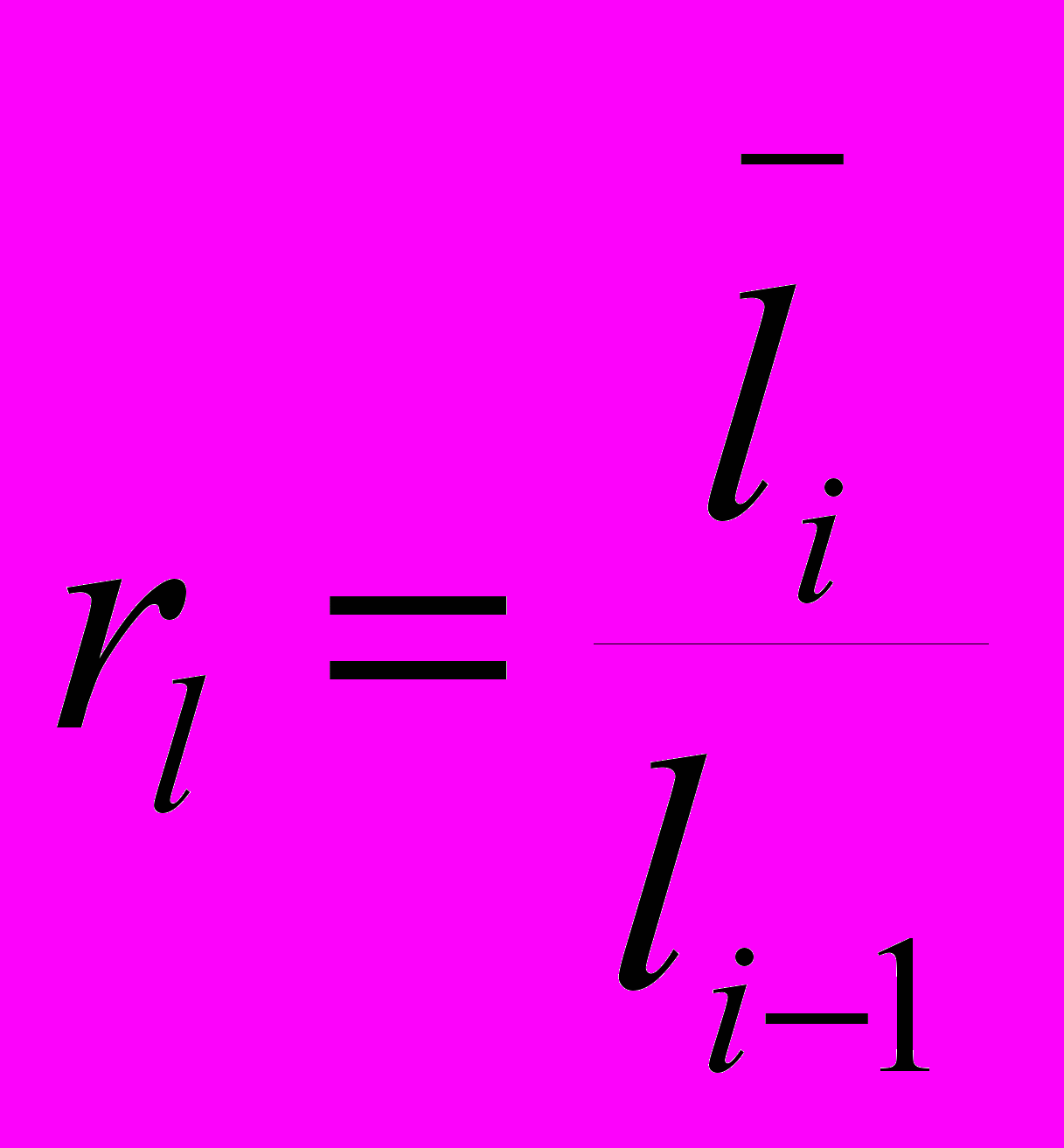, (1.8)

де - середня довжина компонентів i- го порядку в даному ГШ. За думкою цих авторів обчислення по (1.7) і по (1.8) передбачають об’ємні і складні розрахунки на реальному рельєфі і, таким чином, сталість подібних показників може визначатися тільки через розвинений ГІС-аналіз.

Із самої будови флювіальної мережі випливає, що вершини дерева тальвегів є топологічно різнорідними. Виділяються 4 типи вершин. Для їх характеристики теж користуємося елементарними уявленнями теорії графів.

1. Зовнішні (висячі) вершини x₀. Вони є кінцевими елементами дерева. Висячі вершини є фіктивними, тому що тут не відбувається злиття тальвегів. Наголосимо умовність останнього твердження, бо це залежить від масштабу дослідження.
   
2. Порядкотворні вершини при злитті 2-х елементів одного порядку х₁, х₂ ·.., х_п-1 ·
   
3. Старша порядкотворна вершина х_n, з якої розпочинається корінь дерева (елемент мережі найвищого порядку).
   

Непорядкотворна вершина - при впадінні тальвегу нижчого порядку в тальвег вищого порядку (рис. 1.3).

Число дуг, що знаходиться вище кореневої вершини даного рангу, дорівнює S_m - 2^m - 2, де S_m - число дуг; m - ранг вершини. У бінарному дереві, що використовується у структурному аналізі, вершини типу 4 не приймаються до уваги. Для функціонального аналізу враховуються будь-які елементи, що знаходяться вище від точки фіксації, бо вони, незалежно від розміру, приймають участь у флювіальному процесі.

Складними елементами топологічної структури дерева тальвегів є трійники при вершинах 2-4-го типів. Трійник (з точки зору теорії графів) твориться сполученням трьох дуг і однієї вершини.

У ньому дві дуги сполучаються кінцевими, а третя - початковим елементами. У природі цій формальній структурі відповідають два тальвеги, що зливаються у вершині дерева (є вхідними щодо цієї вершини) і третій – похідний від них (тобто більш високого порядку - нижчий щодо зазначеної вершини).




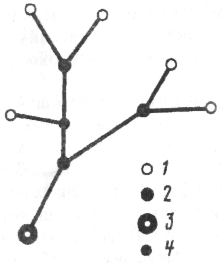
Рис. 1.3. Типи вершин "дерева" тальвегів: 1 - кінцева (висяча); 2 - порядкотворна; 3 - коренева; 4 – непорядкотворна


Нижче наводяться топологічні закономірності, що характеризують трійники, уперше виділені у якості первинних структурних утворень автором і повно описані як структурні вузли рельєфу С.В.Костріковим (див. рис. 2.8 у частині 2).

A. Симетрія щодо осі, що збігається з кінцевим (тобто низхідним у системі флювіальної мережі) елементом дуги і вершиною трійника.Б. Співвідношення порядків дуг при вершині.

B. Кут між початковими (вхідними щодо флювіальної мережі) елементами дуг.

М. Кут між бісектрисою кута В и віссю симетрії (показник асиметрії).

Д. Кути між віссю симетрії і кінцевими елементами дуг.

Властивості В, Г, Д називають ангулярними властивостями ¹³.

За ⁴⁶,⁵⁰, число вершин Р_m, що знаходяться вище кореневої (без зовнішніх вершин), складає Р_m = 2^m-1 - 2.

Завдяки цим відносинам, можна сформулювати одну з найважливіших структурних властивостей мережі тальвегів:

- два дерева, що відображають дві мережі тальвегів, топологічно ізоморфні, якщо мають корінь одного рангу.

Як узагальнення цих досліджень, наведемо таблицю 1, де відображено сукупність залежностей, виявлених переважно західними авторами у мережі тальвегів флювіального рельєфу, що нещодавно була складена Р.Доддсом та Д. Ротманом (див. ⁵²).

Структурними властивостями володіють, крім тальвегів, ще два типи ліній: вододіли і перегини схилів.


1.5.3. Ієрархія вододілів


Властивості мережі вододілів подібні, але не тотожні мережі тальвегів. Порівняння показує, що мережі тальвегів властива вища, ніж вододілам, організація, що полягає в її орієнтованості, обумовленій функціональним значенням тальвегів як середовища впорядкованого стоку до гирла основної ріки. Орієнтованість існує об‘єктивно й абсолютно, тобто незалежно від детальності розгляду мережі. Різним є характер наростання порядків тальвегів і вододілів: у першому випадку переважає бінарне дерево, у другому – певне число дерев різних порядків із загальним "коренем". За термінологією теорії графів - це "ліс".

Головні відмінності мереж тальвегів і вододілів полягають у наступному.

1. Мережа тальвегів орієнтована, вододілів - не орієнтована. Тому лінійні елементи системи тальвегів мають топологічно загальний напрям, мережі вододілів - ні.
   
2. У мережі вододілів немає чіткої залежності поміж рангом вершини і порядком ребер, що у ній сходяться (у термінах теорії графів). В одному вузлі можуть бути безладно поєднані вододіли різних порядків, на той час у мережі тальвегів переважає дихотомія. В ієрархії вододільних ліній відсутня дихотомія як норма.
   
3. Ієрархія вододілів залежна від ієрархії долин, тому що останні первинні в структурному відношенні: вони задають структуру рельєфу, будучи прогресивними елементами; вододіли консервативні.
   

5. Оскільки ієрархія вододілів визначається ізоморфізмом щодо мережі долин, визначення їхніх порядків доцільно здійснювати за залежною схемою за правилом, запровадженим В.П. Філософовим ³⁷: поміж двома тальвегами будь-яких порядків існує один вододіл, порядок якого відповідає порядкові топологічно молодшого тальвегу.


1.5.4. Лінії перегину схилів


Лінії перегинів схилу утворені точками параболічного виду. Поняттям "перегин схилу" поєднуються три види ліній: власне перегини схилу, бровки і підошви схилів.

Власне перегин схилу - це лінія нульової кривизни схилу. Якщо розітнути схил профілями в хрест простягання, то перегинові схилу буде відповідати точка, у якій увігнута й опукла частини схилу зчленовуються. Стосовно кривої можна говорити про знак кривизни.

В увігнутої частини схилу він від‘ємний, в опуклої - додатний, у точки їхнього зчленування є нульова кривизна. Лінії бровки і підошви в перетині профілем не характеризуються нульовою кривизною на відміну від споріднених до них ліній перегину. Навпаки, по відношенню до перегинів схилу, кривизна лінії профілю в точках перетину ним бровки і підошви максимальна.

На рис. 1.4 зображені лінії перегину схилу на опукло-увігнутому схилі. Угорі (див. рис. 1.4, а) наведений фрагмент гіпсометричної карти схилу, за якою приблизно відбиваються бровка і підошва схилу. По лінії ab складений профіль.

На рис. 1.4, б показаний профіль схилу. На ньому виділені точки максимальної кривизни: точка верхнього перегину (k_m1), чи бровка, точка нижнього перегину (k_m2), чи підошва схилу, і точка нульової кривизни - середнього перегину опукло-вгнутого схилу (k₀).

На рис. 1.5, а показаний складний схил з декількома перегинами схилу. 1, 2,..., 9 - поперечні профілі схилу.

На рис. 1.5, б ті ж поперечні профілі побудовані проектуванням на вісь абсцис точок перетинання ліній профілів з горизонталями рельєфу. Видно, що профілі змінюють свій вигляд від прямого (1), опукло-вгнутого (2-5) до складного з двома увігнутостями (7-9). Знаком "плюс" позначені лінії перегину додатного, "колечком"- від‘ємного значень кривизни. З рис. 1.5, б видно, що лінії перегину схилу можуть зникати, тобто вони не становлять зв'язну мережу. Таким чином, вони не мають тих властивостей, що притаманні деревоподібним мережам тальвегів і вододілів.



Рис. 1.4. Лінії перегину схилу. Рис. 1.5. Перспективне зображення

складного схилу.


Позначення на обох рисунках: а - планове зображення схилу балки (в ізогіпсах); б – профіль (в абсолютних висотах); k_m1 - верхній перегин (бровка), k_m2 - нижній перегин (підошва), k₀ - середній перегин (лінія нульової кривизни)


Переривчасто-фрагментарна мережа перегинів схилу, утворена різнорідними лініями - бровками, підошвами схилів і лініями нульової кривизни - топологічно несхожа з іншими мережами.

Узагальнимо властивості ліній перегину схилу:

1. Сукупність наявних у флювіальному рельєфі перегинів схилу незв'язна, тобто не створює суцільної мережі. На складних схилах можливі локальні мережі перегинів скатів. На плоских схилах немає ліній нульової кривизни, тому що тут лінія вироджується у площину. Вона ж знову відроджується в місцях переходу плоского схилу в опукло-увігнутий. На опуклих і увігнутих схилах лінії перегину відсутні.
   
2. Локальна мережа перегинів схилу циклічна на складних схилах.
   

З. У локальних мережах перегинів схилу немає природної ієрархії, котру можна було б використовувати як об‘єктивну основу їхнього упорядкування.

Лінії та їх мережі є границями або упорядниками різних процесів, бо вони організують флювіальний геоморфогенез у цілому, надаючи потокам речовини-енергії односпрямованого руху. При цьому самі ці потоки сприяють самозбереженню інваріантних ліній чи їхньому новоутворенню. Водночас, в умовах антропогенного тиску на природну поверхню мають місце й протилежні процеси реградації структурних мереж. У одній з найбільш фундаментальних вітчизняних робіт з екологічної геоморфології І.П. Ковальчук переконливо (на достовірному й досконало опрацьованому фактичному матеріалі) і наочно (за допомогою топологічних схем) показав, що протягом 100 років один з річкових басейнів Поділля (р. Золота Липа) втратив від 30 до 65 % тальвегів нижчих порядків, через що відбулося пониження рангу тальвегів високих порядків.

Сукупність сталих, інваріантних ліній поверхні земного рельєфу утворює його топологічний інваріант. Виявлення останнього достатнє для того, щоб відтворити сам рельєф, що використовується в моделюванні рельєфу і відтворенні палеорельєфу по окремих фрагментах. Характерні лінії рельєфу створюють його морфологічний вигляд. "Малюнок рельєфу" служить засобом виявлення його походження, історії розвитку, використовується для діагностики сучасних процесів.

Перераховані елементи рельєфу водночас складають каркас його внутрішньої метрики. За допомогою математичних процедур ці елементи можна однозначно вичленувати, якщо є модель рельєфу. Основна властивість елементів внутрішньої метрики - їхня стійкість. Вони зберігають незмінність взаємного положення, тобто топологічної інваріантості, при будь-яких переміщеннях давніх рельєфів, наприклад, тектонічних підняттях чи опусканнях, деяких деформаціях поверхні, її згинаннях без розриву (у геометричному змісті) і перекосів. Такі деформації бувають обумовлені регіональною тектонікою, гляціодислокаціями, ізостатично нерівномірними переміщеннями блоків літосфери і т.ін.

Елементарний тальвег рано чи пізно зустрінеться з іншою ерозійною формою. У залежності від порядку останньої, в точці зустрічі відбудеться впадання (молодшого тальвегу у старший) чи злиття. Будемо розглядати другий випадок, тобто злиття, що відбувається між однопорядковими формами (у даному випадку 1-го порядку).

У точці злиття утвориться вузол 1-го порядку. З цього вузла виходить нова ерозійна форма – тальвег 2-го порядку. Це трійник. Він - найбільш характерна елементарна система в складній системі ерозійного розчленовування, бо тут уперше відбувається саморегулювання.


1.5.5. Формалізація двовимірних структурних мереж тальвегів


Існує певна асиметрія у дослідженнях структурних мереж флювіального рельєфу. Як повідомлялось вище, основні зусилля геоморфологів, особливо зарубіжних, спрямовані на визначення законів організації плоскої мережі тальвегів. З нашої ж точки зору, лінії тальвегів з'єднують точки одного (параболічного) виду і являють собою лінії мінімумів поверхні, тому функціонально відносяться до водозливного гідрологічного типу. Їх легко виділити по топографічній карті і на місцевості як 3-вимірну структуру.

У двовимірному вигляді, лінії тальвегів творять зв'язну мережу у межах ФГМС. Її зв‘язність визначається тим, що усередині однієї флювіальної системи з будь-якої точки будь-якого тальвегу можна потрапити в будь-яку іншу точку того ж чи іншого тальвегу. Мережа, що має зазначені властивості, називається деревоподібною, чи просто "деревом", також - "кістяком", "каркасом". Деревоподібна мережа може досліджуватися засобами теорії графів, як це було вже показано вище на елементарному рівні.

Мережу тальвегів і граф, що її відображає, можна розглядати різними способами. У морфометрії прийнято аналізувати цю мережу з урахуванням усіх її особливостей, насамперед відповідно до реального положення на реальному рельєфі. Такий підхід назвемо топографічним аналізом. Він загальновідомий. Якщо ми розглядаємо структурні співвідношення у системі флювіальної мережі, то такий аналіз є, відповідно, структурним. У таких випадках обираються лише певні відрізки мережі. Частину структурного аналізу, що обмежується визначенням інваріантних структур флювіальної мережі, доречно називати топологічним аналізом.

Ієрархію мережі тальвегів відображає засобами теорії графів бінарне "дерево", елементами якого служать вершини і дуги. До топологічних властивостей такого дерева віднесемо топологічну відстань - число дуг на шляху від однієї вершини до іншої; порядок дуги (аналогічний порядку тальвегу за схемою Філософова-Стралера); ранг вершини - число на одиницю більше порядку дуг, що входять у дану вершину, і рівне порядку дуги, що виходить з цієї вершини.

Кінець кінцем, подамо зведення законів ієрархії тальвегів за різними авторами (табл. 1.1).

Перші 5 законів встановлено Хортоном-Стралером. Інші закони й кількісні відношення проаналізовано у тексті досить об‘ємної статті, що надрукована у Науковому щорічнику досліджень планети Земля, виданому Міжнародним центром теоретичної фізики (США).

До таблиці ми додали 2 правила визначення чисел вершин та відрізків дерева тальвегів (закони 16, 17), встановлені нами (1979) і наведені вище.

1.5.6. Тривимірні мережі ФГМС


Для метричної оцінки дискретних елементів і форм рельєфу звичайно використовуються узагальнені характеристики. Найчастіше це середня абсолютна і відносна висоти, середній ухил чи кут нахилу, довжина і ширина (вимірювані в площині горизонтального проложення).

Усі метричні характеристики рельєфу-поля (у розумінні автора (див. 27, 51) можна розділити на дві групи. До першої групи відносяться метричні показники, що залишаються незмінними незалежно від того, у якому положенні розглядається рельєф. Для прикладу, можна привести морфометричні характеристики форм рельєфу на рельєфній топографічній карті. Це такі показники:

• кривизна поверхні в довільній точці,
  
• площа поверхні,
  
• довжина лінії на поверхні.
  

Вони не міняються, навіть якщо змінюється положення рельєфу у зовнішньому просторі (або система координат). Наприклад, якщо ми змінимо положення цієї рельєфної карти (див. приклад у Вступі, рис. В-1) чи будемо розглядати її під певним довільним кутом зору, зазначені характеристики залишаються сталими, тому що вони визначають форму самої поверхні безвідносно до її положення в просторі. Відповідно до традицій диференціальної геометрії, будемо називати їх внутрішньою метрикою рельєфу.


Таблиця 1.1. Закони ієрархії річкових мереж

№ пп	Закон	Прізвище відкривача чи назва закону	Масштабні співвідношення
1	Tv = Ti (RT)v-1	Токунага	( Ti,,RT)
2	nω+1/nω =Rn	Хортон –закон числа потоків	Rn = Rr
3	ēω+1/ēω =Re	Хортон – закон порядку сегментів стоку	R e= RT
4	ĺω+1/ĺω =Rl	Хортон – закон порядку основного русла	Rl = RT
5	āω+1/āω=Ra	Хортон – закон площ водозборів	Ra = Rn
6	l œ Ld	Афінної самоподібності елементарних тальвегів	d
7	l œ a h	Закон Хака	h = log Rl / log Rn
8	a œ LD	відношення площ водозборів	D = d/h
9	L┴ =LH	Відношення «of basin widths»	H = d/h - 1
10	P(a) œ a -τ	---------------
11	P(l) œ l -γ		τ = 2 – h
12	Λ œ aβ	Закон Лангбейна	γ = 1/h
13	λ œ Lф	Уточнення закону Лангбейна	Ф= d
14	ˉΛ œ a β	Доддса та Ротмана (1)	β = 1+h
15	˜Λ œ Lф	Доддса та Ротмана (2)	Ф= d
16	Рm = 2 m-1 - 2	Число вершин дерева тальвегів (див. вище)	m –ранг кореневої вершини
17	Sm - 2m - 2	Число відрізків флювіальної мережі (див. вище)	-“-