Анотація структура та обсяг роботи

Вид материала

Диплом

Содержание 3.3Обґрунтування методу розв’язання 3.4Опис методів розв’язання

Подобный материал:

• Правила оформлення конкурсної роботи, 125.68kb.
• Анотація матеріалів, 321.56kb.
• Схема: ”Структура виконання учнівської науково-дослідницької роботи та її захист, 47.06kb.
• Програма підготовки до складання комплексного іспиту за фахом на отримання освітньо-професійного, 109.09kb.
• Завдання для самостійної роботи по курсу «Страхування» Тем Сутність, принципи та роль, 87.96kb.
• Структура програми навчальної дисципліни 3 правила роботи у програмі асистент 8 зразок, 1160.56kb.
• Завдання для самостійної роботи, 83.76kb.
• Та рекомендації до виконання практичної, індивідуальної та самостійної роботи, 911.62kb.
• 4 семестр, у обсязі навчальної роботи 72 год., 2 кр. Загальний обсяг аудиторної роботи, 198.34kb.
• Методика написання реферату. Загальні правила оформлення результатів наукових досліджень., 17.56kb.

3.3Обґрунтування методу розв’язання

Задача (3.1)-(3.4) є класичною задачею лінійного параметричного програмування (ЗЛП) [7], а задача (3.5) може бути зведена до ЗЛП, тому розв’язувати їх будемо використовуючи алгоритми розроблені для даного класу задач.

Загальним методом розв’язання задач даного класу є симплекс-метод. Симплекс-метод – метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по допустимим базисним розв’язкам до знаходження оптимального розв'язку; симплекс-метод також називають методом поступового покращення плану. Метод був розроблений американським математиком Джорджем Данцигом у 1947 році.

В основі методу параметричного програмування для ЗПП з параметром у цільовій функції лежать процедури прямого симплекс-методу з деякою модифікацією, отже для задачі (3.1)-(3.4) будемо застосовувати процедури алгоритму саме цього методу.

Стосовно задачі (3.5), то вона зводиться до задачі лінійного програмування, що дозволить розв’язати її симплекс-методом.

3.4Опис методів розв’язання

Основною математичною задачею, яку розв’язує даний комплекс, є задача параметричного програмування з параметром у цільовій функції.

Параметричне програмування – це метод визначення того, як міняється розв’язок задачі зі зміною всіх компонент вектора коефіцієнтів ЦФ.

Нехай при 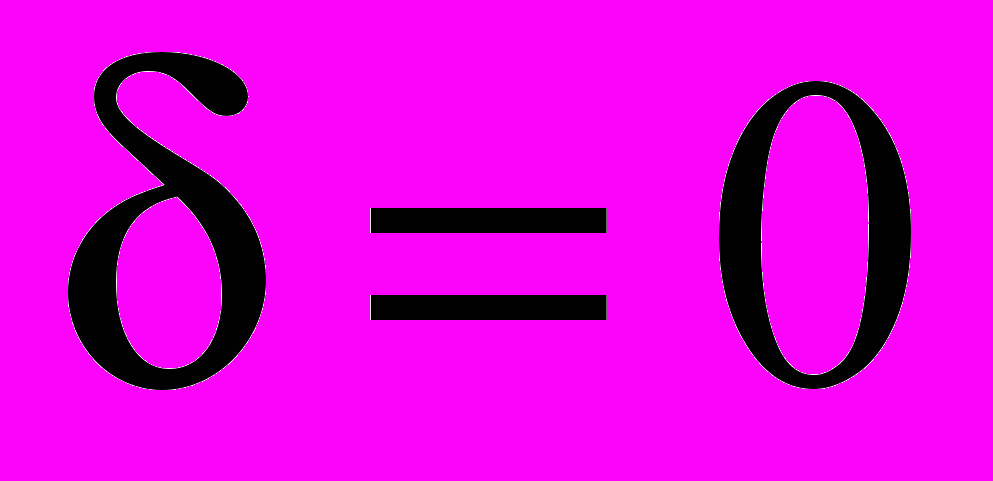задача має оптимальний розв’язок 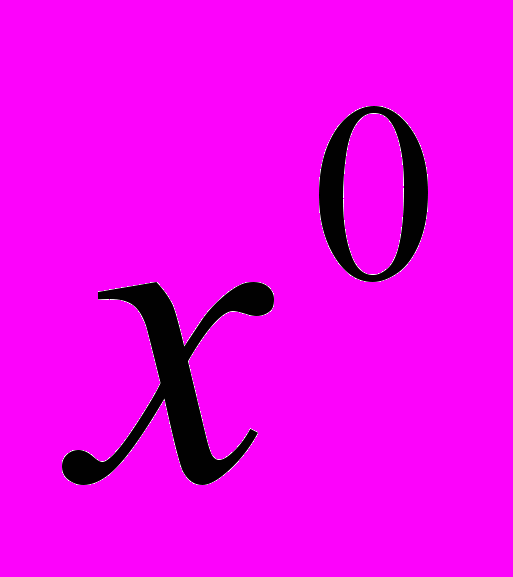. Без втрати загальності припустимо, що в оптимальному розв’язку небазисні змінні мають номери 1,…,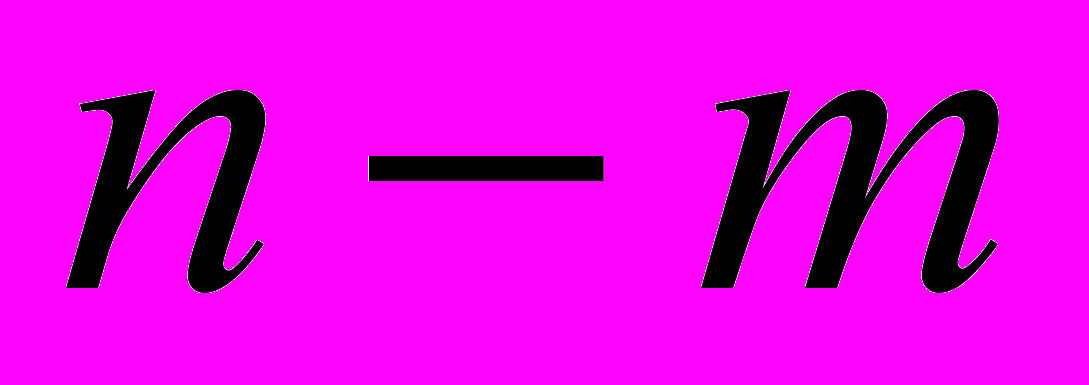. Запишемо перетворену задачу, відповідну оптимальному розв’язку ()

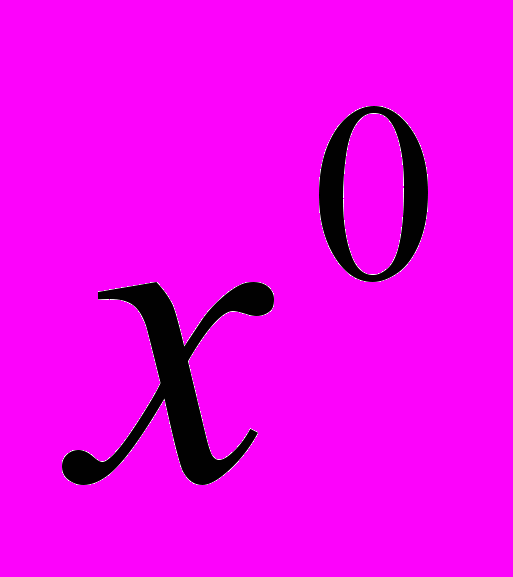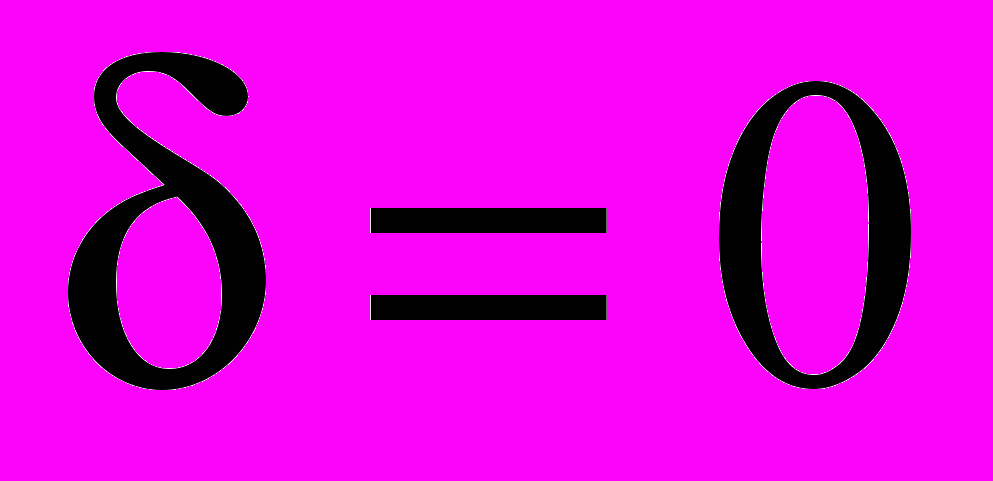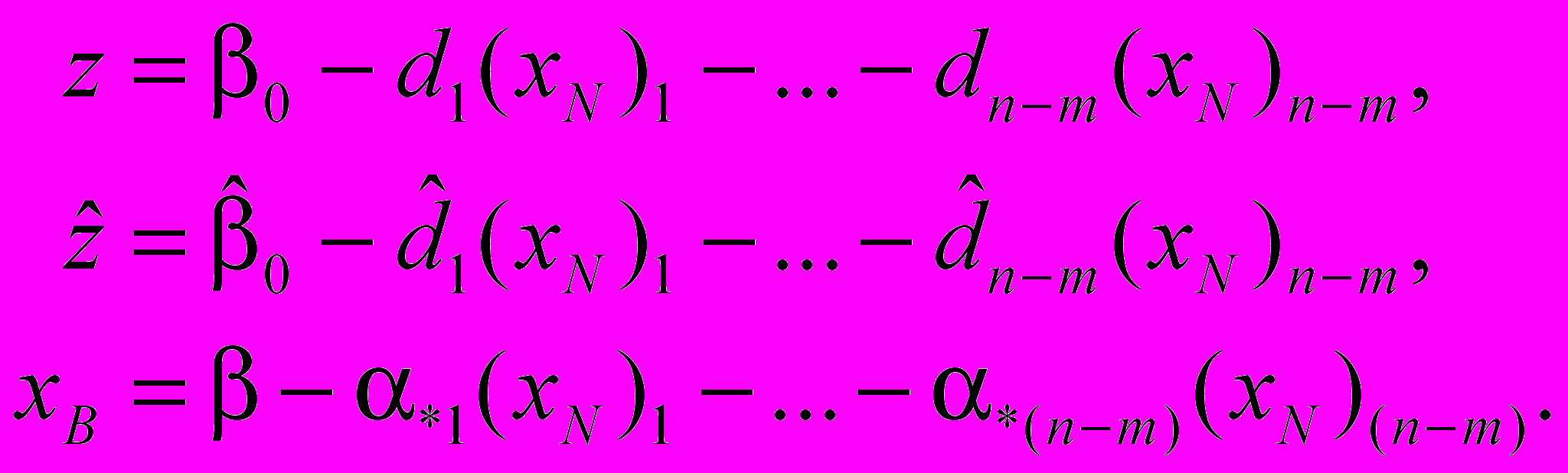(3.8)

де

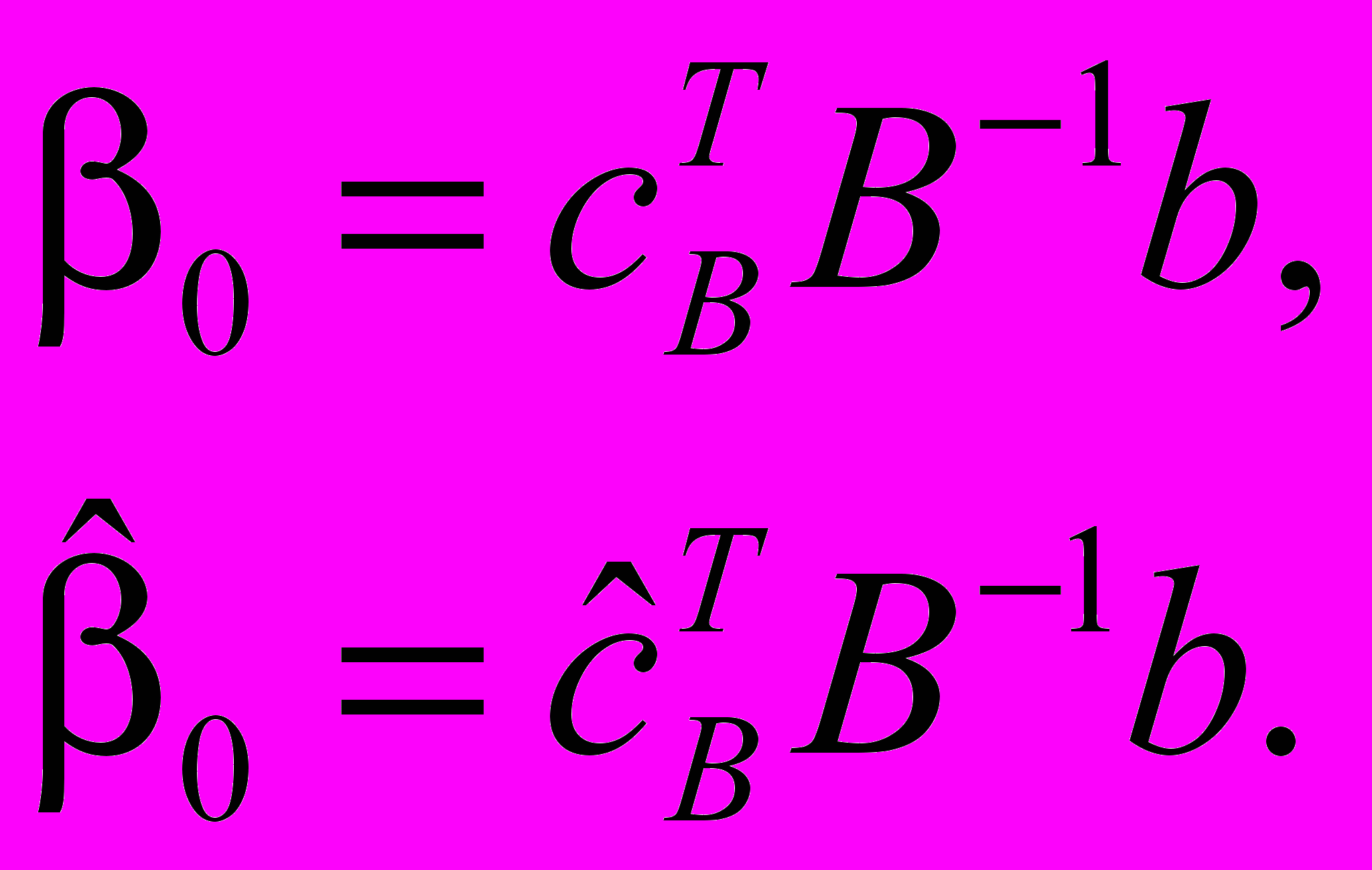(3.9)

Тут коефіцієнти складової обчислені на основі базису, оптимального відносно ЦФ при 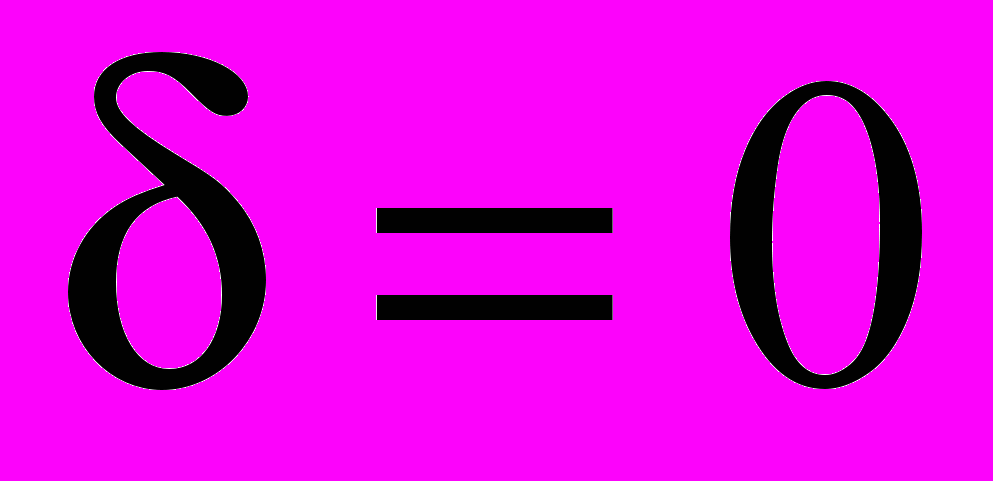, так що компоненти вектора 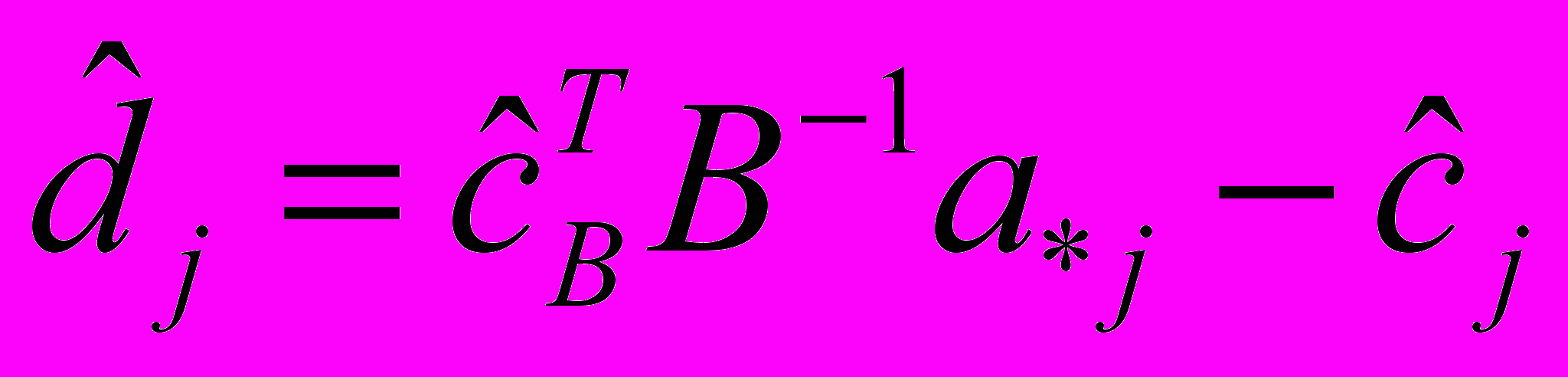не обов'язково невід’ємні. О
скільки розв’язок 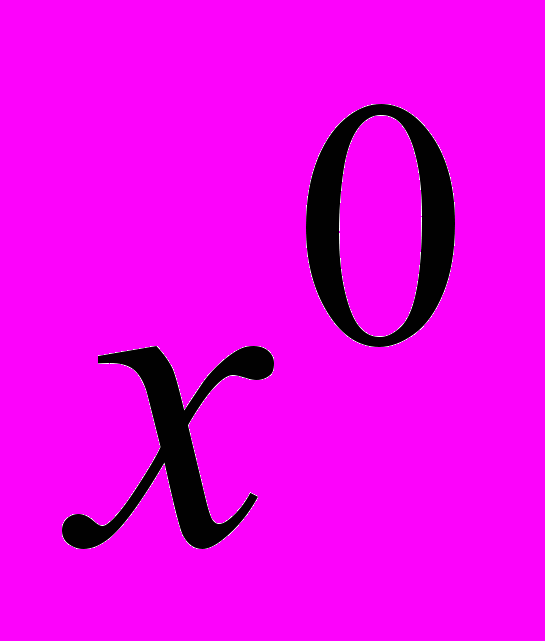оптимальний відносно , то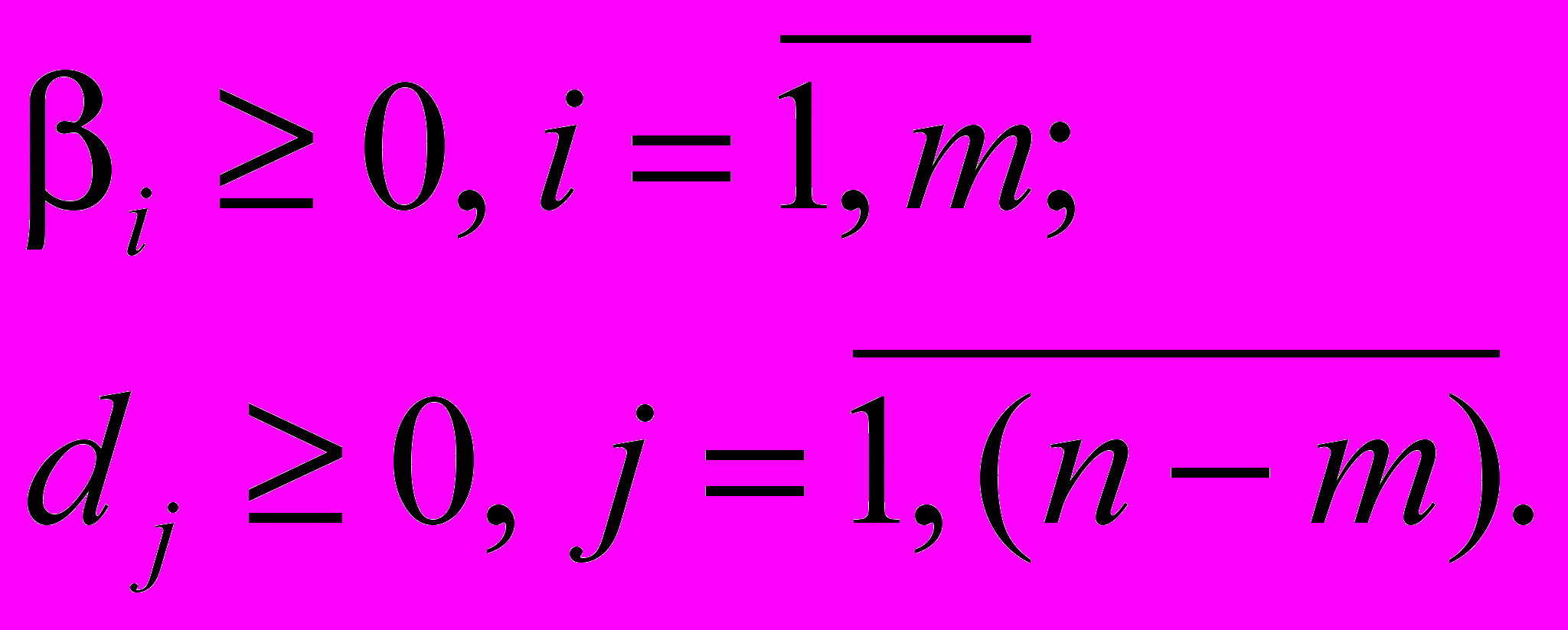

(3.10)

При 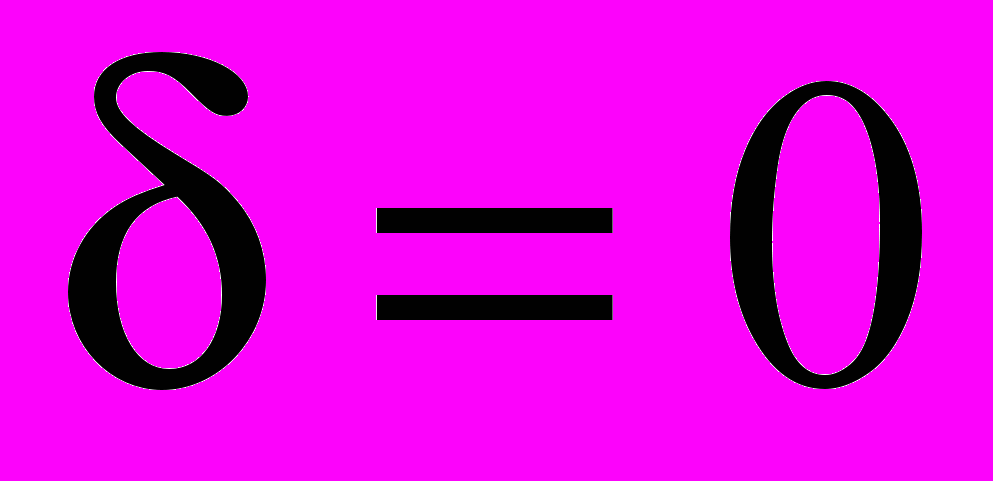параметрична складова не грає ніякої ролі. При збільшенні 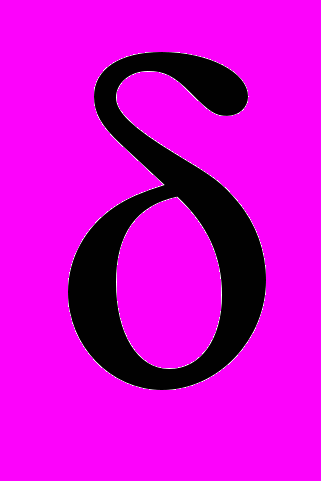від нуля відбувається поворот вектора-нормалі ЦФ 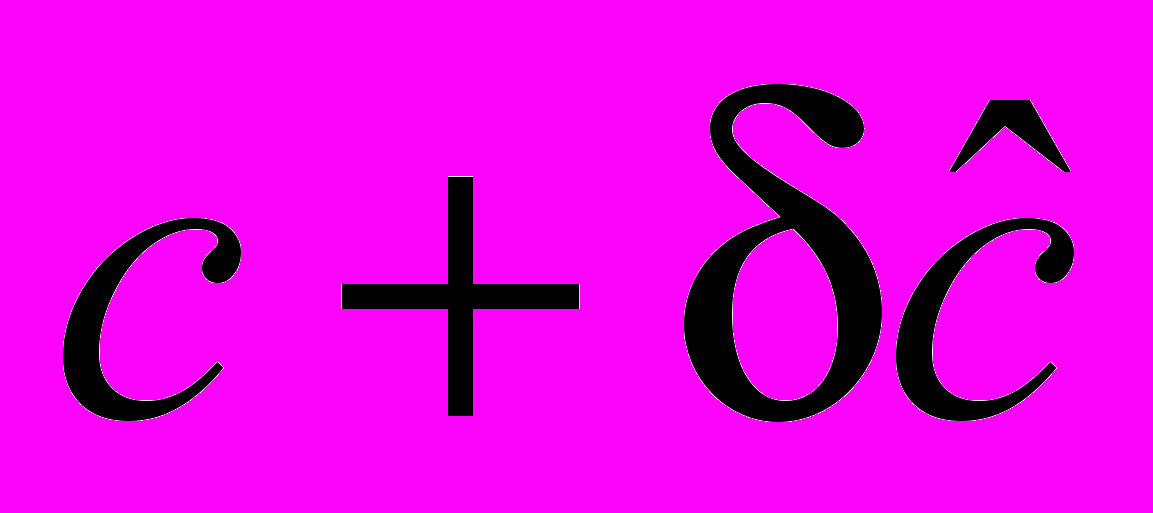, при досягненні 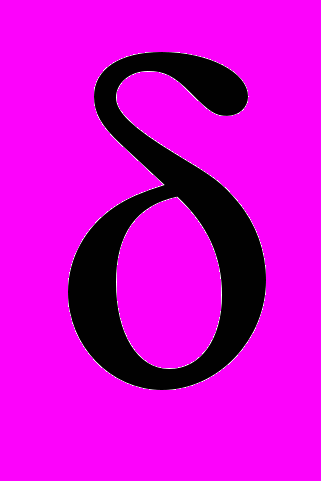певного значення це може призвести до зміни оптимуму.

Продовжимо аналіз задачі. При збільшенні 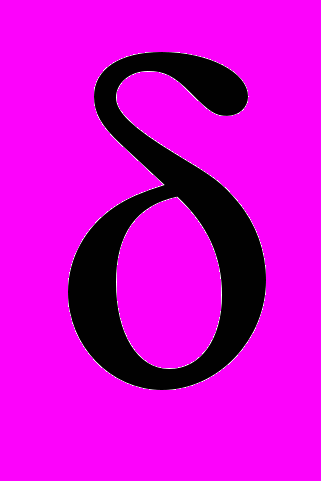від нуля загальна ЦФ набуває значення

.

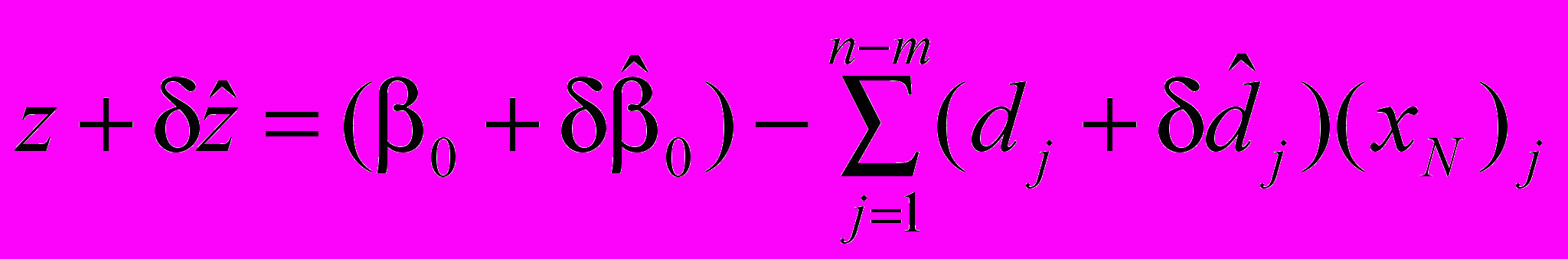(3.11)

Розв’язок 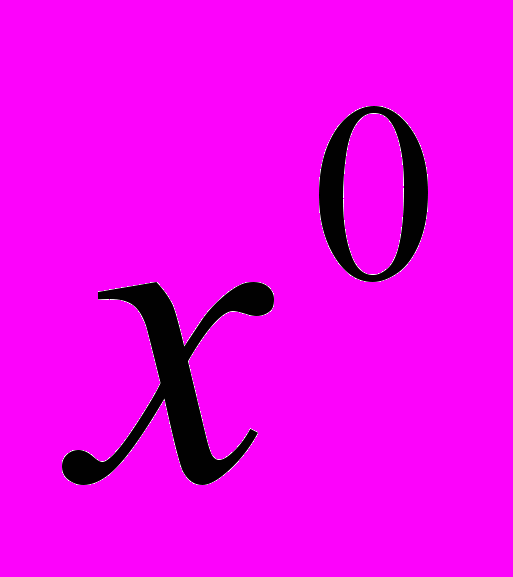залишається оптимальним до тих пір, поки виконуються умови:

.

(3.12)

.........

Узагальнимо описаний вище метод у вигляді покрокового алгоритму:

Крок 0. ЗНАЙТИ розв’язок початкової ЗЛП при .

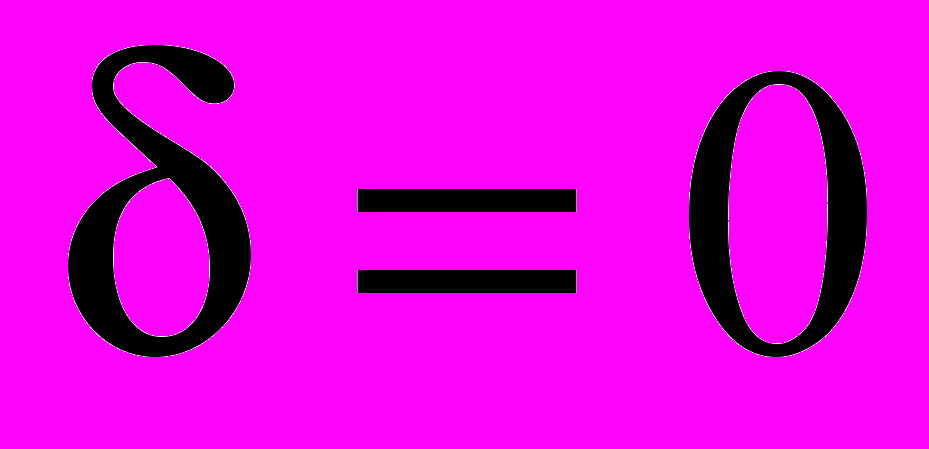Крок 1. ЯКЩО 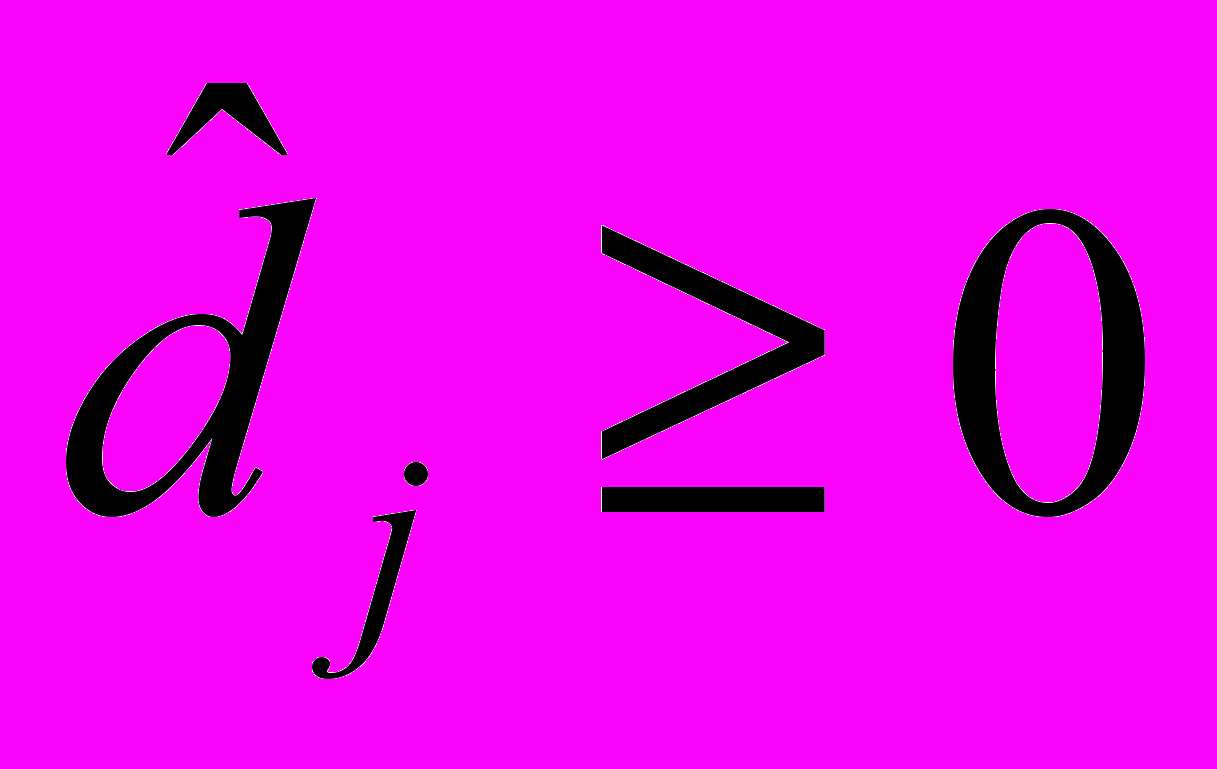для всіх 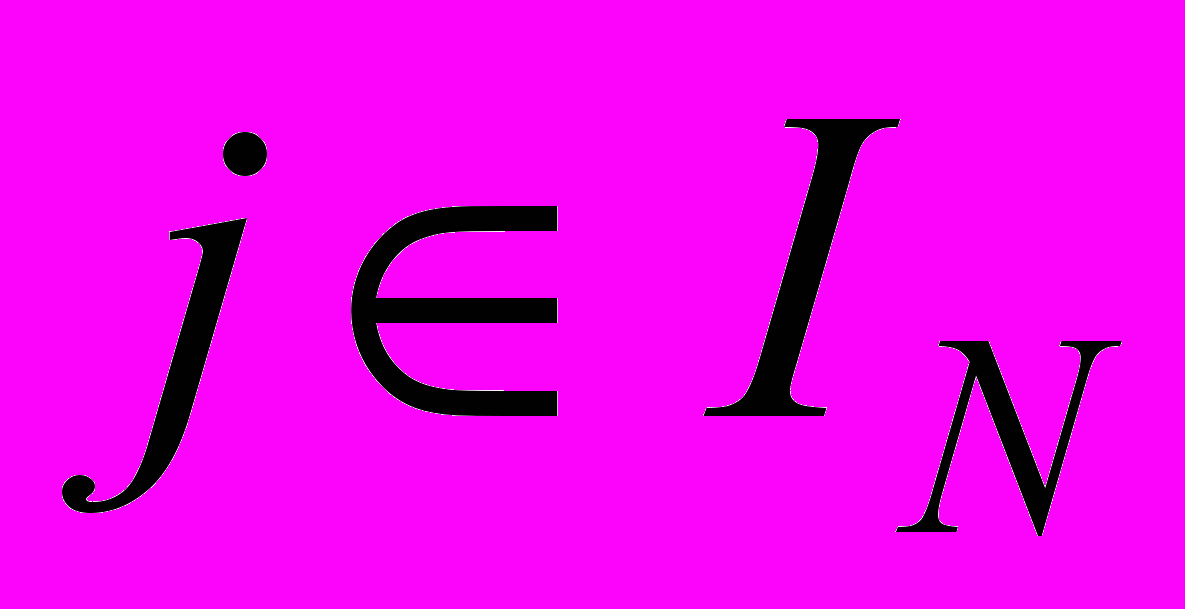( 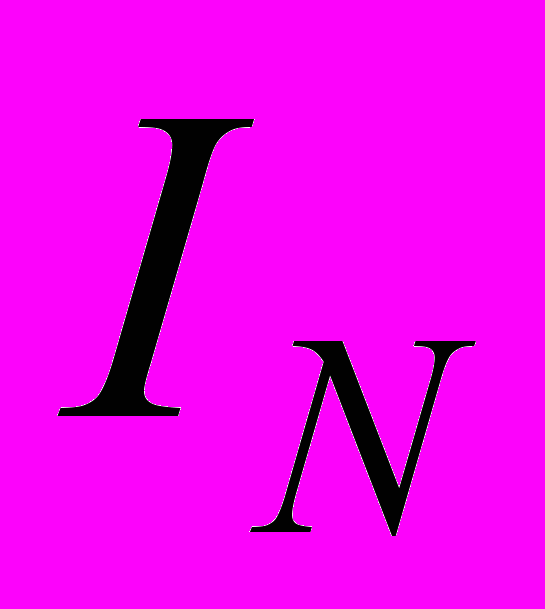- множина індексів небазисних змінних), поточний розв’язок залишається оптимальним при всіх скільки завгодно великих 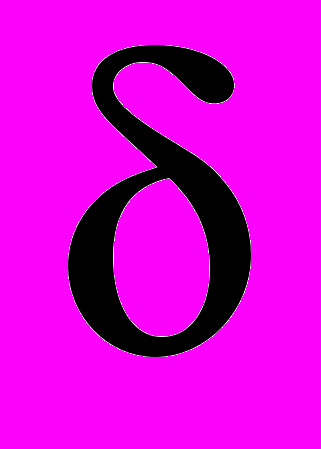, СТОП. ІНАКШЕ ЗНАЙТИ

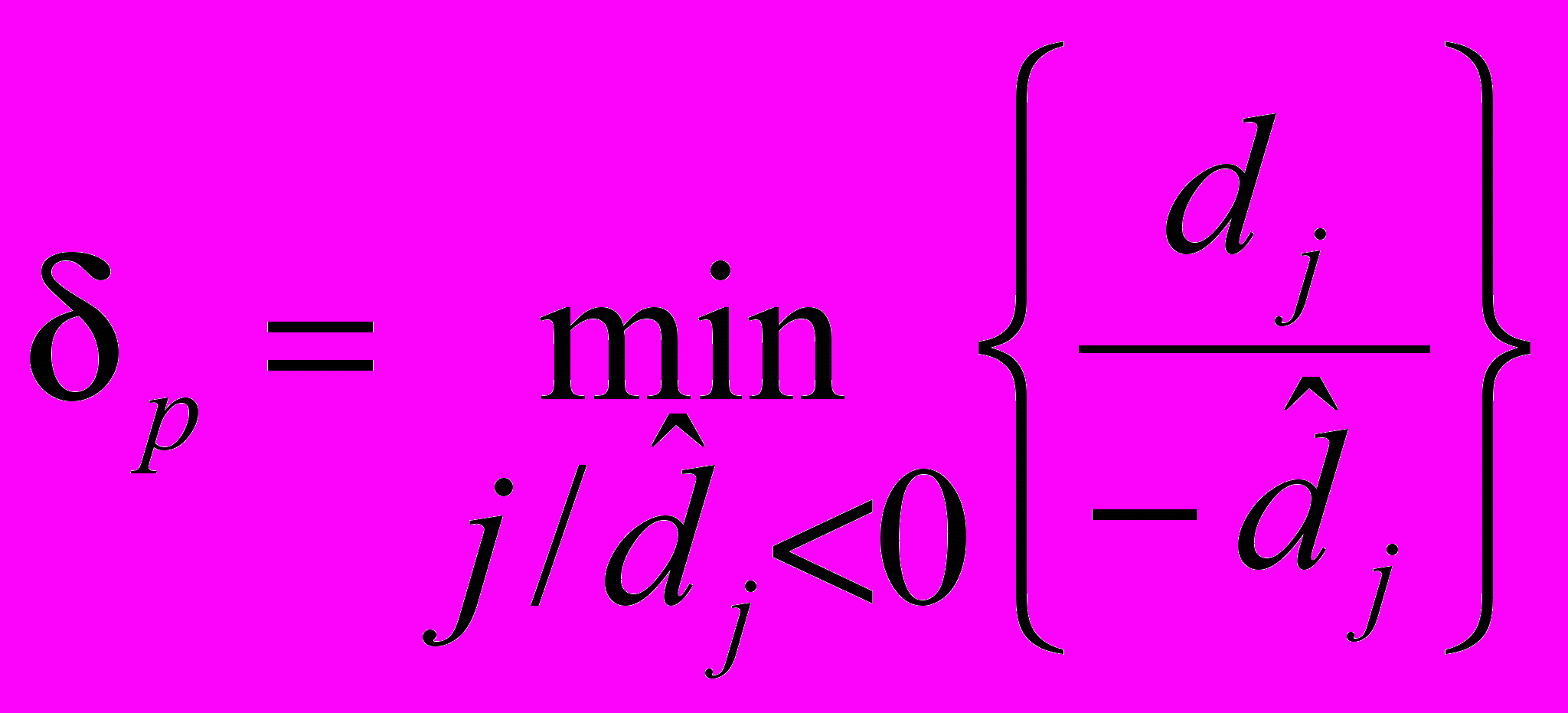і відповідне .

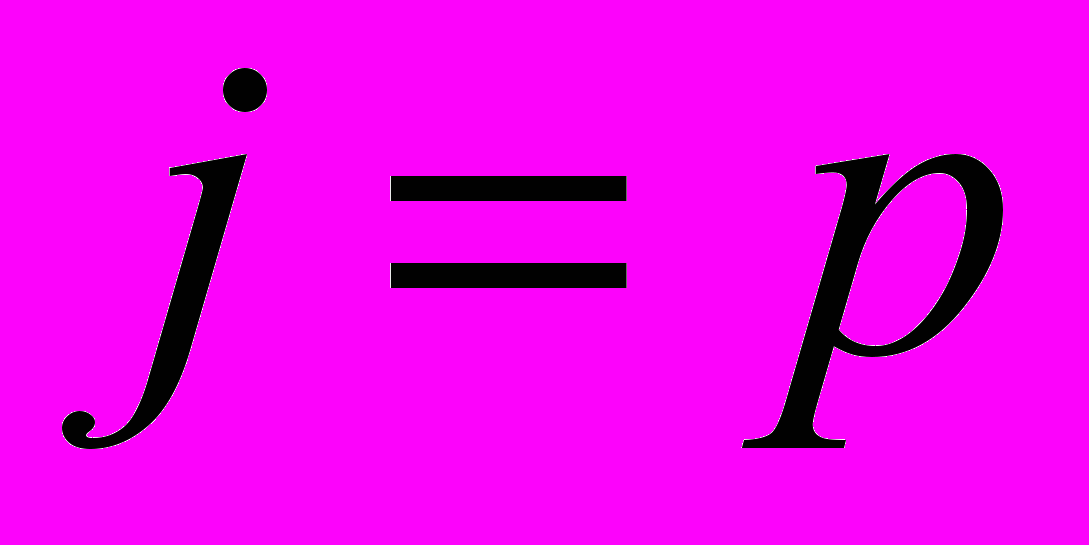Крок 2. ЯКЩО 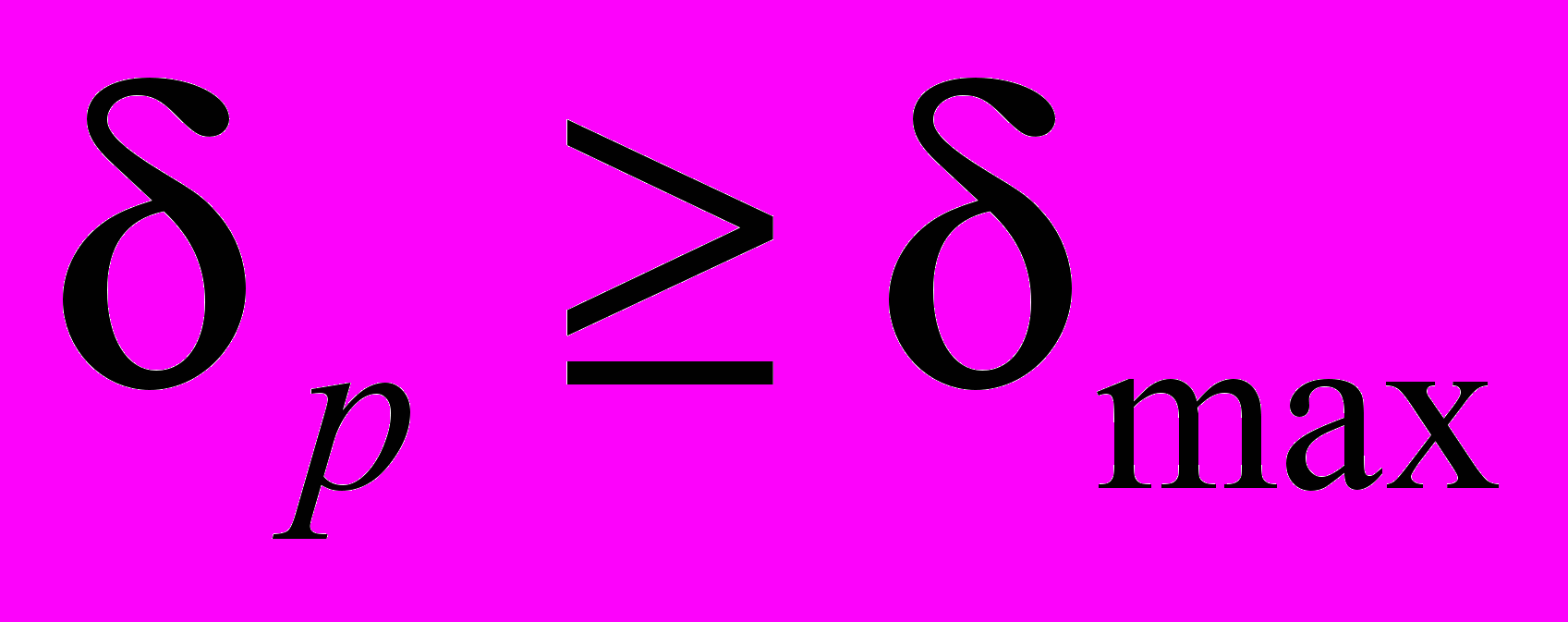, то ми визначили всі розв'язки в наперед заданому діапазоні зміни параметра 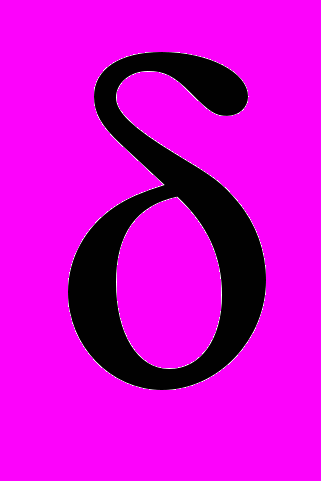, СТОП.

Крок 3. ЯКЩО 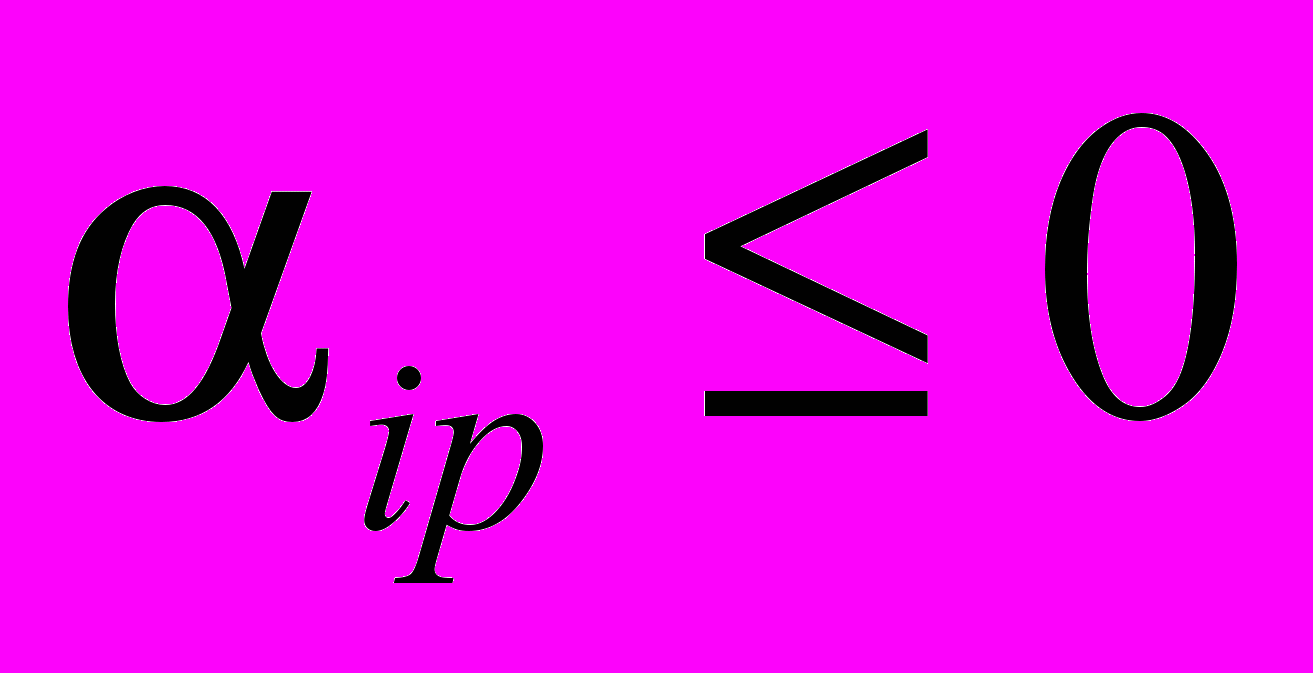для всіх 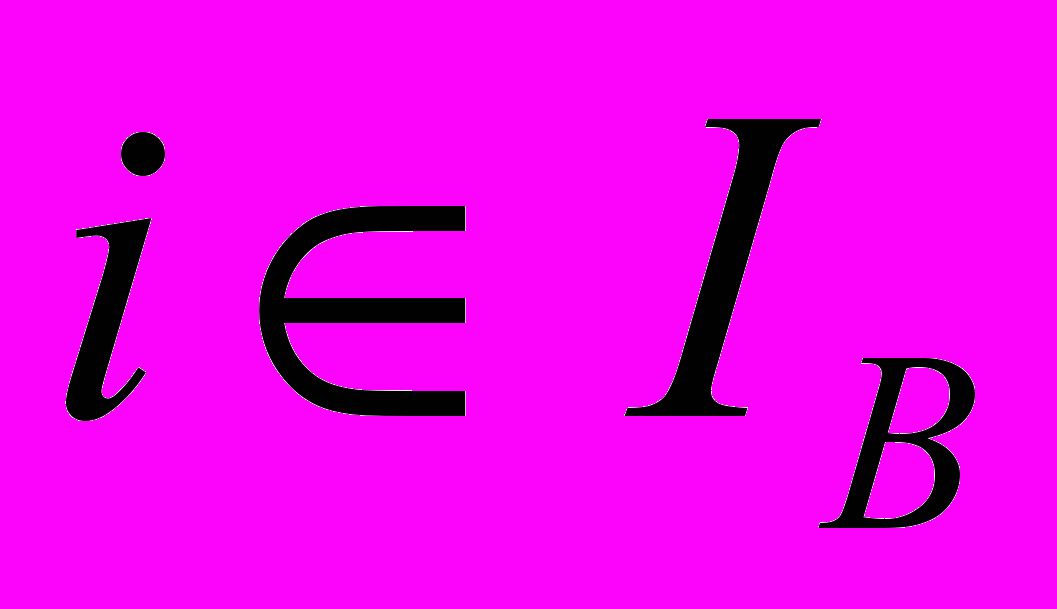( 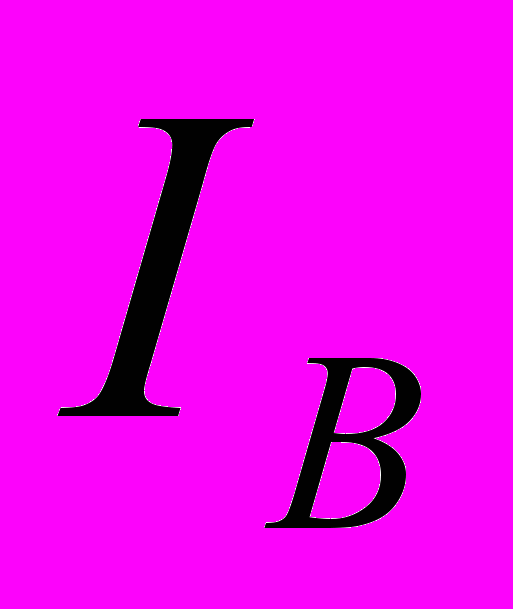- множина індексів базисних змінних), то при зміні базису ЦФ стає необмеженою (якщо в стовпці, що відповідає змінній 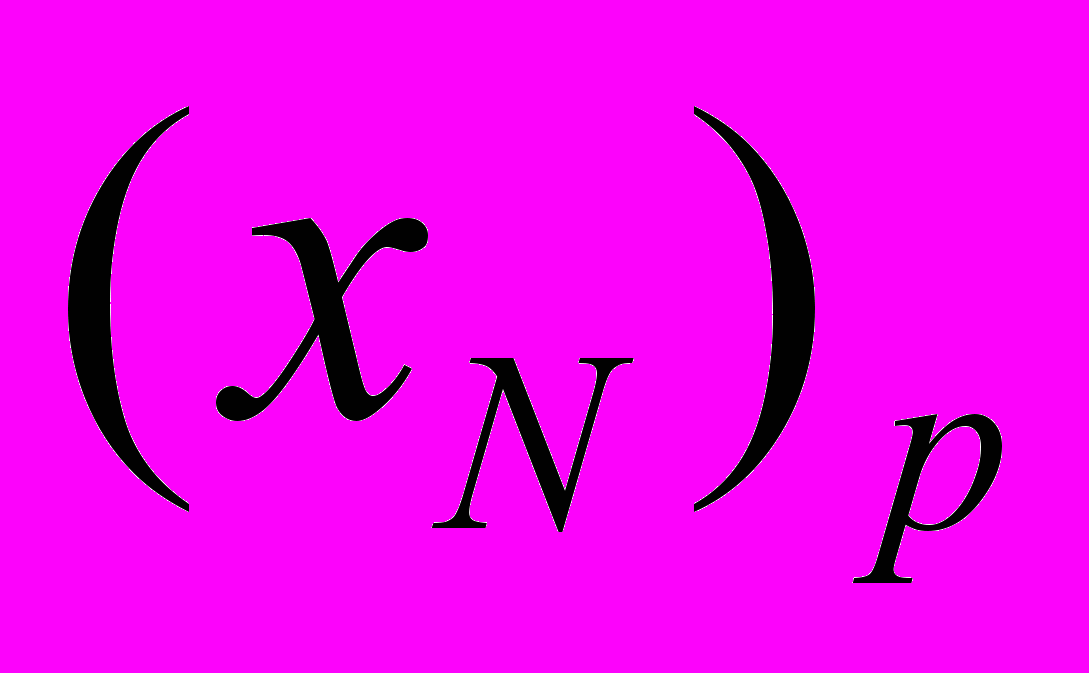, всі коефіцієнти не додатні, то при всіх 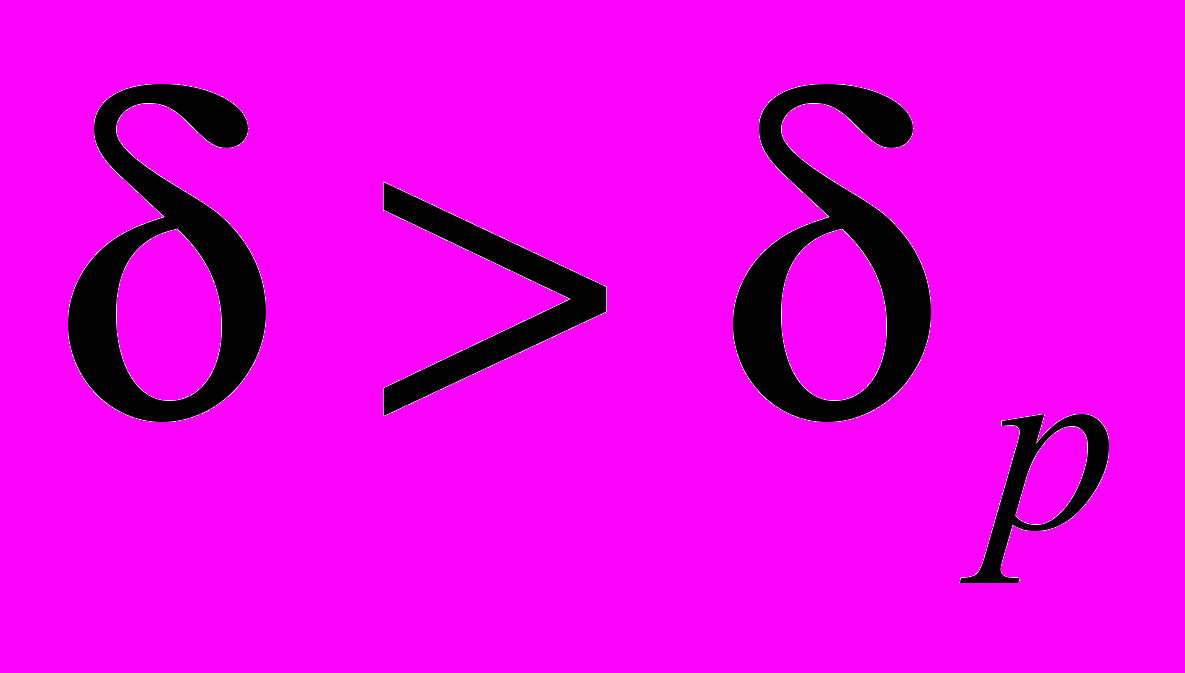ЦФ необмежена зверху), СТОП.

ІНАКШЕ ЗНАЙТИ змінну, яку виводимо з базису, за допомогою виразу

.

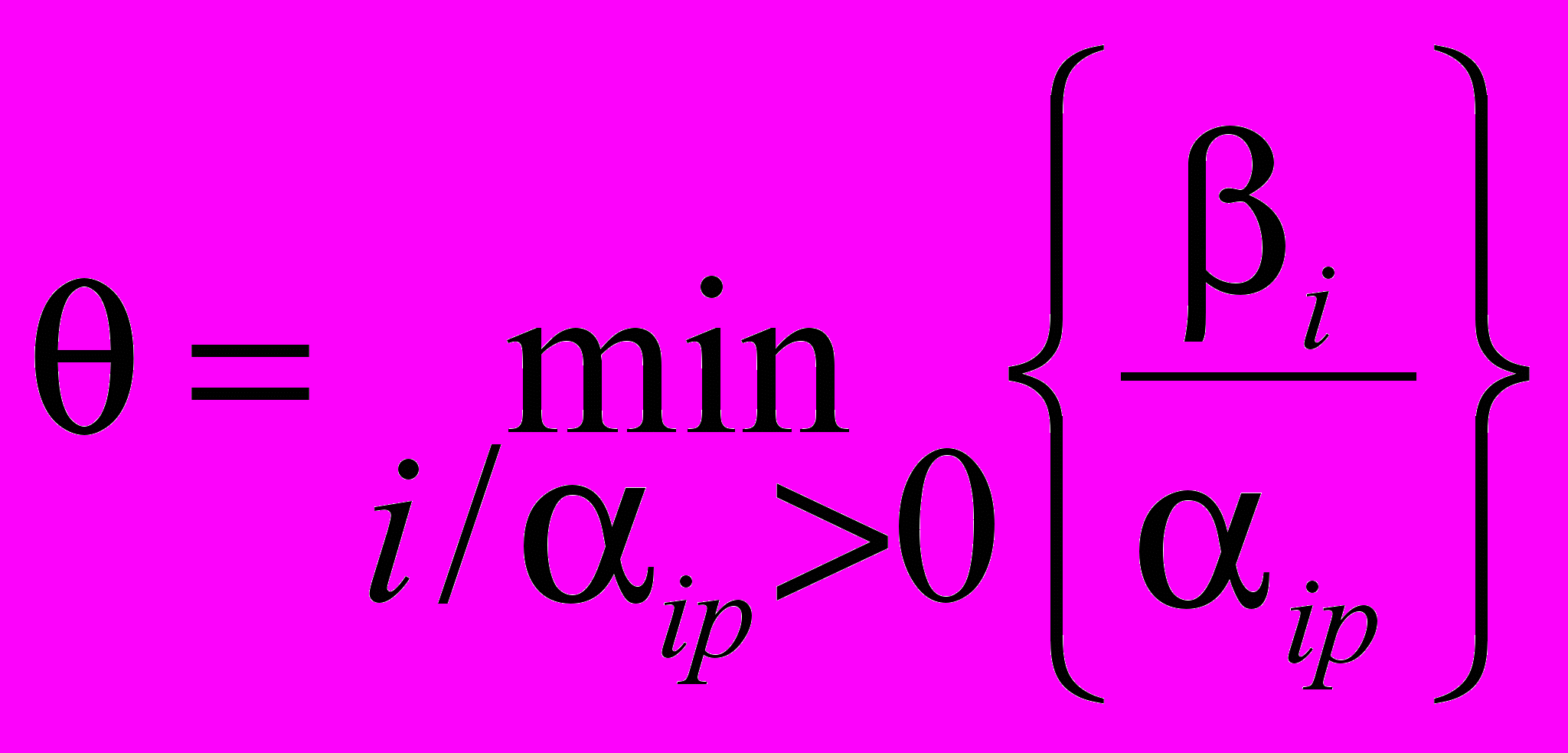Нехай мінімум відповідає індексу .

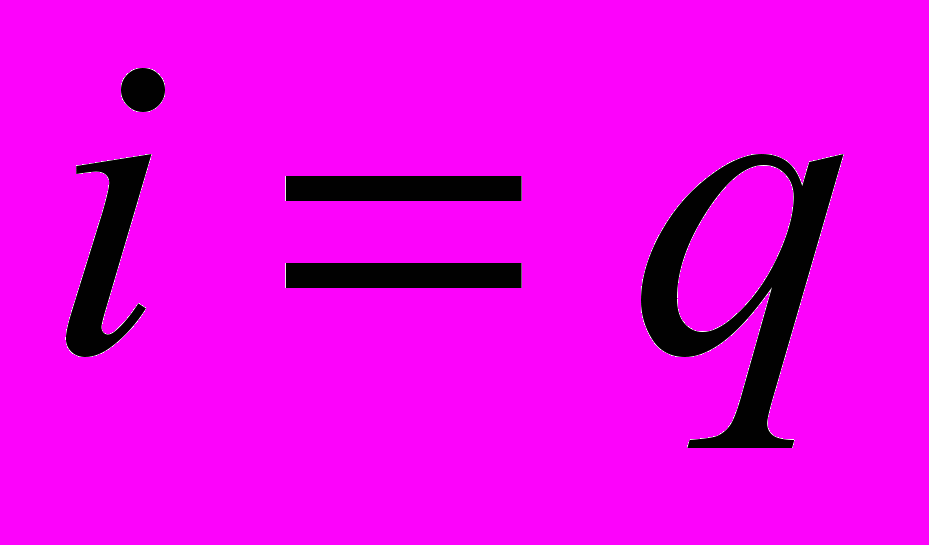Крок 4. ВИКОНАТИ операцію заміщення: ввести в базис змінну 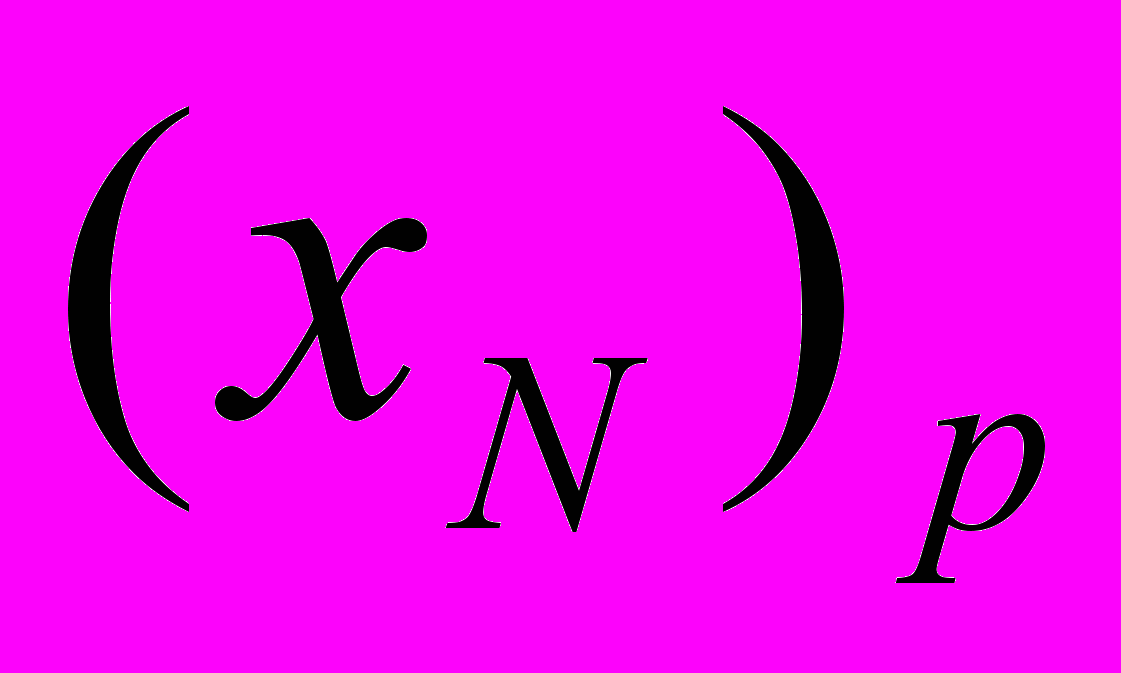, вивести з базису змінну .

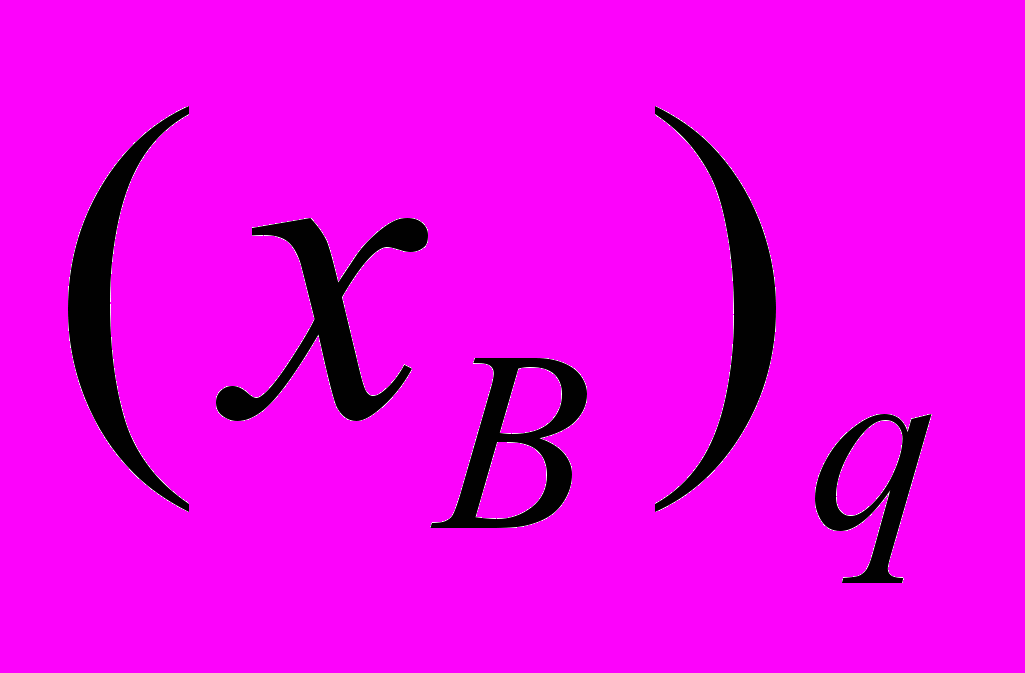Крок 5. ПЕРЕЙТИ на Крок 1.