3 теоретический анализ психолого- педагогической литературы по проблеме развития алгоритмического мышления учащихся 3-го класса

Вид материала

Реферат

Содержание Развернутое словесное описание алгоритмов. 2. Экспериментальное изучение проблемы развития алгоритмического мышления учащихся 3-го класса на уроках математики 1 2 в разрядную сетку _1 2 2) 1 2 2.2. Описание хода эксперимента и анализ полученных результатов Список использованной литературы Имя и фамилия ученика

Подобный материал:

• 3 анализ психолого-педагогической литературы по проблеме активизации познавательной, 401.02kb.
• 3 анализ психолого-педагогической литературы по проблеме интеллектуальной готовности, 505.23kb.
• 3 теоретический анализ литературы по проблеме мотивации женской измены, 761.78kb.
• 3 теоретический анализ литературы по проблеме готовности к риску современных предпринимателей, 461.9kb.
• Программа занятий по коррекции агрессивного поведения у детей Повторная диагностика., 79.73kb.
• 3 теоретический анализ литературы по проблеме особенностей образа «Я» у детей из неблагополучных, 399.1kb.
• 3 глава 1 теоретический анализ литературы по проблеме гендерных различий в агрессивном, 613.56kb.
• Методологическую основу исследования составили, 38.84kb.
• Психолого-акмеологические механизмы развития стратегического мышления руководителя, 89.34kb.
• Психолого-педагогические основы развития творческого мышления детей, 454.14kb.

1.3. Педагогические условия использования алгоритмов в курсе математики начальной школы


Одной из характеристик развития общества является получение, накопление, обработка и потребление информации. В современном обществе без умения использовать компьютер для решения определенных задач трудно представить реализацию творческих возможностей человека в различных сферах жизни.

Проблема «общения» с компьютерной техникой требует умения понимать различного рода алгоритмические языки, а также наличия определенного уровня сформированности алгоритмического мышления. Отсюда и возникает задача формирования элементов алгоритмической грамотности уже в начальной школе [5, с.99].

В нашей стране практика переноса курса «Информатика» в сферу начального образования начала складываться в начале 90-х гг. ХХ в. Большинство программ для начальной школы ориентировано на формирование логического и алгоритмического мышления, все они содержат раздел, посвященный алгоритмам.

Но, к сожалению, не во всех школах есть возможность ввести курс «Информатика» в учебный план. В такой ситуации ведущая роль принадлежит учителю, который может организовать работу с алгоритмическими обучающими средствами на уроках математики, способствуя тем самым развитию алгоритмического мышления.

Осветим часть вопросов возможности формирования элементов алгоритмической грамотности при изучении курса математики в начальных классах, что является требованием современного общества.

А. И. Газейкина выделяет следующие комплексы методических приемов, применение которых способствует развитию алгоритмического мышления:

1. Создание нового алгоритма, его запись, проверка и исполнение самим обучаемым или выбранным исполнителем.
   
2. Усвоение алгоритмов решения основных типовых задач.
   
3. Поиск и исправление синтаксических и семантических ошибок в алгоритме.
   
4. Оптимизация готового алгоритма [1, с.16].
   

Формирования элементов алгоритмической грамотности должно осуществляться на основе логических знаний и умений учащихся. Учитывая связи между элементами логической и алгоритмической грамотности, возможен следующий план реализации единой логико-алгоритмической линии в курсе математики:

Лог.:

• Умение узнавать предмет по данным признакам.
  
• Умение сравнивать.
  
• Умение распределять предметы по определенным признакам группы.
  

Алг.:

• Понимание сущности алгоритма, его свойств.
  
• Умение читать алгоритм.
  

Лог.:

• Умение устанавливать соотношения общего и частного.
  
• Понимание смысла слов: и, или, все, каждый, некоторые.
  

Алг.:

• Умение четко исполнять алгоритм.
  
• Знакомство с основными типами алгоритмов.
  
• Умение преобразовывать алгоритм.
  
• Умение выбирать рациональный алгоритм.
  

Лог.:

• Умение получать умозаключение.
  
• Умение обосновывать умозаключение.
  
• Умение составлять алгоритм.
  
• Умение проверять правильность алгоритма.
  

Учащимся начальной школы доступны следующие способы описания алгоритмов: граф-схемы; блок-схемы; таблицы; развернутое словесное описание.

Граф-схемы. Уже в первом классе рассматриваются линейные граф-схемы. Можно также использовать граф-схемы в виде дерева, которые характеризуют разветвляющийся процесс.

Целесообразно использовать следующие виды заданий:

1. Произвести вычисления по заданной граф-схеме.
   
2. Дать различные интерпретации для данных граф-схем.
   

Можно предлагать граф-схемы, в которых не заданы ни числовые значения, ни отношения между ними. Наряду с приведенными граф-схемами можно предлагать и такие, которые частично заполнены. Такие схемы можно использовать для отработки особых случаев, например действий с нулем и единицей. Цель задания этого типа – совершенствование вычислительных навыков и иллюстрация такого свойства алгоритмов, как массовость.

Таблица. Следующий способ задания – таблица, содержащая несколько строк. Указан способ ее заполнения. Заполнение таблицы готовит к восприятию идеи описания циклических процессов.

Развернутое словесное описание алгоритмов. Известно, что результат действия во многом зависит от того, насколько человек осознает алгоритмическую сущность своих действий. Начиная уже с первого класса важно учить детей видеть алгоритмы, выделять элементарные действия как-либо действия. Начинать эту работу следует с простейших алгоритмов, доступных и понятных детям, т.е. само действие не должно вызывать затруднений. Так, например, можно составить вместе с детьми алгоритм перехода улицы или лепки снеговика [5, с.100-110].

Формирование и развитие алгоритмического мышления может происходить, когда и учитель, и ученик действуют совместно, идут навстречу друг другу, когда в учебный процесс включены элементы коллективной деятельности. Весь учебный процесс должен быть направлен на то, чтобы у детей сначала появилось желание, эмоциональный настрой, а потом и потребность учиться. Определенные приемы позволяют добиться полной успеваемости, качественного ее роста, развивают творческое мышление и познавательную активность учащихся.

Перед учителем математики стоят следующие задачи:

• организовать совместную деятельность, обеспечивающую комфортность участников обучения, способствующую культурному и интеллектуальному развитию учащихся;
  
• развивать мышление и творческие способности учащихся;
  
• формировать культуру общения, т.е. умения вести дискуссию, слушать и слышать, уважать мнение партнера, аргументировать свою точку зрения.
  

Необходимо учитывать и возрастные особенности учащихся в начальном звене, их способность и потребность познать себя как личность. У человека, достигшего решения поставленной задачи, появляется вера в свои силы, понимание путей достижения цели.

Адекватное и успешное обучение и воспитание можно вести только при правильной оценке и учете возрастных и индивидуальных особенностей детей, поэтому при проведении уроков выбираются такие методы и приемы, которые соответствовали бы психологическим особенностям детей данного возраста.

Для младших школьников характерны трудолюбие, старательность, у них начинают развиваться высшие психические функции, возникают элементарные логические рассуждения об объектах, происходит процесс классификации объектов по отдельным важным признакам.

Основные логические структуры мышления формируются в возрасте 5-11 лет. Запоздалое формирование этих структур протекает с большими трудностями и часто остается незавершенным. Следовательно, обучать детей в этом направлении целесообразно с начальной школы.

Учет этих возрастных особенностей позволяет успешно развивать у детей алгоритмическое мышление и творческие способности, поддерживать постоянный интерес к предмету, дает возможность на высоком уровне изучать математику.

Задачей курса математики является формирование вычислительной культуры, развитие алгоритмического мышления и творческих способностей учащихся. Алгоритмическое мышление на уроках математики развивается с помощью игр, сюжет которых основан на известных сказках; творческие способности учащихся развиваются посредством художественной деятельности, при подготовке и проведении викторин, конкурсов рисунков [11, с.114].

Современное общество требует от нового поколения умения планировать свои действия, находить необходимую информацию для решения задачи, моделировать будущий процесс. Поэтому школьный курс математики, развивающий алгоритмическое мышление, формирующий соответствующий стиль мышления, является важным и актуальным.

Таким образом, на основе теоретического анализа психолого-педагогической литературы по проблеме развития алгоритмического мышления учащихся 3-го класса, мы приходим к следующим выводам:

Мышление – это высший познавательный психический процесс, в результате которого порождается новое знание на основе творческого отражения и преобразования человеком действительности. Различают предметно-действенное, наглядно-образное и словесно-логическое.

Кроме того, выделяют алгоритмический стиль мышления, который представляет собой специфический стиль мышления, предполагающий умение создать алгоритм, для чего необходимо наличие мыслительных схем, которые способствуют видению проблемы в целом, ее решению крупными блоками с последующей детализацией и осознанным закреплением процесса получения конечного результата в языковых формах.

Алгоритмическое мышление включает в себя ряд особенностей, свойственных логическому мышлению, однако требует и некоторых дополнительных качеств. Основными из них считаются умение находить последовательность действий, необходимых для решения поставленной задачи и выделение в общей задаче ряда более простых подзадач, решение которых приведет к решению исходной задачи. Наличие логического мышления не обязательно (хотя и достаточно часто) предполагает наличие мышления алгоритмического. В основе развитого алгоритмического мышления, безусловно, лежит сформированное и развитое логическое мышление

Проблема развития и алгоритмического мышления в начальной школе – одна из важнейших в психолого-педагогической практике. Основной способ ее решения – поэтапное формирование логических приемов мышления с постепенным переходом непосредственно к элементам алгоритмизации. Ведущая роль в этом принадлежит учителю, который может организовать работу с алгоритмическими обучающими средствами на уроках математики, способствуя тем самым развитию алгоритмического мышления.


2. ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ПРОБЛЕМЫ РАЗВИТИЯ АЛГОРИТМИЧЕСКОГО МЫШЛЕНИЯ УЧАЩИХСЯ 3-ГО КЛАССА НА УРОКАХ МАТЕМАТИКИ


2.1. Изучение педагогического опыта использования алгоритмов при обучении младших школьников математике


Нами был изучен опыт использования алгоритмов при обучении учащихся 3-го класса на уроках математики, накопленный учителем начальных классов средней школы № 4 г.Лунинца Брестской области Киселевой Валентиной Ивановной.

Беседа с преподавателем и посещение открытого урока математики по теме «Организация усвоения алгоритма письменного деления на однозначное число» позволили нам обобщить опыт Валентины Ивановны, основные положения которого мы и приводим ниже.

Алгоритм письменного деления является одной из наиболее трудных тем начальной школы. Во всех существующих учебниках отдельно рассматривается письменное деление на однозначное число и письменное деление на многозначное число. Это вызвано тем, что, будучи одинаковыми по технике выполнения, эти алгоритмы имеют принципиальное различие: письменное деление на однозначное число опирается на знание таблицы умножения, а подбор цифр в частное при делении на многозначное число осуществляется с помощью прикидки. Между тем хорошее усвоение алгоритма письменного деления на однозначное число является необходимым условием понимания алгоритма письменного деления на многозначное число.

Формально алгоритм письменного деления на однозначное число заключается в следующем: 2356:4. Выясняем, что цифра, стоящая в старшем разряде – 2, не делится на 4. Присоединяем к ней следующую цифру и делим на 4 число 23. Получаем неполное частное 5 и остаток 3, к которому сносим следующую цифру 5 и делим на 4 число 35 и т.д. Традиционная методика ориентирует на то, чтобы давать детям некоторое количество примеров, в ходе выполнения которых ученики могли бы уловить смысл алгоритма и запомнить его. Такой подход способствует, конечно, тому, чтобы большинство детей усвоили алгоритм, однако этот процесс можно ускорить и увеличить долю сознательности усвоения.

Алгоритм можно сделать более содержательным, если воспользоваться следующей моделью натурального числа: единицы – отдельные палочки, десятки – связанные в пучки 10 палочек, сотни – пучки из 10 пучков-десятков и т.д. Эта модель удобна еще и тем, что может быть широко использована при обучении сложению и вычитанию, то есть научить работать с ней можно уже в первом классе, а к третьему она станет привычным рабочим инструментом. Первый шаг алгоритма можно представить себе так: 2 пучка-тысяч пытаемся разложить на 4 равные части. Этого сделать нельзя. Тогда развяжем их, получим 20 пучков-сотен. Вместе с имеющимися 3 сотнями на 4 равные части нужно разделить 23 пучка-сотен. В результате этого деления получается 5 сотен в каждой части и 3 сотни остается. Их превращаем в десятки, операция повторяется и т.д. Использование этой модели, с нашей точки зрения, позволяет детям лучше усвоить каждый шаг алгоритма, осознать поразрядовый смысл деления (делится не 23, а 23 сотни), понять смысл приписывания последующей цифры к остатку от деления предыдущего разряда. При необходимости можно выполнить 1–2 задания «вручную», раскладывая на равные части поочередно пучки-сотни, пучки-десятки и отдельные палочки. Выполнение подобных предметных действий, которое находит широкое применение в методике начальной школы, в данном случае позволит повысить эффективность и сознательность усвоения алгоритма.

Как видно из всего сказанного выше, для того чтобы воспользоваться этой моделью, необходима хорошая усвоенность деления с остатком, для которого, в свою очередь, необходима усвоенность табличного деления. Организацию усвоения деления с остатком мы рассмотрим ниже. Сейчас не будем исходить из того, что этот материал усвоен.

Предварительная работа с моделью числа подготавливает детей к усвоению алгоритма письменного деления. На этапе последующего объяснения важно, чтобы предметом сознания детей по-прежнему оставался поразовый смысл письменного деления. Поэтому мы считаем удобным использовать на этом этапе в качестве ориентировочной следующую запись:

т с д е

3 3 1

_ 1 3 2 4 : 4 - Делимое помещается

1) 1 2 в разрядную сетку

_1 2

2) 1 2

_ 0 4

3) 4

0

Частность также записывается в разрядную сетку над делимым. Такая запись используется в некоторых зарубежных учебниках математики. Нам она кажется удобной тем, что позволяет подчеркнуть, что в первом шаге мы делим не 12, а 13 сотен и получаем при этом 3 сотни. Это же должно подчеркиваться учителем и в устных пояснениях, а также найти отражение в контроле над выполнением каждого шага алгоритма. Например, работа может проводиться следующим образом: 2742 : 3.

1. Поместим делимое в разрядную сетку:
   

т с д е

9 1 4

_ 2 7 4 2 : 3

1) 2 7

_0 4

2) 3

_ 1 2

3) 1 2

0

2. Что делим в первом шаге? Что получаем? (Так как 2 тысячи нельзя разделить на 3, то превращаем их в сотни и делим 27 сотен на 3. Получаем 9 сотен. В остатке 0 сотен)
   
3. Что делим во втором шаге? Что получаем? (Во втором шаге делим 4 десятка. Получаем 1 десяток. В остатке 1 десяток)
   
4. Что делим в третьем шаге? Что получаем? (Оставшийся десяток превращаем в единицы – это 10 единиц, да еще 2 единицы. Делим 12 единиц на 3. Получаем 4 единицы. Осталось 0 единиц. Число разделилось полностью)
   

После того как алгоритм в общем усвоен, можно переходить к обычной записи, принятой в нашей школе. Перейдя к обычной записи, еще 1–2 задания необходимо выполнить с подробным комментированием. Эти задания должны включить случай, когда в середине частного получается 0. Как хорошо известно учителям, это наиболее трудный случай письменного деления на однозначное число. Ошибка, когда дети забывают писать 0 в середине частного, является очень распространенной. Чтобы ее избежать, авторы многих школьных учебников предлагают ставить в частном точки, количество которых должно соответствовать количеству цифр частного. Такой выход из положения представляется нам не очень удачным с точки зрения дальнейшего обучения. Этот прием перестанет срабатывать в пятом классе после изучения десятичных дробей. Но так как он прочно усваивается в начальной школе, то дети и в дальнейшем пытаются применить его при делении натуральных чисел. Например: 173 : 5 (5-й класс) – первое неполное делимое 17, значит, в частном будет две цифры. Примерно так будет рассуждать ребенок, перенося знания из начальной школы в новую ситуацию. Эти рассуждения неверны с точки зрения 5-го класса и приводят к трудностям и ошибкам. Раскрытие поразрядового смысла деления с помощью работы с моделью числа, разрядной сеткой и нетрадиционной записью может помочь детям понять и выполнять без ошибок этот трудный случай деления, избежав при этом формирования ненужного стереотипа. Образец подробного комментирования при переходе к обычной записи может быть следующим:

_2128 7

21 304

_02

0

_28

28

0

2 тысячи мы не можем разделить на 7 частей. Превращаем их в сотни. Вместе с имеющейся 1 сотней получится 21 сотня. Делим 21 сотню на 7. Получаем 3 сотни. В остатке 0 сотен. Делим следующий разряд – десятки. 2 десятка делим на 7. Получаем 0 десятков, в остатке 2 десятка. Оставшиеся десятки превращаем в единицы. Всего – 28 единиц. Делим 28 единиц на 7. Получаем 4 единицы, в остатке 0 единиц. Число разделилось полностью: 2128 : 7 = 304. Контроль последующих заданий осуществляется по конечному результату. Однако при возникновении ошибок или затруднений учитель может попросить подробно объяснить решение или в случае необходимости вернуться к записи в разрядной сетке.


2.2. Описание хода эксперимента и анализ полученных результатов


Для выявления эффективности использования алгоритмов в обучении учащихся 3-го класса математике, мы провели исследование, которое проводилось в три этапа. На первом этапе эксперимента мы провели констатирующий срез для определения глубины и прочности программных знаний, умений и навыков учащихся по математике.

Второй этап эксперимента – формирующий – заключался в проведении с учащимися занятий по математике с использованием алгоритмов.

На третьем этапе – контрольном – нами был определен итоговый уровень глубины и прочности программных знаний, умений и навыков учащихся по математике и проведен анализ полученных результатов.

Итак, цель эксперимента: выявление эффективности использования алгоритмов в обучении учащихся 3-го класса математике.

В исследования приняли участие 9 учеников 3 класса Лунинской школы Лунинецкого района Брестской области.

Для проведения констатирующего среза нами был проведена проверочная работа (приложение 1).

Результаты проверочной работы отражены в таблице 1, где знаком «+» отмечены правильно выполненные задания (приложение 2).

Из таблицы 1 видно, что дети имеют разные уровни знаний, умений и навыков:

• большинство детей – 6, что составляет 66,7%, выполнили от 5 до 8 заданий правильно;
  
• два ученика (22,2%) смогли решить только 1-2 задачи;
  
• и только 1 испытуемый (11,1%) смог выполнить правильно все задания.
  

На формирующем этапе нами были проведены занятия по математике с использованием алгоритмов (примерные конспекты уроков – приложение 3).

На заключительном – контрольном – этапе эксперимента мы провели контрольный срез для определения глубины и прочности программных знаний, умений и навыков учащихся.

Для проведения среза мы опять использовали проверочную работу, по результатам которой была составлена таблица 2 (приложение 4).

Сравнивая результаты констатирующего и контрольного этапов эксперимента можно заметить, что показатели знаний детей значительно улучшились.

Динамику изменения уровня знаний учащихся мы представили на диаграмме 1. На диаграмме отражено количество правильно выполненных во время проверочных работ заданий.

Диаграмма 1




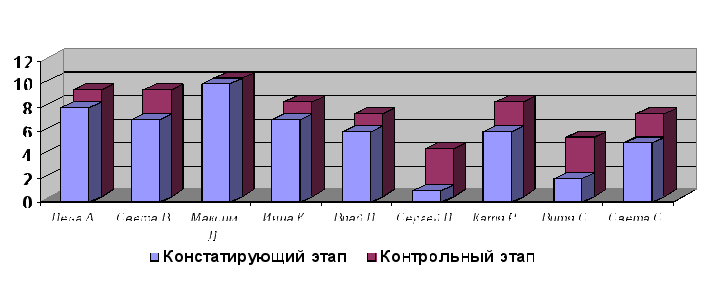
Итак, проведя анализ полученных данных по результатам эксперимента, мы констатируем, что уровень глубины и прочности программных знаний, умений и навыков учащихся повысился, поэтому мы можем сделать вывод об эффективности использования алгоритмов в обучении учащихся 3-го класса математике.


ЗАКЛЮЧЕНИЕ


Современный уровень развития науки и техники требует включения в обучение школьников знакомство с моделями и основами моделирования, а также формирования у них навыков алгоритмического мышления. Без применения моделей и моделирования невозможно эффективное изучение исследуемых объектов в различных сферах человеческой деятельности, а правильное и четкое выполнение определенной последовательности действий требует от специалистов многих профессий владения навыками алгоритмического мышления.

Алгоритмический стиль мышления представляет собой специфический стиль мышления, предполагающий умение создать алгоритм, для чего необходимо наличие мыслительных схем, которые способствуют видению проблемы в целом, ее решению крупными блоками с последующей детализацией и осознанным закреплением процесса получения конечного результата в языковых формах.

Алгоритмическое мышление включает в себя ряд особенностей, свойственных логическому мышлению, однако требует и некоторых дополнительных качеств. Основными из них считаются умение находить последовательность действий, необходимых для решения поставленной задачи и выделение в общей задаче ряда более простых подзадач, решение которых приведет к решению исходной задачи. Наличие логического мышления не обязательно (хотя и достаточно часто) предполагает наличие мышления алгоритмического.

Проблема развития и алгоритмического мышления в начальной школе – одна из важнейших в психолого-педагогической практике. Основной способ ее решения – поэтапное формирование логических приемов мышления с постепенным переходом непосредственно к элементам алгоритмизации, т.е. следует развести понятия логическое мышление и алгоритмическое мышление, хотя в основе развитого алгоритмического мышления, безусловно, лежит сформированное и развитое логическое мышление. Ведущая роль в этом принадлежит учителю, который может организовать работу с алгоритмическими обучающими средствами на уроках математики, способствуя тем самым развитию алгоритмического мышления.

Обучение школьников умению «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют, начинается с простейших алгоритмов, доступных и понятных им (алгоритмы пользования бытовыми приборами, приготовления различных блюд, переход улицы и т.п.). В начальном курсе математики алгоритмы представлены в виде правил, последовательности действий и т.п. Например, при изучении арифметических операций над многозначными числами учащиеся пользуются правилами сложения, умножения, вычитания и деления многозначных чисел, при изучении дробей – правилами сравнения дробей, и т.д. Программа позволяет обеспечить на всех этапах обучения высокую алгоритмическую подготовку учащихся.

Целью экспериментального исследования курсовой работы было определение эффективности использования алгоритмов при изучении математики в 3 классе.

После проведения с детьми занятий по математике с использованием алгоритмов мы зафиксировали повышение уровня глубины и прочности программных знаний, умений и навыков учащихся, на основании чего сделали вывод об эффективности использования алгоритмов в обучении учащихся 3-го класса математике. Результаты исследования представлены нами во второй части работы.

Таким образом, цель исследования – изучить особенности развития алгоритмического мышления учащихся 3-го класса на уроках математики – достигнута; задачи реализованы. Гипотеза – использования алгоритмов при изучении математики в 3 классе положительно влияет на процесс усвоения учащимися знаний и умений – подтверждена.


СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

1. Газейкина А.И. Стили мышления и обучение программированию // Информационные технологии в общеобразовательной школе. – 2003. - № 6. – С.12-19.
   
2. Доморяд А.П. Математические игры и развлечения. – М.: ГИФМЛ, 1961. – 68 с.
   
3. Дубровина И.В., Андреева А.Д. и др. Младший школьник: развитие познавательных способностей: Пособие для учителя. – М.: Академия, 2002. – 360 с.
   
4. Кнут Дональд Э. Алгоритмическое мышление и математическое мышление/ Пер. И.В.Лебедева. – М.: Изд. иностр. лит-ры, 1999. – 110 с.
   
5. Козлова Е.Г. О возможностях формирования у младших школьников способности к работе с алгоритмизованными обучающими средствами // Начальная школа. – 2004. - № 2. – С.99-112.
   
6. Коляда Е.П. Развитие логического и алгоритмического мышления учащихся 2 класса //Информатика и образование. – 1996. - № 1. – С.86-88.
   
7. Копаев А.В. О практическом значении алгоритмического стиля мышления // Информационные технологии в общеобразовательной школе. – 2003. - № 6. – С.6-11.
   
8. Ландо С.К., Семенов А.Л. Алгоритмика. 5-7 классы. Пропедевтический курс. – М.: Инфра-М, 2005. – 120 с.
   
9. Первин Ю.А. Алгоритмические этюды, тетрадь № 2. – М.: АО КУДИЦ, 1993. – 110 с.
   
10. Первушина О.Н. Общая психология: Методические рекомендации. – М.: Вектор, 2003. – 210 с.
    
11. Побединская И.В. Развитие алгоритмического мышления и творческих способностей учащихся в начальном звене // Начальная школа. – 2000. - № 4. – С.110-116.
    
12. Реан А.А., Бордовская Н.В., Розум С.И. Психология и педагогика: Учебник для вузов. – СПб: Питер, 2002. – 432 с.
    
13. Рубинштейн С.Л. О мышлении и путях его исследования. – М.: Прогресс, 1958. – 410 с.
    
14. Рубинштейн С.Л. Основы общей психологии. – СПб: Питер, 2000. – 520 с.
    
15. Теплов Б.М. Практическое мышление// Хрестоматия по общей психологии: Психология мышления. – М.: МГУ, 1981. – 395 с.
    
16. Чабатарэўская Т.М. Матэматыка ў 3 класе. – Мн., 2000.
    

ПРИЛОЖЕНИЯ


Приложение 1

Проверочная работа по математике

Реши следующие задачи:

1. Купили 6 стульев и 4 табуретки по одинаковой цене. За стулья заплатили 54 рубля. Сколько стоят табуретки?
   
2. Хозяйка засолила несколько банок помидоров, по 3кг в каждой банке. После того, как съели 12 кг помидоров, осталось 18 кг. Сколько банок помидоров засолила хозяйка?
   
3. На 3 грузовиках привезли 180 мешков муки. Сколько потребуется грузовиков, чтобы доставить 420 таких же мешков муки?
   
4. Костюм стоит 120 рублей, а платье в три раза дешевле. На сколько костюм дороже платья?
   
5. Рыбаки поймали 64 форели, а сазанов на 48 меньше. Во сколько раз меньше поймали сазанов, чем форели?
   
6. У Сережи 14 рублей, а у Вити 13 рублей. Сколько наклеек они смогут купить, если одна наклейка стоит 3 рубля?
   
7. В ведре 8 л воды, что в 8 раз меньше, чем в бочке. Сколько литров воды в ведре и в бочке?
   

Запиши уравнения и реши их:

1. Число 40 увеличили на произведение числа 6 и неизвестного и получили 76.
   

Составь уравнение и реши задачи:

1. В корзине 28 красных и желтых мячей. Сколько красных мячей в корзине, если желтых 13?
   
2. В трех группах 27 учеников. В первой группе на 3 ученика меньше, чем во второй группе, и на 6 учеников больше, чем в третьей. Сколько учеников в третьей группе?
   

Приложение 2

Таблица 1


Результаты констатирующего этапа эксперимента

Имя и фамилия ученика	№№ заданий	Кол-во правильных ответов
1	2	3	4	5	6	7	8	9	10
Лена А.	+	+		+	+	+		+	+	+	8
Света В.	+	+		+	+		+	+		+	7
Максим Д.	+	+	+	+	+	+	+	+	+	+	10
Инна К.	+	+	+		+		+		+	+	7
Влад Л.	+	+		+	+		+	+			6
Сергей П.		+									1
Катя Р.	+	+		+	+		+	+			6
Витя С.		+			+						2
Света С.	+	+			+		+	+			5

Приложение 3

Конспекты уроков математики