Рабочая программа методические указания контрольные задания для студентов специальности 1-36 04 02 «Промышленная электроника» заочной формы обучения
| Вид материала | Рабочая программа |
- Финанс ы методические указания и контрольные задания для студентов заочной формы обучения, 825.1kb.
- Низкотемпературных и пищевых технологий, 526.64kb.
- Методические указания и контрольные задания для студентов заочной формы обучения Составитель:, 672.87kb.
- Методические указания и контрольные задания для студентов заочной и очно-заочной форм, 985.16kb.
- Методические указания к практическим занятиям для студентов экономических специальностей, 560.21kb.
- Программа, методические указания и контрольные задания для студентов специальности, 1197.59kb.
- Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.
- Программа, методические указания и контрольные задания по учебной дисциплине «риторика», 1732.52kb.
- Учебно-методический комплекс Рабочая учебная программа Методические указания и индивидуальные, 2260.36kb.
- Методические указания и контрольные задания для студентов 1 курса железнодорожных специальностей, 785.04kb.
4.11 Фильтрация измерительных сигналов (Тема 2.4)
При приёме измерительных сигналов возникают следующие основные задачи:
– обнаружение (выделение) сигнала на фоне помех;
– выделение конкретного сигнала из смеси нескольких сигналов присутствующих в данный момент времени;
– оценка с максимальной точностью одного или нескольких постоянных во времени параметров сигнала (например, амплитуды, частоты, фазы, временного сдвига);
– воспроизведение первоначальной формы сигнала, или фильтрацию сигнала;
– предсказание поведения сигнала во времени (экстраполяция).
Если в канале передачи сигнала действуют помехи, то плотности вероятности шума и смеси сигнал + шум перекрываются и принципиально невозможно достоверно указать, какая принятая реализация (или её часть) сигнала соответствует переданной.
Поэтому наиболее важной является задача выделения сигнала на фоне помех, цель которой максимизация отношения сигнал/помеха. Она может решаться как путём совершенствования структуры сигналов (например, использование кодов Баркера), так и созданием таких устройств для их обработки, которые наилучшим образом выделяют сигнал из помех. Линейные цепи, отвечающие критерию максимизации отношения сигнал/помеха на выходе цепи
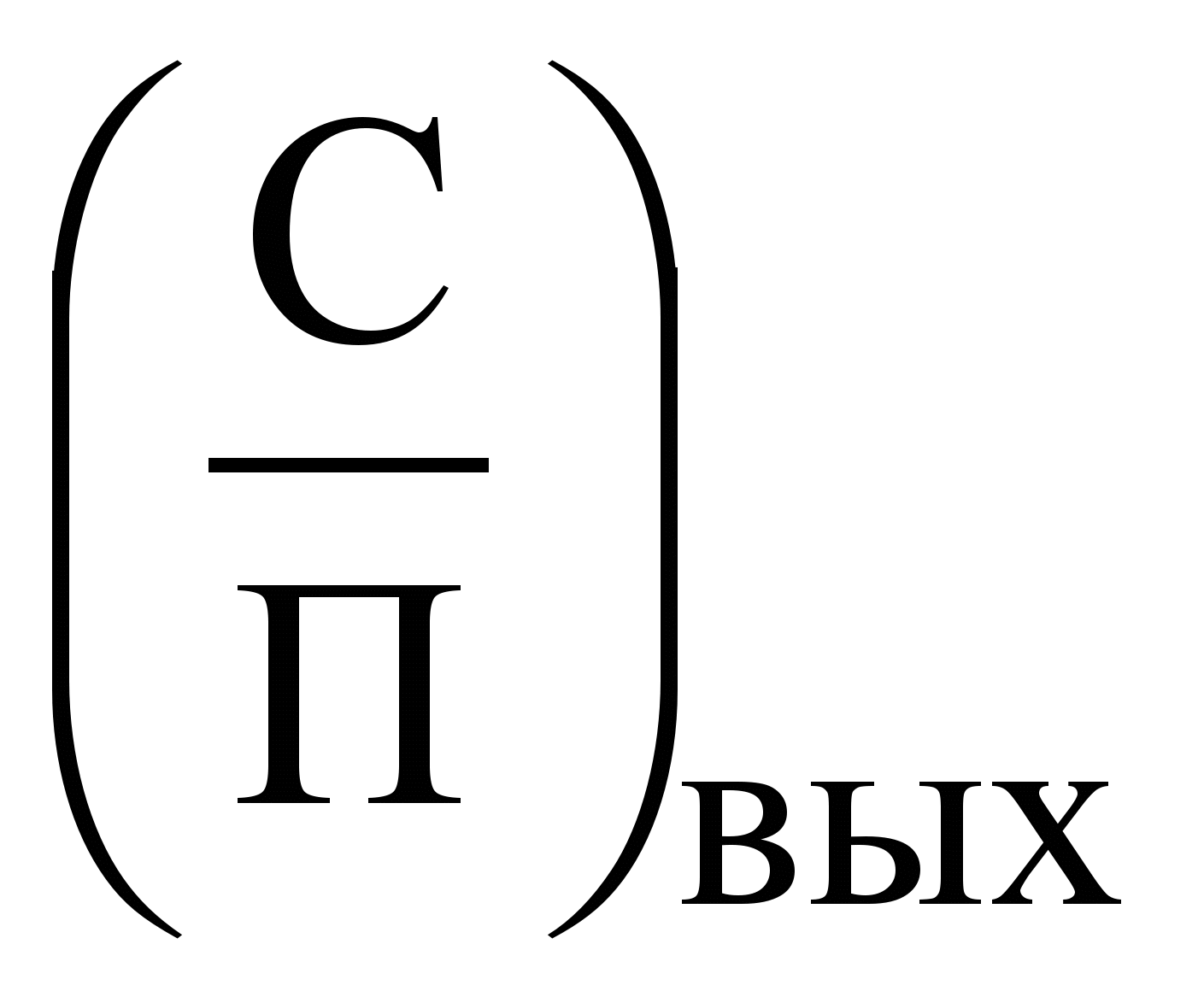– называются оптимальными.Необходимо изучить принцип работы оптимального приемника на основе коррелятора и его структурную схему. Знать основные характеристики оптимального (согласованного) фильтра и соотношения Коши-Буняковского. Уметь оценивать различие между оптимальным приемником на основе согласованного фильтра и коррелятором.
Аналоговые устройства, которые могут производить обработку не квантованных дискретных сигналов по алгоритмам, аналогичным алгоритмам цифровой фильтрации, называют дискретными фильтрами. Необходимо знать дискретное преобразование Фурье, его свойства и построение не его основе дискретных фильтров.
Цифровые устройства, производящие линейную обработку сигнала, называют цифровыми фильтрами (ЦФ). Основной технический показатель ЦФ – его быстродействие, оно зависит как от скорости протекания переходных процессов в микроэлектронных компонентах, так и от сложности алгоритма фильтрации. Предельные частоты сигналов, обрабатываемых с помощью ЦФ, составляют сотни мегагерц, и достижения современной микроэлектроники непрерывно расширяют этот диапазон. Необходимо изучить обобщенную структурную схему устройства цифровой обработки непрерывных сигналов, алгоритм линейной цифровой фильтрации, импульсную и частотную характеристики цифрового фильтра и схемы их построения.
Контрольные вопросы
1. Какие задачи стоят при приеме сигналов на фоне помех?
2. Что представляет из себя оптимальный приемник?
3. Какой приемник называется оптимальным и почему?
4. Сформулируйте неравенство Коши-Буняковского.
5. Как описывается импульсная характеристика согласованного фильтра?
6.Какова структурная схема оптимального приемника на основе согласованного фильтра?
7. В чем разница оптимального приемника на основе согласованного фильтра и коррелятора?
8. Чем характеризуются дискретные фильтры и каковы их свойства?
9. Какова обобщенная структурная схема цифрового линейного фильтра?
10. Запишите алгоритм линейной цифровой обработки непрерывных сигналов.
11. В чем отличие трансверсальных нерекурсивных от рекурсивных фильтров?
12. Какими характеристиками описываются цифровые фильтры?
4.12 Преобразователи частоты (Тема 3.1)
Преобразователем частоты (ПЧ) называется устройство, предназначенное для переноса спектра частот исходного сигнала из одной области частот в другую без изменения соотношения между составляющими спектра. Они широко применятся в радиовещании, телевидении и т. д. Необходимо изучить принцип работы, способы схемного построения и предъявляемые к ним треования.
Контрольные вопросы
- Каков принцип работы преобразователя частоты? В чем суть квазилиней-
ной теории преобразования частоты?
- Какие требования предъявляются к преоразователю частоты?
- Какие знаете схемы построения преобразователей частоты? Поясните
принцип их работы.
4.13 Умножители и делители частоты (Тема 3.2)
Умножители частоты (УЧ) предназначены для умножения частоты ЗГ в заданное число раз. Умножители используются при построении радиопередащих устройств, в измерительной технике для получения сетки частот и т. д. Используется несколько способов построения умножителей частоты:
– с помощью генератора гармоник и полосовой фильтрации;
– с помощью «захвата» частоты вспомогательного генератора;
– с помощью устройства фазовой автоподстройки частоты (ФАПЧ), а также их комбинации.
Необходимо знать принципы получения умножения частоты, схемное построения умножителей.
Делители частоты предназначены для деления частоты в заданное число раз. Различают делители частоты регенеративного типа и цифровые счетчикового типа. Необходимо изучить принцип работы и уметь нарисовать их структурные схемы.
Контрольные вопросы
1. На каком принципе основано умножение частоты с помощью генератора гармоник?
2. Какие знаете схемы построения умножителей частоты? Поясните принцип их работы.
3. Поясните работу делителя частоты регенеративного типа?
4. Нарисуйте структурную схему делителя частоты счетчикового типа.
4.14 Модуляторы АМ-сигналов (Тема 4.1)
Модуляция есть процесс изменения одного или нескольких параметров высокочастотного модулируемого колебания под воздействием относительно низко-частотного модулирующего сигнала, содержащего определенную информацию. Из выражения, описывающего высокочастотные колебания тока
I(t) = Imcos(0t + )
следует, что такими параметрами являются амплитуда Im, частота 0 и фаза . Поэтому можно осуществлять амплитудную, частотную или фазовую модуляции. В результате модуляции спектр управляющего сигнала переносится в область высоких частот, где передача электромагнитных сигналов в свободном пространстве посредством излучения более эффективна. Роль переносчика информации выполняет высокочастотное колебание, называемое несущим. Устройства, предназначенные для получения модулированных колебаний, называются модуляторами. Для получения амплитудной модуляции (АМ) в качестве модулятора используются нелинейные четырехполюсники, которыми на практике служат транзисторы и электронные лампы. Необходимо изучить принцип работы амплитудного модулятора, какие схемы применяются для построения модуляторов (с балансной модуляцией, однополосной модуляцией), какими временными функциями описываются соответствующие модулированные колебания и какими спектральными диаграммами они характеризуются.
Контрольные вопросы
- На чем основан процесс модуляции?
- Нарисуйте схему базового модулятора. Каков принцип его работы? Каки-
ми характеристиками описывается его работа?
- Нарисуйте схему балансного модулятора? Модулятора на одной боковой
частоте? Каков принцип их работы? Какие спектральные диаграммы выходного сигнала им соответствуют?
4.15 Методы получения угловой модуляции (Тема 4.2)
Методы осуществления угловой модуляции (УМ) можно разделить на две группы: прямые и косвенные. При частотной модуляции (ЧМ) прямой метод означает непосредственное управление частотой колебаний генерируемых задающим генератором (автогенератором), а при фазовой модуляции (ФМ) прямой метод реализуется воздействием на электрические цепи (усилители сигнала, умножители частоты) определяющие фазу несущего колебания. Косвенные методы осуществляют преобразования ФМ в ЧМ или ЧМ в ФМ.
Необходимо изучить, как можно в случае прямого метода получать ЧМ, используя включение варикапа в колебательный контур автогенератора. Уметь нарисовать схему такого модулятора и пояснять принцип его работы. Уметь пояснять косвенные методы получения ЧМ и ФМ на примере структурных схем.
Контрольные вопросы
- Каким образом, используя варикап в схеме автогенератора, можно полу-
чить ЧМ?
- Какие способы получения ЧМ и ФМ знаете?
- На чем основан метод преобразования АМ в ФМ? Какова структурная
схема такого модулятора и принцип ее работы?
4. Нарисуйте структурную схему модулятора с частотной манипуляцией.
- Демодуляция АМ-сигналов (Тема 4.3)
Демодуляцией (детектированием) называют процесс восстановления модулирующего напряжения из модулированных колебаний, т. е. процесс обратный модуляции. В зависимости от вида модуляции напряжение на выходе детектора должно воспроизводить закон изменения амплитуды, частоты или фазы детектируемого колебания. Детектирование сопровождается преобразованием спектра высокочастотного сигнала (ВЧ) содержащего несущее колебание и колебания боковых частот. На выходе демодулятора выделяется напряжение с низкочастотным спектром (НЧ) передаваемого измерительного процесса. Так как при
детектировании происходит трансформация частотного спектра, то такой процесс не может быть осуществлен без применения нелинейных элементов или линейных но с переменными параметрами, а также фильтра для выделения необходимого спектра частот.
При детектировании АМ-колебаний необходимо получить колебания, совпадающие по форме с огибающей модулированного высокочастотного сигнала. Элементом, в котором осуществляется преобразование частоты, может быть как управляемое (транзистор, триод), так и неуправляемое (диод) нелинейное сопротивление, так и линейное сопротивление с переменными параметрами. В качестве фильтра используется фильтр нижних частот (ФНЧ) в виде RC-цепи, который выделяет все составляющие продетектированного сигнала и не пропускает высокочастотные составляющие.
Необходимо знать схемы диодных детекторов (с открытым и закрытым входами), принцип их работы, требования к постоянной времени нагрузки, их характеристики. Знать, в чем отличие диодного детектора в линейном и квадратическом режимах работы, как это влияет на нелинейные искажения.
Контрольные вопросы
1. Какие знаете схемы диодных детекторов? Поясните принцип их работы?
2. Какими характеристиками описываются диодные детекторы? От чего зависят их параметры?
3. Как выбирается постоянная времени цепи нагрузки и на что это влияет?
4. Чем характеризуется линейный режим работы диодного детектора?
5. В чем особенность нелинейного режима работы диодного детектора?
6. От чего зависят нелинейные искажения при детектировании АМ-сигналов?
- Демодуляция сигналов с угловой модуляцией (Тема 4.4)
При детектировании ЧМ- и ФМ-сигналов они предварительно преобразуются в колебания с неглубокой амплитудной модуляцией и затем детектируются амплитудным детектором. Подобное преобразование необходимо потому, что нелинейные элементы реагируют на изменение только амплитуды, а не частоты или фазы колебаний. Необходимо изучить принцип работы частотного детектора, основанного на преобразовании ЧМ а АМ с использованием колебательных контуров, настроенных на одну частоту и с расстроенными контурами (частотный дискриминатор), а также фазово-частотных дискриминаторов.
Фазовым детектором называется устройство, напряжение на выходе которого зависит от разности фаз двух сравниваемых напряжений одной частоты или очень близких частот. Фазовые детекторы применяются в широком диапазоне часто. Необходимо изучить принцип работы фазового детектора, знать его схемы построения.
Контрольные вопросы
- На каком принципе работает фазовой детектор? Какова его характеристи-
ка детектирования?
- Нарисуйте схему фазового детектора на основе операционного усилителя.
- На каком принципе работает синхронный детектор? Нарисуйте его схему
и поясните принцип работы.
5. КОНТРОЛЬНЫЕ ЗАДАНИЯ
Выполнение контрольных заданий является одной из важнейших частей самостоятельной работы студентов. Оно способствует успешному усвоению материала, приобретению практических навыков подготовки к измерениям, обработки и оформления результатов, облегчает подготовку к зачёту по дисциплине. Поэтому выполнению контрольных заданий должно быть уделено большое внимание. Для более детальной проработки вопросов дисциплины рекомендуется также решить другие задачи, не вошедшие в индивидуальное задание.
ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ ЗАДАНИЙ
Контрольное задание состоит из 10 задач, которые охватывают разделы 1 – 4 . Номера задач, подлежащих включению в индивидуальное задание, определяются по двум последним цифрам шифра студента. Номера варианта соответствуют последней цифре шифра. Задачи, решённые не по варианту либо не по заданию, не засчитываются, а работа возвращается студенту без проверки.
Приступать к решению задачи следует только после полной проработки соответствующей и предыдущих тем. Условия должны быть записаны в тетрадях с контрольными решениями полностью. Решения и ответы на поставленные вопросы должны быть обоснованными и, по возможности, краткими, содержать необходимый иллюстративный материал (схемы, чертежи, графики) и выполняться в строгом соответствии с действующими стандартами.
Задачи следует решать в общем виде и только затем подставлять числовые значения в стандартных единицах физических величин. Недостающие данные (если это необходимо ) следует задавать самим в общем виде или в пределах реальных значений. Обязательно следует приводить пояснения хода решения. Задачи, представленные без пояснений, могут быть не зачтены. При решении задач с большим объёмом вычислений рекомендуется использовать ЭВМ. Программу следует составлять на языке высокого уровня, а её распечатку приложить к контрольной работе. При этом следует предусмотреть вывод на печать основных результатов промежуточных и окончательных вычислений, а также дать пояснения к алгоритму и привести основные расчётные соотношения.Окончательные результаты расчетов должны быть представлены в соответствии с МИ 1317 - 86 или ГОСТ 8.207 - 76 с указанием размерности физической величины . Решения задач должны заканчиваться чётко сформулированными выводами .
Контрольные задания должны выполняться в отдельной тетради, на обложке
которой должно быть указано наименование учебной дисциплины, фамилия и инициалы студента, номер шифра и группа. Если студент желает, чтобы проверенное задание было выслано ему почтой, следует указать почтовый адрес и индекс отделения связи.
При решении контрольных задач необходимо пользоваться методическими
указаниями, изложенными в [3.1.9 – 3.1.10].
ЗАДАЧИ
Задача 1. На рисунке 1 заданы периодические последовательности видеоимпульсов различной формы и скважности, параметры которых определены в таблице 1 соответствующим вариантом. Выполнить спектральный анализ заданного видеоимпульса с амплитудой Е, длительностью и периодом повторения T = a.
Таблица 1
| Единицы/ десятки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | а11 | б21 | в31 | г41 | д11 | е21 | ж31 | з41 | и11 | а21 |
| 10 | б31 | в41 | г11 | д21 | е31 | ж42 | з12 | и22 | а32 | б42 |
| 20 | в12 | г22 | д32 | е42 | ж12 | з22 | и32 | а42 | б12 | в22 |
| 30 | г33 | д43 | е13 | ж23 | з33 | и43 | а13 | б23 | в33 | г43 |
| 40 | д13 | е23 | ж33 | з43 | и13 | а23 | б24 | в34 | г44 | д14 |
| 50 | е24 | ж34 | з44 | и14 | а14 | б21 | в32 | г42 | д12 | е22 |
| 60 | ж32 | з42 | и12 | а22 | б32 | в42 | г13 | д24 | е32 | ж41 |
| 70 | з13 | и23 | а33 | б44 | в11 | г23 | д33 | е43 | ж13 | з23 |
| 80 | и34 | а43 | б13 | в24 | г34 | д41 | е12 | ж24 | з31 | и42 |
| 90 | а12 | б41 | в13 | г14 | д42 | е14 | ж44 | з14 | и33 | а44 |
Для этого необходимо:
- используя разложение в ряд Фурье, определить все гармонические сос-
тавляющие спектров амплитуд и фаз в пределах от 0 до 4;
- построить в соответствующем масштабе графики спектров амплитуд и
начальных фаз;
3) для полученных гармонических составляющих рассчитать их мощность на сопротивлении нагрузки в 1 Ом и построить график спектра их мощностей. Какова будет огибающая?
4) пользуясь равенством Парсеваля, определить суммарную мощность всех составляющих, включая и постоянную составляющую (если она имеется);
5) рассчитать мощность заданного сигнала на том же сопротивлении нагрузки;
6) определить (в процентах) какая часть мощности приходится на рассчитанные гармонические составляющие;
7) по спектральному графику мощностей определить полосу частот f, в которой сосредоточена рассчитанная мощность спектральных составляющих заданного сигнала;
8) построить спектр периодической последовательности радиоимпульсов, несущая частота которой f0 = 10 МГц, а огибающая S(t) является сигналом, заданным соответствующим вариантом.
Вид импульсного сигнала на рисунке 1, значение амплитуды импульсов Е, его длительность и величина а, устанавливающая связь между T и задаются с помощью кода таблицы вариантов (таблица 1) и соответствующих таблиц: таблица 2 (значение Е) и таблицы 3 (значение и а).
Например, студент должен выполнить вариант № 36. По таблице 1 этому номеру варианта соответствует код и43. Следовательно, форма импульса приведена на рисунке 1, и, амплитуда импульса Е = 5 В, длительность импульса = 5 мкс, при этом а = 5 и Т = 5.
Таблица 2 Таблица 3
| Первая цифра кода таблицы 1 | Е |
| 1 | 1 В |
| 2 | 2 В |
| 3 | 4 В |
| 4 | 5 В |
| |
| Вторая цифра кода таблицы 1 | | а |
| 1 | 1 мкс | 2 |
| 2 | 2 мкс | 4 |
| 3 | 5 мкс | 5 |
| 4 | 10 мкс | 6 |
| 5 | 20 мкс | 8 |
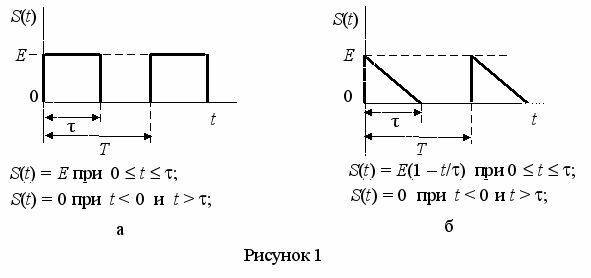
Продолжение рисунка 1
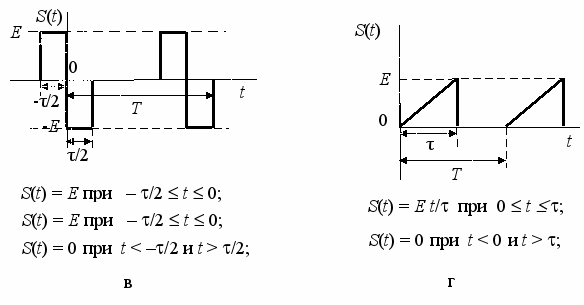
τ/2
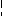
Е
0
-τ/2
-Е
T
t
ж
S(t)
S(t) = – E при – /2 t 0;
S(t) = E при 0 t /2;
S(t) = 0 при t < –/2 и t > /2;
з
Е
0
-τ/2
T
t
S(t)
τ/2
S(t) = – 2Et/ при –/2 t 0;
S(t) = 2Et/ при 0 t /2;
S(t) = 0 при t < – /2 и t > /2;
S(t)
S(t)
Е
Е
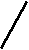
0
0
t
t
-τ/2
τ/2
τ/2
-τ/2
T
T
S(t) = E при –/2 t /2;
S(t) = 2E(t + /2)/ при –/2 t 0;
S(t) = 0 при t < –/2 и t > /2;
S(t) = 2E(/2 – t)/ при 0 t /2;
S(t) = 0 при t < – /2 и t > /2;
д
е
Рисунок 1
Продолжение рисунка 1
Задача 2. Высокочастотное косинусоидальное колебание с частотой f0 и амплитудой U подвергается модуляции. Вид модуляции (амплитудная – АМ, частотная – ЧМ), модулирующий низкочастотный сигнал E(t) заданы в таблице 4.
Необходимо составить в общем виде аналитические выражения для модулированных колебаний с учетом заданного варианта по таблице 1.
Таблица 4
-
Буква кода
таблицы 1
Вид
модуляции
Модулирующая
функция E(t)
а
АМ
u(1 + cos 1t)
б
ЧМ
сos3t
в
АМ
u(1 + sin2t)
г
ЧМ
сos23t
д
АМ
u(1 + cos21t)
е
ЧМ
sin3t
ж
АМ
u(1 + sin22t)
з
ЧМ
sin23t
и
АМ
u(1 + cos1t + cos2t)
Для АМ-колебаний:
- определить парциальные коэффициенты модуляции для каждой состав-
ляющей модулирующей функции E(t);
- построить в соответствующем масштабе спектральную диаграмму моду-
лированного колебания и определить полосу частот, занимаемую сигналом;
- считая нагрузку резистивной и равной 10 Ом, рассчитать мощности коле-
баний на несущей частоте и на всех боковых частотах;
- определить, какая часть мощности относительно несущего колебания
приходится на боковые составляющие.
Исходные данные заданного варианта находятся с помощью кода по таблицам 1, 4, 5, 6
Таблица 5 Таблица 6
| Первая цифра кода таблицы 1 | U, В | u, В | f0 , МГц |
| 1 | 1 | 0,1 | 1 |
| 2 | 2 | 0,2 | 2 |
| 3 | 4 | 0,4 | 4 |
| 4 | 5 | 0,3 | 0,5 |
| |
| Вторая цифра кода таблицы 1 | f1=1/2 | f2=2/2 |
| 1 | 10 кГц | 14 кГц |
| 2 | 15 кГц | 18 кГц |
| 3 | 20 кГц | 16 кГц |
| 4 | 8 кГц | 13 кГц |
| 5 | 12 кГц | 7 кГц |
- определить индекс частотной модуляции ;
- используя разложение в ряд по функциям Бесселя, определить амплитуды
гармонических составляющих модулированного колебания для несущей частоты, а также для ближайших четырех боковых составляющих спектра ЧМ-колебания (значения функций Бесселя от величины приведены в Приложении 1);
Таблица 7 Таблица 8
| Первая цифра кода таблицы 1 | U, В | f0 , МГц |
| 1 | 2 | 5 |
| 2 | 4 | 10 |
| 3 | 6 | 15 |
| 4 | 6 | 20 |
| |
| Вторая цифра кода таблицы 1 | f3=3/2 | f=/2 |
| 1 | 4 кГц | 24 кГц |
| 2 | 6 кГц | 72 кГц |
| 3 | 10 кГц | 50 кГц |
| 4 | 12 кГц | 108 кГц |
| 5 | 8 кГц | 80 кГц |
- нарисовать в соответствующем масштабе спектральную диаграмму моду-
лированного колебания и определить полосу частот, занимаемую сигналом для рассчитанного индекса частотной модуляции;
4) рассчитать мощности колебаний на несущей частоте и на определенных выше гармонических составляющих модулированного колебания, считая сопро-
тивление нагрузки равной 10 Ом. Определить. какая часть мощности относительно несущего колебания приходится на боковые составляющие.
Исходные данные заданного варианта находятся с помощью кода по таблицам 1, 4, 7, 8.
Задача 3. Закон распределения плотности вероятности задан функцией p(x). Вид функции и интервалы изменения случайной величины х определяется таблицей 1 и буквой кода таблицы 9, а исходные данные приведены в таблицах 10 – 11.
Таблица 9
-
Буква кода
таблицы 1
Вид
функции p(x)
Интервал изменения
случайной величины х
Численные значе-
ния постоянных
а
сos x
(– /2, /2)
-
б
1/( – )
х ;
= 2; = 5
в
sin x
(– /2, /2)
-
г
a/x
1 x 3
а = 4
д
ax2
1 x 5
а = 3
е
1 – сos x
(– /2, /2)
-
ж
1/( + )
х ;
= 3; = 6
з
1 – sin x
(– /2, /2)
-
и
1/ax2
1 x 4
а = 2
Таблица10 Таблица 11
| Первая цифра кода таблицы 1 | Числовые значения постоянной а |
| 1 | 3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 5 |
| Вторая цифра кода таблицы 1 | Численные значения постоянных | |
| | | |
| 1 | 2 | 5 |
| 2 | 1 | 4 |
| 3 | 3 | 6 |
| 4 | 5 | 8 |
| 5 | 0,5 | 2,5 |
Необходимо определить математическое ожидание и дисперсию.
Задача 4. На вход нелинейного элемента, вольтамперная характеристика которого приведена на рисунке 2, подается входной сигнал uвх(t).
Необходимо:
- аппроксимировать заданную вольтамперную характеристику нелинейно-
го элемента степенным полиномом n степени;
- определить ток на выходе нелинейного элемента и построить его спек-
трограмму;
- по полученной аппроксимированной функции построить аппроксимиро-
ванную характеристику на одном графике совместно с заданной. Из построенных графиков определить погрешность аппроксимации.
Исходные данные для выполнения задания находятся в зависимости от кода варианта (таблица 1) и таблиц 12 – 14.
Таблица 12
| Буква кода таблицы 1 | а | б | в | г | д | е | ж | з | и |
| № рисунка | 2, а | 2, б | 2, в | 2, г | 2, д | 2, е | 2, ж | 2, з | 2, и |
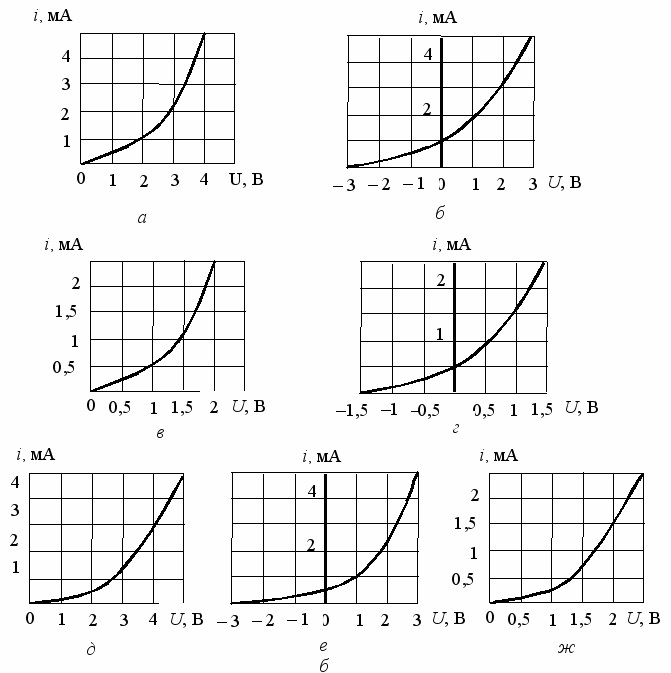
Рисунок 2
П
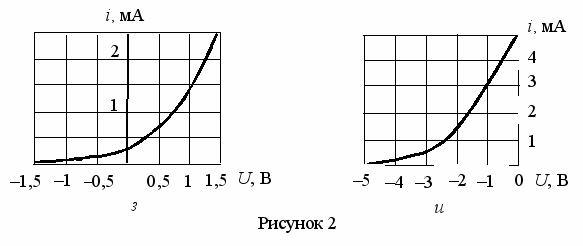родолжение рисунка 2Таблица 13 Таблица 14
| Первая цифра кода таблицы 1 | Степень поли- нома n |
| 1 | 2 |
| 2 | 3 |
| 3 | 3,укорочен. |
| 4 | 2 |
| |
| Вторая цифра кода таблицы 1 | Входной сигнал uвх(t), В |
| 1 | 2cos 1t + cos 2t |
| 2 | sin 1t + 2sin 2t |
| 3 | 2cos 1t + 4sin 2t |
| 4 | 2sin 1t + 4cos 2t |
| 5 | cos 1t + 2sin 2t |
При построении спектрограмм необходимо положить, что 1 > 2.
Задача 5. К нелинейному элементу (рисунок 3), вольтамперная характеристика которого имеет кусочно-линейную аппроксимацию с напряжением запирания Eз = А В и крутизной характеристики S = В мА/В , приложено напряже-
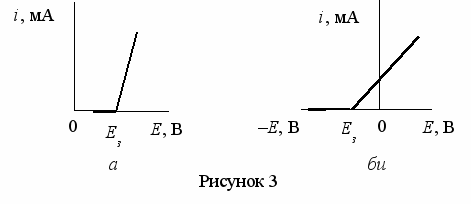
ние uвх = (Е0 + Umcos t) В. При заданных соответствующим вариантом (табли-
ца 1) и исходных параметров в таблицах 15 – 17 определить:
- смещение Е0 и угол отсечки , при которых амплитуда n гармоники будет
максимальной;
- для определенного угла отсечки определить амплитуды гармонических
составляющих тока I0 , I1, I2, I3 ;
- по полученным величинам токов рассчитать коэффициент нелинейных
искажений kг выходного сигнала;
- для заданного сигнала и рассчитанного смещения Е0 построить графичес-
ки на вольтамперной характеристике сигнал на входе и выходе нелинейного устройства.
Таблица 15
-
Буква кода
таблицы 1
Номер
рисунка
А , В
В , мА / В
а
3, а
1
5
б
3,б
– 2
3
в
3, а
2
4
г
3, б
– 1
8
д
3, а
0,5
4
е
3, б
– 0,5
5
ж
3, а
4
2
з
3, б
– 3
6
и
3, а
0,75
7
Таблица 16 Таблица 17
| Первая цифра кода таблицы 1 | Номер гармоники, n |
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
| 4 | 2 |
| |
| Вторая цифра кода таблицы 1 | Амплитуда сигнала Um, В |
| 1 | 2 |
| 2 | 4 |
| 3 | 5 |
| 4 | 6 |
| 5 | 3 |
Задача 6. Задан узкополосный полосовой фильтр, представляющий собой параллельный резонансный колебательный контур (рисунок 4), имеющий неполное включение для согласования с нагрузкой Rн.
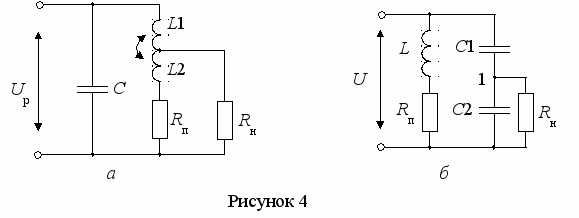
Задача 6.1 Для задачи рисунка 4, а :
1) рассчитать по данным, заданным в таблицах 18 – 20, сопротивление параллельного колебательного контура Zк на резонансной частоте f0 или при расстройке на f от резонансной частоты f;
2) определить при заданной расстройке f или при f0.707 напряжение на контуре U, если на резонансной частоте оно равно Uр (предполагается, что внутреннее сопротивление источника сигнала Ri значительно больше сопротивления контура Zк ,то есть Ri >> Zк);
3) определить величины индуктивностей L1 и L2 , обеспечивающие согласование с нагрузкой Rн на резонансной частоте при некотором коэффициенте включения p. Взаимной индуктивностью M между катушками пренебречь;
4) рассчитать и построить амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики фильтра. По этим характеристикам определить полосу пропускания фильтра на уровне 0.707 (2f0.707) и его добротность Q.
Вариант задания определяется по таблице 1.
Таблица 18
-
Буква кода
таблицы 1
Номер
рисунка
Uр, В
U, В
f0 ,
МГц
f ,
МГц
Расстройка
f , кГц
а
4, а
0,5
–
0,8
б
4,б
–
3
0,6
в
4, а
2
–
–
0,5
+10
г
4, б
–
7
0,4
д
4, а
5
–
0,7
е
4, б
–
2,5
0,5
ж
4, а
4
–
0.4
– 8
з
4, б
–
6
0,7
и
4, а
3
–
1,0
Таблица 19
| Первая цифра кода таблицы 1 | Индуктивность контура L , мкГн | Емкость контура C, пФ |
| 1 | 400 | – |
| 2 | – | 300 |
| 3 | 500 | – |
| 4 | – | 250 |
| Таблица 20 |
| Вторая цифра кода таблицы 1 | Сопротивление нагрузки Rн, кОм | Коэффициент включения p | Сопротивление потерь в контуре Rп , Ом | Добротность контура Q |
| 1 | 2 | – | 20 | – |
| 2 | – | 0,2 | – | 30 |
| 3 | 5 | – | 10 | – |
| 4 | – | 0,15 | – | 20 |
| 5 | 3 | – | 15 | – |
Задача 6.2 Для задачи рисунка 4, б :
1) рассчитать по данным, заданным в таблицах 18, 21 – 22 элементы L, C1, C2, добротность Q и характеристическое сопротивление колебательного контура, обеспечивающего согласование с сопротивлением нагрузки Rн ;
2) в режиме согласования для заданного коэффициента включения p определить величину сопротивления нагрузки Rн ;
3) с учетом коэффициента включения p определить напряжение на сопротивлении нагрузки Rн, если на вход контура подается напряжение U на резонансной частоте f0;
Таблица 21 Таблица 22
| Первая цифра кода таблицы 1 | Сопротивление потерь в контуре Rп , Ом | Емкость контура C, пФ |
| ||||||||||||
| 1 | 4 | 200 | |||||||||||||
| 2 | 6 | 300 | |||||||||||||
| 3 | 10 | 150 | |||||||||||||
| 4 | 8 | 250 |
4) рассчитать и построить амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики фильтра. По этим характеристикам определить полосу пропускания фильтра на уровне 0.707 (2f0.707) и его добротность Q. Сравнить с рассчитанным значением.
Вариант задания определяется по таблице 1 а исходные данные для задачи
6.1 задаются таблицами 18 – 20, а для задачи 6.2 по таблице 1 определяется вариант задания, а по таблицам 18, 21–22 исходные данные для расчетов.
Указания:
– при решении этой задачи под режимом согласования понимается, что сопротивление контура на резонансной частоте Zк,р связано с сопротивлением Zк1 в точке включения 1 сопротивления нагрузки Rн через коэффициент включения p соотношением Zк1