Лекция №1 «Общие сведения о моделировании систем»

Вид материала

Лекция

Содержание 2. Основные понятия теории моделирования систем Системный подход 3. Классификация моделей Комбинированное (аналитико-имитационное) 4. Основные подходы к построению математических моделей систем

Подобный материал:

• Рабочей программы дисциплины Моделирование систем управления по направлению подготовки, 25.88kb.
• Общие сведения  Название направления, 222.63kb.
• Реферат по курсу Моделирование Вычислительных Систем Тема: «Механизм генерации транзактов, 128.48kb.
• Механизм генерации транзактов в модели, 121.16kb.
• Лекция № Введение в оау. Общие сведения. Общие понятия, 48.78kb.
• Разработка информационных систем для организации автоматизированных рабочих мест преподавателей, 43.3kb.
• Тема Введение. Общие сведения о системах электросвязи лекция 1 системы электросвязи, 253.51kb.
• 2 Анализ сетей Петри, 29.67kb.
• Учебное пособие Оглавление Лекция Общие сведения о гомилетике Лекция Можно ли научиться, 1476.59kb.
• Матрицы и матричные операции широко используются при математическом моделировании самых, 552.31kb.

Лекция № 1

«Общие сведения о моделировании систем»


1. Моделирование как метод научного познания

Все то, на что направлена человеческая деятельность, называется объектом. В реальной жизни достаточно часто возникают задачи создания новых и совершенствования существующих объектов, решение которых невозможно без проведения предварительных теоретических исследований. Как правило, данные исследования начинаются с выдвижения гипотез - определенных предсказаний, предположения о свойствах исследуемых явлений и процессов, основывающиеся на ограниченном количестве опытных данных, наблюдений или догадок. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения имеют аналогии. Аналогией называют суждение о каком-либо частном сходстве двух объектов познания. Данные суждения основываются на научных положениях, проверенных на практике, или имеющихся опытных данных. Например, процесс изменения во времени емкости конденсатора в колебательном контуре аналогичен процессу изменения угла отклонения маятника. Таким образом, аналогия связывает гипотезу с экспериментом.

Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны быть наглядны и сводится к удобным для исследования логическим схемам. Такие логические схемы, упрощенные рассуждения и логические построения или эксперименты, в результате которых уточняется природа явления, называются моделями. Другими словами, модель – это объект-заместитель оригинала объекта, явления или процесса, обеспечивающий изучение некоторых (необходимых исследователю) свойств оригинала.




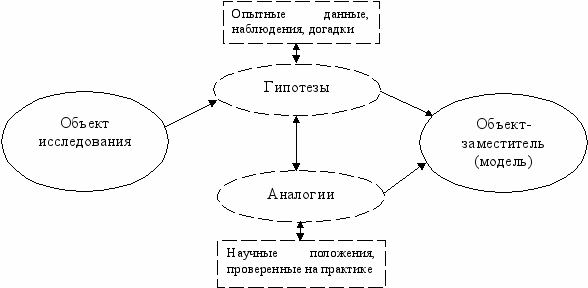
Сам процесс замещения реальных объектов моделями называется моделированием. А теория замещения объектов-оригиналов объектами-моделями и исследования свойств объектов на их моделях называется теорией моделирования.

Если полученные данные о процессах, протекающих в модели, подтверждаются накопленным научным и практическим опытом, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев.


2. Основные понятия теории моделирования систем

В качестве определения системы будем использовать следующее: система – это целенаправленное множество взаимосвязанных элементов. Ключевое слово в данном определении, характеризует общее свойство всех систем (в том числе и систем управления) - стремление к достижению некоторой цели. Любая система функционирует в реальном мире. Поэтому при моделировании систем необходимо учитывать внешнюю среду – множество существующих вне системы элементов любой природы, оказывающих влияние на систему или находящихся под ее воздействием.

При анализе и синтезе систем управления специалистами используются два основных подхода – классический и системный.

Разработка модели системы на базе классического подхода предусматривает переход от частного к общему и синтезирует систему путем слияния ее компонент, разрабатываемых раздельно. При этом каждая из компонент решает свои задачи и изолирована от других частей модели. Поэтому классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно независимое рассмотрение отдельных сторон функционирования реальной системы. Процесс синтеза модели на основе классического подхода можно проиллюстрировать следующим образом. Реальная система разбивается на отдельные подсистемы, то есть выбираются исходные данные Д для моделирования и ставятся частные цели Ц, отображающие отдельные стороны процесса моделирования. По отдельной совокупности исходных данных ставится отдельная частная цель моделирования отдельной стороны функционирования системы, на базе которой формируется некоторая компонента К будущей модели. Совокупность компонент объединяется в модель М.

Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель функционирования системы.

Суть системного эффекта заключается в том, что целевое функционирование системы рассматривается во взаимодействии с внешней средой. При этом в зависимости от целей моделирования могут рассматриваться различные аспекты взаимодействия системы с внешней средой. Системный подход позволяет решить проблему построения сложной системы с учетом всех факторов и возможностей, пропорциональных их значимости на всех этапах исследования системы и построения ее модели.

Процесс синтеза модели на базе системного подхода заключается в следующем. Рассмотрение системы как интегрированного целого при разработке модели начинается с формулировки цели ее функционирования Ц. Далее осуществляется определение структуры моделируемой системы S как совокупности связей между ее элементами, отражающими их взаимодействие в процессе достижения указанной цели. На основе исходных данных {ИД}, которые известны из анализа внешней среды (надсистемы) Е и ограничений {Огр}, накладываемых на систему сверху, и на основе цели функционирования Ц формируется совокупность исходных требований Т к модели системы М. На базе этих требований формируются подсистемы П как совокупности элементов {Э}. Моделирование данных подсистем является основой построения общей модели системы. После чего с использованием совокупности критериев выбора {КрВ}, формулируемых исходя из общей цели функционирования системы, осуществляется наиболее сложный этап синтеза – выбор подсистем, которые образуют синтезируемую модель системы М.

Характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических задач, к основным из которых относятся:

- идентификация реальных объектов (определение их структуры и параметров);

- выбор вида модели;

- построение модели и ее машинная реализация;

- взаимодействие исследователя с моделью в ходе машинного эксперимента;

- проверка правильности полученных в ходе моделирования результатов;

- выявление основных закономерностей, исследованных в процессе моделирования.


3. Классификация моделей

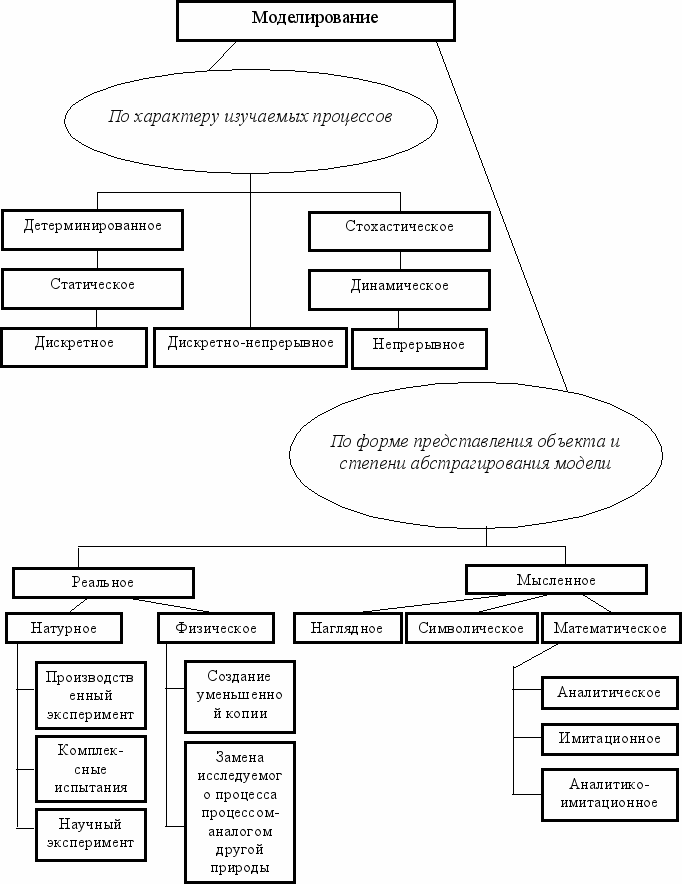
В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть разделены на:

- детерминированные и стохастические;

- статические и динамические;

- дискретные, непрерывные и дискретно-непрерывные.

Детерминированные модели отображают процессы, в которых предполагается отсутствие всяких случайных воздействий. Стохастические модели отображают вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики. Статические модели служат для описания поведения объекта в какой-либо момент времени, а динамические модели отражают поведение объекта во времени. Дискретное моделирование служит для описания дискретных процессов, непрерывное – для непрерывных, а дискретно-непрерывное – для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.

В зависимости от формы представления объекта и степени абстрагирования модели различают реальное и мысленное моделирование.

При реальном моделировании используется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части. Основными разновидностями реального моделирования являются натурное и физическое моделирование.

Натурным моделированием называют проведение исследований на реальном объекте. В рамках натурного моделирования различают производственный эксперимент, комплексные испытания и научный эксперимент.

Физическое моделирование - это исследование реального объекта (системы) путем замещения изучаемого физического процесса подобным ему процессом той же физической природы.

Мысленное моделирование часто является единственным способом моделирования объектов (систем), которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического. Наглядное и символическое моделирование связано с созданием на базе представлений человека о реальных объектах мысленных объектов и логических макетов, учитывающих причинно-следственные связи между входом и выходом изучаемого объекта. Их применение ограничено достаточно простыми объектами.

Наибольшее распространение для исследования характеристик различных систем получило математическое моделирование. Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Математическая модель - это система математических зависимостей, описывающих изучаемый процесс. Вид математической модели зависит как от природы реального объекта (физики моделируемых процессов), так и задач исследования объекта и требуемой достоверности и точности решения этой задачи. Любая математическая модель описывает реальный объект лишь с некоторой степенью приближенности к действительности. По методу исследования характеристик процесса функционирования объектов (систем) математические модели можно разделить на аналитические, имитационные и комбинированные.

Аналитические модели основаны на представлении процессов функционирования объектов (систем) в виде явных аналитических зависимостей между входными и выходными величинами, которые исследуются либо путем прямого получения выражений для искомых характеристик в явном виде, либо путем использования численных методов.

Имитационное моделирование рассматривается как эксперимент со сложной математической моделью описывающей поведение системы, реализуемой на ЭВМ. Имитационная модель может иметь большую размерность по числу переменных и связей, стохастический характер, нелинейность и ограничения различных типов, различное математическое описание элементов модели и реакции, зависящие от времени. При этом сохраняется логическая структура и последовательность протекания во времени исследуемого процесса, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени.

Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие процессы и для тех из них, где это возможно используются аналитические модели, а для остальных подпроцессов строятся имитационные модели.




4. Основные подходы к построению математических моделей систем

Основой создания математической модели является формальная модель объекта (исследуемой системы), которую можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:

- совокупность входных воздействий

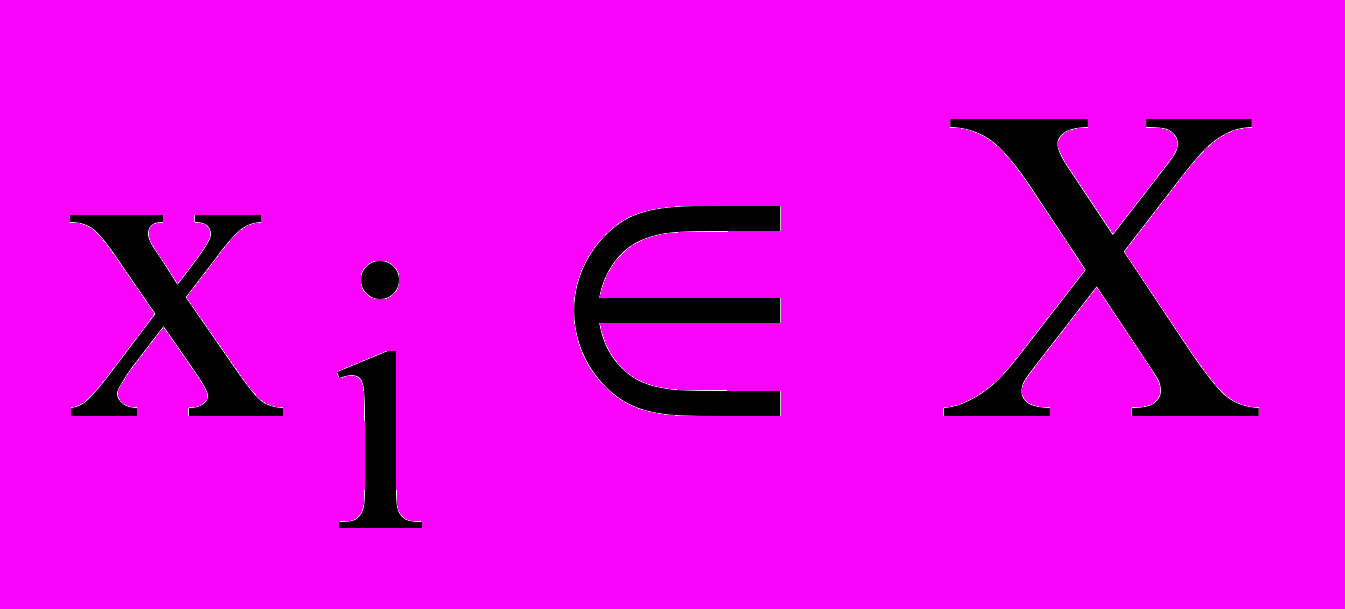, i = 1, ..n _x

- совокупность воздействий внешней среды

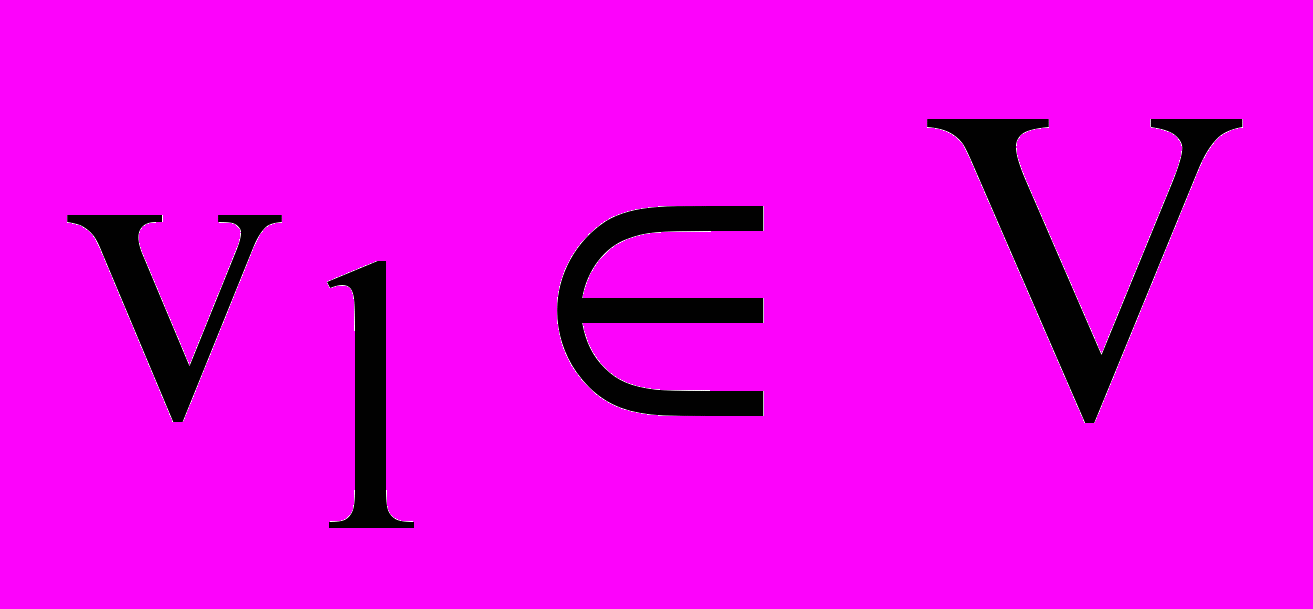, l = 1, ..n _v

- совокупность внутренних (собственных) параметров

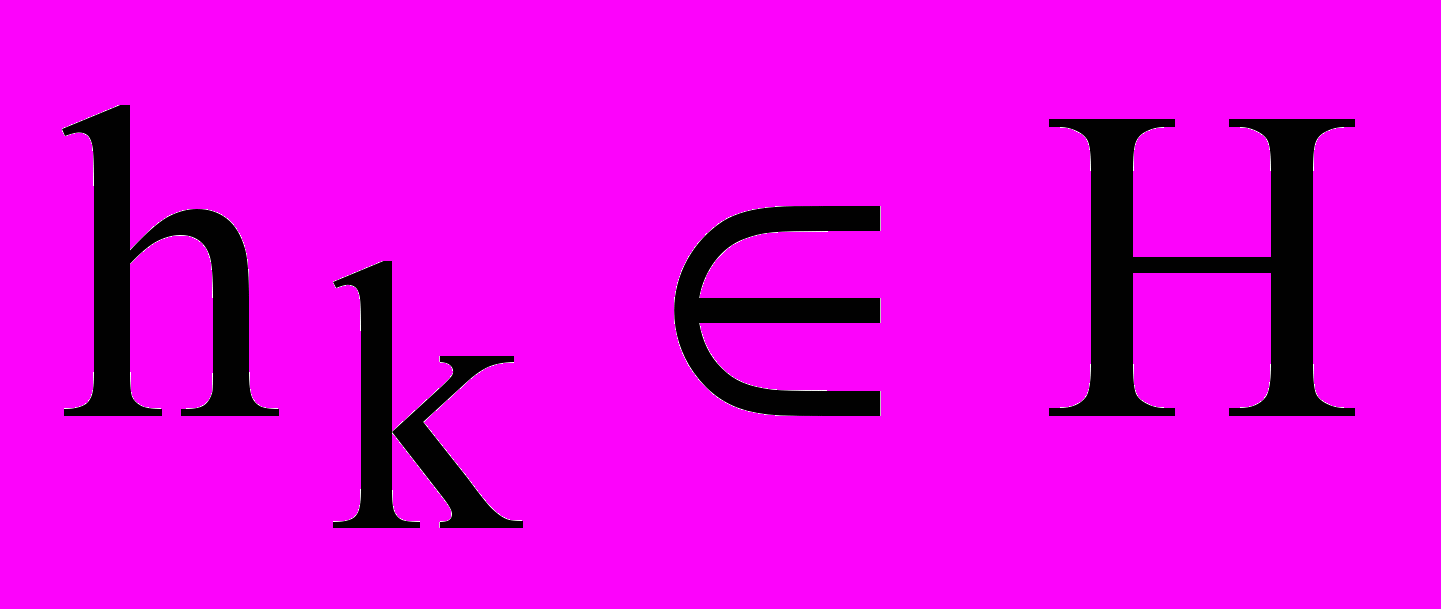, k= 1, ..n _h

- совокупность выходных характеристик

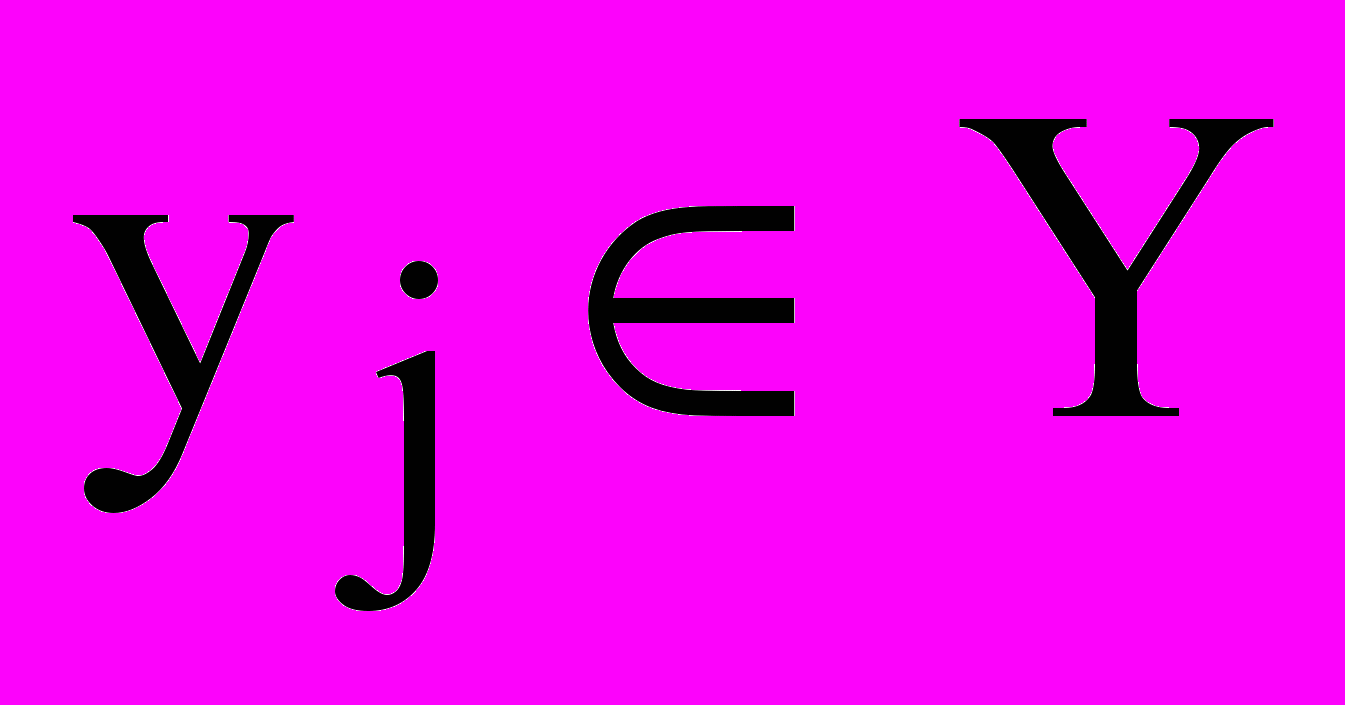, j = 1, ..n _y.

В этих подмножествах можно выделить управляемые параметры (x_i и у_i) и неуправляемые (v_l и h _k). В общем случае все эти подмножества могут иметь как детерминированные, так и стохастические составляющие.

При моделировании системы входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменным, которые в векторной форме имеют соответственно вид:

, ,

.

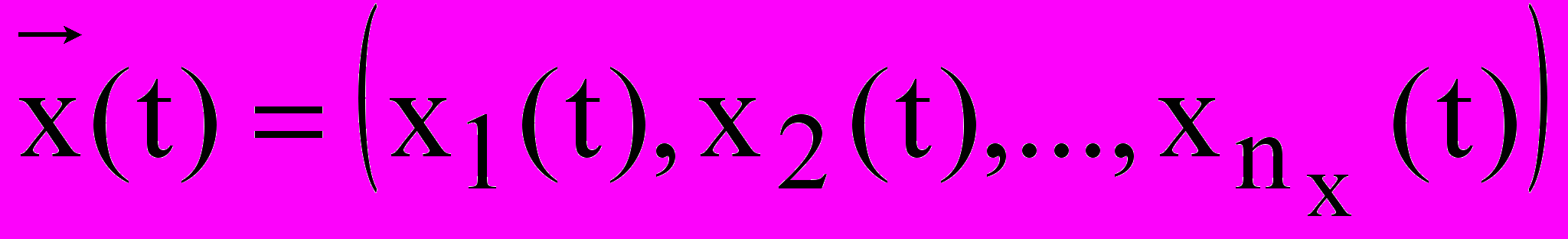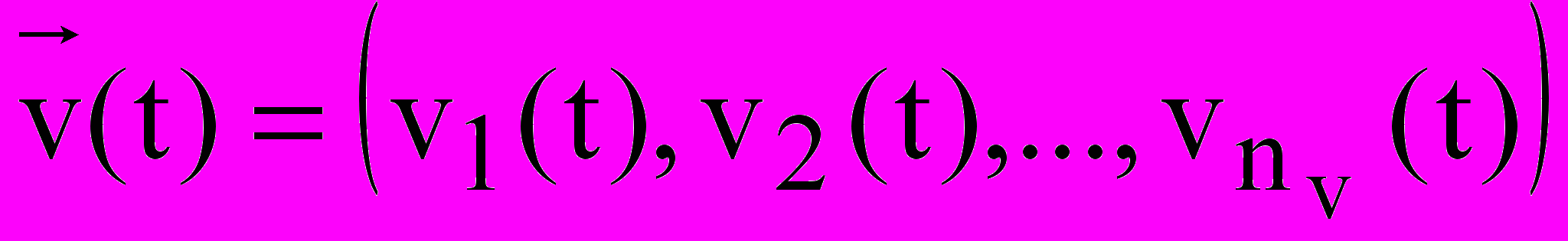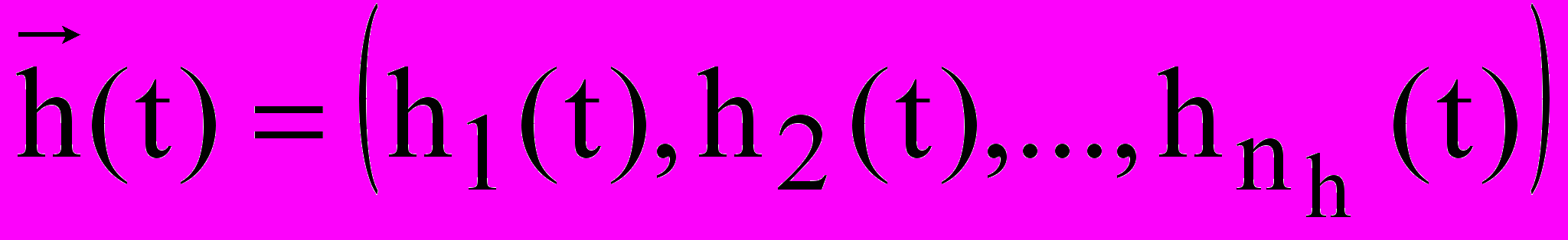Выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид:



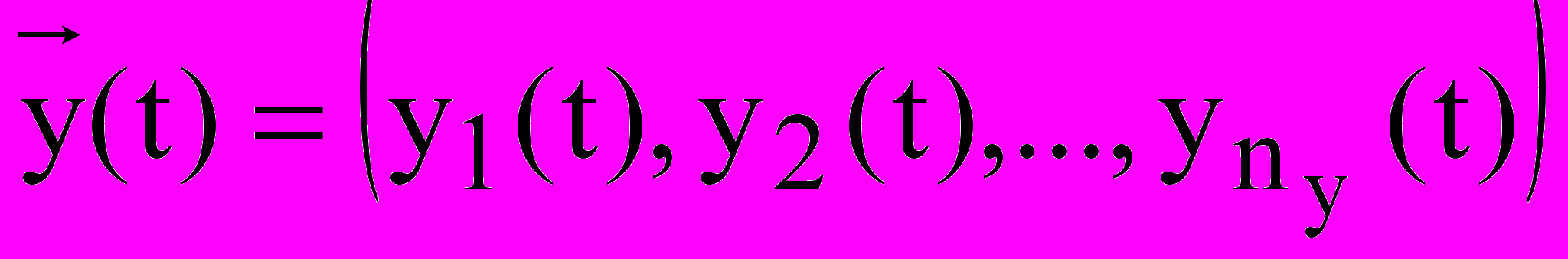
Процесс функционирования системы S описывается во времени оператором F связывающим по определенному алгоритму выходные (зависимые) характеристики с независимыми величинами:

. (1)

Данная зависимость называется законом функционирования системы. Весьма важным для описания и исследования системы S является понятие алгоритма функционирования A_S, под которым понимается метод получения выходных характеристик с учетом входных воздействий 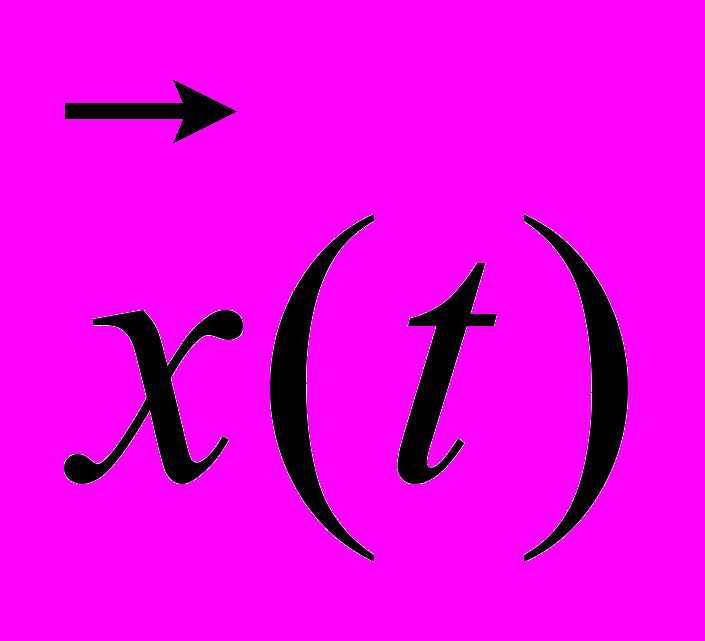, воздействий внешней среды 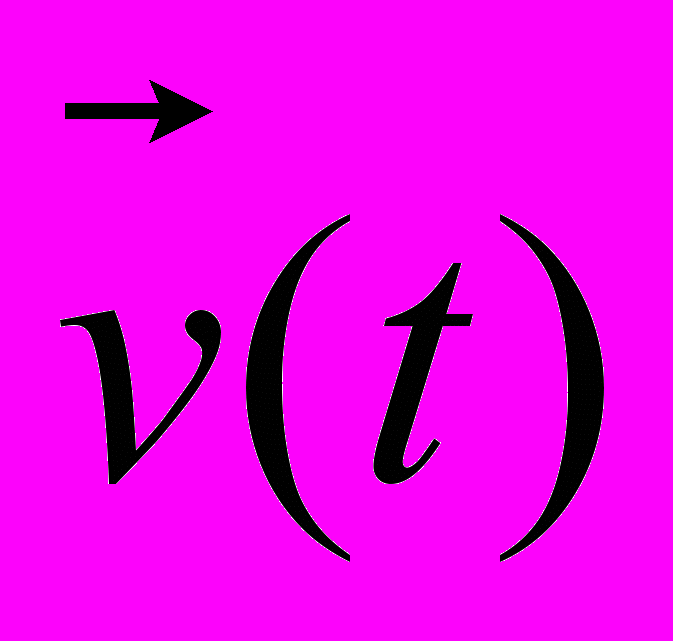и собственных параметров системы 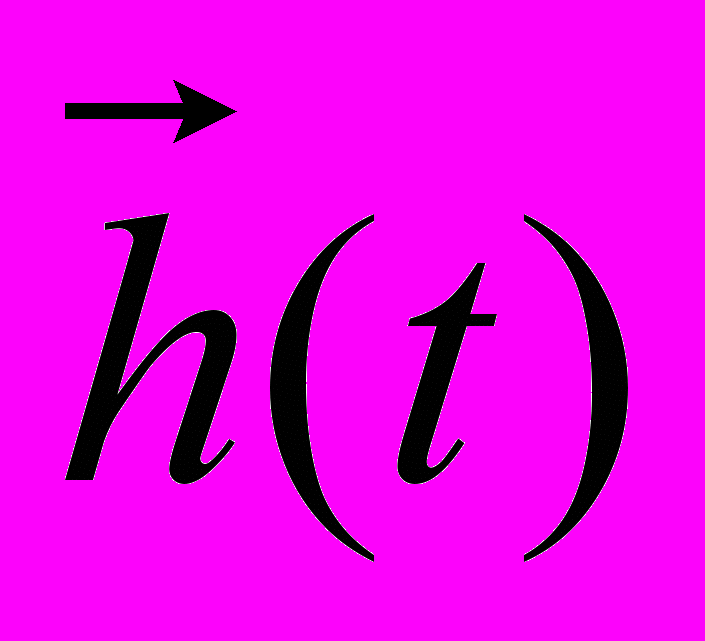. Очевидно, что один и тот же закон функционирования F_S системы S может быть реализован различными способами, то есть с помощью различных алгоритмов функционирования A_S.

Соотношение (1) является математическим описанием поведения системы во времени, то есть отражает ее динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями.

Для статических моделей математическая модель (1) представляет собой отображение между двумя подмножествами свойств моделируемой системы Y и {X, V, H}, что в векторной форме записывается в виде:

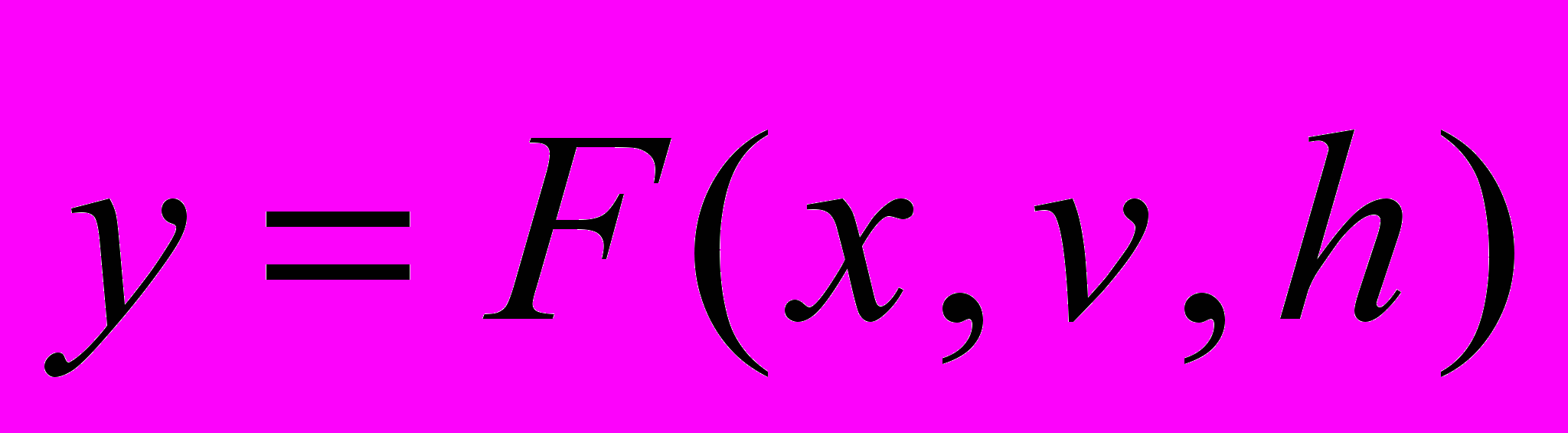. (2)

В общем случае соотношения (1) и (2) могут быть заданы в любой математической форме (в виде функции, функционала, алгоритмической или табличной форме и т.п.).

Таким образом, под математической моделью объекта (системы) понимают конечное подмножество переменных {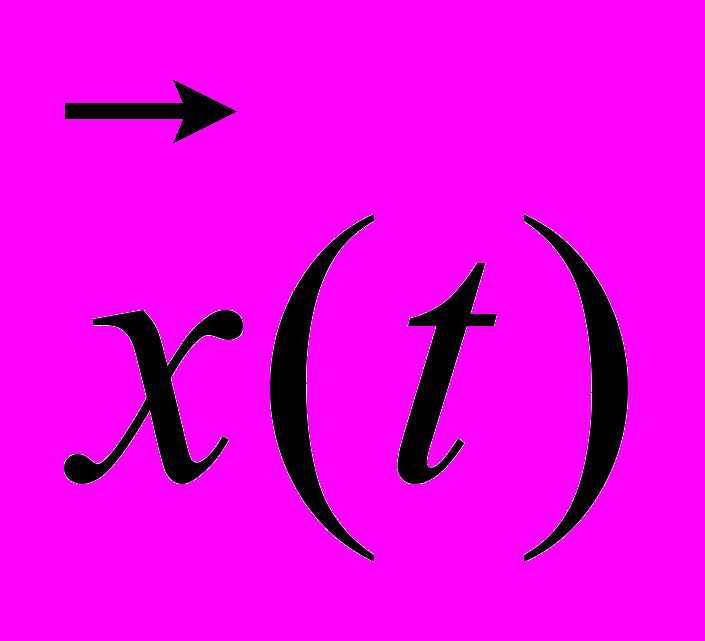, , 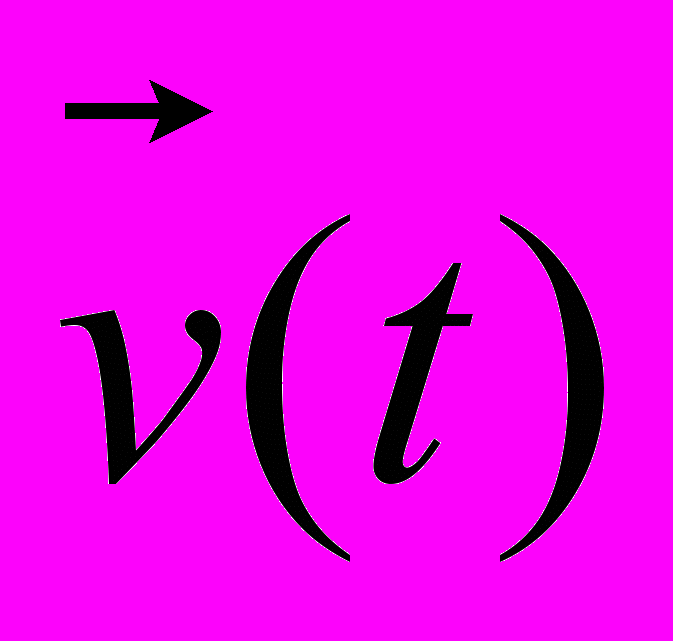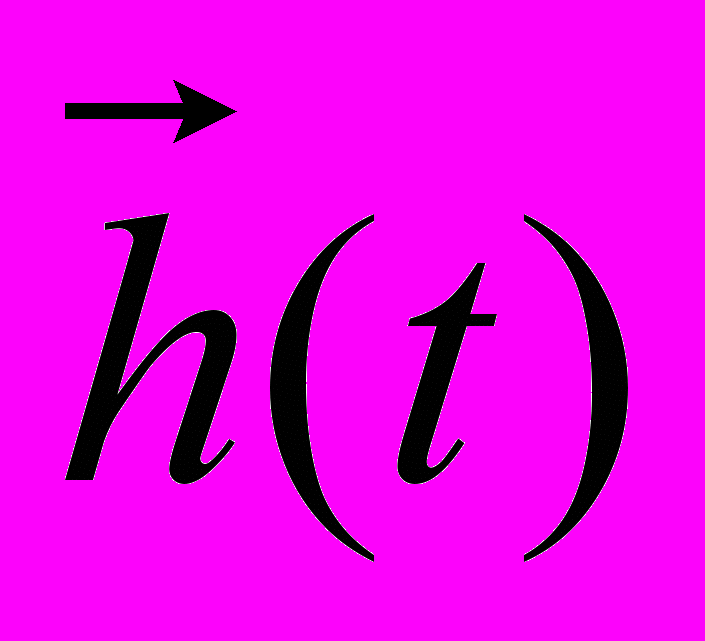} вместе с математическими связями между ними и характеристиками .

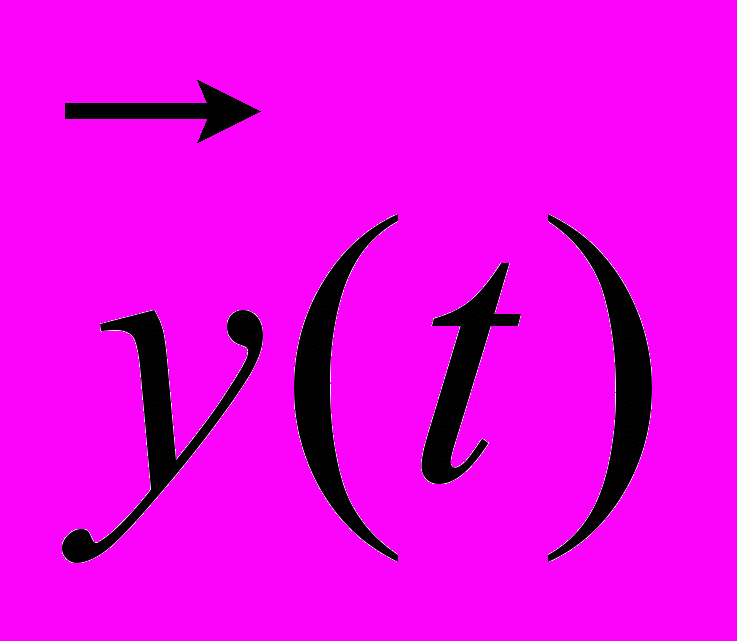Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, то есть стохастические воздействия внешней среды и стохастические внутренние параметры отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

.

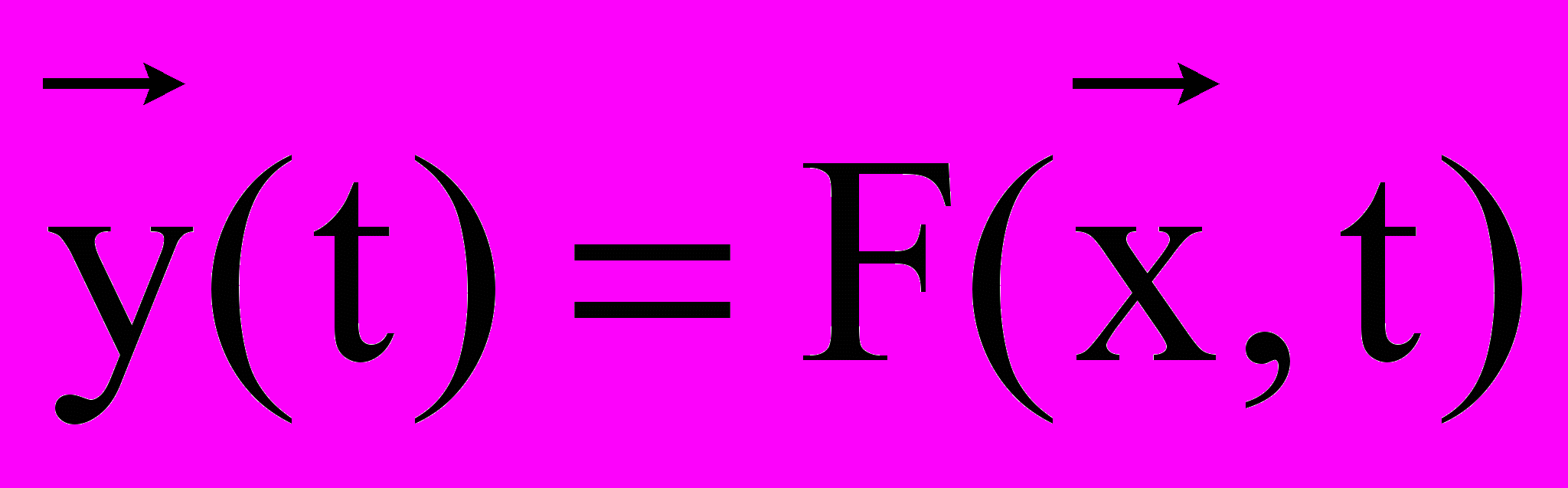Очевидно, что детерминированная модель является частным случаем стохастической модели.