2 Анализ сетей Петри

Вид материала

Документы

Содержание К. При проектировании автоматизированных систем опреде­ление К

Подобный материал:

• Моделирование динамики конфигураций организационных систем на сетях петри, когнитивных, 33.91kb.
• И. Ф. Бабалова московский инженерно-физический институт (государственный университет), 39.62kb.
• Я. А. Трофимов международный университет природы, общества и человека «Дубна», Дубна, 71.95kb.
• Сравнительный анализ социально-сетевых проектов, 231.35kb.
• Рабочей программы учебной дисциплины б3+ Администрирование компьютерных сетей Уровень, 72.29kb.
• Доклад Сазанов Владимир Михайлович, Россия, предприниматель, 411.36kb.
• Интерфейсы, протоколы, стеки протоколов, 593.76kb.
• Темы курсовых работ (проектов) по курсу: «Программно-аппаратные средства обеспечения, 99.03kb.
• Лекция №10. Конвергенция компьютерных и телекоммуникационных сетей, 127.96kb.
• Динамическое моделирование и прогноз вращения Земли, 95.4kb.

2.4.5. Анализ сетей Петри

При имитационном моделировании сложных систем на базе сетей Петри задают входные потоки заявок и определяют соот­ветствующую реакцию системы. Выходные параметры рассчи­тывают путем обработки накопленного при моделировании статис­тического материала.

Возможен и другой подход к использованию сетей Петри для анализа сложных систем. Он не связан с имитацией процессов и основан на исследовании таких свойств сетей Петри, как ограни­ченность, безопасность, сохраняемость, достижимость, живость.

Ограниченность (или К-ограниченность) имеет место, если число меток в любой позиции сети не может превысить значе­ния К. При проектировании автоматизированных систем опреде­ление К позволяет обоснованно выбирать емкости накопителей. Воз­можность неограниченного роста числа меток свидетельствует об опасности неограниченного роста длин очередей.

Безопасность - частный случай ограниченности, а именно это

1-ограниченность. Если для некоторой позиции установлено, что она безопасна, то ее можно представлять одним триггером.

Сохраняемость характеризуется постоянством загрузки ресурсов, т.е.

∑ А_i N_i = const,

где N_i— число маркеров в i-й позиции; А_i - весовой коэффициент.

Достижимость М_k → М_j характеризуется возможностью достижения маркировки М_j из состояния сети, характеризуемого маркировкой М_k.

Живость сети Петри определяется возможностью срабатыва­ния любого перехода при функционировании моделируемого объекта. Отсутствие живости либо означает избыточность аппаратуры в проектируемой системе, либо свидетельствует о возможности воз­никновения зацикливаний, тупиков, блокировок.

В основе исследования перечисленных свойств сетей Петри ле­жит анализ достижимости.

Один из методов анализа достижимости любой маркировки из состояния М₀ - построение графа достижимости. Начальная вер­шина графа отображает М₀, а остальные вершины соответствуют другим маркировкам. Дуга из М_i в М_j означает событие М_i → М_j и соответствует срабатыванию перехода t. В сложных сетях граф может содержать чрезмерно большое число вершин и дуг. Однако при построении графа можно не отображать все вершины, так как многие из них являются дублями (действительно, от маркировки M_t всегда порождается один и тот же подграф независимо от того, из какого состояния система пришла в М_k). Тупики обнаружива­ются по отсутствию разрешенных переходов из какой-либо верши­ны, т.е. по наличию листьев - терминальных вершин. Неограни­ченный рост числа маркеров в какой-либо позиции свидетельству­ет о нарушениях ограниченности.

Приведем пример анализа достижимости.

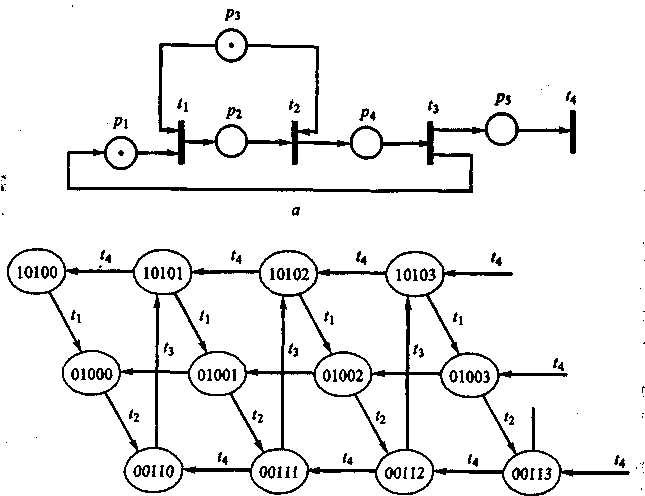
ПримерЗ. На рис. 2.12, а показана сеть Петри, а на рис. 2.12,б - соответствующий ей граф достижимых разметок.

Вершины графа на рис. 2.12,б соответствуют маркировкам (со­стояниям сети Петри), представленным в виде последовательнос­ти цифр, цифры означают количества меток в позициях, перечисля­емых в порядке p₁, р₂, р₃, р₄, р₅ . Дуги помечены обозначения­ми срабатывающих переходов. Живость сети очевидна, так как срабатывают все переходы, тупики отсутствуют, сеть не является K – ограниченной.




б

Рнс. 2.12. Сеть Петри (а) и граф достижимости (б) для примера 3