Рабочая программа по алгебре 11 класс 3ч/нед. (102 ч.)

Вид материала

Содержание

Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.
Ответ оценивается отметкой «4»
Отметка «3» ставится в следующих случаях
Оценка «1» ставится в случае
Отметка «3» ставится, если
Отметка «1» ставится, если
II. Календарно-тематическое планирование.
Раздел программы
Формы контроля
I. Повторение курса Х класса (3 ч.)
II. Тригонометрические функции (15 ч.)
III. Производная и ее применение (26 ч).
VI. Перечень рекомендуемой литературы для учителя.

Подобный материал:

МОУ Марьевская сош

Утверждено: Согласовано: Рассмотрено на заседании

Директор школы Зам. директора по УВР ШМО естественно-математического цикла

. Руководитель ШМО

Моисеева О.И. _________ Попивненко Е.В ______ Сурженко С.А. _________

РАБОЧАЯ ПРОГРАММА

ПО АЛГЕБРЕ 11 КЛАСС

3ч/нед. - (102 ч.)

Составил:

Сурженко С.А. – учитель

математики МОУ Марьевской сош

с. Марьевка

2010г.

Пояснительная записка.

Естественно-математическое образование в системе общего среднего образования, занимает одно из ведущих мест. Математика, являясь обязательной составной частью всеобщего среднего образования, одновременно образует прочный фундамент всего естествознания. Включение ее в качестве основного учебного предмета в школьный учебный процесс ни у кого не вызывает сомнения.

На сегодняшний день, в соответствии с Базисным учебным планом, на ее изучение в рамках курса 11 класса отводится 5 часов в неделю (на изучение алгебры и начал анализа – 3 учебных часа в неделю, геометрии – 2 часа), что составляет 170 часов за год.

Назначение математического образования можно охарактеризовать с двух сторон: практической, связанной с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности и духовной, связанной с мышлением человека, с овладения определенным методом познания и преобразованием мира математическим методом.

Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. С другой стороны математическое образование вносит свой вклад в формирование общей культуры человека, способствует эстетическому воспитанию, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идей симметрии. Таким образом, без базовой математической подготовки невозможна постановка образования современного человека.

Роль математики в развитии общества в целом и формировании личности каждого отдельного человека определяет цели и задачи обучения математике в общеобразовательной школе:

овладение конкретными математическими знаниями, необходимыми для применения в конкретной практической деятельности, для изучения смежных дисциплин, доля продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общечеловеческого прогресса.

Цель изучения курса алгебры и начал анализа в Х-ХI классах - систематическое изучение функции, как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.

Цель изучения курса геометрии в Х-ХI классах - систематическое изучение свойств геометрических тел в пространстве, развитие пространственных представлений учащихся, освоение способов вычисления практически важных геометрических величин и дальнейшее развитие логического мышления учащихся.

Рабочая программа ориентированна на усвоение обязательного минимума математического образования, позволяет работать без перегрузок в классе с детьми разного уровня обучения и интереса к математике.

В процессе реализации рабочей программы решаются не только задачи общего математического образования, но и дополнительные, направленные на:

использование личностных особенностей учащихся в процессе обучения;
формирование у учащихся математического стиля мышления.

В основе построения программы лежат принципы единства, преемственности, вариативности, выделения понятийного ядра, деятельностного подхода, системности.

Основные разделы: курс «Алгебра и начала анализа. 11 класс» - «Тригонометрические функции», «Производная и ее применение», «Применение производной к исследованию функций», «Интеграл», «Повторение. Решение задач»; курс «Геометрия. 11 класс» - «Метод координат в пространстве», «Цилиндр, конус, шар», «Объемы тел», «Обобщающее повторение. Решение задач». Изменений в тематике и часовом распределении, определенных в Программе для общеобразовательных школ, гимназий, лицеев «Математика. 7-11 классы» - нет.

Курс алгебры и начал анализа XI класса характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учетом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса является систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков учащихся, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения.

Курсу геометрии в ХI классе также присущи систематизирующий и обобщающий характер изложений, направленность на закрепление и развитие умений и навыков, полученных в основной школе. При доказательстве теорем и решении задач активно используются изученные в курсе планиметрии свойства геометрических фигур, применяются геометрические преобразования, векторы и координаты. Высокий уровень абстрактности изучаемого материала, логическая строгость систематического изложения соединяются с привлечением наглядности на всех этапах учебного процесса и постоянным обращением к опыту учащихся.

Принципиальным положением организации математического образования становится дифференциация обучения в школе. При этом достижение уровня обязательной подготовки становится непременной обязанностью ученика в его учебной работе. В организации учебно-воспитательного процесса важную роль играют задачи. В обучении математики они являются и целью, и средством обучения и математического развития школьников. Организуя решение задач, следует иметь в виду, что теоретический материал осознается и осваивается преимущественно в процессе решения задач, организуя их решение, целесообразно использовать дифференцированный подход к учащимся, основанный на достижении обязательного уровня подготовки. Это способствует нормализации нагрузки школьников, обеспечивая их посильной работой, и формирует у них положительное отношение к учебе.

Важным условием правильной организации учебно-воспитательного процесса является выбор рациональной системы методов и приемов обучения. Необходимо реализовать сбалансированное сочетание традиционных и новых методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, использование технических средств. Учебный процесс необходимо ориентировать на рациональное сочетание устных и письменных видов работы, как при изучении теории, так и при решении задач. Внимание должно быть направлено на развитие речи учащихся, формирование у них навыков умственного труда - планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов.

В школе математика является опорным предметом средней школы: она обеспечивает изучение других дисциплин, прежде всего предметов естественно-научного цикла, в частности физики, основ информатики и вычислительной техники, химии. Например, на уроках физики, изучение понятий и законов механики осуществляется с использованием знаний о векторах, действиях с ними, координатах точки, проекциях вектора, линейной функции и ее графике, квадратных уравнениях, окружности, касательной к ней. Практические умения и навыки математического характера необходимы для трудовой подготовки школьников. При изучении отдельных тем курса математики возможна опора на знания, полученные учащимися на других предметах. Например, знания, полученные при изучении механики: о мгновенной скорости развиваются при введении производной; о свободных колебаниях - используются при рассмотрении дифференциальных уравнений; о перемещении в равноускоренном движении, о работе переменной силы – при изучении интеграла.

Требования к математической подготовке учащихся:

Вычисления и преобразования:

В результате изучения курса математики учащиеся должны:

находить значение корня, степени, логарифма, значения тригонометрических выражений на основе определений. С помощью калькулятора или таблиц;
выполнять тождественные преобразования иррациональных, степенных, показательных, логарифмических и тригонометрических выражений;

Уравнения и неравенства:

В результате изучения курса математики учащиеся должны:

решать иррациональные, показательные, логарифмические, и тригонометрические уравнения;
решать системы уравнений с двумя неизвестными;
решать рациональные, показательные, логарифмические неравенства;
иметь представление о графическом способе решения уравнений и неравенств;

Функции:

В результате изучения курса математики учащиеся должны:

определять значение функции по значению аргумента при различных способах задания функции;
иметь наглядные представления об основных свойствах функций; иллюстрировать их с помощью графических изображений;
изображать графики основных элементарных функций; опираясь на график описывать свойства этих функций; уметь использовать свойства этих функций для сравнения и оценки ее значений;
понимать механический и геометрический смысл производной; находить производные элементарных функций, пользуясь таблицей производной и правилами дифференцирования суммы, произведения и частного, формулой производной функции вида 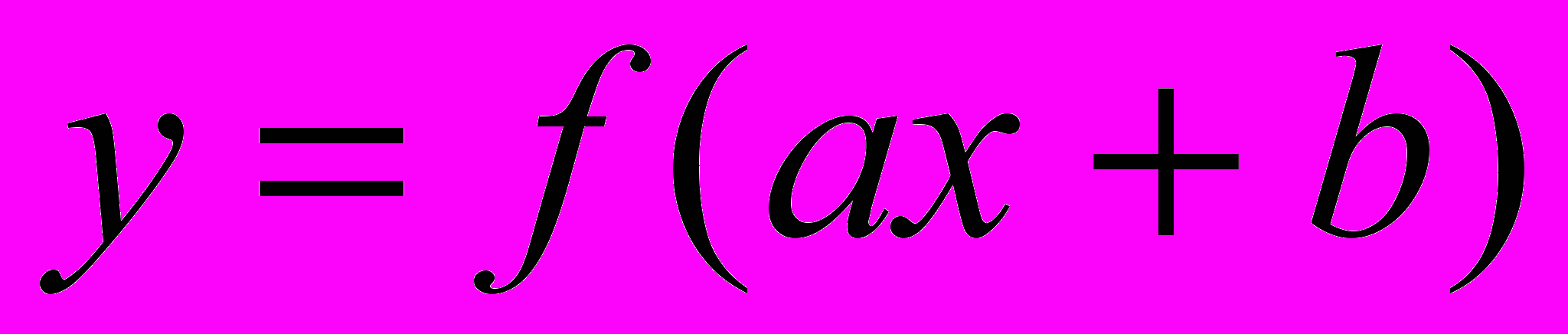; в несложных ситуациях применять производную для исследования функции на монотонность и экстремумы, для нахождения наибольших и наименьших значений функций и для построения графиков;
понимать смысл понятия первообразной, находить первообразные для суммы функций и произведения функции на число;
вычислять в простейших случаях площадь криволинейной трапеции.

Геометрические тела и их свойства.

Измерение геометрических величин.

В результате изучения курса математики учащиеся должны:

выполнять чертеж по условию стереометрической задачи;
понимать стереометрические чертежи;
решать задачи на вычисление геометрических величин, проводя необходимую аргументацию;
решать несложные задачи на доказательство;
строить сечения геометрических тел.

Требования к уровню усвоения дисциплины.

Рекомендации по оценке знаний, умений и навыков учащихся по математике.

Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.

Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Среди погрешностей выделяются ошибки и недочеты.

Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.

Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

Оценка ответа учащихся при устном и письменном опросе производится по пятибалльной системе.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.
Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.

Оценка устных ответов учащихся.

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя.

Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Отметка «3» ставится в следующих случаях:

неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка «1» ставится в случае, если:

ученик обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных контрольных работ учащихся.

Отметка «5» ставится в следующих случаях:

работа выполнена полностью.
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);

Отметка «4» ставится, если:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);

Отметка «3» ставится, если:

допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере.

Отметка «1» ставится, если:

работа показала полное отсутствие у учащегося обязательных знаний, умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

II. Календарно-тематическое планирование.

«Алгебра и начала анализа».

№ п/п	Раздел программы	Общее количество часов	Примерные календарные сроки	Кол-во контрольных работ
1	Повторение курса Х класса.	3	01.09 –7.09.
2	Тригонометрические функции	15	8.09.-13.10.	1
3	Производная и ее применение.	26	14.10-19.12.	1
4	Применение производной к исследованию функций	22	20.12-22.02.	1
5	Интеграл	12	24.02.-23.03.	1
6	Повторение. Решение задач.	24	24.03. – 30.05.	1
Итого	6 тем	102		5

III. Тематическое планирование.

«Алгебра и начала анализа».

№ п/п	Тема раздела		Кол-во ча-сов	Номера уроков и сроки	Средства обучения		Формы контроля		Формы входящего, рубежного, итогового контроля		Литера-тура.
1	2		3	4	5		6		7		8
I. Повторение курса Х класса (3 ч.)
1	Повторение курса 10 класса		2	№№1-2
2	Диагностирующая работа		1	№3					входящий контроль
II. Тригонометрические функции (15 ч.)
3	Область определения и множество значений тригонометрических функций.		2	№№ 4-5							§38
4	Четность, нечетность, периодичность тригонометрических функций		2	№№ 6-7				С. р.			§39
5	Свойства функции y=cosx и ее график		2	№№ 8-9							§40
6	Свойства функции y=sinx и ее график		2	№№ 10 -11				С. р.			§41
7	Свойства функции y=tgx и ее график		2	№№ 12 -13							§42
8	Обратные тригонометрические функции		1	№14							§43
9	Решение задач		3	№№ 15-17
10	Контрольная работа №1		1	№ 16				К.р.
III. Производная и ее применение (26 ч).
1		2	3	4		5		6		7		8

11	Производная	3	№№ 19 - 21
12	Производная степенной функции	3	№№ 22 – 24	С.р.
13	Правила дифференцирования	3	№№ 25 – 27

14	Производные некоторых элементарных функций	5	№№ 28 - 32		С.р.		§47
15	Геометрический смысл производной	6	№№ 33 - 38		С. р.		§48
16	Решение задач	5	№№ 39 - 43		С.р.
17	Контрольная работа №2	1	№44		К.р.
18	Возрастание и убывание функций	2	№№ 45 - 46		С.р.		§49
19	Экстремумы функций	4	№№ 47 - 50		С.р.		§50
20	Применение производной к построению графиков функций	5	№№ 51 - 55		С. р.		§51
21	Наибольшее и наименьшее значение функции	5	№№ 56- 60		С.р.		§52
22	Выпуклость графика функции. Точки перегиба.	2	№№ 61 - 62				§53
23	Решение задач	3	№№ 63 - 65		С.р.
24	Контрольная работа №3	1	№ 66		К.р.
25	Первообразная	1	№67				§54
26	Правила нахождения первообразных	2	№№ 68 - 69		С.р.		§55
27	Площадь криволинейной трапеции и интеграл	1	№ 70				§56
28	Вычисление интегралов	2	№№ 71-72
29	Вычисление площадей с помощью интегралов.	2	№№ 73 - 74		С.р.
30	Применение производной и интеграла к решению практических задач	1	№ 75
31	Решение задач	2	№№ 76-77
32	Контрольная работа №4	1	№ 78		К.р.
1	2	3	4	5	6	7
33	Числа и алгебраические преобразования	3	№№ 79-81
34	Функция, исследование функций.	4	№№ 82 – 85		С.р.
35	Уравнение и системы уравнений	4	№№ 86 - 89
32	Неравенства и системы неравенств	3	№№ 90 - 92		С.р.
33	Решение заданий, содержащих параметр	5	№№ 93-97		С.р.
34	Решение комбинированных заданий	2	№№ 98-99
35	Итоговая контрольная работа	3	№№ 100-102		К.р.

VI. Перечень рекомендуемой литературы для учителя.

Кузнецова Г.М., Миндюк Н.Г. «Программа для общеобразовательных школ, гимназий, лицеев: Математика. 7-11 класс». М: Дрофа, 2001г.

Алимов Ш. А., Колягин Ю. М. , Сидоров Ю. В. и др. «Алгебра и начала анализа. 10-11 класс». Учебник для обще6образовательных учреждений. М: «Просвещение», 2003г.

Федорова Н.Е., Ткачева М. В. «Изучение алгебры и начал анализа в 10 – 11 классах: Книга для учителя», М: Просвещение, 2004г.

Дорофеев Г. В., Кузнецова Л. В., Кузнецова Г.М. и др. «Оценка качества подготовки выпускников средней школы по математике», М: Дрофа, 2000г.

Ивлев Б. М., Саакян С. М., Шварцбурд С. И., «Дидактические материалы по алгебре и началам анализа для 11 класса», М: Просвещение, 2004 год.

Башмаков М. И., Братусь Т. А., Жарковская Н. А. и др. «Алгебра и начала анализа. 10-11 класс: учебно-методическое пособие», М: Дрофа, 2001 г.

Атанасян Л. С., Бутузов В. Ф, Кадомцев С. Б. и др.»Геометрия, 10-11 класс: учебник для общеобразовательных учреждений», М: Просвещение, 2003 г.

Саакян С. М., Бутузов В. Ф. «Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику: Книга для учителя», М: Просвещение, 2003г.

Рогулева А. В. «Геометрия 11 класс. Рабочая тетрадь в 2 – х частях» Саратов: Лицей, 2005 г

Лысенко Ф. Ф., Калашников В.Ю., Неймарк А. Б. и др. «Математика. ЕГЭ – 2006, вступительные экзамены». Ростов – на –Дону: Легион, 2005г.

Blog

Рабочая программа по алгебре 11 класс 3ч/нед. (102 ч.)

Содержание

Раздел программы